1. 서 론
2. 이론적 배경
2.1 복층터널 분기구간 정의
2.2 지반조건 및 지보재 관련 설계기준
2.3 강도응력비(Strength Stress Ratio)
3. 수치해석 모델링
3.1 해석단면 및 지반조건 설정
3.2 굴착조건 및 해석영역 설정
4. 해석결과 분석 및 고찰
4.1 굴착공법에 따른 선행굴착 영향
4.2 벤치길이에 따른 선행굴착 영향
4.3 선행굴착 영향에 따른 강도응력비 결과
5. 결 론
1. 서 론
국내에서 경제가 발전하고 도심 인구가 증가함에 따라 도심지 도로의 정체가 심각해지고 이를 해결하기 위하여 지속적으로 도로를 확충하고 있으나 도심지의 경우 지상공간의 한계, 환경 영향 등으로 인하여 상습적인 정체를 해소하기 쉽지 않은 상황이다. 해외에서는 이를 해결하기 위하여 지하에 도로를 건설하고 운영 중에 있고 국내에서도 서부간선도로와 동부간선도로, 경부고속도로의 지하화를 계획하거나 일부는 이미 추진 중에 있어 점차 도심지 정체가 개선될 것으로 기대된다. 이에 따라 가까운 미래에는 지하도로가 새로운 도로의 모델이 될 것으로 예상된다. 해외에서는 지하도로의 형태로서 복층구조로 되어 있는 복층터널이 주를 이루고 있으며, 국내에서도 경부고속도로 지하화 시 복층터널로 검토하는 등 복층터널에 대한 관심이 높아지고 있다. 복층터널은 일반적인 병렬터널과 비교하여 동일 굴착면적당 더 많은 교통량을 처리할 수 있고 굴착공사로 인한 영향 범위도 적어 지하공간의 활용과 안정성 측면에서 유리하다. 그러나 복층터널이 도로의 기능을 온전히 수행하기 위해서는 지상의 주요 지점과 연결되는 진 ‧ 출입로가 필요하고, 그에 따라 지상과 연결을 위한 분기구가 존재하게 되어 단층 터널의 분기구 보다 기하학적으로 복잡한 구조를 띄게 되어 분기구 굴착 시 안정성에 대한 검토가 특별히 중요하다(La and Kim, 2016; 2020).
터널 분기구의 본선과 분기터널과 같이 인접한 터널에 대한 연구는 주로 병렬터널에 대하여 근접에 따른 안정성 영향을 평가하는 내용에 관한 연구가 주를 이루고 있다(Ghaboussi and Ranken, 1977; Xie et al., 2004; Gerçek, 2005; Chehade and Shahrour, 2008; Kim and Bae, 2008; Hsiao et al., 2009; Kim et al., 2012; Kim and Lee, 2013; Chung et al., 2013; Jung et al., 2014; Lim and Son, 2014; Das et al., 2017; Kim and Kim, 2017; La et al., 2018). 그러나 복층터널의 분기구간은 필라의 안정성이 확보되지 않는 단면에 대하여 터널의 형상이 모자 형태 또는 대단면 형태를 갖는 ‘분기 전 확폭구간’과 두 터널 간 일정거리 이상의 이격거리가 발생하여 안정성이 확보되는 ‘분기 후 구간’으로 나눌 수 있으며, 이 때 분기 전 확폭구간의 단면이 분기 후 구간의 터널 단면에 비해 매우 크기 때문에 분기 전과 분기 후를 포함한 분기구의 굴착 안정성에 관한 검토가 심층적으로 이루어질 필요가 있으나, 현재까지 이에 관한 연구는 미미한 실정이다.
따라서 본 연구에서는 암반에서 시공되는 NATM 방식의 2차로 대심도(40 m) 본선 복층터널에서 1차로 단층터널인 분기터널로 분기되는 조건을 대상으로 3차원 유한요소해석을 수행하여 굴착공법 및 벤치길이를 변화시키며 분기 후 본선터널과 분기터널의 이격방향(0°, 30°, 60°)을 고려하여 분기 전 확폭구간 굴착(선행굴착)이 분기 후 구간 굴착(후행굴착)에 미치는 영향을 분석하였다.
2. 이론적 배경
2.1 복층터널 분기구간 정의
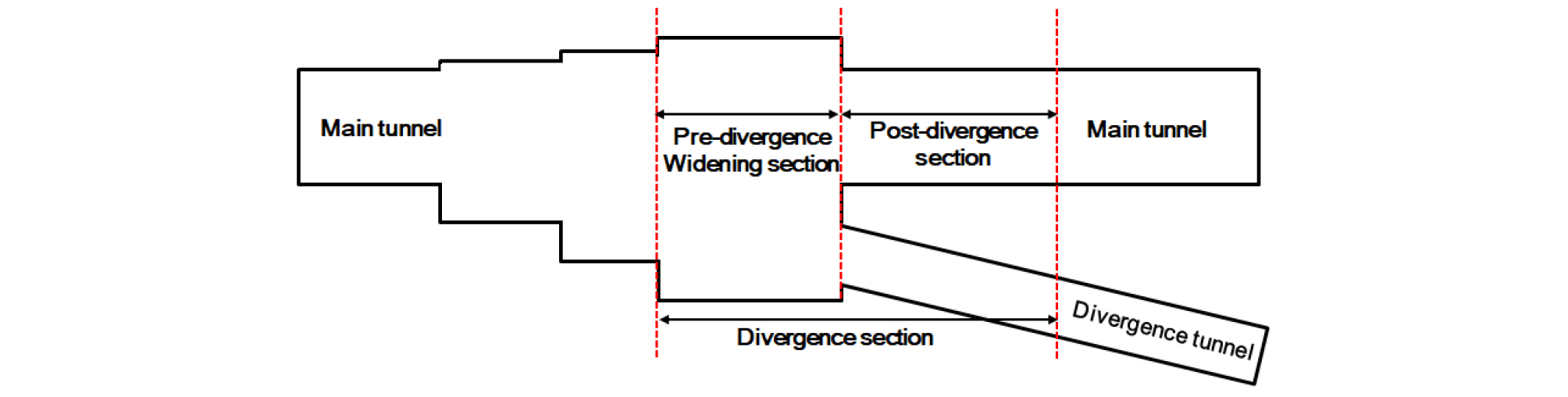
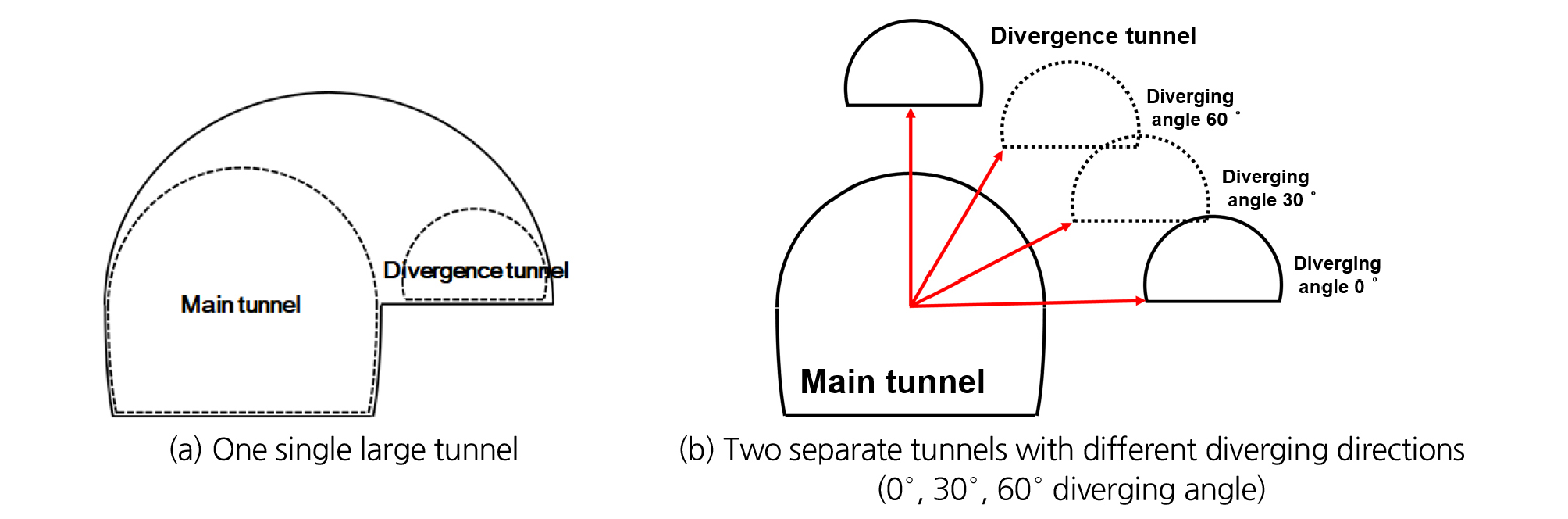
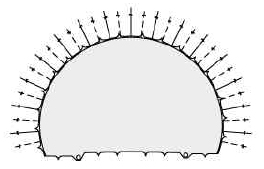
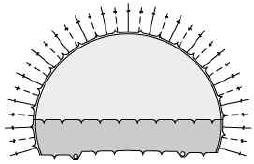
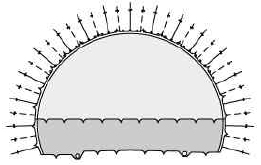
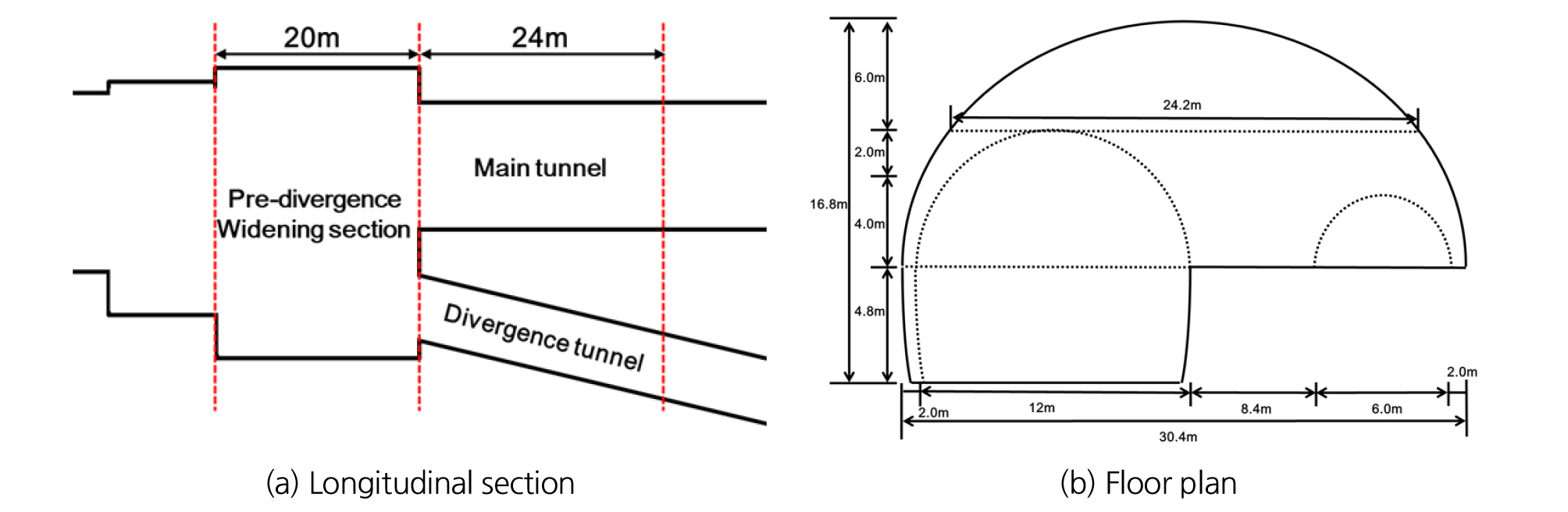
복층터널 분기구간은 Fig. 1과 같이 분기 전 확폭구간과 분기 후 구간으로 나눌 수 있다. 복층터널의 상층 우측부에서 분기가 발생한다고 가정하면 안정성이 확보되지 못하여 두 터널을 분리된 형태로 시공할 수 없는 분기 전 확폭구간의 단면은 Fig. 2(a)와 같이 모자형태의 대단면이 된다. 이격거리가 충분하여 안정성이 확보되는 분기 후 구간 단면은 Fig. 2(b)와 같이 본선터널과 분기터널이 각각 독립적으로 분리된 형태가 된다. 복층터널 분기구간의 안정성 확보에 있어 분기 후 구간의 본선터널과 분기터널 간 상대 위치 변화도 큰 영향을 미치게 되지만 2차원 수치해석에서 고려되지 못하는 분기 전 확폭구간의 굴착으로 발생된 선행굴착 역시 분기구간 전체 안정성에 영향을 미치게 된다. 따라서 복층터널의 계획 및 설계 시 분기구간의 안정성 분석은 분기 후 구간의 본선터널과 분기터널 간 상대 위치 변화뿐만 아니라 분기 전 확폭구간의 굴착 영향성도 반영되어야 한다.
2.2 지반조건 및 지보재 관련 설계기준
터널설계기준(Ministry of Land, Infrastructure and Transport, 2016)에서 암반등급은 “RMR에 의한 암반 분류는 5등급으로 분류하는 것을 원칙으로 하되, 터널의 크기, 용도 및 지역특성을 고려하여 5등급 이상으로 세분화할 수 있다”로 명시하고 있고 그 내용은 Table 1과 같고, 도로설계편람 터널편(Ministry of Oceans and Fisheries, 2011)에서 일반 터널과 대단면 터널에 대하여 숏크리트와 록볼트의 지보패턴은 Table 2와 같이 제시하고 있다. 따라서 본 연구에서는 지반조건 설정과 숏크리트와 록볼트의 지보패턴 결정 시 Tables 1, 2를 참조하여 분기 전 확폭구간과 분기 후 구간의 수치해석 물성치를 결정하였다.
Table 1.
Rock mass rating system (Design Guidelines for Road, 2016)
Table 2.
Pattern of tunnel reinforcement (Road Design Manual, 2011)
2.3 강도응력비(Strength Stress Ratio)
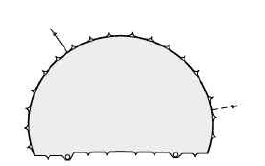
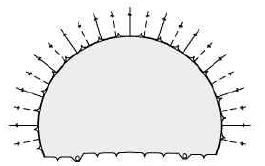
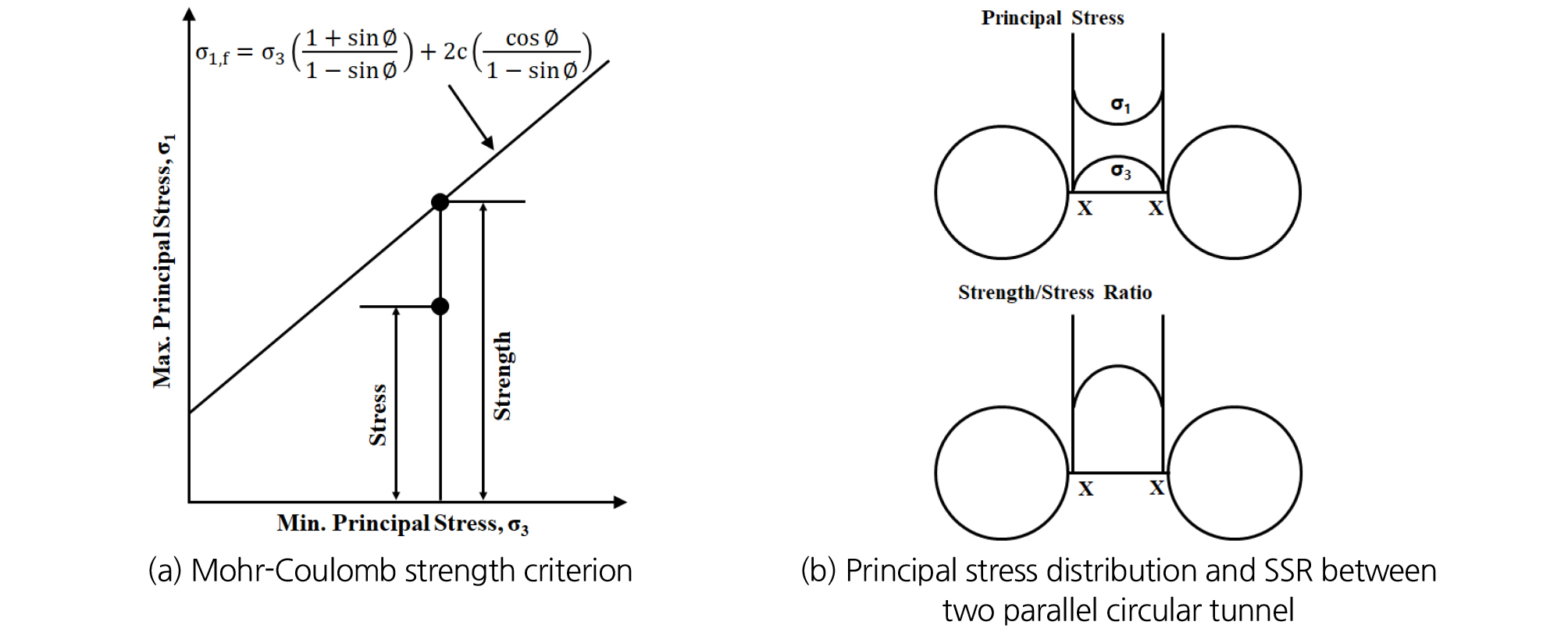
암반이 Mohr-Coulomb 파괴기준을 따른다고 가정하면 두 터널 사이의 지반(필라부)의 안정성은 Fig. 3(a)와 같이 암반의 구속압력(σ3)에 대하여 암반 필라의 강도와 작용응력(σ1)의 비로 나타낼 수 있으며 암반의 강도가 작용응력 보다 클 경우 강도응력비는 1.0 이상이 된다. 또한, 인접한 두 터널을 순서대로 굴착하게 되면 두 터널 사이의 지반(필라부)의 주응력 분포와 강도응력비 분포는 Fig. 3(b)와 같다.
암반이 Mohr-Coulomb 파괴기준을 따른다고 가정했을 때, 주어진 구속압(σ3) 조건에서 해당 암반의 파괴 시 축방향 응력은 식 (1)과 같이 표현된다.
| $$\sigma_{1,f}=\sigma_3\left(\frac{1+sin\phi}{1-sin\phi}\right)+2c\left(\frac{cos\phi}{1-sin\phi}\right)$$ | (1) |
여기서, σ1,f : 파괴 시 축방향 응력(강도)
σ3 : 구속응력
c : 암반의 점착력
ϕ : 암반의 내부 마찰각
위 식을 통해서 최종적으로 강도응력비(Strength Stress Ratio, SSR)는 식 (2)와 같이 정의된다.
| $$\mathrm{강도응력비}(SSR)=\frac{\sigma_{1,f}}{\sigma_1}$$ | (2) |
여기서, σ1 : 최대 주응력
필라의 강도응력비가 필라 전체의 안전율을 대변하지는 않지만, 진행성 파괴(progressive failure)나 응력 전이과정(stress transfer progress)을 고려하여 필라 중앙 단면에서의 평균 강도응력비(average strength stress ratio)가 1.0 이하가 되면 필라 전체가 불안해지는 것으로 알려져 있다(Hoek and Brown, 1980).
3. 수치해석 모델링
3.1 해석단면 및 지반조건 설정
복층터널 분기 전 확폭구간의 선행굴착 영향을 분석하기 위해 굴착공법, 벤치길이 및 분기방향을 매개변수로 범용 지반 유한요소해석 프로그램인 Midas GTS NX를 사용하여 Mohr-Coulomb 파괴기준에 따른 3차원 유한요소해석을 수행하였다. 해석 대상 터널로는 분기 전 확폭구간의 길이를 20 m, 상층의 우측분기를 가정하여 모자형 대단면 터널(폭 30.4 m, 높이 16.8 m)로 설정하였고 분기 후 구간은 2차원 단면 해석과 같이 가상의 복층터널 편도 2차로의 본선 터널(폭 12 m, 높이 10.8 m)과 편도 1차로의 분기 터널(폭 6 m, 높이 4 m) 단면을 적용하였다(Fig. 4 참조).
지반조건은 3등급에서 5등급 암반까지 변화하는 것으로 가정하였고 지반의 암반등급별 설계지반정수는 김포도시철도 설계보고서(Gimpo Goldline, 2015)와 서울특별시 건설안전본부의 토질조사보고서(Seoul Metropolitan Government Construction Safety Management Headquaters, 2007)를 참고하여 Table 3과 같은 물성을 적용하였다. 또한, 수치해석 시 분기 전 확폭구간은 2.2절의 대단면 터널에 대하여 제시하고 있는 숏크리트와 록볼트의 지보패턴을 참고하여 Table 4와 같은 지보패턴으로 해석을 수행하였다.
Table 3.
Rock mass properties used in analysis
| Rock mass |
Unit weight (kN/m3) |
Elastic modulus (MPa) |
Cohesion (kPa) |
Friction angle (°) |
Poisson ratio (ν) |
| V | 23 | 580 | 170 | 34 | 0.26 |
Table 4.
Pattern of tunnel reinforcement
| Type | Shotcrete (mm) | Rock bolt (m) | |
| Length | Interval (vertical/horizontal) | ||
| Widening section | 300 | 6.0 | 1.2/1.2 |
3.2 굴착조건 및 해석영역 설정
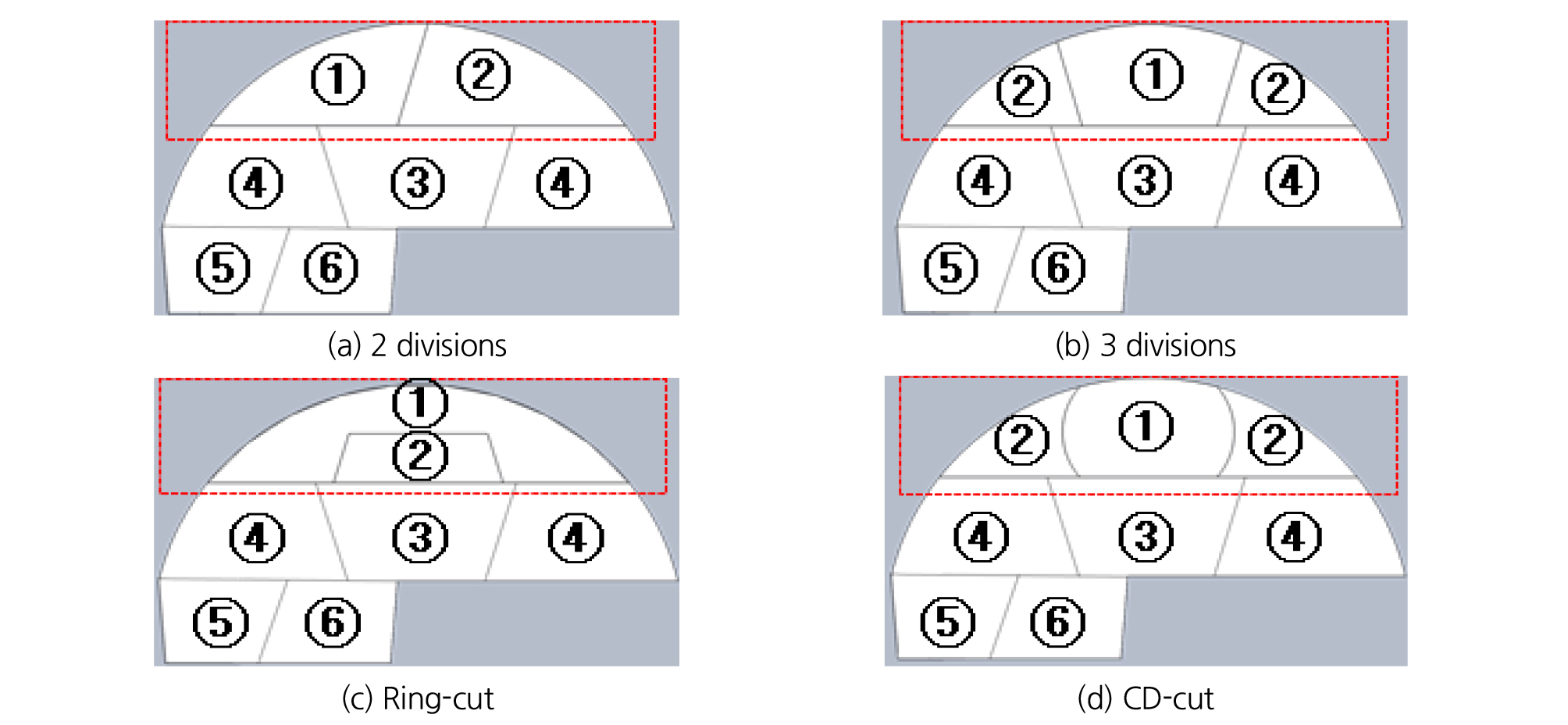
분기 전 확폭구간의 선행굴착 영향을 분석함에 있어 굴착공법 간의 차이를 확인하기 위하여 Fig. 5와 같이 분기 전 확폭구간 단면의 상부를 2분할(2 divisions), 3분할(3 divisions), 핵남기기(Ring-cut), 중벽분할(CD-cut) 4가지 굴착조건을 설정하여 굴착공법에 대한 선행굴착 영향을 분석하였다.
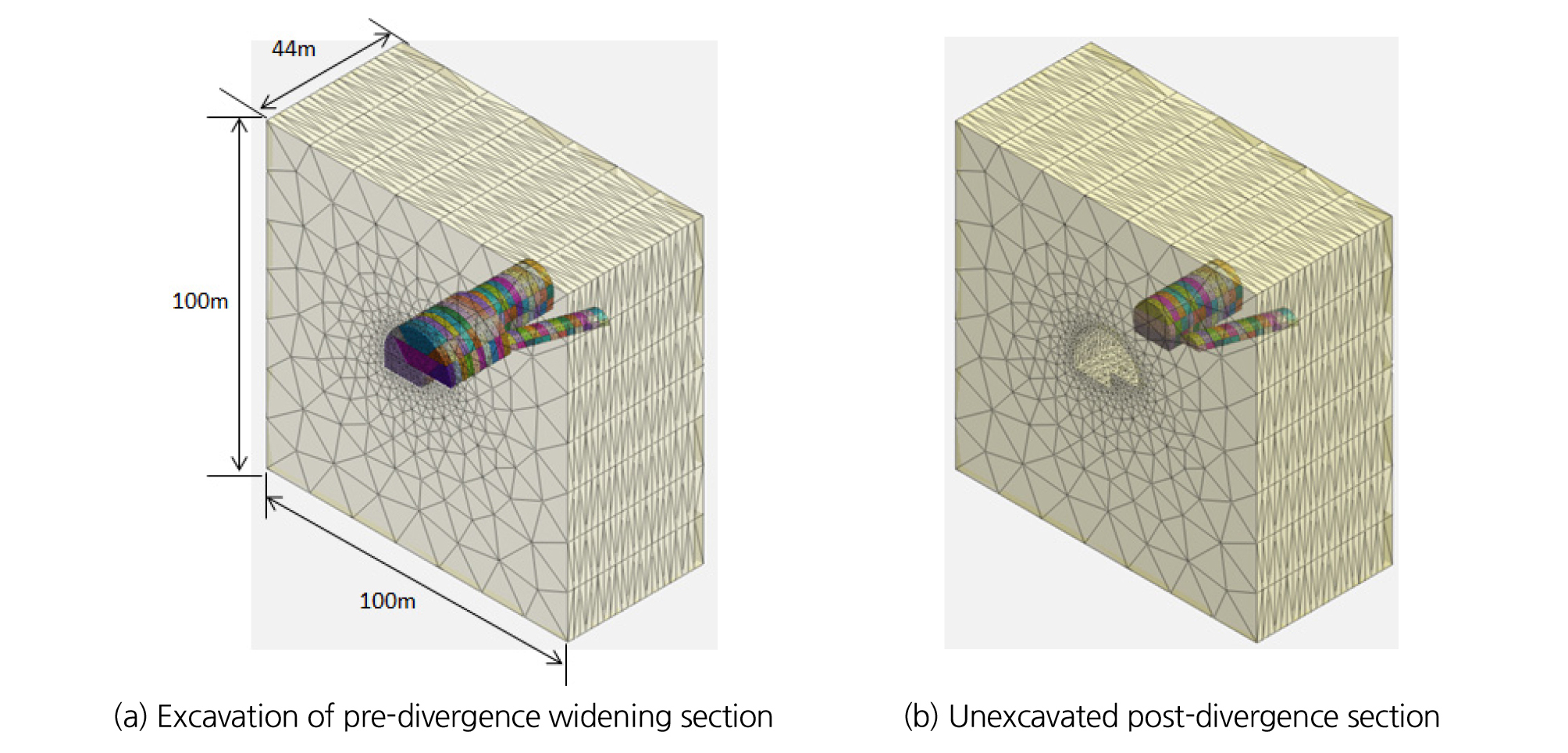
전체 해석영역은 Fig. 6(a)와 같이 높이 100 m, 길이 100 m, 폭 44 m로 설정하여 지반경계가 해석결과에 영향을 미치지 않도록 고려하였다. 또한, Fig. 6(b)와 같이 분기 전 확폭구간의 시공단계를 고려하여 굴착을 진행하였고 분기 전 확폭구간 굴착이 끝난 후 선행굴착 영향을 분석하였다. 또한, 벤치길이에 따른 선행굴착 영향을 판단하기 위하여 Fig. 7과 같이 벤치길이를 2 m, 4 m, 10 m, 20 m 4가지 조건으로 변화하여 선행굴착 영향을 분석하였다.
4. 해석결과 분석 및 고찰
4.1 굴착공법에 따른 선행굴착 영향
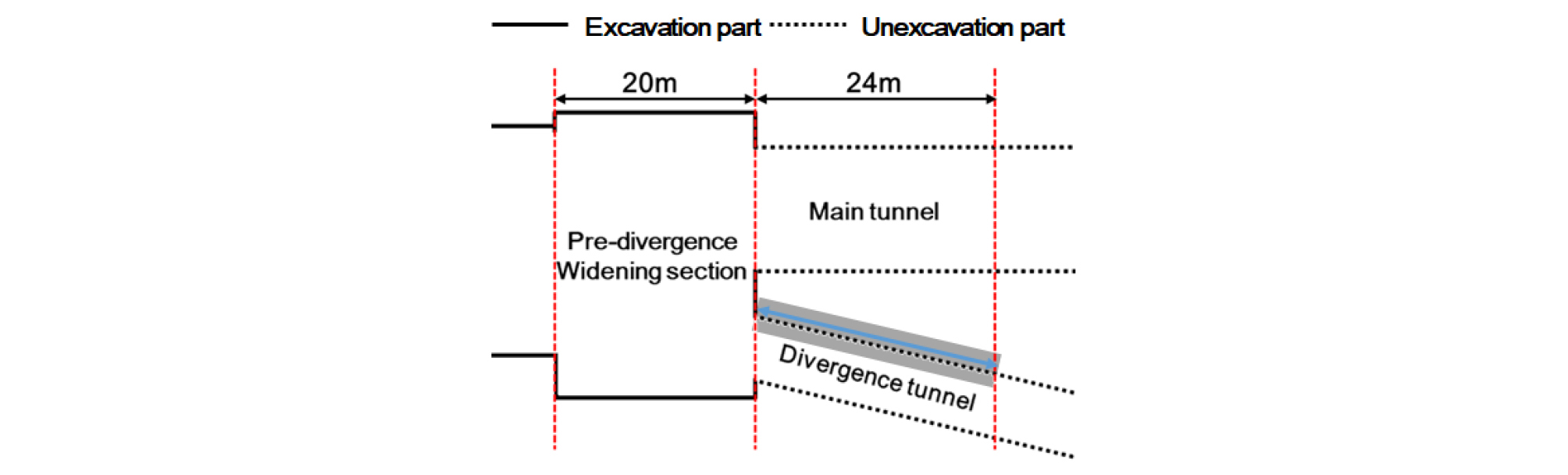
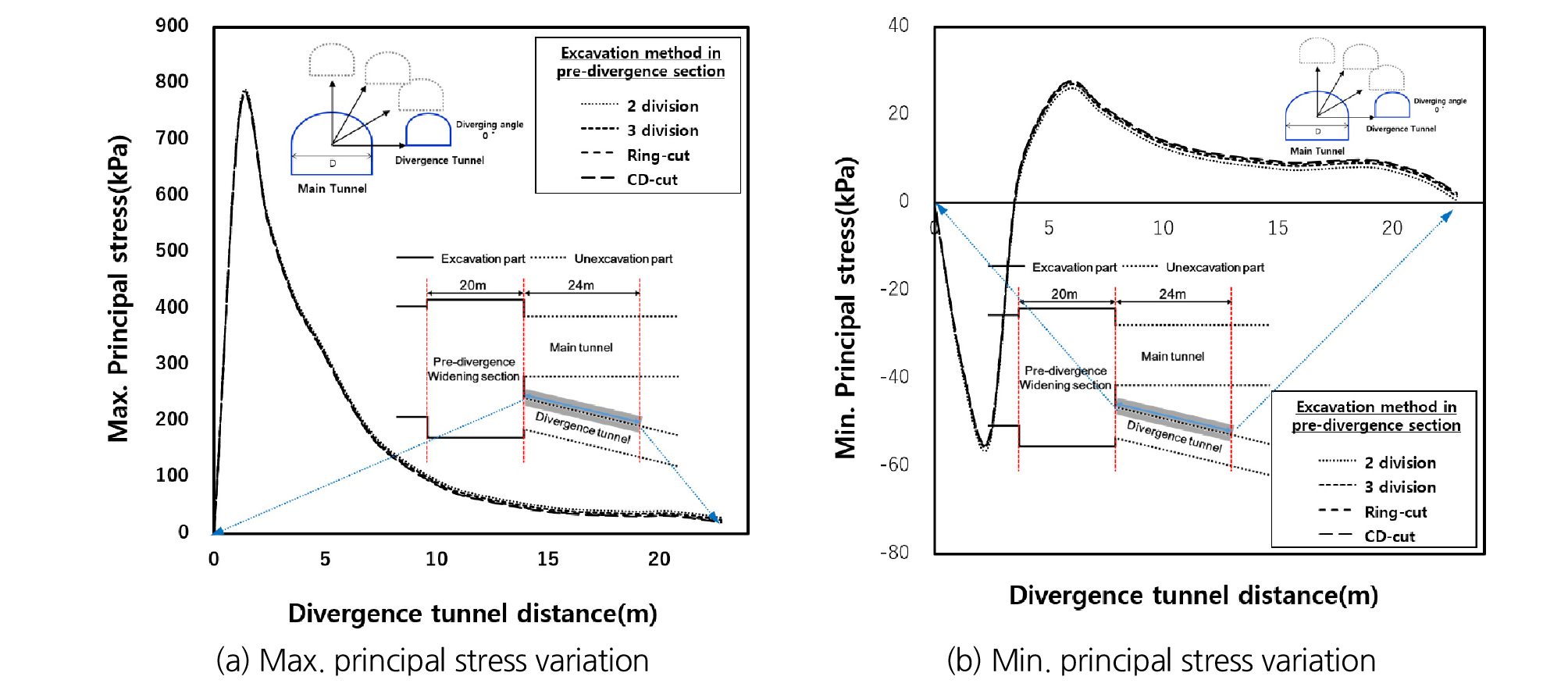
선행굴착 영향을 분석하기 위해서 시공단계에 따라 분기 전 확폭구간 굴착이 종료되면 Fig. 8과 같이 굴착되지 않은 가상의 분기 후 구간 중 음영부분의 분기터널 좌측부 선을 따라 굴착 전과 굴착 후에 대한 최대주응력과 최소주응력의 변화량을 살펴보았다.
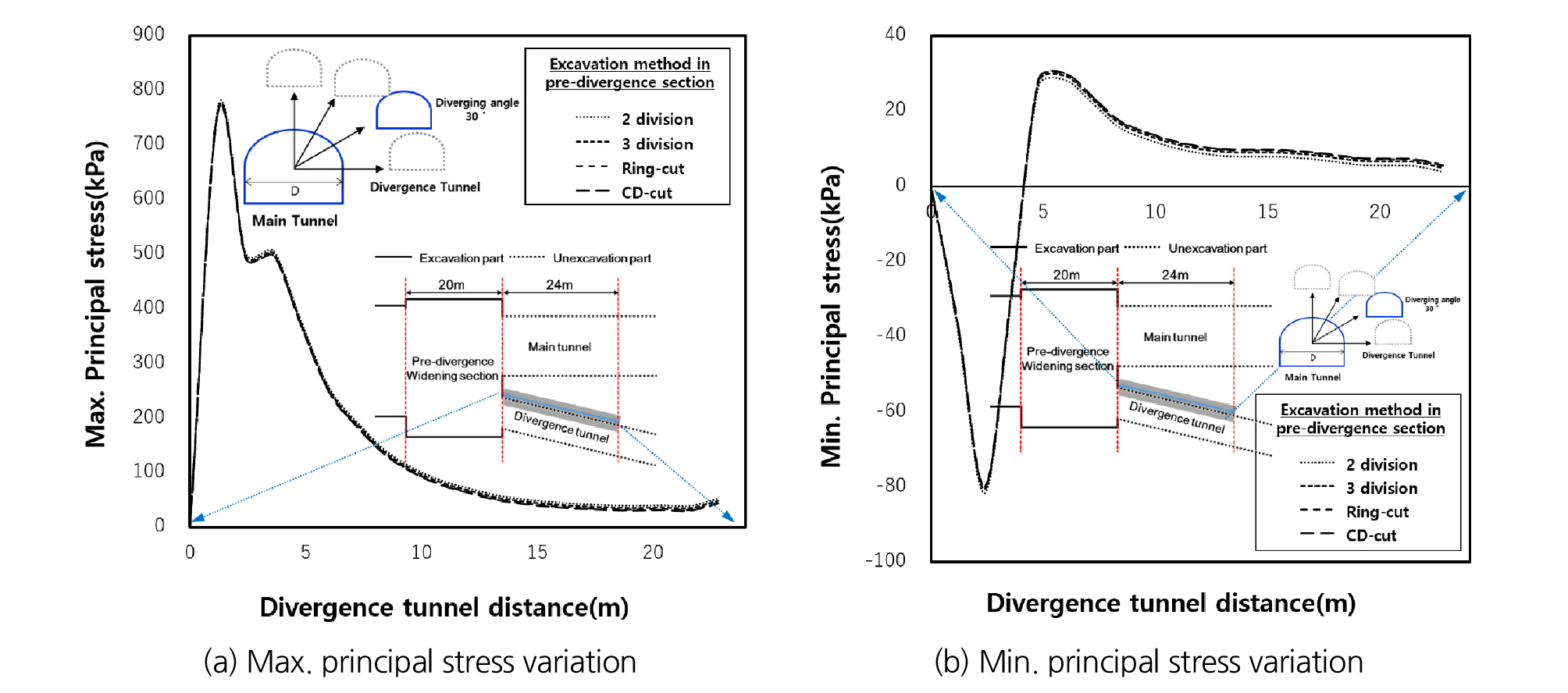
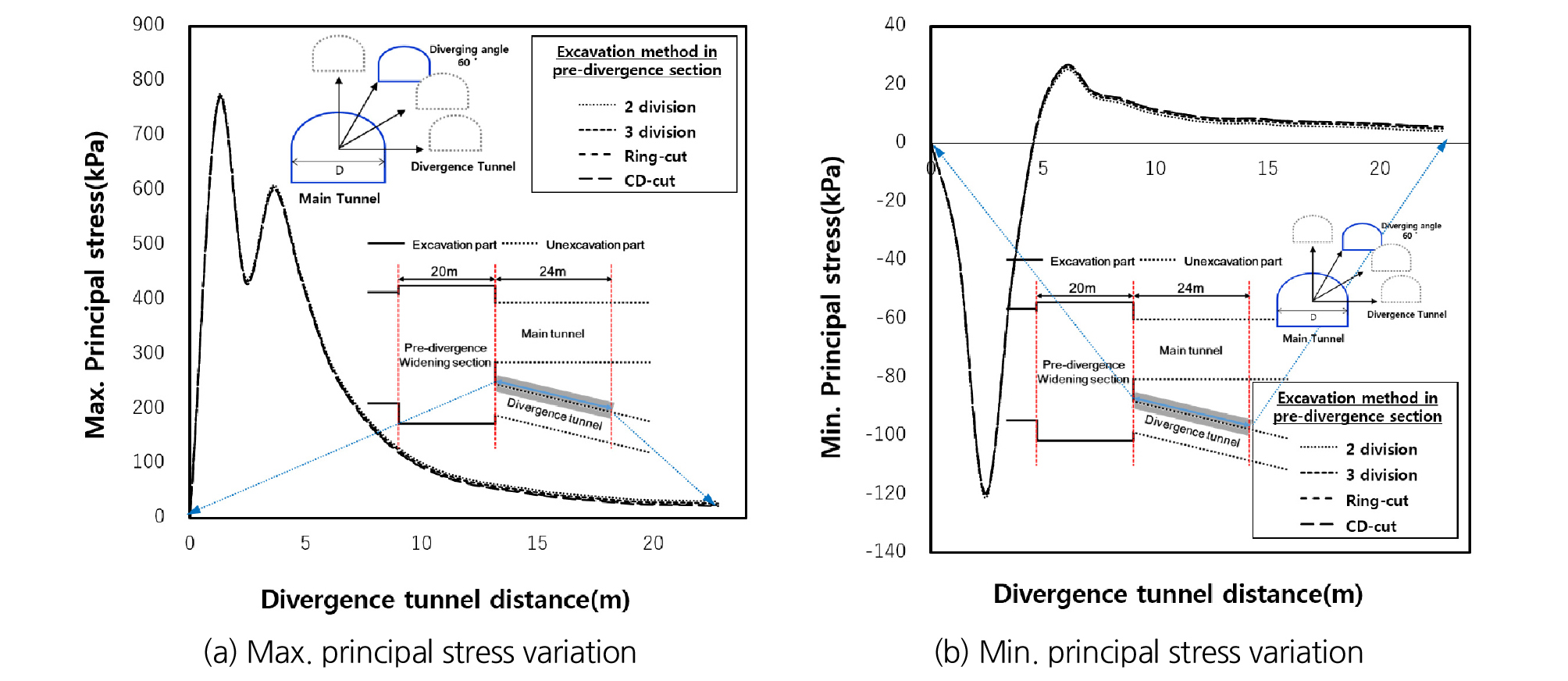
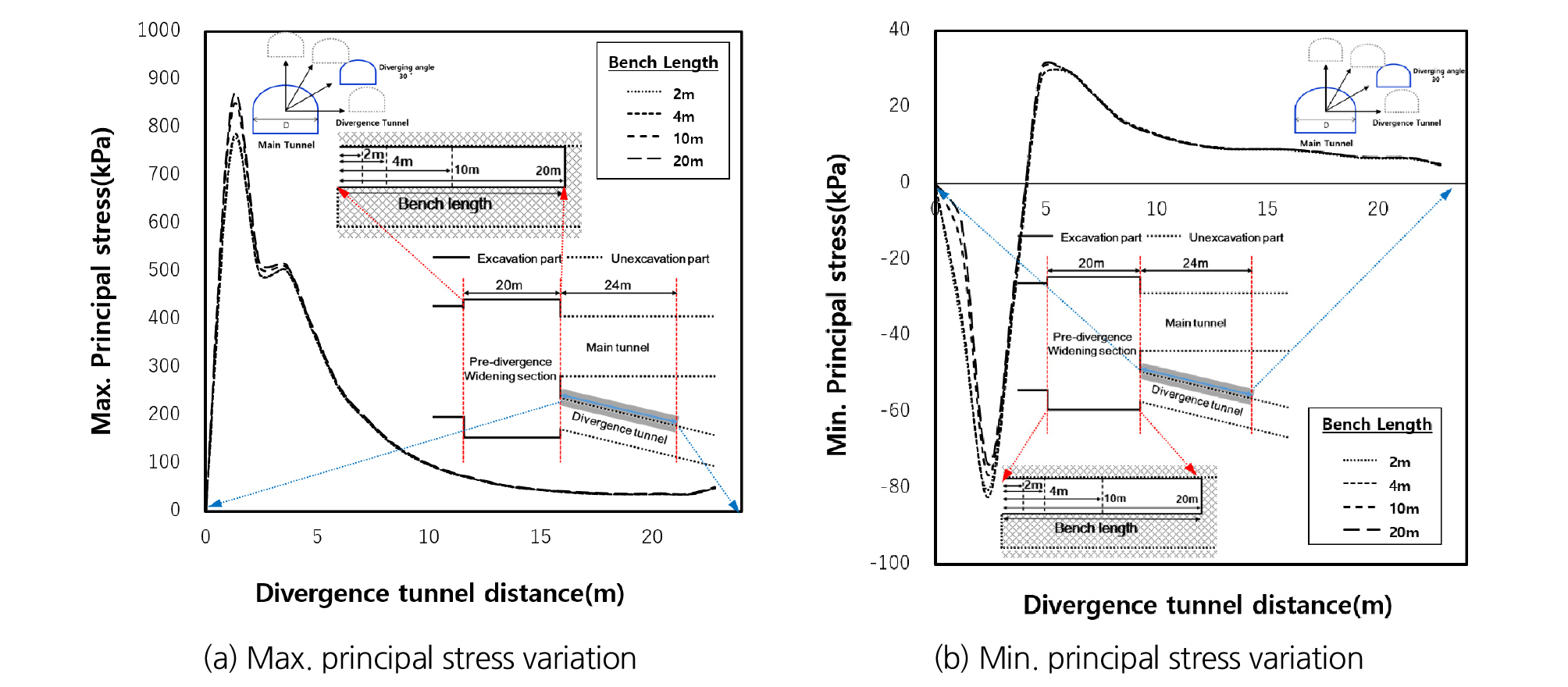
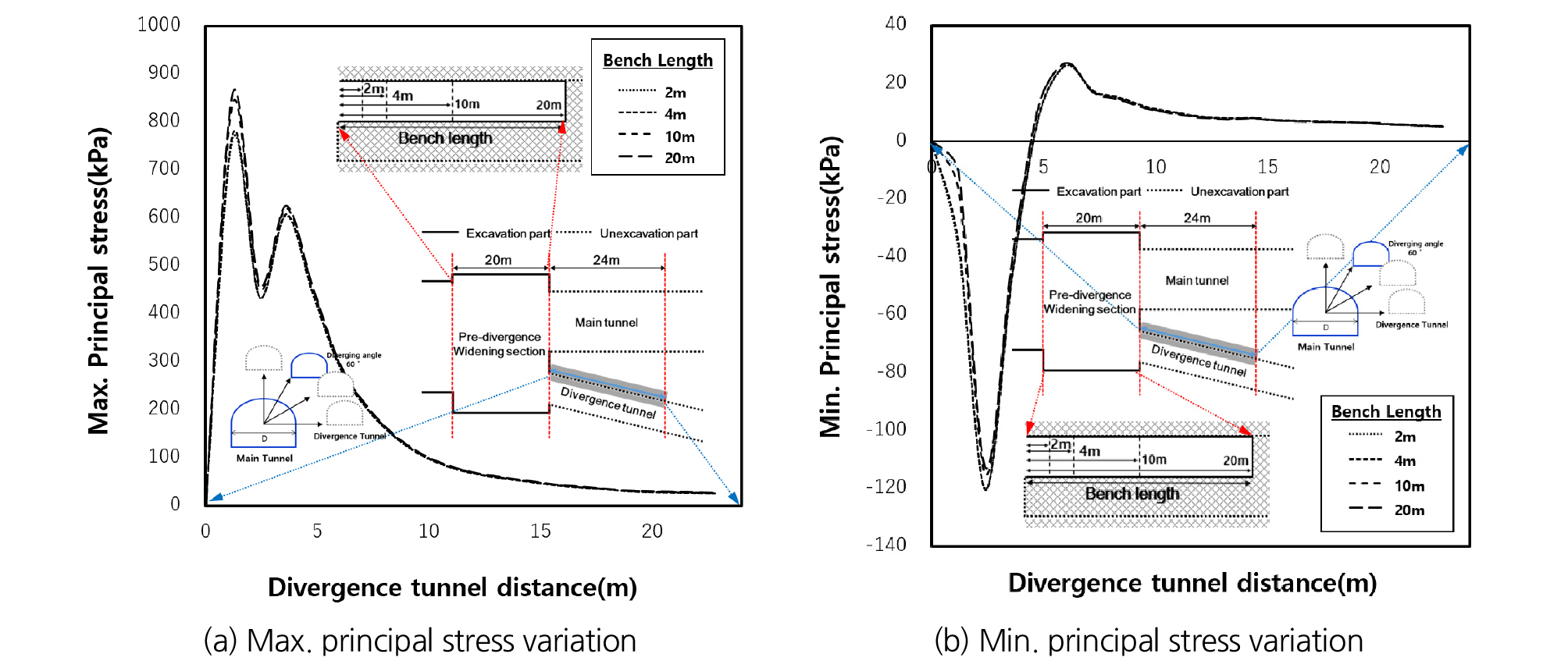
굴착공법에 따른 선행굴착 영향을 분석하기 위해 최대주응력과 최소주응력 변화량에 대한 결과를 본선터널과 분기터널 사이 각도에 따라 Figs. 9~11에 나타내었다. 그 결과, 최대주응력의 최대 크기 차이는 780 kPa, 최소주응력의 최대 크기 차이는 58 kPa로 나타났고, 4가지 굴착공법 간 차이가 거의 발생하지 않는 것으로 나타났으며 분기각이 커짐에 따라 최대주응력의 최대크기 차이는 없지만 최소주응력의 최대 크기차이는 58 kPa, 82 kPa, 121 kP로 증가하는 것을 확인하였다. 굴착공법 간의 차이는 미미하나 분기 전 확폭구간의 선행굴착 영향은 분기 후 구간에 충분히 영향을 줄 만큼 큰 응력으로 판단하였다. 최대주응력은 굴착 후 약 16 m 이격된 지점, 최소주응력은 10 m 이격된 지점부터 변화량의 차이가 없는 것으로 나타나 확폭구간 폭 16.8 m의 약 1.0배 이격된 지점부터 선행굴착 영향이 거의 없는 것으로 판단되었다.
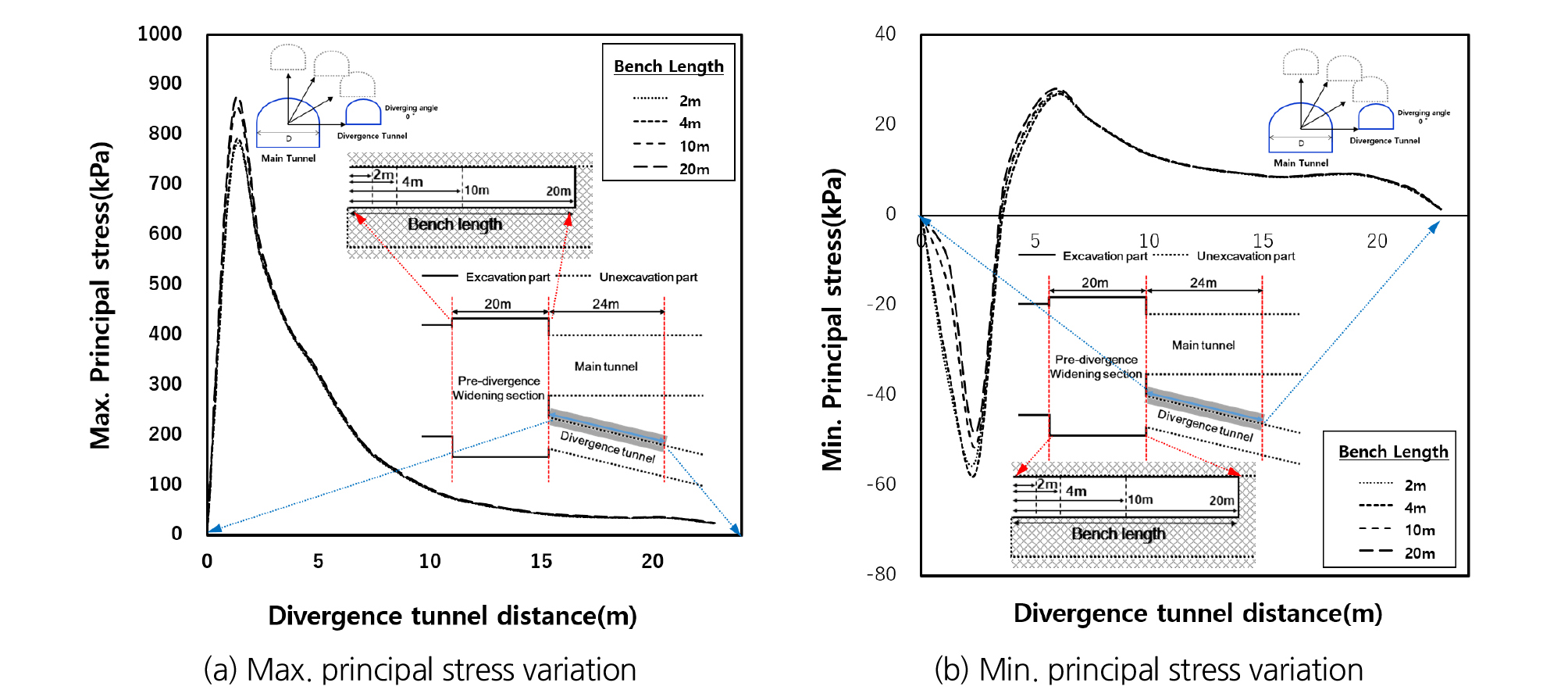
4.2 벤치길이에 따른 선행굴착 영향
벤치길이에 따른 선행굴착 영향 분석을 위해 최대주응력과 최소주응력 변화량 결과를 메인 터널과 분기 터널 사이 각도에 따라 Figs. 12~14에 나타내었다. 그 결과, 메인터널과 분기터널 사이 이격각도가 0°일 때, 벤치길이 2 m일 때 최대주응력의 최대 크기 변화량은 763 kPa, 벤치길이 20 m일 때 최대주응력의 최대 크기 변화량은 858 kPa로 95 kPa의 차이가 발생하였고, 벤치길이 2 m일 때 최소주응력의 최대 크기 변화량은 58 kPa, 벤치길이 20 m일 때 최소주응력의 최대 크기 변화량은 48 kPa로 10 kPa의 차이가 발생하였으며 이격각이 커짐에 따라 최대주응력의 최대크기 차이는 없었지만 최소주응력의 최대 크기차이는 58 kPa, 82 kPa, 120 kPa로 증가하는 것을 확인하였다. 따라서 벤치길이에 따른 선행굴착 영향은 어느 정도 발생하는 것으로 판단되며 굴착공법에 따른 변화와 같이 확폭구간 폭 16.8 m의 약 1.0배 이격된 지점부터 선행굴착 영향이 거의 없는 것으로 판단되었다.
4.3 선행굴착 영향에 따른 강도응력비 결과
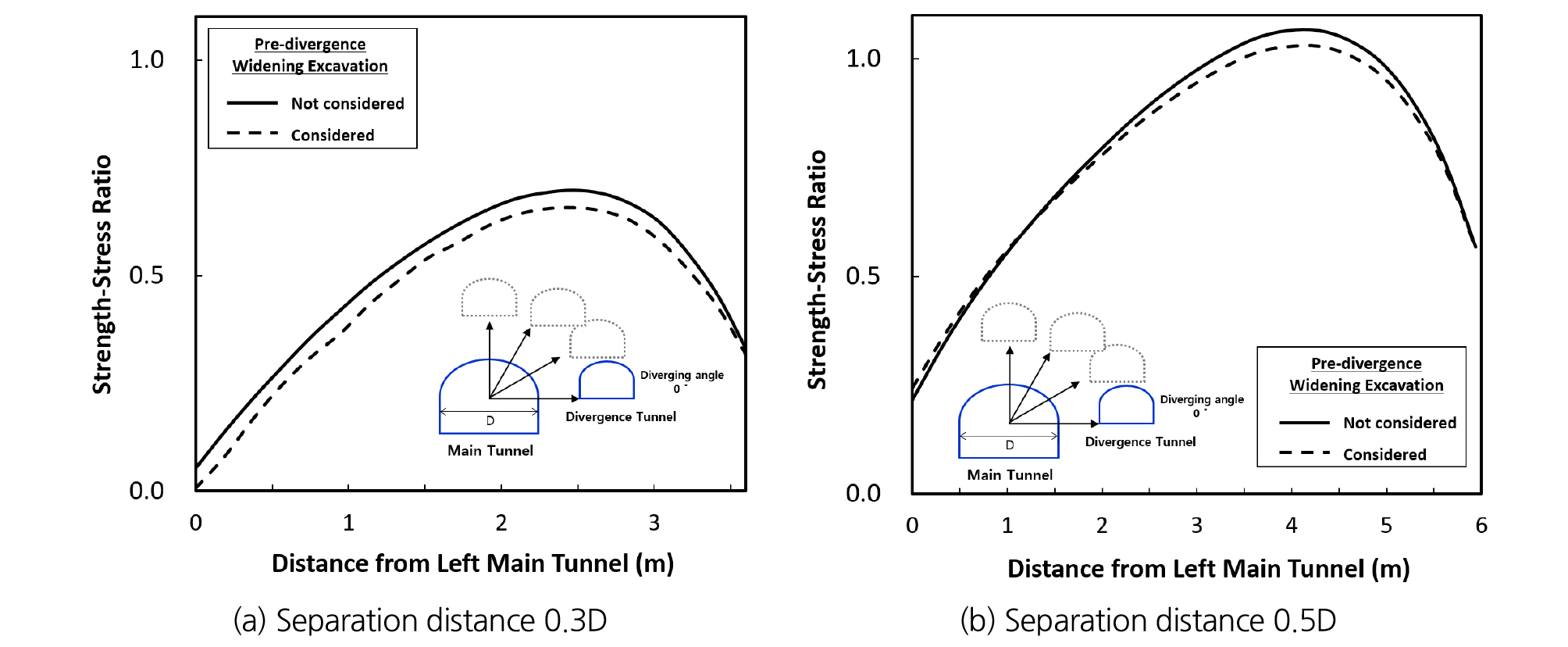
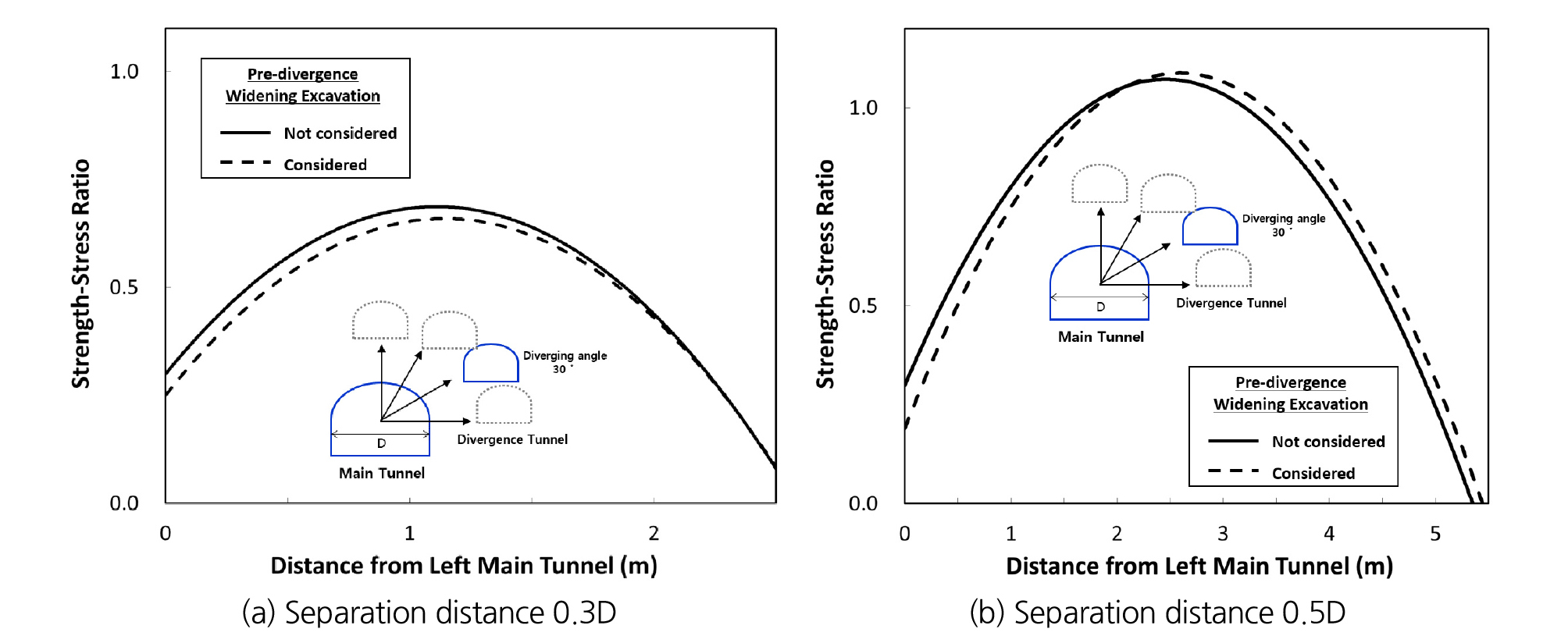
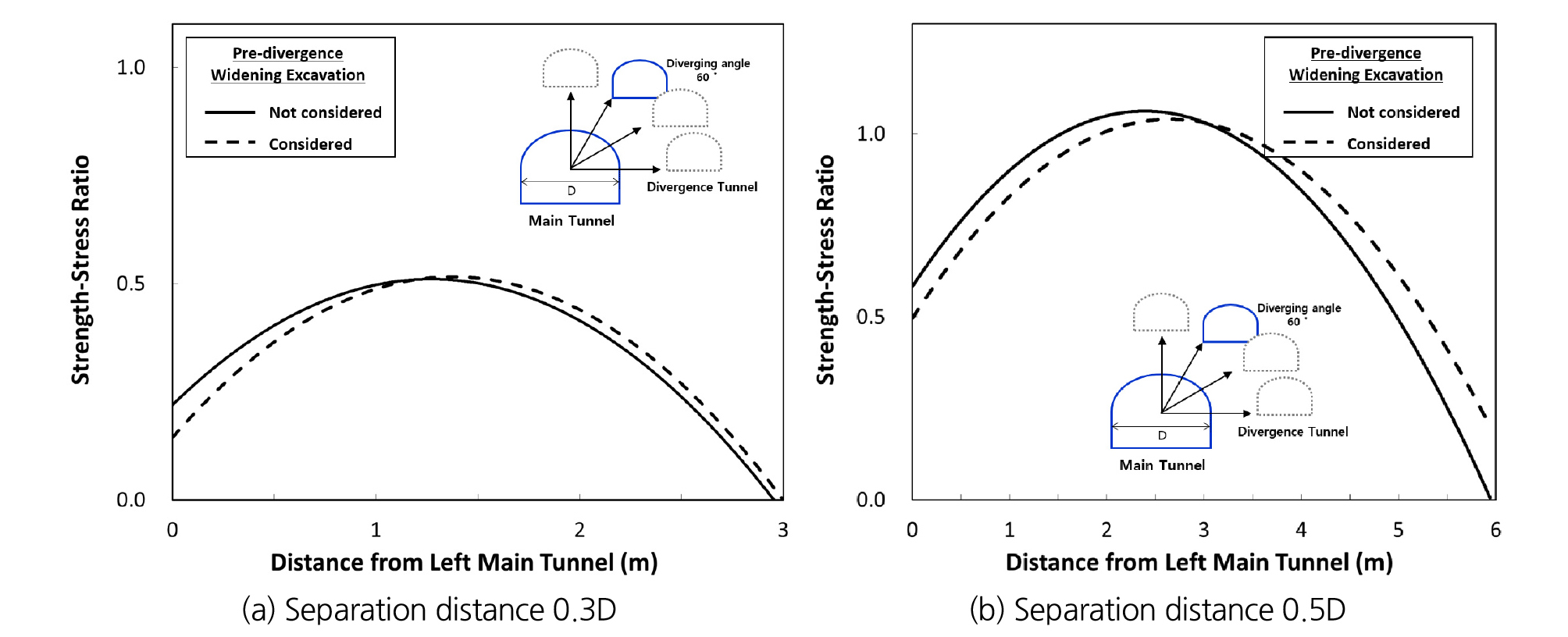
2차원 수치해석 해석대상은 5등급 암반의 이격각도 0°(수평), 30°, 60°이고 분기터널의 접속각도는 20°로 설정하여 수행하였고 선행굴착 영향을 반영한 결과와 선행굴착 영향을 반영하지 않은 결과를 비교하기 위하여 Figs. 15~17에 이격각도에 따른 두 방법 간 강도응력비 결과의 차이를 나타내었다. 5등급 암반의 분기 전 확폭구간으로 부터 약 2 m이격된 본선터널 폭 기준 이격거리 0.3D, 이격각도 0°지점의 경우 Fig. 15(a)와 같이 선행굴착 영향을 반영한 결과가 선행 굴착 영향을 반영하지 않은 강도응력비 값이 낮은 것을 확인하였다. 또한, 이격거리가 증가할수록 선행굴착 영향이 감소하여 Fig. 11(b)와 같이 본선터널 폭 기준 이격거리 0.5D 지점에서 강도응력비 차이가 이격거리 0.3D일 때 보다 감소하는 것으로 나타났으며 메인터널과 분기터널의 이격각도에 따라 강도응력비가 최대로 발생하는 메인터널에서의 거리가 다르다는 것을 확인하였다.
5. 결 론
본 연구에서는 암반에서 시공되는 NATM 방식의 2차로 대심도(40 m) 본선 복층터널에서 1차로 단층터널로 분기되는 조건을 대상으로 분기 전 확폭구간 굴착 시 굴착공법, 벤치길이, 이격각도의 변화에 따라 발생되는 선행굴착 영향에 대한 연구를 수행하였다. 이를 위해 3차원 유한요소해석을 수행하고 분기 전 확폭구간 굴착으로 발생된 선행굴착이 분기 후 구간에 미치는 영향을 분석하였으며, 다음과 같은 결과를 얻었다.
1. 3차원 수치해석 결과 분기 전 확폭구간의 굴착공법에 따른 선행굴착 영향에서 굴착공법 간 최대주응력 증감량은 약 780 kPa, 최소주응력 증감량은 약 58 kPa로 그 차이는 크지 않았으며, 최소주응력의 증감은 메인과 분기터널 사이 분기각에 영향을 받는 것을 확인하였다. 이로써, 분기 전 확폭구간의 선행굴착은 분기 후 구간의 굴착 안정성에 영향을 줄 만큼 큰 응력의 변화를 유발하는 것으로 나타났다.
2. 벤치길이 2 m와 20 m에 대해서 최대주응력과 최소주응력 변화량의 차이가 각각 95 kPa, 10 kPa 발생하여 벤치길이에 따른 분기 전 확폭구간의 선행굴착 영향은 상대적으로 크지 않은 것으로 나타났다.
3. 선행굴착 영향을 반영한 결과와 선행굴착 영향을 반영하지 않은 결과에 대한 강도응력비 산정 결과, 분기 전 확폭구간으로 부터 약 2 m이격된 본선터널 폭 기준 이격거리 0.3D 지점의 경우 선행굴착 영향을 반영한 결과가 2차원 수치해석 결과보다 강도응력비 값이 확연히 감소하는 것을 확인하였고, 확폭구간으로 부터 이격거리가 증가하여 선행굴착 영향이 감소한 분기 전 확폭구간으로 부터 약 8 m 이격된 본선터널 폭 기준 이격거리 0.5D 지점에서 강도응력비 차이가 크지 않은 것으로 나타나 설계 시 분기 전 확폭구간과 이격거리가 작은 지점에서는 선행굴착 영향을 반드시 고려해야할 것으로 판단된다.