1. 서 론

최근 국내의 경우 도시화로 인한 교통량이 증가하고 차량의 증가와 대형화로 인한 교통문제가 증가하고 있다. 이러한 교통문제를 해결하기 위해 종래에는 도로와 터널을 신설하였으나 도로의 경우 현재 토지 보상비가 증가하고 민원이 빈번하게 발생하여 도심지 내의 도로신설이 어려우며 터널의 경우 지하철, 지하상가 등 각종 지장물이 있어 저심도 터널 시공에 어려움이 있다. 따라서 기존 지하 구조물과 간섭을 피하고 보상이 적어 지하 공간 개발이 용이한 대심도 복층 분기 터널의 중요성이 증가하고 있으며, 국내에서도 일반적인 터널보다 단면이 작고 지하에서 다른 터널과 교차하는 네트워크형으로 계획한 소형차 전용 터널을 계획하고 있다.

You et al. (2017)은 대심도 복층 터널의 확폭 단면 형상 및 보강방법에 관한 안정성 연구에서 확폭부의 단면이 아치 형상보다 박스형 확폭 단면이 안정성이 높게 나타나는 것으로 평가하였다. 또한, 기존 쉴드 터널 단면과 박스형 확폭부의 접합부에 있어서 Seo et al. (2016)은 기존의 강재 보가 콘크리트에 매립되어 볼트접합 연결되는 기존 하이브리드 접합법의 한계와 단점을 개선하기 위하여 단순한 강접합 절점을 갖는 하이브리드 PC 콘크리트 보 시스템을 개발하여 휨 거동을 평가하였다.

Kwon et al. (2017a)은 강재 기둥과 접합된 하이브리드 H-보-철근 콘크리트 보(HSRC)의 반복 휨 거동을 평가하였다. 또한 Kwon et al. (2017b)은 시공성이 단순한 연성형 절점을 갖는 HSRC 하이브리드 보 시스템의 콘크리트 보 영역에서의 일축 전단 및 연결 절점 영역에서의 전단 마찰 거동을 평가하였다. Lee et al. (2015)은 하이브리드 OCB (Optimized Composite Beam)을 개발하여 부모멘트 구간에서는 노출강연선으로 보강된 H형강으로 구성되고 정모멘트 영역에서는 PSC 구조로 구성된 건축용 OCB의 휨실험을 실시하고 구조거동 및 안전성을 평가하였다. 그러나 기존 연구는 건축구조에 있어서 장경간을 위한 강재 보와 RC보의 하이브리드 구조의 연결부에 관한 상세로 신설 구조물에 적합한 접합부이며 본 연구 대상과 같이 기존 구조물을 확장하여 신규 구조물과 기존 구조물을 접합하는 접합부에 관한 연구는 미흡한 실정이다.

따라서 본 연구에서는 쉴드 터널 분기부에 있어서 기존 구조물과 신규 구조물의 접합부에 있어서 기존의 전단면 강재접합부 대신 휨모멘트가 최대로 발생하는 부분에만 강재를 사용하는 부분 강재-콘크리트 접합부 상세를 제안하였다. 또한, 쉴드 터널 분기부 확폭구간의 3차원 거동효과를 반영하기 위해 확폭부 시종점에서의 기둥 효과와 확폭구간 종방향 부재의 강성효과를 고려할 수 있는 2차원 해석모델을 검토하였다. 종방향부재의 스프링상수는 세그먼트와 확폭부(박스)의 연결부에 종방향으로 설치가 가능한 부재의 단면 강성과 작용력을 고려하여 부재 처짐을 산정하고 이때 발생 최대처짐을 스프링상수로 변환하여 적용하였다.

2. 구조해석

2.1 지반반력계수 검토

2.1.1 적용 지반 물성

구조해석시 적용하는 지반 물성치는 국내에서 복층 터널의 시공이 예상되는 암반조건이 양호할 것으로 예상되는 대심도 조건을 고려하여 연암조건을 가정하였으며, 해석시 적용한 암반의 물성치는 Table 1과 같다.

Table 1. Analysis ground material properties

2.1.2 적용식

지반반력계수 산정을 위해 지반공학적 특성을 반영한 AFTES식을 적용하였다(AFTES - WG7, 1993).

여기서, Ks는 단위접선 길이 당 스프링 계수, Es는 주변지반의 탄성계수, R은 Lining의 등가반경( R＝$\sqrt{\frac{\mathrm{A}}{\mathrm{\pi }}}$ ), L은 부재 중앙과 중앙 사이의 길이, υ은 포아송비이다.

2.1.3 산정 값

식 (1)을 적용하여 지반반력계수를 산정하였으며, 산정된 지반반력계수 값은 Table 2와 같다.

Table 2. Subgrade reaction modulus

2.2 세그먼트 연결부의 스프링 상수

본 연구에서는 세그먼트 연결부는 연결의 회전 강성과 전단 강성을 고려하여 다음과 같이 모델링 하였다.

2.2.1 회전스프링 상수

보-스프링 구조해석모델의 경우 세그먼트 이음부 강성을 반영하여 실제 거동에 가까운 모사가 가능하므로 이음부에 회전 강성을 적용하였으며, 회전스프링 상수 산정은 다음의 3개의 공식을 비교 검토하여 적용하였다.

(1) 일본 터널표준시방서(Japanese Standard Specification for Tunneling, 2016)

이음부에 인장부재가 없는 압축을 받는 조건에서의 회전스프링 상수는 다음과 같다.

여기서, M은 휨모멘트, θ는 휨모멘트로 인한 회전각, x는 세그먼트의 회전으로 생기는 압축영역 거리, h는 세그먼트 높이, b는 세그먼트 폭, Ec는 콘크리트 탄성계수이다.

여기서, x = h인 경우(하중 편심률 0, 이음부에 인장부재 없음) 회전스프링 상수는 $k_m=\frac{h^{2}b{E}_c}{24}$이 된다.

기존 국내에서는 하중편심률을 고려하여 $x=\frac{n\bullet A_b}{b}(-1+\sqrt{1+\frac{2bd}{n{A}_b}})$ 또는 $x=\frac{n\bullet A_b}{b}(-1+\sqrt{\frac{2bd}{n{A}_b}})$를 적용한 식을 적용하여 왔다. 국내에서 적용해온 회전스프링 상수 값은 x = h를 적용한 값보다 작은 값이 적용되었다.

(2) Loenhardt 식(JSCE, 2010)

각 세그먼트 이음마다 하중편심률(m)에 따른 회전스프링상수가 고려된다.

여기서, m = 하중편심률 = e / a = M / (N × a), M은 휨모멘트, N은 축력, a는 세그먼트 접촉 높이, e는 편심거리, θ는 휨모멘트로 인한 회전각, x는 세그먼트의 회전으로 생기는 압축영역 거리, b는 세그먼트 폭, Ec는 콘크리트 탄성계수이다.

(3) Janssen 식(Janssen, 1983)

여기서, M은 휨모멘트, N은 축력, l_t는 세그먼트 접촉 높이, b는 세그먼트 폭, E는 콘크리트 탄성계수이다.

세그먼트가 압축만 받는 경우에는 일본 토목구조물 설계표준 ‧ 동해설 식과 Leonhardt 식, Janssen 식은 동일한 값을 나타낸다. 기존 국내에서는 일본 토목구조물 설계표준 ‧ 동해설 식보다 작은 회전스프링상수 값을 적용해 왔으므로 단면력이 크게 산정되어 강도조건에서 볼 때 최적철근량보다 많은 철근량이 산정되어 비경제적인 단면이 적용되어 왔다. 본 연구에서는 기존 국내에서 적용한 회전스프링 상수값을 적용하여 해석을 수행하였다. 위의 3개의 식을 적용한 회전스프링 상수 값은 Table 3과 같다.

Table 3. Rotational spring constant

2.3 작용하중 검토

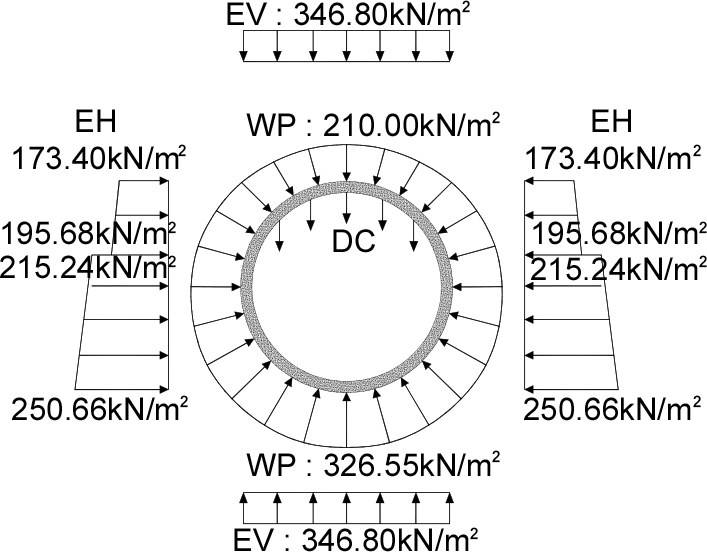
2.3.1 작용하중

본 연구에서 검토한 쉴드터널 단면은 ○○현장에 적용된 대단면(외경 7.770 mm, 두께 350 mm, 길이 3,614 mm, 폭 1.5 m) 조건을 준용하였으며, 하중 종류에 따른 적용값과 하중재하도는 Table 4와 같다.

Table 4. Applied load

Fig. of applied load	Applied load
	Load Per unit area (m2) Per unit length (m) DC Automatically loaded in program EV 346.80 kN/m2 520.200 kN/m EH (top) 173.40 kN/m2 260.100 kN/m EH (2nd) 195.68 kN/m2 293.520 kN/m EH (3rd) 215.24 kN/m2 322.860 kN/m EH (bottom) 250.66 kN/m2 375.990 kN/m WP (top) 210.00 kN/m2 315.000 kN/m WP (bottom) 326.55 kN/m2 489.825 kN/m

2.3.2 하중조합

콘크리트와 강재의 단면 검토 시 적용한 하중조합은 Table 5와 같다. 콘크리트 단면 검토 시에는 극한하중조합을 사용하였으며, 강재 단면의 응력 검토 시에는 사용하중조합을 사용하였다.

Table 5. Load combination

2.4 기존 해석모델 검토

2.4.1 검토모델 및 해석모델

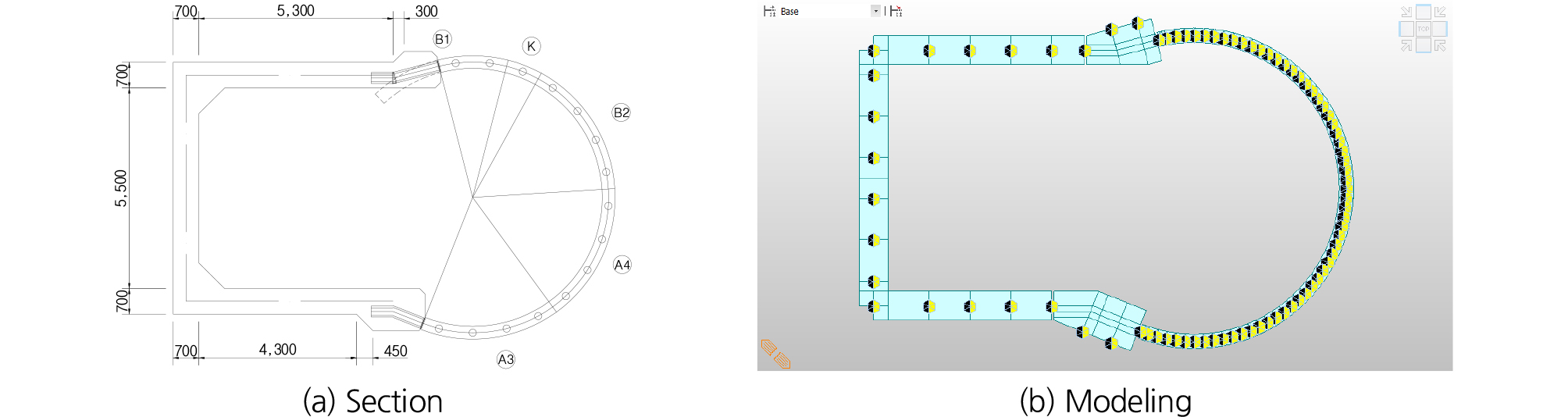
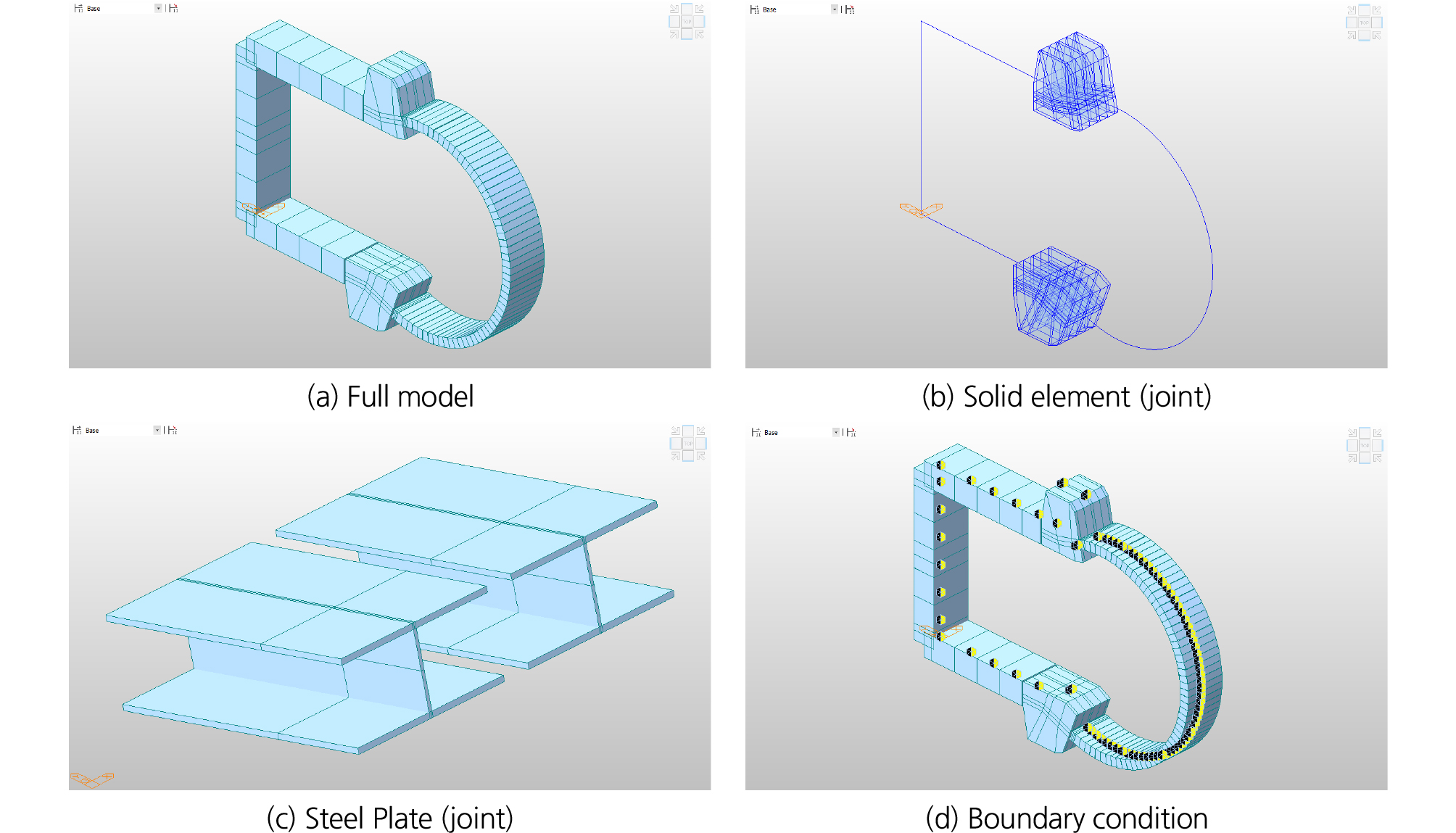
기존 쉴드 세그먼트 터널과 확폭부(박스부)의 단면도 및 해석모델은 Fig. 1과 같으며 경계조건은 Fig. 1(b)와 같이 지반스프링을 적용하였다.

Fig. 1.

Analysis model (section and modeling)

2.4.2 해석결과 및 검토

기존 검토모델과 작용하중을 고려한 해석결과는 Fig. 2와 같다.

Fig. 2.

Results of previous model

기존 모델의 구조해석결과 박스부(확폭부)의 최대작용모멘트 Mu = 4,750 kN-m, 세그먼트부의 최대 발생모멘트 Mu = 947 kN-m (하중조합 CO2)로 분석되었다. 세그먼트부의 저항모멘트 ΦMn = 649 kN-m이다. 기존 모델의 구조안전성 검토결과 세그먼트부에서 Mu = 947 kN-m > ΦMu = 649 kN-m으로 구조안전성을 확보하지 못하는 것으로 검토되었다. 쉴드 터널 분기부에서는 기존 세그먼트와 확폭부의 연결로 지간이 길어져 큰 모멘트가 발생하게 된다.

따라서 본 연구에서는 발생모멘트를 감소시키기 위하여 정거장 개구부 보강거더와 같이 연결부에 내부 거더와 기둥시스템을 설치하여 연결부에서 중간지점효과를 고려할 수 있는 시스템과 해석기법을 제안하였다. 세그먼트와 확폭부의 접합부에서 종방향 부재와 확폭부의 시 ‧ 종점부의 기둥 효과를 고려할 수 있는 종방향 부재를 도입하였다.

종방향 부재의 강성은 2차원 횡방향 해석 모델에서 세그먼트와 확폭부의 접합부 스프링지지 효과를 고려할 수 있도록 종방향 스프링 지점으로 모델링하여 3차원 거동효과를 고려할 수 있도록 하였다.

2.5 종방향 부재의 강성 고려

2.5.1 검토모델 및 해석모델

쉴드 터널 분기부의 확폭구간의 해석은 3차원 거동효과를 반영하기 위해 확폭부 시종점 구간의 기둥 효과와 종방향 부재의 강성효과를 고려할 수 있는 2차원 해석모델을 검토하였다. 확폭부 시종점 구간의 종방향 부재의 강성을 횡방향 모델에서 연결부의 탄성스프링 지점으로 고려하여 종방향 부재의 강성과 시종점부의 기둥효과를 반영하는 해석모델을 선정하였다.

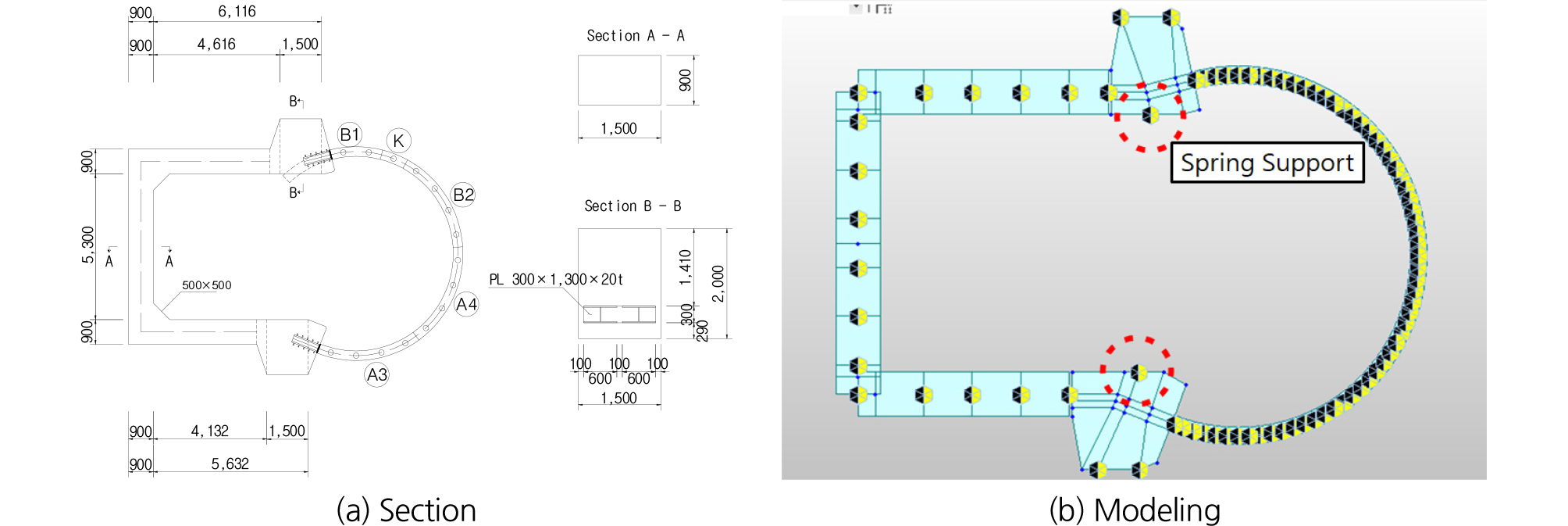
종방향 부재의 강성 효과를 검토하기 위한 단면도 및 해석모델은 Fig. 3과 같다. 종방향 부재 강성 효과를 검토하기 위한 모델의 경계조건으로 지반스프링을 적용하였으며, 연결부에 종방향 부재의 강성을 스프링 지점으로 적용하였다(Fig. 3(b)).

Fig. 3.

Analysis model (section and modeling) for stiffness effects of longitudinal member

2.5.2 종방향 부재 스프링 상수에 따른 단면력 변화

종방향 부재 스프링상수 값은 k = 0~100,000 kN/m의 범위에서 적용하였으며 Table 6에 스프링상수 변화에 따른 박스부(확폭부)와 세그먼트의 발생 단면력을 정리하였다.

Table 6. Member forces according to the change of spring constant (K)

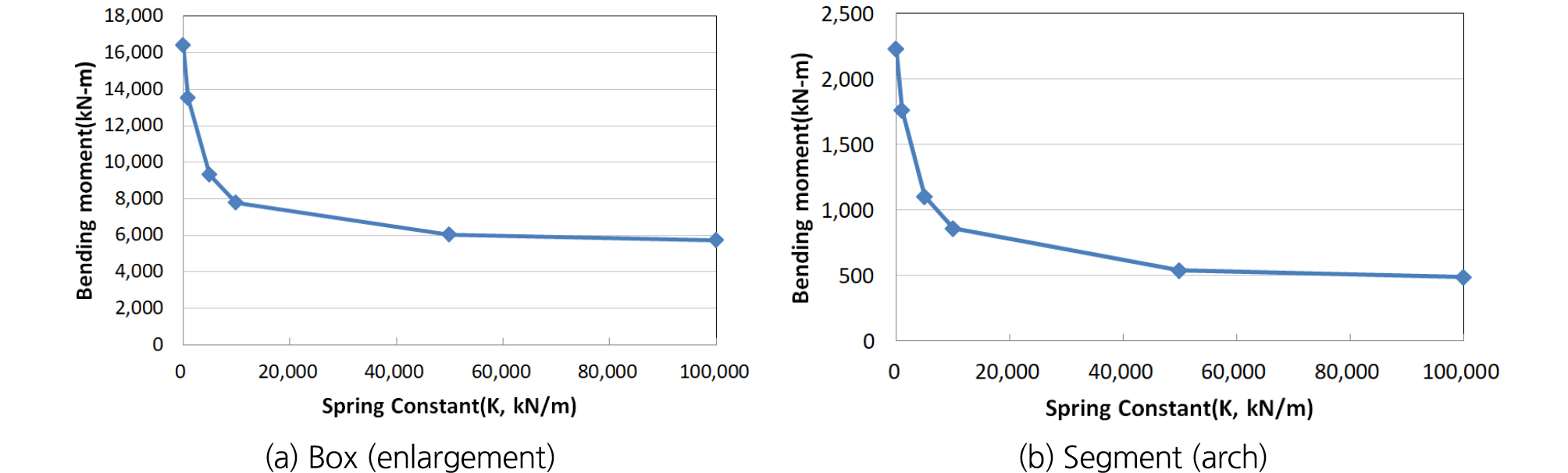
종방향 부재의 스프링 상수값의 변화에 따른 휨모멘트를 보면(Fig. 4) 스프링 상수가 증가함에 따라 박스부와 세그먼트에 발생하는 휨모멘트는 감소하는 것을 확인할 수 있다.

Fig. 4.

Sensitive analysis of spring constant (k)-bending moment

따라서 확폭부와 기존 세그먼트 연결부의 휨모멘트를 저감시키는 종방향 부재의 내부 거더 효과를 고려하기 위하여 2차원 모델링시에 종방향 상수를 고려한 모델링 기법이 필요하다고 판단된다. 또한, 종방향 스프링상수 값 k = 50,000 kN/m 이상의 범위에서 세그먼트 아치부의 작용력이 단면의 저항강도 이하로 작아지는 것을 확인하였다.

2.5.3 종방향 부재 해석

(1) 해석 기법

세그먼트 아치부의 휨모멘트를 감소시키고 보-기둥효과를 적용하기 위한 종방향 부재의 해석 기법은 다음과 같다.

∙ 세그먼트와 박스의 연결부에 종방향으로 설치가 가능한 부재의 단면 강성과 작용력을 고려하여 부재 처짐을 산정한다.
∙ 발생 최대 처짐과 작용력을 이용하여 스프링 상수 계산한다(스프링 상수 = 작용력/최대처짐).
∙ 횡단면 모델의 연결부에 강성스프링의 경계조건을 고려하여 구조해석을 수행하고 단면을 검토한다(3차원 거동을 고려한 2차원 해석기법 적용).

3. 부분 강재-콘크리트 세그먼트 구조 안전성 검토 및 보강 상세

3.1 구조해석

세그먼트부와 박스부는 Frame으로 모델링 하였으며, 연결부는 Plate와 Solid 모델을 사용하여 작용 외력에 의한 강재에 작용하는 응력을 검토할 수 있도록 하였다. Fig. 5에 해석모델 및 경계조건을 나타내었다. 해석모델에 작용하는 하중 및 하중조합은 2.3 작용 하중과 동일하게 적용하였다.

Fig. 5.

Analysis model and boundary condition

3.2 해석결과 및 단면 검토

3.2.1 해석결과 및 콘크리트 단면 검토

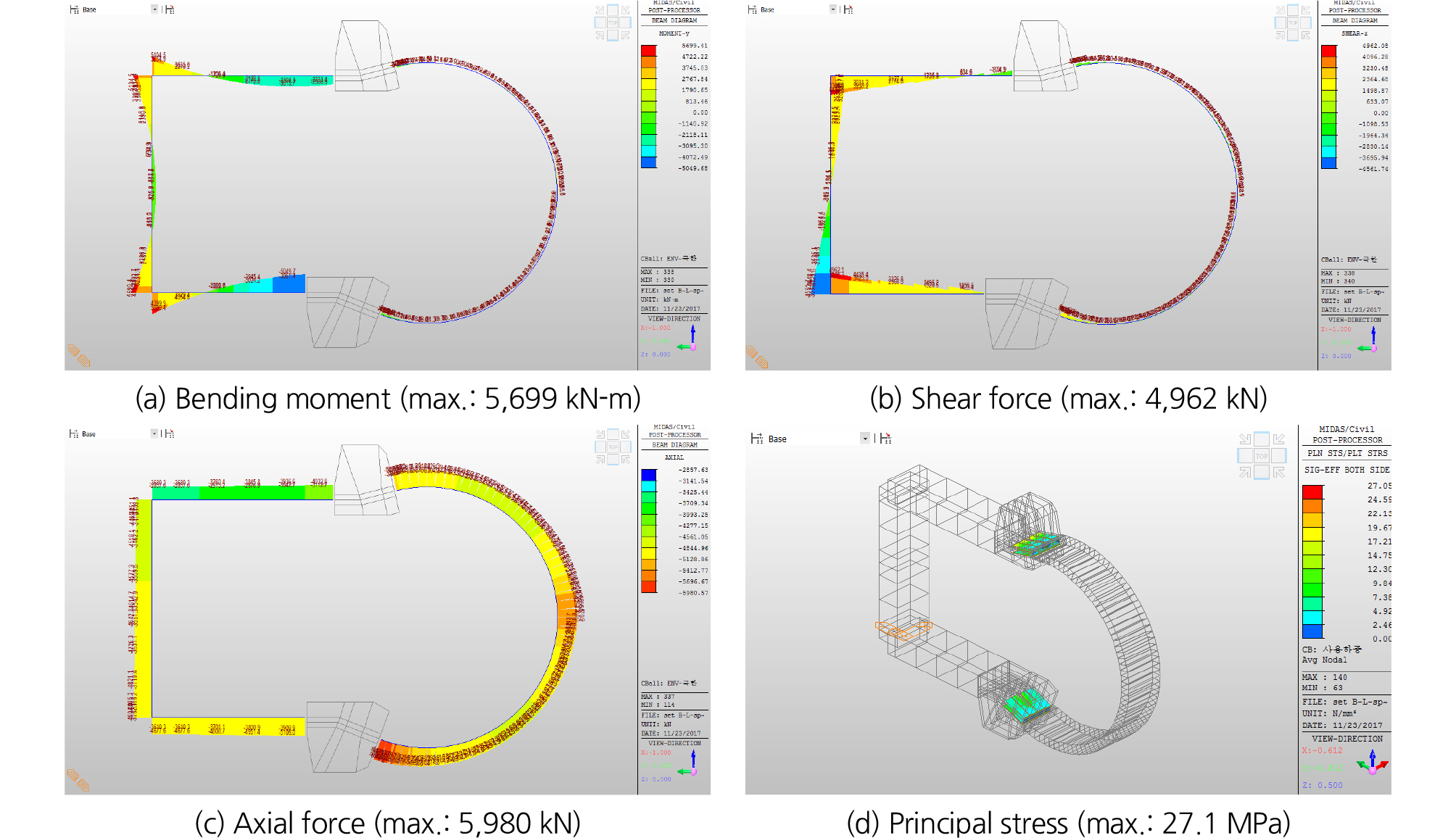
종방향 부재의 강성을 연결부의 스프링지점으로 반영한 해석모델의 구조해석결과 콘크리트부(박스부, 세그먼트 라이닝부)에서의 최대모멘트는 5,699 kN-m, 최대전단력은 4,962 kN, 최대축력은 5,980 kN으로 분석되었다(하중조합: CO2). 접합부 강재의 최대발생응력은 사용하중조합인 CO-S에서 27.1 MPa로 허용응력 140 MPa 이내로 확인되었다(Fig. 6). 박스부(확폭부)의 단면 검토 결과는 Table 7과 같다.

Fig. 6.

Results of partial steel-concrete joint model

Table 7. Section review of box section (enlargement)

3.2.2 부분 강재-콘크리트 접합부 상세

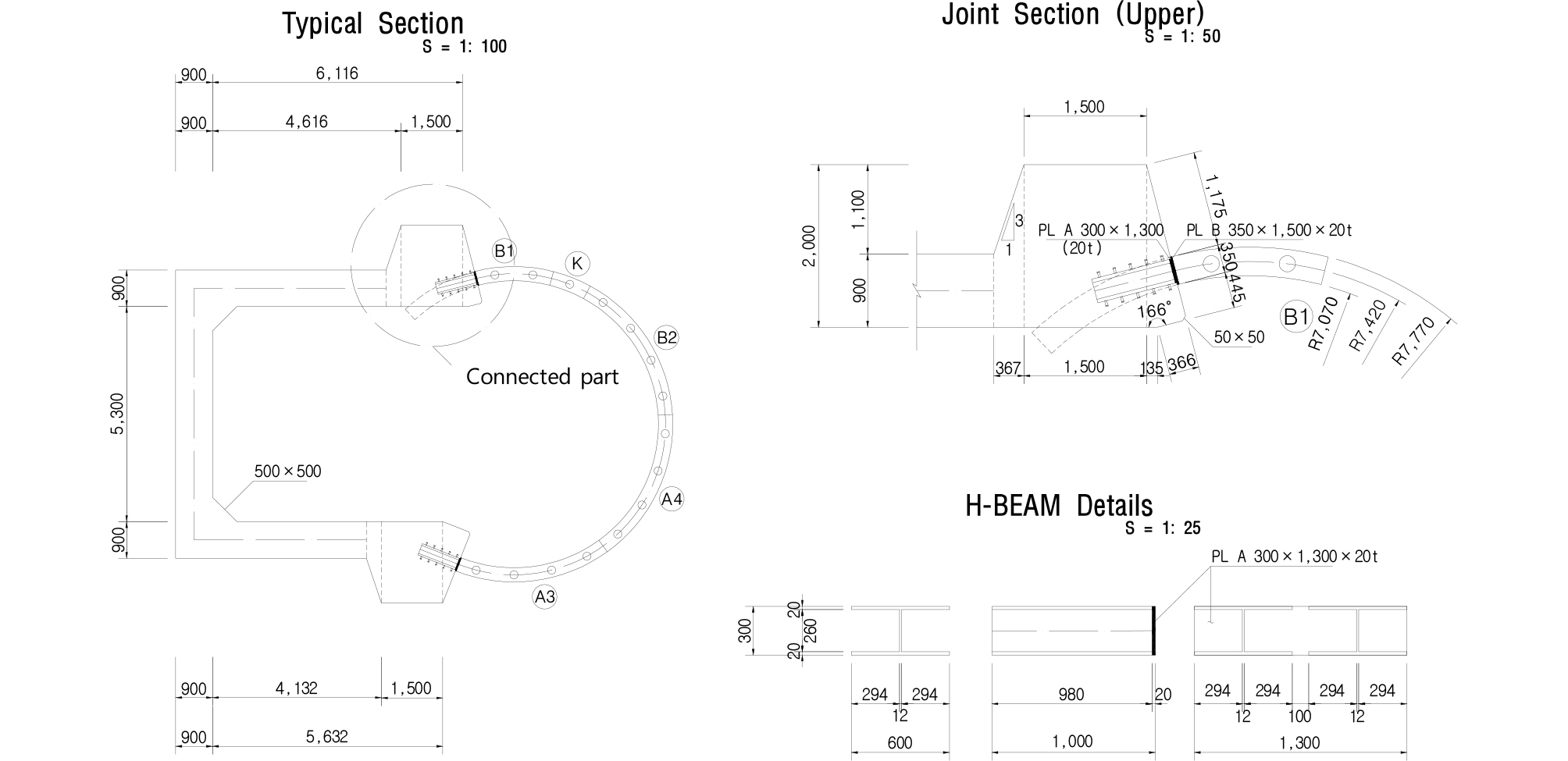
본 연구에서 제안한 부분 강재-콘크리트 접합부 상세를 Fig. 7에 나타내었다. 쉴드 터널라이닝과 박스확폭부의 연결부는 H-BEAM으로 연결하였으며, 확폭부 시종점부의 기둥과의 보-기둥 효과를 고려하고 접합부 및 박스부의 휨모멘트를 감소시키기 위해 연결부에 종방향부재(폭 1.5 m, 높이 2.0 m, 길이 20.0 m)를 설치하였다.

Fig. 7.

Details of partial steel-concrete joints

4. 결 론

쉴드 터널 분기부의 세그먼트라이닝과 박스부(확폭부) 접합부의 안전성 검토 및 보강 상세 제안을 위해 종방향 부재를 고려한 구조해석을 통해 단면의 안정성을 검토한 결과 다음과 같은 결론을 얻을 수 있었다.

1. 전단면 강재세그먼트 대신 휨모멘트가 크게 발생하는 쉴드 터널과 분기부 접합 부분에 국한적으로 강재세그먼트를 적용하는 부분 강재-콘크리트 세그먼트의 구조 특성을 분석하고 구조안전성을 확보하는 구조 상세를 제안하였다.

2. 쉴드 터널 분기부 확폭 구간의 해석은 3차원 거동효과를 반영하기 위해 확폭부 시 ‧ 종점부의 기둥 효과와 확폭 구간 종방향 부재의 보 효과를 고려할 수 있는 2차원 해석 기법을 제안하였으며 확폭 구간구간의 종방향 부재의 강성을 횡방향 모델에서 연결부의 탄성스프링 지점으로 고려하여 종방향 부재의 강성(보 효과)과 시종점부의 기둥효과를 반영하였다.

3. 종방향부재의 강성을 스프링 지점으로 적용한 2차원 해석 모델의 해석 결과 일정값 이상의 강성을 갖는 종방향 부재를 도입하면 접합부와 박스부의 휨모멘트를 저감시킴으로써 부분 강재-콘크리트 세그먼트의 구조 안전성을 확보할 수 있는 것으로 검토되었다.