1. 서 론
국제표준화기구(International Organization for Standardization, ISO)에서는 신뢰성을 기반으로 한 설계(General Principles on Reliability for Structures)를 국제 표준(ISO 2394)으로 채택하고 있고, 토목분야 설계에 있어서 신뢰성 이론을 기반으로 한 설계가 보편화되는 추세이다. 이러한 추세는 설계변수에서 나타나는 불확실성을 설계에 고려함으로써 보다 합리적이고 정량적이며 안정성 및 경제성 부분에서 최적화된 기준을 수립하기 위한 것이라 할 수 있다. 신뢰성 기반의 설계를 위해서는 우선 설계변수의 불확실성을 대상 구조물에 적용 가능한 확률분포로 생성한 후, 몬테카를로 시뮬레이션(Monte Carlo Simulation, MCS) 기법을 이용하여 해석과정에 반영하거나 설계변수의 변동계수(Coefficient of Variation, COV) 결정을 통해 해석과정에 반영한다. 이때 설계변수가 구조물의 안정성과 경제성에 미치는 영향은 크다. 설계변수의 불확실성은 결국 설계의 신뢰성을 좌우하며 과대 또는 과소설계의 주요 원인으로 작용하므로 합리적인 구조물 설계를 위해서는 설계변수의 불확실성을 최소화한 특성 값 결정이 중요하다.
지반공학 분야에서 신뢰성 기반의 설계를 위해서는 지반정수의 변동성을 합리적으로 결정하는 것이 중요하다. 따라서 지반정수의 변동성과 관련한 국외에서는 Lumb (1974), Asoake and A-Grivas (1982), Baecher (1982), Lacasse and Nadim (1996), Phoon and Kulhawy (1999), Duncan (2000), Baecher and Christian (2003) 등에 의해 수행되었고, 국내에서는 Yoon et al. (2008), Kim et al. (2008), Kim et al. (2009a), Kim et al. (2009b), Kim et al. (2010))에 의해 연구가 활발히 수행되고 있다. 이러한 연구들은 대부분 실내 및 현장시험에 의해 나온 지반정수들을 통계적인 방법을 이용하여 변동성을 평가하고 있다.
쉴드 터널의 경우 단순히 지반정수의 변동성만 결정한다고 신뢰성 기반의 설계가 가능한 것이 아니다. 일반적으로 쉴드 터널의 설계는 작용하는 하중에 의한 응력 및 변형을 구하고 부재단면의 안전성을 검토하여 적합한 단면을 결정하게 된다. 이때 설계변수는 지반정수가 아닌 작용하는 하중이 되기 때문에 이에 대해 현장실험을 통해 변동성을 구해야 하나 쉴드 터널에 실제 작용하는 하중을 실험에 의해 구하기는 현실적으로 불가능하며 안전성에 가장 크게 영향을 미치는 토압을 정확히 계산하기 쉽지않다. 또한 쉴드 터널은 교량 구조물과 달리 비선형 경계 조건으로 인해 구조물에 외력이 동시에 작용할 때 그것이 미치는 영향(예, 휨모멘트. 전단력, 축력 등)이 모두 개개의 외력에 의한 영향의 총합과 같고 하중의 순서에도 관계없는 중첩의 원리가 성립하지 않기 때문에 작용하는 하중에 대한 변동성을 결정하는 것이 필요하다. 따라서 본 논문에서는 쉴드 터널의 신뢰성 기반의 설계를 하는데 필요한 설계변수 중에서 구조물의 안전성에 가장 큰 영향을 미치는 하중인 토압에 대한 변동계수를 제시하였고 이를 바탕으로 터널 구조물의 전체 작용하중의 변동계수를 제시하였다.
2. 설계에 사용되는 하중
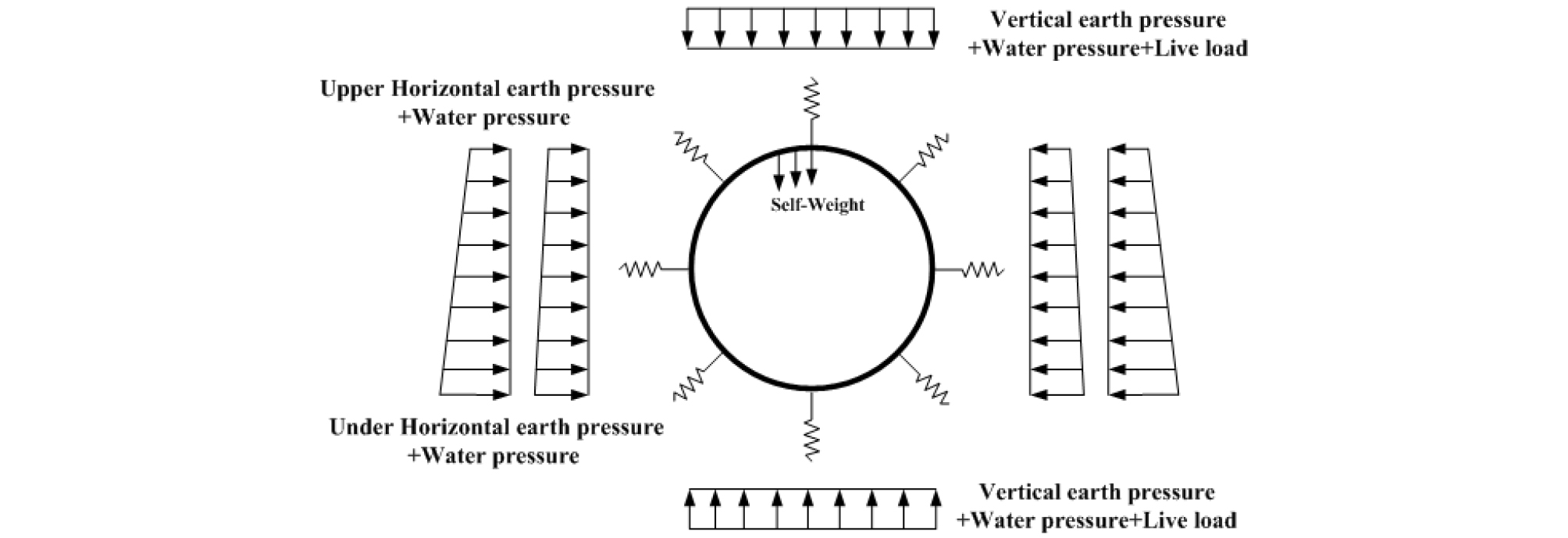
쉴드 터널 세그먼트에 작용하는 하중은 Fig. 1에서와 같이 크게 토압, 수압, 상재하중, 자중, 내부하중, 지진하중, 지반반력, 특수하중 등으로 구분할 수 있으며 이러한 작용하중에서 비교적 규모가 큰 하중은 토압과 수압으로 볼 수 있다(Korean Tunnelling and Underground Space Association, 2008). 이 중에서 수압의 경우 작용방향이 구조체의 도심축(원의 중심)을 향하여 작용하므로 원형 형상의 세그먼트를 고려할 때 대부분이 축력의 형태로 전환되므로 하중의 크기에 비하여 세그먼트의 안정성에 미치는 영향은 비교적 작다고 할 수 있다(Chun et al., 2014). 따라서 세그먼트 안정성에 가장 큰 영향을 미치는 하중은 토압으로 평가할 수 있으므로 이에 대한 변동성을 결정하는 것은 신뢰성 기반 설계에서 가장 중요한 요소이다.
쉴드 터널이 주로 통과하는 암반층의 경우 토압의 형태가 이완하중으로 작용하게 되는데 본 연구에서는 토압에 대한 변동계수를 산정하기 위한 방법으로 Terzaghi (1946) 이론식을 사용하였다. Terzaghi (1946)는 터널이 굴착되면 굴착면의 상부에 하부로 이동하는 활동면이 형성되고 이 활동면을 따라 상향의 저항력이 발생한다고 고려하였다. 따라서 활동면의 저항력으로 지지할 수 없는 부분을 이완범위로 보고 이를 하중으로 정의하였다. 또한 실험을 통해 터널의 폭(B)에 상당한 높이에 걸쳐서 측압계수가 점차 증가하며 일정높이(2.5B) 이상에서는 하부의 변위가 응력 상태에 영향을 미치지 않음을 확인하여 식 (1)을 제안하였다(Chun et al., 2014). 식 (1)은 점착력 특성을 반영한 식이다.
| $$P_\nu=\frac{\gamma B-2c}{2K{\tan}\phi}(1-e^{-K{\tan}\phi\frac{2H}B})$$ | (1) |
여기서, , 는 이완하중, 는 이완영역, 는 토피고, 는 지반단위중량, 는 내부마찰각, 는 측압계수, 은 터널의 높이, 는 터널의 폭, 는 점착력이다.
3. 이완하중의 통계적 특성치 제시
Terzaghi (1946) 이론식에 관계되는 변수는 토피고, 이완영역의 폭, 측압계수, 터널의 높이, 터널의 폭, 단위중량, 내부마찰각, 점착력이 있는데 이중에서 지반과 관련된 단위중량, 내부마찰각, 점착력을 확률변수로 결정하였다.
본 연구에서 사용된 확률변수에 대한 통계적 특성치는 국내 도심지 구간에 해당하는 45개 현장의 지반 조사 자료를 분석하여 풍화토 및 풍화암에 대한 평균, 표준편차, 변동계수를 산정하였다. 이때 풍화토는 N치에 의해 N ≦ 15, 15 < N ≦ 30, N > 30의 경우로 구분하여 산정하였다. 확률변수에 대한 통계적 특성치는 Table 1에서 보여준다.
Table 1. Soil material probability variables
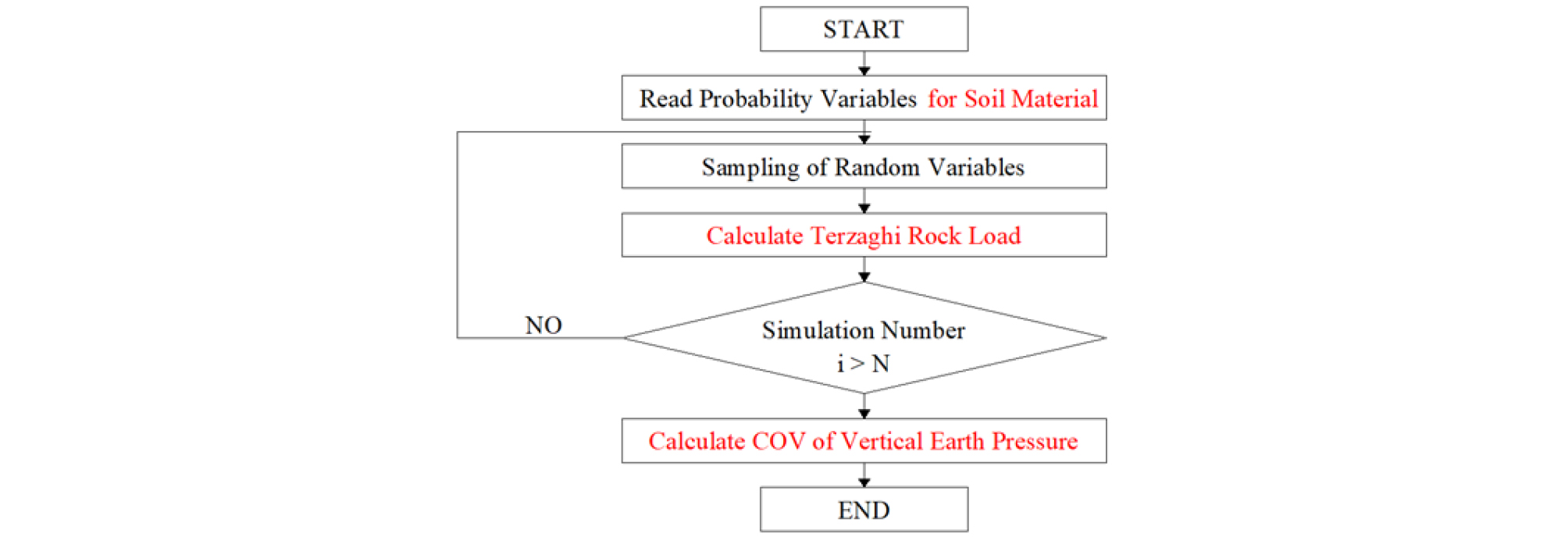
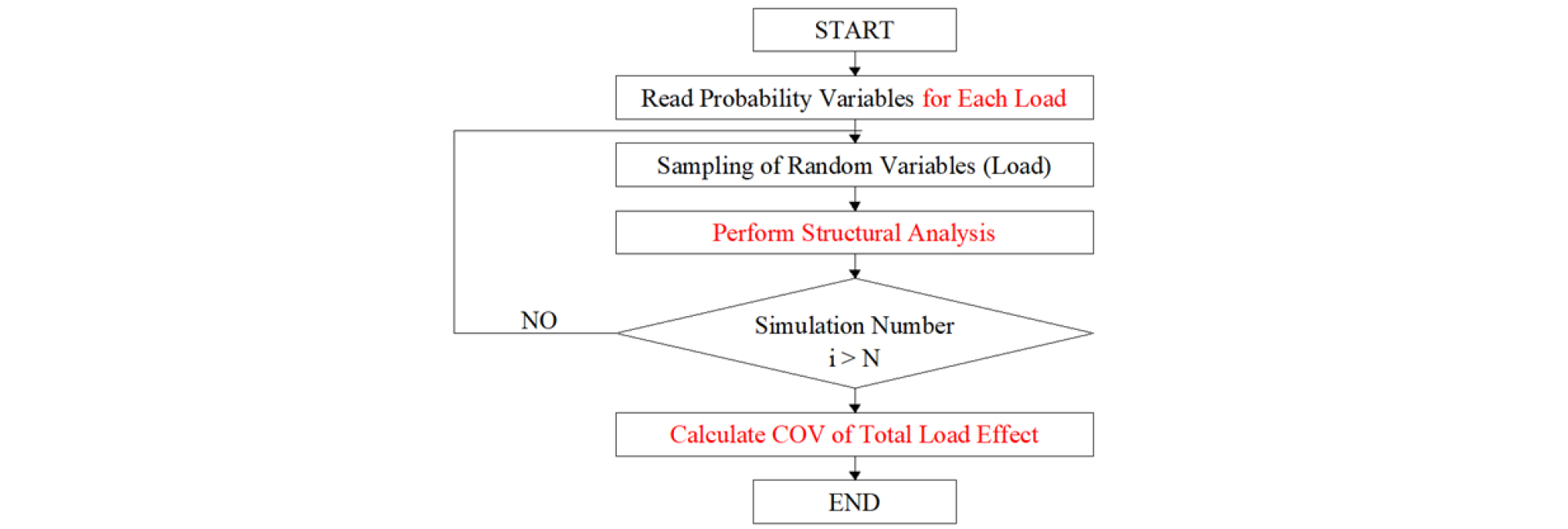
설계 변수인 이완하중에 대한 통계적 특성치 결정을 위해서 본 논문에서는 MCS 기법을 활용하였으며 절차는 Fig. 2에서 보여준다.
앞서 결정된 확률변수의 통계적 특성치를 통해 Table 2와 같은 조건에 대한 분석을 실시하여 이완하중의 통계적 특성치를 산정하였다. Table 2에서 Case I, Case II, Case III은 공동구 터널을 고려한 조건이며 Case IV는 지하철터널을 고려한 조건이다.
Table 2. Review cases
| Tunnel diameter (m) | Tunnel depth (m) | |
| Case I | 3.5 | 20.0 |
| Case II | 3.5 | 15.0 |
| Case III | 3.5 | 10.0 |
| Case IV | 7.2 | 20.0 |
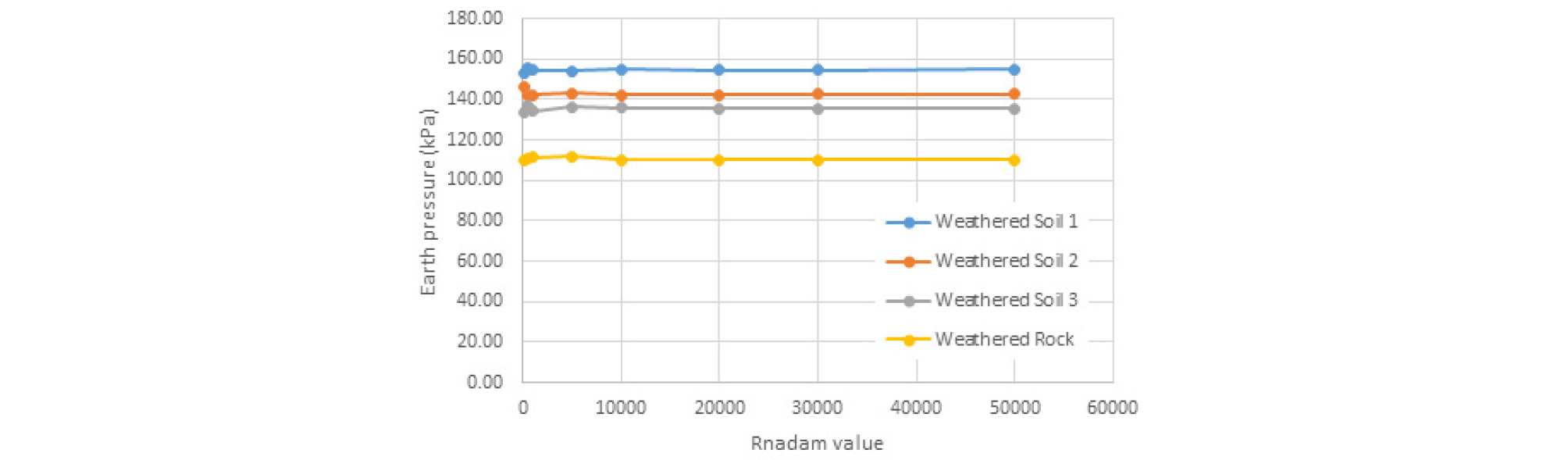
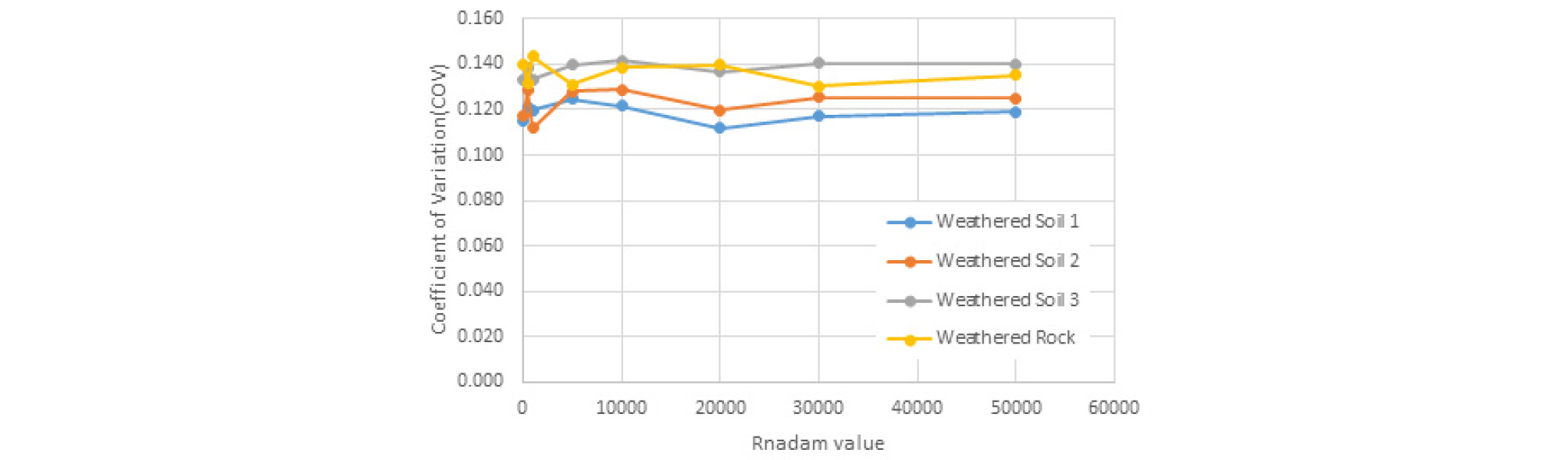
확률변수에 대해 난수들을 반복적으로 추출하여 이완하중을 계산하였고, 이때의 평균과 변동계수를 산정하여 조건별 비교 분석을 실시하였다. 일반적으로 난수의 개수를 많이 발생시킬수록 보다 정확한 값을 얻을 수 있지만 그만큼 시간이 소요되므로 본 연구에서는 적절한 난수의 개수를 결정하기 위한 예비 시뮬레이션을 수행하였다. Case I인 직경 3.5 m, 심도 20 m의 공동구 터널 조건으로 시뮬레이션을 수행한 결과 이완하중 평균값과 변동계수 결과 30,000회 이상 수행되면 수렴하는 것으로 나타났으며 본 논문에서는 50,000회까지 시뮬레이션을 수행하였다. Fig. 3과 4에서 시뮬레이션 결과를 보여준다.
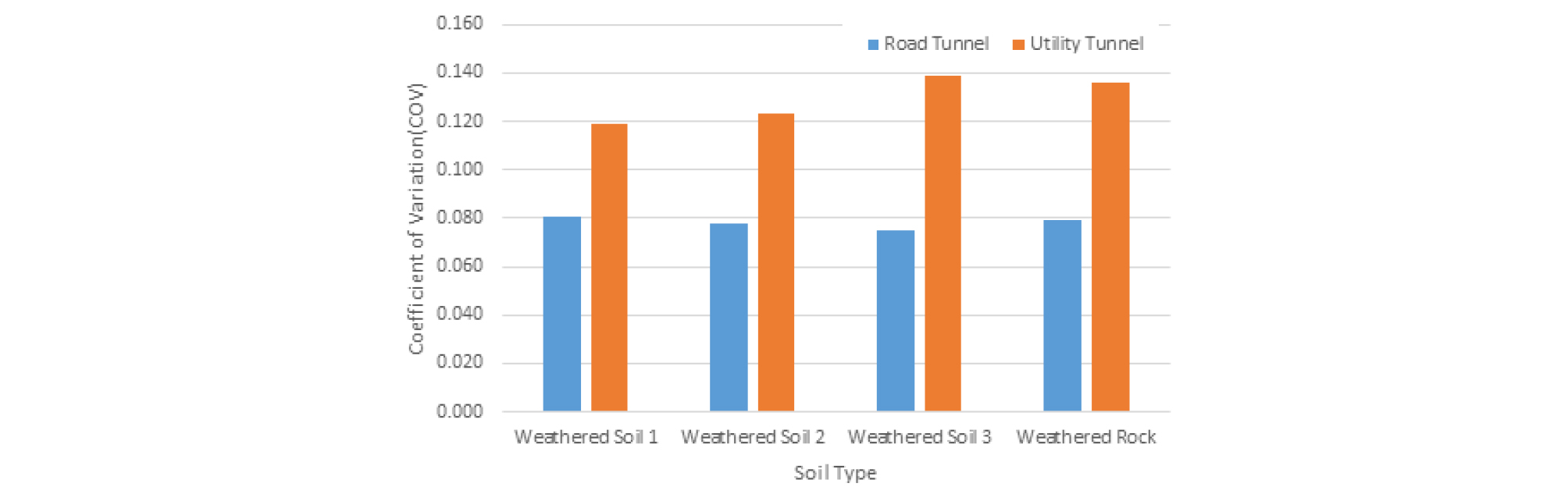
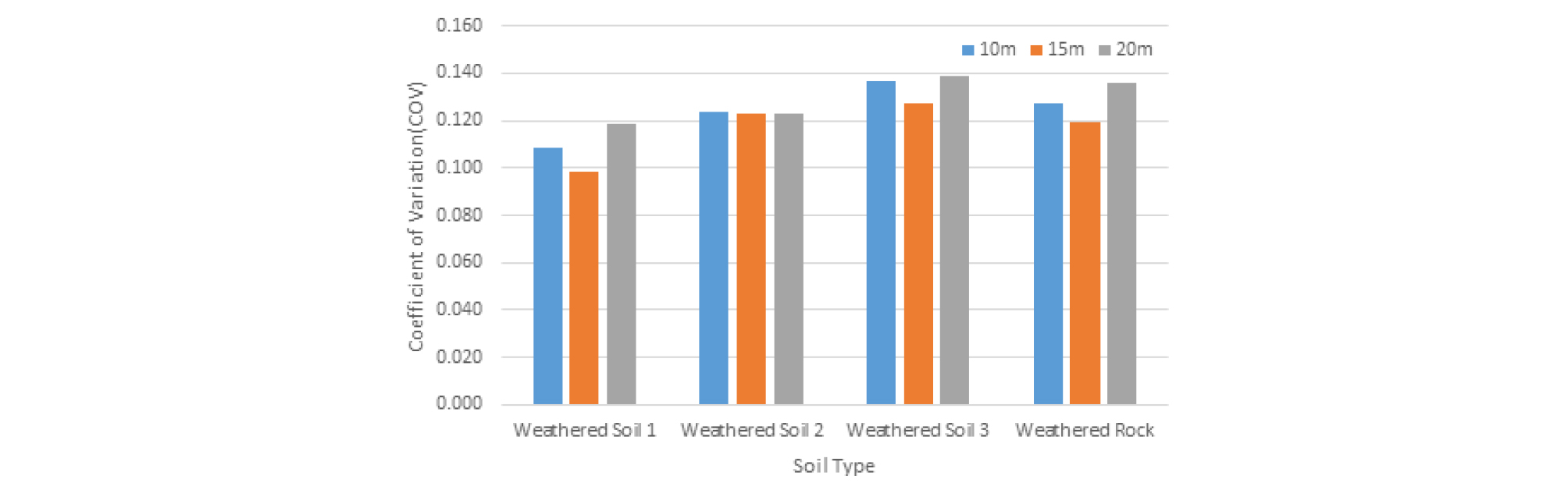
Case I의 조건으로 50,000회의 시뮬레이션을 통해 이완하중의 평균 및 변동계수를 산정하였다. 그 결과 평균은 풍화토 1 (N ≦ 15)은 154.62 kPa, 풍화토 2 (15 < N ≦ 30)은 142.97 kPa, 풍화토 3 (N > 30)은 135.43 kPa, 풍화암은 110.54 kPa로 나타났으며, 변동계수는 풍화토 1 (N ≦ 15)은 0.119%, 풍화토 2 (15 < N ≦ 30)은 0.123%, 풍화토 3 (N > 30)은 0.139%, 풍화암은 0.136%로 나타났다.
Case II의 조건으로 시뮬레이션 결과 이완하중의 평균은 풍화토 1 (N ≦ 15)은 134.28 kPa, 풍화토 2 (15 < N ≦ 30)은 124.36 kPa, 풍화토 3 (N > 30)은 117.74 kPa, 풍화암은 97.72 kPa로 나타났으며, 변동계수는 풍화토 1 (N ≦ 15)은 0.109%, 풍화토 2 (15 < N ≦ 30)은 0.124%, 풍화토 3 (N > 30)은 0.137%, 풍화암은 0.127%로 나타났다.
Case III의 조건으로 시뮬레이션 결과 이완하중의 평균은 풍화토 1 (N ≦ 15)은 104.65 kPa, 풍화토 2 (15 < N ≦ 30)은 97.52 kPa, 풍화토 3 (N > 30)은 91.88 kPa, 풍화암은 78.26 kPa로 나타났으며, 변동계수는 풍화토 1 (N ≦ 15)은 0.982%, 풍화토 2 (15 < N ≦ 30)은 0.123%, 풍화토 3 (N > 30)은 0.128%, 풍화암은 0.119%로 나타났다.
Case IV의 조건으로 시뮬레이션 결과 이완하중의 평균은 풍화토 1 (N ≦ 15)은 238.89 kPa, 풍화토 2 (15 < N ≦ 30)은 232.30 kPa, 풍화토 3 (N > 30)은 229.51 kPa, 풍화암은 215.77 kPa로 나타났으며, 변동계수는 풍화토 1 (N ≦ 15)은 0.08%, 풍화토 2 (15 < N ≦ 30)은 0.078%, 풍화토 3 (N > 30)은 0.075%, 풍화암은 0.08%로 나타났다.
Table 3에서 각 조건별 시뮬레이션 결과를 보여주는데 국내 지반 특성을 고려했을 때 풍화토 및 풍화암에 대한 이완하중의 변동계수는 0.08~0.14의 범위로 나타났다.
Table 3. Calculate results COV by review cases using MCS
각 조건별 비교 분석을 실시하였다. 공동구 터널의 심도에 따른 분석을 위해 Case I, Case II, Case III의 결과를 비교 분석한 결과 Fig. 5에서 나타난 것과 같이 심도가 깊어짐에 따라 변동계수가 증가하는 것으로 나타났다. 공동구 터널(Case I)과 지하철 터널(Case IV)의 비교 분석한 결과는 Fig. 6에서 나타난 것과 같이 터널의 단면 직경이 작을수록 변동계수가 증가하는 것으로 나타났다.
4. 신뢰성 기반의 설계를 위한 총 작용하중의 변동계수 제시
쉴드 터널에서 신뢰성 기반의 설계를 위해서는 서론에서 서술한 바와 같이 세그먼트에 작용하는 하중 각각의 통계적 특성치가 아닌 세그먼트에 작용하는 하중의 총 하중의 통계적 특성치를 산정해야 한다. 이에 본 연구에서는 MCS 기법을 사용하여 총 작용 하중의 통계적 특성치인 변동계수를 산정하였으며 Fig. 7에서 절차를 보여준다. 먼저 각 하중의 통계적 특성치를 결정한 후에 이 값들 사용하여 난수를 추출하고 구조해석을 수행하여 작용하는 하중의 전체 하중을 도출하였다. 그리고 최종적으로 최대 휨 모멘트 결과를 사용하여 변동계수를 산정하였다.
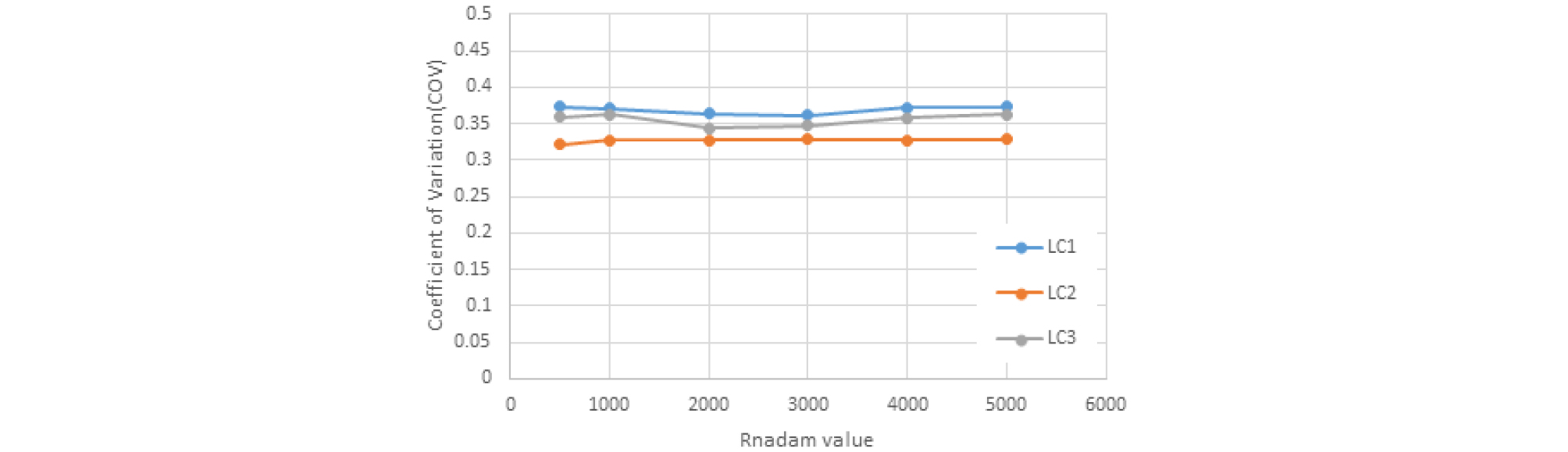
변동계수를 산정하기 위해 세그먼트에 작용하는 하중은 자중, 토압(수평 및 연직), 수압, 활하중으로 선정하고 Table 4에서와 같이 쉴드 터널 설계에 사용되는 하중조합으로 분석하였다. 변동계수를 산정하기 위해 MCS를 위해 난수는 5,000회까지 시뮬레이션을 수행하였으며, 확률분포는 신뢰성 해석 기법간의 비교와 계산의 용이성을 위해 정규분포를 따르는 것으로 고려하였다. Table 5 하중 구성 요소에 대한 변동계수를 나타냈는데 토압을 제외하고는 국외 문헌(Nowak and Collins, 2013)을 참고로 하였다. 토압의 경우 앞서 도출된 변동계수 범위에서 가장 큰 값인 0.14를 적용하여 보수적으로 총 작용 하중의 값을 산정하였다. 변동계수 산정 결과 Table 6과 Fig. 8에서와 같이 LC1 = 0.38, LC2 = 0.33, LC3 = 0.37로 나타났으며, 이 결과는 쉴드 터널의 세그먼트에 대한 신뢰성 기반 설계 시 활용이 가능할 것으로 판단된다.
Table 4. Load combinations
| Load combinations | |
| LC1 | Self weight + Earth pressure |
| LC2 | Self weight + Earth pressure + Hydrostatic pressure |
| LC3 | Self weight + Earth pressure + Hydrostatic pressure + Live load |
Table 5. Statistical parameters of load components
| Statistical Parameters | COV |
| Dead load | 0.10 |
| Hydrostatic pressure | 0.15 |
| Earth pressure | 0.14 |
| Live load | 0.18 |
Table 6. Calculate results COV by load components using MCS
| N | 500 | 1000 | 2000 | 3000 | 4000 | 5000 | COV |
| LC1 | 0.373 | 0.371 | 0.364 | 0.362 | 0.372 | 0.373 | 0.38 |
| LC2 | 0.321 | 0.327 | 0.327 | 0.328 | 0.327 | 0.328 | 0.33 |
| LC3 | 0.359 | 0.363 | 0.344 | 0.347 | 0.358 | 0.363 | 0.37 |
5. 결 론
본 논문에서는 쉴드 터널의 신뢰성 기반의 설계를 하는데 필요한 설계변수들 중에서 구조물의 안전성에 가장 큰 영향을 미치는 하중인 토압에 대한 변동계수를 제시하였고, 이를 바탕으로 터널 구조물의 총 작용하중의 변동계수를 제시하였다. 이를 위해 MCS 기법을 적용하여 설계에 사용되는 이론식을 바탕으로 토압의 변동계수와 세그먼트에 작용하는 전체 하중의 변동계수를 산정하였다. 본 연구에서 얻어진 결론은 다음과 같이 요약된다.
1. 국내 도심지 구간에 해당하는 지반 조사 자료를 분석하여 풍화토 및 풍화암에 대한 평균, 표준편차, 변동계수를 산정할 수 있었으며 이 값들을 Terzaghi (1946) 이론식을 근거로 MCS 기법을 통해 변동계수를 산정할 수 있었다.
2. MCS 기법을 적용하여 이완하중의 변동계수를 산정한 결과, 국내 지반 특성을 고려했을 때 풍화토 및 풍화암에 대한 이완하중의 변동계수는 0.08~0.14의 범위로 나타났다.
3. 공동구 터널의 경우 심도가 깊어짐에 따라 변동계수가 증가하는 것으로 나타났으며 공동구 터널과 지하철 터널의 비교 분석한 결과는 터널의 단면 직경이 작을수록 변동계수가 증가하는 것으로 나타났다.
4. 각 설계 하중의 변동계수를 바탕으로 구조해석을 수행하여 작용하는 총 하중에 대한 변동계수를 산정한 결과, LC1 (자중 + 토압) = 0.38, LC2 (자중 + 토압 + 수압) = 0.33, LC3 (자중 + 토압 + 수압 + 활하중) = 0.37로 나타났으며, 이렇게 제시된 변동계수는 쉴드 터널의 세그먼트에 대한 신뢰성 기반 설계 시 활용이 가능할 것으로 판단된다.