1. 서 론
2. 디스크 커터 교체 유무 예측을 위한 분류기법
2.1 Support Vector Machine, SVM
2.2 k-Nearest Neighbor Algorithm, kNN
2.3 Decision Tree, DT
3. 예측 모델 데이터 구성
3.1 지반 조건
3.2 쉴드 TBM 기계데이터
3.3 예측 모델 구성
4. 분류성능 평가 지표 및 분석비교 결과
4.1 분류성능 평가 지표
4.2 예측 모델 비교 평가
5. 결 론
1. 서 론
최근 국내 도심지에서 터널 시공은 소음과 진동이 적고 주변 지반 손상을 최소화하며 터널 시공 중 높은 안정성을 확보할 수 있는 쉴드 TBM (Tunnel Boring Machine) 공법이 많이 사용되고 있는 추세이다. 쉴드 TBM공법은 기계전면에 디스크 커터를 장착하여 커터헤드를 회전시키고 암석을 파쇄하며 터널을 굴착하는 공법이다. 발파식 공법(NATM)에 비해 공사비가 많이 들지만 보다 정밀하고 인접구조물의 지반 손상을 최소화시키면서 안전사고의 위험이 적다는 장점이 있다.
TBM 공법은 쉴드 TBM 장비의 추력으로 암반을 압쇄 및 절삭하는 과정에서 디스크 커터의 마모가 발생하고, 마모의 형태는 암반의 강도와 디스크 커터의 조건에 따라 다양한 형태로 발생된다. 이러한 디스크 커터의 마모, 비정상적인 파손, 탈락은 굴착하는 과정에서 암반의 압쇄능력이 감소하면서 연쇄적으로 주변 디스크 커터를 훼손하는 결과를 발생시켜 추력 상승, 굴진속도 저하 등 쉴드 TBM 굴진 효율을 현저히 저하시킨다. 또한 현장에서 마모된 디스크 커터의 교체 소요시간은 길고 전체 쉴드 TBM 직접공사비의 10~15%까지 차지하며 공사비 절감 측면에서 디스크 커터의 수명 예측은 매우 중요하다.
디스크 커터 마모율 및 수명 예측 모델은 국내 외 많은 연구자들이 제안하였는데 국외 모델로는 미국 콜로라도 광산대학의 CSM 모델(Rostami and Ozdemir, 1993), 프랑스의 Gehring 모델(1995), 노르웨이 과학기술 대학의 NTNU 모델(Bruland, 2000)이 있다. 국내에서 개발된 KICT-SNU 모델(Yu, 2007)은 선형 절삭시험으로부터 디스크 커터 수명을 예측하는 방법을 제시하였고, Kim et al. (2017)은 양방향 마모를 발생시켜 새로운 디스크 커터 마모도 예측 시험과 이를 통한 마모지수를 새롭게 제시하였다. 지금까지 제안된 디스크 커터 마모 예측 모델들은 균질한 암석을 재료로 마모지수를 산정하였기 때문에 균질한 암반층을 통과하는 쉴드 TBM 공사에서의 디스크 커터 교체 예측에만 적합하다. 그러나 국내에서 시공된 터널공사들은 두 가지 이상의 지층이 혼합되고 지층 변화가 심한 복합지층에서 시공되었다. 실제 한 지하철 현장에 대한 굴진자료 분석 후 기존 예측모델들을 적용하여 비교한 결과, 디스크 커터 소모량을 가장 가깝게 예측한 NTNU 모델조차 실제 총 소모량보다 2배 이상의 마모가 발생한 것으로 보고되었다(Chang et al., 2011).
따라서 본 연구에서는 쉴드 TBM의 굴진 데이터와 지반정보 데이터를 이용해 머신러닝(Machine Learning) 기법들을 적용함으로써 디스크 커터의 교체 유무를 판단하는데 도움이 될 수 있는 모델을 제시하고자 한다. 머신러닝 기법은 인공지능의 한 분야로서 일정 수준의 데이터를 학습하여 습득 된 데이터를 기반으로 새로운 결과를 도출하는 기법으로 복잡하고 불확실성이 많은 요소들을 고려해야하는 예측 모델에 매우 효과적인 도구가 될 수 있다.
본 연구에서는 디스크 커터 교체 유무를 분류하기 위해 머신러닝 분류기법 중 서포트 벡터 머신(Support Vector Machine, SVM), 최근접이웃(k-Nearest Neighbor, kNN) 알고리즘, 의사결정트리(Decision Tree, DT) 알고리즘을 적용하고 분류성능지표를 통하여 알고리즘의 적절성을 비교 판단하였다. 디스크 커터의 교체시기에 관한 기준은 각 현장여건에 따라 다양한 요소를 고려해야하기 때문에 머신러닝 기법을 이용한 디스크 커터 교체 유무 예측 모델 개발은 쉴드 TBM 공사기간 단축과 공사비 절감을 가능케 하여 터널산업 향상에 크게 기여할 수 있을 것으로 기대한다.
2. 디스크 커터 교체 유무 예측을 위한 분류기법
머신러닝(Machine Learning)에서 분류기법(Classification Methods)은 지도학습(Supervised Learning)의 한 기법으로 주어진 입력데이터를 학습하여 결과값에 따라 카테고리를 정하는 방법으로 두개의 클래스로 분류하는 이진분류와 셋 이상의 클래스로 분류하는 다중 분류로 나누어진다. 본 연구에서는 디스크 커터 교체 유무 예측을 위하여 서포트 벡터 머신(Support Vector Machine, SVM), 최근접이웃(k-Nearest Neighbor, kNN) 알고리즘, 의사결정트리(Decision Tree, DT) 알고리즘을 적용하였다.
2.1 Support Vector Machine, SVM
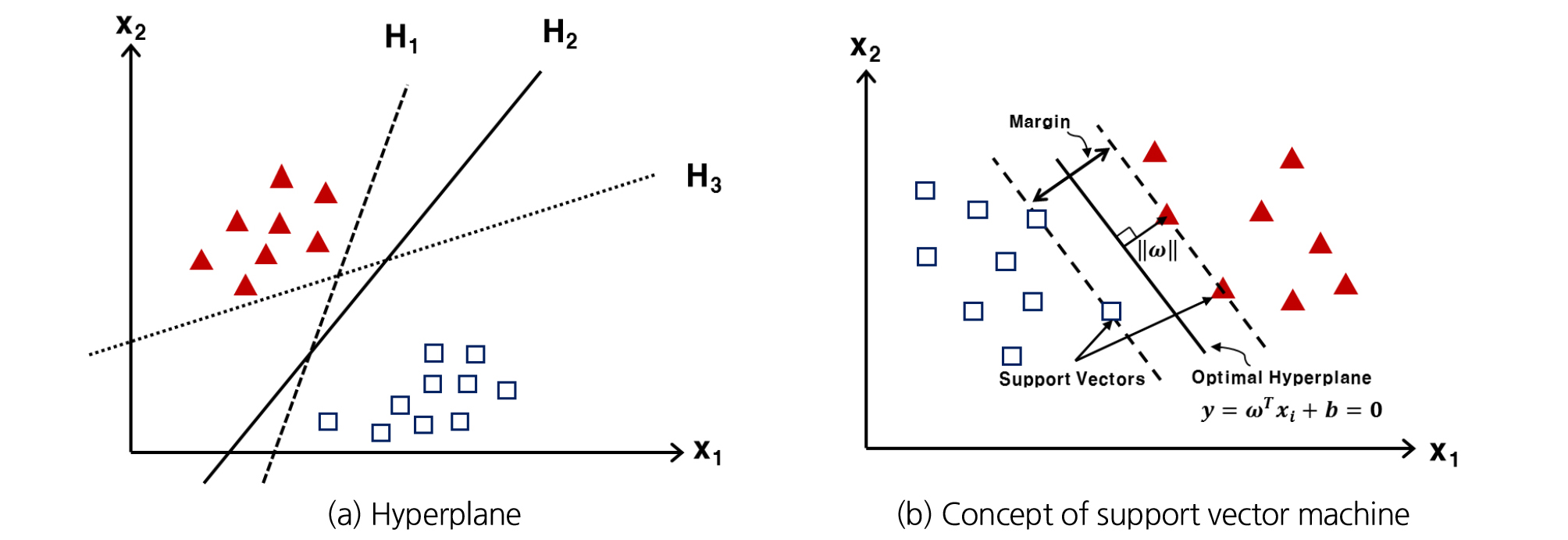
SVM 기법은 Vapnik (1995)에 의해 제안된 학습이론으로 두 개 이상 클래스의 분류 문제를 다루는 기법이다. 데이터 간의 여백(Margin)을 최대화할 수 있는 결정 초평면(Hyperplane)을 찾아 데이터를 최대한 잘 분류하는 것으로 결정 초평면을 직선으로 나눌 수 있으면 선형 SVM 모델, 그렇지 못하면 비선형 SVM 모델로 구분된다. SVM은 선형 또는 비선형 분류뿐 아니라 회귀, 이상치 탐색 등 여러 분야에서 널리 활용되고 있으며, 구조적 위험 최소화(Structural risk minimization)를 기반으로 하고 있기 때문에 일반화의 오류를 감소시키는 점에서 기존의 방법들보다 우수한 성능을 가진다고 알려져 있다(Burges, 1998).
선형적으로 분류가 가능한 SVM에서는 두 개의 범주로 구성된 N개의 객체가 p차원 공간에 위치한다고 가정할 때, p차원 공간에서 두 범주를 구분하는 분리 경계면은 Fig. 1(a)와 같이 무수히 많은 초평면으로 나눌 수 있는데, 최적의 초평면은 Fig. 1(b)와 과 같이 +1 및 -1로 치환된 해석결과를 가장 잘 분류할 수 있는 직선으로 나타낼 수 있으며, 여기서 경계선(Boundary)을 설정하고 경계선의 거리(마진)를 정의하는 변수를 서포트 벡터(Support vector)라 한다.
현재 차원에서 선형 분리가 되지 않는 경우에는 비선형 SVM 문제로 데이터를 고차원의 특성 공간으로 매핑(Mapping) 시킨다. 매핑을 시켜주는 커널함수들은 여러 가지가 존재하고 그 중 대표적으로 다항식(Polynomial)과 방사기저함수(Radial Basis Function, RBF)가 사용된다. 여기서, RBF는 다변량 데이터의 보간을 위해 제안된 근사모델로 차원이 무한한 특성 공간에 매핑하는 방식으로 사용된다.
2.2 k-Nearest Neighbor Algorithm, kNN
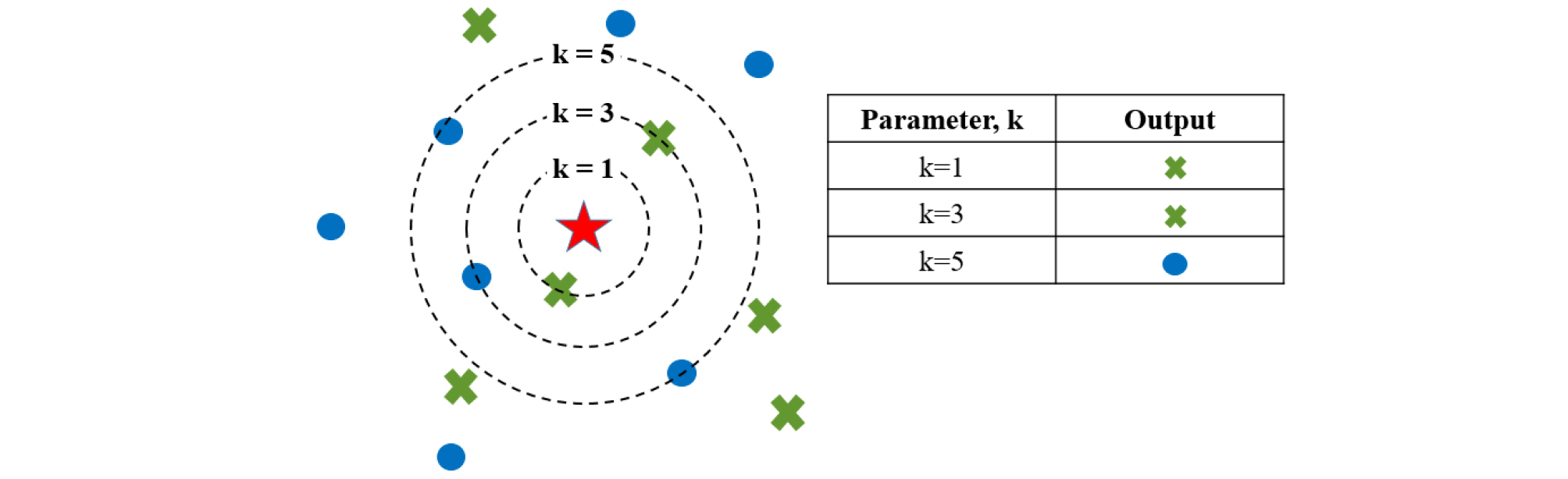
최근접 이웃 알고리즘은 기계학습 분류 기법 중 하나로 Fig. 2와 같이 기존 데이터와 예측하고자 하는 데이터 사이의 거리를 측정하여 가장 유사한 k개의 데이터로 범주를 예측한다. kNN은 간단하고도 직관적인 알고리즘으로 모델을 구성할 때 하이퍼 파라미터인 k 값과 다양한 거리척도를 계산하는 거리척도 함수의 선택이 모델의 정확성을 높여주며 모델의 변형이 용이하기에 많은 분야에서 활용한다. 또한, k 값을 선택할 시, k 값이 너무 작으면 각각의 데이터에 민감하게 반응하여 과대적합(Overfitting)의 위험이 있으며, k 값이 너무 크면 과소적합(Underfitting)의 문제가 발생한다. kNN 알고리즘에서 거리척도로 사용할 수 있는 유클리드(Euclidean), 정규화 유클리드(Standardized Euclidean), 상관관계(Correlation) 방정식을 다음과 같이 식 (1), (2), (3)에 제시하였다. 이 외에도 체비쇼프(Chebychev), 도시블록(Manhattan), 코사인(Cosine)거리 측정 등 여러가지 방정식이 존재하며 kNN 알고리즘에 적용하는 다양한 거리측정법은 Abu Alfeilat et al. (2019)에 제시되어있다.
| $$ED(x,y)=\sqrt{\sum_{i=1}^n\vert x_i-y_i\vert^2}$$ | (1) |
| $$SED(x,y)=\sqrt{\sum_{i=1}^n\vert x_i-y_i\vert^2/V(x_i)}$$ | (2) |
2.3 Decision Tree, DT
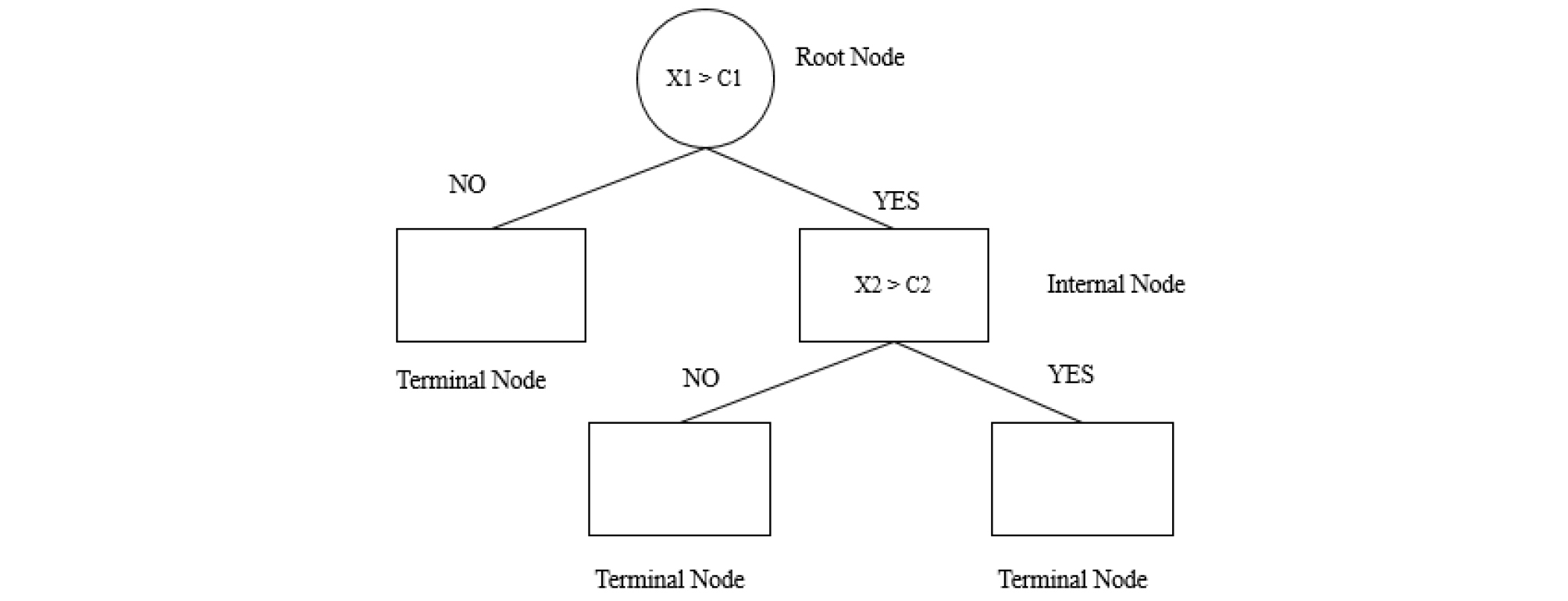
의사결정트리 학습법은 Fig. 3과 같이 데이터를 나무구조로 도표화하여 어떤 문제에 대한 관측값과 목표값을 연결해주는 예측모델로써 Breiman et al. (1984)에 의해 제시되었으며 CART (Classification And Regresstion Trees) 라고 불린다. 이 기법은 데이터 마이닝에서 주로 사용하며 기본적으로 결정트리는 결정에 도달하기 위해서 예/아니오 질문을 이어 나가면서 학습하며 트리가 어떻게 작동하는지에 대한 중요도를 확인 할 수 있다는 장점이 있다.
앙상블은 여러 머신러닝 모델을 연결하여 더 강력한 모델을 만드는 기법으로 랜덤 포레스트(Random Forest)와 그레이디언트 부스팅(Gradient Boosting) 두 앙상블 모델이 분류와 회귀 문제에 효과적이라고 입증이 되었으며 이 두 모델 모두 기본 요소로 결정트리를 사용한다.
3. 예측 모델 데이터 구성
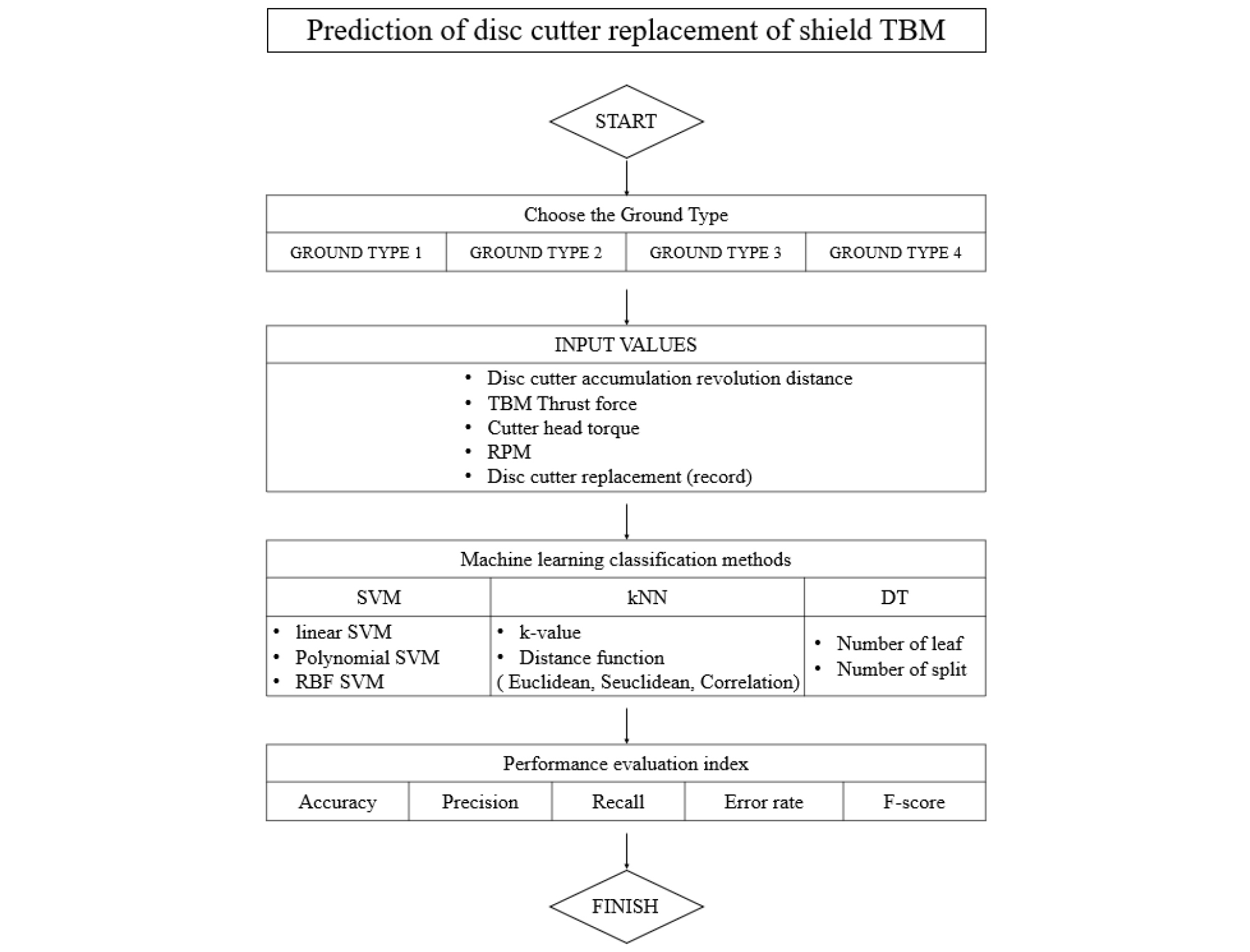
본 연구에서 쉴드 TBM 디스크커터 교체 유무를 판단하기 위해 국내 00~00 고속철도 00-0 공구로 쉴드 TBM 현장 데이터를 수집하였다. 현장의 쉴드 TBM 구간 중 모델 구축에 사용된 데이터는 약 550 m 구간으로 여러 지층이 혼합된 복합지반의 형태가 많아 굴착이 진행됨에 따라 지반을 4가지로 분류하였고, 수집한 쉴드 TBM 기계 데이터 및 디스크 교체 이력 자료를 토대로 예측의 정확성을 높이기 위하여 디스크 커터 마모에 영향을 주는 요인으로 입력변수를 선정하였다. 전처리 작업이 끝난 입력데이터는 MATLAB 프로그램에 분류기법인 SVM, kNN, DT 기법에 학습데이터 및 예측데이터로 사용하여 디스크 커터 교체 유무 예측을 수행하였다. 머신러닝 모델이 학습 후 예측한 결과의 성능을 평가하기 위하여 분류성능평가 지표들을 도입하여 비교 및 분석하였다. 디스크커터 교체 유무를 판단하기 위한 연구의 흐름도를 Fig. 4와 같이 제시하였다.
3.1 지반 조건
본 연구에서 수집된 쉴드 TBM 굴착구간에 대해서 현장시험인 시추조사 10공, 전기비저항탐사 및 종내재하시험으로 지층의 상태를 확인하였고 실내시험인 토질 시험 및 암석 시험을 토대로 암반의 강도를 확인하여 지층의 상태를 확인하였다. 그 결과 모델을 수행하고자 하는 쉴드 TBM 구간은 풍화층과 퇴적층이 혼합되어있고 구간별로 연암과 경암이 출현하는 복합 지층으로 확인되었기에 본 연구에서 지반조건을 Fig. 5와 같이 분류하였다. 터널 노선에 따라 풍화암이 주를 이루는 혼합층(Ground type 1)과 풍화층(Ground type 2), 연암이 주를 이루는 혼합층(Ground type 3)과 퇴적층(Ground type 4)으로 나누었다. 지반 조건에 대한 보다 자세한 내용은 La et al. (2019b)에 기술되어 있다.
3.2 쉴드 TBM 기계데이터
쉴드 TBM 장비는 독일 HERRENKNECHT사에서 제작된 이수가압식 쉴드 TBM 장비로 주요 제원 Table 1과 같으며 복합 지층 대응용으로 제작되었다.
Table 1.
Summary of the slurry TBM specification
| TBM type | Slurry shield TBM |
| TBM outer diameter | 8,410 mm |
| TBM length | 10,500 mm |
| Number of motor | 8 |
| RPM | Max 3.1 |
| Torque | 4,680~6,786 kN ‧ m |
현장 굴진자료에서 쉴드 TBM 기계데이터 중 총 추력, 토크, 회전속도를 예측모델의 입력변수로 설정하였으며 각 디스크 커터별 누적전주거리도 디스크 커터 교체 유무 예측 모델에서 입력변수로 포함시켰다. 쉴드 TBM의 추력(Thrust force)은 디스크 커터에 작용하는 힘으로 소모량에 직접 영향을 미치며, 일반적으로 암반의 강도가 높을수록 추력의 크기도 커지는데 본 연구에서 적용한 현장은 추력의 크기가 약 15.0~36.5 MN의 범위에 있었으며 지층 변화가 심하고 복합지반으로 추력의 크기가 크고 변화가 심한 것 나타났다. 토크(Torque) 역시 디스크 커터의 상태와 관련성이 높은 인자로 당 현장에서는 약 0.5~4.0 MN ‧ m의 범위로 추력과 마찬가지로 변화 폭이 큰 것으로 나타났다. 커터 헤드의 회전속도 역시 혼합 지층이 많고 지층 변화가 크기 때문에 1.0~2.5 RPM의 낮은 범위에서 운전하여 시공 트러블이 발생하지 않도록 굴착을 진행하였으며, 비교적 일정한 크기로 회전속도를 유지하였음을 알 수 있다. 보다 자세한 기계데이터의 내용은 La et al. (2019a)에 기술되어 있다.
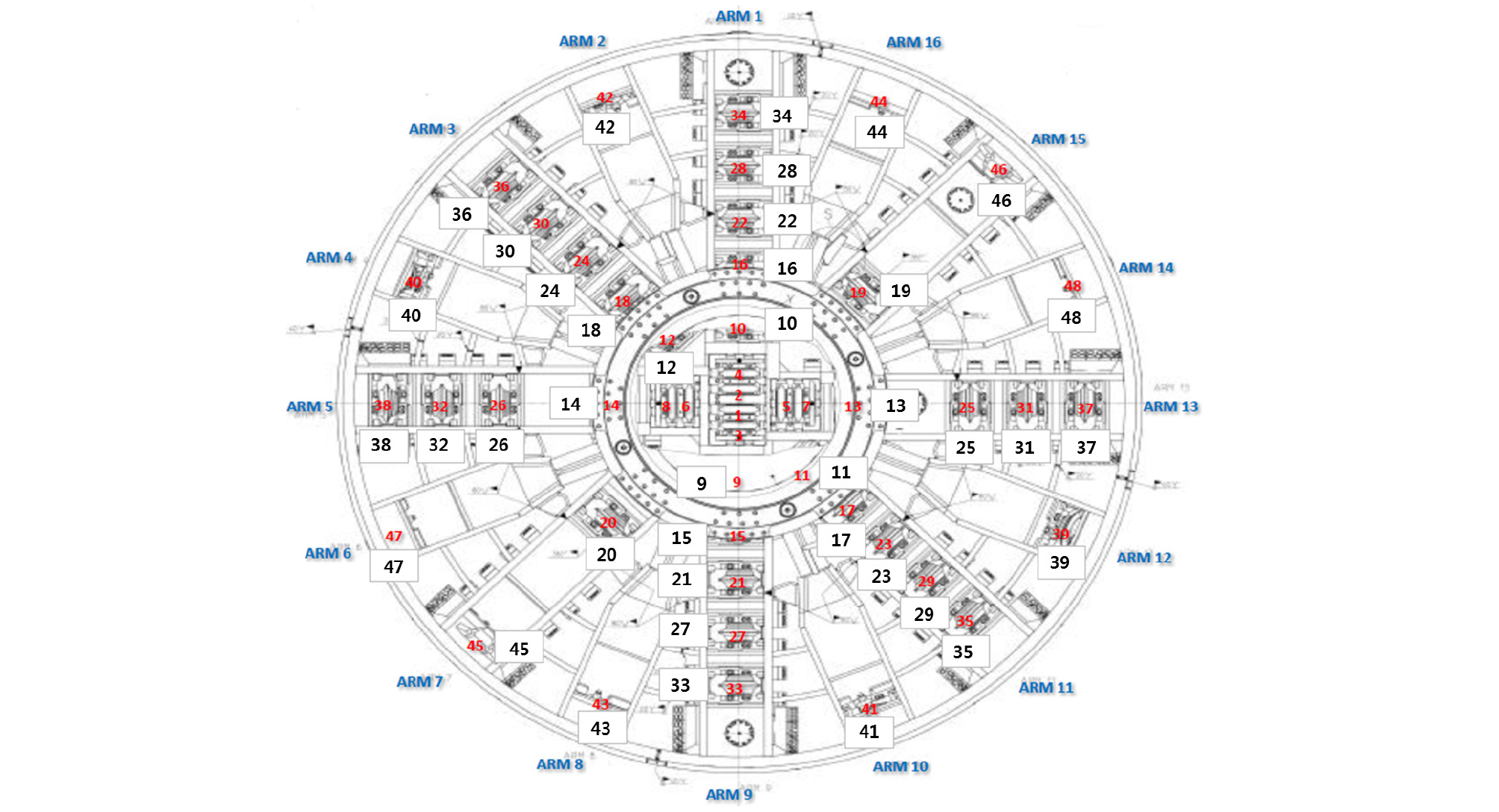
디스크 커터는 Fig. 6과 같이 쉴드 TBM 면판 헤드에 부착되어 있으며 본 기계에 장착된 싱글 디스크 커터는 총 40개로 직경은 17 inch이며 모델의 예측데이터로 사용하였다.
3.3 예측 모델 구성
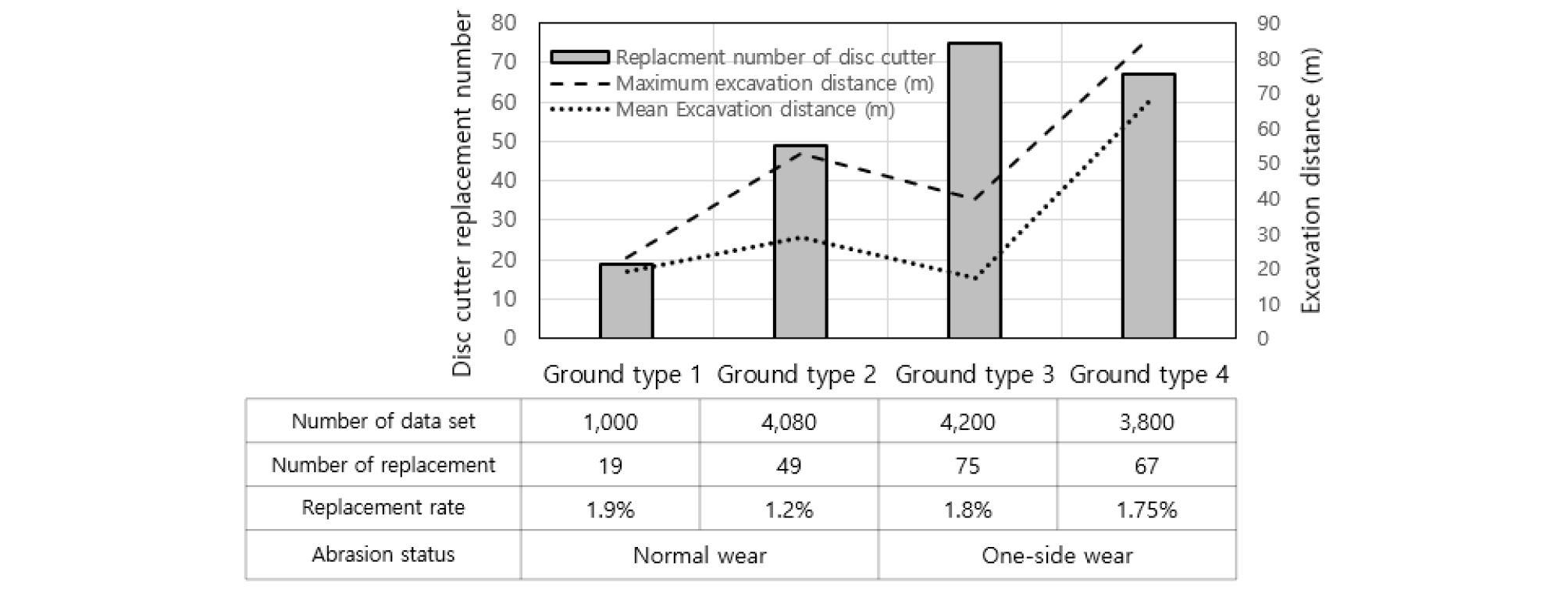
데이터가 수집된 굴착 구간에 대해서 Table 2와 같이 지반을 분류하였고 지반 조건 별로 디스크 커터의 교체 개수와 최대, 평균굴착 거리를 Fig. 7에 제시하였다. 현장에서 교체된 디스크 커터의 개수는 풍화암이 많은 혼합층(Ground type 1), 풍화암층(Ground type 2), 연암이 주된 혼합층(Ground type 3), 퇴적층(Ground type 4)에서 각각 19개, 49개, 75개, 67개이다. 이는 각 지반조건별 전체 데이터 세트에서 교체한 디스크 커터의 교체비율이 1.9%, 1.2%, 1.8%, 1.75%로 현저히 낮아 분류기법으로 모델을 예측하기에는 신뢰도가 매우 낮다고 판단하였기에 디스크 커터 교체 기준을 마모율 70%로 임의 설정하여 데이터 세트의 교체 수를 증가시켜 모델을 수행하였다. 디스크 커터의 교체에 관한 기준을 보면 디스크 커터의 마모율 및 교환 위치는 지반조건, 쉴드 TBM 형식이나 회전 거리 등 다양한 요소 및 현장여건에 따라 교체 시기가 달라지기 때문에 위와 같은 임의 설정은 문제가 없다고 판단하였다.
Table 2.
Specifications of ground condition in different ground types
Table 3은 본 연구에서 선정한 분류기법인 SVM, kNN, DT를 보여주며 기법들의 정확도를 높이기 위한 알고리즘 내 하이퍼파라미터 변수 및 함수들을 보여준다. 한 분류기법에서도 최적의 분류성능을 얻기 위하여 다양한 모델들을 구축하여 예측을 시도하였다. 현장에서 수집한 데이터 세트는 랜덤으로 추출한 80%의 데이터 세트만 학습에 사용하고 나머지 20%는 예측데이터로 사용하였다.
4. 분류성능 평가 지표 및 분석비교 결과
본 연구에서 3가지 분류기법(SVM, kNN, DT)을 사용하여 디스크 커터 교체 유무 예측 모델을 수행하고 실제 현장에서의 커터 교체 여부와 모델이 학습하여 내놓은 결과를 비교 분석하기 위하여 분류성능평가 지표들을 활용하여 평가하였다. 오차행렬(Confusion Matrix)의 기반으로 평가를 수행할 수 있는 지표인 정확도(Accuracy), 정밀도(Precision), 재현율(Recall), 오분류율(Error rate), f-점수(f-score)를 통하여 모델의 예측 성능을 비교평가하였다.
4.1 분류성능 평가 지표
이진분류기법에서 모델 성능평가를 할 수 있는 오차행렬(Confusion Matrix)은 Table 4에 제시하였으며 이 때, 진실 양성(TP)은 실제 현장과 예측 결과 모두에서 디스크 커터를 교체한 경우, 그리고 거짓 양성(FP)은 실제 현장에서는 교체하지 않았으나 예측에서는 교체한 경우, 거짓 음성(FN)은 실제로 교체하였으나 예측에서는 교체하지 않은 경우, 마지막으로 진실 음성(TN)은 현장과 예측 모두 교체하지 않은 경우를 각각 의미한다. 오차행렬에서 많은 정보를 얻을 수 있지만 매우 수동적이기에 오차행렬분석을 통해 수치로 쉽게 모델을 파악할 수 있는 지표는 정확도(Accuracy), 정밀도(Precision), 재현율(Recall), 오분류율(Error rate), f-점수(f-score)이다.
Table 4.
Confusion matrix of binary classification
| Predicted class | |||
| Replaced | Not replaced | ||
| Actual class | Replaced |
TP (true positive) |
FN (false negative) |
| Not replaced |
FP (false positive) |
TN (true negative) | |
정확도(Accuracy)는 식 (4)와 같이 전체 데이터 중 정확하게 예측이 된 데이터의 비율을 의미하며, 실제로 디스크 커터를 교체 여부를 예측 모델이 정확하게 예측한 경우의 비율을 의미한다.
| $$\mathrm{Accuracy}\;(\%)=\frac{TP+TN}{TP+TN+FP+FN}\times100$$ | (4) |
정밀도(Precision)은 교체했다고 모델이 예측한 경우에서 실제로 디스크 커터의 교체가 일어난 비율을 의미하며 식 (5)와 같다. 정밀도는 양성 예측도(Positive Predictive Value, PPV)라고도 불리며 거짓 양성의 수를 줄이는 것이 목표일 때 성능 지표로 사용한다.
| $$\mathrm{Precision}\;(\%)=\frac{TP}{TP+FP}\times100$$ | (5) |
재현율(Precision)은 실제로 디스크커터가 교체한 데이터 중 예측모델이 교체했다고 판단한 비율을 의미하며 이는 민감도(Sensitivity), 진짜 양성 비율(True Positive Rate, TPR)이라고도 불린다. 식 (6)과 같으며 모든 양성 데이터를 식별 해야하고 거짓 음성(FN)을 원치 않을 경우에 성능지표로 사용한다.
| $$\mathrm{Recall}\;(\%)=\frac{TP}{TP+FN}\times100$$ | (6) |
오분류율은 식 (7)과 같이 실제로 디스크 커터가 교체되지 않았지만 교체된 것으로 잘못 분류한 경우의 비율을 의미한다.
| $$\mathrm{Error\;rate}\;(\%)=\frac{FP}{FP+TN}\times100$$ | (7) |
정밀도와 재현율이 매우 중요한 측정 방법이지만 재현율의 최적화와 정밀도의 최적화는 상충되는 지표이므로 이 둘의 조화평균인 f-score 지표를 사용한다. 일반적인 f-score는 식 (8)과 같으며 β 값에 정밀도나 재현율의 가중치를 둘 수 있다. 즉, 정밀도와 재현율의 가중치를 동일하다고 한다면(β = 1), f1-score라고 표시하고 다음 식 (9)와 같다.
| $$\mathrm{f-score}=\frac{(1+\beta^2)(Precision\times Recall)}{\beta^2\;Precision+Recall}$$ | (8) |
| $$\mathrm{f1-score}=\frac{2\cdot(Precision\times Recall)}{Precision+Recall},\;(\beta=1)$$ | (9) |
4.2 예측 모델 비교 평가
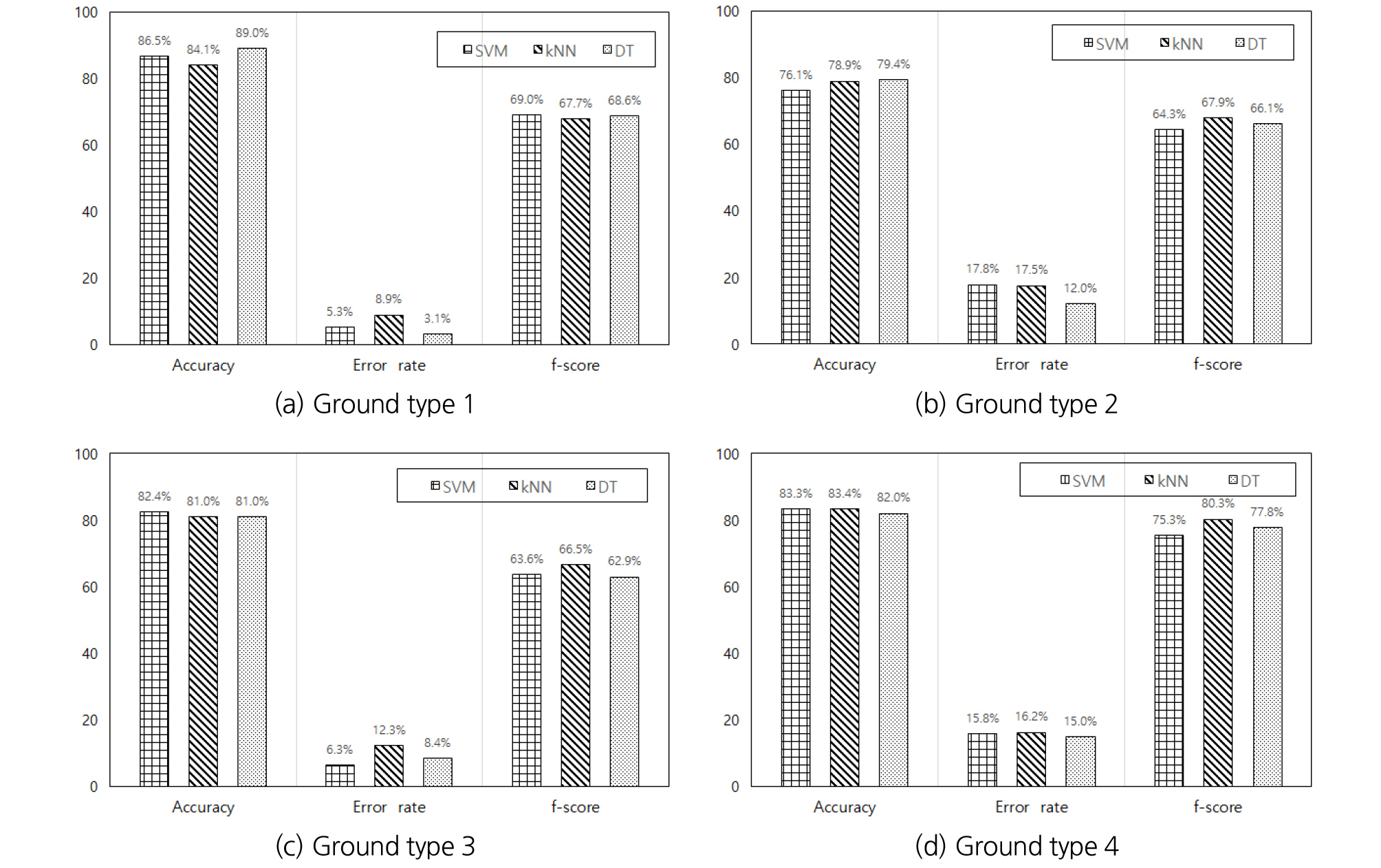
4종류의 지반 조건에 따라 SVM, kNN, DT 기법을 사용하여 디스크 커터 교체 유무에 대한 예측 모델을 수행한 결과 각 기법에서 최적의 분류 성능 평가 지표를 Table 5와 Fig. 8에 나타내었다. Table 5에서는 각 지반조건에 대하여 정확도, 정밀도, 재현율, 오분류율, f-score 5가지의 지표를 나타내었으며, Fig. 8에서는 f-score값이 정밀도와 재현율의 조화평균값이기에 정확도, 오분류율, f-socre 지표만 나타내었다. 지반조건 1로 분류된 풍화암이 많은 혼합층에 대해서는 Fig. 8(a)와 같이 정확도가 89%이며 오분류율이 3.1%로 가장 적고 f-score는 68.6%로 비슷한 값을 보여 최적 예측모델은 의사결정트리모델로 확인하였다. 지반조건 2로 분류된 풍화암 층에 대해서는 Fig. 8(b)와 같이 정확도가 79.4%, 오분류율이 12%, f-score가 66.1%로 지반조건 2의 최적 예측 모델은 의사결정트리모델로 확인하였다. 또한, 연암이 많은 혼합층 지반조건 3에 대해서는 Fig. 8(c)와 같이 정확도 82.4%, 오분류율 6.3%, f-score 63.6%로 SVM 예측 모델을 최적예측모델로 판단하였다. 마지막으로 지반조건 4로 분류된 퇴적층에 대해서는 Fig. 8(d)와 같이 f-score이 80.3%로 가장 높고 정확도 83.4%, 오분류율이 16.2% 결과가 나타난 kNN 예측모델이 최적이라고 판단하였다.
Table 5.
Summary of the performance evaluation index of the prediction model
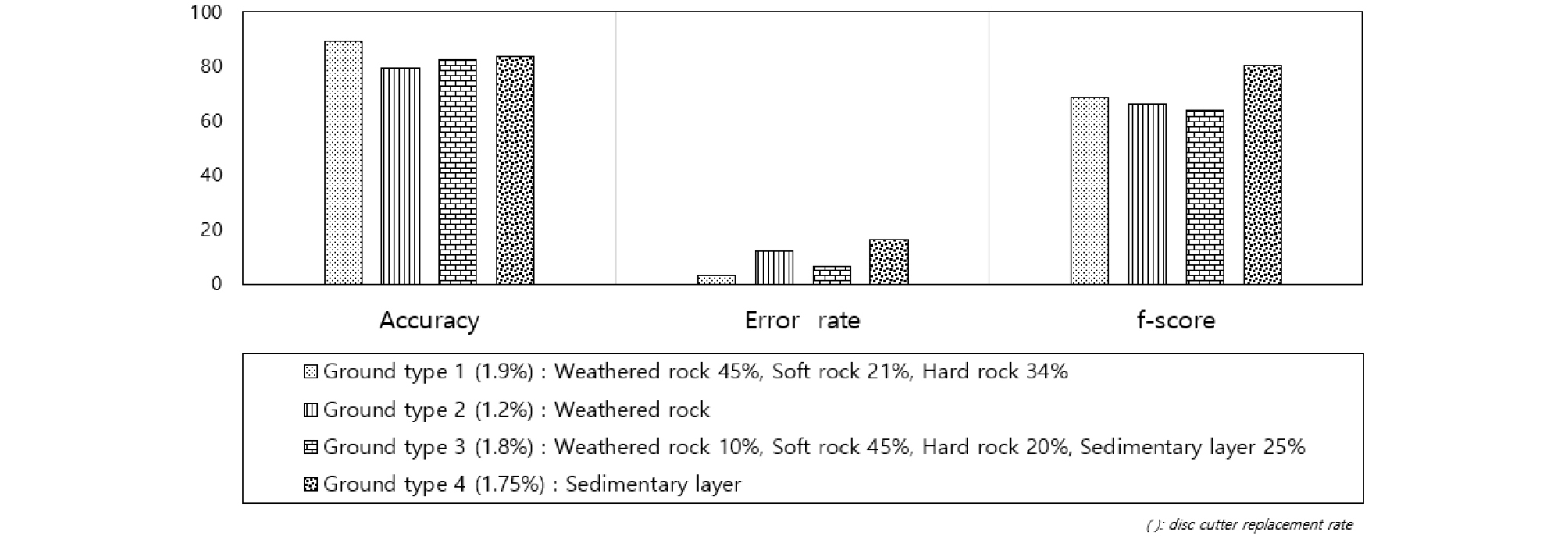
그리고 Fig. 9에 제시한 바와 같이 지반 조건에 따라 비교했을 때 정확도는 Ground type 1, Ground type 4, Ground type 3, Ground type 2 순서로 높았고 오분류율은 Ground type 1, Ground type 3, Ground type 2, Ground type 4의 순서로 낮았으며 f-점수 지표는 Ground type 4, Ground type 1, Ground type 2, Ground type 3 순서로 높은 것을 확인하였다.
5. 결 론
본 연구에서는 쉴드 TBM 터널 디스크 커터의 교체 유무 판단을 위해 머신러닝 분류기법 알고리즘의 적용성을 검토하였으며 예측모델로는 SVM, kNN, DT 알고리즘을 활용하였다. 모델간의 예측 결과 성능을 평가하기 위해서 분류성능평가 지표를 토대로 비교 분석하였고 연구결과를 요약하면 다음과 같다.
1. 디스크 커터 교체 유무 예측 모델을 SVM, kNN, DT 알고리즘을 활용하여 지반조건별로 적용한 결과 지반조건 1과 2에 대해서는 DT 모델을 최적 모델로, 지반조건 3에서는 SVM 모델, 지반조건 4에서는 kNN 모델의 성능이 좋다고 판단하였다. 각 지반조건별로 최고의 예측모델 기법을 판단하였지만 성능평가지표들을 확인하였을 때 각 예측기법에서의 지표들의 차이는 크지 않게 나타났다. 따라서 기법의 중요성보다 모델 구축 시 지반 조건 및 입력데이터와 출력데이터의 상관관계 모델 안의 속성을 어떻게 구성하는지가 더 중요하다고 판단한다.
2. 디스크 커터 유무 판단을 위한 kNN 기법으로 만들어진 예측모델에서 다양한 거리 척도 함수를 사용하였는데 성능의 차이는 많이 나타나지 않았다. 하지만 하이퍼 파라미터 k 값이 커질수록 성능이 전체적으로 낮게 평가되었다. 이는 디스크 커터 교체 여부 판단에 적절하지 않다는 것을 의미하며 이는 실제로 디스크 커터의 교체율이 매우 낮아서라고 판단된다.
3. TBM 디스크 커터 교체 여부를 판단하는데 머신러닝의 분류기법이 이용될 수 있을 것이며, 향후 더 많은 쉴드 TBM 굴진, 지반 데이터와 디스크 커터 교체이력 데이터 등을 축적하여 디스크 커터의 소모량을 머신러닝 알고리즘으로 판단하게 된다면 실무 적용성이 매우 클 것으로 기대한다.