1. 서 론
2. 수치해석
2.1 해석개요 및 경계조건
2.2 적용 구성모델 및 물성치
2.3 수치해석 과정 및 분석
3. 해석결과 분석
3.1 말뚝의 설계지지력 결정
3.2 말뚝의 축력 분포
3.3 말뚝의 전단응력 분포
3.4 터널굴착에 따른 말뚝 두부 침하
3.5 말뚝의 상대변위 분포
3.6 기존연구를 통한 말뚝 비교 분석
4. 요약 및 결론
1. 서 론
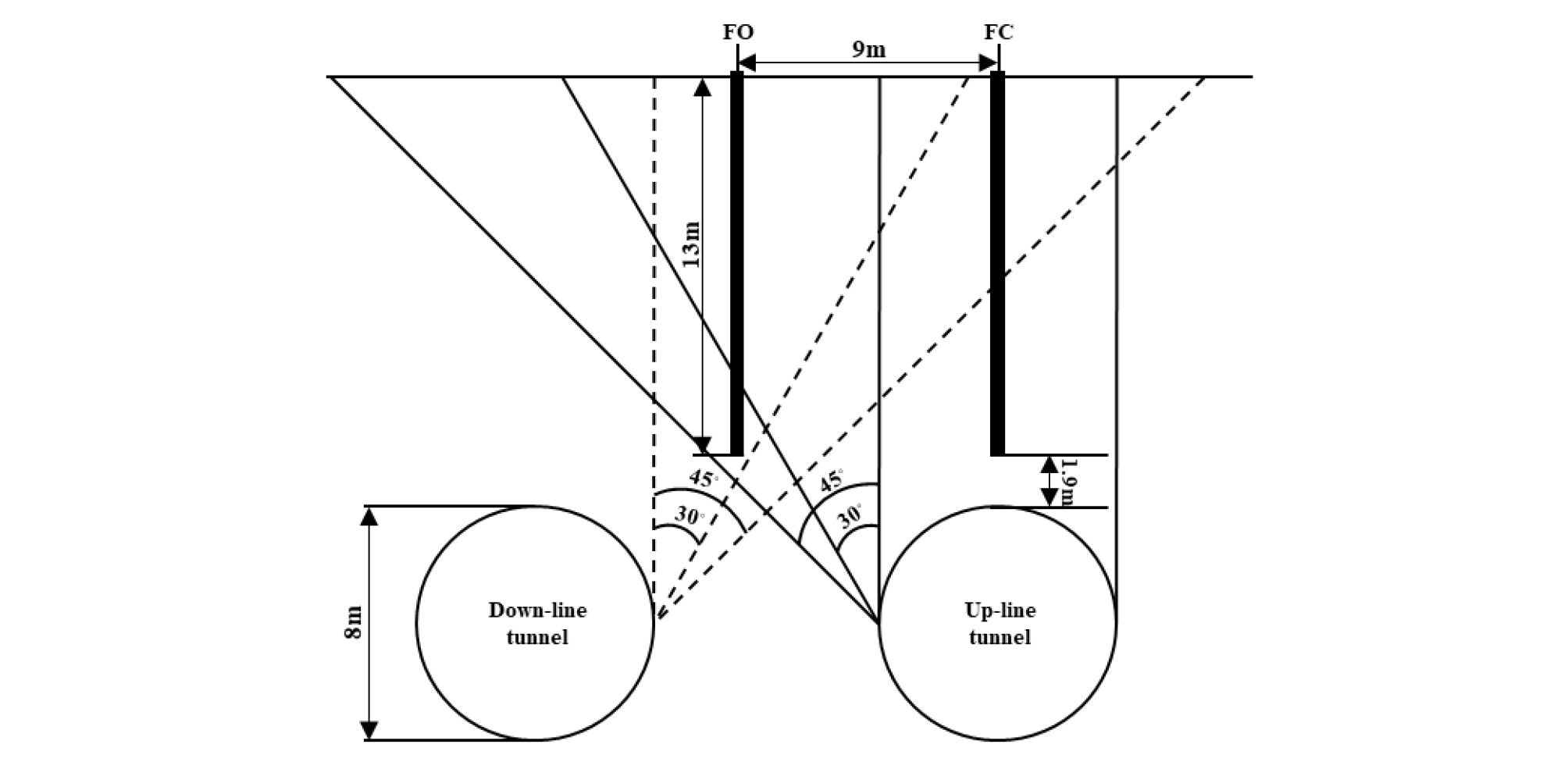
최근 도심지에서 기 존재하는 말뚝 기초에 근접하여 다양한 터널시공이 이루어지고 있으며, 이러한 터널시공은 지반의 침하를 유발하여 말뚝의 공학적 거동에 영향을 미치게 된다(Lee, 2012a). 또한, 현재까지 수행되어온 기 연구성과에 의하면 터널시공은 터널 주변지반의 침하를 필연적으로 발생시키며 이로 인해 터널과 인접한 말뚝에는 변형이 유발되고 축력분포 역시 변하게 되어 말뚝의 사용성에 큰 영향을 받는다고 보고되었다(Lee, 2012a). 이러한 문제를 해결하기 위해 수치해석 연구, 이론적 연구, 실내모형실험 및 원심모형실험 연구와 같은 많은 연구들이 수행되었다(Jacobsz, 2002; Pang, 2006; Cheng et al., 2007; Lee and Chiang, 2007; Lee, 2008; Marshall, 2009; Lee, 2012a; 2012b; 2012c; Ng et al., 2013; Dias and Bezuijen, 2014a; 2014b; Hartono et al., 2014; Liu et al., 2014; Ng and Lu, 2014; Ng et al., 2014; Williamson, 2014; Hong et al., 2015; Lee and Jeon, 2015; Jeon and Lee, 2015; Jeon et al., 2015; Lee et al., 2016; Jeon et al., 2017; Soomro et al., 2018). 이에 비해 현장실측자료 분석을 통한 연구는 상대적으로 제한적인데, Selemetas (2005), Pang (2006), Liu et al. (2014), Mair and Williamson (2014), Williamson (2014) 및 Selemetas and Standing (2017)은 터널굴착으로 인한 인접말뚝의 거동을 현장실측을 통하여 연구한 바 있다. Fig. 1은 Selemetas and Standing (2017)이 보고한 런던점토에서 수행된 EPB 타입 TBM 터널 초근접 시공의 단면도를 보여주고 있으며, 저자들은 터널굴착으로 인한 말뚝의 거동을 현장실측 및 이론적 연구를 통하여 분석하였다.
최근 국내에서는 터널시공에서 전통적으로 적용되어온 NATM 공법에 비해 지반의 변형 및 민원 발생을 최소화할 수 있는 shield TBM 공법이 최적의 대안으로 대두되고 있다. Shield TBM 공법의 경우 굴진 시 막장압을 작용시켜 지반침하를 최소화 할 수 있으며, 굴착과 동시에 세그먼트 조립 및 그라우트를 주입하는 연속공정으로 타 터널굴착공법에 비해 공기를 단축시킬 수 있다는 장점이 있다. 반면에 shield TBM 공법적용에 따른 인접말뚝의 거동에 대한 연구는 현재까지 미흡한 상태이고 이에 대한 명확한 연구가 필요한 실정이다. Kaalberg et al. (2005)의 경우 TBM 공법을 적용한 현장실측 및 수치해석을 통하여 터널시공에 따른 지반 및 말뚝 침하의 영향을 분석하였으며, 터널로부터 말뚝선단의 상대적인 위치를 터널굴착 시 발생하는 지반침하 영향권과 비교하여 연구를 수행하였다. Mroueh and Shahrour (2008)은 일정한 막장압을 유지한 상태에서의 터널굴착을 수치해석으로 모사하여 터널굴착에 따른 지표면 침하 및 터널인근지반의 변형을 분석하였다. Lee et al. (2012)은 TBM 공법 적용에 따른 상부구조물의 거동을 터널로부터 상부구조물의 이격거리를 고려하여 수치해석을 통한 연구를 수행하였다. 이들의 보고에 의하면 터널과 구조물의 이격거리에 따라 구조물의 거동이 상이하게 나타나므로 현장조건과 구조물의 이격거리를 고려한 터널시공이 이루어져야 한다고 보고하였다. Lee et al. (2012), Cho et al. (2014a; 2014b), Xu et al. (2015), You and Kim (2017) 및 Ahn et al. (2018)의 기존 관련 연구들은 터널굴착으로 인한 지반침하와 이로 인해 유발되는 말뚝의 거동을 막장압의 변화를 고려하지 않은 조건에서 연구를 수행하였다. 반면, Jeon et al. (2018)은 막장압의 변화를 고려하여 shield TBM 터널 근접시공에 따른 말뚝의 거동 연구를 수치해석을 활용하여 수행하였다. 또한 터널굴착 영향권 내에 말뚝이 존재하는 경우 터널굴착 영향권 밖에 존재 하는 말뚝에 비해 말뚝의 겉보기 안전율이 낮게 나타나는 것으로 알려져 있으나 아직까지 그 거동을 명확하게 규명하지 못하고 있는 실정이며, 이에 대한 체계적인 연구가 시급하게 요구되고 있다(Williamson, 2014).
이에 본 연구에서는 터널로부터 말뚝선단의 이격거리를 고려한 shield TBM 공법을 모사하여 막장압의 변화에 따른 지반 및 말뚝의 거동을 3차원 유한요소해석을 통해 수행하였으며, tunnelling-induced 말뚝두부침하, 축력, 상대변위 및 경계면에서의 전단응력 등을 고찰하였다.
2. 수치해석
2.1 해석개요 및 경계조건
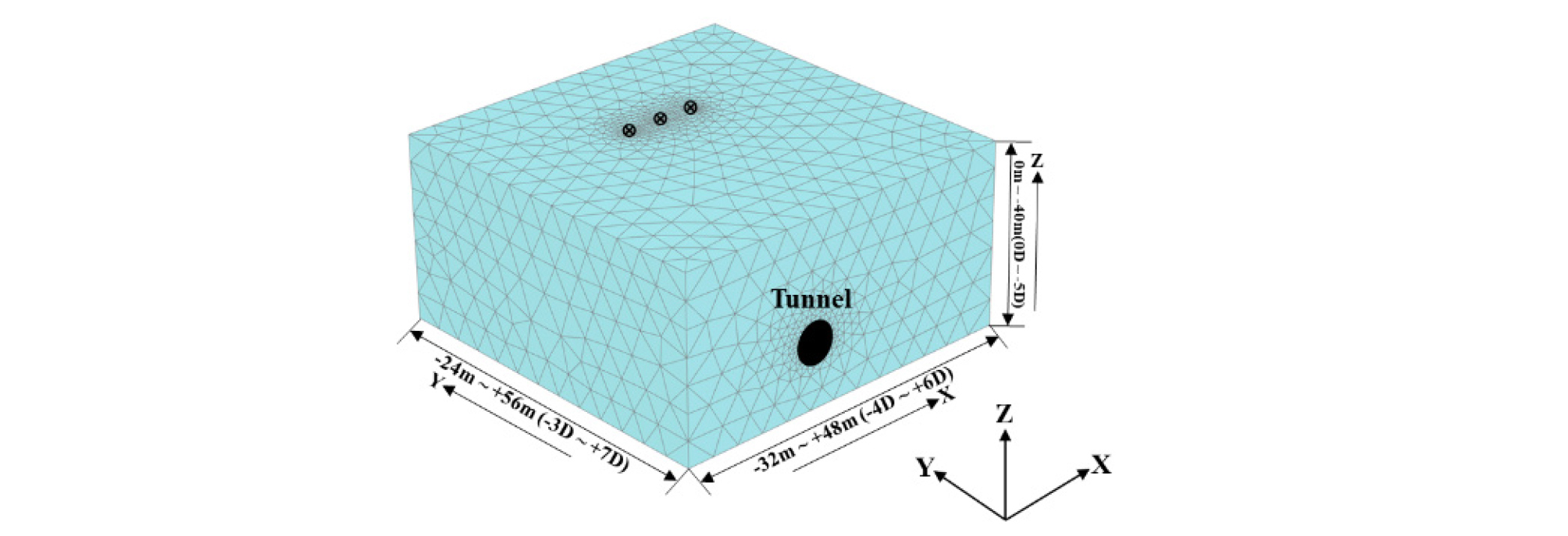
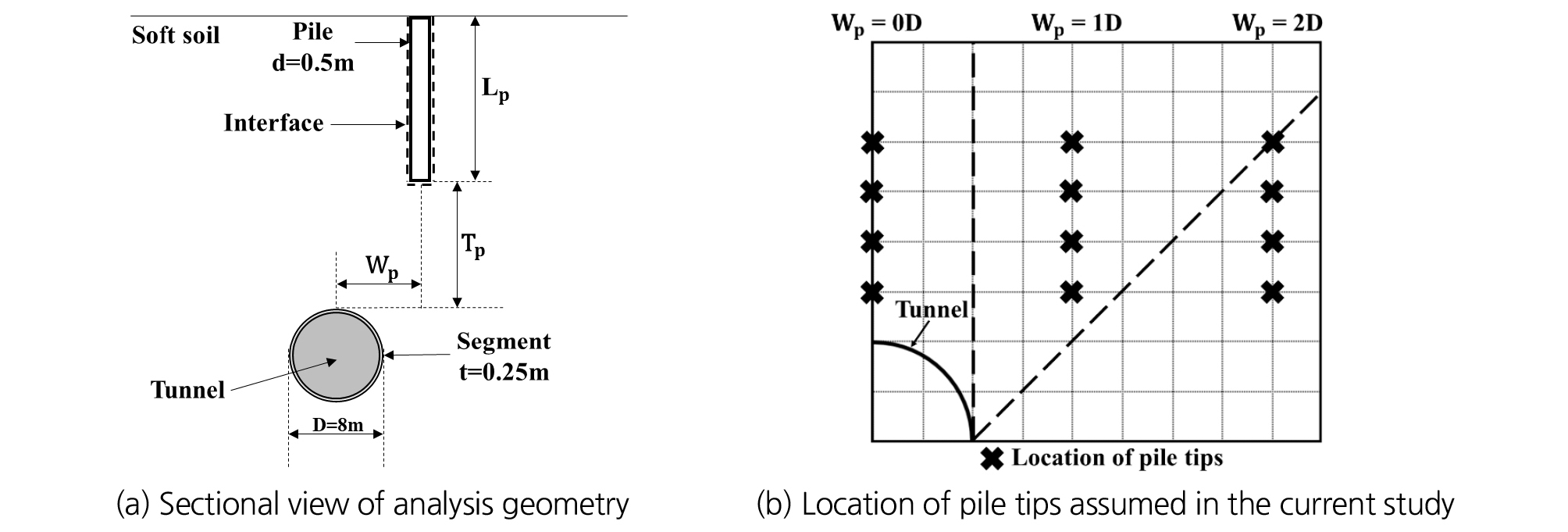
본 연구에서는 3차원 유한요소해석 프로그램인 Plaxis 3D (2018)를 이용하여 터널로부터 말뚝선단의 이격거리를 고려한 shield TBM 공법을 모사함으로써 막장압의 변화에 따른 말뚝의 거동을 분석하였다. Fig. 2는 해석에서 적용된 대표 유한요소 mesh를 나타내고 있다. Fig. 3(a)는 본 해석에서 적용한 해석단면도를 보여주고 있고, Fig. 3(b)는 터널로부터 말뚝선단의 위치를 표시하였다. 해석에서 가정한 shield TBM 터널의 굴착 직경(D)은 세그먼트 두께(t = 250 mm)를 포함하여 8 m이며, 터널의 중심부(springline)는 지표면으로부터 26 m 하부에 위치하고 있다. 말뚝의 직경(d)은 0.5 m이며, 길이(Lp)는 14 m, 16 m, 18 m 및 20 m로 Tp = 1.00D, 0.75D, 0.50D 및 0.25D에 대응된다. 여기서, Tp는 터널 크라운(crown)에서 말뚝선단까지의 수직이격거리를 의미한다. 한편 터널의 중심으로부터 말뚝의 중심을 횡방향으로(X-축) 0 m, 8 m 및 16 m 이격시켜 해석을 수행하였다(Wp = 0D, 1D 및 2D). 여기서, D는 터널의 직경을 나타내고, Wp는 터널의 중심부에서 말뚝의 중심까지 수평이격거리를 의미한다(Fig. 3(a)).
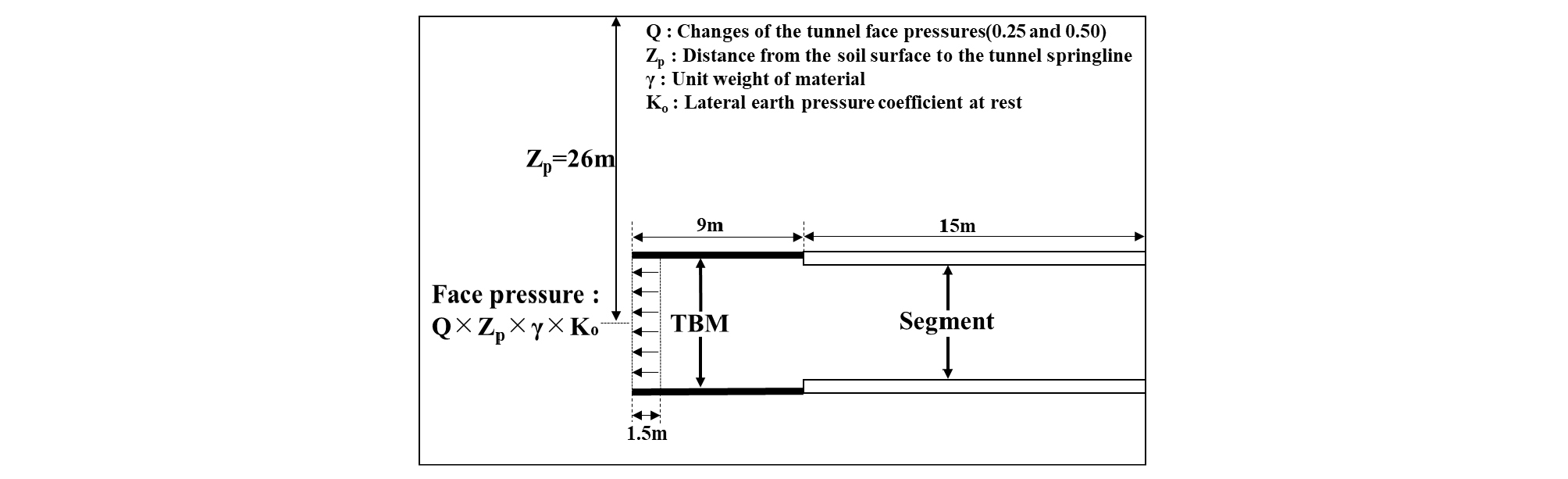
본 연구에서는 Fig. 4에 나타나 있듯이 9 m 길이의 shield TBM 장비를 모사하기 위해 판요소(plate element)를 적용했으며, 1회 굴착장(세그먼트의 폭)은 1.5 m로 하였다(Plaxis 3D, 2018). 또한, 터널의 굴착을 모사하기 이전에 기 제작된 15 m 길이의 세그먼트가 설치되었다고 가정하였다(Fig. 4). 터널굴착과 관련된 내용은 2.3절에서 상세히 설명하였다. 막장압은 터널굴착면에 대하여 일정하게 작용한다고 가정하였으며, 그 크기는 지표면으로부터 터널 중심부까지의 거리(Zp)를 고려하여 Q × Zp × γ × Ko식(Q = 막장압의 크기 변화(본 연구에서는 0.25 및 0.50 적용), Zp = 지표면에서 터널 중심부까지의 거리, γ = 흙의 단위중량, Ko = 정지토압계수)으로 산정하였다(Mroueh and Shahrour, 2008). Table 1은 본 연구에서 실시한 해석이 요약되어 있으며, Greenfield 조건, 다양한 말뚝선단의 위치 및 막장압의 변화 조건을 포함하여 총 20회의 해석이 수행되었다. Table 1에 나타나 있듯이 막장압의 경우 터널굴착 이전 터널 중심부에서의 초기 수평토압(260 kPa)의 25% 및 50%를 적용하였다(65 kPa 및 130 kPa). 본 연구에서는 Mroueh and Shahrour (2008)의 선행연구를 참조하여 터널 굴착 이전 springline에서의 수평토압에 비해 작은 막장압을 작용시켰다. 또한 본 연구에서 가정한 최저 막장압 65 kPa은 Bolton (1991)에 의해 제시된 식 (1)로 유도된 사질토 지반에 시공되는 터널 붕괴 시 막장압의 크기(σFP)인 86 kPa 보다 약간 작지만, 이는 근사적으로 터널붕괴 상태의 막장압의 크기와 유사하다고 간주할 수 있다. 한편 각 막장압에 대해 공식 (2)의 load factor (LF)를 적용하여 막장압 크기의 영향을 고찰하였다. 이때 LF = 1은 터널붕괴를 의미하며 LF는 근사적으로 안전율의 역수로 가정할 수 있다.
| $$\sigma_{FP}=\left[1-\left(\frac D{2C+D}\right)^{(K_p-2)}\times\left[\frac{\gamma D}{2(K_p-2)}\right]\;\right]$$ | (1) |
| $$LF=\frac{q+\gamma Z_p-\sigma_F}{q+\gamma Z_p-\sigma_{FP}}$$ | (2) |
여기서, γ는 흙의 단위중량, Zp는 지표면에서 터널의 중심까지의 거리, q는 표면 상재하중, σFP는 터널 붕괴시의 막장압 크기, σF는 실제 적용 막장압, D는 터널의 직경, Kp는 수동토압계수, C는 터널 크라운에서 지표면까지의 거리를 말한다. 본 해석에서는 지표면 상재하중 및 지하수위는 고려하지 않았다.
Table 1. Summary of numerical analyses (D: tunnel diameter)
2.2 적용 구성모델 및 물성치
터널의 굴착을 모사하기 위하여 탄-소성해석을 실시하였으며 특히 지반과 말뚝 경계면에서 소성항복(plastic yielding)이 발생할 경우 미끄러짐(slip)의 발생을 허용하는 경계요소(interface element)를 적용하였다. Fig. 3(a)의 말뚝 주면에 표시된 점선이 경계요소(interface element)를 의미한다. 따라서 말뚝과 인접 지반 경계면에서의 전단응력 전이 과정을 분석 할 수 있도록 하였으며, 특히 말뚝에 인장력이 작용할 경우 말뚝선단과 지반이 서로 분리 될 수 있도록 말뚝선단에도 경계요소를 지정하여 수행하였다. 또한, shield TBM 장비를 모사하기 위하여 판요소(plate element)를 사용하였으며, 터널의 막장면을 제외한 터널과 지반 사이에도 경계요소(interface element)를 지정하였다. Table 2는 수치해석에서 적용한 지반, 말뚝, shield TBM 장비 및 세그먼트의 일반적인 물성치를 정리하였다(Mroueh and Shahrour, 2008; Plaxis 3D, 2018). 지반에는 비관련 흐름 법칙(non-associated flow rule)과 Mohr-Coulomb의 파괴기준(failure criterion)을 따르는 탄-소성 모델이 적용되었으며 말뚝, shield TBM 장비 및 세그먼트에는 등방탄성모델(isotropic elastic model)이 적용되었다. 말뚝의 시공에 의한 말뚝주면-지반 및 말뚝선단-지반 경계면에서의 전단강도 상수(c'int, φ'int)가 감소되는 것을 고려하기 위하여 Brinkgreve et al. (2015)의 지침을 참고하여 강도감소 계수(strength reduction factor) Rint = 0.7를 적용하고 식 (3) 및 (4)을 통해 적절한 전단강도 상수를 산정하였다.
| $$\mathrm c'_{\mathrm{int}}={\mathrm R}_{\mathrm{int}}\times\mathrm c'_{\mathrm{soil}}$$ | (3) |
| $$\tan(\varphi'_{\mathrm{int}})={\mathrm R}_{\mathrm{int}}\times\tan(\varphi'_{\mathrm{soil}})$$ | (4) |
여기서, c'soil은 지반의 점착력, Rint는 강도감소 계수, φ'soil은 지반의 내부마찰각, φ'int는 interface 마찰각(19.6°)이다.
Table 2. Material parameters assumed in the numerical modelling
| Material | Model |
γ (kN/m3) |
E’ (MPa) |
c’ (kPa) |
φ' (°) | Ko | ν |
| Soil (Mroueh and Shahrour, 2008) | Mohr-Coulomb | 20 | 30 | 5 | 27 | 0.5 | 0.3 |
| Shield TBM machine (Plaxis 3D, 2018) | Elastic | 247 | 200,000 | - | - | - | - |
| Segment (Plaxis 3D, 2018) | 27 | 31,000 | - | - | 0.01 | 0.1 | |
| Pile | 25 | 30,000 | - | - | 0.01 | 0.2 |
2.3 수치해석 과정 및 분석
수치해석에서는 말뚝 시공 시 발생하는 근입효과에 따른 지반의 응력변화는 포함시키지 않았으므로 본 연구에서 가정한 말뚝은 현장타설말뚝과 유사하다고 볼 수 있다. 터널의 굴착은 종방향(Y)에 대하여 0D에서 +7D (0 m ~ +56 m) 구간 사이에서 실시되었다(Fig. 2). 이는 앞서 설명하였듯이 터널의 굴착 시작에 앞서 15 m 길이의 터널굴착이 이미 완료되었다고 가정하였으며, shield TBM 장비의 길이는 9 m로 모사하였기 때문에 종방향 Y = 0 m에서 최초 굴착이 수행되었다(Fig. 4). 또한 각각의 해석 단계에서는 1.5 m씩 굴진하면서 총 37단계에 걸쳐 실시하였다. 초기 평형단계 도달 이후 터널굴착 이전 말뚝두부에는 별도의 해석(PL1, PL2, PL3 및 PL4)을 통해서 결정한 설계하중 Pa을 작용시켰으며(Lp = 20 m [600 kN], Lp = 18 m [500 kN], Lp = 16 m [408 kN] 및 Lp = 14 m [313 kN]), 터널굴착 이전 말뚝두부에는 단계적으로 하중을 증가시켜 설계하중을 작용시켰다. 또한 각 해석단계별로 굴착과 세그먼트의 조립을 동시에 적용하였다. 터널 막장압의 경우 앞서 2.1절에서 설명하였듯이 지표면에서 터널중심부까지의 거리(Zp = 26 m)와 흙의 단위중량(γ) 및 토압계수(Ko = 0.5)를 고려하였으며 터널막장에 대하여 심도와 무관하게 일정한 크기로 작용한다고 가정하였다. 해석결과의 분석을 위하여 임의의 심도에서 말뚝의 축력 P는 P = σzz_avg × Ap 식으로 산정하였다. 여기서 σzz_avg는 특정심도에서 말뚝 수직응력의 값을 평균한 것이고 Ap는 말뚝의 단면적이다. 한편 말뚝-지반 경계면에서의 전단응력은 임의의 심도에서의 값을 평균하여 산정하였다.
3. 해석결과 분석
3.1 말뚝의 설계지지력 결정
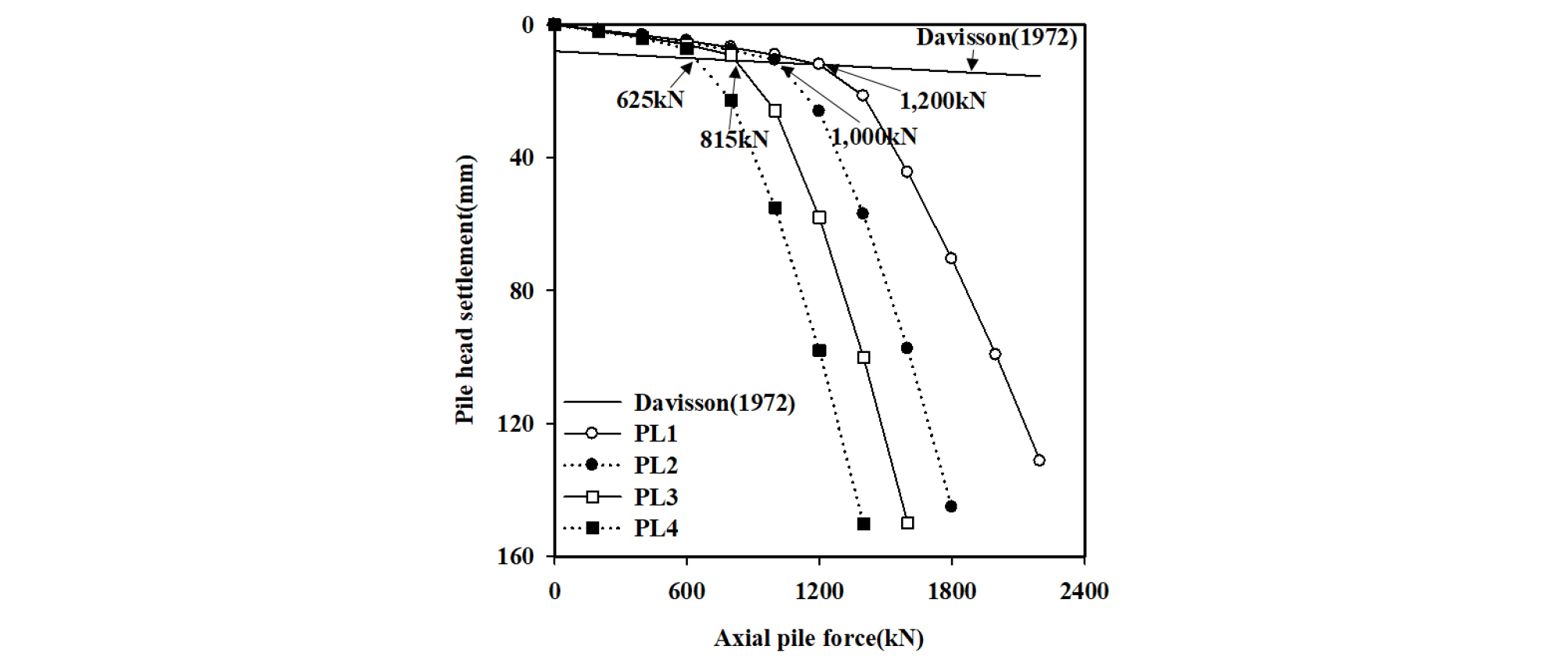
Fig. 5는 말뚝의 설계지지력을 결정하기 위해 말뚝재하시험 모사를 통하여 산정된 말뚝의 하중-침하 관계를 보여주고 있다. 또한, 터널의 굴착이 포함되지 않은 말뚝의 하중-침하 관계를 보여주고 있으며, 말뚝의 길이 변화에 따라 Tp = 0.25D (20 m, PL1), Tp = 0.50D (18 m, PL2), Tp = 0.75D (16 m, PL3) 및 Tp = 1.00D (14 m, PL4) 조건의 말뚝에서 실시되었다. 말뚝 하중재하시험을 모사하기 위하여 말뚝두부에 단계별로 압축력을 증가시켰다. PL1의 경우 말뚝두부의 하중이 약 1,190 kN 인근에 도달할 때까지는 말뚝하중과 말뚝두부침하 사이에 거의 선형적인 관계를 보이고 있으나, 이를 초과하는 하중이 작용하는 경우 급격한 침하가 발생하고 있다. 또한 PL2~PL4 말뚝의 경우 PL1 말뚝과 비슷한 경향을 보이고 있으나 그 값은 다르게 나타났다. 본 연구에서는 말뚝에 발생된 하중-침하 관계로부터 말뚝의 설계지지력을 결정하기 위하여 널리 사용되는 Davisson (1972)의 방법을 적용하였으며 이를 통하여 Fig. 5에 나타나 있듯이 PL1 말뚝의 파괴하중(failure load)을 1,200 kN으로 산정하였다. 여기에 안전율 2.0을 적용하여 말뚝의 설계하중(Pa)은 600 kN으로 결정되었다(1,200 kN/2 = 600 kN). Davisson (1972) 그래프의 경우 말뚝의 길이(PL1~PL4)에 따라 각각 다르게 계산되지만 그 값들이 매우 유사하므로 PL1 말뚝에 대한 하나의 Davisson (1972) 그래프를 대표로 이용하여 나타내었다. 따라서 PL2~PL4 말뚝의 경우 말뚝의 파괴하중은 각각 1,000 kN, 815 kN 및 625 kN으로 나타났으며, 여기에 안전율 2.0을 적용하여 설계하중을 각각 500.0 kN, 407.5 kN 및 312.5 kN으로 산정하였다. 이때 PL1~PL4의 말뚝두부의 침하량(δ)은 각각 5.3 mm, 4.8 mm, 4.3 mm 및 3.7 mm로 평가되었다. 말뚝 설계하중 작용 하에서 말뚝-지반 사이의 경계면 굴착으로 인한 기 시공된 말뚝의 거동을 심도있게 분석하기 위해 터널굴착 이전 말뚝두부에 3단계에 걸쳐 하중을 단계별로 증가시켜 설계하중(Pa)을 작용시켰다. 이를 통해 사용 중인 말뚝의 거동을 모사하였으며 이후 터널의 단계별 굴착을 진행시켰다.
3.2 말뚝의 축력 분포
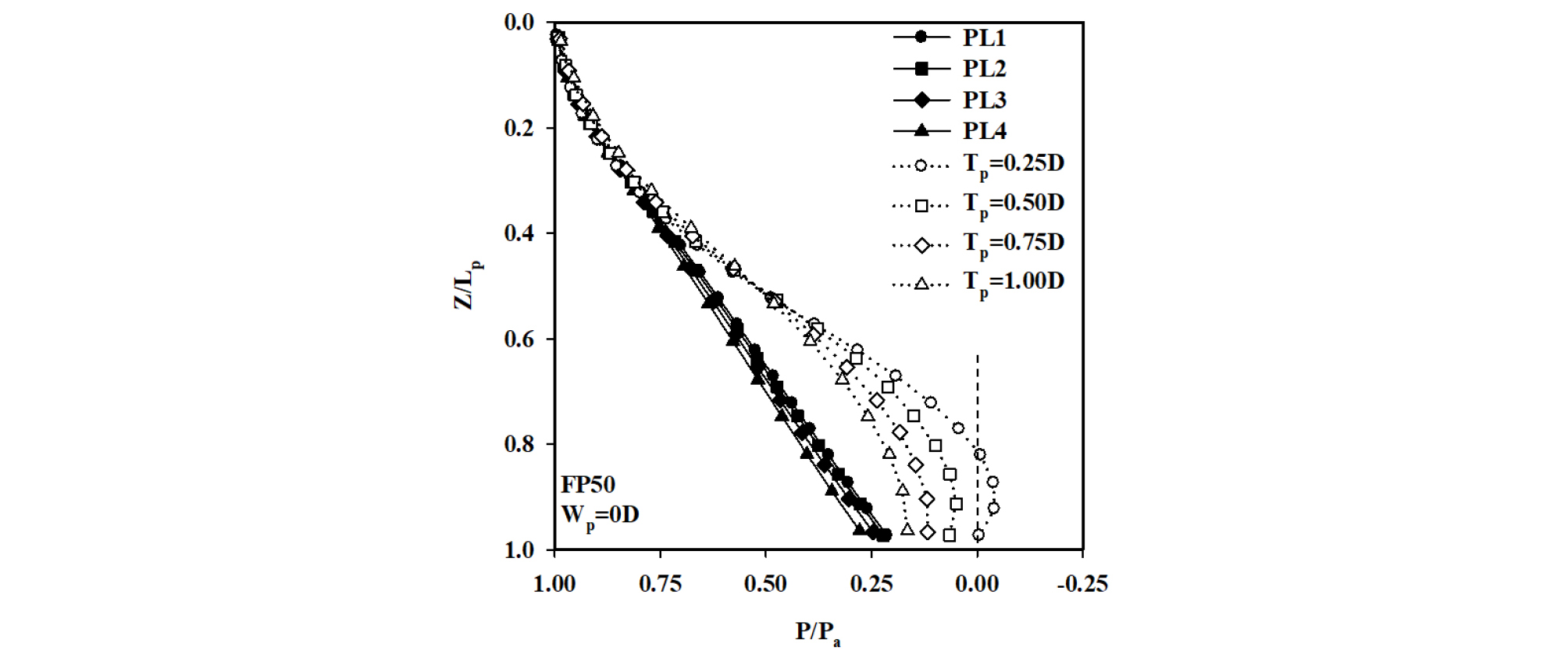
Fig. 6은 막장압 FP50 조건에 대하여 터널굴착 종료 후 Wp = 0D 위치에서 말뚝선단의 이격거리(Tp = 0.25D, 0.50D, 0.75D 및 1.00D)에 따른 정규화된 말뚝 축력(P/Pa)의 분포를 정규화된 말뚝의 심도(Z/Lp)에 대하여 보여주고 있다. 여기서, P는 임의 심도에서 말뚝의 축력을 의미하고, Pa는 터널굴착 이전 말뚝두부에 작용한 설계하중이다. Fig. 6은 터널굴착 이전 말뚝두부에 작용한 설계하중(pile loading)의 축력분포 및 터널굴착 종료에 따른 축력의 분포를 포함하고 있다. 설계하중(pile loading) 작용 하에서 말뚝의 축력은 모든 조건의 말뚝에 대해 비슷한 경향을 보이고 있으며, 말뚝 선단에서 축력의 값은 약 P/Pa = 0.20~0.28으로 나타났다. 터널굴착 종료 후 모든 말뚝의 선단부근에서는 축력이 설계하중시의 축력보다 상대적으로 감소하였는데 이는 선단에 의해서 지지되던 하중의 일부가 주면마찰력에 의해 지지되는 전단응력 전이현상으로 설명될 수 있다. 특히, Tp = 0.25D 말뚝의 경우 Z/Lp = 0.8~1.0 부근에서 인장력을 나타내는 (-) 값이 발생하였으나(최대 P/Pa = -0.04, P = 24.7 kN, Pa = 600 kN), 이 값은 콘크리트의 인장강도를 8 MPa로 가정하였을 때의 말뚝의 허용 인장강도인 1,570 kN의 1.6% 정도에 불과하여 말뚝의 사용성에는 별다른 지장을 초래하지 못할 것으로 분석된다.
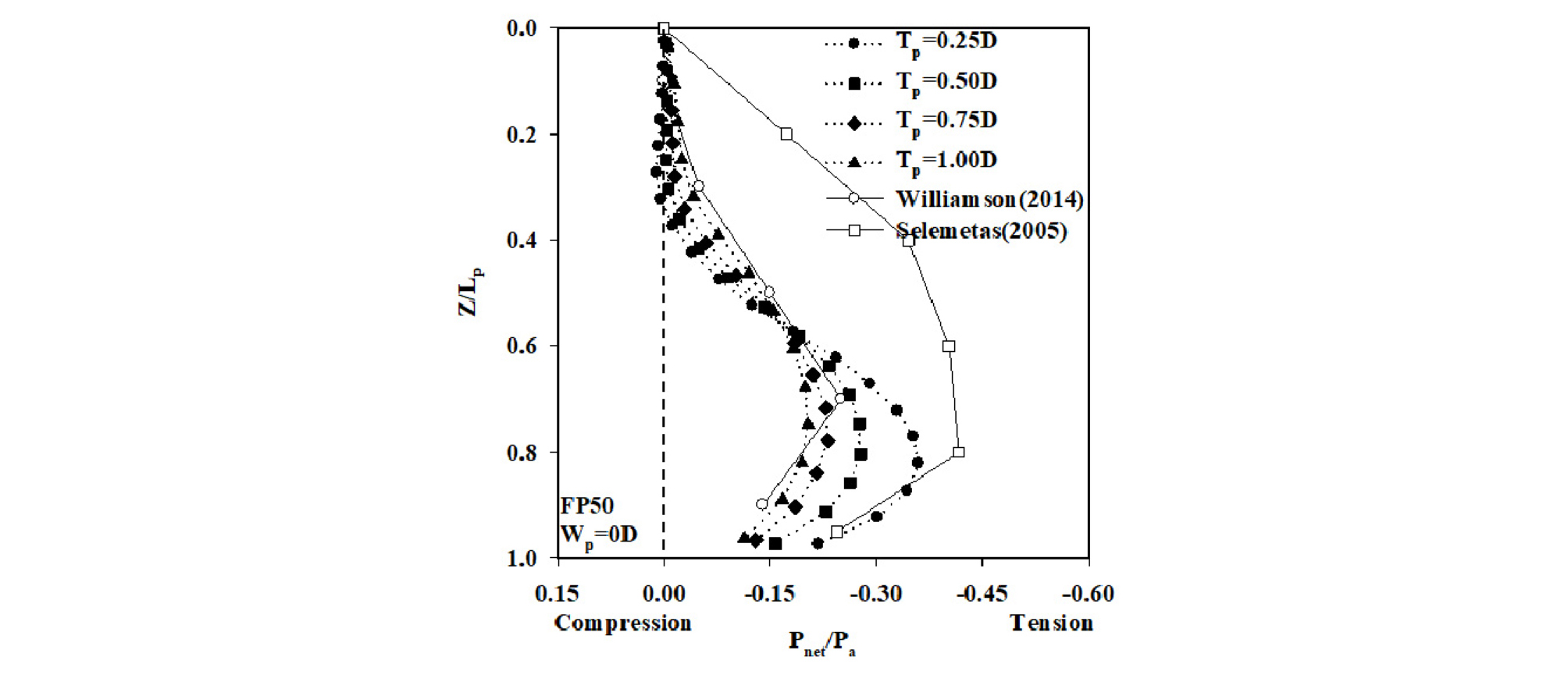
Fig. 7은 터널굴착에 의한 말뚝의 축력변화를 명확하게 규명하기 위하여 막장압 FP50 조건에서 일정한 말뚝의 횡방향 이격거리(Wp = 0D)에 대하여 다양한 수직 이격거리(Tp = 0.25D, 0.50D, 0.75D 및 1.00D)에 따라 정규화된 tunnelling-induced 말뚝 축력(Pnet/Pa)의 분포를 정규화된 말뚝의 심도(Z/Lp)에 대하여 보여주고 있다. 여기서, Pnet은 순수하게 터널의 굴착에 의해서 발생한 말뚝의 축력(tunnelling-induced)이다. 본 연구에서 수행된 모든 조건의 말뚝 축력은 지표면에서부터 Z/Lp = 0.8 부근까지 터널의 굴착으로 인해 감소하는 것을 알 수 있다. 또한, Tp = 0.25D 및 Tp = 1.00D 말뚝의 경우 Pnet_(-)max/Pa의 값이 각각 -0.36 및 -0.20으로 나타났다. 여기서, Pnet_(-)max/Pa은 말뚝에 발생한 최대인장력의 값을 의미한다. 터널 크라운(crown)으로부터 말뚝선단까지의 수직 이격거리가 증가 할수록 말뚝에 작용하는 최대인장력의 값이 감소하는 것을 알 수 있다. 한편, Fig. 7에는 Selemetas (2005) 및 Williamson (2014)이 각각 현장실측 및 원심모형실험을 통해 측정한 Pnet/Pa를 같이 포함하고 있다. Selemetas (2005) 및 Williamson (2014)에 의해 계산된 말뚝의 Pnet_(-)max/Pa의 값은 각각 -0.42 및 -0.25로 나타났다. Selemetas (2005) 및 Williamson (2014)의 연구에서도 말뚝에 tunnelling-induced 인장력이 발생하는 것으로 나타났으며, 본 연구에서 산정된 결과와 비슷한 경향을 보이고 있어 본 연구의 적합성을 입증하고 있다.
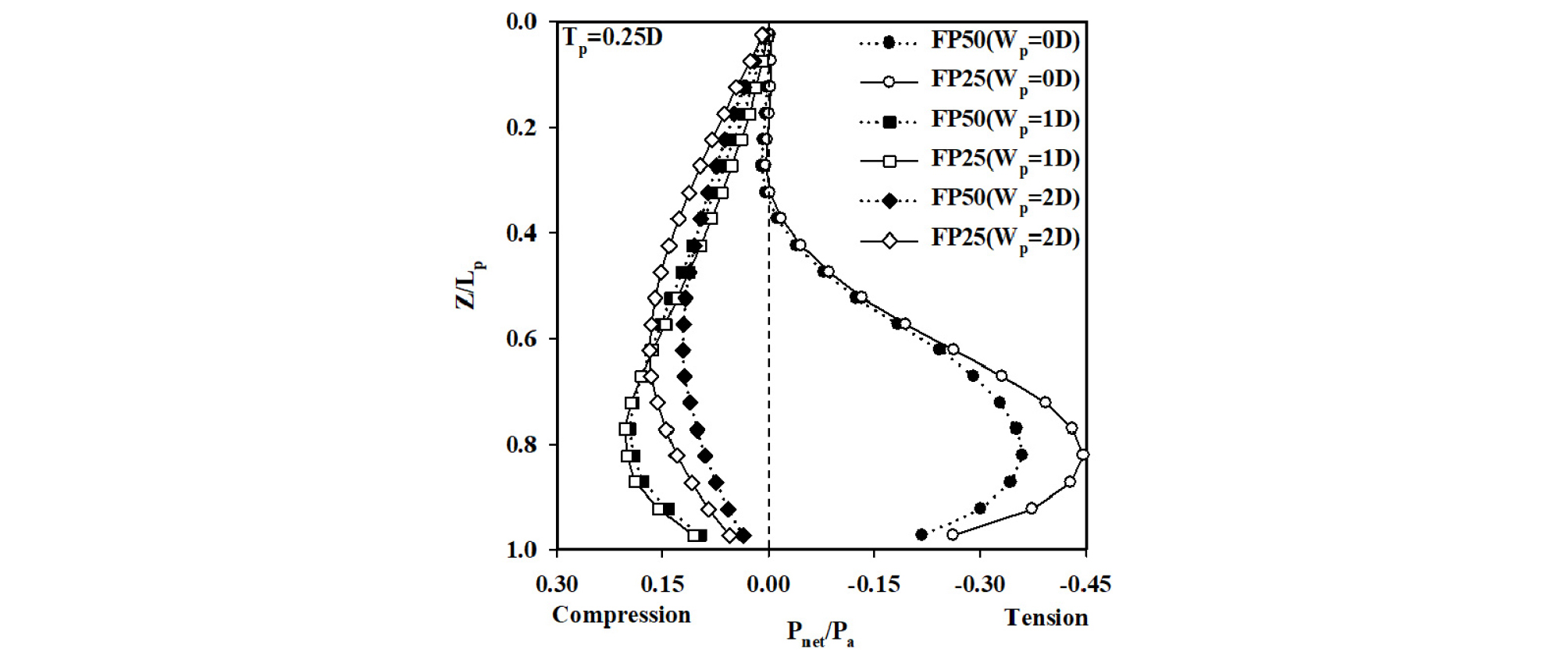
Fig. 8은 막장압 FP50 및 FP25 조건에서 터널로부터 말뚝선단의 일정한 수직 이격거리(Tp = 0.25D, Lp = 20 m)에 대하여 다양한 횡방향 이격거리(Wp = 0D, 1D 및 2D)를 고려하여 정규화된 tunnelling-induced 말뚝 축력(Pnet/Pa)의 분포를 정규화된 말뚝의 심도(Z/Lp)에 대하여 보여주고 있다. Fig. 8에 나타나 있듯이 터널 크라운 상부에 위치한 FP50 (Wp = 0D) 및 FP25 (Wp = 0D) 말뚝의 경우 말뚝에는 터널굴착으로 인하여 인장력 형태의 축력이 발생하는 것을 알 수 있으며, 터널로부터 Wp = 1D 및 2D 이격된 말뚝의 경우 압축력 형태의 축력이 발생하였다. 이와같이 말뚝의 축력 분포는 터널로부터 말뚝선단의 상대적인 위치에 영향을 받는 것으로 나타났다. 또한, FP25 조건에 대한 Wp = 0D 및 2D 위치 말뚝의 경우 FP50 조건의 말뚝보다 축력의 값이 크게 발생하였는데, 이는 막장압의 크기가 작을수록 지반의 침하를 크게 유발하여 말뚝과 지반 사이에 전단강도의 발현이 크게 나타나기 때문으로 판단된다. 터널굴착 영향권 내부에 존재하는 FP25 (Wp = 0D) 말뚝의 경우 말뚝에 작용하는 인장력 형태의 최대 축력값은 Pnet/Pa = -0.45로 나타났으며, 터널굴착 영향권 외부에 존재하는 FP25 (Wp = 1D) 말뚝의 경우 압축력 형태의 최대 축력값은 Pnet/Pa = 0.2로 산정되었다. 결론적으로 막장압의 변화에 따라 지반 침하 및 말뚝 침하가 상이하게 나타나므로 막장압의 크기를 고려한 연구가 필요하다고 판단된다.
3.3 말뚝의 전단응력 분포
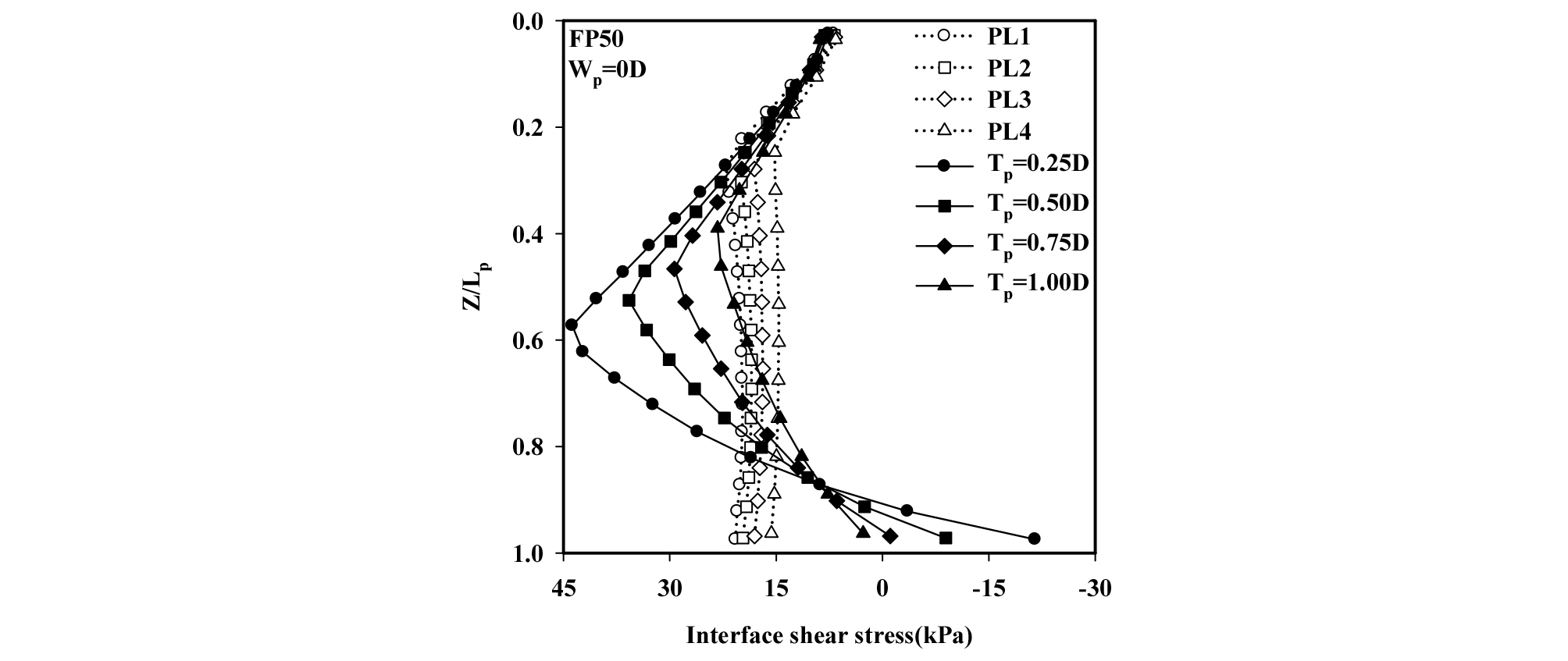
Fig. 9는 막장압 FP50 조건에 대하여 터널굴착 종료 후 산정된 말뚝-인접지반 경계면에서의 전단응력의 분포를 Wp = 0D 위치에서 말뚝선단의 이격거리(Tp = 0.25D, 0.50D, 0.75D 및 1.00D)를 고려하여 정규화된 말뚝의 심도(Z/Lp)에 대해 보여주고 있다. 또한, 터널굴착 이전 설계하중작용(pile loading)에 의한 전단응력 및 터널굴착 종료 후의 전단응력의 분포도 같이 보여주고 있다. 터널굴착 이전 말뚝에 작용한 설계하중에 의해 발생한 전단응력의 경우 모든 조건의 말뚝에서 비슷한 경향을 보이나, 말뚝의 길이가 길수록 상대적으로 더 큰 전단응력이 발생하는 것을 관찰할 수 있다. 또한, 설계하중 작용 하에 있는 말뚝의 경우 말뚝의 두부에서부터 Z/Lp = 0.3 부근까지 말뚝 심도의 증가에 따라 전단응력이 증가하였으나 이후 말뚝의 선단까지는 약간의 변화만 있을 뿐 일정하게 나타났다. 반면, 터널의 굴착이 수행되고 난 후 말뚝과 지반 사이에는 소성항복의 범위가 확장되었으며, 터널로부터 말뚝선단의 이격거리가 짧을수록 그 범위가 크게 발생하였다. 말뚝의 특정심도에서 전단응력의 부호가 (+)에서 (-)로 변하는 것을 알 수 있는데 이는 전단응력의 작용방향이 반대로 변했음을 나타낸다. 다시 말해 부호가 바뀌는 부근을 기점으로 상부에서는 상향의 전단응력이 하부에서는 하향의 전단응력이 발생하는 것을 의미한다(Lee, 2012a). 터널굴착 종료 후 Tp = 0.25D 말뚝의 경우 Z/Lp = 0.57 부근까지 전단응력이 증가하는 것을 알 수 있으며, 그 이후 말뚝의 하부까지 점차적으로 감소하여 선단부근에서는 (-) 값으로 관찰되었다. 또한, 다른 타 조건의 말뚝의 경우도 말뚝의 두부에서 Z/Lp = 0.39~0.53 부근까지 전단응력이 증가하였으며, 그 이후 말뚝의 선단까지 점차적으로 감소하였다. 이러한 사실로부터 말뚝두부에서 특정심도까지 전단강도가 완전히 발현하고, 그 하부에서는 전단강도의 일부만이 발현됨을 알 수 있다.
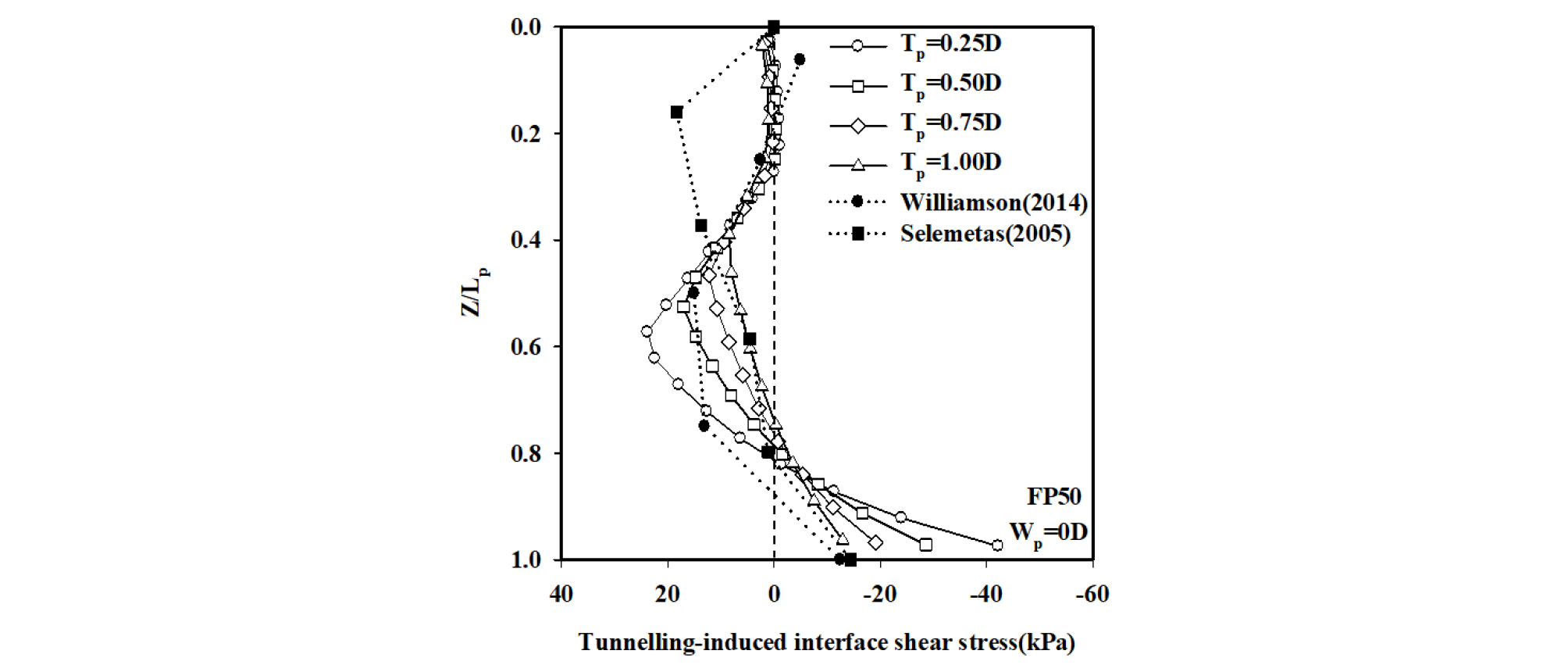
Fig. 10은 막장압 FP50 조건에서 일정한 말뚝의 횡방향 이격거리(Wp = 0D)에 대하여 다양한 수직 이격거리(Tp = 0.25D, 0.50D, 0.75D 및 1.00D)를 고려한 순수하게 터널굴착(tunnelling-induced)으로 유발된 말뚝의 전단응력 분포를 정규화된 말뚝의 심도(Z/Lp)에 대하여 보여주고 있다. Fig. 10에 나타나 있듯이 모든 조건의 말뚝에서 비슷한 경향을 보이고 있으며, 말뚝두부에서 심도 Z/Lp = 0.30 까지 매우 작은 전단응력의 변화만이 나타났다. 이는 앞서 설명하였듯이 터널굴착 이전 설계하중으로 인해 말뚝 두부에서 특정심도까지 전단강도가 전부 발현되었기 때문으로 판단된다. Tp = 0.25D 말뚝의 경우 심도 Z/Lp = 0.30~0.57 까지 전단응력이 점차적으로 증가하여 최대 전단응력의 값이 관찰되었으며, 이후 말뚝 하부까지 전단응력이 감소하여 말뚝선단에서는 (-)의 값을 나타냈다. 또한, 타 조건의 말뚝에서도 이와 같은 경향이 발생하였다. 한편, Fig. 10은 앞서 설명한 Selemetas (2005) 및 Williamson (2014)의 실측된 말뚝축력의 값으로부터 도출된 정규화된 말뚝의 심도(Z/Lp)에 대한 전단응력의 분포도 나타내고 있다. 이는 본 연구에서 분석된 결과들과는 약간의 차이를 보이지만, 본 연구에서 산정된 전단응력 분포의 경향과는 일치하는 것으로 나타났다.
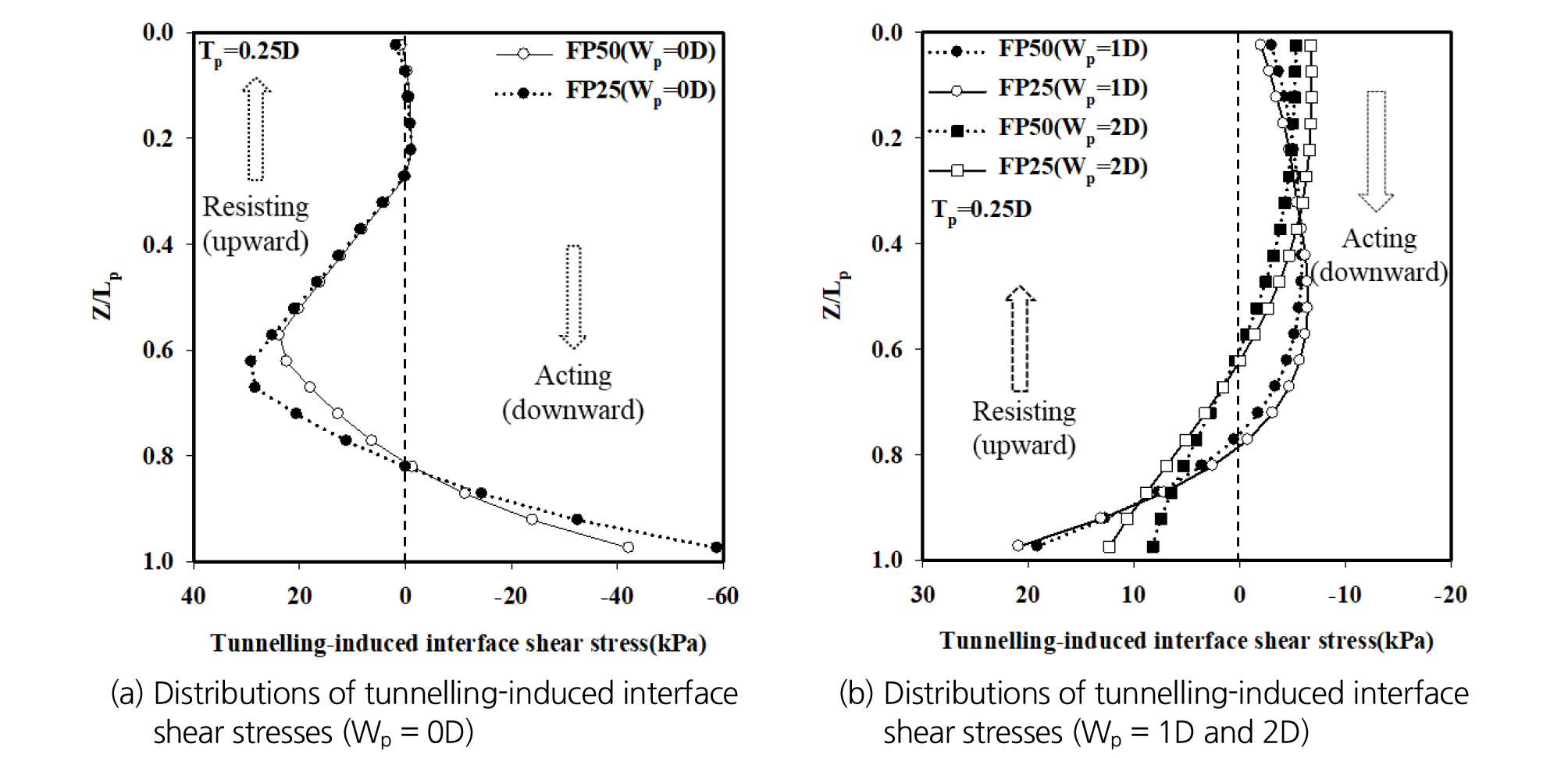
Fig. 11(a) 및 11(b)는 막장압 FP50 및 FP25 조건에서 일정한 수직 이격거리(Tp = 0.25D, Lp = 20 m)에 대하여 말뚝의 다양한 횡방향 이격거리(Wp = 0D, 1D 및 2D)를 고려한 순수하게 터널굴착(tunnelling-induced)으로 유발된 말뚝의 전단응력 분포를 정규화된 말뚝의 심도(Z/Lp)에 대하여 보여주고 있다. Fig. 11(a)에 나타나 있듯이 FP50 (Wp = 0D) 및 FP25 (Wp = 0D) 조건의 말뚝의 경우 말뚝의 상부에는 말뚝의 침하가 지반의 침하를 초과하는 상향의 전단응력이 발생하였으며, 반대로 말뚝의 하부에는 지반의 침하가 말뚝의 침하를 초과하는 하향의 전단응력이 나타났다. 이러한 현상으로 인해 말뚝에는 인장력 형태의 축력이 발생하며 앞서 3.3절에 설명한 내용을 다시 한 번 입증하였다. 또한, 막장압의 감소는 지반의 침하를 증가시켜 말뚝과 지반 사이의 상대변위를 크게 유발하므로 전단응력의 값 또한 증가시키게 된다. 따라서 FP25 (Wp = 0D)의 경우 FP50 (Wp = 0D)와 비교하여 최대 (+) 전단응력의 값과 최소 (-) 전단응력의 값이 계산되었다. 말뚝의 선단이 터널굴착 영향권 밖[FP50 (Wp = 1D), FP25 (Wp = 1D), FP50 (Wp = 2D) 및 FP25 (Wp = 2D)]에 존재하는 말뚝의 경우 Fig. 11(b)에 나타나 있듯이 Fig. 11(a)의 경향과 반대로 나타났다. 다시 말해 말뚝의 상부에서는 하향의 전단응력이 발생하였으며, 말뚝의 하부에서는 상향의 전단응력이 발생하여 압축력 형태의 축력을 유발시켰다.
3.4 터널굴착에 따른 말뚝 두부 침하
Table 3은 다양한 말뚝선단의 위치에 대하여 막장압의 변화를 고려한 해석을 통해 산정된 정규화된 tunnelling-induced 최대 말뚝두부 침하(δp,net_max/δgr_50,max) 및 정규화된 tunnelling-induced 최대 말뚝축력(Pnet_max/Pa)을 정리하였다. 여기서, δp,net_max은 순수하게 터널굴착으로 발생한 최대 말뚝 두부 침하를 의미하고, δgr_50,max는 Greenfield 해석조건의 막장압 FP50에 대하여 터널굴착에 의한 Wp = 0D 위치의 지표면 최대침하를 의미한다(δgr_50,max = 10.8 mm). 또한 Pnet_max는 말뚝에 작용하는 최대 축력값(인장력 및 압축력)을 나타낸다. 말뚝두부 침하의 경우 막장압의 크기를 가장 작게 고려한 FP25 조건에서 가장 크게 나타났으며, 터널 크라운(crown) 상부에 위치한 말뚝은 막장압의 크기에 관계없이 인장력 형태의 축력이 발생하였다. 본 내용과 관련하여 아래에서 상세히 설명하였다.
Table 3. Computed maximum pile head settlement and maximum axial pile forces
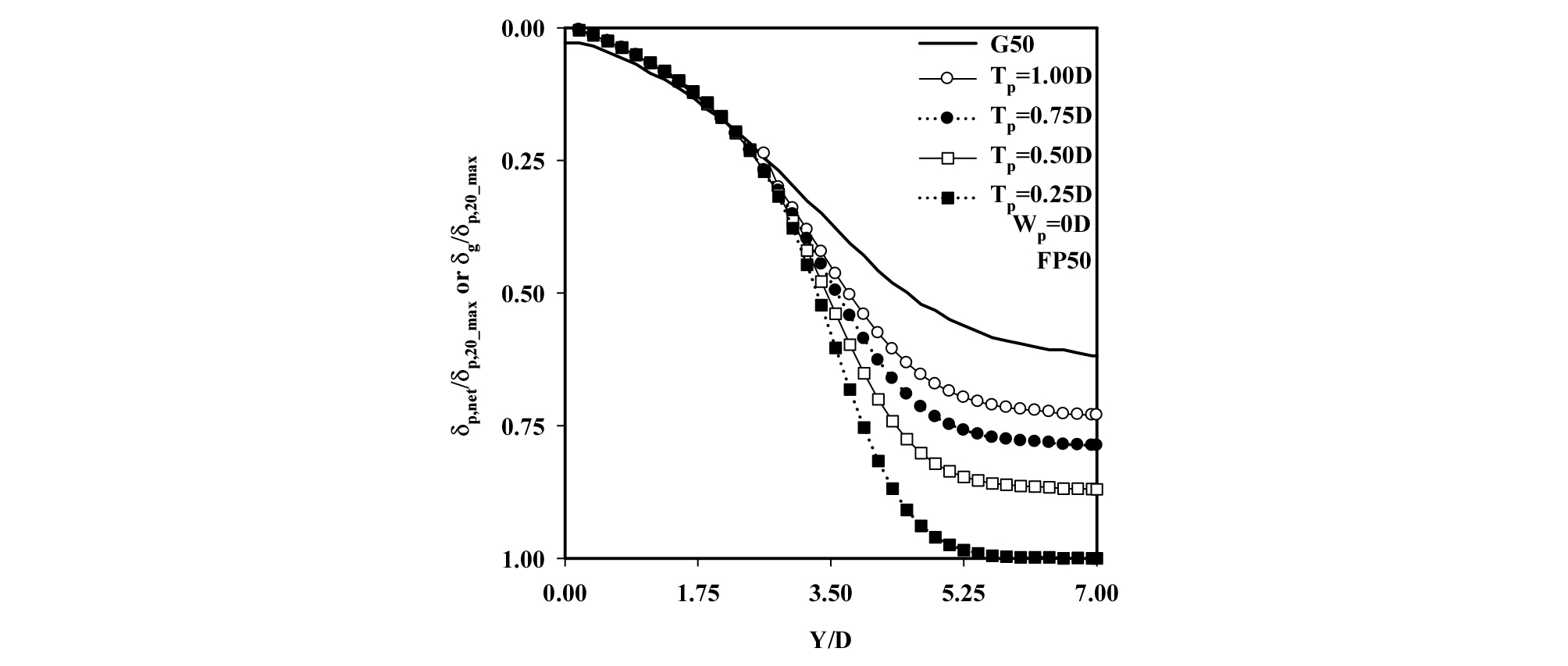
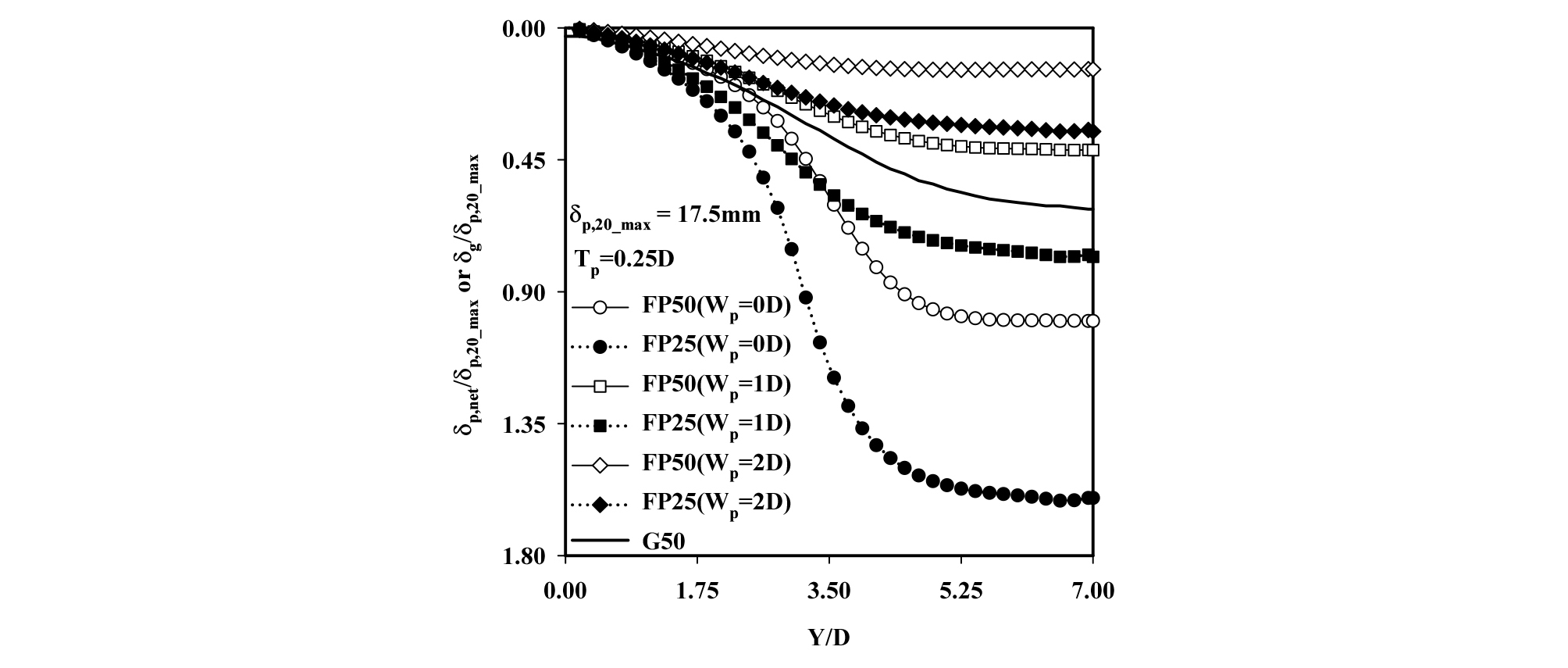
Fig. 12는 막장압 FP50 조건에서 말뚝의 선단이 터널 크라운 바로 상부(Wp = 0D)에 존재하는 경우에 대해 다양한 수직이격거리(Tp = 0.25D, 0.50D, 0.75D 및 1.00D)를 고려하여 해석을 통해 산정된 터널굴착 단계별(X/D = 0D ~ +7D) 정규화된 말뚝두부 침하(δp,net/δp,20_max) 및 지반침하(δg/δp,20_max) 분포를 보여주고 있다. 여기서, δp,net은 순수하게 터널굴착에 의해서 발생한 터널굴착 단계별 말뚝두부의 침하(tunnelling-induced pile head settlement)를 나타내며, δg는 지중에 말뚝이 존재하지 않는 Greenfield 해석조건에서 막장압 FP50 조건에 대한 말뚝 중심 위치에서의 터널굴착 단계별 지표면 침하를 의미한다. 또한, δp,20_max는 FP50 조건에서 Wp = 0D에 위치한 20 m 길이의 말뚝에 대해 터널굴착에 의해 발생한 말뚝두부의 최대침하를 의미한다(δp,20_max = 17.5 mm). Fig. 12에 나타나 있듯이 정규화된 침하 δp,net/δp,20_max 및 δg/δp,20_max은 터널의 굴착이 진행될수록 점차 증가함을 알 수 있다. 터널굴착 단계에서 말뚝두부의 침하비율이 가장 크게 발생하는 경우는 터널굴착이 말뚝 중심을 기준으로 Y/D = ±1 구간에서 수행될 경우이며, 이는 말뚝의 직하부(Y/D = 3.5) 부근을 통과할 때 이다. 또한 δp,net_max의 약 80%가 발생하였다. 여기서, δp,net_max은 tunnelling-induced 말뚝두부 최대침하를 의미한다. 그 이후 터널굴착에 따른 침하의 비율은 현저히 감소되는 것으로 분석되었다. 추가적으로 터널의 굴착이 말뚝 중심을 기준으로 ±0.5D 구간에서 수행될 경우 최대 말뚝두부 침하(δp,net_max)의 약 37%가 발생하였다. 모든 말뚝에 대해 대부분의 터널굴착 구간에서 Greenfield 조건의 지표면 침하를 초과하는 침하가 발생하였으며, 터널굴착 종료 후 말뚝선단의 수직이격거리가 증가할수록 말뚝두부의 침하는 점차적으로 감소하였으며, Tp = 0.25D, 0.50D, 0.75D 및 1.00D의 경우 δp,net/δp,20_max의 값이 각각 1.00, 0.87, 0.79 및 0.73으로 분석되었다. 특히, 터널굴착 종료 후 말뚝두부의 침하는 Tp = 1.00D 말뚝이 Tp = 0.25D 말뚝과 비교하여 약 27% 감소되는 것으로 나타났으며, 이는 지반의 침하가 터널에서부터 지표면 상부로 올라갈수록 감소하기 때문으로 판단된다.
Fig. 13은 막장압 FP50 및 FP25 조건에서 터널로부터 말뚝선단의 수직 이격거리가 일정(Tp = 0.25D, Lp = 20 m)하고 횡방향 이격거리가 변하는 경우(Wp = 0D, 0.5D 및 1D)를 고려하여 해석을 통해 산정된 터널굴착 단계별(Y/D = 0D ~ +7D) 정규화된 말뚝두부 침하(δp,net/δp,20_max) 및 지반침하(δg/δp,20_max) 분포를 보여주고 있다. 여기서, δp,net은 순수하게 터널굴착에 의해서 발생한 터널굴착 단계별 말뚝두부의 침하(tunnelling-induced pile head settlement)를 나타내며, δp,20_max는 FP50 조건에서 Wp = 0D에 위치한 20 m 길이의 말뚝에 대해 터널굴착에 의해 발생한 말뚝두부의 최대침하를 의미한다(δp,20_max = 17.5 mm). 터널굴착 종료 후 말뚝두부의 침하는 다른 타 조건의 말뚝에 비해 FP50 (Wp = 0D) 및 FP25 (Wp = 0D) 조건의 말뚝에서 큰 침하가 나타났으며, 이는 말뚝선단이 터널 크라운 바로 상부에 위치해 있으므로 터널굴착의 영향을 가장 크게 받아 지반의 침하가 크게 나타나기 때문이다. 또한, FP25 (Wp = 0D) 말뚝의 경우 터널굴착 종료에 따른 말뚝두부의 침하는 FP50 (Wp = 0D) 말뚝의 두부침하보다 약 1.6배 크게 나타났으며, FP50 (Wp = 2D) 조건의 말뚝보다는 약 11배 크게 분석되었다. FP25 (Wp = 1D) 말뚝의 경우 Y/D = 0.00~3.45 구간까지 FP50 (Wp = 0D) 말뚝 보다 큰 침하를 보였으나 말뚝두부의 최종침하는 작게 나타났다. 이는 막장압 조건 변화에 따른 터널의 굴착이 지반의 침하를 다르게 발생시키기 때문으로 판단되며, 따라서 터널굴착 영향권을 고려한 심도있는 분석이 요구된다.
3.5 말뚝의 상대변위 분포
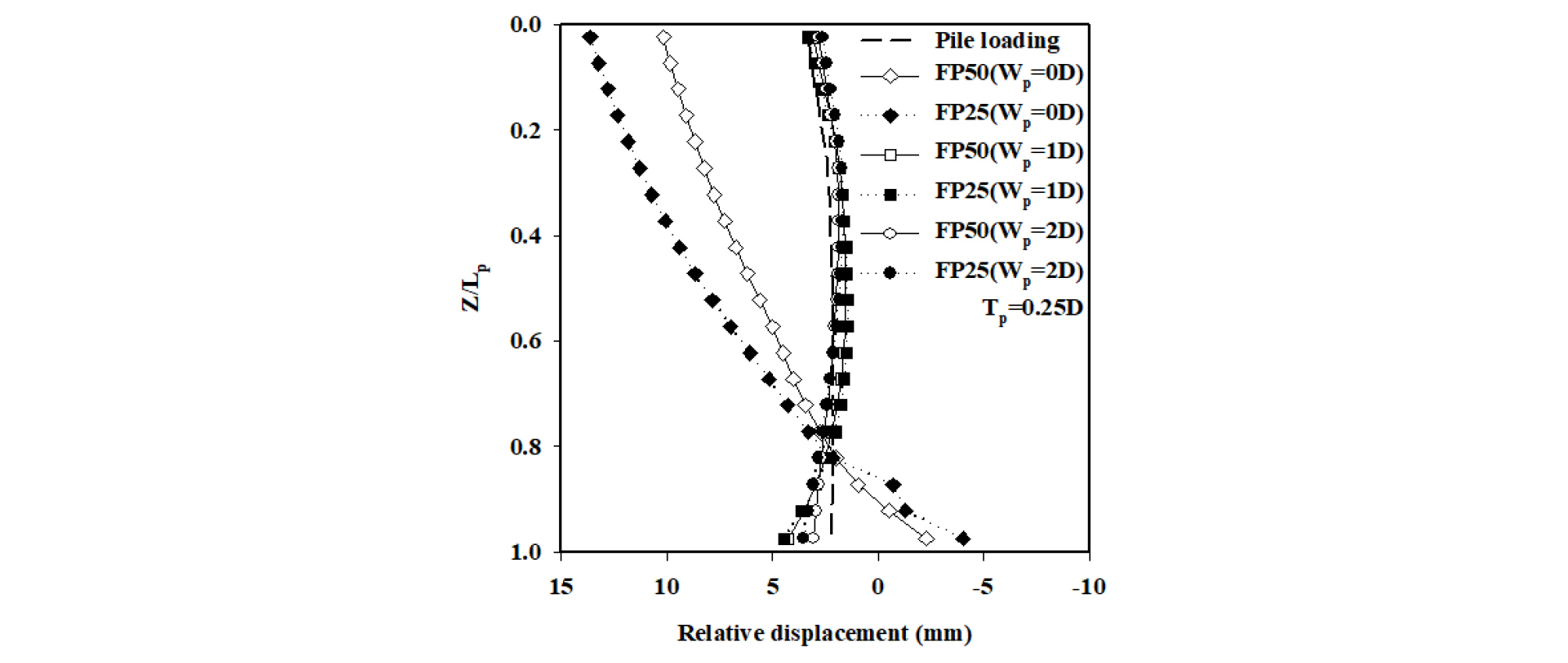
Fig. 14는 터널굴착 종료 후 막장압 FP50 및 FP25 조건에서 터널굴착에 의해 산정된 말뚝-지반 사이에 존재하는 interface 요소의 상대변위 분포를 일정한 수직 이격거리(Tp = 0.25D, Lp = 20 m)에 대하여 말뚝의 다양한 횡방향 이격거리(Wp = 0D, 1D 및 2D)를 고려하여 정규화된 말뚝의 심도(Z/Lp)에 따라 보여주고 있다. 터널굴착 이전 말뚝두부에 작용한 설계하중으로 인해 말뚝 전체 구간에서 말뚝의 침하가 지반의 침하를 초과한다. Wp = 0D에 위치한 말뚝의 경우 터널굴착 이후 말뚝에 발생된 상대변위의 값은 상당히 크게 나타났으나, Wp = 1D 및 2D에 위치한 말뚝의 경우 Wp = 0D에 위치한 말뚝과 비교하여 상대적으로 상대변위의 값이 작게 발생하였다. 즉, 말뚝 선단의 위치에 따라 상대변위의 변화 경향이 상이하므로 순수하게 터널 굴착으로 인해서 유발된 상대변위(tunnelling-induced relative shear displacement)를 검토할 필요가 있다.
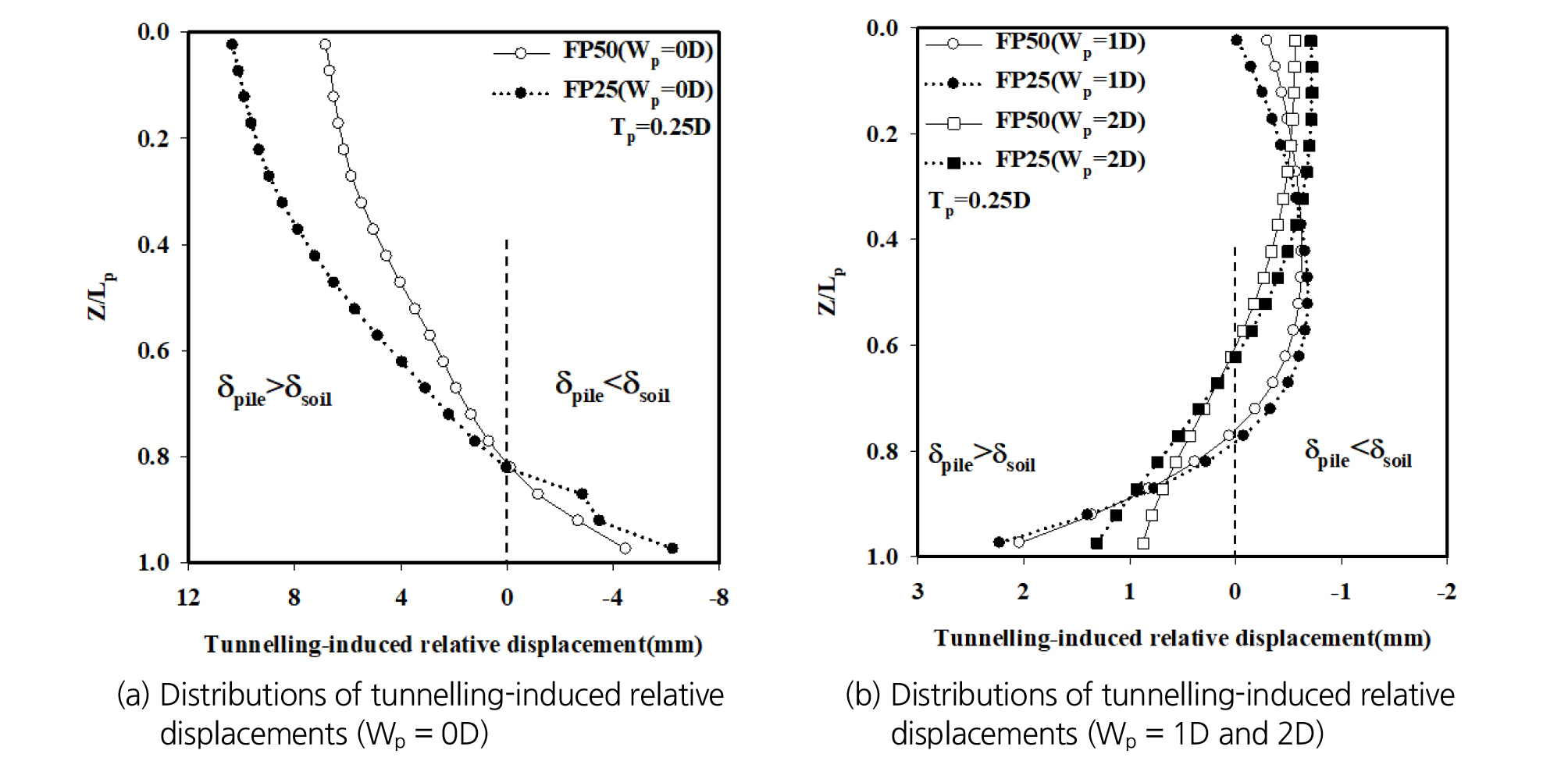
Fig. 15(a) 및 15(b)는 막장압 FP50 및 FP25 조건에서 tunnelling-induced 상대변위의 분포를 일정한 수직 이격거리(Tp = 0.25D, Lp = 20 m)에 대하여 말뚝의 다양한 횡방향 이격거리(Wp = 0D, 1D 및 2D)를 고려하여 정규화된 말뚝의 심도(Z/Lp)에 따라 보여주고 있다. 막장압 FP25 조건의 경우 FP50 조건에 비해 상대적으로 큰 상대변위가 발생하였으며, 이로 인해 말뚝에 작용하는 전단응력 값 또한 FP25 조건이 FP50 조건 보다 크게 나타난다. Wp = 0D에 위치한 말뚝의 경우 터널굴착 종료 후 말뚝두부에서 약 Z/Lp = 0.8 부근까지는 말뚝의 침하가 인접지반의 침하를 초과하고 있으며, 그 하부에서는 반대의 경향을 보인다. 즉, Z/Lp = 0.8 부터 말뚝선단까지는 터널굴착으로 인한 지반침하로 하향의 마찰력이 말뚝에 작용하며, 반대로 말뚝두부에서 Z/Lp = 0.8 까지는 지반이 말뚝의 침하에 대해 저항하는 형태의 상향의 마찰 저항력이 발현되는 것으로 보인다. 따라서 앞서 설명한 전단응력의 분포를 tunnelling-induced 상대변위를 통하여 재차 입증하였다. 추가적으로 Wp = 1D 및 2D에 위치한 말뚝의 경우 Wp = 0D 조건의 말뚝과 반대의 경향이 나타났으며, 이는 앞서 설명되어진 것을 다시 한 번 입증하였다.
3.6 기존연구를 통한 말뚝 비교 분석
Fig. 16은 Dias and Bezuijen (2014b)에 의해 보고된 연구 결과의 일부분을 인용하였으며, 지표면 최대침하(δgr_max)에 대한 순수하게 터널굴착으로 유발된 말뚝두부의 침하(Pnet)의 비()를 정규화된 심도() 및 정규화된 횡방향 이격거리()에 따라 보여준다. 또한, Fig. 16에 나타낸 표시점(mark)들은 말뚝 선단의 위치를 의미하며 기존 연구들의 결과 값을 표시점 옆에 나타냈다. 여기서, Z는 지표면에서부터 터널중심부까지의 거리를 의미하며 Lp, Wp 및 D는 Fig. 3(a)에 표시했다. 추가적으로 본 연구에서 수행된 수치해석의 결과 값은 네모칸(box)으로 나타냈다. = 0.0~0.5 사이에 존재하는 말뚝은 Jacobsz et al. (2004)에 의해 제안된 0.77을 제외하고 모두 1보다 큰 값을 보이며, 이러한 결과 값은 본 연구에서 수행된 수치해석의 결과값과 유사하게 나타났다. 또한, 말뚝의 선단이 = 0.5~1.5 사이에 존재하는 경우에 의 값은 1보다 크거나 작게 나타나는 다양한 분포를 보였다. 터널로부터 횡방향 이격거리()가 1.5를 초과하는 말뚝의 경우 기존 연구 및 본 연구에서 수행된 수치해석 모두 의 값이 1보다 작게 계산되었다. 여기서, 의 값이 1을 초과하는 경우 말뚝 두부의 침하가 지반의 침하를 초과하는 것을 의미하며, 1을 초과하지 않는 경우는 반대의 경향을 의미한다. 또한, Fig. 16에는 Selemetas et al. (2005)에 의해 보고된 터널굴착 영향권이 표시되어 있으며, Selemetas et al. (2005)에 의하면 Zone A에 존재하는 말뚝의 경우 말뚝의 침하가 지반의 침하를 초과한다고 보고하였다. 추가적으로 Zone B의 경우 말뚝침하와 지반의 침하가 같고 Zone C의 경우 지반의 침하가 말뚝 침하를 초과한다고 제안하였다. 이와 같이 기존 연구 및 본 연구에서 수행된 수치해석의 결과 모두 Selemetas et al. (2005)이 제안한 터널굴착 영향권과 비슷한 경향이 나타났다.
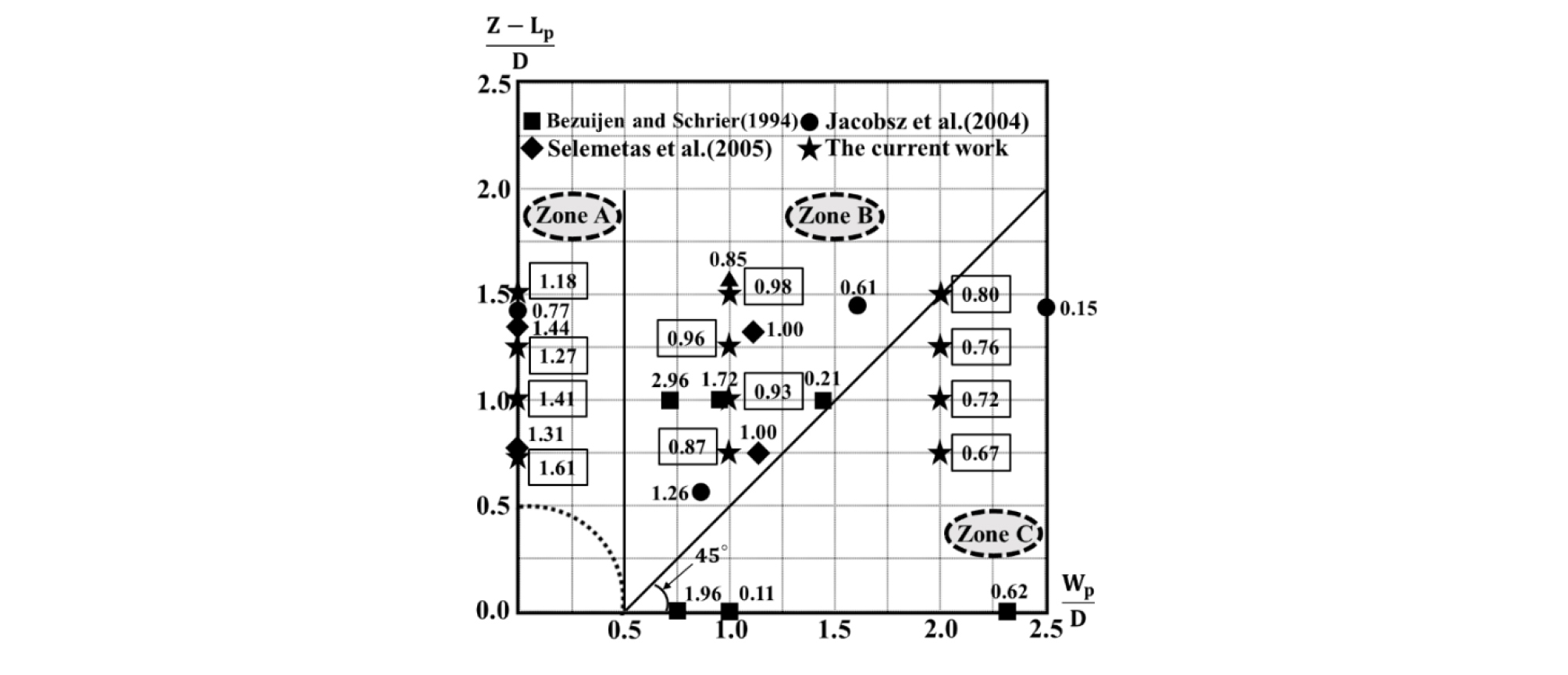
Fig. 16.
Pile/Surface settlement ratio calculated on current works and reported on literature (Dias and Bezuijen, 2014b)
Fig. 17(a) 및 17(b)는 Dias and Bezuijen (2014b)에 의해 보고된 연구 결과의 일부분을 인용하였으며, 정규화된 심도() 및 정규화된 횡방향 이격거리()에 따라 말뚝 선단의 위치를 고려하여 Fig. 17(a)에 표시된 말뚝선단 위치에서의 tunnelling-induced 말뚝 축력분포를 Fig. 17(b)에 보여주고 있다. 여기서, C1, C2, C3 및 C4의 경우 본 연구에서 수행된 막장압 50% 상태의 말뚝의 축력분포 의미한다. 터널 크라운 상부에 위치한 S1, C1, S2 및 C2 말뚝의 경우 말뚝 축력분포가 모두 (-) 부호로 나타났으며, 이는 인장력을 의미한다. C1 및 C2 말뚝의 경우 인접한 S1 및 S2 말뚝에 비해 상대적으로 큰 축력의 값이 나타났으나 말뚝에 발생한 축력분포의 경향은 전반적으로 비슷하게 발생하였다. 반면, 터널의 측면에 가장 인접하게 위치한 L1 및 F1 말뚝의 경우 압축력 형태의 축력 분포가 보고되어졌다. 이는 터널 크라운 바로 상부에 위치한 말뚝과 비교하여 반대의 축력분포를 보여주며 다시 말해 터널로부터 근접한 위치에 존재하는 말뚝이라도 터널-말뚝선단의 상대위치에 따라 말뚝의 거동이 상이하게 나타나는 것을 의미한다. 따라서 터널굴착 영향권 및 터널-말뚝의 상대위치를 고려한 지속적인 연구가 필요할 것으로 판단된다.
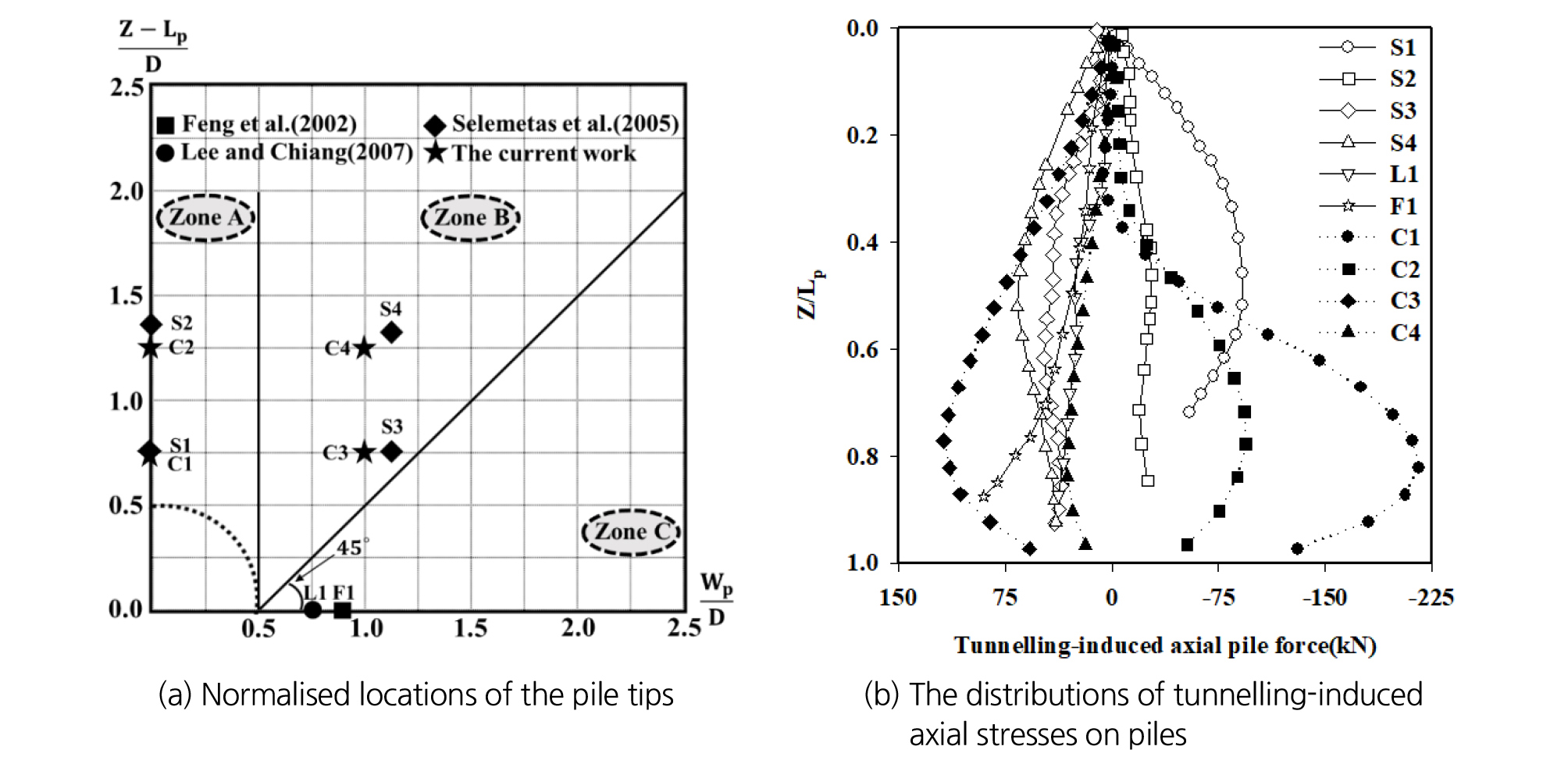
Fig. 17.
Axial pile stresses from the current works and reported in literatures (Dias and Bezuijen, 2014b), S: Selemetas et al. (2005) [F: Feng et al. (2002), L: Lee and Chiang (2007), C: Current study]
4. 요약 및 결론
본 연구에서는 3차원 유한요소 해석을 실시하여 막장압의 크기 및 말뚝선단의 위치를 고려한 shield TBM 터널굴착을 모사함으로써 근접 터널시공으로 발생하는 말뚝의 거동분석을 수행하였다. 이를 통해 터널굴착으로 유발된 말뚝침하, 축력, 전단응력 및 상대변위를 분석하였고 그 결과 다음과 같은 결론을 도출하였다.
말뚝의 선단이 터널 크라운(crown) 상부에 위치할 경우 말뚝두부의 침하는 greenfield 조건의 지표면 침하를 초과하는 침하가 나타났다. 또한 터널굴착 단계에서 말뚝 두부의 침하는 터널이 말뚝선단 하부를 통과하는 Y/D = ±1.0 구간에서 가장 크게 발생하였으며, 최종침하의 약 80%가 이 구간에서 나타났다. 터널 크라운 상부에 위치한 말뚝에 대하여 초기수평토압의 25%를 적용한 막장압에서의(FP25) 말뚝두부의 침하는 초기수평토압의 50%를 고려한 막장압 조건(FP50)의 말뚝 두부침하보다 약 1.6배 크게 발생하였다. 반면, 터널로부터 가장 멀리 이격된 FP50 조건의 말뚝의 경우 말뚝의 침하가 가장 작게 나타났으며, 말뚝의 침하가 가장 크게 발생한 조건에 대비하여 약 10%의 말뚝침하가 발생하였다.
터널 크라운 상부에 위치한 말뚝의 경우 tunnelling-induced 인장력의 값은 말뚝 심도가 증가할수록 감소하였으며, 이는 기 연구자료와 같게 나타났다. 말뚝에 작용한 정규화된 최대 인장력의 값은 터널굴착 영향권 내부에 위치한 FP25 조건의 말뚝에서 Pnet/Pa = -0.45로 발생하였다. 반면, 말뚝에 작용하는 정규화된 최대 압축력의 값은 터널굴착 영향권 외부에 위치한 FP25 조건의 말뚝에서 Pnet/Pa = 0.20으로 나타났다. 따라서 말뚝의 거동은 터널과 말뚝의 상대적인 위치에 큰 영향을 받는 것으로 관찰되었다.
터널굴착 영향권 내부인 Wp = 0D에 위치한 말뚝의 경우 말뚝의 상부에서는 상향의 전단응력이 발생하고 말뚝의 하부에서는 하향의 전단응력이 발생한다. 반면, 터널굴착 영향권 외부인 Wp = 1D 및 2D에 위치한 말뚝에서는 터널굴착 영향권 내부의 말뚝과 반대로 말뚝의 상부에서는 하향의 전단응력이, 말뚝의 하부에서는 상향의 전단응력이 나타났다. 상대전단변위의 경우 막장압 FP25 조건이 막장압 FP50 조건에 비해 상대적으로 크게 나타났으며, 이는 전단응력의 분포에 직접적으로 반영되었다.
기 연구자료를 바탕으로 본 연구 결과와의 비교분석을 실시한 결과 터널굴착 영향권 내부에 존재하는 말뚝의 경우 대부분의 말뚝에서 지표면 침하에 대한 말뚝 두부침하의 비가 1보다 크게 나타났다. 반면, 터널굴착 영향권 외부에 존재하는 말뚝의 경우 기존 연구 및 본 연구에서 수행된 결과 모두 Pnet/δgr_max의 값이 1보다 작게 계산되었다. 이와 같이 기존 연구 및 본 연구에서 수행된 수치해석의 결과 모두 제시된 터널굴착 영향권과 비슷한 경향이 나타나 본 연구의 타당성을 입증하였으며, 터널과 말뚝선단의 상대위치 및 막장압의 크기 변화에 따라 말뚝의 거동이 상이하게 나타나므로 이에 대한 추가적인 연구가 필요할 것으로 판단된다.