1. 서 론

국내에서 지하공동 발생으로 기인한 지반함몰 현상이 최근 빈번하게 발생하는 추세이다. Choi et al. (2016)에 의하면, 지반함몰은 보통 지중매설관의 노후 및 접합 불량 등에 기인한 누수에 의해서 발생하거나, 터널 굴착 및 지하구조물 시공 시 잘못된 공법의 선택 또는 관리 부실로 인한 지하수의 유입으로 지하공동이 발생되어 일어난다고 제시하였다. 정부에서는 이러한 국민 불안감 해소를 위한 방안으로 2018년 1월을 기점으로 지하안전관리에 관한 특별법을 시행하였다. 지난 1년여 간의 제도 시행에 따라서 많은 전문기관에서 지하 굴착 시 안전영향에 대한 보고서 작성 및 평가 등의 과정을 통해서 경험을 축적 중이다. 하지만, 이제 시작단계이기 때문에 많은 개선과 보완이 이루어져야 할 것으로 판단된다. 특히, 지하 굴착공사 완료 후, 운영 단계에 있는 건설구조물 인근에 대한 지반조사로 지하공동이 발견되면, 이에 대한 안정성 평가를 위한 절차가 세부적으로 제시되고 있지 않은 상황이다. 이에 본 연구진은 소규모 지하공동의 형상을 고려한 전단강도감소기법(shear strength reduction method, SSRM) 기반의 안정성 평가에 관한 선행 연구를 수행하였다. 지하공동의 형상을 타원형, 원형 및 구(sphere)형으로 구분해서 형상 별 안전율 경향을 분석하였다. 연구를 통해서 지하공동에 대한 SSRM 기반의 지반 안정성 평가가 가능하다는 결과를 제시하였다(An et al., 2018a, An et al., 2018b).

SSRM은 전통적으로 사면안정해석에 많이 사용되고 있다. 사면의 안전율 산정 시, 한계평형법 기반의 결과와 유한요소해석에 포함되는 SSRM으로 산정된 결과는 오차 범위 안에서 일치한다는 연구 결과가 다수 제시되었다(Matsui and San, 1992; Cheng et al., 2007; Fu and Liao, 2010). 본 연구에서는 사면안정해석 시 잠재 파괴면 근처에 소규모 지하공동이 존재하는 경우를 가정하여, SSRM 수행 과정에서 지하공동과 잠재파괴면과의 상호 영향관계를 파악하는 것에 주안점을 두었다. 지하공동 발생이 사면의 안정성에 미치는 영향에 대해서 파악하였다.

많은 연구자들이 SSRM을 사용해서 지하공동 및 사면의 안정성 평가 방법을 제안하였다. Park and You (1998)는 절리암반 터널 안정성 평가에 대해서 SSRM을 적용한 안전율 기반의 수치해석적 접근을 시도하였다. FLAC 2D 프로그램에서 구현 가능한 편재절리모델(ubiquitous joint model)을 사용해서 연구를 수행하였다. Song et al. (2002)은 석탄광 주변에 건설되는 터널이 채굴공동의 붕락으로 인해 지반침하에 미치는 영향에 대해서 연구하였다. 2차원 FDM 수치해석 프로그램인 FLAC2D를 사용하여 채굴공동이 터널에 미치는 영향을 분석하였다. Drumm et al. (2009)은 석회암 공동발달지역의 잔적토 지반함몰에 대한 안정성 평가 연구를 수행하였고, 연구 결과를 기반으로 한 안정성 도표를 제안하였다. 구형 공동을 4분원 형태로 모델링하여 적용하였으며, 내부마찰각($\varphi$)의 범위에 따른 불안정 영역을 도표로 제시하였다. 2차원 FEM 지반 범용해석 프로그램인 $Phas{e}^2$를 사용하여 SSRM을 통한 안전율을 산정하였다. Matsui and San (1992)은 유한요소법에 기반한 사면안정해석을 위한 SSRM을 검증하는 연구를 수행하였다. 전단변형율의 파괴기준이 사면의 잠재파괴면으로 정의됨을 검증하였다. Bishop법 등 사면안정해석에 널리 사용되는 한계평형법(limit equilibrium method, LEM)과의 결과 비교를 통해서 연구를 수행하였다. Cheng et al. (2007)은 LEM과 SSRM을 비교하는 연구를 수행하였고, 단일 지층의 경우에는 $\varphi$가 0인 경우를 제외하면 두 방법이 잘 일치하며, 지반 물성치(soil parameter) 및 해석 영역 크기(domain size)는 일반적으로 민감하지 않다고 제시하였다. Fu and Liao (2010)는 Hoek-Brown 모델에 SSRM을 적용하기 위한 연구를 수행하였고, 동일 방법으로 Hoek-Brown 이외에 다른 비선형 파괴 기준에도 적용할 수 있는 방법임을 제시하였다. Hammah et al. (2007)은 blocky/jointed 상태의 암반에 대해서 SSRM을 적용하기 위한 연구를 수행하였다. 개별요소법 프로그램인 UDEC의 결과와 FEM 프로그램으로 수행한 연구 결과를 비교하여 신뢰성을 확보했다고 제시하였다. Lee and Jang (2010)은 석회석 광산에서 암반사면의 전체적인 거동을 파악하기 위해 유한요소법 기반의 SSRM을 이용한 연구를 수행하였다.

하지만, 전술한 선행 연구들은 사면안정해석에 관한 SSRM 적용에 관한 독립적인 연구 또는 지하공동에 관한 안정성 평가를 위한 SSRM 적용성에 관한 독립적인 연구이다. 사면의 잠재파괴면 근처에 지하공동이 발생한 경우에 대해서 동시 조건으로 SSRM을 적용한 연구 사례는 없었던 것으로 판단된다.

본 연구는 빙하학(glaciology)으로부터 영감을 받아서 진행되었다. Fowler (1987)는 빙하 속에 존재하는 공동(subglacial cavitation)이 빙하 덩어리의 기반 경계면에서 슬라이딩 활동에 영향을 미치고 있다고 제시하였다. 공동의 존재가 빙하 내 배수통로 시스템 확장으로 전개되고, 이후 빙하 덩어리 내부의 배수속도가 빨라져서 최종적으로는 공동이 빙하 덩어리의 유효압력(effective pressure)을 감소시켜서 슬라이딩 활동을 촉진한다고 제시하였다.

본 연구에서는 지반범용 유한차분해석 프로그램인 FLAC3D (Itasca Consulting Group, Inc., 2017)를 사용하였고, SSRM이 일반적으로 사용되고 있는 사면안정해석 분야에 적용성을 검토해보고자 사면 상부에 존재하는 도로 또는 사면 내 소단 부근 하부 지반에서 발생 가능한 소규모 지하공동을 대상으로 하였다. 지하공동이 없는 사면에 대한 잠재파괴면의 위치를 파악하고, 잠재파괴면 부근에 지하공동이 발생한 경우를 가정하여 SSRM을 수행한 후, 지하공동의 존재가 사면 안전율 산정 시 미치는 영향에 대한 연구를 수행하였다.

2. 국내외 산악지형 및 사면 내 지하공동

지하안전관리에 관한 특별법이 시행됨에 따라서 국내 대다수 설계기준에서 지하공동에 대한 사항들이 추가되어 반영되고 있는 실정이다. 예를 들어, 한국철도시설공단의 철도설계기준 터널조사 편(KR, 2017)에서는 터널 계획 시 지하공동 및 싱크홀의 유무, 규모, 상태, 발생원인 등을 확인하기 위한 조사를 실시하여야 한다고 개정된 내용을 반영하였다. 터널 시공 시 용출수 및 지하수위 측정 등을 통해 주변 지하수 변동을 파악하여야 하고, 터널 시공에 의해 영향을 받을 수 있는 범위를 선정한 후, 이 범위에 포함되는 근접구조물 및 매설물(상하수도관, 송유관, 통신 및 전력 케이블, 도시가스관, 기타 지중 구조물 등)에 대하여 각 시설의 관리 주체 및 관리대장, 노후도, 장래확장 계획 여부를 조사하고 누수 등으로 인하여 지반함몰이 예상되는 경우에는 상세조사를 시행하여 설계 시 기초자료로 활용한다고 제시하였다. 산악지형에 대해서는 예외조항을 두어 지하공동 조사를 생략하는 경우도 있지만, 터널 갱구부 사면 등 주요 지역에 대해서는 지하공동에 대한 조사가 필수적으로 이루어져야 할 것으로 판단된다. 본 장에서는 산악지형에 발생 가능성이 있는 지하공동의 유형을 조사하였다.

2.1 석회암 지대에서의 지하공동

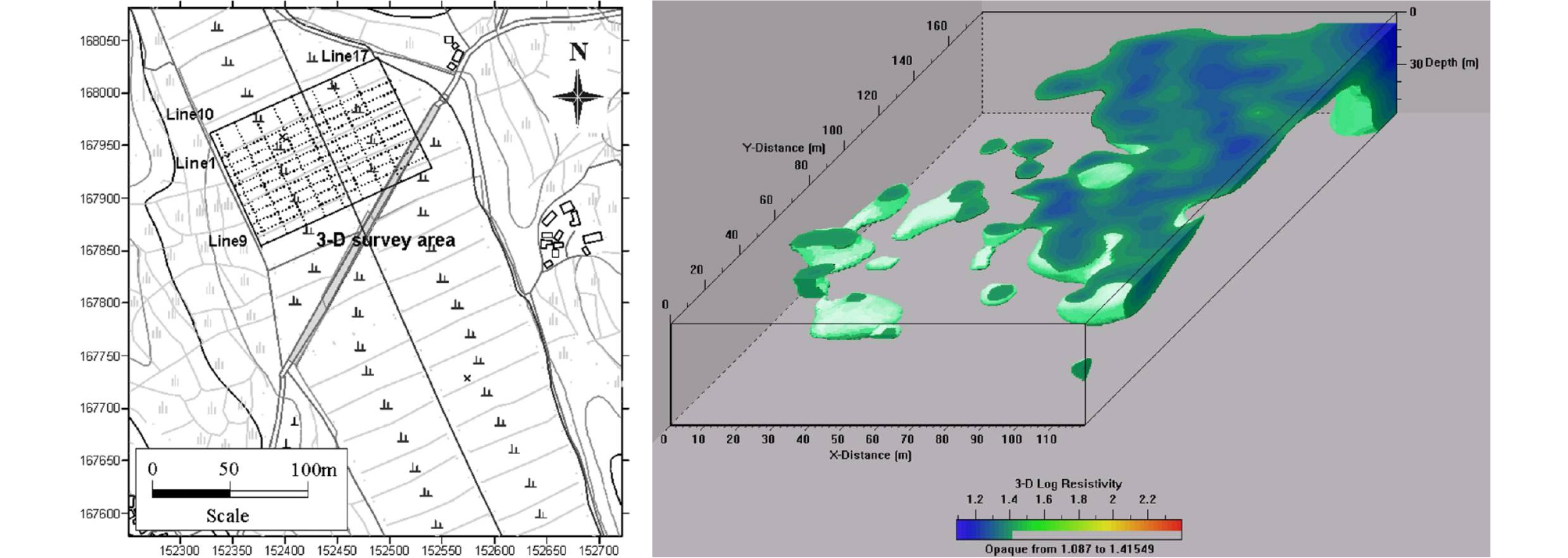
카르스트(Karst) 지형은 석회암 등 물에 용해되기 쉬운 암석으로 구성되어 우수 또는 지하수 등에 의한 용해 작용이 발생된 지형을 말한다. 이러한 카르스트 지형에서는 지반 안정성에 위해 요소로 평가할 수 있는 지하공동의 발달이 필연적으로 발생한다. El Aal (2017)은 사우디아라비아 수도인 리야드(Riyadh) 인근 Tuwaiq 산 지역의 지하공동 조사 및 처리 방안에 대한 연구를 수행하였다. 지표면 근처의 연약 지반 내에 존재하는 지하공동이 지반함몰, 도로 및 건축구조물의 붕괴사고로 이어질 수 있음을 제시하였다. Fig. 1에서는 전기비저항탐사 방법으로 발견한 Tuwaiq 산 지표 근처의 지하공동을 보여주고 있다. 국내에서도 석회암 지대에 대한 지하공동 탐사는 지속적으로 이루어지고 있다. Park et al. (2006)은 석회규산염암 공동에 의한 지반침하 지역에 3차원 전기비저항탐사를 실시하여 지하공동 영상화 작업을 시도하였다. Fig. 2에서는 석회규산염암이 분포하고 있는 전라남도 무안군 용월리 일대에서 실시한 전기비저항탐사 결과 및 지하공동의 분포를 보여주고 있다.

Fig. 1.

(a) Stratigraphic columnar section of Jabal Tuwaiq Formation illustrating the upper and lower contact, (b) and (c) solution side wall developed caves. The Tuwaiq Mountain Limestone foundation bedrock (d), (e) and (f) the occurrences of caves and open fractures and (g) solution of side caves affecting the side wall rocks (El Aal, 2017)

Fig. 2.

3-D electrical resistivity survey (Park et al., 2006)

2.2 사면 내 지하공동

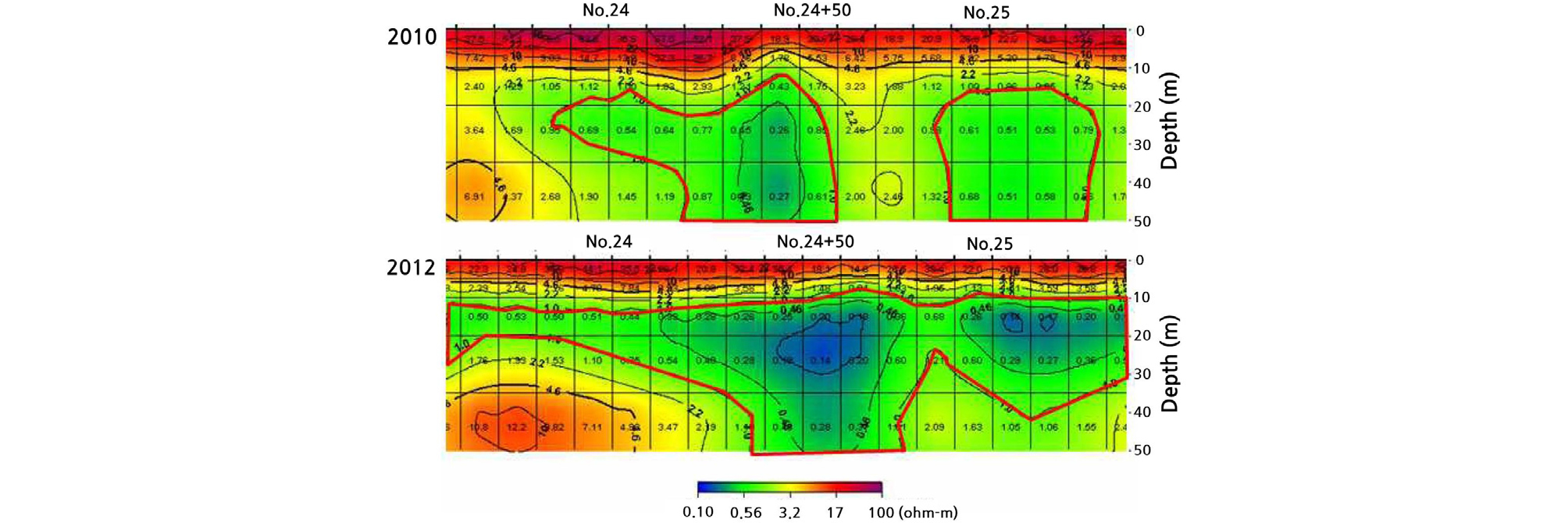
아직까지 보고된 사례가 드물긴 하지만, 도심지에서는 노후된 상하수관의 누수로 인한 소규모 지하공동의 발생사례가 많다. 이에 비추어 판단해보면, 사면 상부에 위치한 도로 구조물 또는 사면 측구에 존재하는 배수로 주변 또는 사면 선단부에서는 지하공동이 발생할 가능성이 많은 것으로 판단된다. 다른 유형으로 판단되지만, 댐 및 방조제에서는 필연적으로 사면이 형성된다. 이러한 사면을 포함한 구조물에 대해서는 다양한 지구물리학적 방법으로 유지관리에 노력하고 있는 실정이다. Yong et al. (2013)은 지구물리학적 방법을 이용한 방조제 유지 및 관리 체계를 제안하는 연구를 수행하였다. Fig. 3에서는 새만금 2호 방조제 내측사면 아래 5 m 이격된 제체 종방향 측선을 따라 2차원 전기비저항 탐사를 수행한 형상을 보여주고, Fig. 4에서는 발견된 사면 내 이상대를 가시화한 형상을 보여주고 있다. 이러한 이상대가 지하공동이라고 정확하게 평가하기는 무리가 따르지만, 사면활동에 영향을 미치는 인자임은 분명한 사실이다. Park and Kim (2013)은 연구에서도 취약대가 존재하는 제방의 누수 탐지를 위한 전기비저항 탐사의 적용성을 파악하였다. 이러한 취약대를 지하공동으로 모사하지는 않았지만, 누수가 발생하는 통로로 판단하고 실내시험 및 수치해석을 수행하였다.

Fig. 3.

Survey lines for 3D resistivity monitoring on sea dike 2 (Yong et al., 2013)

Fig. 4.

Comparison results for an inverted section on sea dike 2 (Yong et al., 2013)

2장에서 살펴본 바와 같이, 사면활동에 대한 안정성 평가에 지하공동이 영향을 미칠 수 있을 것으로 판단된다. 이러한 인과관계를 파악해보기 위해서, 본 연구에서는 지하공동의 크기 변화 및 위치 변화 등에 따른 사면안정해석을 전단강도감소기법 기반으로 수행하였다.

3. 전단강도감소기법 적용 분야

3.1 터널 및 지하공동 안정성 평가

터널 굴착, 광산 갱도 굴착, 지하저장시설 구축을 위한 굴착 등으로 발생되는 인공적인 지하공동에 대해서는 안전율 기반의 안정성 평가 관련 연구가 다수 보고되었다. Park and You (1998)는 연약암반층에 굴착된 터널의 안전율을 산정하기 위해서 SSRM을 사용하는 기법을 제시하였다. 지반의 강도정수인 점착력($c$)과 내부마찰각($\varphi$)을 시험안전율($F^{trial}$)로 시행착오법을 수행하여 안전율을 계산한다. Fig. 5에서는 전단강도와 감소된 전단강도의 관계를 보여주고 있다. 원래의 강도정수 값을 선형 감소시켜서 식 (1)과 식 (2)의 관계를 부여한다. 터널의 파괴가 발생되기 시작하는 시점의 시험안전율을 구하면, 그 값이 터널의 안전율이 된다. Fig. 5 및 식 (1), (2)는 3.2절에서 기술한 사면의 안정성 평가에서도 동일한 원리로 사용된다.

Fig. 5.

Shear strength and trial shear strength relationship (Park and You, 1998)

3.2 사면의 안정성 평가

Park et al. (1999)은 절편법과 유한차분법에 의한 사면안정해석 방법을 비교하는 연구를 수행하였다. 이 연구에서는 사면안정해석 대해서 유한차분법 기반의 전단강도감소기법을 사용하였다. 사용 원리 및 물성치 정의는 3.1절의 내용과 동일하다. Fig. 6에서는 수치해석에 사용한 흐름도를 보여주고 있다. 전단강도를 점진적으로 낮추어 가며 한계상태를 찾아내는 방법도 있지만, 이 연구에서는 이분법(bisection method)을 사용해서 상대적으로 해석속도를 빠르게 하였다. Fig. 6에서 보는 바와 같이 안전율의 상한값($F^{UL}$)과 하한값($F^{LL}$)의 차이가 규정된 오차율(tolerance)보다 작게 되면 해석을 종료하도록 하였다.

Fig. 6.

Flow chart of the routine for the calculation of factor of safety (Park et al., 1999)

3.3 연구에 사용된 전단강도감소기법 흐름도

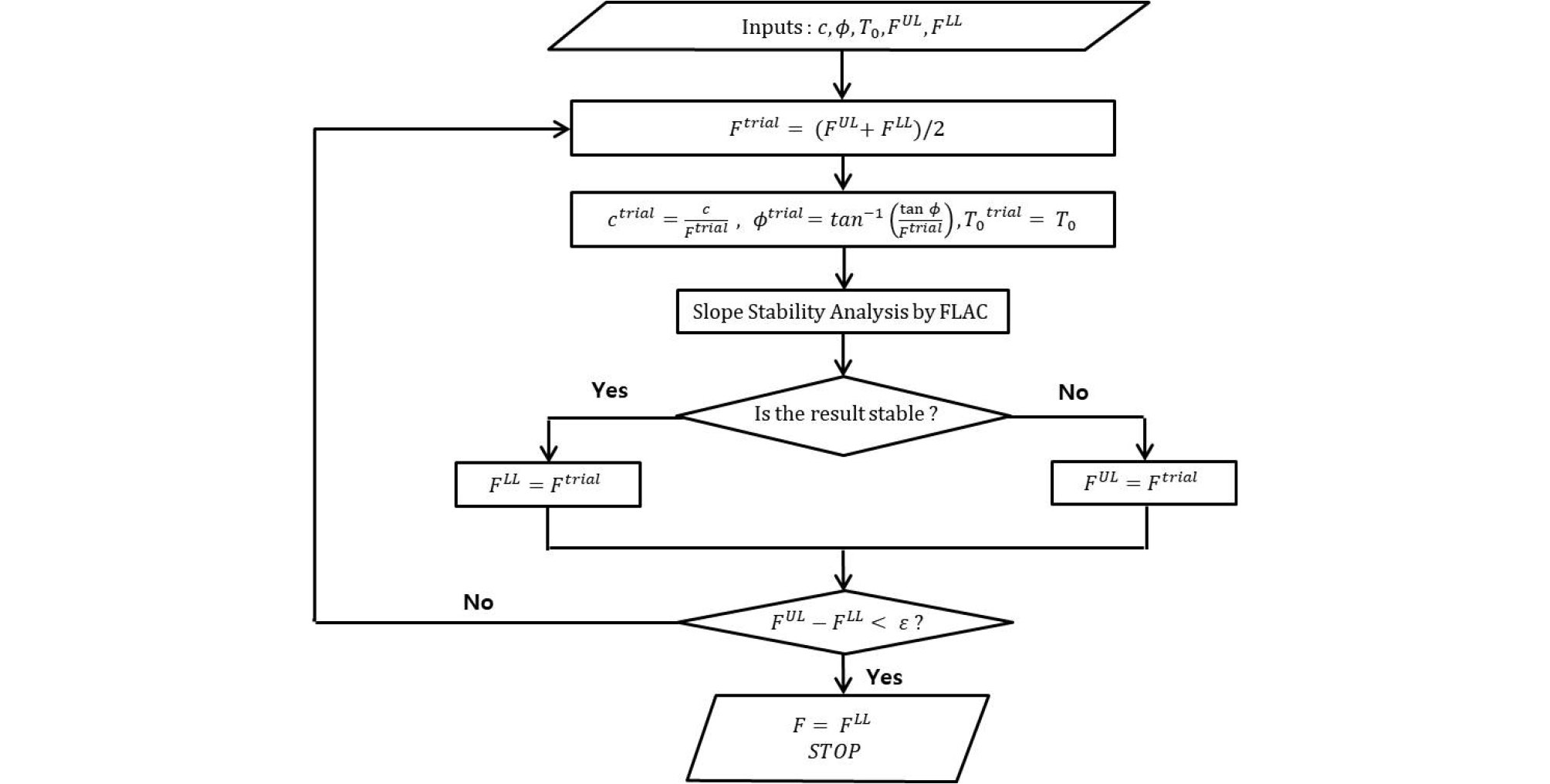
Fig. 7에서는 본 연구에서 사용된 FLAC3D 프로그램에서 지원하는 SSRM 기반의 안전율(Factor of Safety, FS) 계산과정에 대한 흐름도를 보여주고 있다. 일반적으로 SSRM을 많이 사용하고 있는 사면안정해석 분야에서는 FS > 1.0인 안정화되어 있는 사면에 대해서 지반강도정수($c,\varphi$)를 감소시켜서 전단변형율 속도(shear strain rate)가 크게 발생되는 위치를 탐색하여 파괴면을 제시하고, 원지반전단강도 대비 파괴양상이 뚜렷해질 때까지 감소시킨 전단강도의 비를 안전율로 산정한다. 하지만, 파괴된 사면 또는 상대적으로 얕은 심도에서 발견된 소규모 지하공동 등은 FS가 1보다 작은 상태에서 SSRM을 수행한다. 이러한 경우에는 전단강도 값을 감소시키는 것이 아니고, 오히려 FS ≒ 1.0이 될 때까지 증가시켜서 SSRM을 수행해야 한다. 이러한 전단강도 감소 및 증가의 두 가지 경우를 고려해서 SSRM을 수행하기 위해서는 Fig. 7의 오른쪽에서와 보는 바와 같이 불안정/안정(unstable/stable) 상태에 대한 확인과정을 거쳐야 한다. $F_{low}$와 $F_{up}$는 사용자 정의에 의한 시행안전율($F^{trial}$)의 하한 값과 상한 값, $N$값은 탄소성 해석의 반복계산 회수, $R$값은 탄소성 해석의 수렴율(convergence tolerance)이다. 또한, $F_{diff}$는 계산된 시행안전율의 상한 값과 하한 값의 차이를 말하며, 본 연구에서 표기한 모든 안전율은 $F_{diff}$가 0.005 미만인 시행안전율($F^{trial}$)을 의미한다.

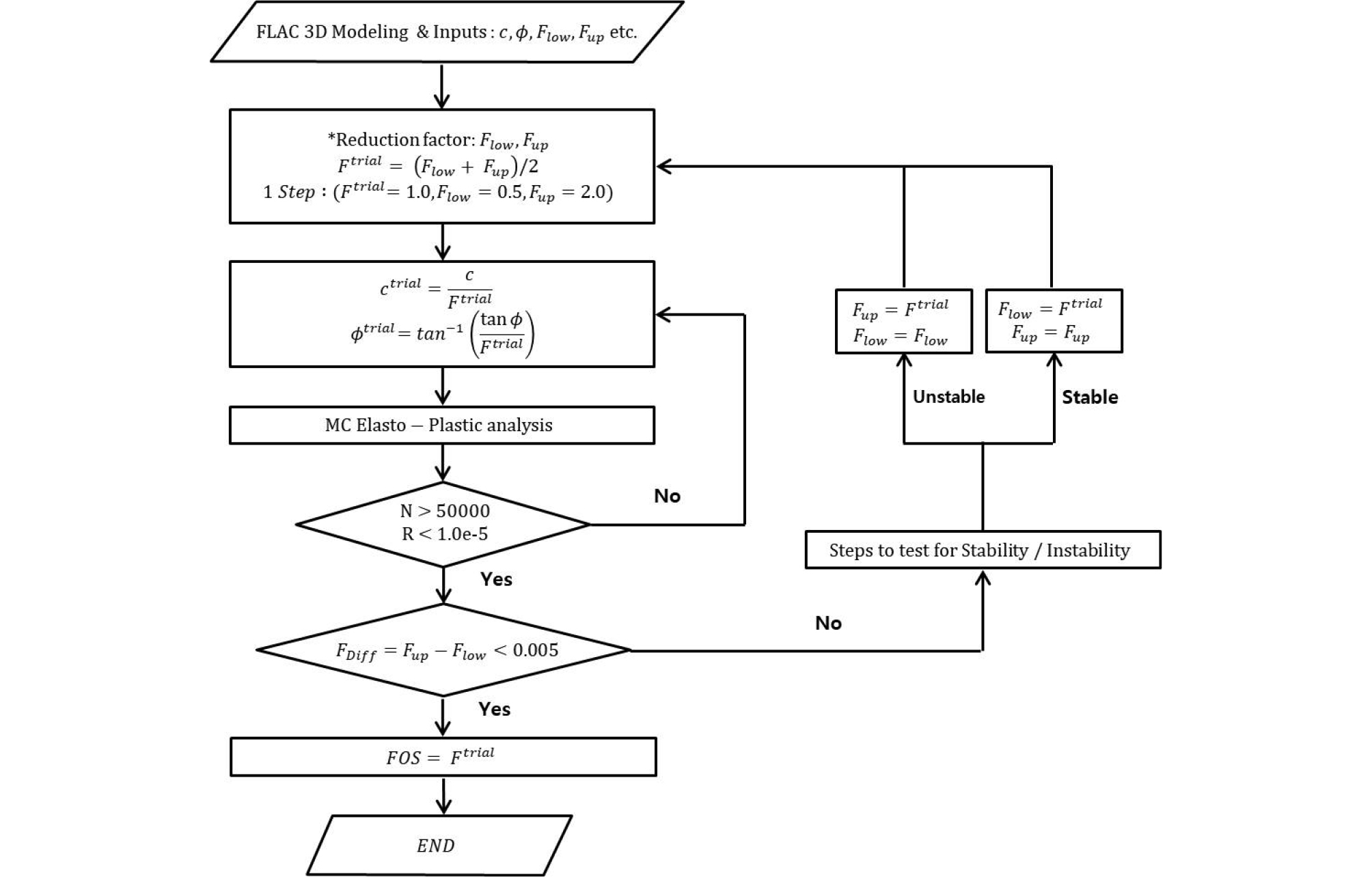
Fig. 7.

Flowchart for the procedure of FLAC3D safety factor calculation by SSRM (Itasca Consulting Group, Inc., 2017)

4. 전단강도감소기법을 사용한 수치해석

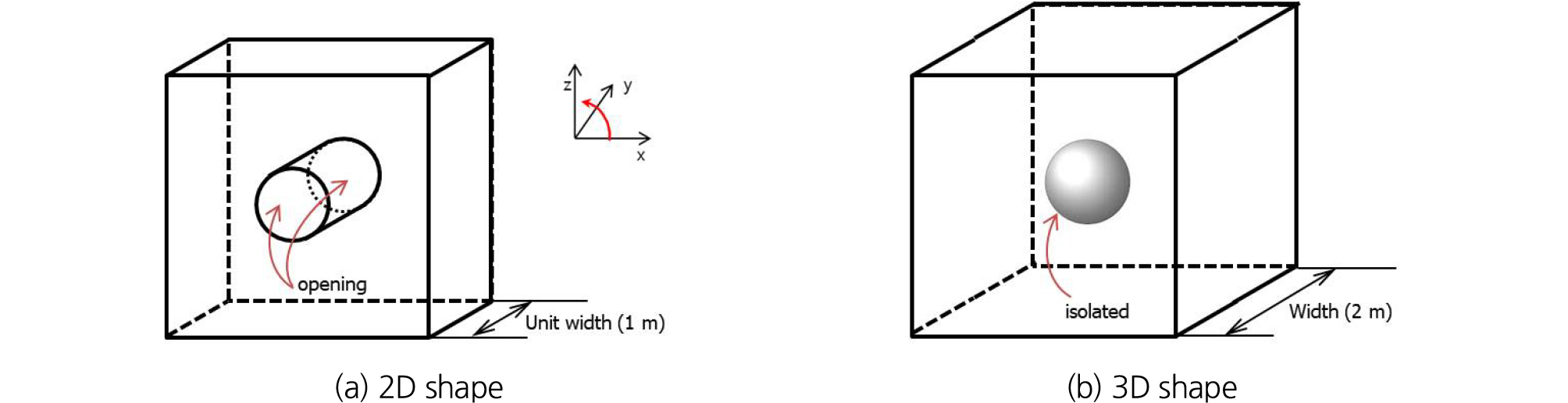
3장에서 설명한 전단강도감소기법을 사용해서 지하공동이 포함된 사면안정해석을 수행하였다. 본 연구의 목적은 지하공동과 사면안정해석의 연관성을 파악하고자 함에 있기 때문에 단순한 사면 형태를 가정하여 수치해석을 수행하였다. 우선 단순사면에 대해서 전단강도감소기법을 사용한 사면의 잠재 파괴면을 확인한 후, 지하공동의 크기, 형상 및 위치 등을 변경해서 사면활동에 미치는 영향을 분석하였다. 또한, 2차원 및 3차원 수치해석을 수행해서 결과를 비교하였다. Fig. 8에서는 2차원 및 3차원 수치해석 적용 시 지하공동의 형상 차이를 보여주고 있다. 3차원 해석에서 해당 모델의 폭은 지하공동의 구(sphere) 형상 최대 크기를 고려해서 수치해석에 영향이 없는 범위를 2 m로 결정하였다. 3차원 해석 영역 대비 지하공동의 의한 영향을 파악하기 위해서 종단방향의 폭을 10, 8, 5, 3, 2 m 순으로 줄여가면서 해석을 수행하였고, 구 형상 최대 크기를 고려했을 때, 안전율 및 파괴형상의 변화가 유사함을 확인하였다. 해석 시간의 단축을 위해서 해석 영역 종단방향의 폭을 2 m로 결정하고, 수치해석을 진행하였다.

Fig. 8.

2D and 3D shape for small underground cavities

4.1 지하공동을 고려한 사면안정해석 개요

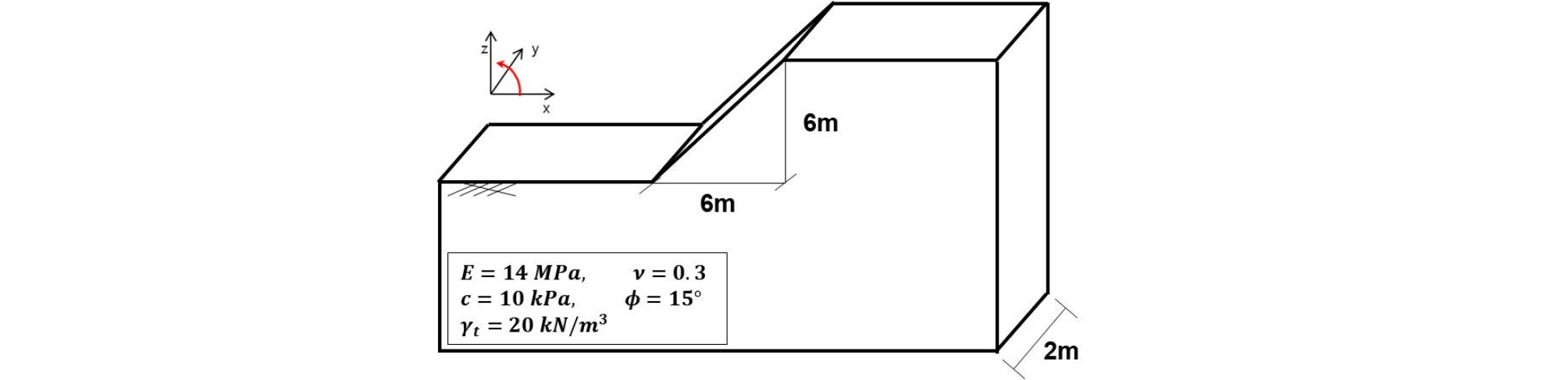
Fig. 9에서는 지하공동이 포함된 사면의 형상을 보여주고 있다. 수치해석에 사용된 토질 강도정수 및 사면의 형상은 Cheng et al. (2007) 및 Shen and Karakus (2013)의 연구 내용을 반영하여 적용하였다. 대상 지반에 대해서 Mohr-Coulomb 모델을 사용하였고, 변형계수($E$)는 14 MPa, 포아송비($\nu$)는 0.3, 전체단위중량(${\gamma }_t$)은 20.0 kN/m³, 점착력($c$)은 10.0 kPa, 내부마찰각($\varphi$)은 15° 그리고 정지토압계수($K_0$)는 0.5를 적용하였다.

Fig. 9.

Boundary and soil conditions for a 3D slope model

4.2 지하공동을 고려하지 않은 사면안정해석

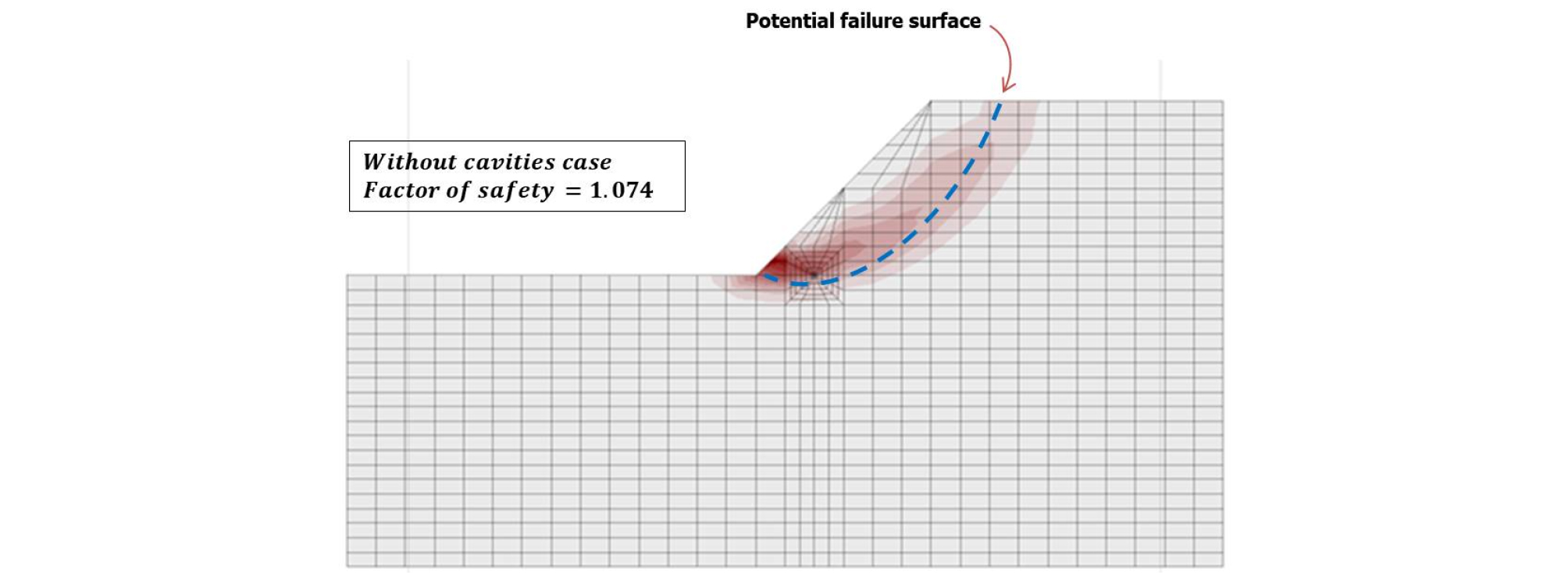
Fig. 10에서는 지하공동이 발생하지 않은 원지반의 수치해석 결과를 보여주고 있다. SSRM으로 수치해석을 진행한 결과, 안전율은 1.074로 산정되었고, 전단변형율 속도(shear strain rate)로 산정한 잠재파괴면의 형상은 Fig. 10에서 보는 바와 같다. 4.3절에서는 여기서 계산된 파괴면을 따라서 지하공동을 배치해서 사면의 잠재파괴면과의 연관성을 파악하였다.

Fig. 10.

Results of SSRM without small underground cavities

4.3 지하공동을 고려한 사면안정해석

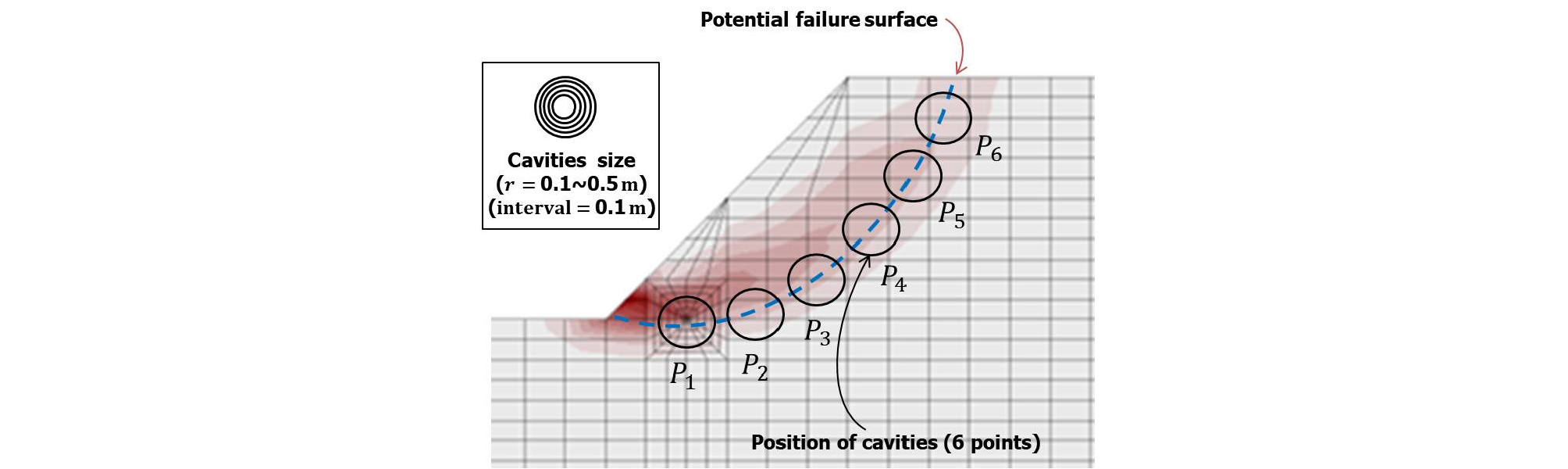
지하공동이 없는 사면의 잠재파괴면을 기준으로 지하공동의 반지름($r$)을 0.1, 0.2, 0.3, 0.4, 0.5 m를 적용하였고 또한, 파괴면을 따라서 사면의 선단부부터 상부 지표면 근처까지 6곳(P₁~P₆)의 위치를 선정해서 해석을 수행하였다. 총 수치해석의 개수는 2차원 30 cases, 3차원 30 cases를 수행하였다. Fig. 11에서는 수치해석 수행 시 지하공동의 크기 및 위치를 보여주고 있다. 지하공동의 위치를 결정하기 위해서 잠재 파괴면 근처가 아닌 곳에서도 수치해석을 수행하였다. 지하공동의 위치가 사면의 잠재파괴면에서 일정 거리 이상 벗어나 있으면, 잠재적인 파괴면 결정에 영향을 미치지 않는 결과가 도출되었기 때문에, 지하공동의 위치가 잠재 파괴면을 따라서 발생되도록 결정하였다.

Fig. 11.

Size and position of small underground cavities in numerical analysis

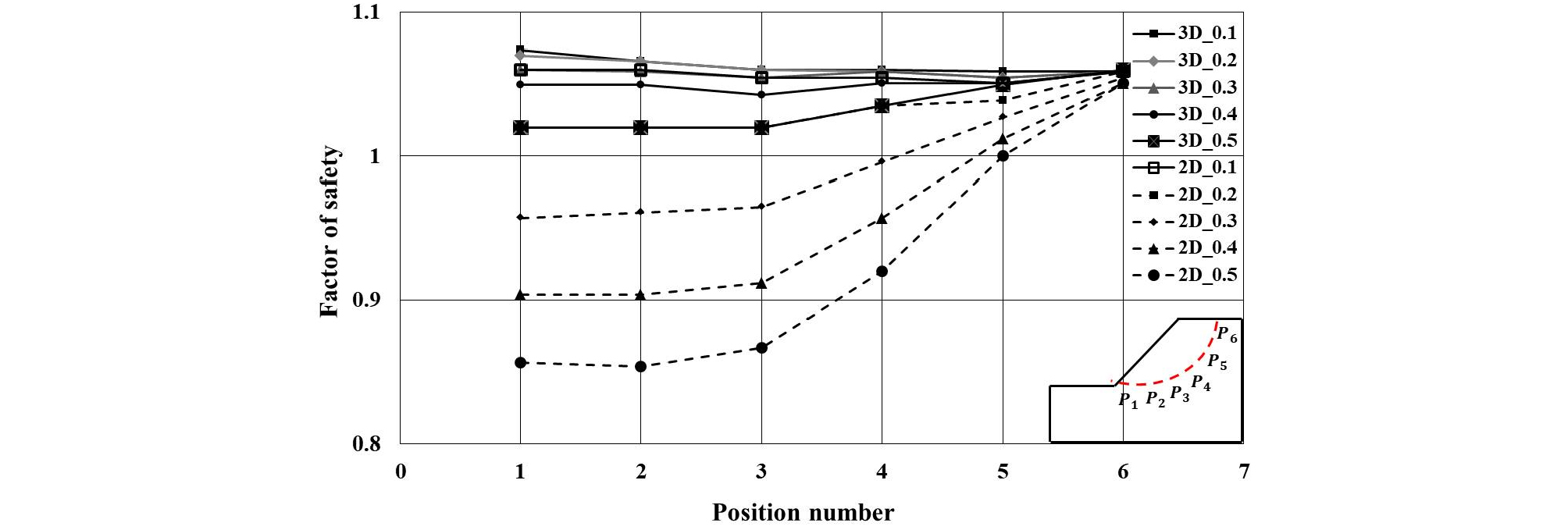
Table 1에서는 전체 수치해석 케이스에 대한 안전율 및 파괴면의 형상에 대해서 보여주고 있다. 지하공동의 형상을 3D로 고려한 해석에서는 크기 및 위치에 관계없이 안전율의 변화가 크지 않았다. 반면에 2D로 고려한 해석에서는 상대적으로 안전율의 변화가 크게 발생함을 확인할 수 있었다. 파괴 형상에 대해서는 사면 선단부에 가깝게 지하공동이 위치한 경우에는 2D 및 3D에서 모두 지하공동 주변으로 국부적인 파괴양상을 보였지만, 사면 상부에 지하공동이 위치한 경우에는 전반적인 파괴양상을 보였다. 또한, 2D 해석에서 상대적으로 국부적인 파괴양상이 더 많이 발생하는 경향을 확인하였다. Table 2에서는 전단변형률 속도의 최대값을 보여주고 있다. 전체 해석에 대해서 분석한 결과, 2차원 및 3차원 해석에 대해서 그 크기에 대해서는 큰 차이를 보이지 않는 경향을 보였다. 지하공동의 반지름 0.4 m, 사면 정상부 위치인 P₆인 경우에 제일 작은 값을 보였고, P₂ 위치에 지하공동이 발생한 경우에 가장 큰 전단변형율 속도를 보이는 것으로 파악되었다. Table 2에서 각 해석 별 전단변형율 속도의 최대값 및 최소값을 음영으로 표현하였다. Fig. 12에서는 지하공동 주변으로 발생하는 국부적인 파괴양상과 사면활동이 전반적으로 발생하는 파괴양상에 대한 대표적인 형상을 보여주고 있고, Fig. 13에서는 지하공동의 위치 및 크기에 따른 안전율의 변화 양상을 그래프로 표현하였다.

Table 1. The results of factor of safety and the shape of failure surface

Table 2. The results of maximum shear strain rate

Fig. 12.

The representative shape of local (L) and global (G) failure surface

Fig. 13.

The comparison of factor of safety using graph

4.3.1 지하공동 위치 변화에 따른 사면안정해석(r = 0.5 m)

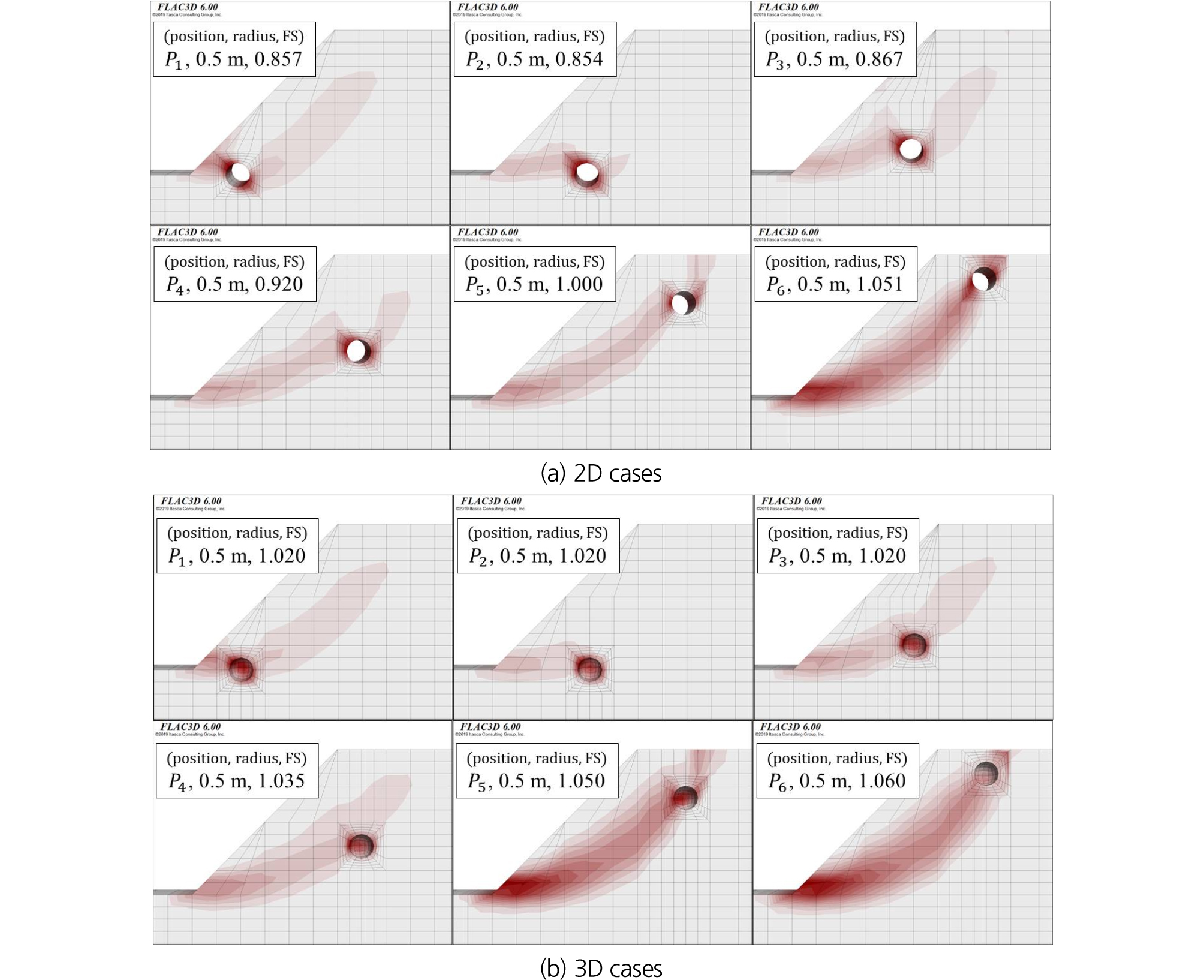
Fig. 14에서는 지하공동의 위치 변화에 따른 안전율 및 파괴양상의 변화를 보여주고 있다. Table 1의 전체 수치해석 케이스 중에서 지하공동의 반지름이 0.5 m인 경우에 대해서 정리하였다. 2차원 형상의 지하공동에 대해서는 안전율 변화가 상대적으로 크게 발생했다. 이러한 결과는 3차원 형상을 2차원으로 가정해서 수치해석에 적용했을 경우에 발생하는 일반적인 경향이라고 판단된다. 2차원 해석에 대한 경우에는 안전율의 변화보다는 잠재 파괴면의 변화 과정을 분석하는 것이 합리적인 설계에 도움이 될 것으로 판단된다. 사면 정상부에 지하공동이 위치하면 안전율이 상대적으로 크게 산정되었고, 사면 선단부에 지하공동이 위치하면 안전율이 큰 폭으로 감소하는 것으로 파악되었다. 이러한 결과는 수치해석 상에서 일반적으로 예상되는 결과이지만, 사면의 전체 안전율 산정 시 지하공동의 영향을 동시에 고려해서 전단강도감소기법을 적용했기 때문에 상대적으로 합리적인 사면 파괴형상이 탐색되었다고 판단된다. 반면에 3차원 지하공동의 형상을 고려한 해석에서는 안전율의 변화는 상대적으로 작은 것으로 산정되었다. 지하공동의 크기가 상대적으로 제일 큰 반지름 0.5 m인 케이스에 대한 파괴면의 형상은 2차원 및 3차원 해석에서 모두 사면 선단부 부근에 지하공동이 위치하면 국부적인 형태, 사면 정상부 부근에 위치하면 전반적인 형태를 보이는 것으로 파악되었다. 사면 선단부 부근에 지하공동이 위치한 경우에 전단변형율 속도의 최대값은 사면의 직각 방향으로 발생하는 경향을 보이며, 지하공동 주변에서 국부적인 파괴양상을 보였다. 반면에 지하공동의 위치가 사면 정상부 부근에 위치하면 전단변형율 속도의 최대값의 방향이 정상부 지표면에 직각 방향으로 발생하는 경향을 보이며, 사면 전체에 대한 전반적인 파괴양상을 보였다. 지하공동의 위치에 따라서 파괴양상이 변하는 것을 확인하였고, 이를 통해서 지하공동이 사면 구조물 주변 지반에 발생한다면 안정성 평가 시 고려해야 할 사항으로 판단된다.

Fig. 14.

The results of SSRM according to the position movement of underground cavities (r = 0.5 m)

4.3.2 지하공동 크기 변화에 따른 사면안정해석(P₁)

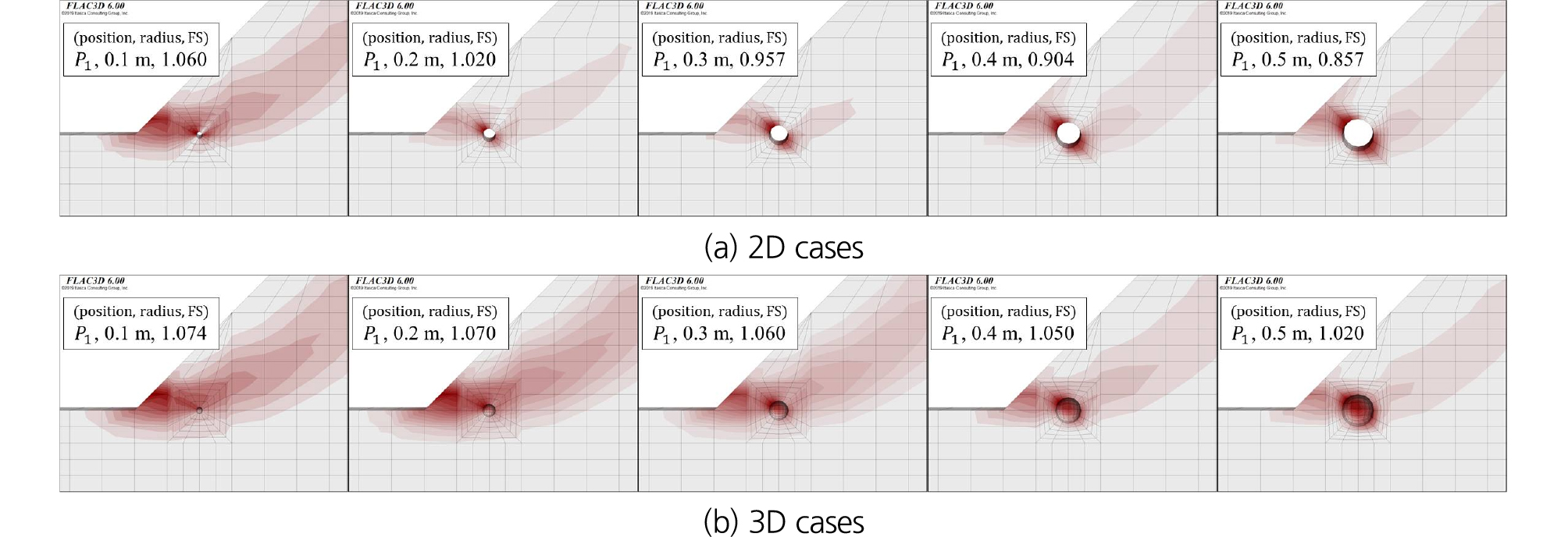
Fig. 15에서는 지하공동의 크기 변화에 따른 안전율 및 파괴양상의 변화를 보여주고 있다. Table 1의 전체 수치해석 케이스 중에서 지하공동의 위치가 사면 선단부 부근인 P₁에 대해서 정리하였다. 위치 변화에서와 유사한 결과를 보였으며, 사면 선단부 부근에 지하공동이 위치하면, 2차원 형상의 안전율 변화가 상대적으로 크게 발생했다. 지하공동의 크기가 커질수록 안전율이 큰 폭으로 감소하는 것으로 파악되었다. 반면에 3차원 지하공동의 형상을 고려한 해석에서는 크기의 변화에 따른 안전율의 변화는 상대적으로 작은 것으로 파악되었다. 파괴면의 형상은 2차원 해석에서는 국부적인 형태 및 전반적인 형태가 지하공동의 크기 변화에 따라서 일정한 경향을 보이지 않는 것으로 파악되었다. 반면에 3차원 해석에서는 크기 변화에 관계없이 전반적인 파괴 형태를 보였다.

Fig. 15.

The results of SSRM according to the size of underground cavities (P₁)

4.4 지하공동의 타원형 3차원 형상을 고려한 사면안정해석

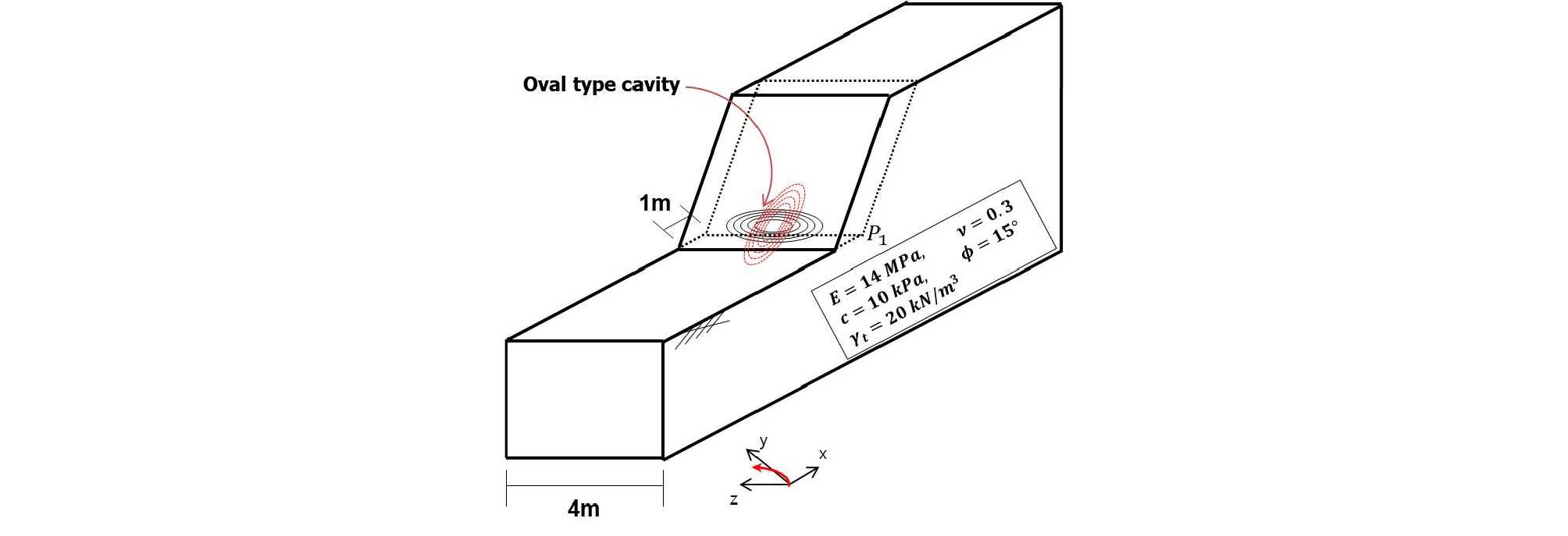
2차원 형상을 고려하고 사면 선단부에 지하공동이 위치하는 경우에, 전단강도감소기법에 의한 안전율의 변화가 상대적으로 큰 폭으로 산정됨을 4.3절에서 확인하였다. 4.4절에서는 이러한 경향을 3차원 해석에 고려하기 위해서 지하공동의 형상을 타원형으로 고려하였고, 지하공동의 장축과 단축의 비(a/b)는 2.0을 적용하여 반영하였다. Fig. 16에서는 수치해석에 적용된 타원형 지하공동의 형상 및 위치를 보여주고 있다. 구(sphere) 형상에 비해서 x축 및 z축 방향으로 길이가 늘어나도록 지하공동의 형상을 고려했고, 이러한 변경사항을 고려해서 전체 모델에 대해서 z축의 길이를 2 m에서 4 m로 변경해서 해석을 수행하였다.

Fig. 16.

Position of oval shape underground cavities in numerical analysis

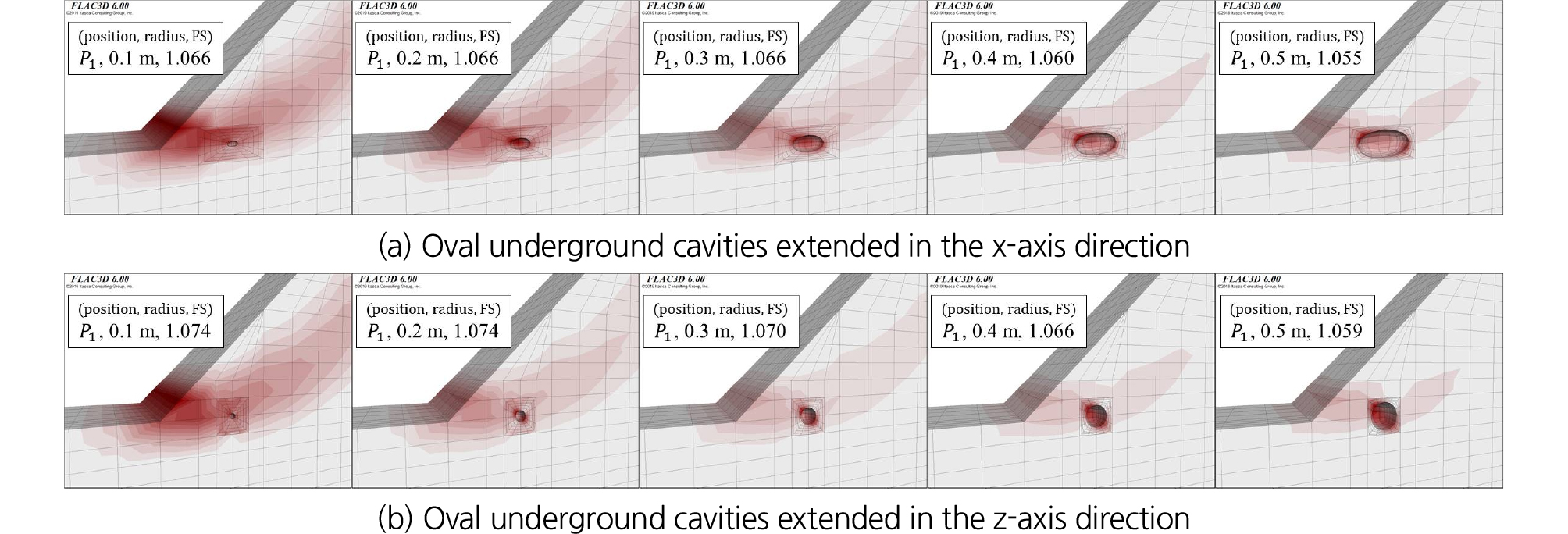
Fig. 17에서는 타원형 지하공동이 사면 선단부 부근에 존재할 때의 전단강도감소기법에 의해서 산정된 안전율 및 파괴면의 양상을 보여주고 있다. x축 및 z축 방향으로 타원형 공동의 장축을 위치시키고, 구형 지하공동의 반지름 0.1, 0.2, 0.3, 0.4, 0.5 m에 대응하는 타원형 공동에 대해서 수치해석을 수행하였다. 사면의 선단 부근에 평면변형율 상태와 유사한 타원형 지하공동이 존재하는 경우에도 구(sphere) 형태의 3차원 해석과 유사하게 안전율의 변화가 크지 않은 것으로 나타났다. 4.3절에 구 형태 및 4.4절의 타원형의 3차원 지하공동 형상을 고려한 수치해석에 의하면, 사면의 3차원 안정 검토 시 소규모 지하공동의 존재는 전체 사면안전율의 변화에는 영향을 미치지 않는 것으로 판단된다. 하지만, 파괴면의 양상은 지하공동의 크기가 증가됨에 따라서 지하공동 주변의 국부적인 파괴 형태로 변화가 발생함을 확인하였다.

Fig. 17.

The results of SSRM according to the size of 3D oval shape underground cavities (P₁)

4.5 결과 분석

사면의 안정성 평가방법 중 전단강도감소기법이 최근 많이 사용되고 있다. An et al. (2018a), An et al. (2018b)의 연구에 의하면 지하공동에 대한 안정성 평가 방법으로 전단강도감소기법이 적용성이 있다고 제안하였다. 본 연구에서는 사면의 잠재적인 활동파괴면 부근에 지하공동이 발생한 경우를 가정하여 지하공동이 사면 활동에 미치는 영향을 분석하였다. 소규모 지하공동을 3차원 형상 중에 구(sphere) 형태로 적용한 경우에는 안전율의 변화에 크게 영향을 미치지 않는 결과를 보였다. 하지만, 2차원 형상을 적용한 경우에는 원통형 지하공동의 반지름 0.3~0.5 m, 지하공동의 위치가 P₁~P₄인 경우에 안전율의 감소가 상대적으로 크게 발생하였다. 또한, 3차원 형상인 경우에 비해서 2차원 형상인 경우에 국부적인 파괴형상이 더 많이 발생하는 결과를 보였다. 사면 선단부 부근인 P₁을 대상으로 3차원 형상 중에 타원형 지하공동을 적용하여 해석한 경우에는 구 형상의 해석 결과와 유사하게 안전율의 변화는 크지 않았지만, 파괴면의 양상 변화는 발생하는 것으로 파악되었다.

5. 결론 및 향후 연구과제

본 연구는 2018년 1월부터 시행된 [지하안전에 관한 특별법] 세부 지침의 지하안전영향평가에 대한 수치해석 적용성에 관한 초기 연구의 일환 및 선행연구(An et al., 2018a, An et al., 2018b)의 후속 연구로 수행되었다. 본 연구의 범위는 단순 사면 지반 내에 잠재파괴면 부근에 발생된 소규모 지하공동에 관한 것으로 제한하였고, 이러한 이유로 지하공동의 반지름 0.1~0.5 m 고려해서 수치해석을 수행하였다. 수치해석 결과를 토대로 분석한 결론은 다음과 같다.

1. Table 1 및 Fig. 13에서 보여주는 바와 같이, 구(sphere) 형상 지하공동을 3차원로 고려한 해석에서는 크기 및 위치에 관계없이 안전율의 변화가 크지 않는 결과를 보였다. 반면에 지하공동의 형상을 2차원으로 고려한 해석에서는 상대적으로 안전율의 변화가 크게 발생함을 확인할 수 있었다. 파괴 형상에 대해서는 사면 선단부에 가깝게 지하공동이 위치한 경우에는 2차원 및 3차원에서 모두 지하공동 주변으로 국부적인 파괴양상을 보였지만, 사면 정상부에 지하공동이 위치한 경우에는 전반적인 파괴양상을 보였다. 또한, 2차원 해석에서 상대적으로 국부적인 파괴양상이 더 많이 발생하는 경향을 확인하였다.

2. 구형 지하공동의 반지름이 0.5 m인 경우에 위치 변화에 따른 안전율 및 파괴양상의 변화를 분석한 결과, 2차원 형상의 지하공동에 대해서는 안전율의 변화가 뚜렷하게 나타났다. 사면 정상부에 지하공동이 위치하면 안전율이 상대적으로 크게 산정되었고, 사면 선단부에 지하공동이 위치하면 안전율이 큰 폭으로 감소하는 것으로 파악되었다. 반면에 3차원 지하공동의 형상을 고려한 해석에서는 안전율의 변화는 상대적으로 작은 것으로 산정되었다. 지하공동의 크기가 상대적으로 제일 큰 반지름 0.5 m인 케이스에 대한 파괴면의 형상은 2차원 및 3차원 해석에서 모두 사면 선단부 부근에 지하공동이 위치하면 국부적인 형태, 사면 정상부 부근에 위치하면 전반적인 형태를 보이는 것으로 파악되었다. 지하공동의 위치에 따라서 파괴양상이 변하는 것을 확인하였고, 이를 통해서 지하공동이 사면 구조물 주변 지반에 발생한다면 그 안정성 평가 시 고려해야 할 사항으로 판단된다.

3. 구형 지하공동이 사면 선단부 위치인 P₁으로 고정하고, 크기 변화에 따른 안전율 및 파괴양상의 변화를 분석한 결과, 지하공동의 위치 변화의 경우와 유사한 결과를 보였으며, 사면 선단부 부근에 지하공동이 위치하면, 2차원 형상의 지하공동에 대해서는 안전율의 변화가 뚜렷하게 나타났다. 지하공동의 크기가 커질수록 안전율이 큰 폭으로 감소하는 것으로 파악되었다. 반면에 3차원 지하공동의 형상을 고려한 해석에서는 크기의 변화에 따른 안전율의 변화는 상대적으로 작은 것으로 파악되었다. 파괴면의 형상은 2차원 해석에서는 국부적인 형태 및 전반적인 형태가 지하공동의 크기 변화에 따라서 일정한 경향을 보이지 않는 것으로 파악되었다. 반면에 3차원 해석에서는 크기 변화에 관계없이 전반적인 파괴 형태를 보였다.

4. 사면의 선단 부근에 타원형 지하공동이 존재하면, 구(sphere) 형태의 3차원 해석과 유사하게 안전율의 변화가 크지 않은 것으로 나타났다. 하지만, 파괴면의 양상은 지하공동의 크기가 증가함에 따라서 국부적인 파괴 형태로 변화하므로 사면 안정성 평가 시 주의해야 할 사항으로 판단된다.

5. 선행 연구(An et al. 2018a, An et al. 2018b)를 통해서 지하공동에 대한 안정성 평가 시 전단강도감소기법의 적용성을 확인하였다. 선행 연구의 결론을 종합해보면, 지하공동의 형상을 수치해석에 반영 시 지하공동 형상 특성을 고려해야 하며, 2차원 형상 보다는 3차원 형상을 고려해야 합리적인 결과를 산정할 수 있을 것으로 판단된다. 본 연구는 일반적으로 사면안정해석 시 파괴면 위치 및 안전율 산정에 사용되고 있는 전단강도감소기법을 지하공동과 동시에 고려할 수 있는지에 대한 적용성 검토를 위해서 수행하였고, 사면의 파괴면 산정 시 지하공동이 수치해석에 영향을 미치는 경향을 파악한 결과, 3차원 형상을 고려하면 사면 활동에 대한 거동의 영향이 지하공동의 발생에 의한 영향 보다 상대적으로 크기 때문에 지하공동은 일종의 파묻힘 현상(고립 현상)으로 안전율에 큰 변화를 보이지 않았다. 이러한 현상은 실제 소규모 지하공동이 사면 내에 존재한다고 해도 사면 파괴로 진행되지 않는 상황과 일치하므로 현실에 더 부합하는 결과로 판단된다. 2차원 형상을 고려한 경우에 안전율의 변화가 상대적으로 크게 발생한 이유는 Fig. 8(a)에서 확인하는 바와 같이 일종의 개방 효과(opening effect)가 반영되어 실제 상황보다 낮은 안전율이 산정되는 것으로 판단된다. 그러므로 사면 내에 존재하는 지하공동의 발현 시 수치해석은 3차원 형상으로 고려하는 것이 실제 상황에 부합되는 결과를 산정할 수 있을 것으로 판단되고, 안전율에 근거한 검토보다는 파괴형상의 변화에 초점을 맞추어 검토를 수행하는 것이 합리적일 것으로 판단된다.

본 연구는 지하공동과 사면안전율과의 관계를 전단강도감소기법을 사용해서 분석한 초기 연구로서, 지하수위 영향, 사면의 다양한 상재하중조건, 지반조건 및 사면 형상 등을 고려하지 못한 한계점이 있다. 또한, 지하공동의 발생 원인을 고려한 수치해석적 접근, 지반조사를 통해서 획득한 사면 내 지하공동의 실제 사례 반영, 암반의 불연속면에 관한 고려하지 못한 한계점도 있다. 향후 연구를 통해서 수치해석의 적용성과 안전율 산정에 영향을 재평가하여 신뢰도를 향상시켜야 될 것으로 판단된다. 하지만, 본 연구의 결과는 내포된 한계점에도 불구하고, 전단강도감소기법을 사용한 사면안정해석 수행 시 사면을 구성하는 지반에서 발견된 지하공동을 포함한 안정성 평가 등에 적용될 수 있을 것으로 판단된다. 향후에는 실제 사면현장에 대한 특성을 반영한 수치해석, 지반조건 변화와 지하공동의 개수를 확대해서 연구를 수행할 예정이다. 또한, GPR 등 지구물리탐사방법에 의한 실제 산악도로 주변의 지하공동 데이터를 기반으로 후속 연구를 수행할 예정이다.