1. 서 론
2. 이론적 배경
2.1 직접법
2.2 최적화 기법
2.3 기존 연구사례
3. 해석 프로그램 및 연구 대상 폐광산
3.1 해석 프로그램
3.2 침하 폐광산
4. 침하 폐광산의 2차원 모델링과 초기 해석 결과
5. 최적설계 적용을 위한 사전 연구
5.1 개 요
5.2 침하 유도 단순화 모델
5.3 최적설계 적용 결과
5.4 설계변수의 상대적 중요도 분석
5.5 단계적 최적설계 적용 결과
5.6 연구결과의 고찰
6. 단계적 최적설계를 통한 ○○광산 지반의 역학적 특성 추정
6.1 개 요
6.2 ○○광산 설계변수의 상대적 중요도 분석
6.3 ○○광산 단계적 최적설계 적용 결과
6.4 연구결과의 고찰
7. 결 론
1. 서 론
국내 폐광산은 전국에 산재되어 있으며 과거 생산위주의 채광활동으로 인해 지반침하에 의한 대책수립이 미흡하여 폐광된 대부분의 광산에서 다양한 형태의 침하를 발생시키고 있다. 또한 이러한 침하는 지표에 존재하는 시설물의 안정성뿐만 아니라 주민들의 안전을 위협하는 잠재적 요인으로 작용한다. 일반적으로 지반침하는 지하 채굴적 및 광산 지하갱도의 함몰, 연약지반의 자연 압밀, 지하수의 양수에 의한 지반 지지력의 상실과 공동의 형성 등 다양한 원인으로 발생한다. 또한, 그 영향인자의 수가 많고 영향인자 각각의 역할이 복잡하게 얽혀있어 그 발생위치 및 시기의 예측과 위험도에 대한 평가가 대단히 어려운 실정이다(MIRECO, 2014).
기존 수치해석을 이용하여 지반침하 위험도를 예측하고 평가한 연구들은 주로 채굴의 직상부에 대한 평가에 초점이 맞추어져 있다. 퍼지이론 및 기타 통계학 기법을 사용하여 영향범위를 산출하며, 채굴적 상부의 지질구조 및 주변 암반 조건에 대해 통합물성을 적용하고 채굴 주변 소성영역을 해석하는데 그치고 있는 실정이다(Choi, 2014). 또한 지질구조 및 지반물성 정보를 확보하는데 있어 항상 제한된 자료밖에 파악할 수 없는 현실적 한계점을 가지며, 이러한 제한된 자료를 입력으로 사용하는 수치해석 결과는 적용 시 신중한 검토가 필요하다. 따라서 수치해석으로 폐광산의 침하예측 및 위험도 평가를 수행하기 위해서는 실제 현장여건에 부합하며 현실적으로 그 현장을 모사하도록 모델링이 가능한 수치해석 기법의 연구가 우선되어야 한다.
역해석 및 최적화 기법은 현재 확보 가능한 광산 정보를 적용하여 광산의 침하이력을 재구성하고, 해당 광산에 맞는 지반의 역학적 특성을 추정할 수 있는 도구이다. 또한 수치해석모델을 실제 현장여건에 부합하며 그 현장을 현실적으로 모사할 수 있는 모델로의 보정이 가능하다. 터널현장에서의 역해석 및 최적화 기법 관련 연구는 1990년도부터 활발하게 수행되어 왔지만 광산현장에의 적용된 연구사례는 아직 보고되지 않고 있다. 수평으로 굴착되는 터널현장과는 달리 경사의 맥을 갖는 광산현장의 경우, 일반적으로 채굴적이 다층의 지반 안에 존재하게 된다. 따라서 최적화 기법을 적용한 폐광산 수치해석모델의 보정연구를 수행하기 해서는 다수의 인자를 추정할 수 있는 역해석 및 최적화 기법의 연구가 병행되어야 한다.
본 연구에서는 실제 침하가 발생한 폐광산 현장을 높은 신뢰수준의 해석모델로 모델링 할 수 있는 수치해석 기법을 연구하였다. 해석모델의 신뢰성을 높이기 위해 광산의 현장 조사 자료를 수집하고 채광이력을 재구성하여 모델링하였으며, 해석모델을 실제 발생한 침하지의 정보를 바탕으로 해당 광산에 맞는 지반 및 절리의 물성을 역해석 및 최적화 기법을 통해 추정하여 보정하였다.
2. 이론적 배경
2.1 직접법
역해석의 기법 중 하나인 직접법은 이미 알고 있는 계측결과와 해석결과를 비교하여 그 차이인 오차함수가 최소의 값을 가질 때까지 미지 매개변수를 수정하여 해석과정을 반복하는 방법이다. 오차함수가 허용범위에 수렴할 때까지 연산과정을 계속적으로 반복하므로 비선형 문제나 입력변수와 해석결과 간의 수학적 배경을 알기 힘든 다양한 문제에 적용 가능하다(Min and Park, 1996). 이 때, 미지변수를 일정한 범위에서 단순히 변화시켜 연산을 반복하고 그 결과들 중에서 오차함수의 최솟값을 찾는다면 연구의 효율성은 매우 저하될 것이다. 예를 들어 3개의 변수를 설정한 범위 내에서 각각 일정한 간격으로 100회씩 변화시켜 해석을 수행한다면 총 100만회의 해석이 필요하다. 만약 1회 1초의 해석시간을 가정한다면 11.5일의 시간이 소요되며 이는 현실적으로 수행이 어렵고 그 자체로 매우 비효율적이다. 이러한 이유로 소요시간의 감소를 위해 변수의 변화되는 값의 크기를 임의로 증가시킨다면 허용범위 내에 수렴하는 미지변수를 추정할 수 없을 가능성이 커지게 된다. 따라서 직접법을 활용한 연구를 수행하기 해서는 이러한 한계점을 보완할 수 있는 연구가 선행되어야 한다.
2.2 최적화 기법
최적화 기법은 직접법에서 반복연산과정의 미지변수를 변화시키는 과정에 적용되는 수치적 알고리즘이다. 미지변수의 값을 오차함수가 허용범위에 수렴되는 효과적인 방향으로 변화시켜 해석시간을 감소시키며 이 모든 과정이 자동적으로 수행된다. 설계범위를 정밀히 탐색하여 인력으로 찾기 힘든 최적의 해를 추정하는 것이 가능하며 이러한 최적화 기법이 적용된 직접법에 의한 역해석을 최적설계라 한다(Choi, 2012).
최적설계에 사용되는 용어를 정리하면 먼저 설계변수는 설계자가 변경가능하고 추정하고자 하는 미지 매개변수를 의미한다. 다음으로 목적함수는 변경되는 설계변수의 방향을 결정하는 함수로써 일반적으로 해석결과와 목표하는 값의 최대 또는 최소 차이로 설정한다. 즉 직접법에서의 오차함수와 그 의미가 유사하며 설정한 목적함수를 만족하는 설계변수를 최적해라 한다. 최적설계는 설계자의 목적을 만족할 때까지 수치해석 또는 연산을 자동으로 반복 수행한다. 설계변수 변화과정에 개입하는 최적화 기법은 최적해를 찾아가는 이론과 알고리즘에 따라 다양한 기법들이 존재한다.
2.2.1 민감도 기반 최적화 기법
민감도 기반 최적화 기법(gradient-based optimization)은 Fig. 1에서와 같이 눈을 감고 울타리가 있는 산을 올라가는 것과 동일한 개념이다. 민감도는 산의 경사를 의미하며 산을 오르는 것은 현재 위치에서 경사가 가장 심한 방향으로 울타리 범위 내에서 최대한 높은 곳으로 이동하는 과정을 반복함으로써 정상에 도달할 수 있다. 이는 다음과 같은 두 단계의 과정을 반복한다. 첫 번째 과정은 방향 탐색의 과정으로 산의 경사를 구한다. 민감도 해석(sensitivity analysis)을 통해 목적 함수와 구속 조건들의 민감도를 계산해 낼 수 있고 이를 조합하여 이동 방향을 구할 수 있다. 두 번째 과정은 울타리 범위 내에서 최대한 높게 이동하는 거리를 찾는 선 탐색(line search) 과정이다. 이러한 반복 과정을 수학적으로 최적조건을 만족할 때까지 되풀이 하면 주어진 설계 조건을 만족하는 최적해를 구할 수 있다(Choi, 2012).
하지만 이 기법은 비선형성이 큰 구조 최적설계에의 적용이 어려운 단점이 있으며 이러한 문제해결을 위해 근사화 기법을 이용한 최적설계 기법이 도입되었다. 근사화와 최적화를 반복하는 순차적 근사화기법(sequential approximate optimization technique)을 사용하며 실제 해석을 근사모델의 생성으로 대체한다. 따라서 본 기법을 통한 설계는 생성되는 근사모델의 신뢰성에 좌우되며, 이러한 이유로 설계변수와 결과값이 특정한 함수적인 관계를 갖지 않는 실제 문제에 적용하는데 있어 많은 제약이 따른다(Kim, 2003).
2.2.2 점진적 2차 반응표면법(PQRSM)
점진적 2차 반응표면법(Progressive Quadratic Response Surface Method, PQRSM)은 근사모델의 생성을 위한 반응표면 모델링과 수렴성 보장을 위한 신뢰영역 알고리즘의 개념을 사용한 순차적 근사 최적설계 기법(sequential approximate optimization)이다. 반응표면이란 실험결과의 추정치들이 지나는 선이나 면을 의미한다. 노이즈가 존재하는 문제에서 최적해의 수렴이 어려운 민감도 기반의 최적설계 기법의 한계점을 극복하기 위해 개발된 반응표면법에서 사용되는 개념이며, 근사모델의 형태는 대부분 이차 함수로 가정한다. 다음으로 신뢰영역 알고리즘은 근사모델이 실제모델에 대해 일정 오차범위 내에 있도록 신뢰영역을 조절하는 기법이다. PQRSM의 신뢰영역 알고리즘은 매 반복단계마다 회전성(rotatability)을 만족하는 실험점들을 사용하여 이차 반응표면 모델로 이차 근사함수를 생성하고, 이를 사용하여 신뢰영역 내에서 근사 최적설계를 수행한다. 이전 반복단계의 정보를 사용하여 현재 반복단계의 정보를 예측하는 기법을 통해 기존의 이차 반응표면 모델을 구하기 위한 실험점보다 적은 실험점만으로 이차 반응표면 모델을 생성할 수 있어 해석 소요시간이 짧은 장점을 갖는다(Choi, 2005).
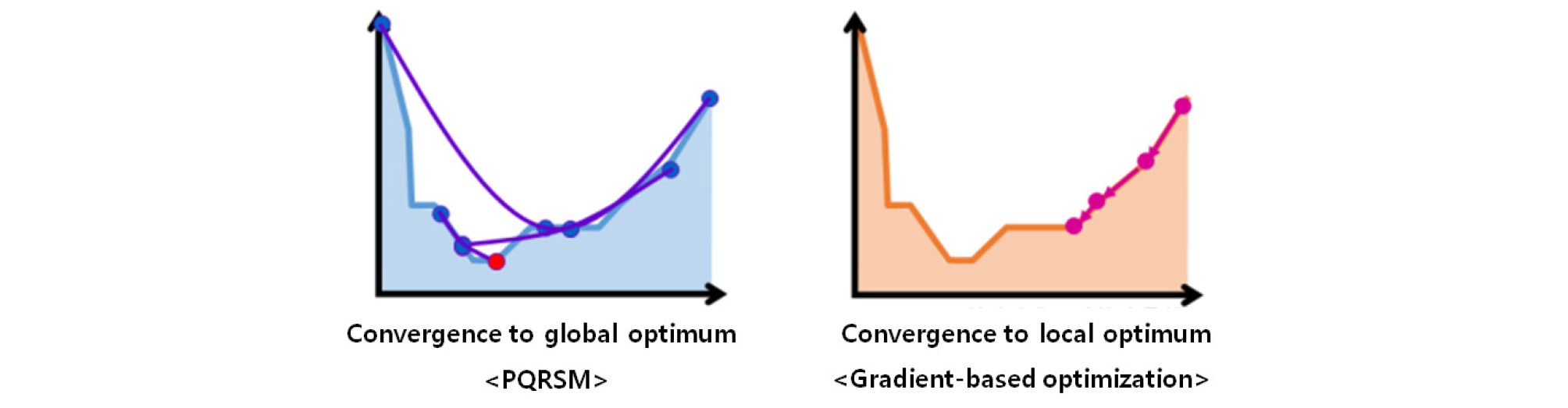
Fig. 2는 최적해 중 국부 최적해(local optimum)와 전역 최적해(global optimum)의 개념을 설명해 주고 있다. 수렴되는 최적해의 종류에 따라 최적설계는 국부 최적설계와 전역 최적설계로 분류될 수 있다. 전역 최적설계는 국부 최적설계와 비교하여 최적해를 찾기 위해 상대적으로 매우 많은 시간이 소요된다. 민감도 기반 최적설계와 PQRSM은 모두 국부 최적설계이나 PQRSM은 민감도가 아닌 함수 기반(function based) 최적설계로서 Fig. 3과 같이 전역 최적해를 찾을 수 있는 약한 전역 최적해 수렴(weak global convergence)의 특징을 가진다. 즉 짧은 소요시간으로 전역 최적해를 구할 수 있는 장점을 갖는다(Hong et al., 2000).
2.2.3 미소 유전자 알고리즘(MGA)
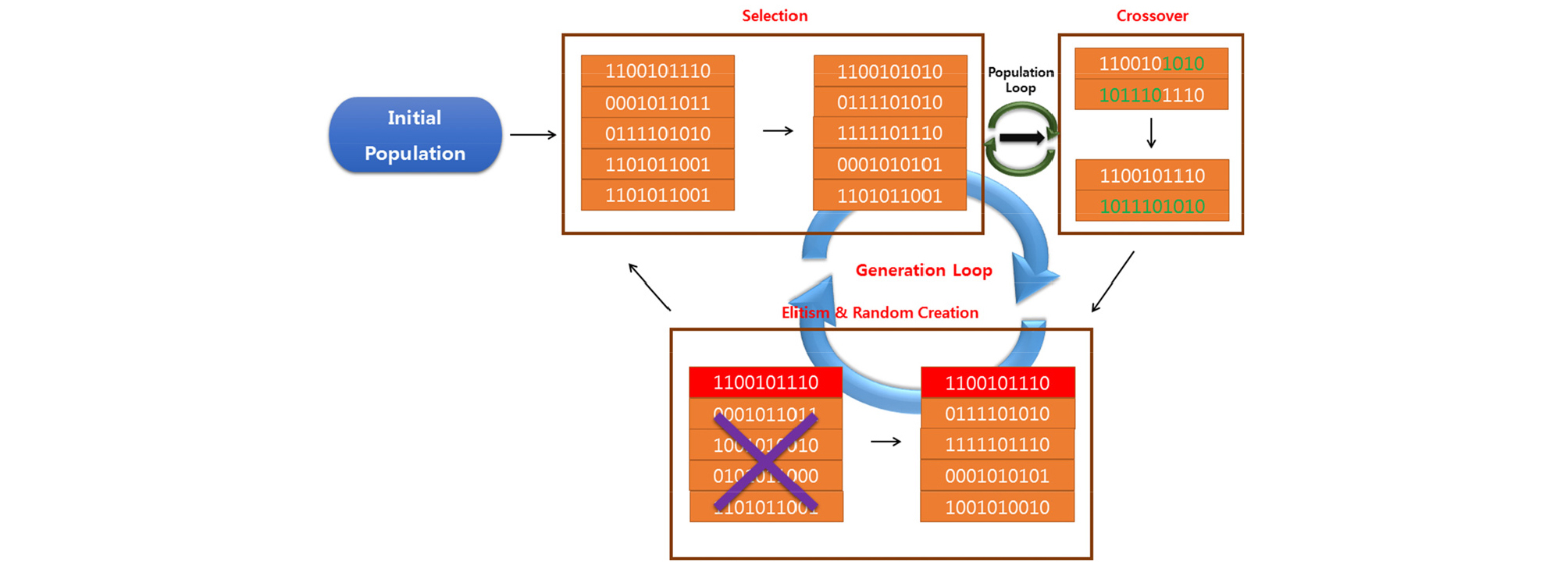
유전자 알고리즘(Genetic Algorithm, GA)은 생물의 진화과정을 모방한 방법으로 1975년 Holland (1975)에 의해 제안되었다. 생명체에 이루어지는 방식과 유사하게 유전자를 혼합하는 교차, 유전자를 일정한 확률로 변화시켜 개체의 다양성을 유지하는 변이의 연산 등을 이용하여 생물의 진화과정을 묘사한다. GA에서 염색체는 유전정보를 담당하는 개체로서 설계변수 각각이 이에 해당하며, 모집단은 염색체들이 모여 이룬 개체집단으로 설계자가 정한 설계영역 내의 설계변수들의 집단이 이에 해당할 수 있다. Fig. 4는 GA의 수행과정을 설명해 주고 있다. n개의 개체를 갖는 모집단을 정하고 그 개체들을 대상으로 교차, 변이, 선택의 단계를 거쳐 새로운 k개의 개체를 가진 모집단을 생성하여 기존을 모집단을 대체하게 된다. 이러한 일련의 과정을 세대라고 표현하며, 목적함수가 허용범위 내로 만족할 때까지 세대가 진행되며, 여러 번의 세대가 흘러가도 성능의 개선이 이루어지지 않는다면 해석이 종료된다. 단일점이 아닌 여러 점을 동시에 사용해 최적점을 탐색하여 전역해에 수렴하는 전역 최적설계로서 함수 값만을 요구하여 확률적인 방법으로 탐색하므로 기울기 정보를 필요로 하지 않으며, 시스템에 존재하는 노이즈에 둔감하고 이산형 설계변수의 분석이 가능하다. 그러나 설계변수를 변환하는 과정이 포함되어 함수계산이 많아 상대적으로 매우 긴 연산시간이 소요된다.
미소 유전자 알고리즘(Micro Genetic Algorithm, MGA)은 GA의 기본 골격은 유지하되 몇 가지 세부 내용을 변형한 것이다. GA는 큰 모집단을 요구하기 때문에 함수 계산이 많아 연산시간이 길다는 단점이 있다. MGA는 이러한 GA의 많은 계산 부담을 줄이고자 작은 집단을 사용하고 이를 효율적으로 다루기 위해 Krishnakumar (1989)가 제안한 방법이다. 생물의 진화과정을 모방하여 여러 개체를 교차, 선택의 세대를 반복하여 최적해를 찾는 원리는 유사하나 Fig. 5와 같이 일반적으로 모집단은 5개의 개체로 구성되며, 변이 과정이 생략되고 선택과 교차가 반복적으로 이뤄지는 내부 순환, 무작위 생성이 수행되는 외부 순환이 동시에 수행되는 이중 구조로 되어 있어 비교적 빠른 수렴성을 보장하는 차이점이 있다. 초기 모집단이 어느 한 점 가까이로 수렴해 가면 집단을 재구성하므로 집단의 다양성이 훼손될 가능성이 적어져 돌연변이 연산이 생략되었으나 이러한 이유로 변수가 많아질 경우 개체군의 다양성이 떨어져 국부해에 수렴할 가능성이 발생한다. 따라서 변수가 적고 빠른 탐색이 필요한 문제에 적합한 방법이다(Joe, 2014).
2.3 기존 연구사례
지반분야에서 역해석 및 최적화 기법이 적용된 연구사례는 주로 터널의 계측변위를 사용하여 지반의 물성을 추정하는 연구가 주를 이루고 있다. 먼저 국내 연구사례로, Min and Park (1996)은 현장 계측데이터를 활용하여 탄성계수와 초기응력을 추정하였으며, Yang and Jeon (2002)는 유한차분해석프로그램 FLAC의 해석과정 내에 직접 탐색법 최적화 알고리즘을 이용한 FISH함수를 삽입하여 탄성계수와 측압계수를 추정할 수 있는 범용적 역해석 프로그램을 개발하였다. 이렇듯 지금까지의 연구들은 주로 터널의 계측변위를 활용하여 변형계수와 초기응력을 추정하는데 그치고 있다. 하지만 지반의 물성은 변형계수와 초기응력뿐만 아니라 매우 다양하나 이러한 다수의 물성을 추정하는 연구가 미흡하며, 복잡한 지반구조를 단일층으로 가정하는 한계점을 갖고 있다. Kim (2006)은 다층지반에서 각각의 층에 대해 단계적으로 역해석을 수행하여 다중 미지변수를 추정하는 연구를 수행하였으나, 이 연구 또한 변형계수와 측압계수만을 추정하였으며 다층의 미지변수를 동시에 고려하지 못하는 한계점을 갖고 있다.
국외 연구사례로 Sakurai and Takeuchi (1983)는 탄성 ‧ 등방성 암반을 대상으로 터널의 계측변위를 통해 초기응력과 영률을 역해석 기법 중 하나인 역산법을 활용하여 이론적으로 추정하였다. 그리고 Hisatake and Ito (1985)는 역해석 기법 중 직접법을 사용하여 변수를 추정하는 과정에 최적화 기법을 적용하여 해석시간을 최소화하는 연구를 수행하였으며, 또한 Hisatake (1986)는 3차원 역해석 연구를 수행하여 탄성계수, 포아송비, 그리고 6개 요소의 3차원 초기응력을 추정하였다. 이렇듯 터널현장에서의 역해석 및 최적화 기법에 대한 연구는 1980년도부터 활발히 수행되어 왔으나 광산 현장에의 적용에 대한 연구는 아직 보고되지 않고 있다. 수평으로 굴착되는 터널 현장과는 달리 급경사의 광맥을 갖는 광산현장의 경우 일반적으로 채굴적이 다층의 지반 안에 존재하게 된다. 따라서 최적설계를 통한 침하 폐광산 지반의 역학적 특성 추정 및 신뢰성 높은 해석모델의 모델링 연구를 수행하기 위해서는 다층의 지반을 고려하여 다수의 물성을 추정할 수 있는 최적설계 기법이 적용되어야 한다.
3. 해석 프로그램 및 연구 대상 폐광산
3.1 해석 프로그램
지반 안정성 분석에 적용되는 수치해석 기법은 크게 연속체 해석과 불연속체 해석으로 나눌 수 있다. 연속체 해석의 경우에는 요소망에 의한 모델구성으로 인하여 해석시간의 단축 및 재료모델의 선정이 용이하다는 장점이 있다. 하지만, 요소사이의 절점이 파괴되지 않기 때문에 대변형이 발생하는 해석조건에 적용하는데 무리가 있다. 반면에 불연속체 해석은 연속체 해석과 달리 모델 구성 요소의 개별적인 변위 및 요소 사이의 분리현상을 모사할 수 있기 때문에 대변형 해석에 적합하며, 실제 침하가 진행되는 과정을 모사할 수 있는 장점이 있다. 개별 요소법 기반의 불연속체 2차원 해석프로그램인 UDEC은 암반의 절리구조를 직접 표현할수 있으며, 대변형 및 불연속면 해석이 가능하다. 또한 요소의 분리현상으로 인한 블록의 유동으로 본 연구의 목적에 유리한 장점을 보유하고 있어 주요 해석 프로그램으로 선정하였다.
다음으로 최적화 기법의 적용을 위해 전문 상용 프로그램인 PIAnO (Process Integration, Automation and Optimization)를 활용하였다. 본 프로그램은 해석 프로세스를 자동화하고 다분야 설계고려사항을 동시에 해석 가능하며, 진보된 설계기법과 연계하여 최적화된 설계를 도출할 수 있는 도구이다. 또한 직접법의 최적화 적용에 있어 설계변수의 변화에 따른 전산해석의 반복작업을 자동화하고 반복과정에 다양한 최적화 알고리즘을 선택적으로 적용하는 것이 가능하다. 뿐만 아니라 설계변수와 해석결과간의 관계를 파악하여 설계하고자 하는 문제에 대해 이해하고 최적설계의 성능을 향상시키는 것이 가능하며, 이를 위해 매개변수 연구, 민감도 분석, 실험설계법과 결과에 대한 통계분석, 신뢰성 분석 등의 다양한 도구를 제공한다. 또한 그 적용사례에 있어 일반실험은 물론 전자, 가전, 자동차 설계, 국방, 항공, 조선, 플랜트, 건축, 발전, 기계, 로봇, 금형, 공정 등 다양한 분야에서 활용되었으며, 수십 편의 관련논문이 제출되어 그 사용성이 검증된 프로그램이다(Choi, 2012). 지반분야에서의 적용된 사례가 아직 보고되지 않았으나 탄성암반의 원형공동 굴착모델에 본 해석프로그램을 적용하여 공동의 천단변위를 목표값으로 설정, 최적설계를 통해 목표변위를 만족하는 물성을 추정한 연구를 통해 지반분야에서의 본 프로그램의 활용 가능성을 사전에 검증하였다(Son, 2017).
3.2 침하 폐광산
한국광해관리공단은 1995년부터 2015년까지 38개 폐광지역에 대해 지반안정성 조사를 실시하였으며, 총 69권에 달하는 지반안정성 기본/정밀/보강 보고서 자료를 보유하고 있다(Kim et al., 2017). 이러한 국내 폐광산 지반안정성 조사 보고서를 활용하여 침하지의 유 ‧ 무 및 위치와 규모, 지반 및 절리의 물성, 채굴적 및 채광 이력 정보를 기준으로 폐광산들을 조사하였으며, 해당 정보들이 모두 수록된 ○○광산을 본 연구의 대상광산으로 선정하였다. 충청북도에 위치한 금속광산인 ○○광산은 화강암에 포획된 반상화강암의 열극을 충전한 열극충전 열수광상이며, 맥의 주향은 N15°W, 경사는 70~80°NE으로 Fig. 6과 같이 폭 약 13 m, 깊이 약 17 m의 함몰형 침하가 발생하였다.
4. 침하 폐광산의 2차원 모델링과 초기 해석 결과
○○광산의 침하가 발생한 지역에 대해 지반안정성 정밀조사 및 실시설계 보고서(MIRECO, 2008)의 단면 및 지반 정보와 Choi (2014)의 연구를 바탕으로 Fig. 7과 같이 모델링하였다. x축은 채굴적 중심을 기준으로 좌로 62 m, 우로 58 m씩 총 120 m이며, y축은 80 m로 해당 단면의 표고 90~170 m에 해당한다. 표토의 표현을 위해 5등급 이하의 낮은 물성의 적용뿐만 아니라 0.5 m 간격의 격자모양 절리를 발생시켰다. 측압계수는 Bae (2005)의 국내 현장계측자료를 통해 조사된 측압계수 결과의 평균값인 2.44를 적용하였으며, 모델에 적용된 암반과 절리의 물성은 각각 Tables 1, 2와 같다. 조사된 채굴적의 채광 후 해석결과는 Fig. 8과 같다. 그림에서와 같이 채굴적으로의 완전침하가 발생하지 않았으며, 1.33 m 발생한 최대 침하량의 위치 또한 실제 침하지의 범위에서 12.6 m 벗어난 결과를 보였다. 이러한 결과로 기존 조사된 보고서의 자료를 활용하여 모델링한 본 해석모델은 현장광산을 현실적으로 모사할 수 없으며, 보정을 위한 추가적인 연구가 필요할 것으로 판단된다.
Table 1. Rock mass properties of ○○mine 2D model (MIRECO, 2008)
Table 2. Rock joint properties of ○○mine 2D model (MIRECO, 2008)
| Normal stiffness (GPa/m) | Shear stiffness (GPa/m) | Cohesion (MPa) | Friction angle (°) |
| 7.07 | 5.55 | 0.03 | 32.4 |
5. 최적설계 적용을 위한 사전 연구
5.1 개 요
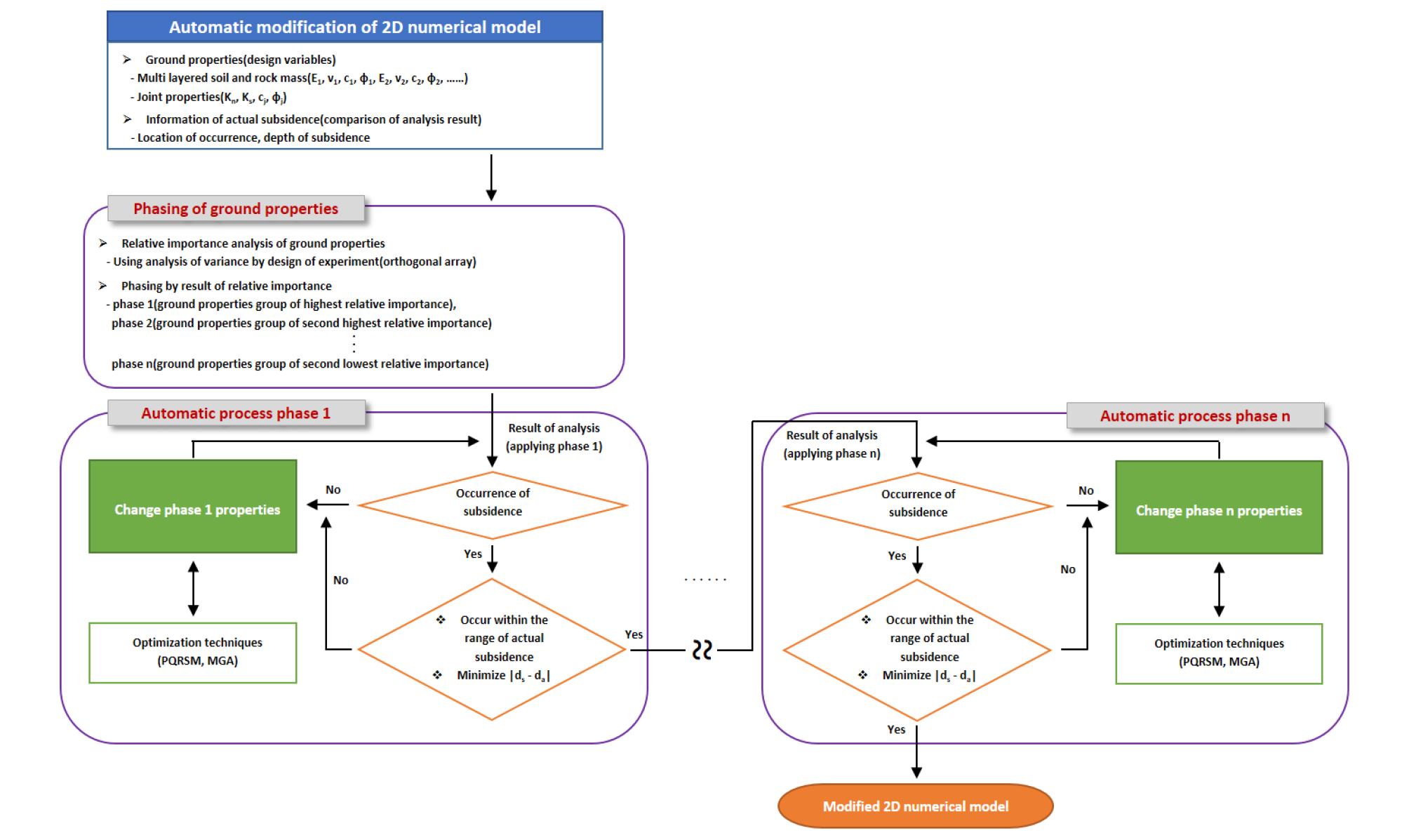
기존 현장 조사 및 실내시험으로 수집된 지질구조 및 지반물성 정보를 바탕으로 한 해석모델의 결과는 실제 침하결과와 상이하여 해당모델의 보정이 수행되어야 할 것으로 판단된다. 이에 본 연구에서는 해석모델에 대해 최적설계를 적용하여 실제 침하결과와 해석결과의 차이를 최소화하는 지반의 물성을 추정하였다. 즉 기존 지반물성을 최적설계로 추정한 물성으로 수정하여 모델을 보정하였으며, 이러한 최적설계에 의한 해석모델 보정 연구를 Fig. 9와 같이 흐름도로 요약하여 나타내었다.
그림에서 E는 변형계수(GPa), ʋ는 포아송비, c는 점착력(MPa), φ는 마찰각(°)으로 다층구조인 토양과 암반의 수에 따라 적용물성이 증가하며 아래첨자로 구분하여 표시하였다. 그리고 Kn는 절리의 수직강성(GPa/m), Ks절리의 전단강성(GPa/m), cj절리의 점착력(MPa), φj절리의 마찰각(°)이고, ds는 실제 침하지의 깊이(m), da는 수치해석으로 지표에서 최대로 발생한 연직변위(m)의 결과이다.
5.2 침하 유도 단순화 모델
복잡한 지질구조를 갖는 ○○모델의 최적설계 적용에 앞서 시행착오를 줄이고 지반모델에 적용되는 최적설계의 특성을 파악하여 연구의 효율성을 높이고자, Fig. 10과 같이 급경사 채굴적을 단순화시킨 모델을 활용한 사전 연구를 수행하였다. 각각의 지반물성과 침하의 연관성을 분석하고 복잡한 지질구조를 갖는 지반모델에서의 최적설계 적용에 관한 가이드라인을 얻는 것이 주 목적으로, 채굴적 상부암반의 붕락 및 침하가 유도되도록 모델링 하였으며 지질구조를 최대한 단순화 시켜 침하에 미치는 영향을 최소화하였다. 그리고 연구의 효율성을 위한 해석시간의 감소를 위해 Whittaker and Reddish (1989)의 침하이론을 바탕으로 수직하는 채굴적의 침하영향 한계각인 35°를 적용하고 영향범위 내에만 0.5 m 간격의 절리를 발생시켰다. 기존 침하이론에 따른 침하영향범위는 채굴적 상부에서부터 지표까지의 범위를 의미하지만 이러한 경우, 매우 작은 영향범위가 설정되어 침하를 유도하는 성능이 저하되므로 본 모델의 주 목적을 위해 침하 영향범위의 증가가 필요할 것으로 판단하여, 채굴적 상부가 아닌 중심에서부터 지표까지의 침하영향범위를 설정하였다. 최적화 기법을 적용하여 채굴적으로의 완전침하 발생과 채굴적 중심의 상부지표에 최대의 침하량을 발생시키는 상부암반 및 절리의 물성을 추정하고자 하며, 총 8개의 설계변수의 물성을 Table 3과 같이 설정하였다. 암반물성의 범위는 ○○광산에 적용된 RMR 1등급에서부터 표토까지 적용된 물성을 참고하였고 절리물성의 범위는 우선 수직강성과 전단강성은 Bandis et al. (1981)이 실험을 통해 제안한 범위를, 점착력과 마찰각은 암반의 점착력, 마찰각과 비슷한 수준으로 설정하였다. 암반물성의 초기값은 3등급 암반의 물성으로 설정하였으며, 절리물성의 초기값은 Table 2의 물성을 적용하였다.
Table 3. Range and initial value of design variables for optimal design
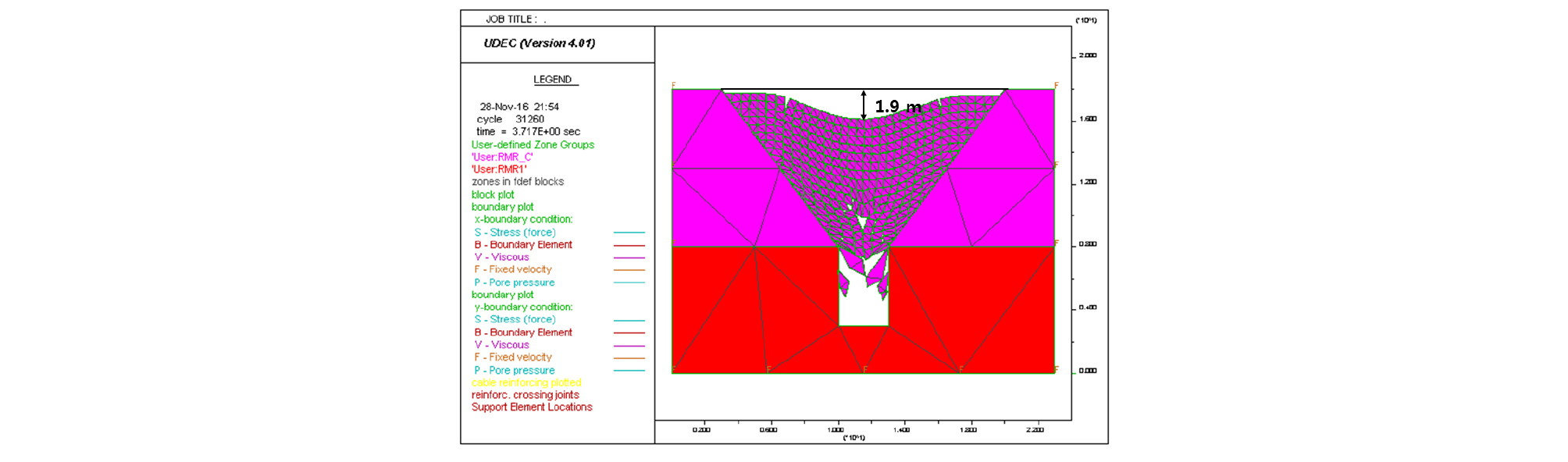
Fig. 11은 Table 3에서 하한 값의 물성을 적용한 해석결과이다. 채굴적 중심의 상부지표에 약 1.9 m의 최대 침하가 발생하였으나 채굴적 내부로의 완전침하가 발생하지 않았으며 이러한 결과로 추가적인 침하 발생을 위한 최적설계의 필요성을 다시 한 번 확인하였다.
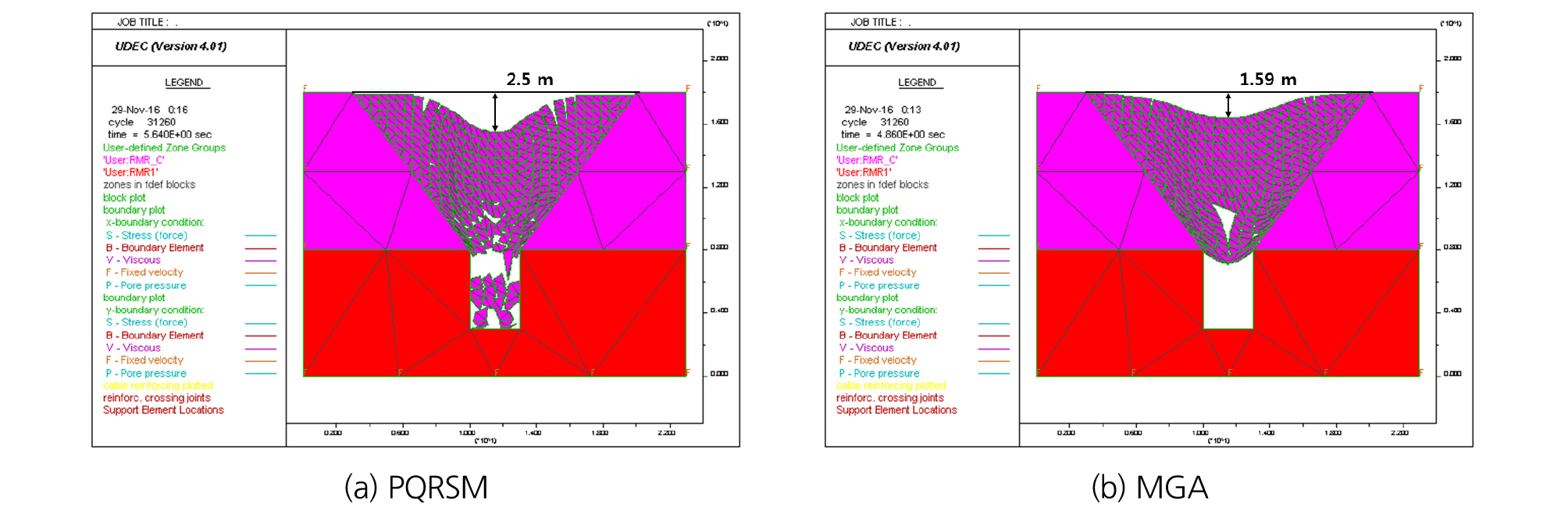
5.3 최적설계 적용 결과
최적설계의 목적함수는 해석결과와 목표변위의 차의 절대값이며, 목적함수의 값이 최소가 되도록 하는 상부암반과 절리의 물성을 추정한다. 목표변위는 3.0 m로 설정하였으며 최적설계 결과 목적함수가 0에 완전히 수렴한다면 목표변위를 증가시켜 추가적인 최적설계를 수행하는 연구계획을 수립하였다. 최적화 기법으로 PQRSM과 MGA를 적용하였으며 그 결과를 Fig. 12와 Table 4에 각각 정리하였다. PQRSM 기법을 적용한 최적설계 결과, 지표변위가 2.5 m 발생하여 하한 값을 적용한 해석결과보다 0.6 m 증가한 향상된 결과를 보였다. 반면에 MGA 기법을 적용한 최적설계 결과, 지표변위가 약 1.59 m 발생하여 하한 값을 적용한 해석결과보다 0.31 m 감소된 결과를 보여 목적함수의 수렴성이 좋지 않은 것으로 판단된다. 이러한 결과의 이유는 확률적으로 탐색하는 MGA의 특성 때문에 PQRSM보다 설계변수의 수와 범위에 더욱 민감한 영향을 받기 때문이며 MGA를 적용한 최적설계의 성능 향상을 위해 설계변수의 수와 범위의 조정이 필요할 것으로 판단된다.
Table 4. Application of optimal design (target displacement: 3.0 m)
| Objective function | Displacement | Analysis time | Number of analysis | |
| PQRSM | 0.5 m | 2.5 m | 1 h 26 m | 171 |
| MGA | 1.41 m | 1.59 m | 7 h 55 m | 951 |
5.4 설계변수의 상대적 중요도 분석
앞서 수행한 최적설계의 성능을 향상시키기 위해 설계변수와 지표침하량과의 상대적인 중요도를 분석하고 중요도에 따라 설계변수를 나누어 적용하는 단계적 최적설계 기법을 고안하였다. 단계적 최적설계를 위한 설계변수의 상대적 중요도 분석을 위해 실험계획법을 활용한 통계분석을 수행하였으며, 실험계획법으로는 Taguchi and Konishi (1987)의 직교배열법, 통계분석으로 분산분석을 수행하여 지표침하량에 대한 각 설계변수의 상대적 중요도를 파악하였다. Table 5는 이러한 실험계획법에 의해 수행된 매개변수 연구의 분산분석 결과이며 백분율 기여도의 값을 통해 상대적 중요도를 평가하였다. 설계변수 중 지반의 점착력의 상대적 중요도가 가장 높게 나타났으며, 특히 지반의 변형계수, 점착력, 절리의 점착력 3개 물성의 상대적 중요도 비율이 약 90%로 대부분을 차지하는 것으로 확인되었다.
Table 5. Results of analysis of variance by design of experiment (orthogonal array)
5.5 단계적 최적설계 적용 결과
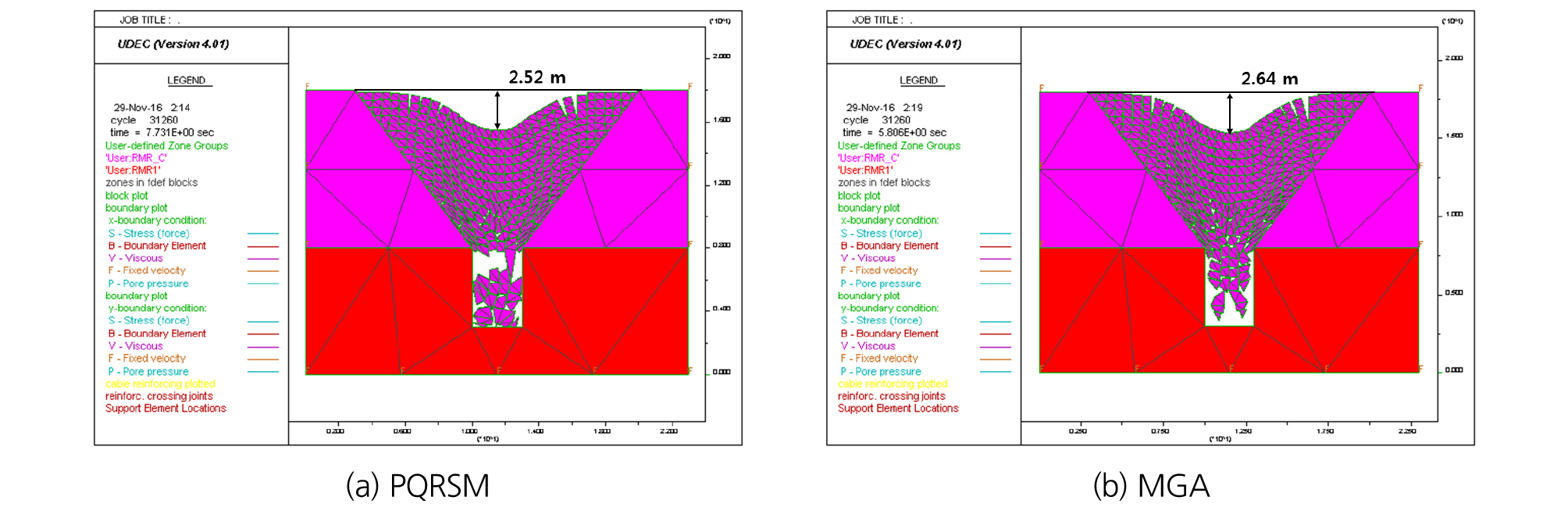
실험계획법에 의한 설계변수와 지표침하량과의 상대적 중요도 결과를 바탕으로 설계변수를 나누어 침하 유도 단순화 모델의 단계적 최적설계를 수행하였다. 8개의 변수를 한 번에 고려했던 방식을 수정하여 상대적 중요도의 결과를 바탕으로 변형계수, 점착력, 절리 점착력의 3개 물성을 먼저 추정하고 이후 나머지 5개의 물성을 추정하는 방식의 단계적 최적설계를 적용하였다. 단계적 최적설계로 추정된 물성과 발생한 최대 침하량, 소요 해석시간 및 횟수를 Table 6에 정리하였으며 Fig. 13은 추정된 물성을 침하 유도 단순화 모델에 적용한 해석결과이다. 먼저 PQRSM 기법의 경우 최종 해석 후 목표변위로 설정한 채굴적 중심위치의 지표에서 최대 침하량이 약 2.52 m 발생하였으며, 총 소요 해석시간은 약 1시간 23분으로 164회의 수치해석이 수행되었고, MGA 기법의 경우 최대 침하량이 약 2.64 m 발생하였으며, 약 25시간 29분 동안 총 3,057회의 수치해석이 수행되었다.
Table 6. Maximum subsidence and estimated properties by phased optimal design array
5.6 연구결과의 고찰
초기에 8개의 설계변수를 동시에 적용한 최적설계와 설계변수를 중요도에 따라 나누어 적용한 단계적 최적설계의 방법을 비교한 결과, MGA 기법의 경우 목적함수의 수렴성이 약 35% 증가하였으며, PQRSM 기법의 경우 목적함수 수렴성의 증가량이 약 1%로 다소 미미하였으나 소요 해석시간이 약 3.5% 감소한 것을 확인하였다. 이러한 결과로 단계적 최적설계는 모든 설계변수를 동시에 고려하지 못하지만 적용되는 설계변수의 수 감소, 민감한 설계변수들만을 고려하게 되는 조건으로 인해 목적함수의 수렴성을 증가시키고 최적설계 결과의 성능을 향상시키는 것으로 판단된다. 또한 첫 번째 단계 이후의 해석에서 초기값이 목표변위에 가까운 값으로 변경되기 때문에 초기값에 민감한 PQRSM 최적설계의 적용 시 문제에 대한 수치적 ‧ 함수적 사전 정보 없이 적용할 수 있으며 보다 감소된 해석시간으로 향상된 결과를 얻을 수 있을 것으로 기대되며, MGA 최적설계는 단계적 기법 적용으로 PQRSM 최적설계와 비교하여 설계영역 변수에 대한 보다 세밀한 검토로 더욱 나은 최적해를 도출해주는 것으로 확인되었다. 하지만 상대적으로 많은 해석시간을 요구하기 때문에 주어진 시간과 연구목적에 따라 적합한 최적화 기법을 선택하여 수행하는 것이 중요할 것으로 판단된다.
6. 단계적 최적설계를 통한 ○○광산 지반의 역학적 특성 추정
6.1 개 요
○○광산 2차원 해석모델의 다층암반과 광맥 및 절리 총 39개의 물성에 대해 지표침하에 대한 상대적 중요도를 실험계획법을 통해 분석 후 그 결과를 바탕으로 고려해야 할 설계변수를 선정하였으며, 선정된 설계변수에 대해 중요도에 따라 나누어 단계적 최적설계를 적용하여 실제 침하지의 위치에서 최대의 지표침하를 유도하는 지반의 역학적 특성을 추정하고 해석모델에 적용하여 그 결과를 확인하였다. 목표변위의 위치를 실제 침하지 중심의 상부 지표로 설정하였으며, 그 크기는 초기 해석에 의한 침하량을 참고하여 5.0 m를 적용하였다. 목적함수는 해석결과와 목표변위의 차의 절대값이며, 최적화 기법으로 PQRSM과 MGA를 활용하여 목적함수의 값이 최소가 되도록 설계변수의 값을 추정하였다. 최적설계의 결과 목적함수가 0에 완전히 수렴한다면 목표변위를 증가시켜 추가적인 최적설계를 수행하는 연구계획을 수립하였으며, 목표변위의 상한값은 실제 침하규모인 17 m이다.
6.2 ○○광산 설계변수의 상대적 중요도 분석
해석모델 입력물성의 지표침하에 대한 상대적 중요도를 실험계획법에 의한 분산분석으로 확인하였다. 그 중 백분율 기여도에 의한 상대적 중요도가 0.01% 이상인 물성의 결과만을 선별하여 Table 7에 정리하였다. 그 결과 표토, 광맥, 절리 물성의 상대적 중요도가 모두 0.01%이상으로 확인되었으며, 그 외 물성은 모두 그 이하의 값이 나타나 상대적 중요도가 미미하였다. 또한 점착력이 약 90%, 광맥과 표토의 마찰각, 절리 점착력이 각각 약 3%의 결과로 나타나 4 개의 설계변수의 총합이 99%로 매우 큰 비율의 상대적 중요도를 보였다.
이러한 결과를 바탕으로 총 39개 물성 중, 상대적 중요도가 0.01% 이상인 12개의 설계변수를 Table 8과 같이 선정하였으며, 사전연구결과를 바탕으로 물성의 범위는 침하 유도 단순화 모델에 적용한 Table 3의 범위에서 상한값을 RMR 2등급으로 조정하였다. 절리의 수직강성과 전단강성의 상한값을 변형계수와 동일하게 설정하였고, 초기값 설정에 있어 우선 암반물성은 4등급 물성으로 설정하였으며, 절리 물성은 Table 2의 물성을 적용하였다. 또한 광맥의 점착력과 마찰각, 표토의 마찰각, 절리 점착력을 대상으로 1단계 최적설계를 수행하고, 2단계로 표토와 광맥의 변형계수, 절리의 수직강성과 전단강성을 대상으로 하였으며, 마지막 3단계에 나머지 변수들을 대상으로 하는 최적설계의 방식을 설정하여 각 단계별 4개씩 설계변수를 고려하는 단계적 최적화 기법을 수행하였다.
Table 7. Results of analysis of variance by design of experiment (orthogonal array)
Table 8. Range and initial value of design variables for optimal design of ○○mine 2D model
6.3 ○○광산 단계적 최적설계 적용 결과
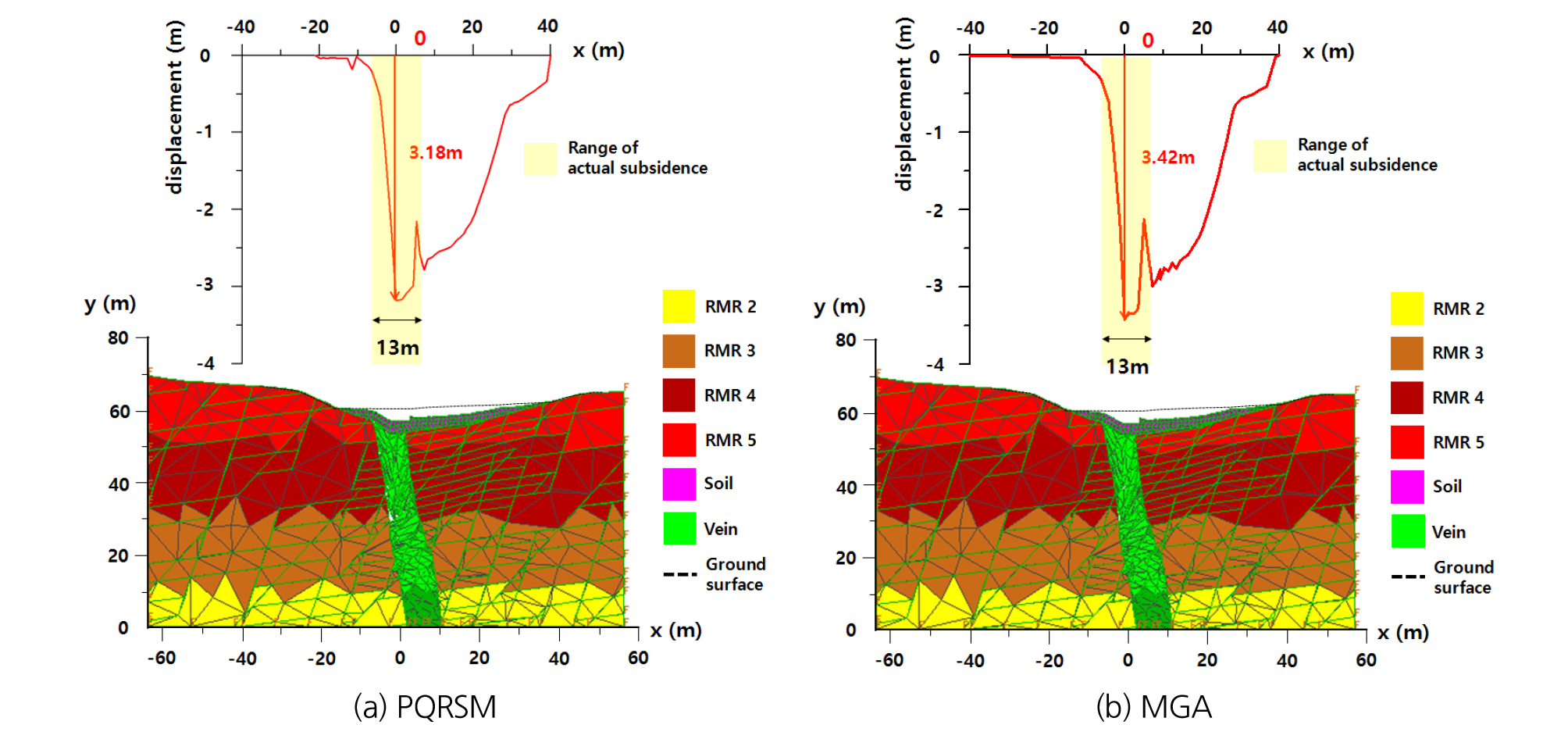
단계적 최적설계의 적용 결과로 추정된 물성과 발생한 최대 침하량, 소요된 해석 시간 및 횟수를 Table 9에 정리하였다. Fig. 14는 최적설계 결과인 최적해를 적용한 수치해석 결과이며 두 최적화 기법 모두 최종 해석 후 채굴적으로의 완전 침하가 발생한 것을 확인하였다. 먼저 PQRSM에 의한 단계적 최적설계 결과, 최종해석 후 실제 침하위치의 범위에서 최대 침하량이 약 3.18 m 발생하였으며, 총 소요 해석시간은 약 6시간 4분 35초로 138회의 수치해석이 수행되었다. 그리고 MGA에 의한 단계적 최적설계의 결과 또한 실제 침하위치의 범위에서 최대 침하가 발생하였으며 그 값은 약 3.42 m로 더 크게 확인되었고, 총 3,208회의 수치해석이 약 135시간 40분 동안 수행되었다.
Table 9. Maximum subsidence and estimated properties of ○○mine model by phased optimal design
6.4 연구결과의 고찰
초기 모델의 해석과 단계 최적설계로 추정된 물성을 적용한 보정 모델의 해석결과를 실제 침하지의 정보와 비교하여 Table 10에 정리하였다. 초기 모델에 대해 최적설계로 보정한 결과, 최대 침하량에 있어 PQRSM의 경우 1.85 m, MGA의 경우 2.09 m 증가하여 실제 침하지의 규모와 보다 근접하였다. 또한 최대 침하량의 발생위치에 있어 12.6 m 벗어난 초기 모델의 해석결과에서 PQRSM과 MGA 모두 실제 침하지의 중심 위치와 일치하도록 보정되어 최적설계에 의한 자동화 보정연구의 적용성과 추정된 물성의 신뢰성을 확인하였다.
Table 10. The comparison of analysis results between initial model and modified model by optimal designs
7. 결 론
본 연구에서는 실제 침하가 발생한 폐광산 현장을 대상으로 2차원 모델링 후 실제 침하지 정보를 바탕으로 최적설계로 추정한 지반의 역학적 특성을 적용하여 보정하였으며, 추정 및 보정의 과정에 있어 자동화된 단계적 최적설계 기법을 제안하였다. 주요 연구결과를 요약하면 다음과 같다.
1. ○○광산을 연구 대상 광산으로 선정하여 실제 침하가 발생한 단면에 대해 2차원 모델링을 수행하였다. 실제 침하지의 정보를 바탕으로 모델에 침하가 발생하도록 보정하였으며, 최적설계를 적용하여 그 과정을 자동화하였다. 복잡한 지질구조를 갖는 실제 모델의 적용에 앞서, 시행착오를 줄이기 위해 침하 유도 단순화 모델에 우선 적용하여 그 특성을 파악하였다.
2. 다수의 설계변수로 인해 최적설계의 성능이 감소되는 문제를 해결코자 설계변수와 지표침하량과의 관계를 통계적으로 분석하고, 중요도에 따라 다수의 설계변수를 나누어 고려하는 단계적 최적설계 기법을 고안하였다. 침하 유도 단순화 모델에 PQRSM과 MGA 최적화 기법을 사용한 단계적 최적설계를 적용한 결과, 모든 설계변수를 그대로 고려하는 기존 최적설계와 비교하여 목적함수의 수렴성이 PQRSM의 경우 약 1%, MGA의 경우 약 35%가 증가하였다. 단계적 최적설계는 모든 설계변수를 동시에 고려하지 못하지만 적용되는 설계변수의 감소, 민감한 설계변수만을 고려, 문제에 대한 사전 정보 제공 등의 조건으로 인해 최적설계의 수행에 유리할 것으로 판단된다.
3. ○○광산 2차원 모델에 단계적 최적설계를 적용하여 보정하였다. 그 결과 지표에 발생한 최대 침하량과 실제 침하지 규모와의 차이가 PQRSM 최적설계에 의해 약 11.8%, MGA 최적설계에 의해 약 13.3% 감소하여 MGA가 PQRSM보다 1.5% 향상된 보정 결과를 보였다. 또한 최대 침하의 발생위치와 실제 침하지 중심위치와의 차이가 12.6 m로 나타난 초기 모델의 결과에서 보정에 의해 정확히 일치되는 것으로 나타나 단계적 최적설계에 의한 자동화 보정연구의 적용성을 확인하였다.
4. MGA는 설계영역의 변수를 더욱 세밀히 검토하여 PQRSM보다 나은 최적해를 도출해준다. 하지만 보정결과의 차이가 크지 않았으며, 약 6시간이 소요된 PQRSM과 비교하여 MGA가 약 135시간 40분으로 약 22.4배 높은 해석시간이 소요되었다. 이렇듯 요구된 시간과 결과의 차이를 감안했을 때, PQRSM을 활용한 단계적 최적설계가 보다 효율적인 것으로 판단된다.
5. 본 연구를 통해 광산현장에 대한 최적설계의 활용가능성을 확인하고, 적용을 위한 단계적 최적설계 기법 및 기초적인 가이드라인을 제안하였다. 하지만 본 연구는 특정조건을 갖는 1개의 광산에 적용한 수치해석적 결과이므로 일반화 하는 것은 다소 무리가 있다. 따라서 향후 다양한 조건의 현장 적용과 실험적 방법을 통한 추가적인 연구가 필요할 것으로 사료된다.