1. 서 론
2. 선형절삭시험
3. 개별요소법을 이용한 수치해석
3.1 암반강도별 미세물성(Micro-property) 결정
3.2 선형절삭시험의 PFC3D 해석
3.3 수치해석의 적정성 검토
4. 디스크커터 최적 간격 산정
5. 결 론
1. 서 론
소음 ․ 진동 등의 환경 피해를 최소화하고 노동력을 절감할 수 있으며, 장대터널에서 급속 시공을 하면 경제적인 터널 시공이 가능하다는 점에서, 터널 기계화 시공의 비중이 더욱 증대되고 있다(Shin, 2015). 그러나 기계식 터널방법의 TBM (tunnel boring machine, TBM)장비의 설계 및 사양검토에 대한 국내 기술력은 미비한 실정이며, TBM의 설계는 노르웨이, 미국, 일본, 독일 등의 기술력에 의존하고 있다.
TBM의 커터헤드 설계에 있어서 디스크커터의 간격 및 압입깊이는 TBM의 암석절삭 효율을 결정하는 중요한 요소이다. 디스크커터가 특정 압입깊이로 암석을 절삭할 때 인접한 디스크커터들 사이에는 최적의 절삭효율을 보이는 최적 커터간격이 존재하게 되는데, 이러한 최적 커터간격보다 크거나 작은 경우 절삭과정에서 에너지 효율이 감소한다(Rostami and Ozdemir, 1993; Acaroglu et al., 2008). 따라서 TBM이 최대의 절삭효율을 발휘하기 위해서는 암반강도 및 압입깊이별로 최적 커터간격을 산정해야 한다. 일반적으로 디스크커터의 최적 절삭조건을 규명하기 위해서는 실대형 선형절삭시험(linear cutting machine, LCM)을 수행하는 것이 가장 신뢰성 있는 방법으로 알려져 있다(Rostami et al., 1996; Chang et al., 2007). 이러한 실대형실험의 경우 경제적, 시간적 제약이 있다. 이러한 제약을 실험의 여러 대안을 정하여 수치해석을 수행함으로써 역학적으로 유리한 대안을 미리 검토해 볼 수 있다(Shin, 2015).
디스크커터의 최적간격 산정과 관련된 연구는 다수 보고되고 있다. Colorado School of Mines에서는 개별 커터에 작용하는 절삭력의 측정을 통해 Semi-theoretical 모델인 CSM 모델을 개발하였으며, Rostami and Ozdemir (1993)는 암석의 일축압축강도 및 인장강도, 커터형상에 따른 절삭력을 이용하여 CSM 모델을 개선하는 연구를 수행하였다. Bakar et al. (2014)은 실대형 절삭실험을 통해, 암반의 함수량이 디스크커터에 의한 암반굴착거동에 미치는 영향에 대한 연구를 수행하였다. Medel-Morales and Botello-Rionda (2013)는 PFC3D를 이용하여 선형절삭시험을 모사하고 Colorado School of Mines의 Cutting force method (CFM)와 비교 ․ 분석하는 연구를 진행한 바 있다. Cho et al. (2010)는 연속체 수치해석 기반의 AUTODYN-3D를 이용하여 선형절삭시험에 대한 3차원 동적 파괴 시뮬레이션을 수행하였으며, 사진측량기법을 사용한 선형절삭시험을 통해 국내 화강암에 대한 디스크커터 절삭효율평가 연구를 수행하였다(Cho et al., 2010). Choi and Lee (2015)는 Particle Flow Code 3D (PFC3D)의 Linear contact bond 모델을 이용하여 부산응회암에 대한 선형절삭시험을 모사하고 최적 커터간격을 산출하는 연구를 진행하였다. 그러나 기존 연구들에서는 몇 개의 특정 암석에 대한 커터간격 산정 연구를 진행하였기 때문에 암반강도에 따른 커터간격의 변화를 파악하기 힘들었다. 따라서 본 연구에서는 암반강도별 최적 커터간격의 범위에 대한 연구를 진행하기 위하여, 개별요소법 기반의 수치해석 프로그램인 PFC3D의 접촉모델 중 입자 간 미끄러짐 및 모멘트에 저항할 수 있는 Linear parallel bond 모델을 이용하여 암반모델을 구성하고 암반강도 및 압입깊이에 따른 선형절삭시험을 시뮬레이션하고 커터간격에 따른 비에너지를 산출하여 최적 커터간격을 산정하였다.
2. 선형절삭시험
선형절삭시험(linear cutting method, LCM)은 실제 TBM을 이용한 터널 굴착 시 발생할 수 있는 커터하중과 관입정도를 모사할 수 있기 때문에 TBM의 성능예측에 직접 적용할 수 있고 시험결과에 대한 크기 효과를 배제할 수 있는 것으로 보고되고 있다(Nilsen and Ozdemir, 1993). 또한 선형절삭시험은 디스크커터의 최적 절삭조건을 규명하는데 있어 가장 신뢰성 있는 방법으로 알려져 있다(Rostami et al., 1996; Chang et al., 2007).
선형절삭시험을 통해 디스크커터 간 최적간격을 산출하기 위해서는 단위부피를 절삭하는데 필요한 에너지인 비에너지(specific energy, SE)의 계산이 필요하다. 비에너지는 굴착 시 커터에 작용되는 회전력(Froll)과 절삭거리(dcut), 절삭부피(Vchip)를 이용하여 계산할 수 있다.
| $$SE=\frac{F_{roll}\times d_{cut}}{V_{chip}}$$ | (1) |
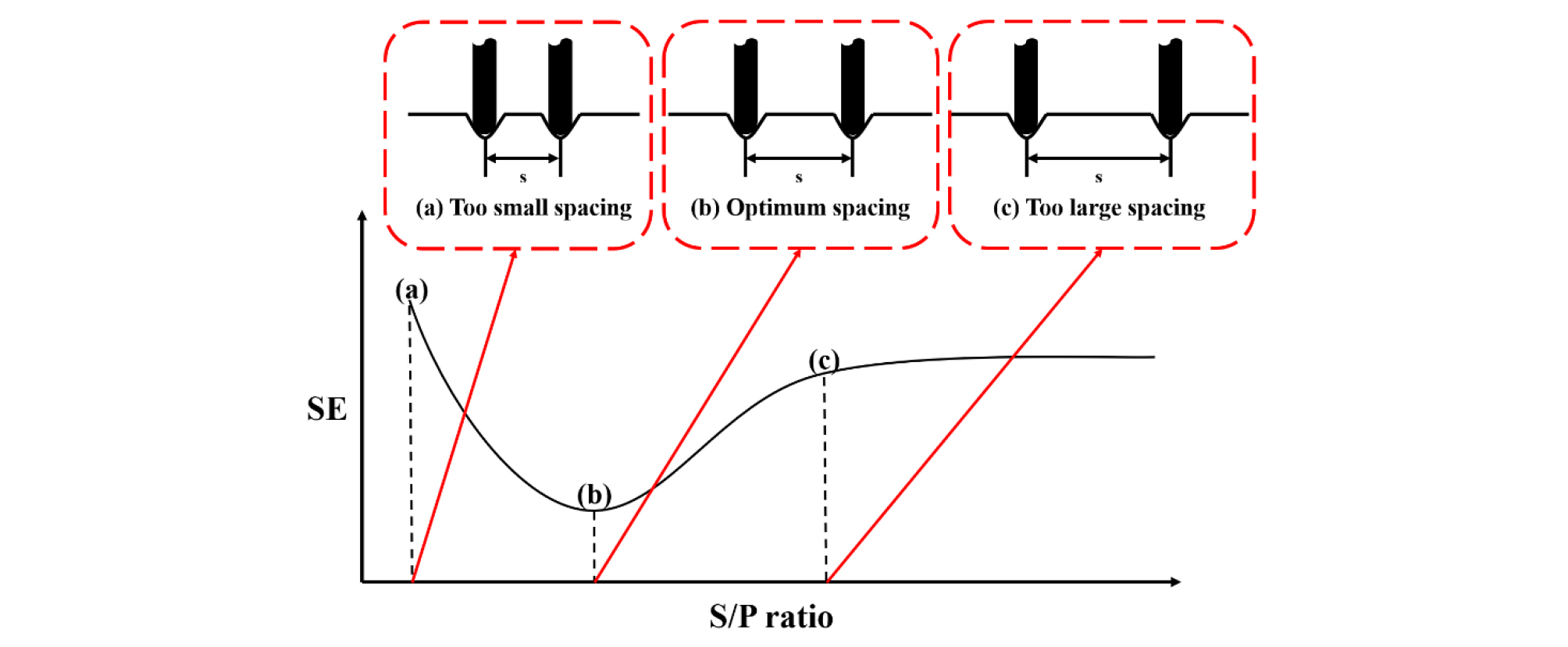
계산된 비에너지를 커터간격(S)과 압입깊이(P)의 비인 S/P비에 따라 도시하면 Fig. 1과 같은 경향을 보이며, 비에너지가 최솟값인 (b)위치에서의 S/P비를 최적 S/P비(S/Popt)로 정의한다.
3. 개별요소법을 이용한 수치해석
본 연구에서는 개별요소법(discrete element method, DEM)을 이용하여 수치해석 연구를 수행하였다. 개별요소법은 불연속체의 거동해석법으로 해석하려는 모델을 단일 입자의 군집으로 이루어져 있다고 가정하고 입자간 결합을 통해 모델을 형성하기 때문에 균열의 전파 및 파괴거동의 시뮬레이션을 보다 잘 모사하는 것으로 알려져 있다(Labra et al., 2017).
본 연구에서는 PFC3D의 두 가지 기본결합모델인 Linear contact bond model과 Linear parallel bond model 중 Linear parallel bond model을 사용하여 수치해석을 진행하였다. Linear contact bond model은 두 입자사이의 한 지점에서 수직 및 전단강성을 형성하며, Linear parallel bond model은 두 입자사이의 접촉면적에 수직 및 전단강성을 형성한다. PFC의 입자는 수직 및 전단방향으로 자유롭게 이동이 가능하며 입자 사이의 회전도 발생한다. 이러한 입자사이의 이동 및 회전은 입자간 모멘트를 유발하지만 Linear contact bond model은 이러한 모멘트에 저항할 수 없으며, Linear parallel bond model의 경우 접촉면에 결합을 형성하기 때문에 모멘트에 저항할 수 있다. 결합을 형성한 후, 작용하는 응력 중 하나가 결합강도를 초과하게 되면 결합이 끊어지게 되며, 결합이 끊어진 이후에는 Linear model과 같은 거동을 보인다. 따라서 본 연구에서는 암반의 파괴거동과 유사한 거동을 보이는 접촉모델인 Linear parallel bond model을 이용하여 접촉결합을 형성하였다. Fig. 2는 Linear parallel bond model의 거동 요약도이다.
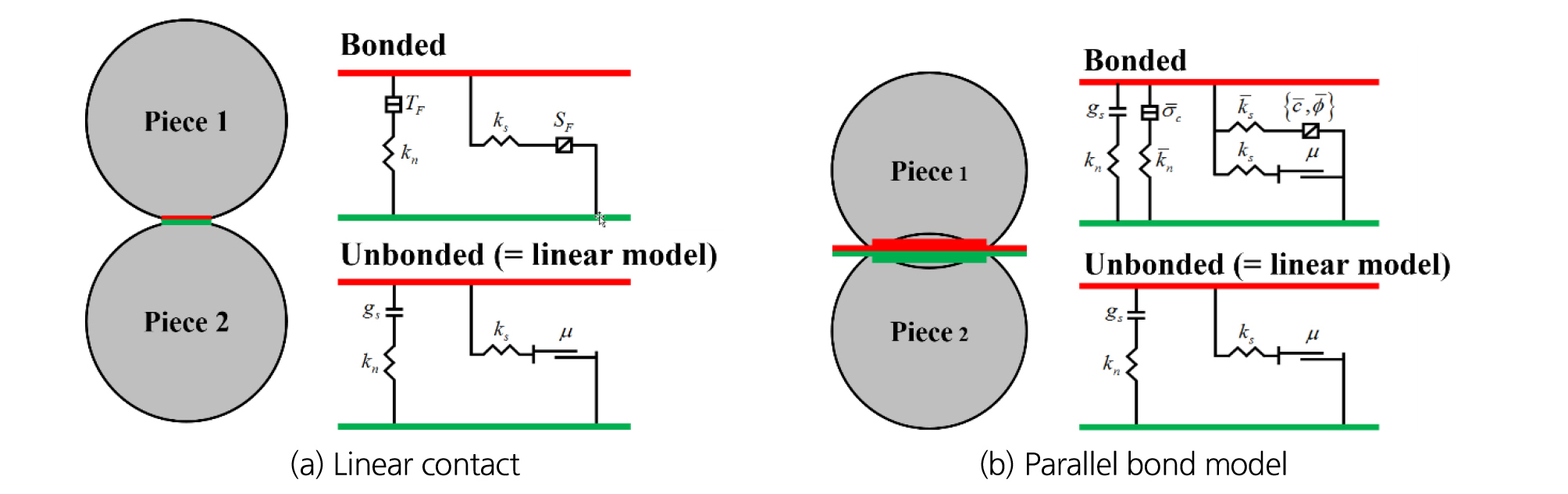
Fig. 2.
Behavior components of the (a) linear contact, (b) parallel bond model (Itasca Consulting Group, 2019)
3.1 암반강도별 미세물성(Micro-property) 결정
개별요소법의 입력 물성은 연속체 해석의 입력물성을 결정하는 방법과 다르다. 연속체해석의 경우 실험을 통해 탄성계수, 전단강도와 같은 입력물성을 산출하여 해석에 적용할 수 있으나, 개별요소법의 경우 실험 대상 암반의 거동특성을 표현할 수 있는 결합모델과 관련된 미세 물성을 결정하여야 한다(Potyondy and Cundall, 2004).
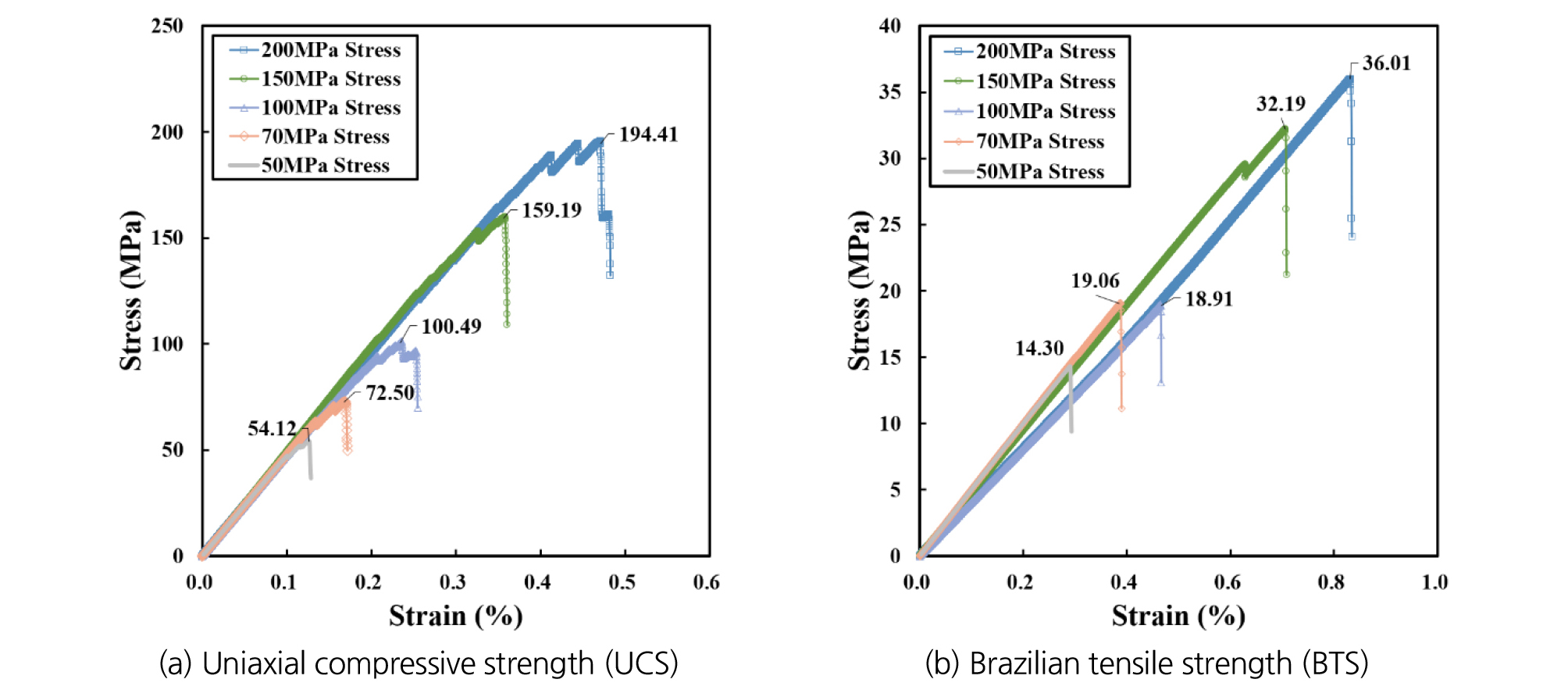
본 연구에서는 5가지의 암반강도(50 MPa, 70 MPa, 100 MPa, 150 MPa, 200 MPa)에 대하여 압입깊이(6 mm, 8 mm)와 커터간격(20~180 mm)을 변경하며 선형절삭시험을 시뮬레이션하였다. 각각의 암반강도에 대한 일축압축시험 및 할렬인장강도 시험을 반복 해석하여 해석 결과를 Fig. 3에 도시하였으며, 결정된 암반강도의 미세물성은 Table 1에 정리하였다.
Table 1.
Micro-properties for various rock strengths
3.2 선형절삭시험의 PFC3D 해석
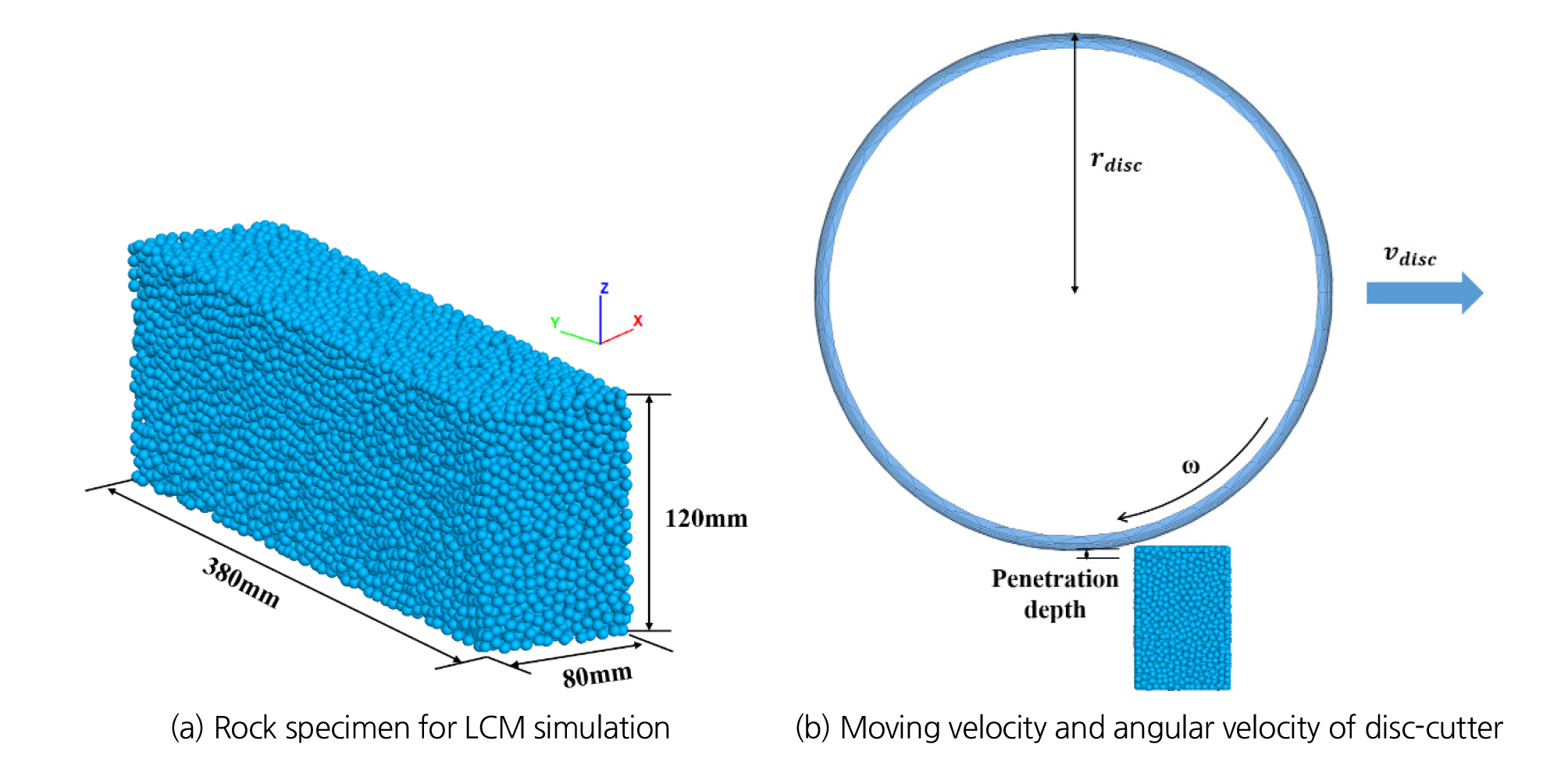
선형절삭시험의 수치해석을 위한 암석시편 및 디스크커터 모델은 Fig. 4와 같다. 암석시편은 380 mm × 80 mm × 120 mm의 크기로 모델링하였으며, 디스크커터는 17인치로 모델링하였다. 디스크커터의 선형절삭속도(vdisc)는 커터의 절삭성능에 뚜렷한 영향을 미치지 않는 것으로 보고된 바 있으며(Sanio, 1985), Choi and Lee (2015)는 개별요소법 수치해석의 해석효율을 제고하기 위해 선형절삭속도를 2 m/s로 적용한 바 있다. 따라서 본 연구에서 디스크커터의 선형절삭속도(vdisc)는 2 m/s로 설정하였다. 디스크커터의 각속도(ω)는 선형절삭속도(vdisc)와 디스크커터의 반경(rdisc)으로 이루어진 식 (2)로 계산할 수 있다. 식 (2)를 이용하여 선형절삭속도(vdisc)가 2 m/s일 때 각속도(ω)는 9.26 rad/s로 설정하였다.
| $$\omega=\frac{v_{disc}}{r_{disc}}$$ | (2) |
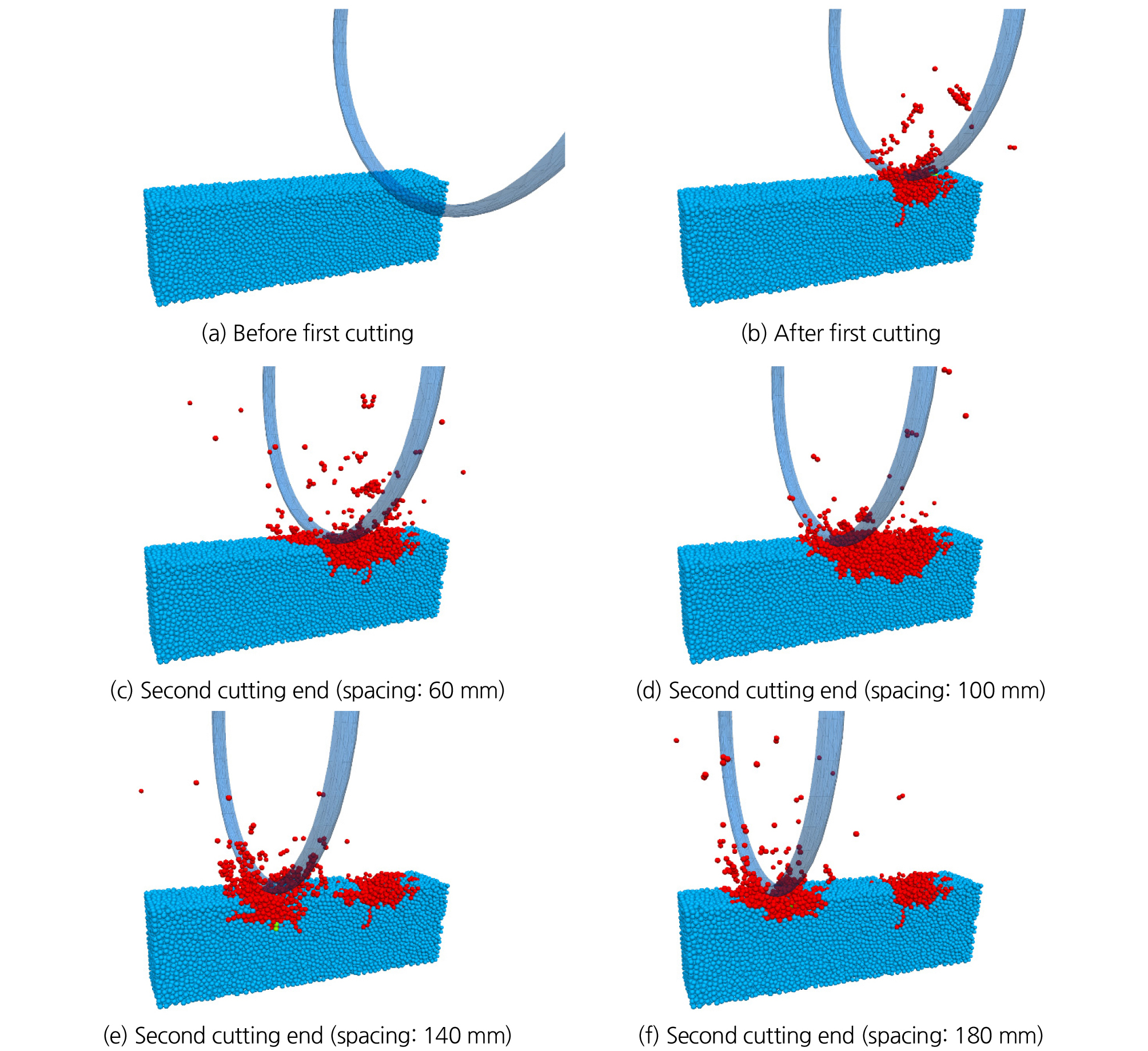
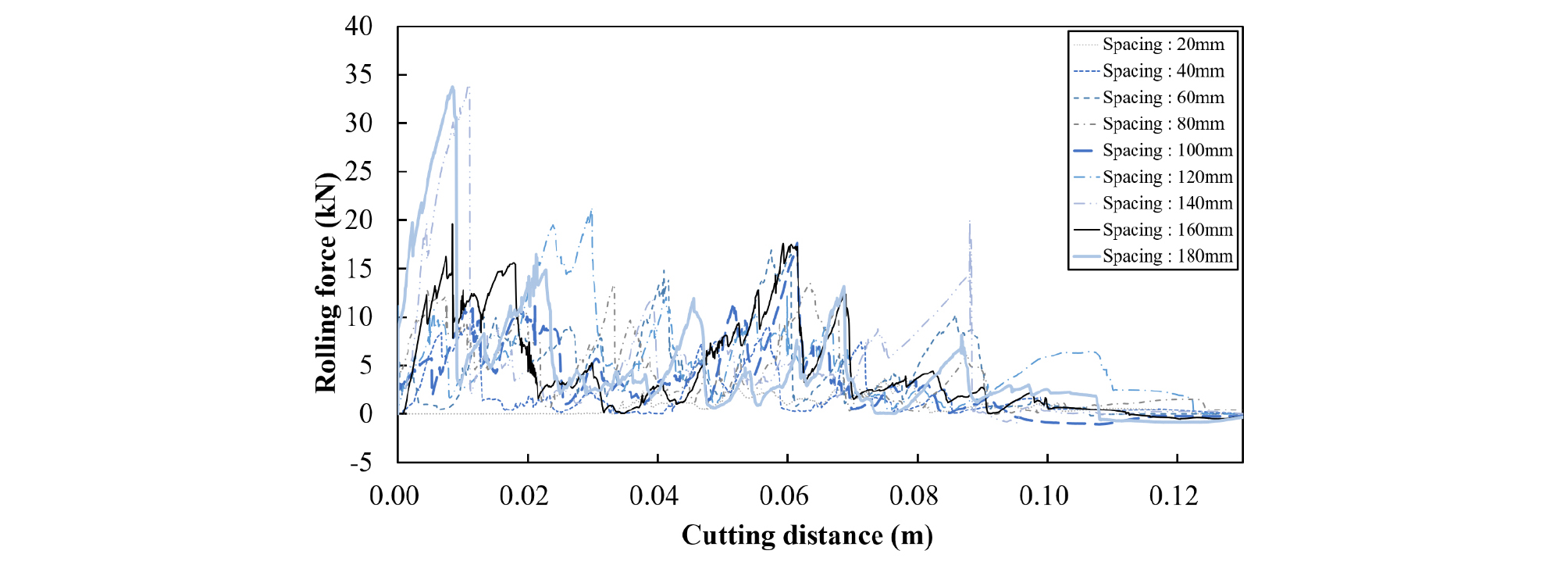
5가지 암반강도(50 MPa, 70 MPa, 100 MPa, 150 MPa, 200 MPa)에 대하여 해석을 수행하였으며, 각각의 암반강도에서 압입깊이 6 mm, 8 mm 및 커터간격 20~180 mm까지 20 mm의 간격으로 해석을 수행하였다. Fig. 5는 일축압축강도 70 MPa와 압입깊이 8 mm에서 커터간격 60 mm, 100 mm, 140 mm, 180 mm에 해당하는 암석시편의 절삭해석결과이며, Fig. 6은 커터간격이 20 mm에서 180 mm까지 20 mm 간격으로 증가시켜가며 절삭해석을 수행한 결과 디스크커터 모델에 작용한 회전력의 측정결과이다.
3.3 수치해석의 적정성 검토
PFC3D를 이용한 수치해석 결과의 검증을 통해 반이론적 모델인 CSM 모델과의 비교 및 분석을 수행하였다. CSM 모델에서 비에너지는 커터의 작용회전력에 비례하며 절삭 부피의 경우 압입깊이, 커터간격, 절삭거리의 곱으로 계산하지만, PFC3D의 해석의 경우 인장균열에 의해 암편이 형성되며 이러한 암편의 부피를 계산할 수 있다. 따라서 절삭 부피의 산정법이 다르기 때문에 직접적인 비교는 불가능하며, 비에너지와 비례하는 커터의 작용회전력의 CSM 모델과 수치해석 결과를 비교하였다.
CSM 모델에서 디스크커터가 관입될 때, 커터에 작용하는 합력은 식 (3)을 이용하여 계산할 수 있으며 이를 통해 커터에 작용하는 회전력을 계산할 수 있다. 이때, 일반적으로 CCS (Constant Cross Section)커터를 사용하는 경우 압력분포상수(ψ)는 커터팁 두께의 증가에 따라 -0.2~0.2 사이의 값을 갖는다고 알려져 있다. 본 연구에서는 압력분포 상수를 0으로 설정하였다.
| $$F_t=\frac{P'\phi RT}{1+\varphi}$$ | (3) |
| $$F_r=F_t\sin\frac\phi2$$ | (4) |
| $$\phi=\cos^{-1}\frac{R-p}R$$ | (5) |
| $$P'=C\;\sqrt[3]{\frac{S\sigma_t\sigma_c^2}{\phi\sqrt{RT}}}$$ | (6) |
여기서, Fn : 커터 수직력(N)
Fr : 커터 회전력(N)
P' : 파쇄영역 작용 압력(Pa)
Ψ : 압력분포함수에 대한 상수
R : 커터 반지름(m)
T : 커터 팁의 두께(m)
p : 압입깊이(m)
C : 무차원계수(2.12)
σc : 암석의 일축압축강도(Pa)
σt : 암석의 인장강도(Pa)
S : 커터사이의 간격(m)
Φ : 커터와 암편의 접촉각도(radian)
Rostami et al. (1996)는 커터 하부의 파쇄영역에서 발생하는 압력(P')에 대해서 식 (6)을 제안했다. 따라서 CSM 모델에서 일축압축강도 및 인장강도, 커터 직경 및 커터 팁의 두께가 같으면 커터회전력은 커터간격에 비례하기 때문에 해석범위에서 커터회전력은 식 (7)과 같이 정규화 하여 표현할 수 있다.
| $$Normalized\;F_r=\sqrt[3]{\frac S{S_{max}}}$$ | (7) |
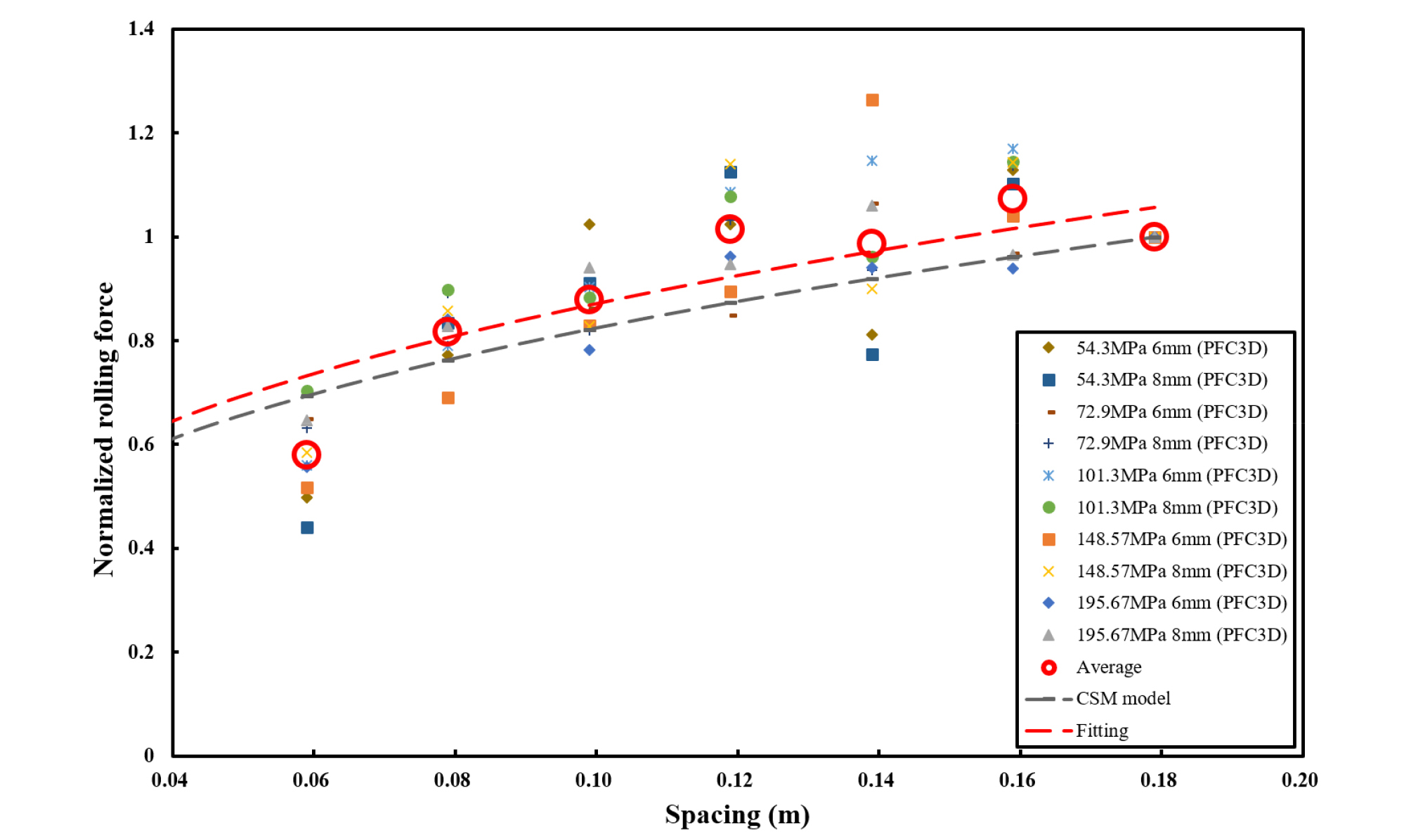
본 연구에서 최대커터간격인 Smax의 경우 180 mm이므로, CSM 모델의 커터회전력은 180 mm의 값을 기준으로 정규화 되게 된다. 따라서 수치해석으로 도출된 데이터를 180 mm를 기준으로 정규화하고 최소제곱법을 사용하여 그래프를 작도하여 CSM 모델과 비교하였다.
비교결과, Fig. 7에 도시된 것과 같이 각 케이스의 최댓값으로 정규화된 회전력의 경향을 CSM 모델과 유사한 경향을 보이는 것을 확인할 수 있었다.
4. 디스크커터 최적 간격 산정
비에너지를 계산하기 위해서는 절삭에 필요한 에너지와 디스크커터의 절삭에 의한 절삭부피를 산출해야 한다. 암석시편의 절삭에 필요한 에너지의 경우 회전력과 절삭거리의 곱으로 산출할 수 있다. 본 연구에서는 2차 컷팅에 의한 비에너지 계산을 위해, 2차 컷팅에 의한 회전력을 절삭거리에 대해 적분하여 절삭에 필요한 에너지를 산출하였다. 절삭 부피는 1차 컷팅에 의해 결합이 끊어진 입자의 부피는 제외하고 2차 컷팅에 의해 기존 암석시편과 결합이 끊어진 입자의 부피를 측정하였다. 이러한 방법은 1차 컷팅에 의해 발생하는 파쇄영영의 부피를 제외함으로써 인장균열에 의해 발생하는 암편의 부피를 계산할 수 있다.
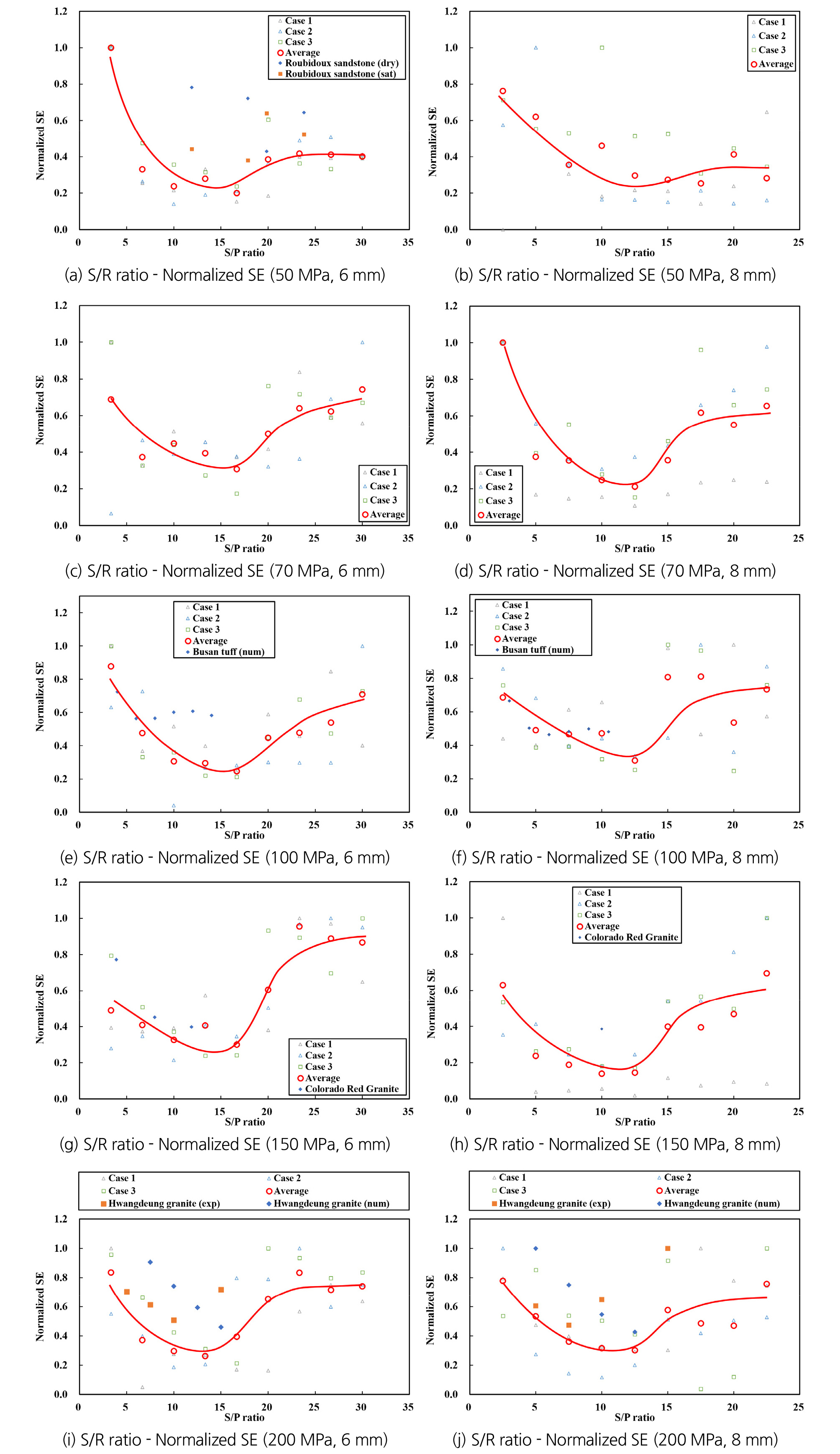
각각의 암반강도에서 압입깊이 및 커터간격에 대한 수치해석을 진행하여 비에너지를 계산하고 수치해석결과의 비교를 위해 기존 연구에서 수행된 LCM 시험결과 중 유사한 UCS와 압입깊이를 갖는 결과들을 Table 2에 정리하였다. 비에너지의 경우 각각의 해석조건에서 발생한 최대 비에너지를 이용하여 정규화했다. 이러한 정규화된 비에너지(normalize specific energy)를 이용하여 S/P ratio - Normalize specific energy 그래프를 Fig. 8에 도시하였다.
Table 2.
Specific energy list (LCM test and numerical analysis data)
| Rock type | Data type | UCS | BTS |
S (mm) |
P (mm) | S/P |
Specific energy (MJ/m3) |
Normalize SE | Reference |
|
Roubidoux sandstone (dry) | LCM test | 51 | 1.02 | 76.2 | 6.4 | 11.9 | 10.44 | 0.78 | Bakar et al. (2014) |
| 114.3 | 17.9 | 9.65 | 0.72 | ||||||
| 127 | 19.8 | 5.72 | 0.43 | ||||||
| 152.4 | 23.8 | 8.60 | 0.64 | ||||||
|
Roubidoux sandstone (sat) | 43 | 1.0 | 76.2 | 11.9 | 6.95 | 0.44 | |||
| 114.3 | 17.9 | 5.98 | 0.38 | ||||||
| 127 | 19.8 | 10.04 | 0.64 | ||||||
| 152.4 | 23.8 | 8.21 | 0.52 | ||||||
| 228.6 | 36.0 | 15.70 | 1.00 | ||||||
|
Busan tuff |
Numerical analysis (DEM) | 115.48 | 25.2 | 24 | 6.0 | 4.0 | 18.56 | 0.73 | Choi and Lee (2015) |
| 36 | 6.0 | 14.44 | 0.56 | ||||||
| 48 | 8.0 | 14.48 | 0.57 | ||||||
| 60 | 10.0 | 15.40 | 0.60 | ||||||
| 72 | 12.0 | 15.55 | 0.61 | ||||||
| 84 | 14.0 | 14.91 | 0.58 | ||||||
| 24 | 3.0 | 17.02 | 0.66 | ||||||
| 36 | 4.5 | 12.88 | 0.50 | ||||||
| 48 | 6.0 | 11.88 | 0.46 | ||||||
| 60 | 7.5 | 12.34 | 0.48 | ||||||
| 72 | 9.0 | 12.76 | 0.50 | ||||||
| 84 | 10.5 | 12.30 | 0.48 | ||||||
|
Hwangdeung granite | LCM test | 209 | 9.2 | 30 | 6.0 | 5.0 | 52.10 | 0.70 | Ministry of Land, Infrastructure and Transport (2015) |
| 45 | 7.5 | 45.30 | 0.61 | ||||||
| 60 | 10.0 | 37.60 | 0.51 | ||||||
| 90 | 15.0 | 53.10 | 0.72 | ||||||
| 40 | 8.0 | 5.0 | 44.80 | 0.61 | |||||
| 60 | 7.5 | 35.00 | 0.47 | ||||||
| 80 | 10.0 | 47.90 | 0.65 | ||||||
| 120 | 15.0 | 74.00 | 1.00 | ||||||
|
Numerical analysis (FEM) | 45 | 6.0 | 7.5 | 59.37 | 0.91 | ||||
| 60 | 10.0 | 48.62 | 0.74 | ||||||
| 75 | 12.5 | 38.93 | 0.59 | ||||||
| 90 | 15.0 | 30.14 | 0.46 | ||||||
| 40 | 8.0 | 5.0 | 65.57 | 1.00 | |||||
| 60 | 7.5 | 49.19 | 0.75 | ||||||
| 80 | 10.0 | 35.77 | 0.55 | ||||||
| 100 | 12.5 | 27.92 | 0.43 | ||||||
|
Colorado red granite | LCM test | 158 | 6.78 | 25 | 6.4 | 3.9 | 77.04 | 0.77 | Gertsch et al. (2007) |
| 51 | 8.0 | 45.00 | 0.45 | ||||||
| 76 | 11.9 | 39.60 | 0.40 | ||||||
| 76 | 7.6 | 10.0 | 38.52 | 0.39 |
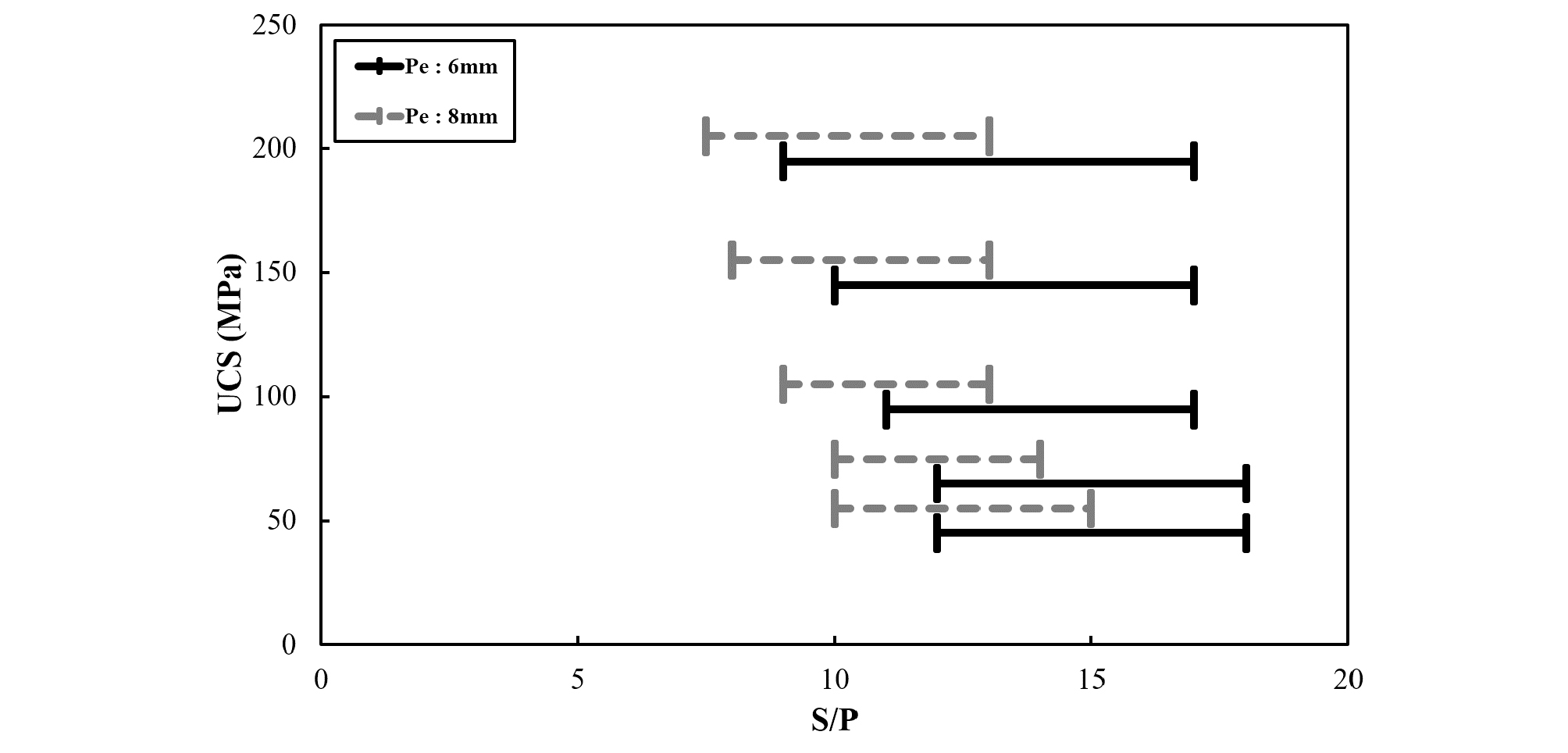
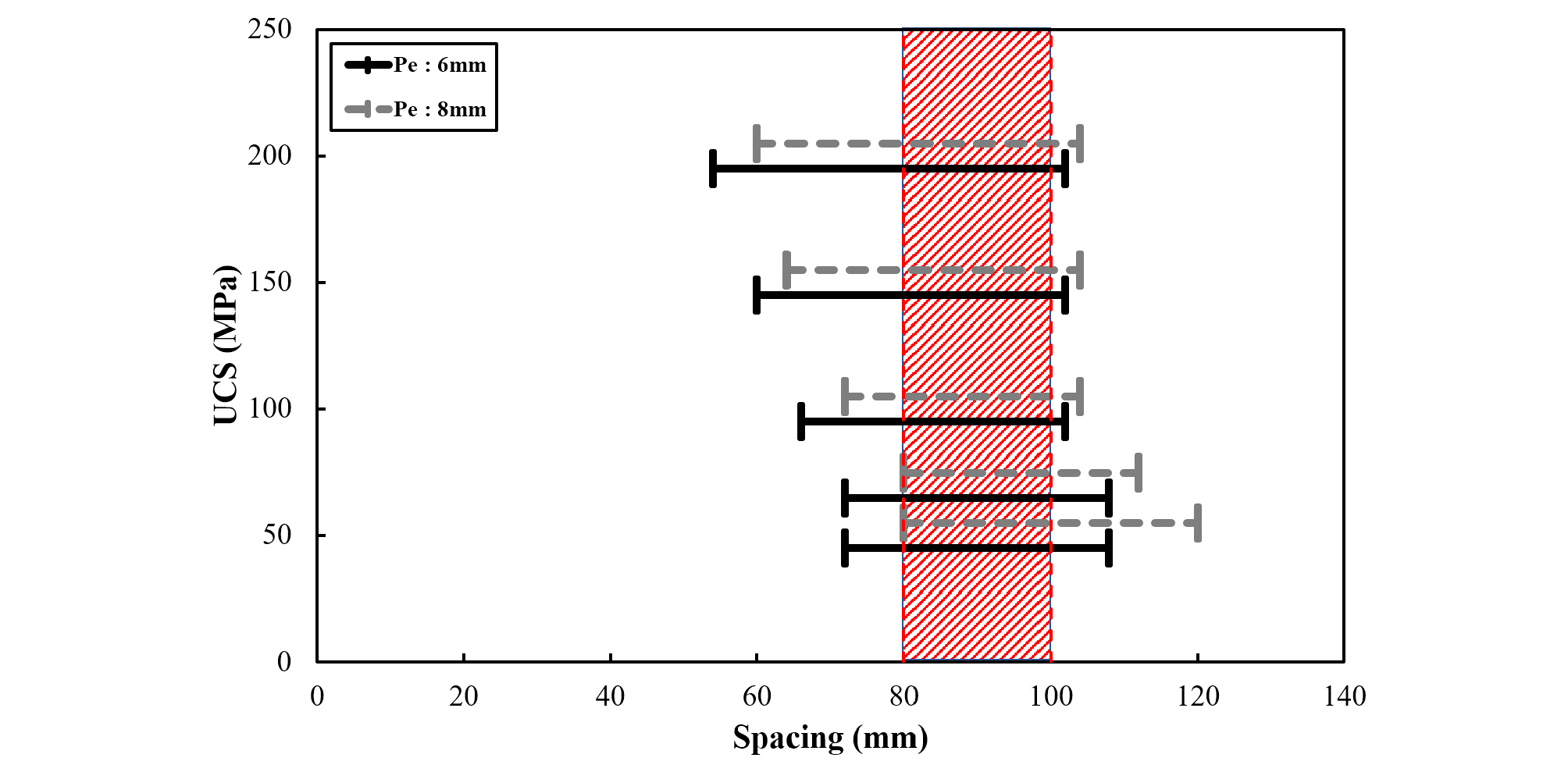
Fig. 9는 5종류의 암반강도에 대한 선형절삭시험을 수행하고 정규화 된 비에너지 - S/P 그래프를 비교한 결과이다. 압입깊이 6 mm, 8 mm의 경우 최적 S/P비의 범위는 암반강도가 커질수록 S/P비의 범위는 감소하는 것을 Table 3을 통해 확인하였고 각각 9.0~18.0, 7.5~15.0 사이의 값을 보이는 것을 확인하였다. 이를 커터간격에 대한 그래프로 작도하여 Fig. 10에 도시하였다. 이를 통해, 디스크커터 간격이 80~100 mm의 범위일 때 5가지 암반종류에 대한 최적 비에너지를 보이는 것을 확인하였다.
Table 3.
Optimum disc cutter spacing
5. 결 론
본 연구에서는 암반강도와 압입깊이의 변화에 따른 선행절삭시험의 개별요소법 수치해석을 진행하고 비에너지를 계산하여 최적 커터간격의 범위를 계산하였다. 또한 디스크커터의 회전력을 반이론적 모델인 CSM 모델과의 비교 ․ 분석을 통해 해석 모델의 적정성을 검토하였다. 해석결과를 정리하면 다음과 같다.
1. 수치해석결과의 신뢰성을 확보하기 위해 커터간격 180 mm의 커터회전력으로 커터회전력을 정규화 하여 반이론적 모델인 CSM 모델과의 비교를 수행하였다. 커터간격이 증가함에 따라 커터회전력의 변화가 CSM 모델과 유사한 경향을 나타내는 것을 확인하였다. 따라서 커터간격의 증가에 따른 커터회전력의 해석결과를 바탕으로 계산된 비에너지의 경향을 신뢰할 수 있을 것으로 판단된다.
2. 상용 개별요소법 프로그램인 PFC3D를 이용하여 암반강도 50 MPa, 70 MPa, 100 MPa, 150 MPa, 200 MPa와 압입깊이 6 mm, 8 mm에 해당하는 선형절삭시험을 모사하고 수치해석을 수행하였다. 해석결과 암반강도가 증가함에 따라 S/P비가 감소하는 경향을 보였으며, 본 연구에서 대상으로 하는 암반강도 범위에서 최적 디스크커터 간격은 80~100 mm의 범위를 갖는다는 것을 확인하였다.
본 연구의 결과를 이용하여 선형절삭시험의 수행이 불가능한 경우 개별요소법 수치해석을 통해 디스크커터의 최적간격을 산정할 수 있다. 그러나 해석을 수행한 모델 또한 선형절삭 시험으로 커터의 회전에 의한 디스크커터의 측력을 고려하지 못하는 단점이 있어 이에 대한 추가적인 연구가 필요할 것으로 생각된다.