1. 서 론
2. 비에너지
3. 머신러닝기법을 이용한 회귀분석모델
3.1 의사결정나무(Decision Tree) 회귀분석
3.2 랜덤 포레스트(Random Forest) 회귀분석
3.3 서포트 벡터 머신(Support Vector Machine, SVM) 회귀분석
4. 자료수집
5. 결과 및 논의
5.1 최소 비에너지에서의 커터 관입깊이와 커터 간격 비
5.2 머신러닝 회귀분석 모델
6. 결 론
1. 서 론
터널시공에 따른 TBM 수요와 그에 따른 생산량은 2013년부터 2018년까지 꾸준한 상승세를 보이고 있다(QYResearch, 2013). TBM은 터널시공에서 주된 역할을 하고 있으며 TBM의 성능을 높이기 위해 현장 지반조건에 더욱 적합하도록 맞춤 설계 및 제작을 하고 있다. 터널굴착에서 실질적으로 지반을 굴착해내는 역할을 하는 부분인 커터헤드는 지반굴착에 직접적으로 영향을 끼치는 여러 가지 부품과 배열의 조합으로 설계되기 때문에 TBM 설계 중에서 가장 중요한 부분이다(Rostami and Ozdemir, 1993; Acaroglu et al., 2008; Cho et al., 2010; Lee et al., 2017). 지반굴착 시 주로 경암과 극경암 지역, 그리고 이러한 암뿐만 아니라 다른 매질과 함께 복합적으로 있는 복합지반에서 장비의 다운타임 등 TBM 굴진에 상대적으로 많은 어려움이 발생되고 있다. 따라서 이러한 지반조건에서 최적의 TBM 굴진을 하기 위한 커터배치에 관한 연구가 수행되어 왔다(Huo et al., 2011; Kim et al., 2012; Bae et al., 2014; Rostami and Chang, 2017; Tao et al., 2017). 효과적인 커터배치를 위해서 커터의 선형 절삭 시험을 통해 커터간격에 따른 절삭 시 소요되는 비에너지를 확인하는 연구가 수행되었고(Chang et al., 2006; Gertsch et al., 2007; Jeong et al., 2011; Ma et al., 2016; Tan et al., 2018), 커터헤드가 원형인 점을 고려하여 커터 개수를 늘여가며 로타리 절삭 시험을 통해 커터간격에 따른 절삭 시 소요되는 최소 비에너지를 찾는 연구가 수행되어왔다(Xia et al., 2012; Pan et al., 2018; Peng et al., 2018). 근래에는 커터헤드 전체를 사용하여 커터헤드의 커터에 의한 절삭시험을 할 수 있는 장비가 개발되어 커터절삭시험이 수행되었다(Geng et al., 2016). 이러한 여러 커터 절삭 시험을 통해 최소 비에너지에서의 커터관입깊이와 커터간격비를 확인 할 수 있으나, 모든 연구가 동일 조건 암반시료에 대해 수행된 것이 아니기 때문에 같은 커터관입깊이와 간격비에서 연구별로 최소 비에너지가 다르며, 관입깊이에 따라 최소비에너지의 커터 간격이 달라지기 때문에 TBM 굴진을 해나가면서 최적의 커터 간격이 달라지게 된다. 커터의 배치는 굴진 중에 바꿀 수 있는 사항이 아니기 때문에 효율적인 커터헤드 설계를 위한 커터의 배치는 어떤 지반에서 TBM을 굴진 시킬 것인지, TBM 굴진거리에서 어떤 조건의 매질이 가장 많이 분포하고 있는지를 고려하고 굴진조건에 대해 가장 효율적인 굴진을 할 수 있는 커터배치를 하여야 한다.
동일한 커터 관입깊이어도 암반조건에 따라서 최소 비에너지가 발생되는 커터 간격이 달라질 수 있기 때문에 커터 관입깊이에 따른 최적 커터 간격을 선형회귀로 예측하기 어렵다. 따라서 여러 절삭시험 연구 결과들을 이용해서 머신러닝 기법 중 의사결정나무기반인 랜덤 포레스트와 서포트 벡터 머신을 이용한 회귀모델을 통해 관입깊이에 따른 최적 커터간격비를 예측해보았다. 의사결정나무기반인 랜덤 포레스트와 서포트 벡터 머신은 대표적인 머신러닝 기법으로써, 두 가지 기법에 의한 결과 비교를 하는 많은 연구가 수행되어 왔다(Larios et al., 2010; Naghibi et al., 2017; Raczko and Zagajewski, 2017; Thanh Noi and Kappas, 2018; Murugan et al., 2019; Aroef et al., 2020).
2. 비에너지
암반 굴착 시 비에너지의 개념적용은 Teale (1965)의 논문에 처음 제시되었으며(Bieniawski et al., 2012), 비에너지는 아래의 식과 같이 산정된다.
| $$E=\frac FA+\frac{2\pi\cdot\omega\cdot T}{A\cdot u}$$ | (1) |
F는 전체 추력이고 A는 굴착되는 면적, ω는 회전속도로 TBM에서 커터헤드의 회전속도를 나타낸다. T는 토크이며 u는 시간당 굴진거리를 의미한다. 지금까지 Teale의 식이 가장 정확성이 높아 Teale의 비에너지 식이 주로 사용되고 있다(Bieniawski et al., 2012). Teale의 비에너지 식은 추력에 관한 항(F/A)과 드릴 또는 커터로 직접 절삭하는 항(2μ ‧ ω ‧ T/A ‧ u), 두 가지로 이루어져 있다. 이 때 ω/u는 커터헤드의 1회전 당 관입깊이(P)로 나타낼 수 있기 때문에 최종적으로 비에너지는 아래의 식으로 나타낼 수 있다.
| $$E=\frac FA+\frac{2\pi\cdot T}{A\cdot P}$$ | (2) |
실내시험에서는 커터가 주가 되기 때문에, 실내시험에서는 많은 연구자들이 직접 절삭에 관련된 항만 고려하여 아래의 식과 같이 커터에 절삭 되는 매질의 단위부피당 소요에너지로 비에너지를 산정하고 있다(Acaroglu et al., 2008; Cho et al., 2010; Jeong et al., 2011; Cho et al., 2013; Tan et al., 2018).
| $$SE(kWh/m^3,\;MJ/m^3)=\frac{F_R\cdot R\cdot t}V=\frac{F_R}A$$ | (3) |
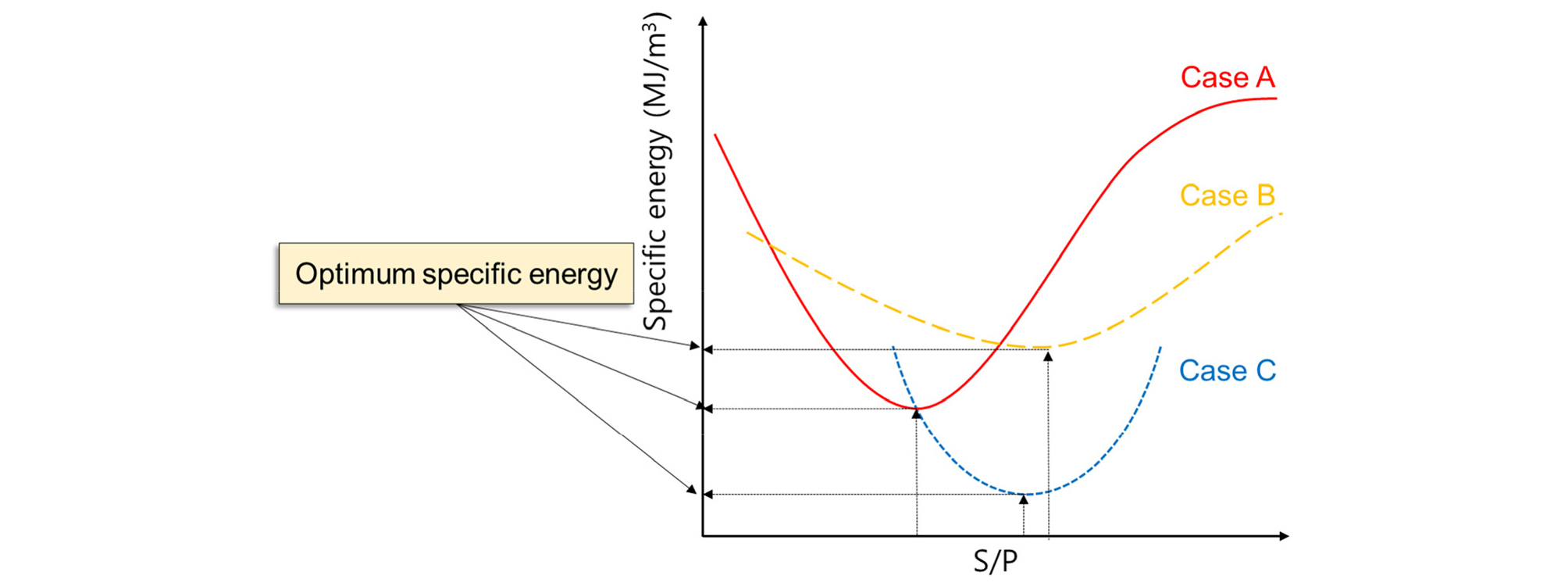
FR은 커터가 진행하는 방향의 힘이며 R은 절삭 속도, t는 절삭 시간, V는 절삭되는 매질의 부피, A는 절삭되는 수직 단면적을 의미한다. 대부분, 암반 절삭에서 비에너지가 최소가 되는 점에서의 커터 간격과 커터 관입깊이의 비를 통해 커터간격을 정하고 있다. 본 논문에서는 각 경우에서의 최소 비에너지를 최적 비에너지(Optimum specific energy)라고 나타내었다(Fig. 1).
3. 머신러닝기법을 이용한 회귀분석모델
3.1 의사결정나무(Decision Tree) 회귀분석
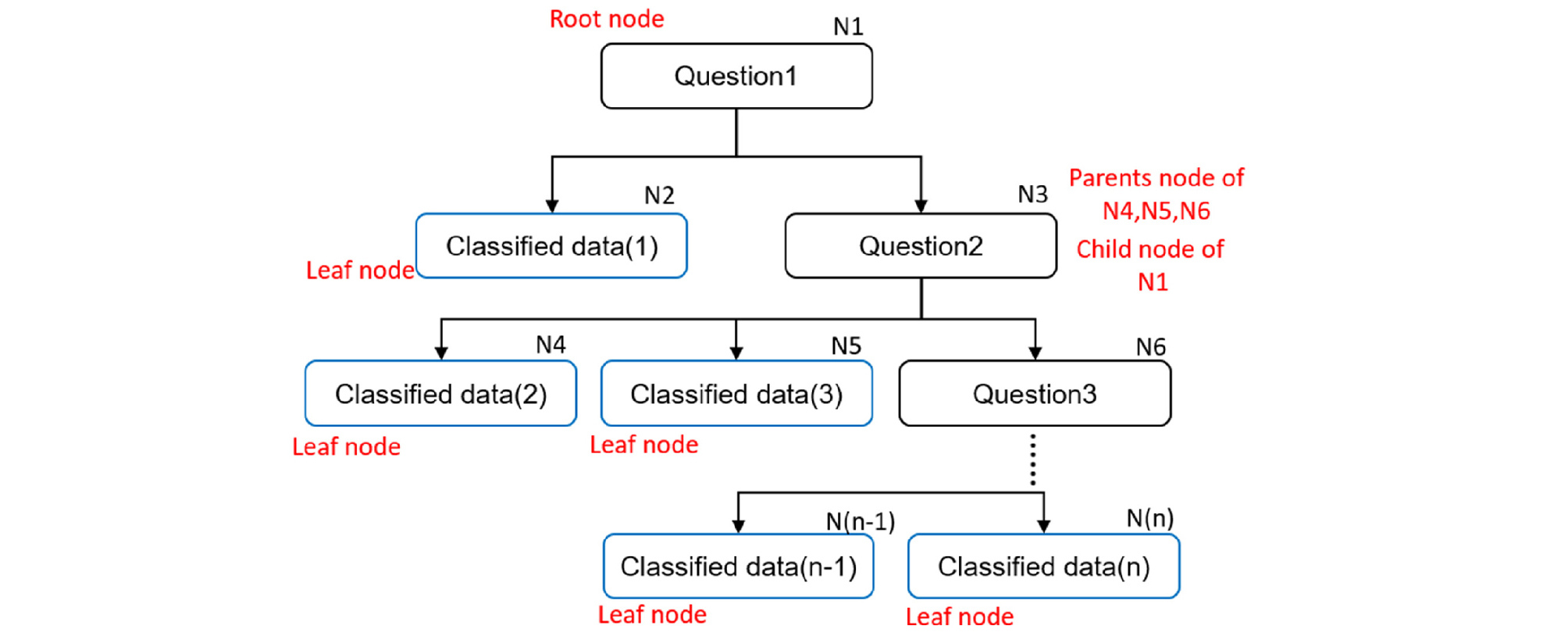
의사결정나무 학습법(Decision tree learning)은 데이터를 각 질문에 따라 차례차례 분류하는 기법이다(Fig. 2). 의사결정나무 학습에서 각 노드에서 분기되어 최종 노드까지 데이터를 분류하게 되며 분기의 깊이(depth)설정값에 따라 2가지 또는 n가지의 단계로 데이터를 분류하게 된다. 이 때, 각 노드에서 분기를 하는 방법은 부모노드에서 정보획득량(Information gain)이 가장 큰 독립 변수와 기준값을 찾아서 자식 노드로 분류하게 된다. 정보획득량은 아래 식과 같이 나타낼 수 있다.
| $$IG(D_p,\;f)=I(D_p)-\sum_{j=1}^n\frac{N_j}{N_p}I(D_j)$$ | (4) |
위의 식에서 Dp는 부모노드(Parents node)에 존재하는 데이터 세트, Dj는 j번째 자식노드(Child node)의 데이터 세트, f는 분기에 따른 특성값, I(Dp)는 Dp데이터의 불순도(Impurity), Np는 Dp의 데이터 개수, Nj는 Dj의 데이터 개수, I(Dj)는 Dj의 불순도를 의미한다. 불순도는 분류된 데이터에 잘못 분류된 데이터가 얼마나 섞여 있는지를 나타낸다. 본 연구에서 일반 분류와 달리 회귀분석을 수행하기 위해 평균 제곱 오차 Mean square error (MSE)로 불순도를 계산하였다.
| $$MSE=\frac1N\sum_{j=1}^n(y_j-\widehat{y_j})^2$$ | (5) |
위의 식 (5)에서 yj는 측정값, 는 예측값을 나타낸다.
3.2 랜덤 포레스트(Random Forest) 회귀분석
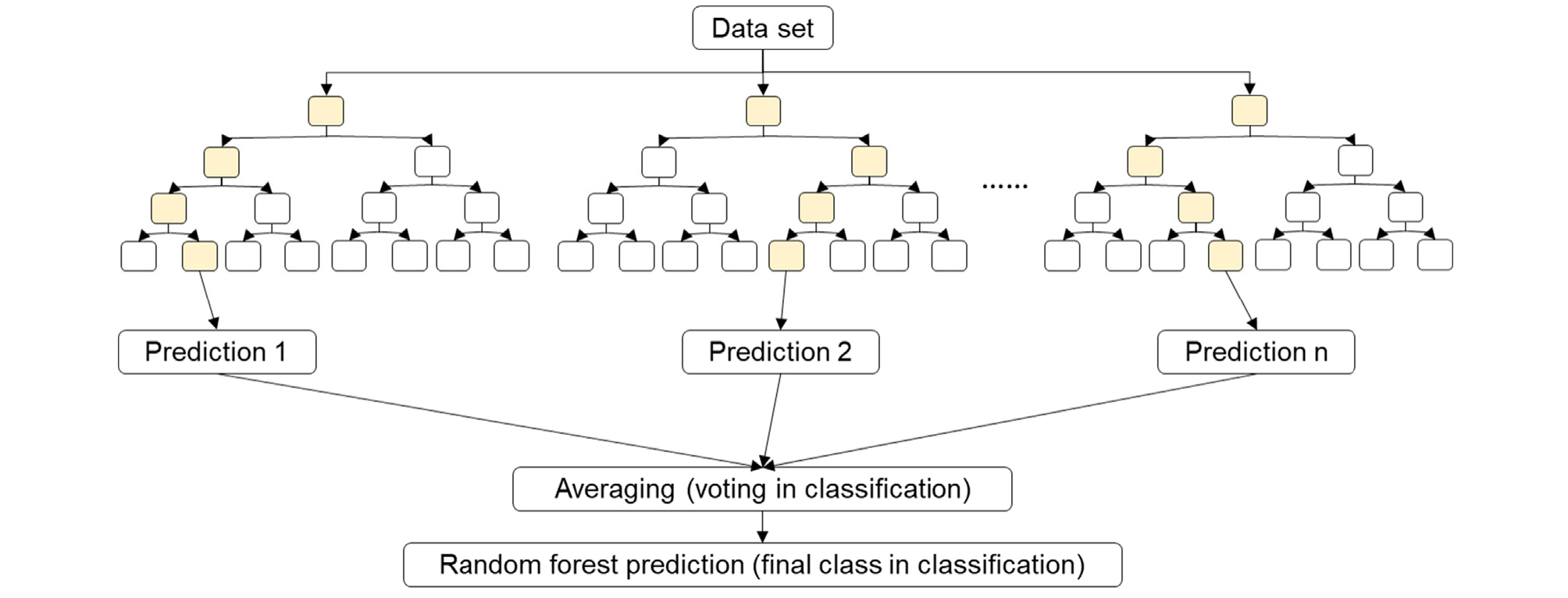
랜덤 포레스트(Random forest) 알고리즘은 주어진 데이터 세트에서 무작위로 n개의 데이터를 샘플링해서 여러 개의 의사결정나무를 만든 후 각각의 의사결정나무의 예측결과를 토대로 다수결에 의해 최종 예측을 결정하는 방식이다(Fig. 3). 따라서 랜덤 포레스트는 분류뿐만 아니라 회귀분석에 적합한 알고리즘을 가지고 있다. 랜덤 포레스트에서 생성되는 의사결정나무수가 많을수록 다수결에 의한 예측 결과의 품질이 높아지게 된다. 하지만, 생성되는 의사결정나무수가 많을수록 분석에 필요한 공간이 더 늘어나게 되며 분석을 수행하는 장비의 더 높은 성능이 요구된다. 본 연구에서는 1,000개의 의사 결정나무를 생성하여 분석하였다. 의사결정나무와 마찬가지로 회귀분석을 위해 정보획득량의 불순도를 MSE를 사용하여 계산하였다.
3.3 서포트 벡터 머신(Support Vector Machine, SVM) 회귀분석
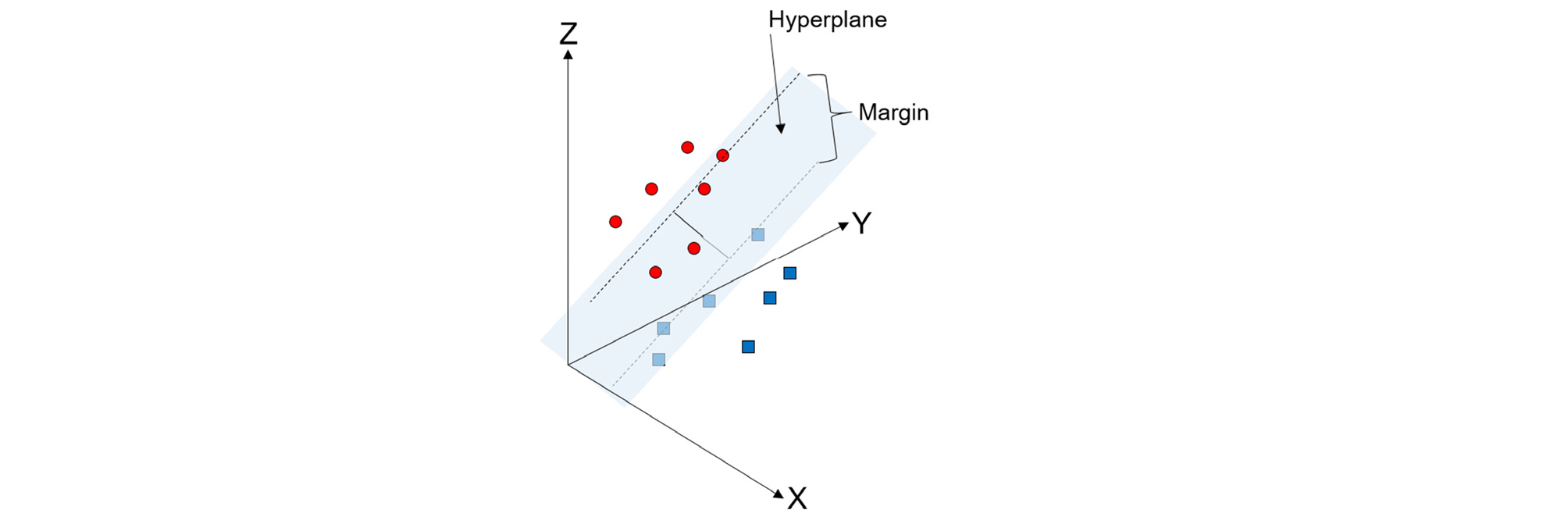
서포트 벡터 머신(SVM)은 2차원에서 구분이 힘든 데이터를 유한 차원 공간에서 초평면(Hyperplane)을 통해 데이터를 분류할 수 있는 알고리즘이다. 주어진 데이터에서 분류하고자 하는 데이터 사이의 간격이 최대가 되는 Margin을 갖는 초평면을 통해 데이터를 정확하게 구분하여 예측할 수 있다(Fig. 4). 이 때, Margin의 경계선에 걸쳐있는 값들을 서포트 벡터(Support vector)라고 하며 서포트 벡터에 의해 Margin값이 달라지게 된다. SVM 기법은 데이터를 선형으로 분류할 수 없는 경우 에도 커널 함수를 사용해서 비선형으로 데이터를 분류할 수 있다(La et al., 2019). 본 연구에서는 두 개의 벡터 xi, xj 벡터를 매개로한 비선형 커널함수인 아래의 가우시안 방사 기저함수인 Radial basis function (RBF) 커널을 사용해서 SVM 회귀분석을 수행하였다.
| $$k(x_i,\;x_j)=exp(-\gamma\parallel x_i-x_j\parallel^2)$$ | (6) |
위의 식에서 γ는 하이퍼파라미터로 데이터 경계면을 결정하는데 영향을 끼치는 인자다. γ값에 따라 가우시안 함수에서 그래프의 곡률이 달라진다. γ값이 클수록 하나의 데이터가 영향력을 행사하는 범위가 넓은 폭이 큰 그래프를 띄게 되며 γ값이 작을수록 폭이 좁은 그래프를 띄게 된다. 본 회귀모델에서 사용되는 데이터의 수가 18개임을 고려하여 데이터가 다른 클래스에 속하는 것을 허용하는 정도인 Cost (C)값을 100으로 설정하고 특성개수의 역수인 1로 γ를 설정하였다.
4. 자료수집
커터절삭시험의 데이터를 토대로 관입깊이에 따른 최적 커터간격비를 제시하기 위해 Chang et al. (2006)의 12개의 선형절삭시험 결과, Cho et al. (2010)의 42개의 선형절삭시험 결과, Jeong et al. (2011)의 17개의 선형절삭시험 결과, Tan et al. (2018)의 16개의 선형절삭시험 결과, 그리고 Lee and Choi (2013)의 6개의 수치해석 결과 총 93개의 결과를 이용하였다. 각 연구에서의 최소비에너지를 구하고 최소비에너지에서의 커터간격과 커터관입깊이의 비를 분석하였다. 각 연구에서 사용한 암의 조건은 Table 1과 같다.
Table 1.
Information for linear cutting machine (LCM) tests
| Reference | Rock type | Rock properties |
Diameter of disc cutter (in) | |
|
Unconfined compressive strength, UCS (MPa) |
Brazilian tensile strength, BTS (MPa) | |||
| Chang et al. (2006) | Hwangdeung granite | 183 | 9.8 | 17 |
| Cho et al. (2010) | Macheon granite | 108 | 10.4 | 17 |
| Cho et al. (2010) | Hudong granite | 91 | 12.3 | 17 |
| Cho et al. (2010) | Sungnam gneiss | 92 | 15.2 | 17 |
| Cho et al. (2010) | Paldang gneiss | 124 | 13.8 | 17 |
| Cho et al. (2010) | Yeongwol limestone | 64 | 8.9 | 17 |
| Cho et al. (2010) | Busan granite | 36 | 4.7 | 17 |
| Cho et al. (2010) | Busan tuff | 115 | 25.2 | 17 |
| Jeong et al. (2011) | Unknown (vertical joint) | 241 | 13.4 | Unknown |
| Jeong et al. (2011) | Unknown (parallel joint) | 186 | 10.7 | Unknown |
| Tan et al. (2018) | Marble | 24.92 | 4.72 | 17 |
| Lee and Choi (2013) | Busan tuff (simulation) | 111 ± 10 | 29.9 ± 5 | 400 (mm) |
5. 결과 및 논의
선형절삭 시험을 통해 커터 관입깊이(Penetration depth, P)를 고정시키고 커터 간격(Spacing, S)을 바꾸면서 찾은 최소 비에너지에서의 적정 커터 간격과 커터 관입깊이 의 비, S/P를 분석하였다(Table 2).
Table 2.
Optimum ratio of cutter spacing to penetration depth
| P (mm) | S (mm) | S/P | Optimum specific energy (MJ/m3) | Reference |
| 2 | 20 | 10 | 6.8 | Tan et al. (2018) |
| 3 | 20 | 6.7 | 19.4 | Tan et al. (2018) |
| 4 | 60 | 15 | 14.6 | Tan et al. (2018) |
| 6 | 40 | 6.7 | 25 | Tan et al. (2018) |
| 2 | 30 | 15 | 4.9 | Chang et al. (2006) |
| 4 | 60 | 10 | 24.5 | Chang et al. (2006) |
| 6 | 60 | 10 | 15.7 | Chang et al. (2006) |
| 4 | 48 | 12 | 14.31 | Lee and Choi (2013) |
| 5.6 | 40 | 10 | 39.4 | Cho et al. (2010) |
| 6 | 48 | 8 | 41.6 | Cho et al. (2010) |
| 6.4 | 48 | 7.5 | 50.0 | Cho et al. (2010) |
| 6.9 | 60 | 8.8 | 29.2 | Cho et al. (2010) |
| 7.3 | 72 | 9.9 | 32.2 | Cho et al. (2010) |
| 7.7 | 72 | 9.3 | 15.5 | Cho et al. (2010) |
| 8.1 | 60 | 7.4 | 26.7 | Cho et al. (2010) |
| 8.6 | 60 | 7 | 42.2 | Jeong et al. (2011) |
| 9 | 60 | 6.7 | 38.7 | Jeong et al. (2011) |
| 9.4 | 80 | 8.5 | 33.8 | Jeong et al. (2011) |
5.1 최소 비에너지에서의 커터 관입깊이와 커터 간격 비
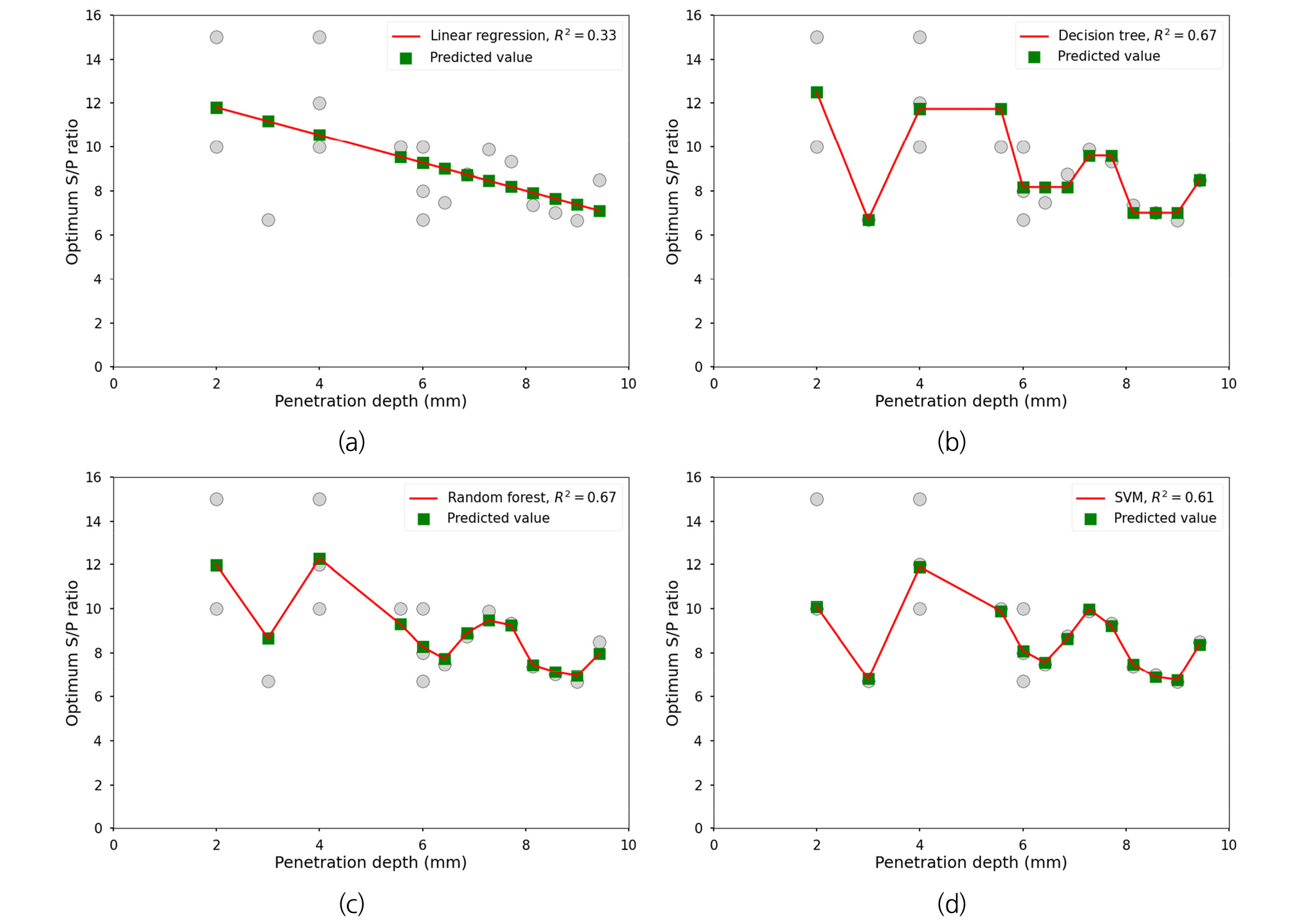
각각의 암반상태가 동일하지 않기 때문에 같은 관입깊이에서 최소 비에너지가 발생되는 커터 간격이 다르게 나타났다. 관입깊이가 클수록 최소비에너지가 발생되는 커터간격은 전체적으로 증가하는 경향성이 약하게 나타났다. 하지만, 관입깊이가 클수록 커터 관입깊이와 커터간격의 비는 전체적으로 감소하는 경향을 보였으며 이는 커터 관입깊이의 증가량보다 커터 간격의 증가량이 상대적으로 작기 때문이다(Fig. 5).
5.2 머신러닝 회귀분석 모델
커터 관입깊이에 따른 최소비에너지가 발생되는 최적 커터간격의 데이터 18개에 대하여 커터 관입깊이를 입력변수로 한 회귀분석결과, 선형회귀의 결정계수 R2 = 0.33보다 의사결정나무, 랜덤포레스트, SVM의 회귀모델 결정계수가 각각 0.67, 0.67, 0.61로 더 높게 나타났다(Fig. 5). 의사결정나무와 랜덤 포레스트 휘귀분석 결과 결정계수가 0.67로 동일하게 나왔으나, 최적 S/P의 범위가 상대적으로 좁은 커터 관입깊이가 6 mm 보다 큰 경우에서 의사결정나무, 랜덤 포레스트, SVM 회귀모델의 MSE는 각각 0.15, 0.08, 0.01로서 랜덤 포레스트 회귀모델과 SVM 회귀모델이 의사결정나무 회귀모델보다 실제 측정값과 잘 맞는 것을 확인 할 수 있었다. 랜덤 포레스트는 의사결정나무를 기반으로 한 여러개의 의사결정나무의 예측결과에 대해 다수결에 따라 최종 예측값을 결정하기 때문에 의사결정나무 회귀모델보다 더욱 정확한 예측값을 도출해 낼 수 있다(Esmaily et al., 2018). 따라서 데이터 개수가 증가함에 따라 랜덤 포레스트 회귀모델의 결정계수값이 의사결정나무 회귀모델의 결정계수보다 조금 더 증가할 것으로 예상된다. 랜덤 포레스트 회귀모델과 SVM 회귀모델에 대하여 전체 18개의 관입깊이와 최적 S/P 데이터 중, Jeong et al. (2011)의 3개 데이터(17%)를 제외한 15개의 데이터(83%)를 훈련 데이터로 사용하고 Jeong et al. (2011)의 새로운 커터 관입깊이에 대한 최적 S/P를 예측한 결과, SVM 회귀모델이 72%의 정확도로 랜덤 포레스트 회귀모델보다 높은 정확도의 예측결과를 보였다(Fig. 6). 현 연구결과에서 일반적인 결론을 이끌기에는 데이터 수와 케이스가 부족하다. 하지만 현재 머신러닝 연구분야의 일반적으로 알려진 결과들을 바탕으로 추정해보면, 랜덤 포레스트 기법은 집단 학습을 통해 데이터를 분류하고 예측하기 때문에 데이터 수에 타 머신러닝 기법보다 상대적으로 민감하다(Ali et al., 2012). 따라서 유한차원에서 비선형으로 데이터를 분류하는 SVM기법이 18개의 적은 데이터 개수에서 랜덤 포레스트 회귀모델보다 새로운 조건에 대한 값을 예측하는데 효율적이다.
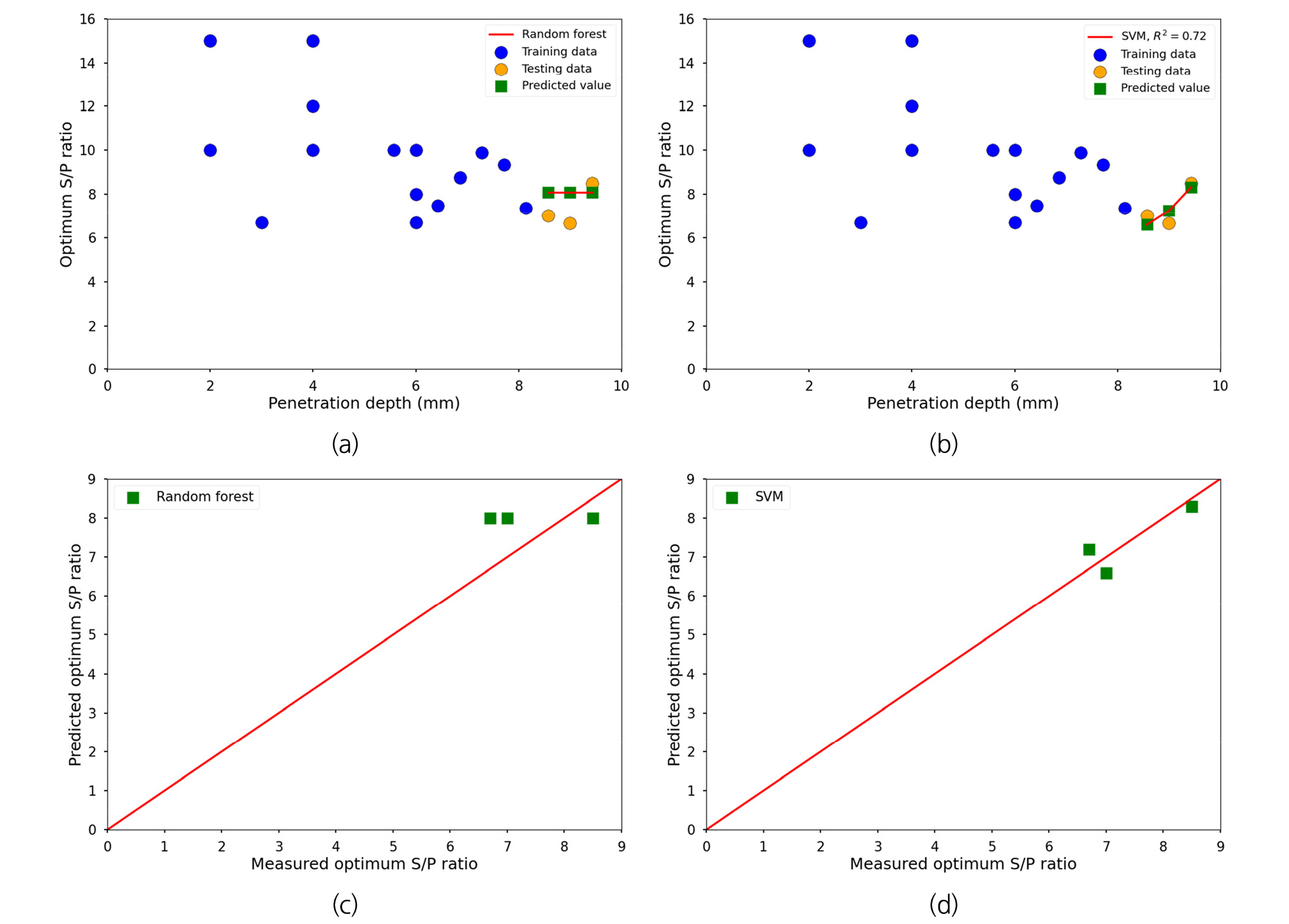
Fig. 6.
Random forest and SVM regressions for predicted optimum S/P with penetration depth by training data: (a) Random forest regression, (b) SVM regression, (c) Relationship between measured optimum S/P ratio and predicted optimum S/P ratio by random forest regression model, and (d) Relationship between measured optimum S/P ratio and predicted optimum S/P ratio by SVM regression model
본 연구에서 훈련된 모델들의 경우, 관입깊이와 최적 S/P간의 물리적 관계를 고려하지 않고 있음을 유의해야 한다. 이는 훈련 데이터 수가 많아질 경우, 보완될 것으로 예상된다.
6. 결 론
커터 관입깊이에 따라 굴착 시 최소 비에너지가 발생되는 최적 커터 간격은 암반의 일축압축강도와 절리 및 조건에 따라 달라 질 수 있다. 따라서 동일한 커터 관입깊이에서 최적 커터 간격이 현장조건에 따라 달라질 수 있기 때문에 선형 회귀분석으로 커터 관입깊이에 따른 최적 커터간격 비를 예측하기 어렵다. 머신러닝 기법 중 데이터 분류뿐만 아니라 회귀모델로도 사용가능한 의사결정나무기반의 회귀분석과 SVM회귀분석을 사용하여 새로운 커터관입깊이에 대한 최적 커터간격비를 예측할 수 있었다. 커터관입깊이에 따른 최적 커터간격비의 데이터 축적을 통해 위의 머신러닝 기법들을 사용할 경우, 더욱 정확한 커터관입깊이에 따른 최적 커터간격비를 예측할 수 있을 것으로 판단된다. 또한, 동일 추력에서 암반의 조건에 따라 관입깊이가 달라 질 수 있지만 커터간격은 커터헤드를 교체하지 않는 이상 변경하기가 어려운 값이기 때문에 암반조건에서의 굴진성능을 고려한 전반적인 커터관입깊이에 따른 커터헤드 설계 시, 커터간격을 설정하는데 SVM 회귀모델이 효율적으로 사용될 수 있을 것으로 판단된다. 뿐만 아니라, SVM 회귀모델은 특정한 커터간격으로 이미 제작된 커터헤드가 어떤 지반에서 효율적으로 사용될 수 있을지 역으로 사용될 수 있을 것으로 판단된다.