1. 서 론
2. 신형식 사변형 격자지보재의 개요
3. 체적비 기반의 격자지보재-숏크리트 합성부재의 등가탄성계수
3.1 체적비 기반의 등가탄성계수 검토를 위한 4점 재하 휨 하중 시험 수치해석 모델
3.2 휨강도 보정을 통한 등가탄성계수의 조정
4. 결 론
1. 서 론
강지보재는 불량한 지반에서 터널의 굴착 직후 터널의 구조 안정성을 확보하기 위해 설치하고 있는 구조재료로써 단면의 기하학적 특성에 따라 다양한 형태를 갖고 있다. H형 강지보재는 일반적으로 단면 높이가 동일한 기존의 격자지보재보다 휨성능이 우수한 것으로 알려져 있으나, H형 강지보재 거치 후 숏크리트 타설 시 플랜지 및 복부판으로 구성된 구조 특성으로 인하여 배면 공극의 발생이 문제시 되고 있다(Kim et al., 2009, Kim et al., 2013).
Lattice Girder는 이러한 문제점을 개선하기 위하여 개발된 격자지보재로 삼각형 형태의 단면을 구성하는데, 격자지보재의 모든 부재는 원형 단면을 갖는 바(Bar) 형태의 부재가 적용된다. 그동안 여러 연구에서 삼각 격자지보재의 구조 성능에 대한 분석이 이루어졌으며, 주로 지보재의 휨성능 평가에 주안점을 두어 연구가 이루어졌다. Moon et al. (1997)은 격자지보재와 숏크리트 간 합성 후 거동에 대한 실험을 수행하여 격자지보재와 숏크리트의 부착성 등을 분석하였다. Yoo et al. (1997), Kim et al. (2007), Kim et al. (2008), Kim et al. (2009), Kim and Bae (2008)는 하중 재하실험을 통해 삼각 격자지보재의 최대지지하중을 평가하고 시험법에 따른 삼각격자지보재의 성능차이를 분석하였다.
선행 연구결과에서 언급되었듯이 삼각 격자지보재는 입체적인 구조 형식을 갖기 때문에 H형 강지보재에서 나타나는 숏크리트 타설 시 나타나는 문제점은 해소할 수 있으나(KICT, 1996; Moon et al., 1997) 기본적으로 동일한 단면 높이를 갖는 지보의 비교에 있어서 H형 강지보재 보다 낮은 구조 성능을 나타낸다. 또한, 원형 단면을 갖는 부재의 결합을 위해 점접촉 방식으로 모든 부재가 접합되는데, 수작업에 의한 용접으로 안정적인 품질 확보가 어렵다는 점이 문제점으로 지적되어 왔다(Kim et al., 2007; Kim et al.,, 2009).
NATM 공법에서 숏크리트가 가장 큰 하중을 부담하는 지보재지만, 초기 타설 시 탄성계수가 매우 작아 변형에 취약하다는 단점이 있다. 이에 따라 불량한 조건의 지반에서는 숏크리트 타설 전에 강지보재를 설치하여 지반의 초기 변형에 저항하고, 숏크리트가 경화 된 이후 일체거동을 하여 지반 거동에 저항하는 목적으로 사용하고 있다. 초기 변형에 저항하기 위해서는 지보 자체의 구조 강도도 우수해야 하고, 숏크리트 타설의 용의성도 확보해야한다(Jung et al., 2016; Kim et al., 2018). 이러한 문제점들을 해결하기 위하여 사변형 격자지보재가 개발되었지만, 이를 수치해석에 적용하기 위한 연구는 미비한 실정이다. 따라서 본 연구에서는 사변형 격자지보재를 터널의 안정해석에 적용할 수 있는 방안으로 숏크리트와 강지보재 합성부재의 등가 물성치 결정법을 제시하였다.
2. 신형식 사변형 격자지보재의 개요
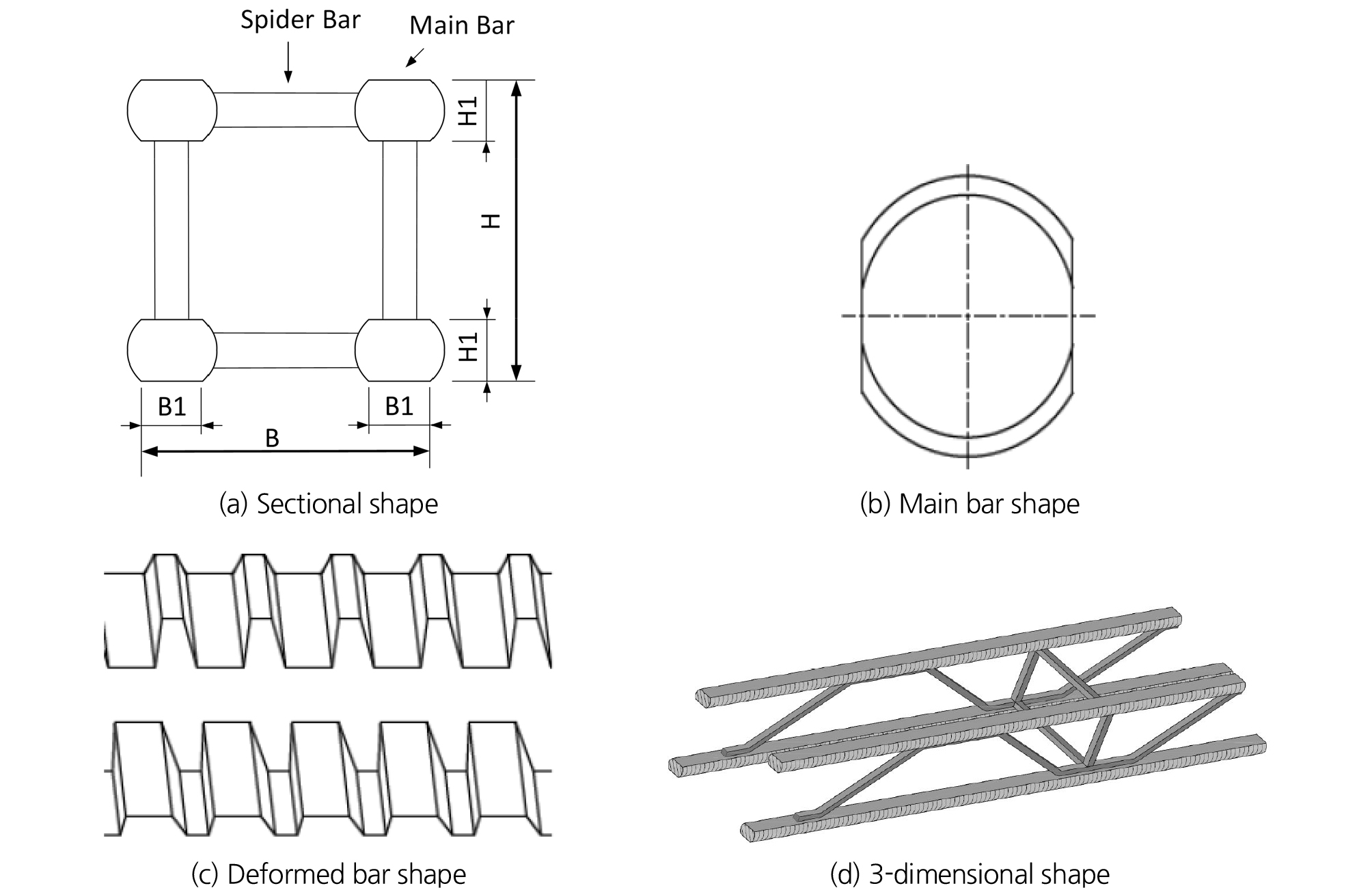
기존 격자지보의 문제점들을 해소하기 위해 Kim et al. (2013)는 사변형 격자지보재에 대한 연구를 수행하였다. 사변형 격자지보재는 부재가 삼각 격자지보재와 같이 선의 형태를 띄는 부재를 사용하여, 면의 형태를 띄는 H형강 지보재에 비해 배면 공동 발생이 저감 될 것으로 예상된다. 또한, 원형 단면 구조 부재를 사용하는 삼각 격자지보재에서 문제점으로 지적되었던 부재간 점접촉 방식에 따른 부재간 연결부 파손 문제를 해결하기 위해 모든 부재를 사각단면을 갖는 바(Bar)를 사용하여 부재 간 면접촉/선용접 방식이 가능하도록 하여 충분한 용접길이를 확보하였다(Kim et al., 2013). 본 연구에서 사용한 신형식 사변형 격자지보재는 기존의 사변형 격자지보재에서 숏크리트와의 부착성을 향상시키기 위해 모든 부재를 나사마디 이형강봉(Fig. 1(c))을 사용하였으며, 수직 및 수평 보강재로 보강하여 격자지보재의 안정성 향상을 도모하였다.
사변형 격자지보재는 지반의 상태에 따라 보다 합리적이고 경제적인 사용을 도모하기 위해 기존 삼각 격자지보재에 대응되는 단면 제원을 기반으로 설계되었다. 각 지보재에 대응되는 단면은 숏크리트 라이닝 두께의 제약 등에 따라 기존 지보재와 같이 총 세 개의 높이를 갖는 단면으로 설계되었다. 사변형 격자지보재 제작에는 터널표준시방서(MOLIT, 2011)의 강지보재 재질기준에 따라 항복강도가 500 MPa 이상인 용접구조용 강재를 사용하였고 사변형 격자지보재의 형상은 아래 Fig. 1과 같으며 상세한 제원은 Table 1에 제시하였다.
Table 1. Dimensions of tetragonal lattice girder
| Tetragonal lattice girder | |||
| Small section | Medium section | Large section | |
| 100 × 100 × 19 | 125 × 110 × 19 | 150 × 130 × 19 | |
| H1 | 17.5 | 17.5 | 17.5 |
| H | 100 | 125 | 150 |
| B1 | 21.5 | 21.5 | 21.5 |
| B | 100 | 110 | 130 |
Diameter of spider bar: 13 mm
3. 체적비 기반의 격자지보재-숏크리트 합성부재의 등가탄성계수
터널 수치해석에서 강지보재를 고려하는 방법은 두 가지로 구분할 수 있다(MOLIT, 2011). 첫 번째 방법은 강지보재와 숏크리트를 각각 보 요소로 모델링하는 방법이다. 실내시험을 통해 각각의 요소 사이의 수직 및 전단강성 값을 획득할 수 있다면 강지보재와 숏크리트를 모델링할 수 있는 가장 현실적인 방법이다. 두 번째 방법은 강지보재와 숏크리트를 합성부재로 가정한 후 모델링하는 방법이다. 첫 번째 방법에 비해 정밀성은 다소 낮지만 입력값 및 결과값 산정과 적용이 다소 편리한 방법이다. 일반적으로 두 번째 방법은 숏크리트와 강지보재가 강결되었다는 가정 하에 단위 폭 또는 강지보재의 설치간격에 해당하는 임의 폭 당 포함되는 단면적비에 따라 등가 탄성계수를 식 (1)과 같이 구하고, 합성부재에 발생한 축력과 모멘트는 숏크리트와 강지보재가 분담을 하며, 합성부재의 축력과 모멘트에 식 (2) 및 (3)과 같은 분담율을 곱하여 각 부재에 작용하는 축력과 모멘트로 분배할 수 있다. 각 부재에 작용하는 부재력을 이용하여 식 (4) 및 식 (5)와 같이 응력을 계산하여 안정성을 평가 할 수 있다(Ha et al., 2008).
| $$E_{eq}=\frac{E_{sh}A_{sh}+E_{st}A_{st}}{A_{sh}+A_{st}}$$ | (1) |
| $$\beta_{sh}=\frac{E_{sh}A_{sh}}{E_{sh}A_{sh}+E_{st}A_{st}}$$ | (2) |
| $$\alpha_{sh}=\frac{E_{sh}I_{sh}}{E_{sh}I_{sh}+E_{st}I_{st}}$$ | (3) |
여기서, 는 등가 탄성계수, , , 는 숏크리트의 탄성계수, 단면적, 단면이차모멘트, , , 는 강지보재의 탄성계수, 단면적, 단면이차모멘트, 는 숏크리트의 축력 분담율, 는 숏크리트의 휨모멘트 분담율이다.
| $$\sigma_{sh}=\frac{N_{sh}}{A_{sh}}+\frac{M_{sh}}{I_{sh}}y_{sh}$$ | (4) |
| $$\sigma_{st}=\frac{N_{st}}{A_{st}}+\frac{M_{st}}{I_{st}}y_{st}$$ | (5) |
여기서, 는 숏크리트의 휨 압축응력, 은 합성부재에 발생한 축력, 은 합성부재에 발생한 모멘트, 는 숏크리트에 분담된 축력(), 는 숏크리트에 분담된 모멘트(), 는 숏크리트의 도심 거리, 는 강지보재의 휨 압축응력, 는 강지보재에 분담된 축력(), 는 강지보재에 분담된 모멘트(), 는 강지보재의 도심 거리이다.
일반적으로 강지보재로 사용하고 있는 삼각 격자지보재 또는 H형 강지보재는 숏크리트와 합성부재로 가정하여 등가탄성계수 계산 시 종방향 단면의 변화가 크지 않기 때문에 단면적으로 고려하고 있는 실정이며, 이는 강지보재의 구조적 특성을 충분히 고려하지 않는 방법이다. 강지보재의 구조적 성능을 과소평가하는 등가탄성계수 산정방법은 과다설계를 유발할 수 있기 때문에, 본 연구에서는 등가탄성계수를 적용한 등가모델에서 강지보재와 숏크리트를 각각 모델링한 상세모델의 휨강도를 나타낼 수 있도록 등가탄성계수를 보정할 수 있는 방법을 제시하였다. 또한 사변형 격자지보재의 경우 수직보강재 및 수평보강재가 있으며, 단면적 기반의 등가탄성계수는 대표단면 위치에 따라 등가탄성계수를 과대 또는 과소평가할 수 있기 때문에 본 연구에서는 체적비 기반의 등가탄성계수 산정법을 제시하였다.
3.1 체적비 기반의 등가탄성계수 검토를 위한 4점 재하 휨 하중 시험 수치해석 모델
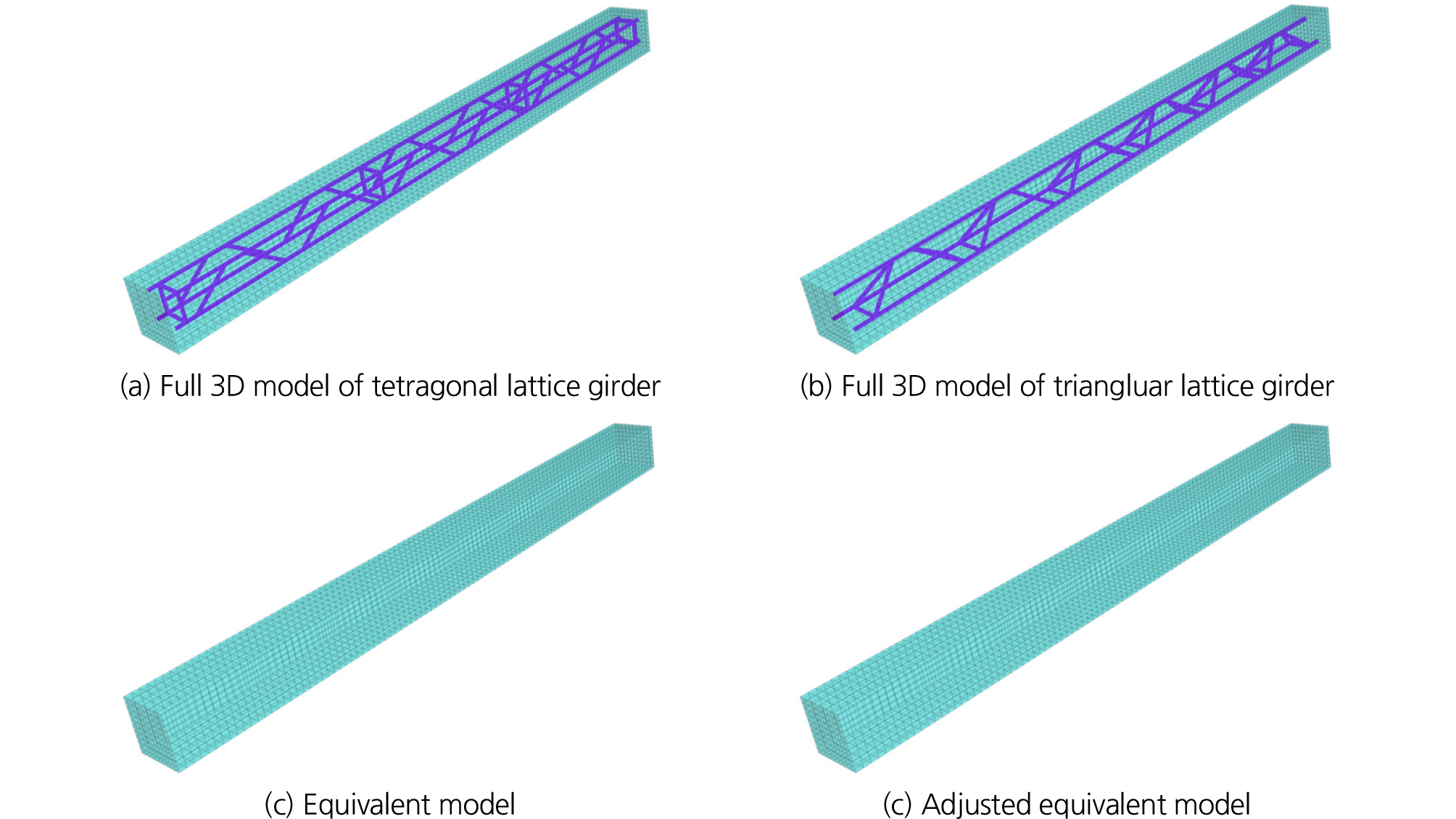
숏크리트와 사변형 격자지보재를 각각 모델링한 경우(Fig. 2(a))와 체적비 기반의 등가탄성계수를 적용한 등가모델(Fig. 2(c))에 대한 3점 휨 재하 시험에 대한 수치해석을 수행하여 휨 강도를 획득하였다. 또한 삼각 격자지보재의 경우에 대해서도 숏크리트와 격자지보재를 각각 모델링한 상세모델(Fig. 2(b))과 체적비 기반의 등가탄성계수를 적용한 등가모델(Fig. 2(d))을 구축하였다. 휨 강도시험에서 사용한 사변형 격자지보재, 삼각 격자지보재, 숏크리트 제원 및 체적비 기반의 등가탄성계수는 Table 2에 정리하였다. 숏크리트는 피복을 고려하여 격자지보재 보다 30 mm씩 증가시켰으며, 수치해석을 위한 격자지보재의 총 길이는 2,100 mm, 숏크리트의 길이는 2,160 mm이다.
Table 2. Derivation of corrected equivalent elastic modulus of shotcrete-lattice girder composit based on volumetric ratio
3.2 휨강도 보정을 통한 등가탄성계수의 조정
숏크리트와 강지보재 합성부재의 부피비에 기반한 일반적인 등가탄성계수의 산정식은 식 (6)과 같다.
| $$E_{eq}=\frac{E_{sh}V_{sh}+E_{st}V_{st}}{V_{sh}+V_{st}}$$ | (6) |
여기서, 는 등가 탄성계수, , 는 숏크리트의 탄성계수 및 체적, , 는 강지보재의 탄성계수 및 체적이다.
본 연구에서는 상세모델과 등가모델의 수치해석 결과를 바탕으로 각 시편의 휨 강도를 역산하였으며, 휨 강도는 시편에 발생하는 변형률이 0.003일 때를 기준으로 계산하였다. 역산식은 KS F 2408 (KS, 2016)에서 제시하고 있는 식 (7)을 적용하였다. 상세모델과 등가모델의 휨 강도 해석결과는 Table 3과 같다.
| $$f_b=\frac{Pl}{bh^2}$$ | (7) |
여기서, 는 휨 강도(MPa), 는 시험기가 나타내는 최대 하중(N), 은 지간(mm), 는 파괴 단면의 너비(mm), 는 파괴 단면의 높이(mm)이다.
Table 3. Correction of elastic modulus based on flexural strength
Table 3의 결과에서 사변형 격자지재보의 경우 상세모델과 등가모델의 휨 강도의 오차율은 평균 130%였으며, 삼각 격자지보재의 경우 평균 50%의 오차율이 발생하였다. 또한 격자지보재의 단면이 증대될수록 크기효과로 인해 휨 강도가 감소하는 경향을 나타낸다. 즉, 해석 결과를 바탕으로 체적비 기반의 등가탄성계수를 수치해석에 그대로 적용하는 것은 강지보재의 구조 성능을 과소평가하게 됨을 알 수 있다. 특히, 사변형 격자지보재는 수직재의 도입을 통해 삼각 격자지보재보다 상세모델의 휨 강도가 더 큰 것으로 확인되었으나, 등가모델의 경우 이러한 차이를 고려할 수 없어서 두 격자지보재의 휨 강도 차이가 크지 않게 나타나는 것으로 확인되었다.
따라서 격자지보재의 구조 성능을 수치해석 또는 설계에 적절히 반영하기 위해서는 체적비 또는 면적비로 계산된 등가탄성계수에 대한 보정이 반드시 필요하다. 일반적인 콘크리트의 휨강도와 탄성계수 관계는 식 (8) 또는 (9)과 같은 선형비례관계를 갖는다(Raphael, 1984; ACI, 1999). 이 식은 일반적인 콘크리트에 대한 관계식이며, 본 연구에서 검토한 재료는 강지보재와 콘크리트의 혼합구조로 위 식을 사용하기에는 부적합하다고 판단하였다. 따라서 콘크리트의 휨강도와 탄성계수 관계가 선형 비례관계인 것을 고려하여 식 (10)과 같이 등가모델의 탄성계수에 상세모델에서 계산된 휨 강도와 등가모델에서 계산된 휨 강도의 오차비를 곱해 등가탄성계수를 보정하였다. 보정된 등가탄성계수를 적용한 격자지보재 합성부재의 휨 강도 및 상세모델과의 오차율을 Table 3에 나타내었다.
| $$f_r=1.92\times\frac E{15,707}$$ | (8) |
| $$f_r=1.92\times\frac E{15,104}$$ | (9) |
여기서, 은 콘크리트 휨강도, 는 콘크리트 탄성계수이다.
| $$E_{ad}=E_{eq}\times\frac{f_r}{f_r'}$$ | (10) |
여기서, 는 보정 후 등가탄성계수, 는 보정 전 등가탄성계수, 은 상세 모델의 휨강도, 은 체적비 기반의 등가탄성계수를 적용한 등가모델의 휨강도이다.
보정한 등가탄성계수를 등가모델에 적용한 결과, 상세모델과의 휨 강도 오차율이 1% 미만으로 발생하였다. 상세모델과 체적비 기반의 등가탄성계수와의 휨 강도를 획득하고 두 휨강도의 오차율을 사용하여 등가탄성계수를 보정하여, 보정된 등가탄성계수를 적용한 등가모델을 통해 터널 해석시 강지보재의 구조성능을 보다 적절히 고려할 수 있다.
이는 강지보재와 보 형태로 결합된 숏크리트 합성부재 요소에 대한 수치해석 결과이며, 실제 터널 현장과는 차이가 있기 때문에 2차원 및 3차원 굴진장을 고려하여 등가탄성계수를 계산하는 과정이 필요하다. 즉, 강지보재 설치 간격을 고려하여 1굴진장에 대한 등가탄성계수를 산정하여 터널 안정해석에 적용하여야 한다.
4. 결 론
본 연구에서는 사변형 격자지보재를 3차원 터널 안정해석에 고려하기 위한 방법으로 체적비 기반의 등가탄성계수 산정에 대한 연구를 수행하였으며 다음과 같은 결론을 도출하였다.
1. 4점 재하 휨 시험 수치해석을 통하여 격자지보재와 숏크리트가 합성된 상세모델과 체적비 기반의 등가물성치를 사용한 등가모델을 비교하였으며, 그 결과로 등가모델은 상세모델에 비해 평균적으로 130% 감소된 휨 강도를 나타내었다.
2. 따라서 체적비 기반의 등가물성치를 수치해석에 그대로 적용하는 경우 강지보재의 휨 성능을 과소평가하여 과다설계를 유발할 수 있기 때문에, 탄성계수와 선형비례관계인 휨강도를 통하여 체적비 기반의 등가탄성계수를 보정하는 방법을 제안하였다. 보정된 등가탄성계수를 적용한 등가모델의 휨강도는 상세모델과 평균 오차율 1% 이내로 나타났다.
본 연구에서는 강지보재를 수치해석에서 반영하기 위한 방법으로 숏크리트와 합성부재를 연속체로 모델링하는 경우 등가탄성계수를 산정하는 방법을 제안하였으며, 합성부재를 구조요소로 고려하기 위해 필요한 등가단면이차모멘트 및 각 부재의 안정성 검토를 위해 필요한 축력 및 모멘트 분담율의 산정을 위해서는 추가적인 연구가 요구된다.