1. 서 론
2. SVM (Support Vector Machine)
2.1 선형적으로 분리가 가능한 SVM
2.2 선형적으로 분리가 불가능한 SVM
2.3 비선형 SVM 문제의 해결
3. 디스크 커터 교체 시점 예측을 위한 SVM 기법 적용
3.1 지반 조건
3.2 디스크 커터 및 전주거리
3.3 쉴드 TBM 기계 데이터
3.4 SVM 모델 구축 및 예측
4. SVM 예측 결과의 신뢰도 평가
4.1 정확도(Accuracy)
4.2 정밀도(Precision)
4.3 오분류율(Error rate)
5. 결 론
1. 서 론
우리나라는 경제 발전과 더불어 토지 사용의 증가로 인해 도로 및 철도시설 확충을 위한 토지의 확보가 어려운 실정이며, 이에 따라 지하 공간 개발의 필요성이 크게 대두되고 있다. 지하 공간의 개발은 주로 터널 건설을 통해 이루어지며, 그 중 터널 굴착기(Tunnel Boring Machine, TBM)를 이용한 기계식 터널 굴착공법이 기존의 Drill and Blast 터널 굴착공법에 비해 소음과 진동이 적고 TBM이 막장면을 자체 지지함에 따라 사고 위험성이 적은 장점이 있어 많이 사용되고 있는 추세이다.
TBM의 굴착 원리는 TBM의 추력을 이용하여 디스크 커터나 커터 비트가 장착된 원형의 커터 헤드를 회전시켜 지반을 압쇄, 절삭하는 것인데, 이 과정에서 자연스럽게 디스크 커터(혹은 비트)에 마모가 발생하고 마모 한계에 도달한 디스크 커터는 TBM의 굴진효율 저하와 과도한 토크 증가의 원인이 되기 때문에 적정 시점에 교체를 하는 것이 중요하다(Jeong et al., 2014; Ko et al., 2014; Kim et al., 2017). 즉, 디스크 커터는 TBM의 굴착 성능을 좌우할 뿐만 아니라 소모성 재료이기 때문에 TBM의 경제성 측면에서 매우 중요한 부품이고, 디스크 커터의 교체에 소요되는 시간과 비용은 TBM 터널의 전체 공사기간과 공사비에 큰 영향을 미칠 수 있다. 따라서 디스크 커터의 교체 시점과 총 소요 개수에 대한 적절한 예측은 설계 단계에서 전체 공사비와 공사기간을 추정하는데 매우 중요한 요소일 뿐 아니라, 시공단계에서도 적절한 굴진관리를 위해 반드시 필요한 요소가 된다.
TBM 디스크 커터의 마모 한계(수명)를 예측하기 위한 기존의 주요 연구들은 대부분 단일 암석에 대한 절삭시험을 바탕으로 수행되었다. 해외의 경우, 미국 콜로라도 광산대학(Colorado School of Mines)의 CSM 모델(Rostami and Ozdemir, 1993), Gehring (1995) 모델, Bieniawski et al. (2009) 모델은 세르샤 마모지수(Cerchar Abrasiveness Index, CAI)를 이용하여 커터 수명을 예측하는 모델을 제안하였고, 노르웨이 과학기술대학(Norwegian University of Science and Technology)에서 개발된 NTNU 모델(Bruland, 2000)은 모형 천공시험(Siever’s J-value test), 취성도 시험(Brittleness test)을 수행하여 커터 수명을 예측하는 모델을 제안하였다. 국내의 경우, 한국건설기술연구원과 서울대학교에서 공동연구로 개발된 KICT-SNU 모델(Yu, 2007)은 국내 8개 암석조건에 대한 선형절삭시험으로부터 디스크 커터 수명을 예측하는 모델을 제안하였고, Kim et al. (2017)은 원형의 디스크를 양방향으로 마모시키는 시험방법과 마모지수를 개발하는 연구를 수행한 바 있다. 그러나 이러한 연구들은 균질한 암석에 대한 절삭시험 결과를 기반으로 하였기에 상대적으로 불균질한 지반이나 디스크 커터가 정상적으로 마모되지 않는 경우에 대해서는 적용에 한계가 있다. 특히, 국내 지반에서 흔히 관찰되는 층리와 발달된 습곡, 여러 지층이 혼합된 복합 지반에서는 디스크 커터에 편마모와 같이 비정상적인 마모가 생기거나 링이 탈락 하는 등 예기치 않게 디스크 커터를 교체해야 하는 상황이 자주 발생한다. 또한, 국내 TBM 터널의 설계와 시공 시 일반적으로 시간과 비용 절감을 위해서 실제 대상 현장 지반의 암석시료에 대해 절삭시험을 통해 디스크 커터의 마모도를 예측하는 경우가 적어 기존 연구들에서 제시한 예측 모델의 활용도가 높지 않은 편이다.
따라서 본 연구에서는 최근 국내에서 적용이 증가하고 있는 쉴드 TBM 터널에 대해서 디스크 커터의 적절한 교체시기를 예측하는데 사용하기 위한 새로운 방법으로서 머신러닝 기법을 이용하는 방법을 제시하고자 하였다. 디스크 커터의 마모에는 지반 조건과 TBM 장비 관련 요소 등 기존 모델들에서 고려하고 있는 요소 이외에도 추력과 토크 등 굴진 데이터와 관련된 요소들도 기존 요소들과 관련성을 맺으며 영향을 미치게 된다. 예측하고자 하는 특정 대상이 다양한 인자들에 영향을 받고 그 인자들 간의 논리적 연관을 모두 명확히 파악하기 어려운 경우에는 머신러닝 기법이 매우 효과적인 예측 도구로 활용될 수 있다. 서포트 벡터 머신(Support Vector Machine, SVM)은 분류 쪽의 성능이 뛰어난 대표적 머신러닝 알고리즘으로 다양한 데이터 분포에서도 잘 작동하는 분류 기법 중 최상의 기법으로 알려져 있다. 본 연구에서는 국내 기 시공된 ○○~○○ 고속철도 쉴드 TBM 터널의 설계 및 시공 데이터를 이용해 디스크 커터의 적절한 교체 시점을 예측하기 위한 SVM 모델을 구축하고 적용성을 검토하였다.
2. SVM (Support Vector Machine)
SVM 기법은 Vapnik (1995)에 의해 제안된 학습이론으로 두 개 이상 클래스의 분류 문제를 다루는 기법이다. SVM은 여러 분야에서 널리 활용되고 있으며, 경험적 위험 최소와 원칙이 아닌 구조적 위험 최소화를 기반으로 하고 있기 때문에 일반화의 오류를 감소시키는 점에서 기존의 방법들보다 우수한 성능을 가진다고 알려져 있다(Burges, 1998).
2.1 선형적으로 분리가 가능한 SVM
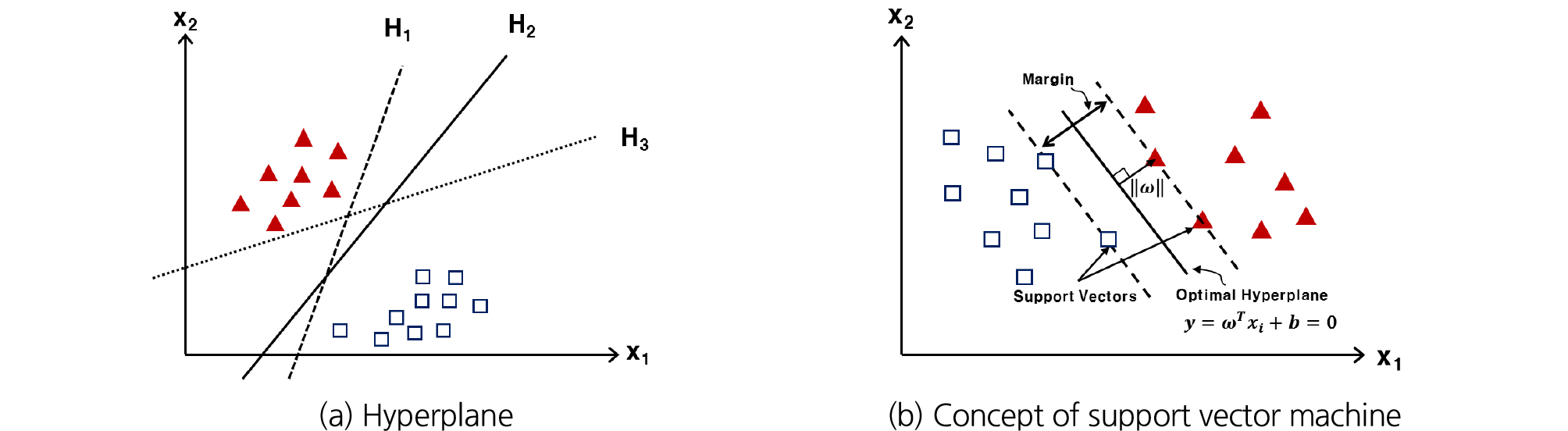
선형적으로 분류가 가능한 SVM에서는 두 개의 범주로 구성된 N개의 객체가 p차원 공간에 위치한다고 가정할 때, p차원 공간에서 두 범주를 구분하는 분리 경계면은 Fig. 1(a)와 같이 무수히 많은 하이퍼플레인(hyperplane)으로 나눌 수 있는데, 최적의 하이퍼플레인은 Fig. 1(b)와 같이 +1 및 -1로 치환된 해석결과를 가장 잘 분류할 수 있는 직선으로 나타낼 수 있으며, 여기서 경계선(Boundary)을 설정하고 경계선의 거리(마진)를 정의하는 변수를 서포트 벡터(support vector)라 한다.
선형 SVM에서 최대 마진을 찾기 위해서는 경계면과 수직인 벡터 가 최소가 되는 값을 결정해야 한다. 또한, 가 최소가 되는 최적화 문제를 해결하기 위해서는 극대 ‧ 극소를 해결하는 방법으로서 개발된 라그랑지 함수(Lagrange function)를 사용한다. 라그랑지 함수 L(, b, )은 변수 와 b에 대해서는 최소화, 라그랑지 승수 에 대해서는 최대화 되어야 가 최소가 되는 문제를 만족하며, 이를 수식으로 표현하면 식 (1)과 같다.
| $$L(\omega,b,\alpha)=\frac12\left\|\omega\right\|^2-\sum_{i=1}^n{\alpha_i(y_i(\omega^Tx_i+b)-1)}$$ | (1) |
식 (1)을 와 b에 대해 미분하면 다음의 식 (2)와 (3)을 얻을 수 있다.
| $$\frac{\partial L(\omega,b,\alpha)}{\partial\omega}=\omega-\sum_{i=1}^n\alpha_iy_ix_i=0$$ | (2) |
| $$\frac{\partial L(\omega,b,\alpha)}{\partial b}=\sum_{i=1}^n\alpha_iy_i=0$$ | (3) |
최대 를 구하기 위해서는 식 (2)와 (3)을 식 (1)에 대입하여 구할 수 있고 를 결정하는 수식은 (4), 조건은 식 (5)와 같게 된다.
| $$\mathrm{Max}\sum_{i=1}^n\alpha_i-\frac12\sum_{i=1}^1\sum_{s=1}^1\alpha_i\alpha_sy_iy_s<x_i,x_s>$$ | (4) |
| $$\mathrm{subject}\;\mathrm{to}:\sum_{i=1}^n\alpha_iy_i=0\;\alpha_i\geq0,\;i=1,\;\cdots,\;n$$ | (5) |
2.2 선형적으로 분리가 불가능한 SVM
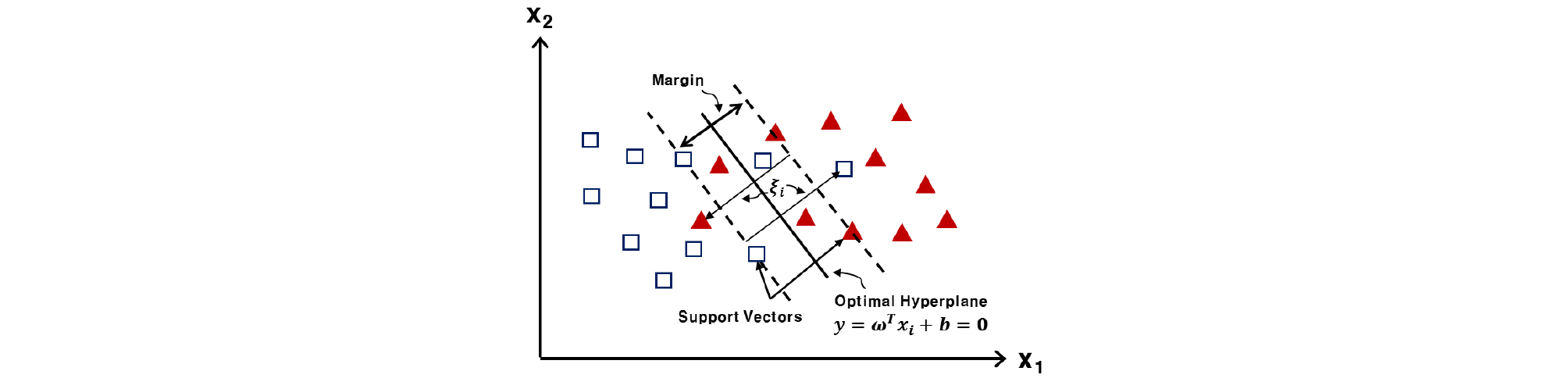
Fig. 2와 같이 데이터를 두 개의 범주로 선형적 분류가 불가능할 경우 이를 해결하기 위해 오분류를 허용하는 여유변수 와 패널티 모수 C를 고려하게 되며, 이러한 경우 가 최소가 되는 최적화 문제는 식 (6), 조건은 식 (7)과 같이 된다(Cortes and Vapnik, 1995; Smola and Scholkopf, 2004; Lee et al., 2018).
| $$\mathrm{Min}\frac12\parallel\omega\parallel^2+C\sum_{i=1}^n\xi_i$$ | (6) |
| $$\mathrm{subject}\;\mathrm{to}:y_i((\omega\bullet x_i)+b)\geq1-\xi_i(1,\cdots,N),\;\xi_i\geq0$$ | (7) |
라그랑지 승수(Lagrange multipliers) 를 이용하여 극대화하는 문제로 변형하여 수식으로 표현하면, 수식은 (8), 조건은 식 (9)와 같게 된다.
| $$\mathrm{Max}\sum_{i=1}^N\alpha_i-\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_ix_j$$ | (8) |
| $$\mathrm{subject}\;\mathrm{to}:0\leq\alpha_i\leq C(i=1,\cdots,N),\;\sum_{i=1}^n\alpha_iy_i=0$$ | (9) |
2.3 비선형 SVM 문제의 해결
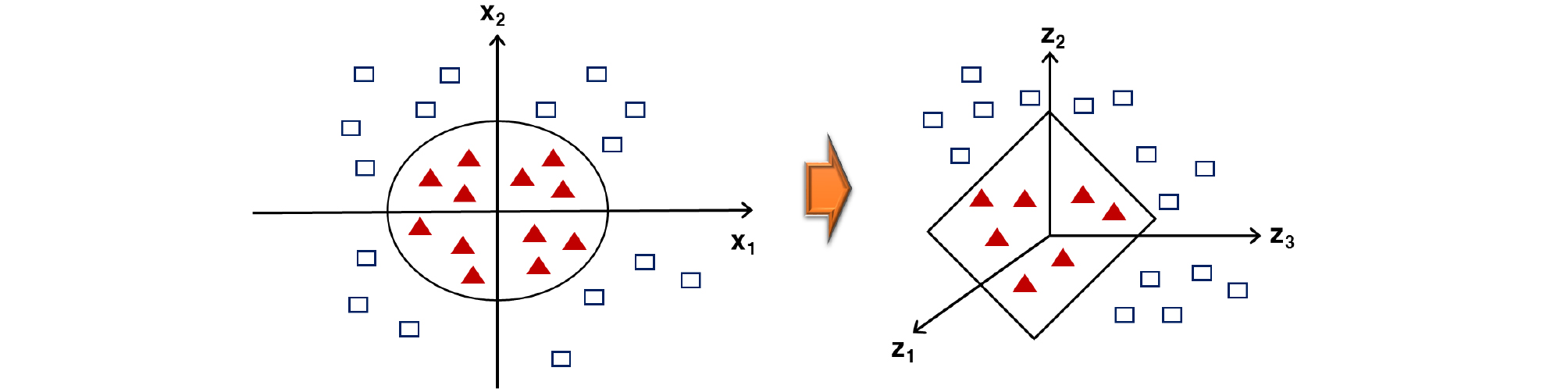
현재 차원에서 선형 분리가 되지 않는 경우에는 SVM은 Fig. 3과 같이 데이터를 고차원의 특성 공간으로 매핑(mapping) 시킨다. 이 때, 공간상의 두 벡터 와 를 매개변수로 갖는 커널함수를 라고 하면, 를 만족하는 기저함수(Basis Function) 가 존재하게 된다. 이 때, 두 벡터 의 내적을 커널함수를 이용하여 계산하게 되고, 이를 통해 식 (4)와 (8)을 변형하면 식 (10) 및 (11)과 같이 된다.
| $$\mathrm{Max}\sum_{i=1}^N\alpha_i-\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)\phi(x_j)$$ | (10) |
| $$\mathrm{Max}\sum_{i=1}^{Nn}\alpha_i-\frac12\sum_{i,s=1}^n\alpha_i\alpha_sy_iy_sK(x_i,x_s)$$ | (11) |
매핑을 시켜주는 커널함수들은 여러 가지가 존재하고 그 중 대표적으로 다항식(Polynomial)과 방사기저함수(Radial Basis Function, RBF)가 커널함수로 사용되며, 그 형태는 다음 식 (12), (13)과 같다. 여기서, RBF는 다변량 데이터의 보간을 위해 제안된 근사모델로 차원이 무한한 특성 공간에 매핑하는 방식으로 사용된다.
| $$K(x_i, x_s) = (x_i \bullet x_s +1)^d ,~d \in N$$ | (12) |
| $$K(x_i,x_s)=\exp\left(-\frac{\left\|x_i-x_s\right\|_{}^2}{2\sigma^2}\right)$$ | (13) |
3. 디스크 커터 교체 시점 예측을 위한 SVM 기법 적용
본 연구에서 제안하는 SVM 기법을 활용한 디스크 커터 교환 주기 예측 모델의 구축을 위해 국내 한 쉴드 TBM 터널 현장의 데이터를 수집하였다. 대상 현장은 ○○~○○ 고속철도 ○○-○ 공구로 터널의 총 연장은 3,930 m이고 이중 쉴드 TBM 구간은 1,160 m이며, 그 중 모델 구축에 사용된 데이터가 수집된 구간은 굴착길이 100 m 지점부터 650 m 지점까지 약 550 m이다. 모델의 구축은 크게 학습과정과 예측과정으로 구분하며, 학습과정에서는 예측이 잘 이루어 질 수 있도록 디스크 커터의 마모(수명)에 영향을 주는 요인과 관련성이 높은 데이터를 입력변수로 설정하여야 한다. 본 연구에서는 모델의 입력과 출력변수로서 디스크 커터의 수명과 높은 상관성을 갖는 것으로 판단되는 지반조건과 디스크 커터의 전주거리, 쉴드 TBM의 추력과 토크, 회전속도(RPM) 등 기계 데이터를 입력변수로, 그리고 디스크 커터의 교체 이력 데이터를 예측변수로 구성하고 모델 학습을 수행하였다. 이 때, SVM 분류함수로서 기본적인 선형 SVM과 커널함수를 사용하는 다항식(Polynomial) SVM 및 RBF (Radial Basis Function) SVM의 3종류를 사용하였으며, 학습된 모델을 이용해 학습에 사용하지 않은 데이터를 가지고 예측을 수행한 후 예측결과에 대한 정확도와 정밀도, 오분류율을 산정하여 모델의 적정성을 평가하였다.
모델의 구성 및 구축 과정과 관련된 세부 사항은 다음과 같다.
3.1 지반 조건
쉴드 TBM 굴착구간의 지반 조사를 위해 시추조사 및 전기비저항 탐사가 수행되었으며, 그 결과 Table 1과 Fig. 4에 나타낸 바와 같이, 터널 노선을 따라 지층은 풍화암이 많은 혼합층과 풍화암층, 그리고 연암이 주를 이루는 혼합층과 퇴적층, 크게 4종류의 지층으로 구분되는 것으로 나타났다. 여기서는 각 지층을 편의상 Ground type 1~4로 표기하였다. 지반 조건과 관련된 보다 상세한 내용은 La et al. (2019)에 기술되어 있다.
Table 1. Ground types of shield TBM excavation site
3.2 디스크 커터 및 전주거리
쉴드 TBM 장비는 독일 HERRENKNECHT사에서 복합 지층 대응용으로 제작된 이수가압식 장비로 쉴드 TBM 면판 헤드에는 총 44개의 디스크 커터와 110개의 스크레퍼가 설치되어 있다. 디스크 커터의 직경은 17 inch이고 더블 커터 4개, 싱글 커터 40개로 구성되어 있으며, 이 중 싱글 커터 40개의 데이터를 디스크 커터 교체 예측 데이터로 사용하였다.
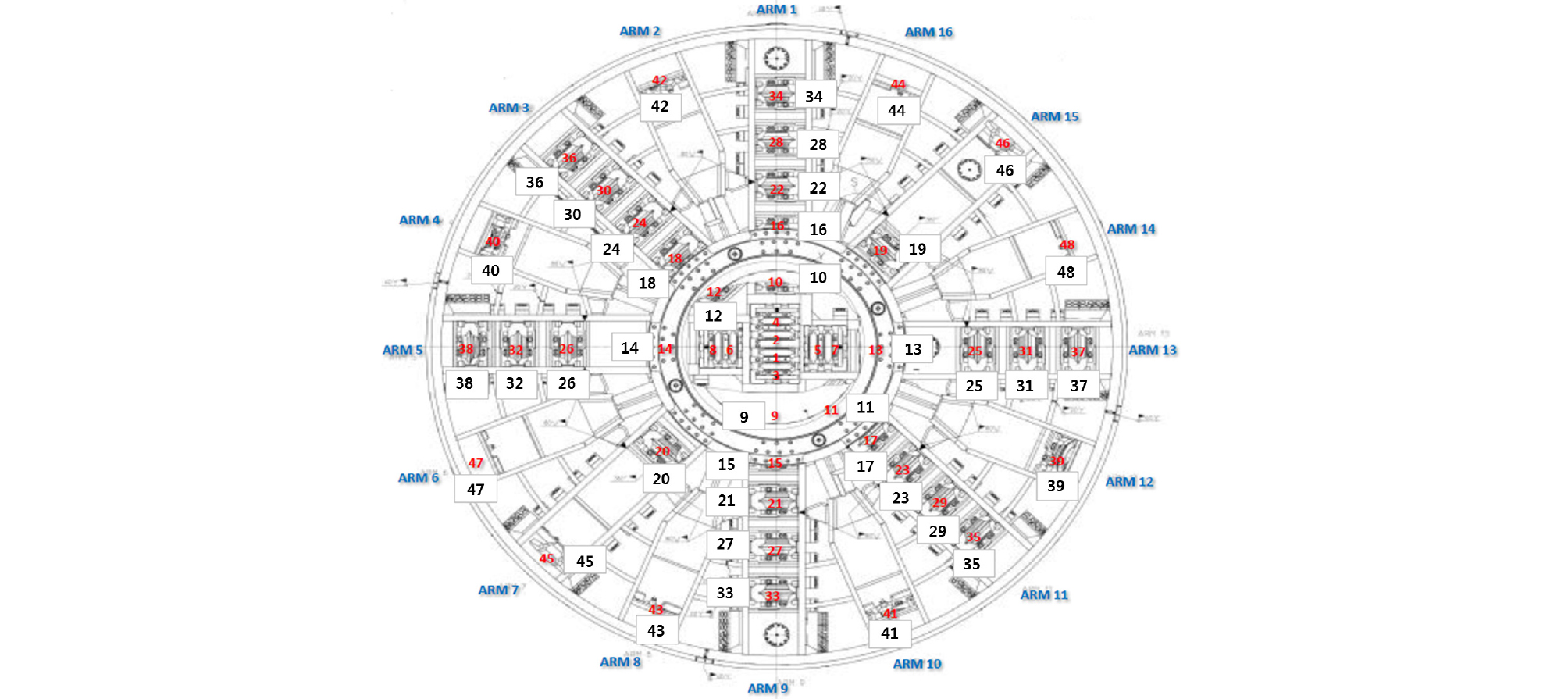
쉴드 TBM 면판 헤드가 회전하면서 지반 굴착을 수행함에 따라 각각의 디스크 커터는 Fig. 5에서 보여 주듯이 디스크 커터의 면판 헤드 상의 위치에 따라서 커터별로 굴진된 거리가 다르게 되며, 면판의 원주가 큰 위치에 있는 디스크 커터의 교체 주기가 상대적으로 짧게 된다. 따라서 각 커터별 전주거리는 디스크 커터 교환 주기에 영향을 미치는 주요한 인자 중 하나이므로 SVM 모델의 입력변수로 설정하였다.
3.3 쉴드 TBM 기계 데이터
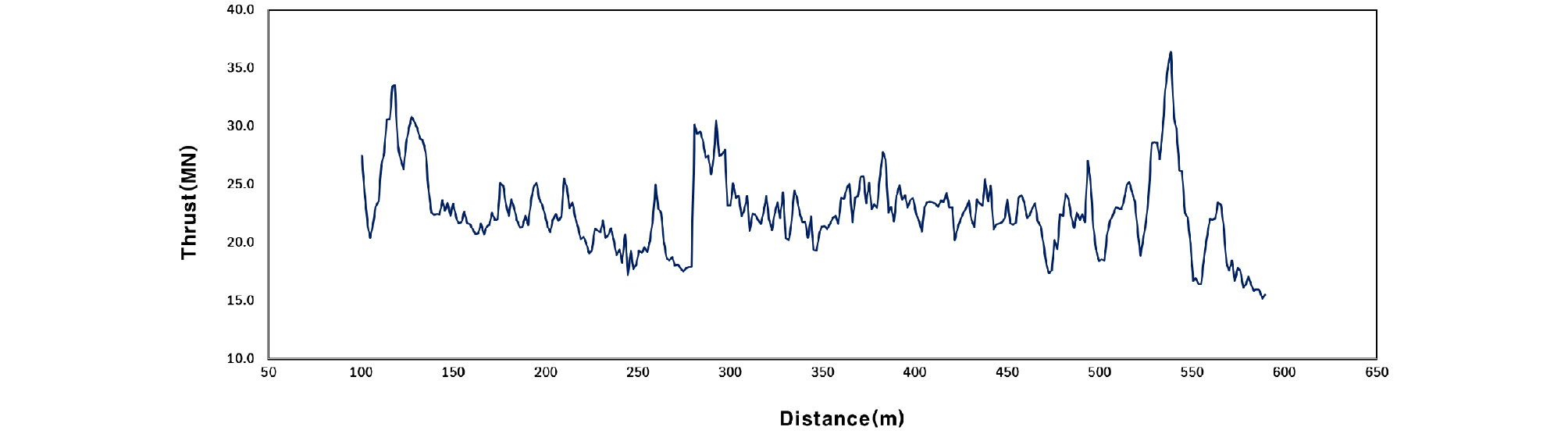
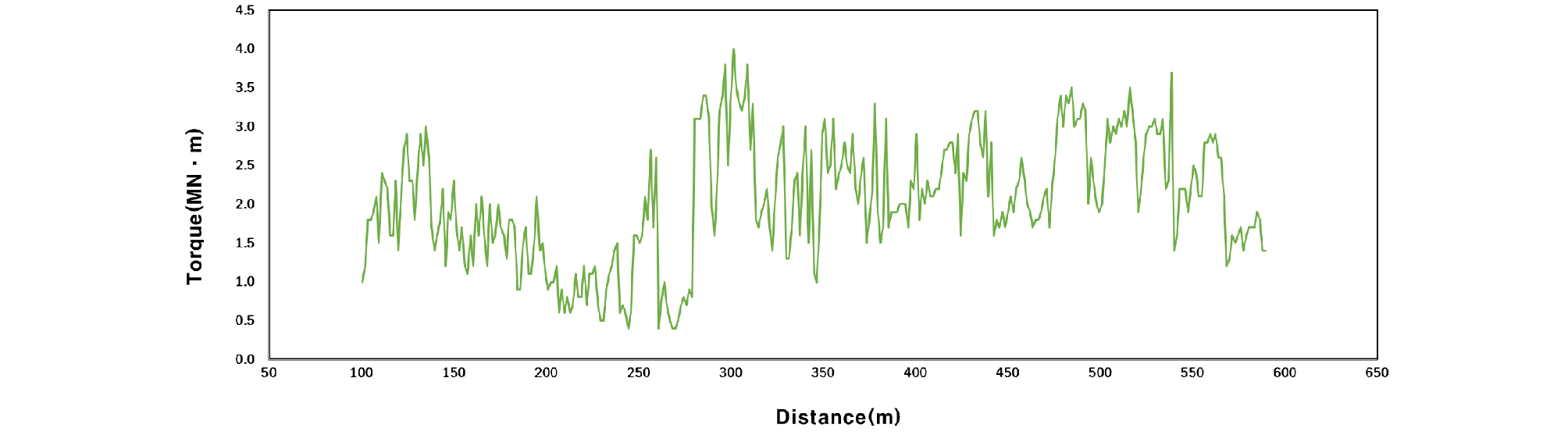
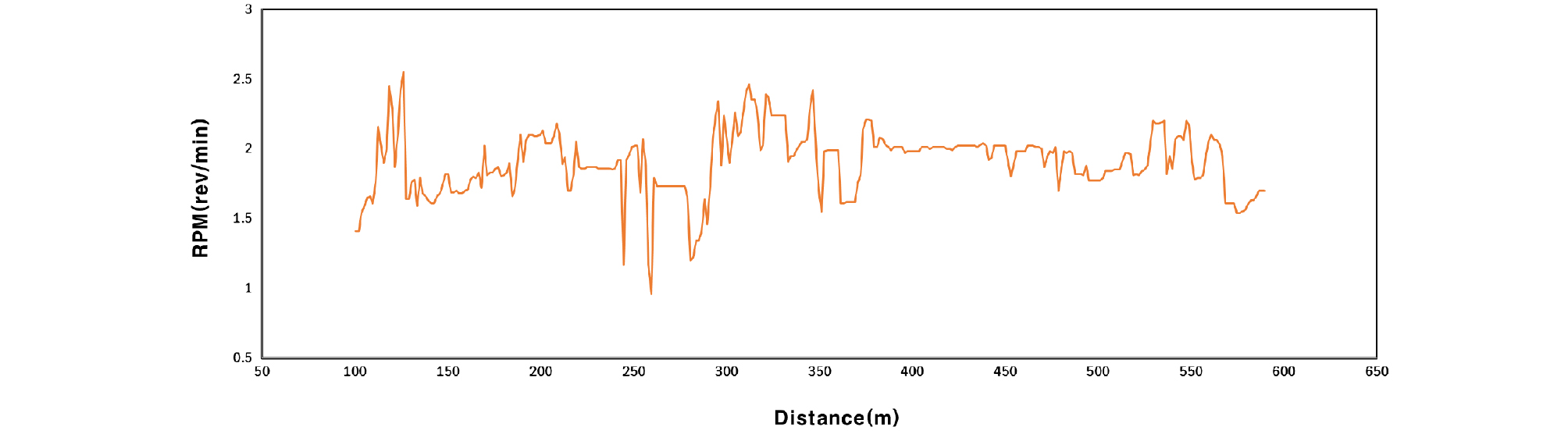
쉴드 TBM 기계 데이터와 관련한 모델 입력변수로는 총 추력과 토크, 회전속도를 설정하였다. TBM의 추력(Thrust force)은 디스크 커터에 가해지는 작용력과 관련성이 높은 인자이며, 일반적으로 암반 강도가 낮을수록 작은 추력에서 굴착이 가능하고 암반 강도가 높을수록 큰 추력을 사용해야 한다. 당 현장에서 TBM 운전에 사용한 추력은 Fig. 6에 보는 바와 같이 약 15.0~36.5 MN의 범위에 있었으며, 터널 굴착 지반의 지층 변화가 심하고 다수의 지반이 복합 지반으로 구성되어 있으며, 비교적 지반의 암반 강도가 높았기 때문에 추력의 크기가 크고 변화가 심한 것으로 나타났다. 토크(Torque) 역시 디스크 커터의 상태와 관련성이 높은 인자로 당 현장에서는 약 0.5~4.0 MN ‧ m의 범위로 마찬가지로 변화 폭이 큰 것으로 나타났다(Fig. 7 참고). 커터 헤드의 회전속도 또한 디스크 커터 교체에 영향을 미치는 중요한 인자로 당 현장에서 터널 굴진시 사용된 회전속도를 Fig. 8에 도시하였다. 혼합 지층이 많고 지층 변화가 크기 때문에 1.0~2.5 RPM의 낮은 범위에서 운전하여 시공 트러블이 발생하지 않도록 굴착을 진행하였으며, 비교적 일정한 크기로 회전속도를 유지하였음을 알 수 있다.
3.4 SVM 모델 구축 및 예측
데이터가 수집된 굴착 구간에 대해서 Table 2에 나타낸 바와 같은 구성으로 개별 데이터 세트가 구성되었고, 지반 조건별로 1,000~4,200개, 총 13,080개 데이터 세트가 SVM에 이용되었다. 해당 구간을 굴착하는 동안 디스크 커터의 교체는 Table 3과 같이 풍화암이 많은 혼합층(Ground type 1)에서 총 19회, 풍화암층(Ground type 2)에서 총 49회, 연암이 주를 이루는 혼합층(Ground type 3)에서 총 75회, 그리고 퇴적층(Ground type 4)에서 총 67회가 이루어졌다. 이를 각 지반 종류에 따라 디스크 커터의 교체율로 나타내면 Ground type 1~4에 대해 각각 1.9%, 1.2%, 1.8%, 1.75%가 된다. 즉, 전체 데이터 세트에서 디스크 커터의 교체에 해당하는 데이터 세트의 수가 차지하는 비율이 낮아 이를 그대로 SVM에 적용하였을 경우 결과를 신뢰하기 어려운 상태가 되었다. 따라서 본 연구에서는 디스크 커터 점검 데이터를 분석하여 디스크 커터의 교체 기준을 마모율 70% (즉, 마모한계까지 30%가 남은 상태)로 임의 설정하여 교체에 해당하는 데이터 세트의 수를 증가시켜 SVM을 수행하였다. 이는 실제 대상 현장과 다른 조건을 적용한 것이나 본 연구의 목적은 실제 대상 현장을 위해 시공 중 예측에 적용하기 위함이 아닌 단지 새로운 접근방법으로서 SVM 기법의 적용성을 평가하기 위함이었으므로 그러한 시도 자체에는 문제가 없다고 판단하였다. 그리고 실제 현장에서는 일반적으로 디스크 커터를 항시 특정한 기준에 따라 교체하는 것이 아니고, 현장 별로, 담당자 별로, 상황에 따라 교체 적용 기준을 달리 적용할 수 있는 상황이다. 따라서 이와 같은 기법을 사용한 예측에 다소 어려움이 예상될 수 있으나 데이터가 지속적으로 축적이 되어 보다 많은 양의 데이터에 대한 학습이 이루어진다면 점차 그러한 어려움들은 해소될 수 있을 것이라 생각한다.
Table 2. SVM variables
Table 3. Statistics of data set and disc cutter replacement condition
| Ground types | Number of data set | Number of replacement | Replacement rate |
| Ground type 1 | 1,000 | 19 | 1.9% |
| Ground type 2 | 4,080 | 49 | 1.2% |
| Ground type 3 | 4,200 | 75 | 1.8% |
| Ground type 4 | 3,800 | 67 | 1.75% |
본 연구에서는 SVM 분류 함수로 선형 SVM, 다항식 SVM, 및 RBF SVM의 3종류를 사용하였으며 전체 데이터 세트에서 랜덤 선택을 통해 80%의 데이터 세트를 학습에 사용하고 나머지 20%의 데이터 세트를 예측에 사용하였다.
4. SVM 예측 결과의 신뢰도 평가
SVM 예측 결과의 신뢰도를 평가하기 위해 SVM 수행을 통해 디스크 커터를 교체한 결과와 실제 현장에서 디스크 커터를 교체한 결과를 비교하고, 정량적인 평가를 위해 SVM 예측 결과의 정확도(Accuracy)와 정밀도(Precision), 오분류율(Error rate)을 산정하였다. Table 4는 그와 같은 신뢰도 평가를 위해 각 클래스 데이터의 수를 TP (True Positive), FP (False Positive), FN (False Negative), 그리고 TN (True Negative) 4종류로 분류한 형태이다. 이 때, TP는 실제 현장에서 디스크 커터를 교체하였고, 예측 결과에서도 교체한 것으로 나타난 경우, 그리고 FP는 실제 현장에서는 교체하지 않았으나 예측에서는 교체한 경우, FN은 실제로 교체하였으나 예측에서는 교체하지 않은 것으로, 마지막으로 TN은 실제 교체하지 않았고 예측에서도 교체하지 않은 것으로 나타난 경우를 각각 의미한다.
Table 4. Classification of predicted results
| Replaced (predicted) | Not replaced (predicted) | |
| Replaced (measured) | TP | FN |
| Not replaced (measured) | FP | TN |
4.1 정확도(Accuracy)
정확도는 식 (14)와 같이 전체 데이터 중 예측이 올바르게 된 데이터의 비율을 의미한다. 즉, 실제로 디스크 커터를 교체한 경우 SVM도 교체로 예측한 경우, 실제로 교체하지 않은 상태를 SVM도 동일한 상태로 예측한 경우의 비율을 의미한다.
| $$Accuracy\;(\%)=\frac{TP+TN}{TP+TN+FP+FN}\times100$$ | (14) |
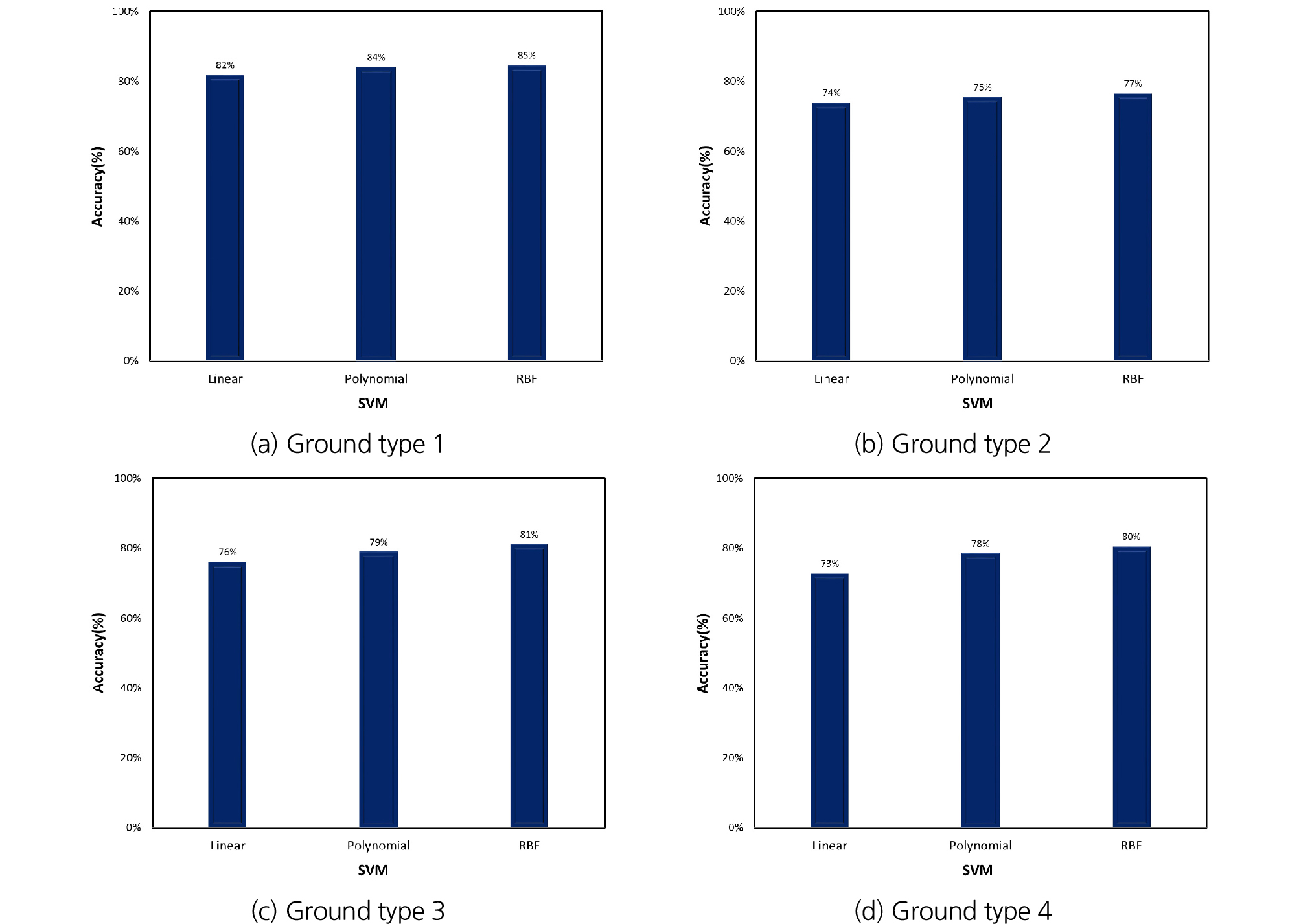
4종류의 지반 조건에 따라 수행된 선형 SVM, 다항식(Polynomial) SVM, RBF (Radial Basis Function) SVM 예측의 정확도 결과를 Fig. 9에 나타내었다. 풍화암이 많은 혼합층(Ground type 1)에 대해서는 Fig. 9(a)에 보는 바와 같이 RBF SVM이 85%로 가장 높은 예측 정확도를 보였고, 다항식 SVM이 84%, 선형 SVM이 82%의 정확도를 나타내었다. 풍화암층(Ground type 2)에 대해서는 Fig. 9(b)와 같이 RBF SVM이 77%로 가장 높은 예측 정확도를 보였고, 다항식 SVM이 75%, 선형 SVM이 74%의 정확도를 보였다. 또한, 연암이 많은 혼합층(Ground type 3)에 대해서는 Fig. 9(c)와 같이 RBF SVM이 81%로 가장 높은 예측 정확도를 보였고, 다항식 SVM이 79%, 선형 SVM이 76%의 정확도를 나타내었다. 마지막으로 퇴적층(Ground type 4)에 대해서는 Fig. 9(d)와 같이 RBF SVM이 80%로 가장 높은 예측 정확도를 보였고, 다항식 SVM이 78%, 선형 SVM이 73%의 정확도를 나타내었다. 정리하면, SVM의 예측 정확도는 전체적으로 RBF SVM이 가장 높은 것으로 나타났고, 그 다음 다항식 SVM, 선형 SVM의 순서로 높은 것으로 나타났다. 그리고 지반 조건에 따라 비교했을 때 디스크 커터 교체율이 높은 순서인 Ground type 1, Ground type 3, Ground type 4, Ground type 2의 순서로 예측 정확도가 높은 것을 확인하였다.
4.2 정밀도(Precision)
정밀도는 식 (15)와 같이 실제로 디스크 커터 교체에 해당되는 데이터가 예측에서도 정확하게 교체로 분류된 데이터의 비율을 의미한다.
| $$Precision\;(\%) = \frac{TP} {TP+FN} \times 100$$ | (15) |
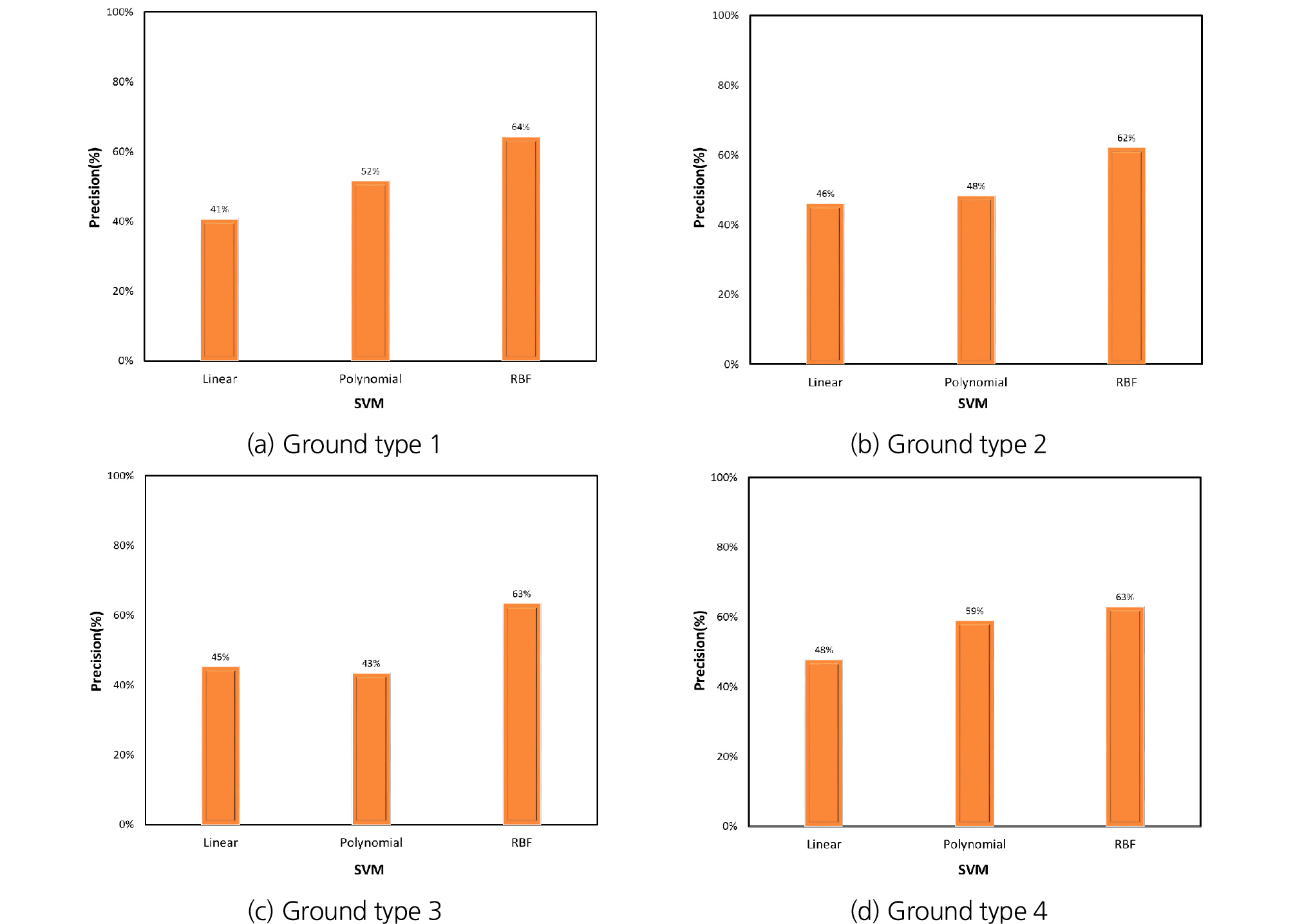
4종류의 지반 조건에 따라 수행된 선형 SVM, 다항식 SVM, RBF SVM 정밀도 결과를 Fig. 10에 나타내었다. 풍화암이 많은 혼합층(Ground type 1)에 대해서는 Fig. 10(a)와 같이 RBF SVM이 64%로 가장 높은 정밀도를 보였고, 다항식 SVM이 52%, 선형 SVM이 41%의 정밀도를 나타내었다. 풍화암층(Ground type 2)에 대해서는 Fig. 10(b)와 같이 RBF SVM의 정밀도가 62%로 가장 높은 것으로 나타났고, 다항식 SVM이 48%, 선형 SVM이 46%로 나타났다. 연암이 많은 혼합층(Ground type 3)에 대해서는 Fig. 10(c)와 같이 RBF SVM이 63%로 가장 높은 정밀도를 보였고, 선형 SVM과 다항식 SVM이 각각 45%와 43%의 정밀도를 나타내었다. 마지막으로 퇴적층(Ground type 4)에 대해서는 Fig. 10(d)와 같이 RBF SVM이 63%로 가장 높은 예측 정밀도를 보였고, 다항식 SVM이 59%, 선형 SVM이 48%의 정밀도를 나타내었다. 정확도(Accuracy) 결과와 마찬가지로 정밀도(Precision)에서도 분류 함수 중 RBF SVM의 결과가 가장 우수한 것으로 나타났으나 정확도에 비해 전반적으로 수치가 낮은 범위로 나타났다. 그리고 지반 조건에 따라 비교했을 때도 정확도와 결과와 동일하게 디스크 커터 교체율이 높은 순서인 Ground type 1, Ground type 3, Ground type 4, Ground type 2의 순서로 정밀도가 높게 나타났다.
4.3 오분류율(Error rate)
오분류율은 식 (16)과 같이 실제로 디스크 커터가 교체되지 않았지만 교체된 것으로 잘못 분류한 경우의 비율을 의미한다.
| $$Error\;Rate\;(\%) = \frac{FP} {FP+TN} \times 100$$ | (16) |
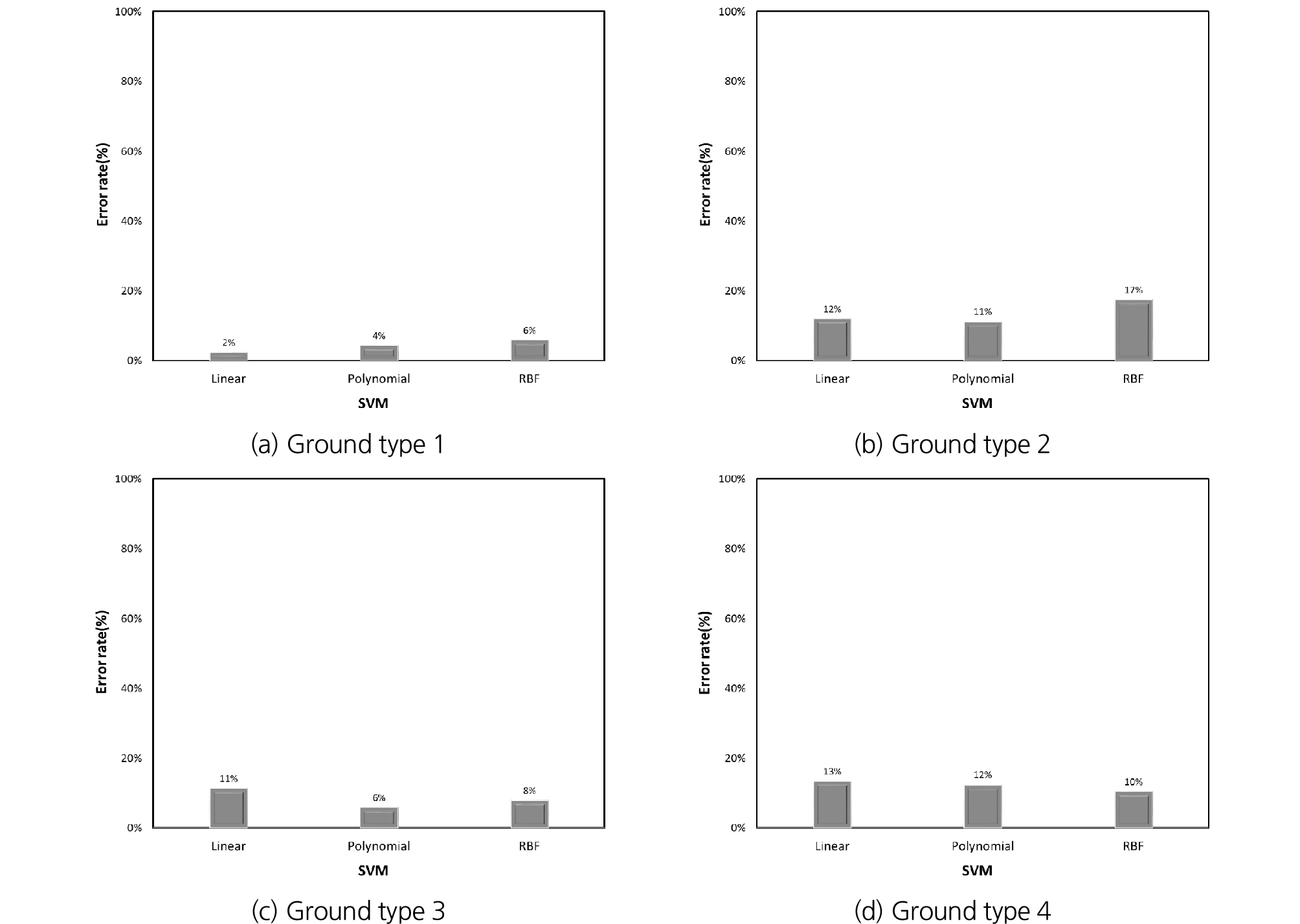
4종류의 지반 조건에 따라 수행된 선형 SVM, 다항식 SVM, RBF SVM의 오분류율 결과를 Fig. 11에 나타내었다. 풍화암이 많은 혼합층(Ground type 1)에 대해서는 Fig. 11(a)와 같이 RBF SVM의 오분류율이 6%로 가장 높게 나타났고, 풍화암층(Ground type 2)에 대해서도 마찬가지로 RBF SVM의 오뷴류율이 17%로 가장 높게 나타났다(Fig. 11(b)). 한편, 연암이 많은 혼합층(Ground type 3)과 퇴적층(Ground type 4)에 대해서는 Fig. 11(c), 11(d)와 같이 선형 SVM의 오분류율이 11%로 가장 높게 나타났다. 즉, 분류 함수별 비교 시 오분류율은 차이가 크지는 않으나 앞서 기술한 정확도 및 정밀도와 일관된 결과를 나타내지는 않았다. 그러나 지반 조건별 비교 시 디스크 커터 교체율이 높은 순서인 Ground type 1, Ground type 3, Ground type 4, Ground type 2의 순서로 오분류율이 낮게 나타났다.
5. 결 론
본 연구에서는 쉴드 TBM 터널 디스크 커터의 적절한 교체 시점을 파악하는 데 활용하기 위한 디스크 커터의 교환 주기 예측 방법으로서 머신러닝 알고리즘의 하나인 SVM의 적용성을 검토하였다. 이를 위해 국내 쉴드 TBM 굴착 현장의 데이터를 대상으로 SVM 모델을 구축하고 예측 성능을 평가하였다. 이를 통해 얻은 결론을 요약하면 다음과 같다.
1. 지반 조건별로 디스크 커터의 마모와 높은 상관성을 갖는 TBM 기계 데이터와 디스크 커터 교체 이력을 분류하였으며, 이들을 SVM의 변수로 사용하여 3종류의 분류 함수를 적용하고 각각 학습을 한 후 예측을 수행하였다. 그리고 예측 결과의 신뢰도를 평가하기 위해 정확도와 정밀도, 오분류율을 산정한 결과, 각 지반 조건에 대해서 3종류의 SVM 분류 함수 중 전체적으로 RBF SVM의 예측 결과가 가장 우수하고, 지반 조건별로 구분 시 디스크 커터 교체 데이터의 수가 많을수록 예측 결과가 좋은 것으로 나타났다.
2. SVM 예측의 정확도는 풍화암이 많은 혼합층(Ground type 1)에 대해서 82%~85%의 범위로 가장 높은 반면, 풍화암층(Ground type 2)에 대해서 74%~77%의 범위로 가장 낮게 나타났다. 그러나 SVM의 정밀도는 전체적으로 50% 내외의 상대적으로 낮은 수치를 나타내었다. 그리고 오분류율의 경우는 4개 지반 조건, 3종류 분류 함수에 대해서 2%~17%를 나타내었다. 결과적으로, 실제 현장 데이터에서 교체 데이터의 수가 비교체 데이터의 수에 비해 매우 적기 때문에 실제 데이터 중 교체 데이터만을 이용하여 산정되는 정밀도를 기준으로 한 경우에 교체와 비교체 데이터 모두를 기준으로 산정되는 정확도와 오분류율에 비해 상대적으로 SVM의 신뢰도를 낮게 평가하게 된 것으로 판단된다.
3. 이상의 결과로부터, TBM 디스크 커터의 적정 교환 주기를 예측하는 방법으로서 SVM과 같은 머신러닝 알고리즘이 이용될 수 있으며, 많은 데이터를 축적하고 이를 모두 활용하여 학습모델을 지속적으로 발전시켜 나간다면 실무 적용성이 매우 클 것으로 기대한다.