1. 서 론
2. 추력과 토크 산정식들
2.1 일본의 계산방법(JSCE, 2007)
2.2 수정된 일본 모델 계산 방법
2.3 CSM (Colorado School of Mines) 계산 방법(Rostami and Ozdemir, 1993)
2.4 NTNU (Norwegian University of Science and Technology) 계산 방법(Bruland, 2000)
3. 모델 비교 및 고찰
4. 결 론
1. 서 론
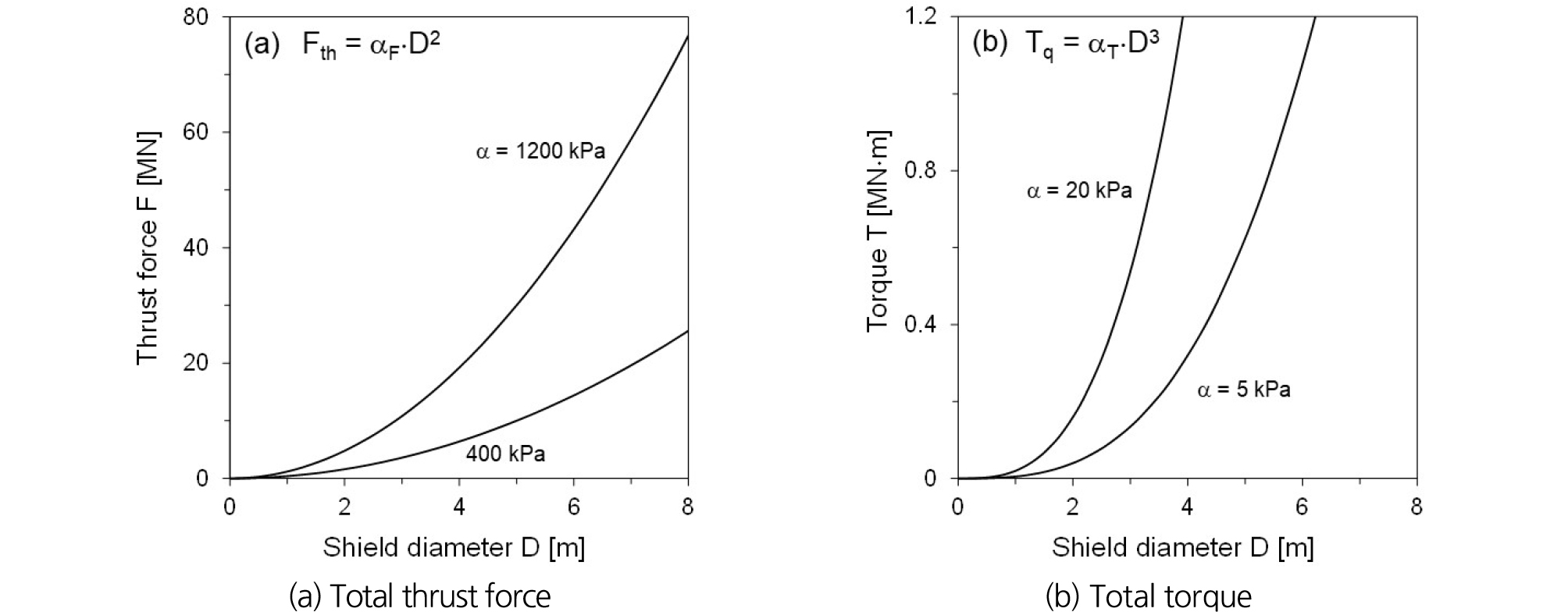
기계식 굴착장비의 하나인 쉴드 TBM (Tunnel Boring Machine) 설계 및 제작에 있어서 가장 핵심적인 부분은 디스크 커터 개수, 커터 배치, 커터 간격, 개구율 등을 고려한 TBM 전면의 커터헤드 설계와 TBM의 굴진 성능에 영향을 미치는 장비의 추력(Thrust)과 토크(Torque)이다. 최근 TBM 설계 당시의 오류로 시공 중 추력과 토크가 부족한 상황이 발생하는 일들이 보고되고 있다(Bilgin and Algan, 2012; Ates et al., 2014). 이처럼 쉴드 TBM을 안정적으로 굴착하기 위해 필수적인 전체 추력(Total thrust force, Fth)과 전체 토크(Torque, Tq)에 대한 설계는 Fig. 1과 같이 지반 조건을 포함한 경험적 인자()와 TBM 직경(D)만을 이용하여 산정되어 왔다(JSCE, 2007). 예를 들어, 직경 6.3 m급 쉴드 TBM에서 추력은 약 20~43 MN까지 매우 넓은 범위의 불확정적인 값을 보여주며 이는 궁극적으로 최적의 추력 유압 시스템을 설계하고 적절한 유압 부품들을 선택하는데 있어서 어려움을 야기한다. 그러므로 쉴드 TBM으로 굴착 시 장비에 가해지는 힘에 영향을 미치는 요소인 지반 조건(굴착깊이, 지하수위, 일축 압축 강도, 횡토압 계수 등), 장비 인자(TBM 직경, TBM 쉴드 프레임 길이, 개구율 등), 운전인자를 반영하여 추력과 토크를 산정하여야 한다. 국내에서는 암반 지반에 적합한 미국 CSM (Colorado School of Mines)모델과 노르웨이 과학기술대학(Norwegian University of Science and Technology, NTNU)에서 개발한 NTNU 모델을 이용하여, 쉴드 TBM의 굴진성능 향상 및 예측을 위한 연구를 수행하였다(Choi et al., 2011; Chang et al., 2013). 또한, 굴착으로 인한 토사 지반의 응력 이완을 반영한 일본의 추력 산정식을 통해 급곡선 구간 시공 시 쉴드 TBM의 구조적 안정성을 검토하였다(Kang et al., 2017). 본 연구에서는 TBM 설계를 위해 이용되고 있는 4가지 추력과 토크 계산식들을 구체적으로 설명하고 정리하였다(토사 지반 적용 - 일본식과 수정된 일본식 모델; 암반 지반 적용 - CSM과 NTNU 모델). 또한, 각각의 방법들을 이용해서 구한 값들을 비교 및 고찰하였다.
2. 추력과 토크 산정식들
2.1 일본의 계산방법(JSCE, 2007)
2.1.1 쉴드 TBM 주변에 작용하는 흙의 응력산정
쉴드 TBM 주변에 작용하는 응력을 산정하기 위해서는 먼저 굴착으로 인해서 터널 상부부터 지표면까지 감소되는 흙의 응력 이완을 반영하여 깊이에 따른 연직 방향 응력을 산정하여야 한다. 지표면과 터널 상부 사이에 미소 요소를 설정하여 주변에 작용하는 힘의 평형을 구하면 다음과 같다(Fig. 2).
| $$\sum_{}^{}F_y=0\rightarrow\sigma'_v\cdot2B_o-(\sigma'_v+d\sigma'_v)\cdot2B_o+\gamma'\cdot2B_o\cdot dh-2(\sigma'_v\cdot ka\cdot u+c)dh=0$$ | (1) |
여기서, 는 터널 상부까지 거리(m), 는 흙의 마찰 계수, 는 흙의 점착력(kPa), 는 흙의 수중 단위 중량(kN/m3), 그리고 는 주동 토압 계수를 의미한다.
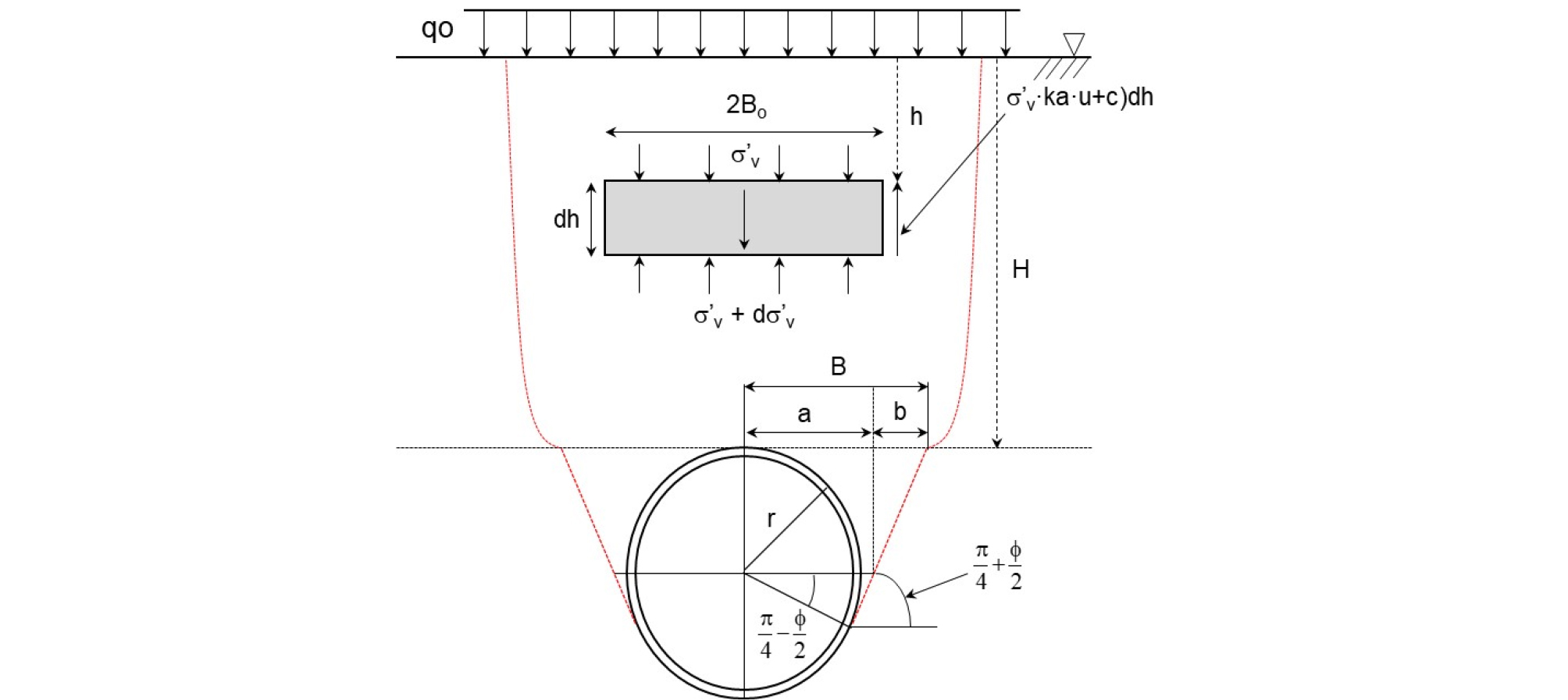
Fig. 2.
Free body diagram of stress relaxation and failure line induced by underground excavation (modified from JSCE, 2007)
특히, 굴착 시에 터널 주변에서 발생하는 아칭 효과(Arching effect)와 터널 측부 근처 흙의 응력 이완으로 인해서, 흙이 터널 방향으로 이동하므로 주동 파괴(active failure)가 발현된다. 양변을 를 나누고, 식 (1)을 정리하면 다음과 같은 1계 선형 비동차 미분 방정식(1st order linear nonhomogeneous differential equation)을 얻게 된다.
| $$\frac{d\sigma'_v}{dh}+\frac{ka\cdot u}{B_o}\cdot\sigma'_v=\gamma'-\frac c{B_o}$$ | (2) |
식 (2)의 해를 구하면, 다음과 같다.
| $$\sigma'_v=e^{-\frac{ka\cdot u}{B_o}\cdot h}\cdot\left[\frac{B_o}{ka\cdot u}\cdot e^{\frac{ka\cdot u}{B_o}\cdot h}\cdot\left(\gamma'-\frac c{B_o}\right)+A\right]$$ | (3) |
지표면에서 상재하중이 가해지는 경계 조건()을 식 (3)에 적용하여, 적분 상수 를 구하고 식을 표현하면 다음과 같다.
| $$\sigma'_v=\frac{B_o}{ka\cdot u}\cdot\left(\gamma'-\frac c{B_o}\right)\cdot\left(1-e^{-\frac{ka\cdot u}{B_o}\cdot h}\right)+qo\cdot e^{-\frac{ka\cdot u}{B_o}\cdot h}$$ | (4) |
식 (4)를 이용하여, TBM 상부에 작용하는 연직 방향 유효 응력을 구하면 다음과 같다(, , ).
| $$\sigma'_v=\frac B{ka\cdot u}\cdot\left(\gamma'-\frac cB\right)\cdot\left(1-e^{-\frac{ka\cdot u}B\cdot H}\right)$$ | (5) |
여기서, 는 터널 중앙에서부터 터널 측부의 주동 파괴선까지의 거리로서, 삼각형 내부 각들의 관계를 이용하여 구하였다.
| $$B=a+b=r\cdot\left[\frac1{\sin\left(\frac\pi4+\frac\phi2\right)}+\frac1{\tan\left(\frac\pi4+\frac\phi2\right)}\right]=r\cdot\cot\left(\frac{\pi/4+\phi/2}2\right)$$ | (6) |
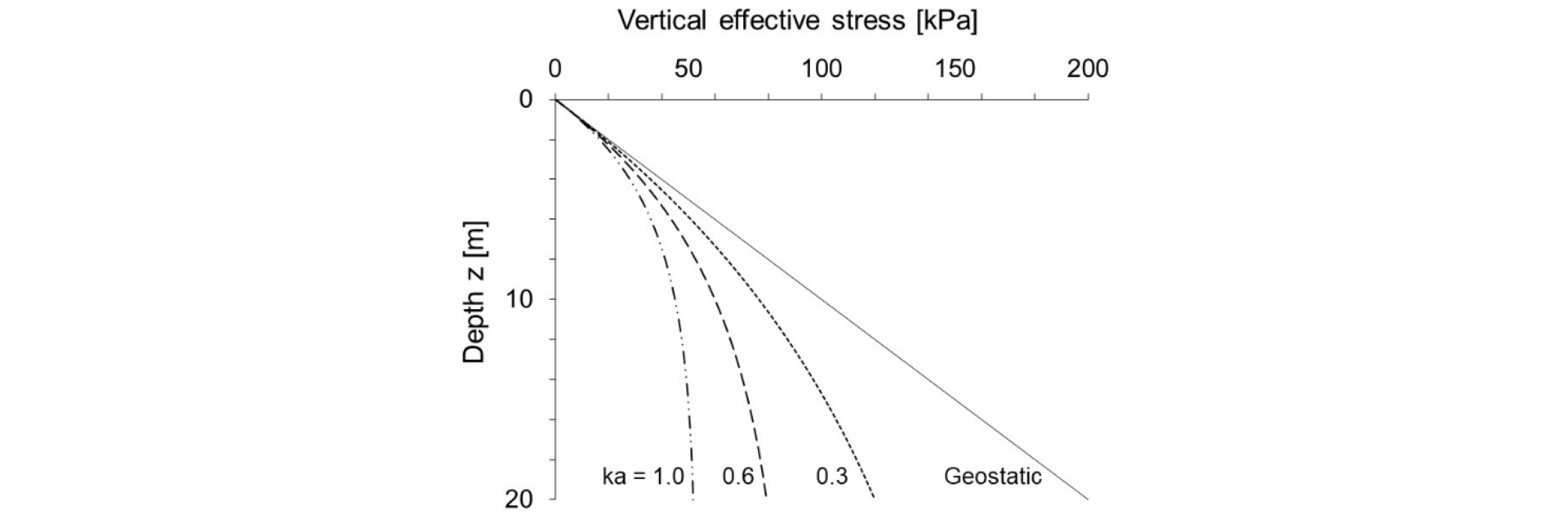
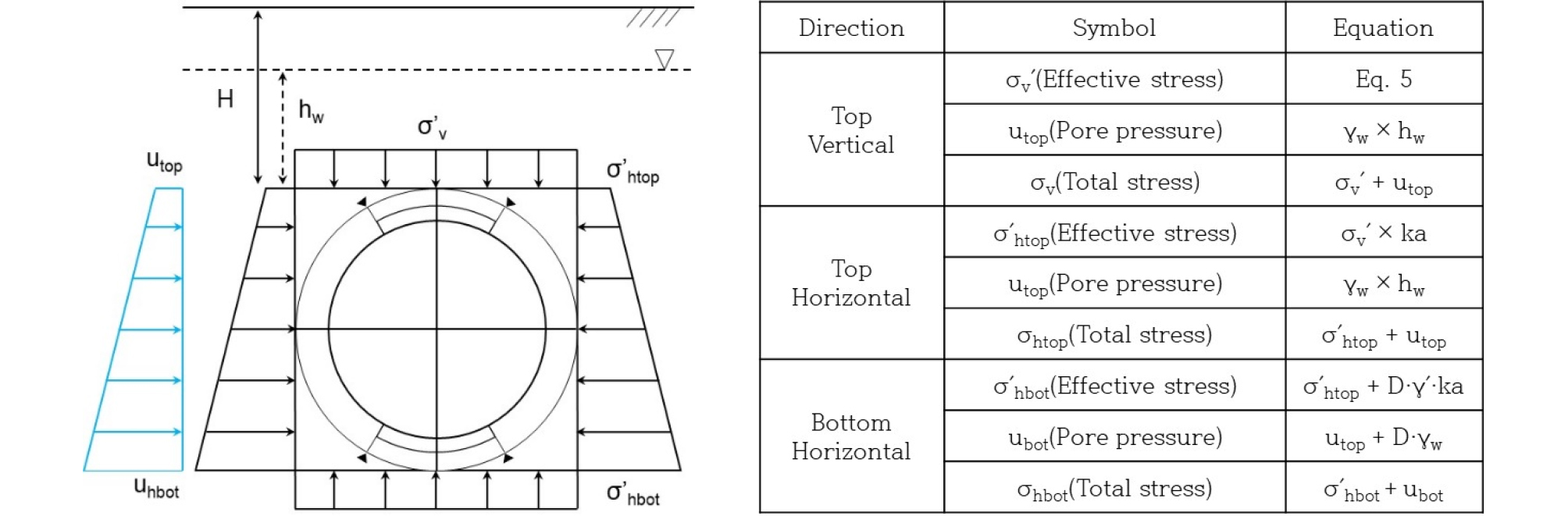
굴착으로 인한 터널 상부에서부터 발현되는 흙의 유효 응력 이완을 정략적으로 분석하였다(Fig. 3). 굴착 이전(Geostatic)과 비교하여 깊이에 따라서 흙의 유효 응력이 감소하였으며, 그 크기는 주동 토압 계수 값이 클수록 더 감소하였다. 실제 터널 굴착으로 인한, 터널 주변에서부터 지표면까지 횡방향 토압 계수는 흙의 변위 정도에 따라서 변하기 때문에 추정하기가 어렵다. 예를 들어서, 터널 상부에서는 굴착으로 인한 주변 흙의 응력 이완으로 인해서, 흙의 변위가 크게 발생하므로, 주동 토압 계수를 적용해야 하지만, 지표면 근처에서는 흙의 응력 및 변위를 발생시키지 못하므로, 정지 토압 계수를 적용하여야 한다. TBM 전면 주변에 작용하는 흙의 유효 응력과 정수압 분포들은 Fig. 4와 같이 가정하였다(관련된 식들은 Fig. 4와 함께 정리하였으며, 다음 섹션에서 설명할 추력 계산식에 사용되었다). TBM 상부에 작용하는 수직 방향 유효 응력은 식 (5)를 이용하여, 터널 직경에 상관없이 등분포를 가정하였으며, TBM 바닥면은 직경만큼의 유효 응력 증가를 고려하였다.
2.1.2 추력
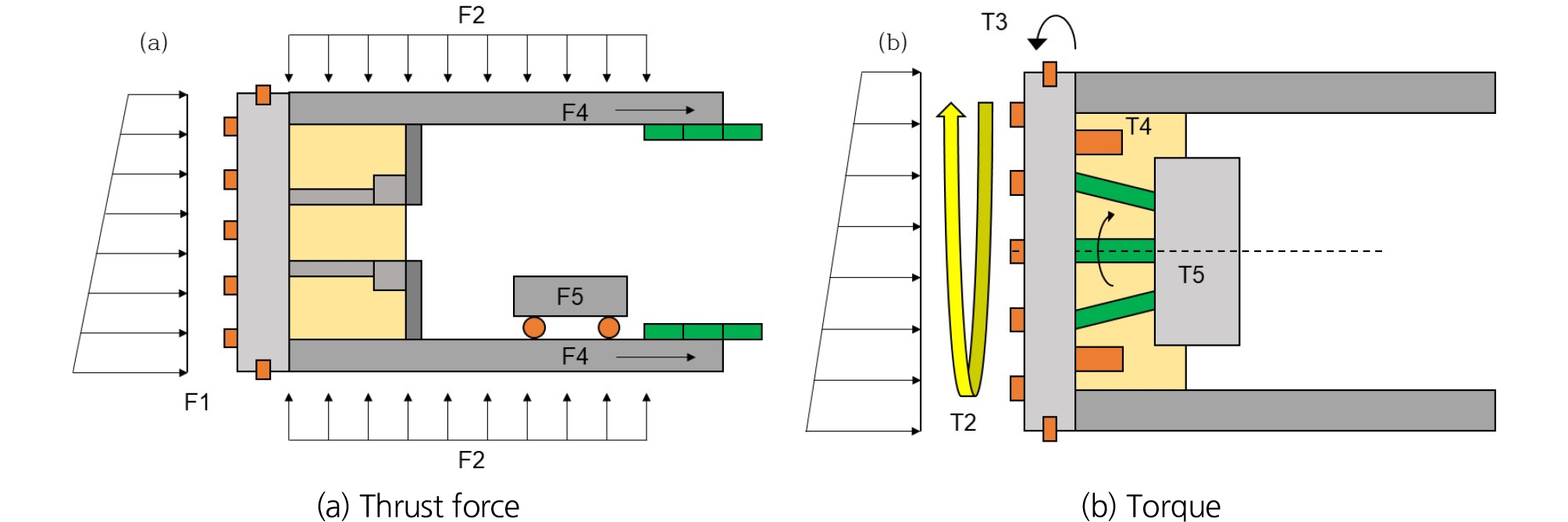
밀폐형 쉴드 TBM에 필요한 설계 추력은 Fig. 5(a)에서 보는 바와 같이 크게 5가지 성분의 합으로 계산된다(JSCE, 2007). 먼저, 쉴드 전면에 가해지는 토압(F1)은 면판에 작용하는 횡방향 전응력()과 커터헤드 면적()을 곱하여 구하였다.
| $$F_1=\sigma_{h-avg}\cdot A_1=\frac{\pi\cdot D^2}4\cdot\left[\left(\frac{\sigma_{htop}+\sigma_{hbot}}2\right)\cdot(1-\rho)+p_c\cdot\rho\right]$$ | (7) |
여기서, 는 챔버압과 는 개구율을 의미한다. 또한, 쉴드 외면과 주변 흙 사이의 마찰 저항력(F2)은 쉴드 외경에 작용하는 평균 유효 응력 을 이용하여 다음과 같이 구하였다.
| $$F_2=\sigma'_m\cdot A_2\cdot\mu_1=\left[\frac{2\sigma'_v+\sigma'_{htop}+\sigma'_{hbot}}4\right]\cdot\pi\cdot D\cdot L\cdot\mu_1$$ | (8) |
여기서, 은 쉴드 프레임 길이(m), 은 쉴드와 주변 지반의 마찰 계수를 의미한다. 특히, 쉴드 주면 토압의 경우에는 전면 마찰 저항과 다르게, 횡방향 응력 산정 시에 정수압의 영향을 제거해 주었다. 국내 지반 특성상 암반지반 굴착 시, 암반 파쇄가 추가적으로 필요하므로, 암반의 일축 압축 강도 과 디스크 커터 재원(순 관입 면적 과 총 커터 개수 )을 반영하여, 암반 파쇄 추력()을 결정하였다. 세그먼트와 쉴드 프레임 마찰 저항(F4)과 백업카 이송 저항(F5)은 현장의 장비 운영에 따라 제외되거나, 총 설계 추력에 비하여 차지하는 비율이 약 2% 미만이므로, 추력성분들에서 제외하였다. 토사와 암반의 경계부나 급곡선 굴진 시에는 일부 추력 성분들의 비율을 조성하여 전체 설계 추력을 계산하여야 한다(Kang et al., 2017).
2.1.3 토크
밀폐형 쉴드 TBM에 필요한 설계 토크는 크게 5가지 성분의 합으로 계산된다(Fig. 5(b)). 우선, 면판에 설치된 디스크 커터들에 작용하는 하중에 의해서 산정이 되는 커터 절삭 토크 T1은 이론적으로 각각의 디스크 커터의 모멘트 하중의 합(각각의 디스크 커터 회전하중과 면판 중심부에서부터 설치된 디스크 커터까지의 거리의 곱들의 합)으로 구해야 한다. 하지만, 디스크 커터들의 회전 하중과 모멘트 거리를 구하는 어려움 등이 있으므로, 다음과 같이 근사식으로 구하였다.
| $$T_1\approx F_r\cdot N_c\cdot\frac r2=\lbrack\sigma_c\cdot w_{cutter}\cdot p\cdot f\rbrack\cdot N_c\cdot\frac r2$$ | (9) |
여기서, 는 전체 디스크 커터 개수, 은 디스크 커터들의 산술 평균 회전 하중으로서, 암반의 일축 압축 강도 , 디스크 커터의 너비 와 관입 깊이 , 그리고 커터 회전 마찰 계수 로 산정된다. TBM 면판 전면 마찰 저항 토크 T2 (전면 토크)는 전면부의 횡방향 평균 유효 응력을 고려하여, 다음과 같이 표현된다.
| $$T_2=\frac{\pi\cdot D^3\cdot(1-\rho)}{12}\cdot\left(\frac{\sigma'_{htop}+\sigma'_{hbot}}2\cdot\mu_1\right)$$ | (10) |
여기서, 는 커터헤드 개구율(Cutterhead opening ratio)로서, 커터헤드 개구부와 전체 커터헤드 면적비(Area ratio)로 계산이 된다. TBM 면판 종류에 따른 개구율 차이는 실제로 면판 전면부에 작용하는 횡토압과 수압의 크기와 분포를 다르게 하지만, 본 논문에서는 이러한 영향들은 고려하지 않았다. 또한, 커터 외경에서 발생하는 저항 토크 T3는 다음과 같다.
| $$T_3=\frac{\pi\cdot D^2\cdot B_g}2\cdot\left(\frac{2\sigma'_v+\sigma'_{htop}+\sigma'_{hbot}}4\cdot\mu_1\right)$$ | (11) |
여기서, 는 커터 헤드의 두께(m)를 의미한다. 이외에, 굴착된 흙이 스크류 컨베이어(Screw conveyor)로 배토를 용이하게 하기 위해서 설치된 챔버(Chamber)내부에서 발생하는 교반 저항 T4와 구동부에 설치된 베어링 마찰 저항 T5는 계산 시에 요구되는 많은 입력 변수들의 불확실성과 설계 토크에 비하여 차지하는 비율이 낮으므로, 토크 성분들에서 제외하였다(Zhou and Zhai, 2018).
2.2 수정된 일본 모델 계산 방법
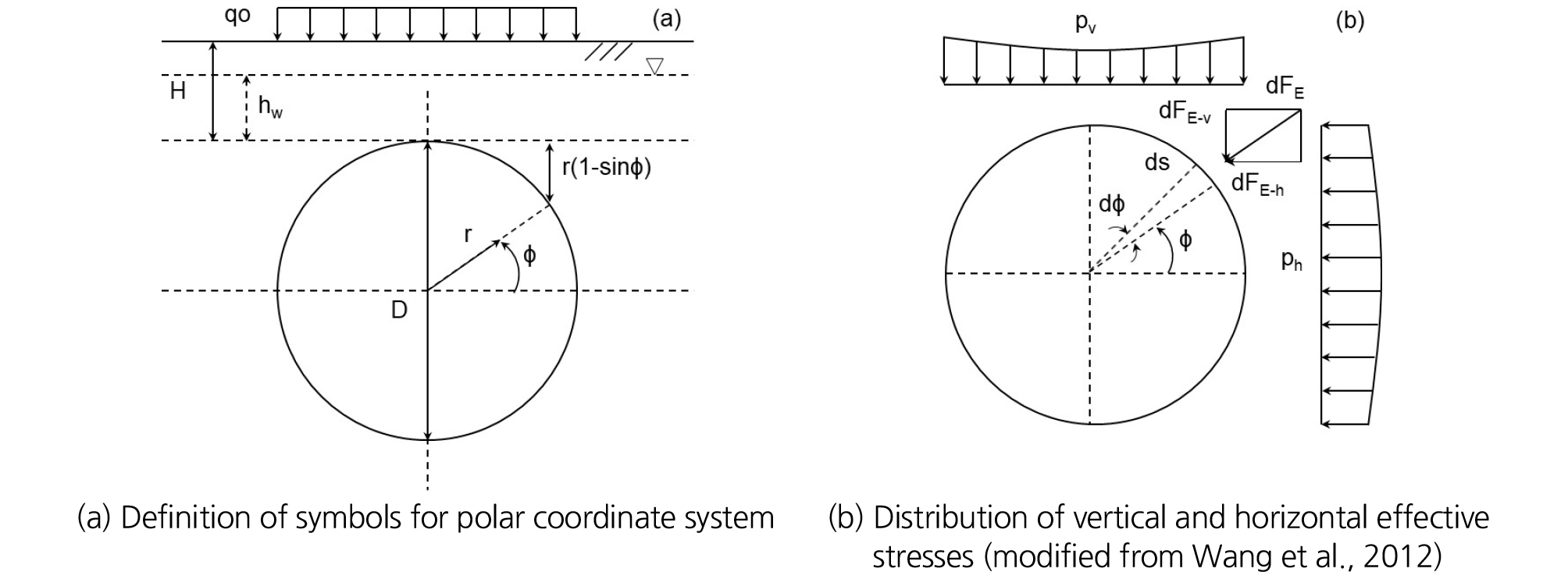
이전에 제시된 일본식 추력과 토크 계산 방법은 TBM 상부와 측면에 작용하는 유효응력을 TBM 직경에 따른 크기의 변화를 고려하지 않았다. 본 섹션에서 소개할 추력과 토크 산정식들은 이러한 부분을 수학적으로 반영하였다(Shi et al., 2011; Wang et al., 2012).
2.2.1 추력
TBM 전면 터널 직경에 따라 변하는 저항력 F1은 극좌표계를 이용하여, 정수압 F11과 횡방향 유효 응력 F12를 다음과 같이 유도하였다(Fig. 6(a)).
| $$F_{11}=\int_0^{2\pi}\int_0^\frac D2\gamma_w\cdot\lbrack h_w+r(1-\sin\phi)\rbrack\cdot rdrd\phi=\frac{\pi\cdot D^2}4\cdot\gamma_w\cdot\left(h_w+\frac D3\right)$$ | (12a) |
| $$F_{12}=\int_0^{2\pi}\int_0^\frac D2ka\cdot\gamma'\cdot\lbrack h_w+r(1-\sin\phi)\rbrack\cdot rdrd\phi=\frac{\pi\cdot D^2}4\cdot\gamma'\cdot ka\cdot\left(h_w+\frac D3\right)$$ | (12b) |
지표면 위에 상재 하중 로 인해서 발생하는 추가적인 전면 하중 F13, 면판 개구율, 그리고 챔버압 을 고려하여 식을 다음과 같이 나타내었다.
| $$F_1=\frac{\pi\cdot D^2}4\left[\left\{\gamma w\cdot\left(h_w+\frac D3\right)+\gamma'\cdot ka\cdot\left(h_w+\frac D3\right)+ka\cdot qo\right\}\cdot(1-\rho)+p_c\cdot\rho\right]$$ | (13) |
쉴드 주면 마찰 저항 F2를 유도하기 위해서 필요한 상부에 작용하는 수직 유효 응력 와 측부에 작용하는 수평 유효 응력 를 다음과 같은 수식으로 표현하였으며, 그 분포들은 Fig. 6(b)와 같이 간략히 도시하였다.
| $$p_v=\gamma'\cdot\left[H+\frac D2(1-\sin\phi)\right]$$ | (14a) |
| $$p_h=\gamma'\cdot ka\cdot\left[H+\frac D2(1-\sin\phi)\right]$$ | (14b) |
식 (14a)와 (14b)를 이용하여, 터널 상부와 측부에 작용하는 각각의 힘들을 구하면 다음과 같다.
쉴드 직경과 프레임을 따라서 가해지는 토압으로 인해서 발생하는 쉴드 주면 마찰 저항 F2는 다음과 같이 표현된다.
| $$F_2=4\cdot(F_{E-v}+F_{E-h})\cdot L\cdot\mu_1=\gamma'\cdot D\cdot L\cdot\left[\frac\pi2\cdot(1+ka)\cdot H+\frac\pi4\cdot(1+ka)\cdot D-\frac D3\cdot(2+ka)\right]\cdot\mu_1$$ | (16) |
암반 파쇄 추력 F3 ()는 일본식을 그대로 이용하였다.
2.2.2 토크
디스크 커터 하중에 의해 산정되는 커터 절삭 토크 T1 ()은 일본식 계산법을 그대로 이용하였다. TBM 전면에 발생하는 전면 토크 T2는 추력과 마찬가지로 극좌표계를 이용하여, 면판 개구율을 고려한 전면 토크를 다음과 같이 유도하였다.
쉴드 외경 토크 T3은 수직 유효 응력 (식 (14a))과 수평 유효 응력 (식 (14b))를 이용하여, 커터헤드 두께를 따라 가해지는 터널 상부와 측부에 작용하는 토크를 구하면 다음과 같다.
| $$T_v=\int_0^{2\pi}p_v\cdot\underbrace{\frac D2\cdot d\phi}_{ds}\cdot\sin\phi\cdot\sin\phi\cdot\frac D2=\frac{\pi\cdot D^2}4\cdot\gamma'\cdot\left(H+\frac D2\right)$$ | (18a) |
| $$T_h=\int_0^{2\pi}p_h\cdot\underbrace{\frac D2\cdot d\phi}_{ds}\cdot\cos\phi\cdot\cos\phi\cdot\frac D2=\frac{\pi\cdot D^2}4\cdot\gamma'\cdot ka\cdot\left(H+\frac D2\right)$$ | (18b) |
| $$T_3=(T_v+T_h)\cdot B_g\cdot\mu_1=\frac{\pi\cdot D^2}4\cdot\gamma'\cdot B_g\cdot\left[H\cdot(1+ka)+\frac D2\cdot(1+ka)\right]\cdot\mu_1$$ | (18c) |
2.3 CSM (Colorado School of Mines) 계산 방법(Rostami and Ozdemir, 1993)
CSM 모델은 장기간 축적된 현장 자료와 실물 크기의 LCM (Linear Cutting Machine) 실험으로부터 얻은 방대한 자료를 근거하여 제시된 암반 절삭력을 이용하여, TBM 굴진 성능 예측을 할 수 있다(Rostami and Ozdemir, 1993; Rostami, 1997). TBM 면판에 설치된 디스크 커터에 작용하는 힘으로 인해서 발생하는 커터 관입 깊이, 암반내의 절삭 압력 분포, 그리고 관련된 기하학적 조건들을 Fig. 7과 같이 도시하였다. 커터 반경과 관입 깊이를 이용하여, 암반과 커터 사이의 접촉 면적과 연관 있는 입사각 (Incidence angle)을 다음과 같이 표현하였다.
| $$\phi=\cos^{-1}\left(\frac{R-p}R\right)$$ | (19) |
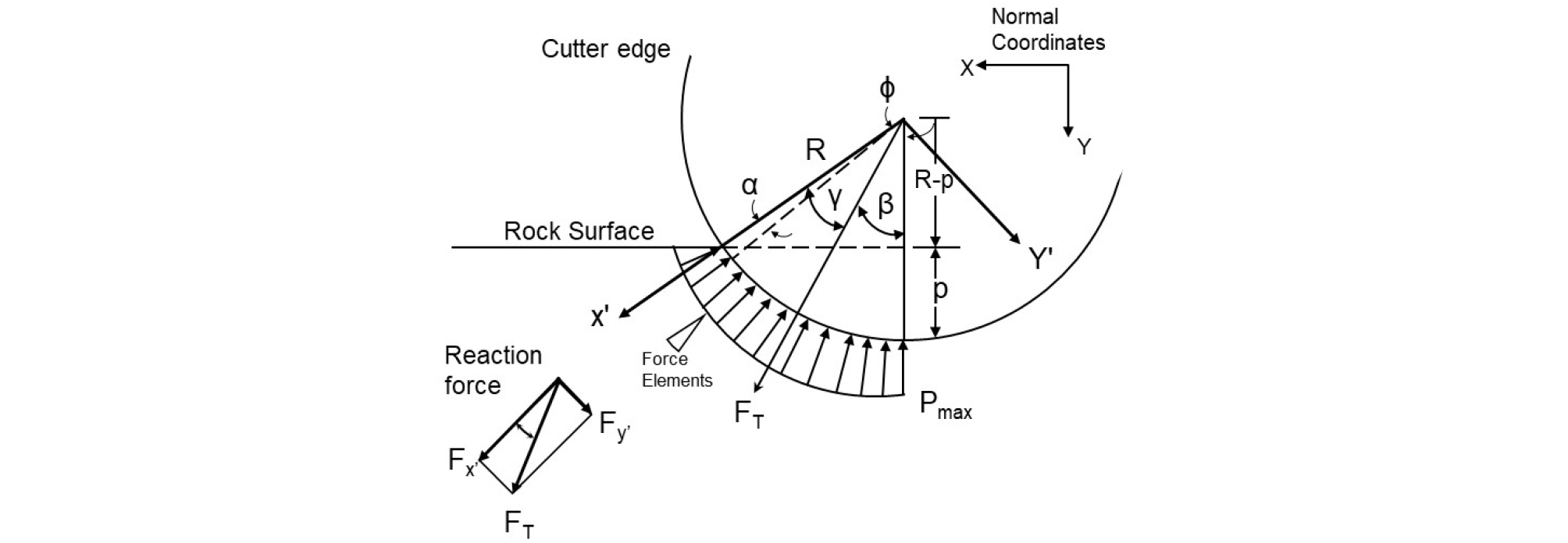
Fig. 7.
Pressure distribution and geometric condition of rock surface cutting with disc cutter (modified from Rostami and Ozdemir, 1993)
디스크 커터 절삭 압력은 입사각, 절삭 지반 조건, 그리고 커터 종류 등에 따라서 다양한 분포를 가지게 된다. 일반화된 절삭 압력은 다음과 같은 수식으로 표현할 수 있다.
여기서, 는 0에서 까지 변하는 입사각, 는 커터 사이의 간격, 는 커터팁 폭, 는 암석 인장 강도, 그리고 는 무차원 계수(≈2.12)를 의미한다. 특히, 압력 형상 계수 는 절삭 압력 분포를 결정한다. 커터의 종류에 따라서 -0.2 (wider tip cutter)~0.2 (V-shape cutter) 까지의 범위를 보인다. 또한, 절삭 암반등의 다른 조건에 따라서 등분포( = 0), 직선 분포( = 1), 그리고 비선형 분포(0 < < 1)를 가지게 된다. 또한, 다른 함수의 형태로 절삭 압력 분포를 가정할 수가 있다(Labra et al., 2017). 절삭면에 작용하는 두 개의 반력을 바뀐 좌표계에서 와 를 일반화된 절삭 압력 함수인 식 (20)을 사용하여 적분식을 유도하고, 테일러 시리즈(Taylor series)를 이용하여 근사적으로 정적분을 계산하고, 반력들의 작용하는 방향 를 표현하면 다음과 같다.
| $$F_{y'}=\int_0^\phi dF\sin\alpha=\int_0^\phi TRp_{max}\left(\frac\alpha\phi\right)^\lambda d\alpha\cdot\sin\alpha=\sum_{i=o}^n(-1)^{i-1}\frac{\phi^{2i+\lambda+2}}{(2i+\lambda+2)(2i+1)}$$ | (21b) |
| $$\gamma=\tan^{-1}\left(\frac{F_{y'}}{F_{x'}}\right)$$ | (22) |
추력과 토크 계산을 위해서는 직교 좌표계에서 전체 합력 의 작용점을 산정해야 한다. 커팅 계수 (Cutting Coefficient)는 회전하는 힘과 연직방향 힘의 비로서, 각에 의해서 다음과 같이 표현된다.
| $$CC=\tan\beta\;\mathrm{where},\;\beta=\tan^{-1}\lbrack\tan(\phi-\gamma)\rbrack$$ | (23) |
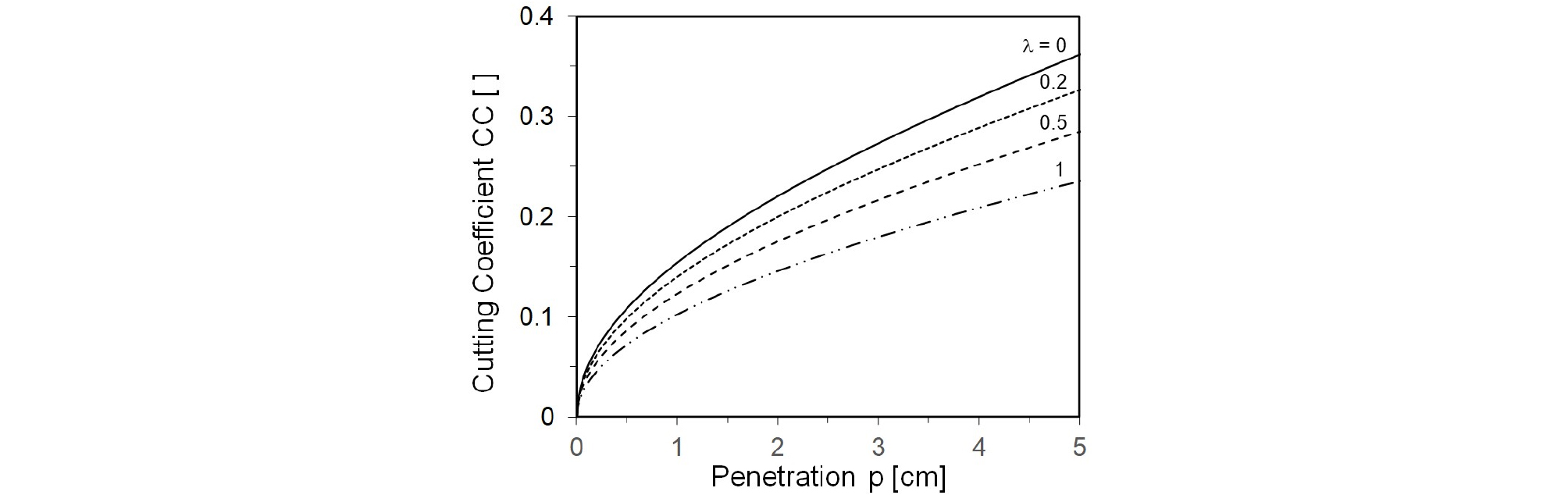
Fig. 8은 관입 형상 계수 에 따른 커터 관입 깊이 와 커팅 계수 의 변화를 보여준다. 관입 깊이가 증가함에 따라서 커팅 계수는 증가한다. 또한, 등분포 압력 분포 형상( = 0)은 같은 관입 깊이일 때, 상대적으로 높은 값을 보여주며, 그 크기는 관입 깊이가 클수록 증가하였다. 절삭 암반에 작용하는 전체 합력은 식 (24)를 이용하여 다음과 같이 구할 수가 있다.
또한, 등분포 압력 분포 형상( = 0)은 같은 관입 깊이일 때, 상대적으로 높은 값을 보여주며, 그 크기는 관입 깊이가 클수록 증가하였다. 절삭 암반에 작용하는 전체 합력은 식 (20)을 이용하여 다음과 같이 구할 수가 있다.
전체 커터 작용 합력 으로부터 얻어진 수직 방향 힘 과 회전하는 힘 은 절삭 압력의 등분포 가정을 이용하여(; 전체 합력의 작용점은 접촉 면적의 중앙점에 위치), 다음과 같이 추력 과 토크 계산식을 표현할 수가 있다.
| $$F_{th}=N_c\cdot F_T\cdot\cos\left(\frac\phi2\right)$$ | (25a) |
| $$T_q=0.3\cdot N_c\cdot D\cdot F_T\cdot\sin\left(\frac\phi2\right)$$ | (25b) |
2.4 NTNU (Norwegian University of Science and Technology) 계산 방법(Bruland, 2000)
NTNU 모델은 노르웨이 과학기술대학(Norwegian University of Science and Technology, NTNU)에서 개발된 방법으로, 노르웨이 지반조건에 대해 수십 년간 축적된 현장자료 및 시험자료에 근거하여 제시된 등가균열계수, DRI (Drilling Rate Index), 그리고 CLI (Cutter Life Index)등의 경험적인 관계들을 이용하여, TBM 굴진 성능을 예측할 수가 있다(Bruland, 2000). 본 연구에서는 추력과 토크 산정 시에 필요한 그래프들의 함수를 선형 회귀 분석을 통해 구하였으며, 해당 그림과 함께 나타내었다. 설계 추력은 다음과 같은 식에 의해서 구할 수가 있다.
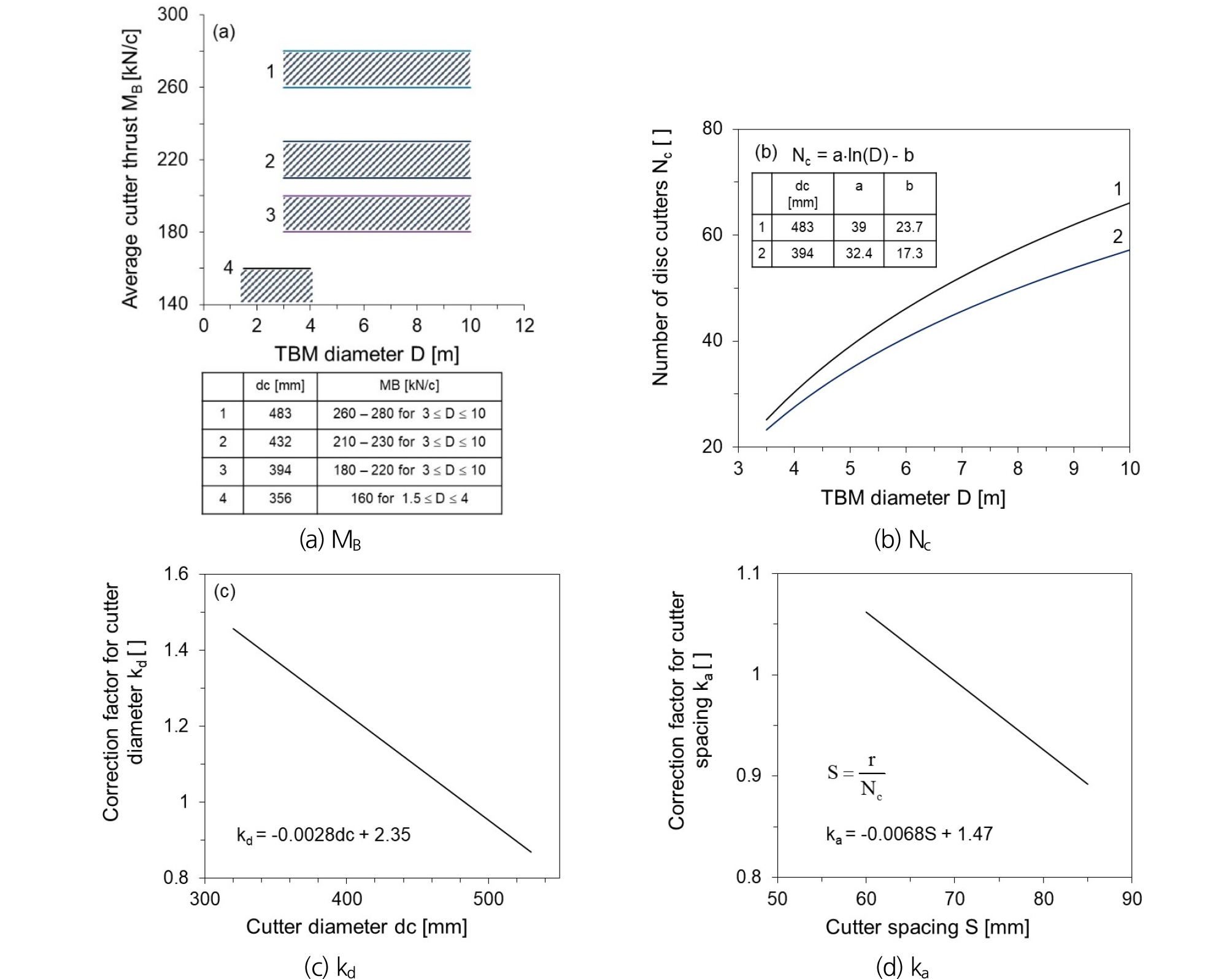
| $$F_{th}=N_c\cdot M_B\cdot k_d\cdot k_a$$ | (26) |
여기서, 는 디스크 커터당 최대 평균 추력(kN/c), 는 커터 직경 계수, 그리고 는 커터 간격 계수를 의미한다. 초기 면판 설계 단계에서 가정된 장비 인자(커터 직경 와 TBM 직경 )를 Fig. 9를 이용하여 필요한 계수들을 산정하면, 설계 추력을 경험적으로 구할 수가 있다.
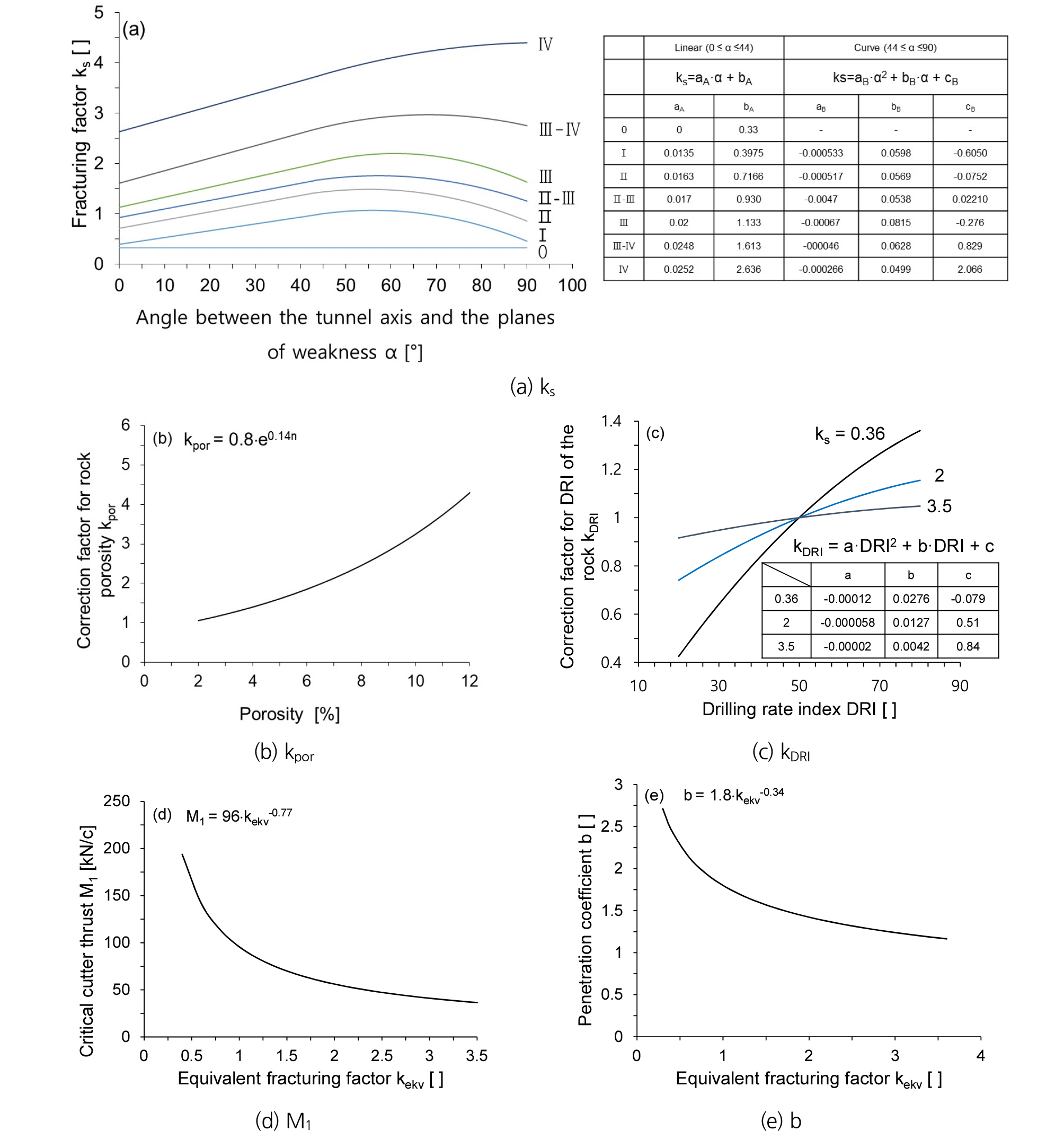
설계 토크는 상대적으로 많은 경험적 계수들이 필요하다. 우선, 암반의 파쇄 정도를 나타내는 파쇄 인자 는 파쇄의 등급과 터널 축이 연약면과 이루는 각도 에 의해서 산정이 된다(Fig. 10(a)). 연약면과 이루는 각도는 주향각과 경사각으로 다음과 같이 표현된다.
| $$\alpha=\arcsin\lbrack\sin\alpha_f\cdot\sin(\alpha_t-\alpha_s)\rbrack$$ | (27) |
여기서, 는 경사 각, 는 주향 각, 는 터널 굴착 방향이다. 하나 이상의 연약면들에 대한 전체 균열 인자는 다음과 같이 계산된다.
| $$k_s=\sum_{i=1}^nk_{si}-(n-1)\cdot0.36$$ | (28) |
파쇄 인자 이외에 암반 공극률 계수 (Fig. 10(b))와 암석의 천공 용이도를 평가하기 위한 DRI 계수 (Fig. 10(c))를 이용하면, 다음 식으로부터 등가 파쇄 요소 를 구할 수가 있다.
| $$k_{ekv}=k_s\cdot k_{DRI}\cdot k_{por}$$ | (29) |
또한, 임계 커터 추력 M1 (1 mm 관입에 필요한 추력)과 관입 계수 는 등가 파쇄 요소 로부터 Fig. 10(d)와 10(e)를 이용하여 구할 수가 있다. 따라서 순 굴진율 는 커터 헤드 회전 속도 RPM을 사용하여, 다음과 같이 표현할 수가 있다.
| $$I=p\cdot\mathrm{RPM}=\left(\frac{M_{ekv}}{M_1}\right)^b\cdot\mathrm{RPM}$$ | (30) |
여기서, 는 등가 추력을 의미한다. 따라서 설계 토크는 다음 식을 이용하여 산정된다.
| $$T_q=0.3\cdot D\cdot N_c\cdot(M_B\cdot k_c)\;\mathrm{where},\;k_c=5\cdot dc^{-0.79}\cdot\sqrt p$$ | (31) |
여기서, 는 커터 계수로서, 커티 직경과 순 관입율로 산정된다.
3. 모델 비교 및 고찰
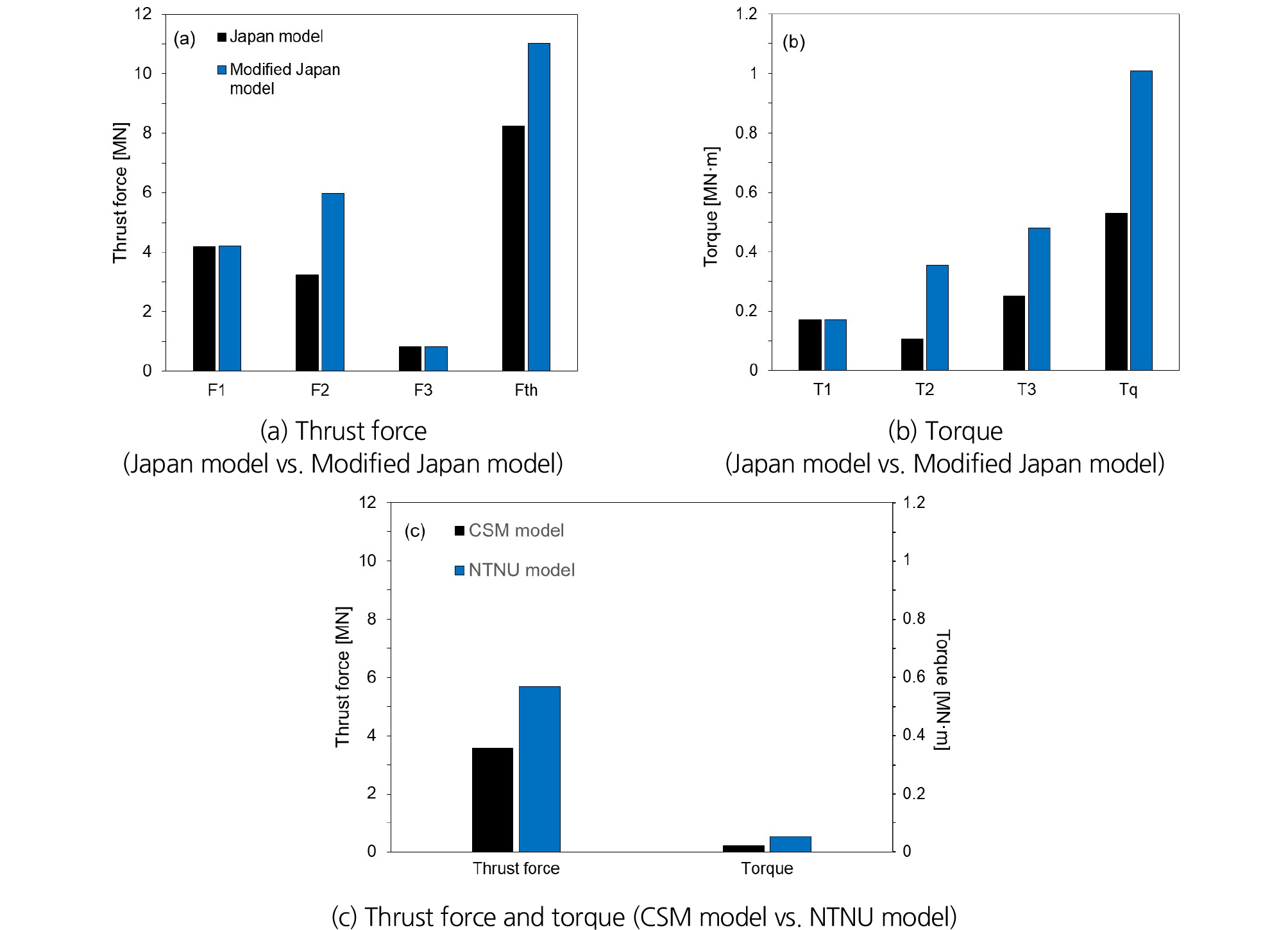
본 연구에서 소개한 4가지 방법을 이용하여 설계 추력과 토크를 계산하였다. 사용된 입력 물성치들은 장비인자, 운전 인자, 그리고 지반인자로 분류하여 Table 1과 같이 정리하였다. Fig. 11에서 보는 바와 같이 TBM 주변에 작용하는 토압을 고려한 일본의 계산 방법과 수정된 일본 모델의 계산 방법으로 계산한 추력 값들에서, 전면부에 작용하는 추력 F1은 비슷한 값을 보였으나, 쉴드 외면과 주변 흙 사아의 마찰 저항력 F2값이 약 2 MN 차이를 보였다(암반 파쇄 추력 F3는 동일한 식을 사용하므로, 같은 값을 가진다). 토크의 경우, 쉴드 전면 토크 T2와 외경 토크 T3가 각각 약 0.2 MN ‧ m 차이를 보였다. 이러한 차이는 본 연구의 수정된 일본 모델 계산 방법이 TBM 직경에 따라서 변하는 수직 유효 응력과 수평 유효 응력을 반영하여, 굴착 시 터널 주변에 발생하는 흙의 응력 이완을 일본식보다 더 고려해 주었기 때문이다. 암반 지반에 적용 가능한 CSM 방법과 NTNU 방법은 전체 추력과 토크에서 값들의 차이를 보였지만, 이는 산정 시 필요한 계수들의 불확실성(터널축과 연약면의 각 로 인한 파쇄 요소)과 낮은 상관 관계의 경험식(일축 압축 강도와 DRI 상관관계) 들로 인해서 야기된 것으로 판단된다. 이런 식들의 차이를 바탕으로 각 모델의 특징을 Table 2에 정리하였다.
Table 1. Input parameters
Table 2. Models characteristics
4. 결 론
TBM 전면의 커터헤드 설계와 TBM의 굴진 성능에 영향을 미치는 장비의 추력(Thrust)과 토크(Torque)는 주로 경험적인 인자와 TBM 직경으로만 간단히 산정되어 왔다. 본 연구에서는 기계 인자과 지반 인자들을 반영한 4개의 추력과 토크 산정식들을 고찰하였으며, 다음과 같은 결론을 도출하였다.
1. 일본식 방법의 경우, 굴착으로 인한 터널상부에서 지표면까지 감소된 흙의 응력 이완을 반영하여, 추력과 토크식들을 유도하였다. 특히, 수직 유효 응력의 크기는 주동 토압 계수 값이 클수록 더 감소함을 보였다.
2. 수정된 일본 모델은 극좌표계를 이용하여 TBM 직경에 따른 수압과 토압 크기의 변화를 정확히 고려하여 추력 및 토크 식을 유도하였다. 일본식 방법과 추력 및 토크 값을 비교한 결과 쉴드 외면과 주변 흙 사이의 마찰 저항력 F2에서 약 2 MN의 차이를 보였고, 전면 마찰 저항 토크 T2와 커터 외경에서 발생하는 저항 토크 T3 각각 약 0.2 MN ‧ m 차이를 보였다. 다른 방법이 흙의 응력 이완을 고려한 일본식의 추력 및 토크 보다 더 큰 것을 확인할 수가 있었다.
3. 암반 지반에 적합한 CSM 모델에서 제안된 추력과 토크식을 소개하였다. 특히, 관입 압력 형상 계수 에 따라서 커터 관입 깊이 와 커팅 계수 의 변화를 확인하였다. 관입 깊이가 증가하면 커팅 계수가 증가하고, 동일 관입 깊이일 때 등분포 형상( = 0) 값이 상대적으로 크다.
4. NTNU 모델은 선형 회귀 분석을 통해 추력과 토크 산정에 필요한 그래프를 제시하였다. CSM 모델과 NTNU 모델의 값 비교 시에 계수들의 불확실성과 낮은 상관 관계의 경험식으로 인해 값의 차이를 보인다.