1. 서 론
2. 쉴드 TBM의 굴착속도 예측 방법
2.1 NTNU 모델
2.2 Graham (1976) 모델
2.3 Tarkoy (1986) 모델
2.4 Hughes (1986) 모델
2.5 Ribacchi and Lembo-Fazio (2005) 모델
3. 지반조건 및 쉴드 TBM 현장 굴진자료 분석
3.1 현장개요 및 쉴드 TBM 장비제원
3.2 지반조건
3.3 쉴드 TBM 현장 굴진자료 분석
3.4 TBM 기계데이터와 굴착속도의 상관관계 분석
4. 기존 굴착속도 예측모델의 적용성 검토
5. 굴착속도 예측모델 제안
6. 결 론
1. 서 론
우리나라는 국토면적이 협소하고 산지가 많은 지형적 영향으로 도로와 철도 등 사회기반시설 확충 시 터널의 건설이 많이 사용되며 국내에서 건설되는 대부분의 터널은 경제적 측면에서 경쟁력이 큰 NATM 공법이 적용되었다. 하지만, NATM 공법은 사고의 위험성이 매우 크고 작업환경이 열악하며 발파 소음, 진동에 대한 민원발생 등의 문제점이 있어 최근에는 쉴드 TBM을 이용한 기계화 터널공법이 적용되는 추세이다. 쉴드 TBM 터널공법은 디스크 커터의 회전력으로 지반을 굴착하고 세그먼트 라이닝을 설치하여 터널을 시공하는 방법으로 NATM 공법에 비하여 낙반사고의 위험성이 적으며 발파진동 및 소음이 적은 장점이 있다. 그러나 쉴드 TBM 터널 시공 시 장비가 투입되어 터널 굴착이 시작되면 장비의 교체나 개조 등 변경이 거의 불가능하기 때문에 설계단계에서 지반조건, 시공기간, 장비조건, 공사비 등에 영향을 미치는 쉴드 TBM 기계의 절적한 굴착속도를 설계하는 것이 무엇보다도 중요하게 된다.
쉴드 TBM 굴착속도 예측에 관한 연구는 암반의 일축압축강도 또는 인장강도를 이용한 굴착속도 예측방법(Tarkoy, 1973; Graham, 1976; Farmer and Glossop, 1980; Hughes, 1986; Tarkoy, 1986), 암반의 불연속면 특성과 강도특성, 암석특성, 장비특성을 고려한 경험적 모델인 미국의 CSM (Colorado School of Mines) 모델과 노르웨이의 NTNU (Norwegian University of Science and Technology) 모델, 암반의 강도특성과 암석특성, 불연속면 특성을 이용한 굴착속도 예측방법(Barton, 1999; Ribacchi and Lembo-Fazio, 2005; Ramezanzadeh et al., 2005; Hassanpour et al., 2009, 2010; Hamidi et al., 2010) 등 많은 연구자들에 의해 수행된 바 있다. 하지만 설계단계에서 제한된 지반조사 결과를 이용하여 설계를 수행하는 국내 여건상 암반의 불연속면 특성과 암석특성을 판단하는 다양한 실내실험 결과를 이용하여 굴착속도를 예측하는 방법은 사용하기 매우 어렵다. 또한 국내 연구진들(Cho et al., 2003; Jung et al., 2010; Han et al., 2011; Chang et al., 2011)에 의해서 기존의 굴착속도 예측방법으로 국내 현장 굴진데이터에 적용하여 굴착속도를 예측하는 연구를 진행한바 있으나, 현장 굴착속도 결과와는 차이가 발생하는 것으로 나타나 적용에 한계가 존재한다. 따라서 국내 설계여건을 고려하고 국내 지반특성이 반영된 예측 정확도가 높은 굴착속도 예측방법이 필요하다.
본 연구에서는 쉴드 TBM 굴착속도 예측시 기존의 연구자들에 의해 제안된 굴착속도 예측 방법보다 적용하기 쉽고 국내지반에 적용 시 정확도가 높은 굴착속도 예측 모델을 개발하고자 하였다. 이를 위해, ○○~○○ 고속철도 TBM 공사구간에 대하여 지반조사 결과와 총 추력, 커터 추력, 토크, RPM, 굴착속도 등 쉴드 TBM 현장 굴진데이터를 분석하고 이를 기존의 예측방법인 일축압축강도와 추력을 사용하는 굴착속도 예측방법과 일축압축강도, 추력, 추가적인 암반의 특성과 장비 특성을 반영한 굴착속도 예측방법에 적용하였다. 또한 현장 굴착속도 결과와 일축압축강도, 추력의 상관관계를 분석하고 이를 통해 TBM 터널 설계 시 쉽게 고려할 수 있는 경험적 굴착속도 예측 모델을 제시하였다.
2. 쉴드 TBM의 굴착속도 예측 방법
2.1 NTNU 모델
NTNU 모델은 노르웨이 과학기술대학(Norwegian University of Science and Technology, NTNU)에서 개발된 방법으로, 노르웨이 지반조건에 대해 수십 년간 축적된 현장자료 및 시험자료에 근거해 얻어진 경험적인 TBM 설계 ‧ 평가 모델이다(Bruland, 2000). NTNU 모델은 모든 활용과정과 시험방법들이 공개되어 있다는 점에서 핵심적인 굴착속도 산출, 커터수명 예측 등에 대해서 공개하지 않은 CSM 모델에 비하여 활용성이 매우 높다. NTNU 모델은 TBM 장비특성 보정에 관한 계수와 암반특성을 고려한 계수로 나눌 수 있으며 Fig. 1과 같이 디스크 커터 직경 보정계수, 암반의 DRI 보정계수, 관입 계수 등 NTNU 모델에 적용 시 사용되는 모든 계수들을 도표를 통하여 그 값을 찾을 수 있다. 필요한 실험으로는 모형 천공시험(Siever’s J-value test)과 취성도 시험(Brittleness test)을 수행하여 하며 DRI (Drilling Rate Index), 암반의 절리간격, 암반의 공극률, 디스크 커터 당 평균 추력, 커터직경, 커터간격 등을 고려하여 굴착속도를 예측한다.
2.2 Graham (1976) 모델
미국 로빈스(Robbins)사에서 축적된 데이터를 바탕으로 제안한 경험적 예측모델로 식 (1)과 같이 암반의 일축압축강도와 디스크 커터의 추력으로 관입속도()를 산출하여 굴착속도()를 계산하는 방법이다. 일반적으로 일축압축강도 140 MPa에서 200 MPa 사이의 암반에서 시공한 사례들을 바탕으로 제안한 모델이며, 이 모델은 암반의 불연속면 특성과 장비특성이 고려되지 않았다.
| $$P_e=3,940\left(\frac{F_n}{\sigma_c}\right)$$ | (1) |
여기서, 은 커터 당 추력(kN), 는 일축압축강도(kPa)이다.
2.3 Tarkoy (1986) 모델
Tarkoy는 식 (2)와 같이 암반의 일축압축강도를 이용한 굴착속도 경험식을 제안하였으며, 이 모델은 암반의 불연속면 특성과 장비특성이 고려되지 않았다.
| $$P_e=-0.909\bullet\ln(\sigma_c)+7.2349$$ | (2) |
여기서, 는 일축압축강도(kPa)이다.
2.4 Hughes (1986) 모델
Hughes는 광산에서 석탄이 포함된 암층의 현장 데이터를 수집하여 식 (3)과 같이 암반의 일축압축강도와 디스크 커터 당 추력, 디스크 커터 직경을 이용한 굴착속도 경험식을 제안하였으며, 이 모델에서 암반의 불연속면 특성은 고려하지 않았다.
| $$P_e=1.167\bullet\ln\left(\frac{F_n}{\sigma_c}\right)^{0.5}\bullet\left(\frac2D\right)^{0.6}$$ | (3) |
여기서, 은 커터 당 추력(kN), 는 일축압축강도(kPa), 는 디스크 커터 직경(m)이다.
2.5 Ribacchi and Lembo-Fazio (2005) 모델
Ribacchi는 평균 150 MPa의 일축압축강도를 갖는 이탈리아의 편마암 지반에서 더블 쉴드 TBM 장비를 이용하여 터널 굴착을 수행한 현장 데이터를 기반으로 식 (4), (5)와 같이 암반의 일축압축강도와 디스크 커터 당 추력, RMR지수를 이용하여 굴착속도 경험식을 제안하였으며, 이 모델에서 장비특성은 고려하지 않았다.
| $$UCS_{cm}=\sigma_c\bullet\exp\left(\frac{RMR-100}{18}\right)$$ | (4) |
| $$P_e=\frac{250\bullet UCS_{cm}^{-0.66}}{F_n}$$ | (5) |
여기서, 은 커터 당 추력(kN), 는 일축압축강도(kPa)이다.
3. 지반조건 및 쉴드 TBM 현장 굴진자료 분석
3.1 현장개요 및 쉴드 TBM 장비제원
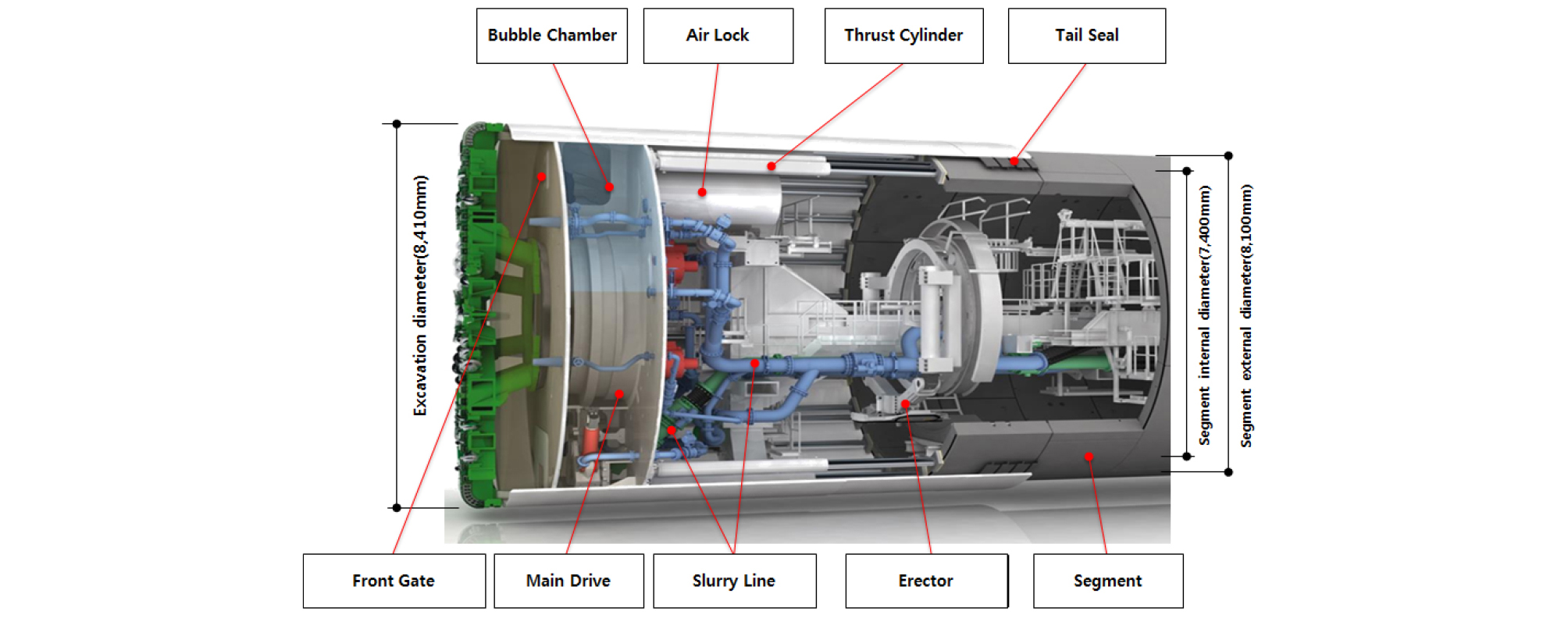
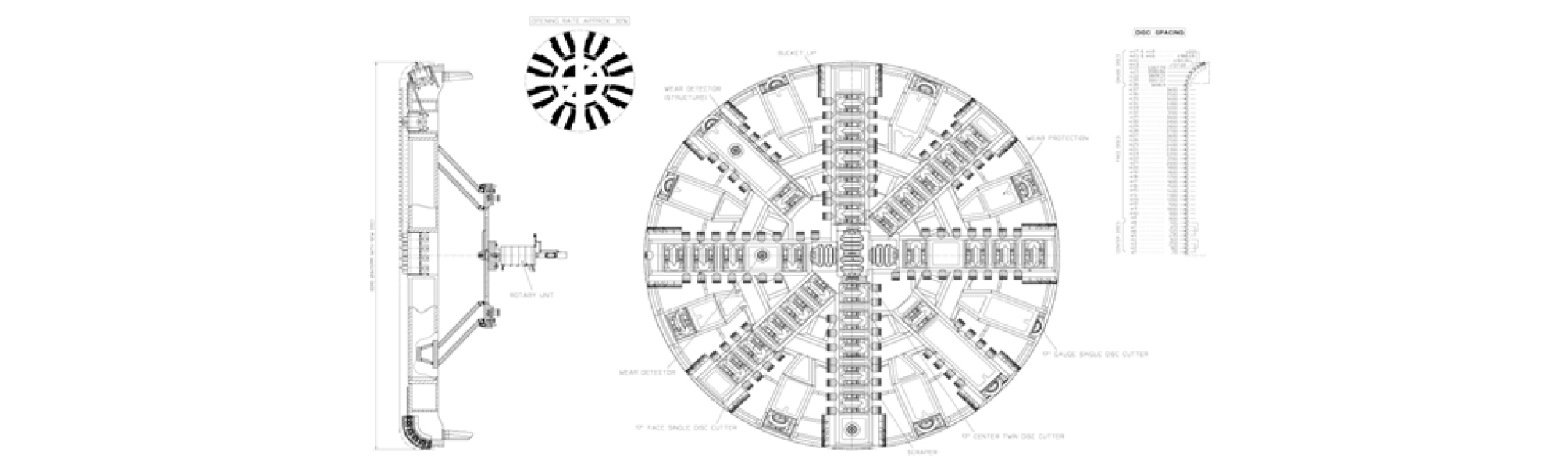
본 연구의 적용대상 현장은 ○○~○○ 고속철도 00-0공구로 남대천 하부를 통과하는 현장이며 터널의 총 연장은 3,930 m이고 이중 쉴드 TBM 구간은 1,160 m이다. 굴착경은 8.41 m (세그먼트 외경 8.1 m / 내경 7.4 m)이며, 콘크리트 세그먼트의 압축강도()는 45 MPa/piece이고 분할 6 + 1 Key, 세그먼트 폭은 1.5 m이다. 이수식 쉴드 TBM 장비는 독일 HERRENKNECHT사에서 제작된 이수가압식 장비로서 주요 제원은 Table 1과 같고 복합지층 대응용으로 제작된 장비로서 터널 굴착 중 발생될 수 있는 문제에 대응하기 위하여 면판 jamming 방지를 위한 면판 전 ‧ 후진 이동장치인 Displacement Cylinder, 사행보정 및 곡선시공 용이성 확보를 위한 Articulation Cylinder, 전방 지질 상태 파악 및 갱내 지반보강을 위한 Drilling Line이 장착되어 있다. 아울러 챔버압 변화에 유연하게 대처하기 위한 Bubble chamber, 굴착 암반 또는 자갈층 파쇄를 위한 Crusher등이 추가 장착되어 복합지반 굴착이 용이하도록 제작되었다. 이외에도 메인베어링 최대 허용압을 5.5 bar로 설계하여 고수압에 대응토록 함과 동시에 송니관 및 배니관 직경은 모두 350 mm로 제작하여 원활한 이수공급 및 배토가 되도록 제작하였다. 또한 면판헤드에는 총 44개의 디스크 커터 및 110개의 스크레퍼가 설치되었으며, 디스크 커터 직경은 17 inch이고 더블커터 4개, 싱글커터 40개로 구성되어 있다. Figs. 2, 3에 쉴드 TBM 장비 주요 구조 및 쉴드 TBM 면판 헤드 구성을 나타내었다.
Table 1. Major specifications of shield TBM
3.2 지반조건
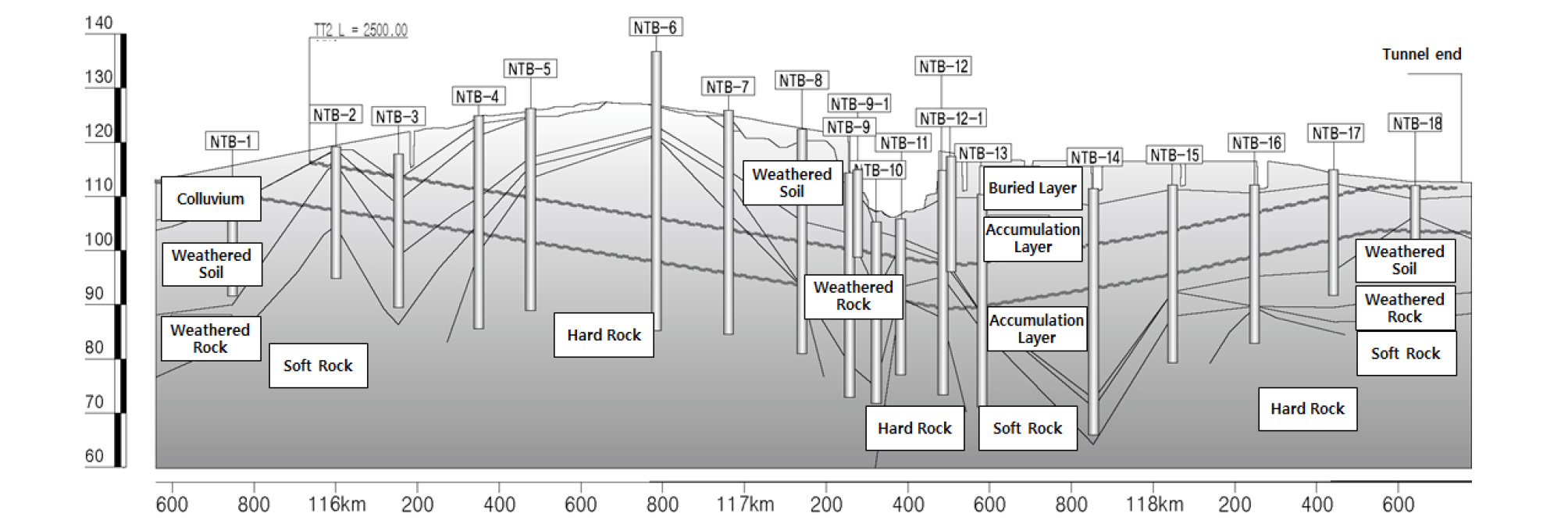
본 연구의 적용대상 현장의 지반조건은 Fig. 4와 같이 쉴드 TBM구간에 대해서 시추조사 10공(NTB-8~NTB-15)을 수행하였으며, 전기 비저항 탐사를 수행하여 지층상태를 확인하였다. 그 결과, 대체적으로 두터운 풍화층과 퇴적층을 이루고 있으며, 일부구간은 연 ‧ 경암이 조기출현 하였다. 또한 쉴드 TBM 구간의 경우 여러 지층이 혼합된 복합지반 형태가 많이 나타나며, 위험예상구간의 지질 상태는 굴착면내 및 굴착바닥면상 ∅18~∅70 cm의 호박돌이 분포되어 있다. 그 외 구간은 충적층이 전면적으로 분포하는 것으로 나타났고 자갈 및 호박돌층은 퇴적과정에서 마모되어 원형을 띠는 전형적인 자갈과 호박돌(풍화저항성이 높음)이 아니어서 퇴적이후에도 풍화작용을 받았으며 충적 모래층과 함께 있는 자갈 및 호박돌이 아니라 홍수시 급격히 퇴적되어 점성이 약간 있는 모래층 내에 박혀있는 것을 확인하였다. 지하수위는 심도 7 m 내외로 충적층(모래질 자갈층)에 위치하고 있다.
3.3 쉴드 TBM 현장 굴진자료 분석
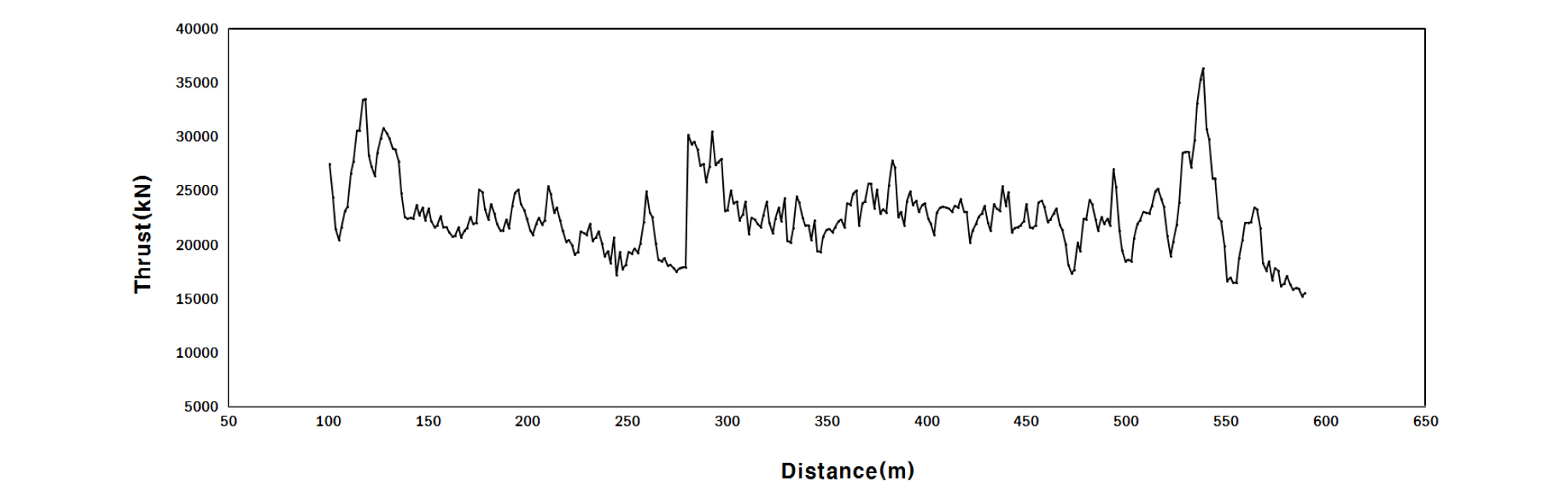
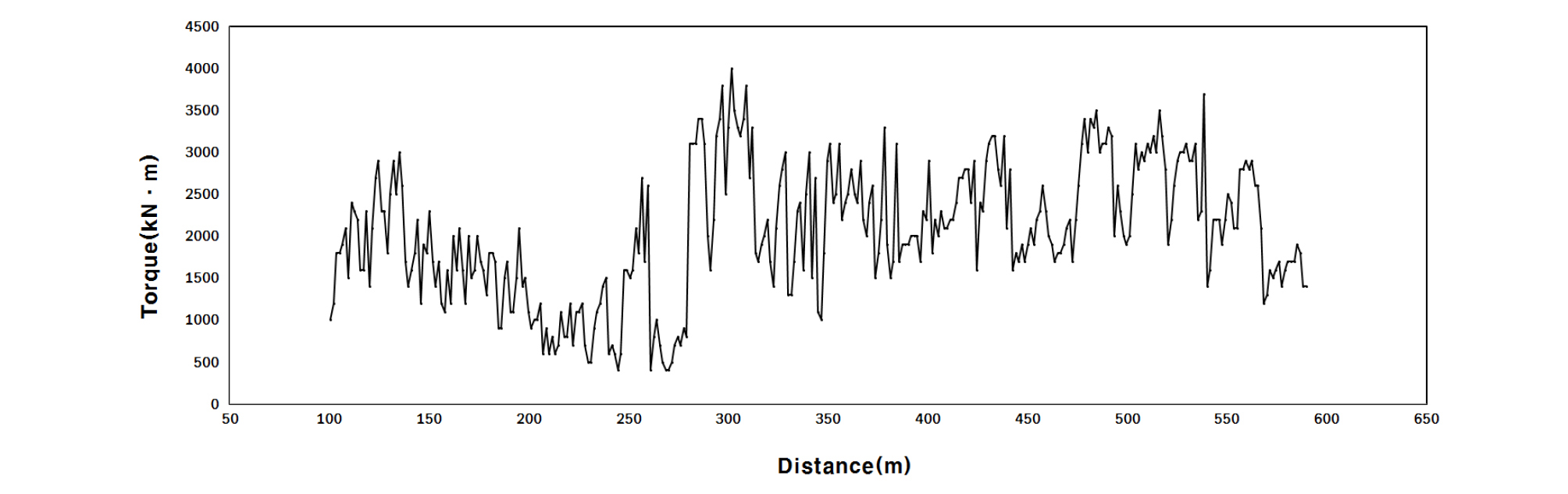
현장 굴진자료 분석에 사용한 데이터는 굴착길이 100 m 지점부터 600 m 지점까지의 이수식 쉴드 TBM 장비로 굴착을 진행한 기계데이터를 사용하였고 이때의 총 추력, 커터 추력, 토크, RPM, 굴착속도 등을 이용하여 굴착성능에 대한 분석을 수행하였다. 쉴드 TBM으로 터널 굴착 시 지반상태를 직접 관찰하기 어렵기 때문에 TBM 장비 데이터 관리는 막장면 안정과 굴착속도 향상을 위하여 매우 중요하다. 추력은 암반의 강도를 판단할 수 있는 가장 기본적인 기준으로 사용되며, 일반적으로 암반강도가 낮을수록 작은 추력에서 굴착이 가능하고 암반강도가 높을수록 큰 추력을 사용해야 한다. 본 현장에서 TBM의 운전에 사용한 추력은 Fig. 5와 같이 15,190~36,387 kN (25,788 ± 10,598 kN)으로 약 40%의 변동성을 보이는 것으로 나타났으며, 이때 커터 당 개별 평균 추력은 316.5~758.1 kN로 운전되어 추력의 크기가 크고 변화가 심한 것으로 나타났다. 이는 터널 굴착 지반의 지층변화가 심하고 비교적 지반의 암반강도가 높기 때문인 것으로 판단된다. 이때, 계측된 토크는 Fig. 6과 같이 500~4,000 kN ‧ m (2,250 ± 1,750 kN ‧ m) 범위에서 운전하여 약 78%의 변동성을 보이며 운전에 사용된 토크의 변화 역시 큰 것으로 나타났다.
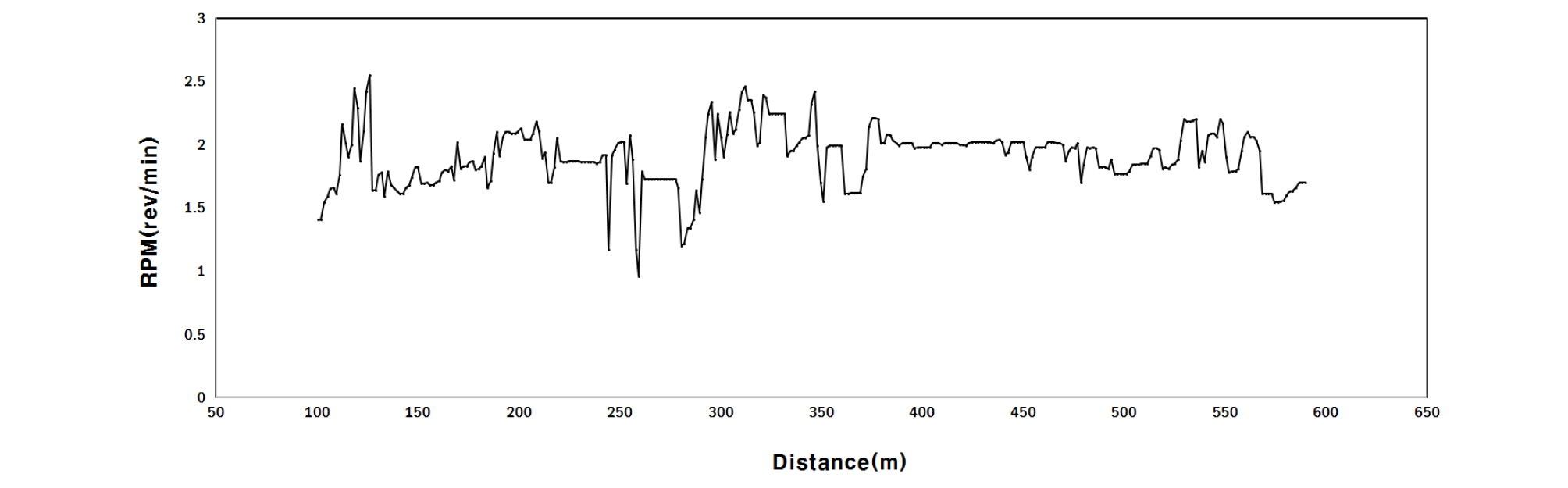
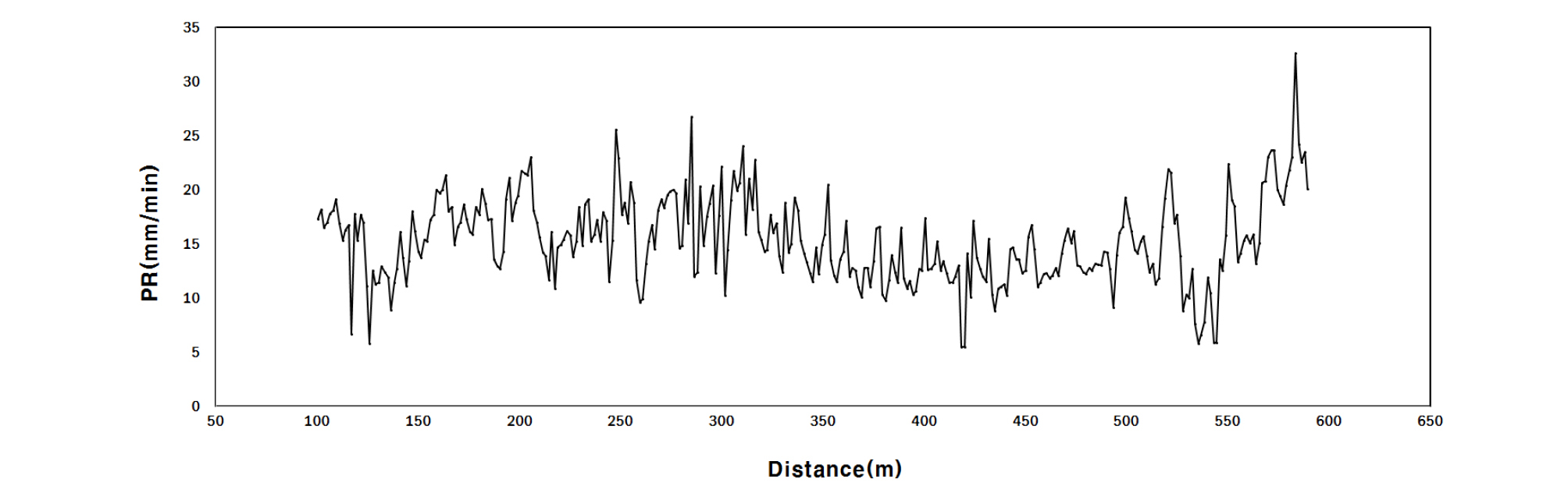
터널 길이에 따른 회전속도(RPM)와 굴착속도를 Fig. 7과 Fig. 8에 도시하였다. 시공 중 RPM은 1~2.5 범위에서 운전되었다. 터널 굴착 지반은 혼합지층이 많고 지층변화가 크기 때문에 RPM을 낮은 범위에서 운전하여 시공트러블이 발생하지 않도록 안전한 굴착을 하였으며, 운전에 사용된 RPM의 변화는 크지 않음을 알 수 있다. 쉴드 TBM의 굴착속도 PR (mm/min)은 디스크 커터 압입깊이(mm/rev)와 커터헤드 회전속도(RPM)의 곱으로 산출되며, 당 현장의 굴착성능에 대해 통계분석 결과 굴착속도는 6~32 mm/min (19 ± 13 mm/min) 범위로 약 68%의 변동성을 보이는 것으로 나타났다. 이는 추력과 토크의 변화가 큰 것과 마찬가지로 터널 굴착 지반의 지층변화가 심하고 비교적 지반의 암반강도가 높기 때문에 굴착속도의 변화 역시 큰 것으로 판단된다.
3.4 TBM 기계데이터와 굴착속도의 상관관계 분석
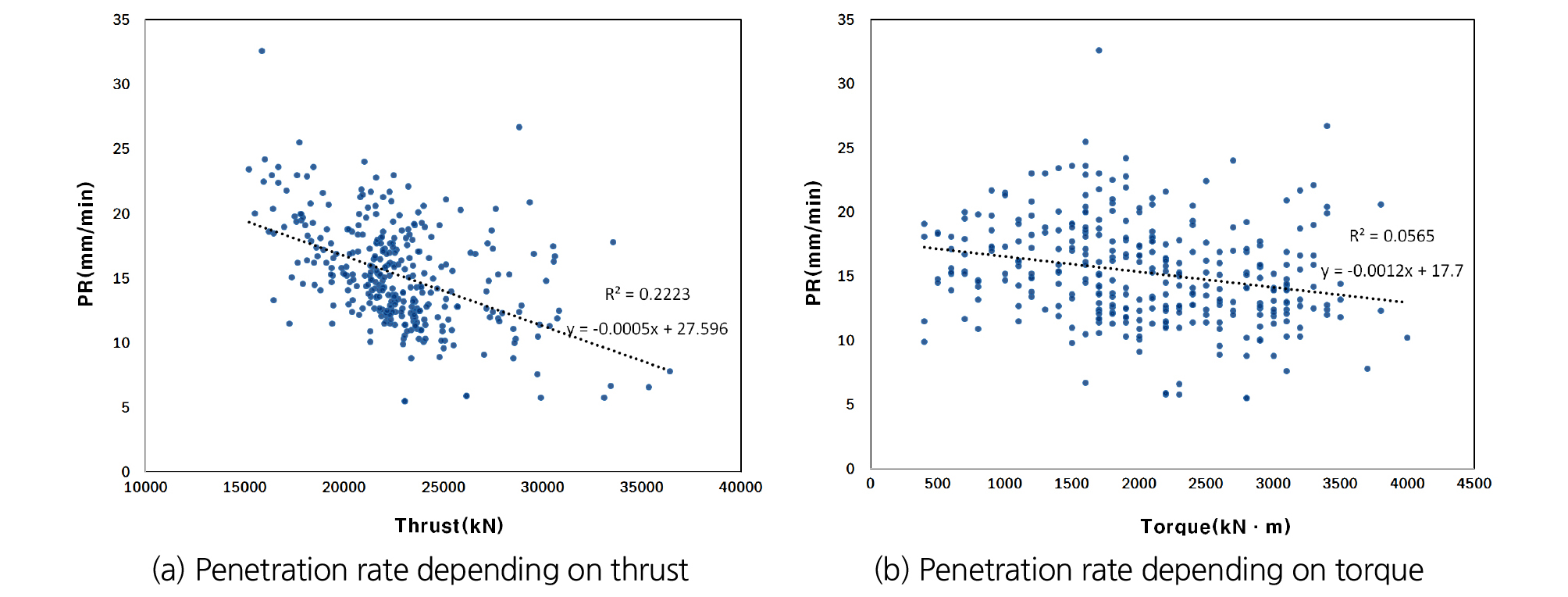
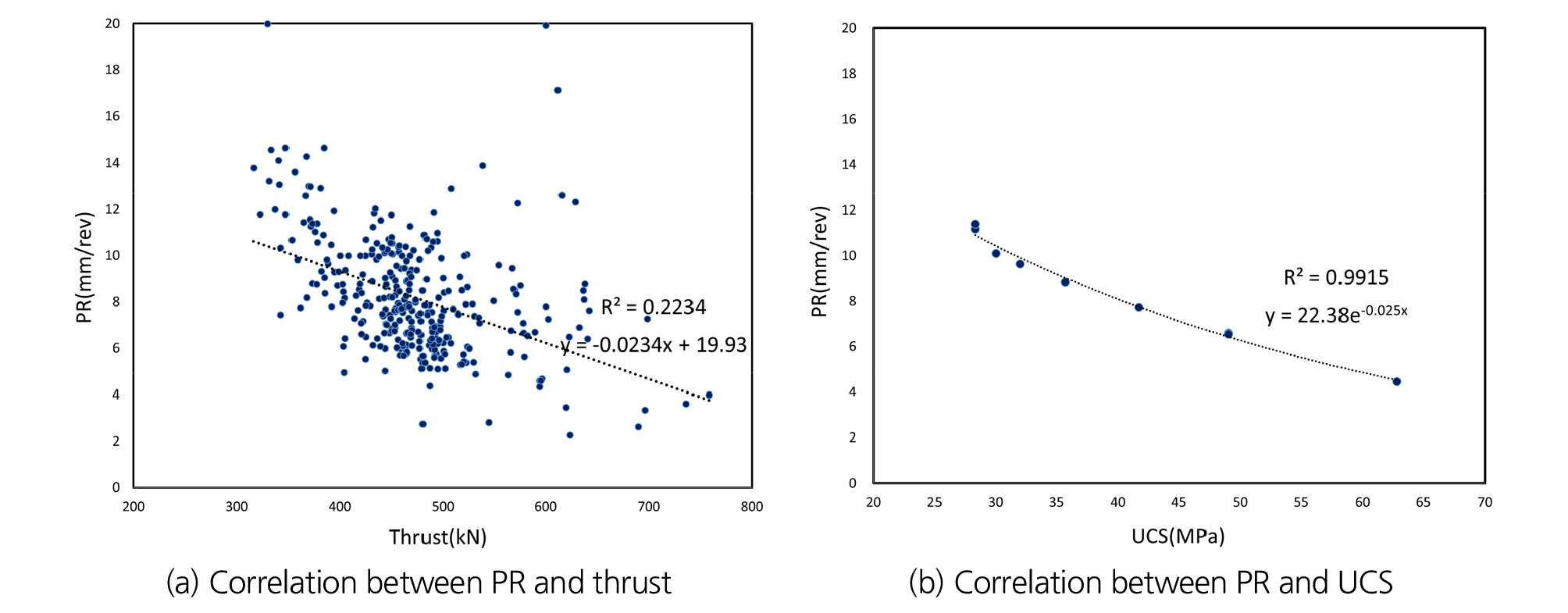
이수식 쉴드 TBM 블랙박스에 기록되는 기계데이터들 중 굴착속도에 영향을 미치는 인자를 파악하고 굴착속도 예측의 정확도를 개선할 수 있는 방안을 모색하고자 굴진특성 인자들을 비교 분석하였다. 본 연구에서 회전속도(RPM)의 경우 3.3절에서 1~2.5 범위에서 비교적 일정하게 운전되는 것을 확인하였기 때문에 TBM 굴진데이터 중 총추력과 토크에 대하여 굴착속도와의 상관관계를 분석하였고 Fig. 9와 같은 결과를 도출하였다. Fig. 9(a)와 같이 총추력과 굴착속도의 관계는 토크에 비해 유의미한 상관성(R2 = 0.22)을 보이는 것으로 나타났고 추력이 증가하면 굴착속도는 감소하는 것으로 나타났으며, 이는 추력이 클수록 암반강도가 크기 때문에 굴착속도가 감소하는 것으로 판단된다. 반면에 Fig. 6(b)와 같이 추력 및 회전속도에 의해 복합적인 영향을 받는 토크는 굴착속도와 뚜렷한 상관관계(R2 = 0.06)를 유추하기 어려웠다.
4. 기존 굴착속도 예측모델의 적용성 검토
실제 현장에서 측정된 굴착속도와 기존의 연구자들에 의해 제안된 예측모델을 통해 산정된 굴착속도를 비교하기 위해 시추조사 지점을 중심으로 지반조건을 세분화하여 굴착속도 예측을 수행하였으며, 그 결과를 식 (6)과 같은 오차율 산정식을 이용하여 상대적인 차이를 비교하였다.
| $$Error\;Ratio\;(\%)=\frac{\sum{\displaystyle\frac{\left|Predicted-Measured\right|}{Measured}}}N\times100$$ | (6) |
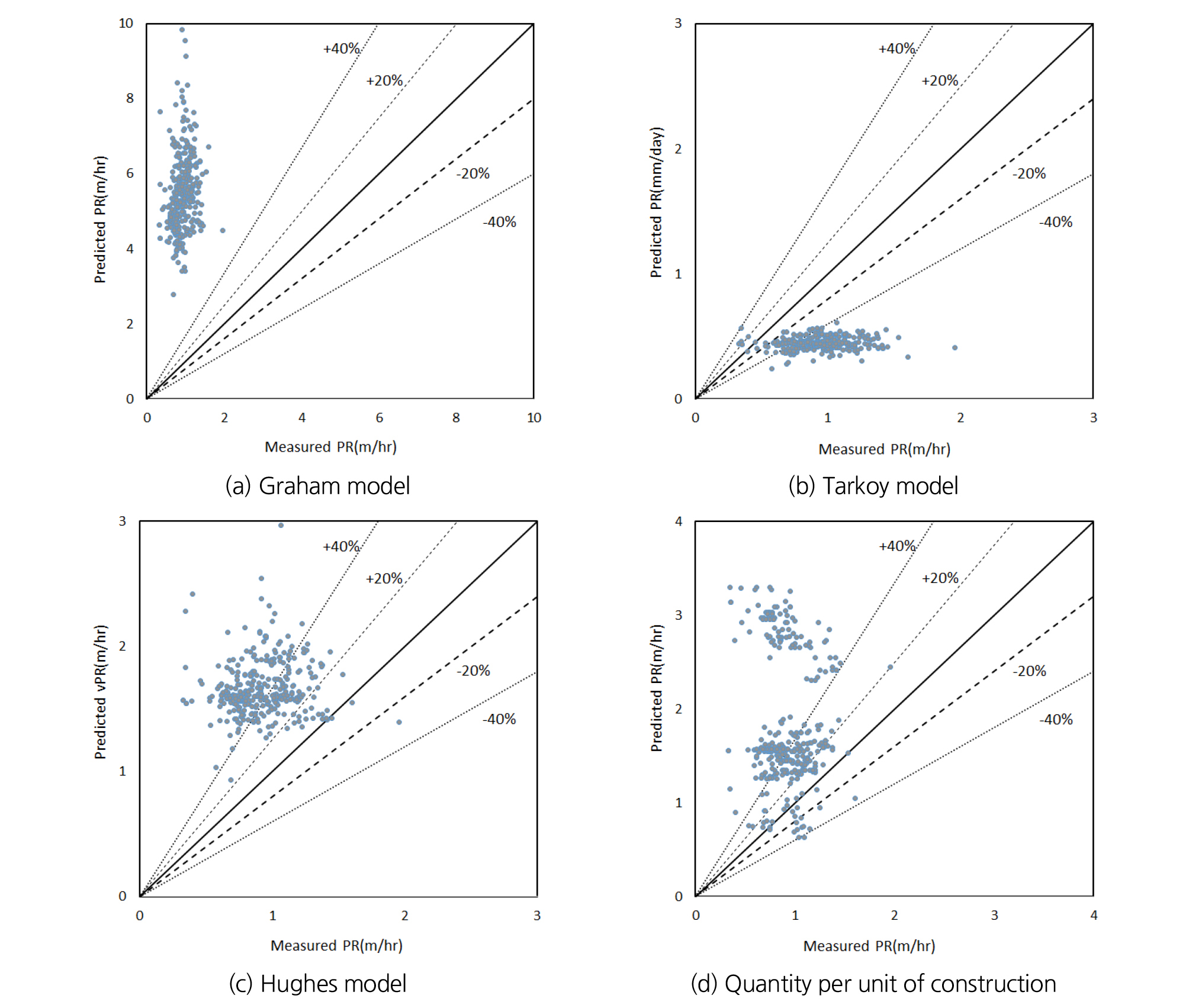
암반의 일축압축강도와 디스크 커터에 작용한 추력만으로 굴착속도를 예측한 Graham (1976), Tarkoy (1986), Hughes (1986), 건설표준품셈 식의 예측결과를 현장의 굴착속도와 비교한 결과를 Fig. 10에 나타내었다. Fig. 10(a)와 같이 Graham (1976) 모델의 경우 현장에서 측정된 굴착속도와 비교하였을 때, 평균 약 500%의 오차율로 가장 큰 차이를 보였다. 이는 Graham 모델이 일축압축강도 140 MPa에서 200 MPa 사이의 암반에서 적용되도록 개발되었기 때문에 일축압축강도가 70 MPa 이하인 대상현장에 적용될 경우 매우 큰 오차를 보이는 것으로 판단된다. Fig. 10(b)와 같이 Tarkoy (1986) 모델의 경우 현장에서 측정된 굴착속도와 비교하였을 때, 평균 약 50%의 오차율로 가장 작은 차이를 보이는 것으로 나타났다. 하지만 이 방법은 기계 데이터 없이 일축압축강도만으로 굴착속도를 예측하기 때문에 모든 예측값이 일정하게 수렴되는 문제가 있어 실제 설계에서는 사용되기 어려울 것으로 판단된다. Fig. 10(c)와 같이 Hughes (1986) 모델의 경우 현장에서 측정된 굴착속도와 비교하였을 때, 평균 약 80%의 오차율을 보이는 것으로 나타났다. 이는 Hughes (1986) 모델의 대상지반이 석탄을 포함한 암반층이기 때문에 현장의 지반조건을 반영하지 못하는 것으로 판단된다. Fig. 10(d)와 같이 대상 현장의 실제 설계에 사용된 건설표준품셈 식의 경우 현장에서 측정된 굴착속도와 비교하였을 때, 평균 약 100%의 오차율을 보이는 것으로 나타났다. 이는 건설표준품셈 식의 경우 대상지반을 풍화암, 연암, 경암 등과 같이 세분화 하지 않기 때문인 것으로 판단된다.
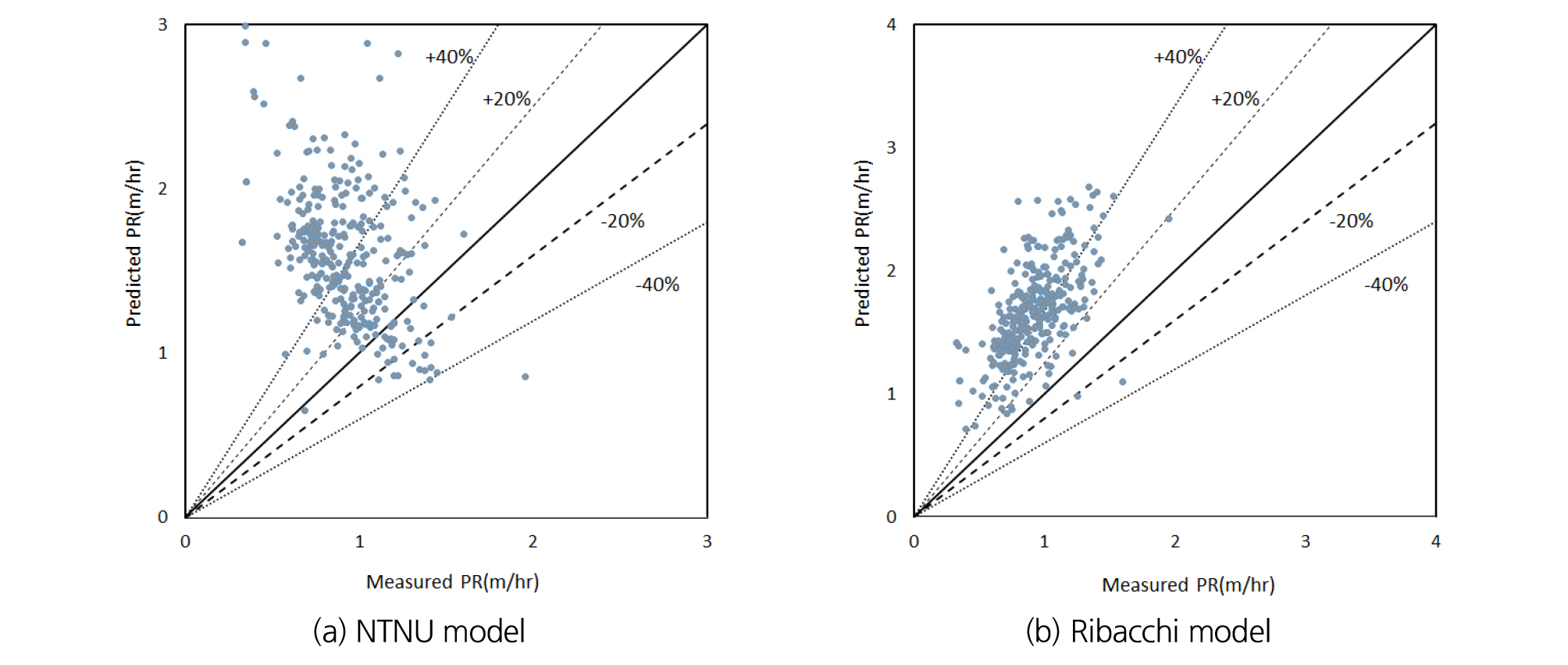
암반의 일축압축강도와 디스크 커터에 작용한 추력, 추가적인 암반의 특성과 장비 특성을 반영한 NTNU, Ribacchi and Lembo-Fazio (2005)의 모델의 예측결과를 현장의 굴착속도와 비교한 결과를 Fig. 11에 나타내었고 그 결과 다양한 특성을 고려한 굴착속도 예측도 현장 굴착속도와는 많은 차이를 보였다. Fig. 11(a)과 같이 NTNU 모델의 경우 현장에서 측정된 굴착속도와 비교하였을 때, 평균 약 74%의 오차율을 보여 일축압축강도와 추력만을 고려한 예측보다는 비교적 작은 경향을 보였다. 하지만 NTNU가 주로 노르웨이 지반을 굴착한 Open TBM의 실적을 통해 산출한 경험식이므로 국내 암반에 적합하지 않을 수 있다(Jung et al., 2010). 또한 현장데이터와 모델 예측값의 비교 결과가 매우 넓은 영역에 분포하는 것을 확인할 수 있으며 따라서 정확한 암반의 특성과 장비 특성 데이터를 사용해야 할 것으로 판단된다. Fig. 11(b)와 같이 Ribacchi and Lembo-Fazio (2005) 모델의 경우 현장에서 측정된 굴착속도와 비교하였을 때, 평균 약 80%의 오차율을 보여 Hughes (1986) 모델을 사용한 예측 결과와 유사한 것으로 나타났다. 하지만 현장데이터와 모델 예측값의 비교 결과가 Hughes (1986) 모델에 비하여 좁은 영역에 분포하는 것을 확인할 수 있다.
5. 굴착속도 예측모델 제안
4장에서 기존 연구자들에 의해 제안된 굴착속도 예측 모델을 현장 굴진데이터에 적용하여 예측한 결과와 현장에서 측정된 굴착속도를 비교한 결과 굴착속도 예측의 정확도가 크게 차이가 나는 것을 확인하였다. 이는 기존 예측 모델들이 국외 지반조건에서의 TBM 실적을 통해 도출된 경험식인 영향이 큰 것으로 판단되기 때문에 국내 설계여건을 고려하여 간편하게 국내 지반조건을 고려 할 수 있도록 해당 현장의 일축압축강도를 이용하여 굴착속도 예측 모델을 개발하고자 하였다. 또한 3.4절에서 쉴드 TBM 기계데이터들 중 추력이 굴착속도에 영향을 미치는 인자인 것을 파악하였기 때문에 커터 당 추력을 굴착속도 예측 모델의 인자로 적용하였다. 이를 위해 Fig. 12와 같이 현장 굴진데이터 중 커터 당 추력과 암반의 일축압축강도에 대하여 관입속도(mm/rev) 결과와의 회귀분석을 수행하였고 이때, 커터 당 추력과 암반의 일축압축강도 이 두 가지 변수에 대하여 최대 R2값을 갖는 회귀식을 도출하는 과정을 수행하였다. 최종적으로 두 가지 회귀식에 곱의 관계를 이용하여 커터 당 추력과 암반의 일축압축강도를 변수로 식 (7)과 같은 예측식을 도출하였다.
| $$PR=\sqrt{(-0.00234\bullet F_n+19.93)\times(22.38e^{-0.025\bullet\sigma_c})}$$ | (7) |
여기서, 은 관입속도(mm/rev), 은 커터 당 추력(kN), 는 일축압축강도(MPa)이다.
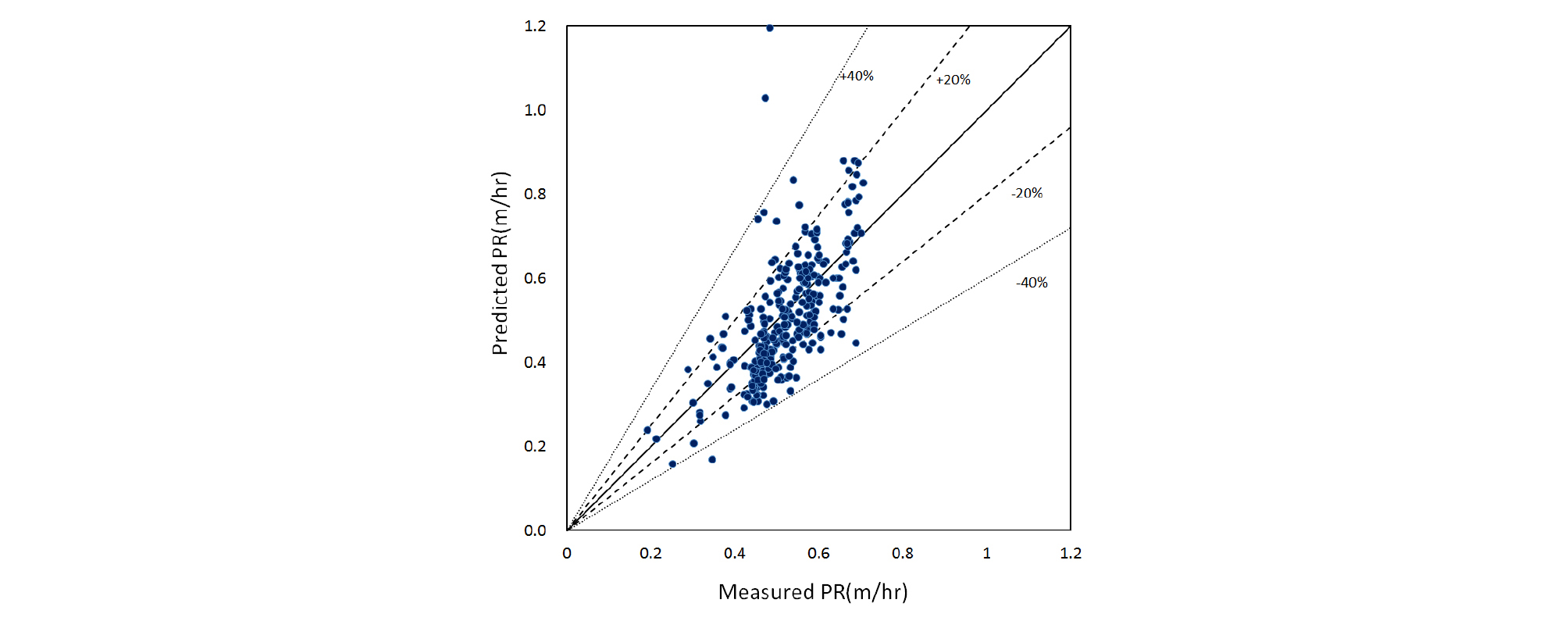
커터 당 추력과 암반의 일축압축강도로 추정된 굴착속도 예측식을 바탕으로 Fig. 13과 같이 해당 현장에 적용하여 굴착속도를 예측하였고 그 결과를 현장에서 측정된 굴착속도와 비교하였다. 4장에서 오차가 가장 큰 Graham (1976) 모델을 제외하고 기존 연구자들에 의해 제안된 굴착속도 예측 모델로 산정된 굴착속도는 현장에서 측정된 굴착속도와의 오차가 평균 약 50~100% 범위인 것에 반하여, 제안된 굴착속도 예측식을 이용하여 산정한 굴착속도는 현장에서 측정된 굴착속도와의 오차가 평균 약 15% 인 것으로 나타나 상대적으로 예측정확도가 높은 것으로 나타났다.
6. 결 론
본 연구에서는 ○○~○○ 고속철도 TBM 공사구간에 대하여 지반조사 결과와 쉴드 TBM 현장 굴진데이터를 분석하고 이를 기존 연구자들에 의해 제안된 경험적 굴착속도 예측방법에 적용하였다. 또한, 현장 굴진데이터 중 커터 당 추력과 일축압축강도의 상관관계를 분석하고 이를 통해 TBM 터널 설계 시 커터 당 추력과 일축압축강도를 변수로 굴착속도를 예측할 수 있는 모델을 제시하였다. 본 연구를 통해 도출한 결론을 요약하면 다음과 같다.
1. 현장 굴진데이터 분석 결과 총 추력은 평균 25,788 ± 10,598 kN으로 약 40%의 변동성을 보였고, 토크의 경우는 평균 2,250 ± 1,750 kN ‧ m 으로 약 78%의 변동성이 측정되었으며 굴착속도는 평균 19 ± 13 mm/min 범위로 약 68%의 변동성을 보이는 것으로 나타났다. 이는 터널이 굴착되는 대상 지반의 경우 혼합지층이 많고 지층변화가 크기 때문에 변동성이 큰 것으로 판단하였다. 또한, 추력의 경우 굴착속도에 영향을 미치는 것으로 나타났지만 토크의 경우 굴착속도에 큰 영향을 주지 않는 것을 확인하였다.
2. 기존 연구자들에 의해 제안된 굴착속도 예측 모델을 이용한 굴착속도 예측 결과 일축압축강도를 사용한 Graham 모델은 현장에서 측정된 굴착속도와 비교하였을 때, 평균 약 500%의 오차율을 보였고, Tarkoy 모델의 경우 평균 약 50%의 오차율, Hughes 모델은 평균 약 80%의 오차율, 건설표준품셈 식의 경우 평균 약 100%의 오차율을 보이는 것으로 나타났다. 또한, 추가적인 암반의 특성과 장비 특성을 반영한 NTNU 모델의 경우 평균 약 74%의 오차율을 보였고 Ribacchi 모델의 경우 평균 약 80%의 오차율을 보이는 것으로 나타났다. 기존에 사용되는 굴착속도 예측 모델을 사용한 결과 전반적으로 오차가 크기 때문에 설계 시 국내 지반에 적용이 어려울 것으로 판단하였다.
3. 따라서 국내 설계여건과 지반조건을 고려할 수 있도록 해당 현장 굴진데이터를 이용하여 디스크 커터 당 추력과 암반의 일축압축강도만을 변수로 굴착속도를 예측할 수 있는 굴착속도 예측모델을 도출하였으며, 이를 통한 예측치와 측정된 굴착속도간의 오차율은 평균 15%로 나타나 향후 유사한 지반조건을 가진 현장에서 이수식 쉴드 TBM 굴착속도 설계 시 적용성이 높을 수 있을 것으로 기대한다.