1. 서 론
2. 이 론
2.1 NATM터널 수치해석
2.2 전면접착형 록볼트 거동 특성
2.3 전면접착형 록볼트 모델링 방법
3. 해석 조건
3.1 대상 터널의 단면 및 해석 조건
3.2 지반 물성 및 지보재 모델링
3.3 록볼트 인발시험 데이터를 활용한 그라우트 물성치 산정
3.4 해석 Case
4. 해석 결과
4.1 록볼트 설치 전 터널 거동 분석
4.2 Cable요소의 그라우트 물성치에 따른 전면접착형 록볼트 거동 분석
4.3 전면접착형 록볼트 모델링 방법에 따른 터널 거동 분석
5. 결 론
1. 서 론
NATM (New Austrian Tunneling Method) 공법은 암반 자체의 지지능력을 활용한 터널 공법으로 현재 국내의 터널 설계 및 시공에 있어 많은 부분을 차지하고 있는 주요 터널 공법이다. NATM 공법의 주 지보재에는 록볼트, 숏크리트, 강지보재가 있다. 이 중 록볼트는 매달림 효과, 보형성 효과, 내압 효과, 아치형성효과 등의 각종 지반 보강효과를 가지고 있으며, 정착 형식에 따라 선단정착형, 전면접착형, 혼합형으로 구분된다(Kim, 2018).
국내 터널 현장에서는 전면접착형 록볼트가 가장 많이 사용되고 있다. 전면접착형 록볼트는 그라우트에 의해 볼트체와 지반 간 상대적인 거동을 구현한다. 그러나 터널 수치해석 시 전면접착형 록볼트는 이러한 거동 특성이 반영되지 못한 방법으로 모델링되는 경우가 많다. 이는 지보재의 부재력을 과소 혹은 과대 평가하는 요인이 될 수 있다.
전면접착형 록볼트는 주로 Truss요소와 Cable요소로 모델링되었다. Heo et al. (2017)은 NATM터널에서 Truss요소로 전면접착형 록볼트를 모델링하여 록볼트 설치각도에 따른 보강효과에 대한 연구를 수행하였다. 그러나 Truss요소는 그라우트를 고려하지 못하기 때문에 록볼트와 지반 간 상대적인 거동을 구현하지 못한다(Swoboda and Marence, 1991). Aydan et al. (1987)은 이러한 문제점을 개선하기 위해 볼트체와 그라우트 간 접촉면을 표현하는 인터페이스를 활용한 전면접착형 록볼트 모델링 방법을 제안하였다. 그러나 인터페이스를 사용하면 모형화의 어려움이 존재하며 해석 시간의 증가에 따른 경제적인 문제가 발생한다(Heo et al., 2017). Cable요소로 전면접착형 록볼트를 모델링할 경우 별도의 인터페이스 모형화 없이 그라우트를 고려할 수 있다. Carranza-Torres (2009)는 터널에 설치된 록볼트의 보강 원리에 대한 연구에서 Cable요소를 사용하여 전면접착형 록볼트를 모델링 하였다. 이 연구에서는 록볼트와 지반을 완전 접착의 상태로 가정하기 위해 Cable요소의 그라우트 물성치를 매우 크게 적용하였다. 그러나 완전 접착을 가정한 모델링의 경우, 전면접착형 록볼트의 거동 특성을 반영한 모델링 방법은 아니기 때문에 합리적인 모델링 방법으로 보기 어렵다. 전면접착형 록볼트의 거동 특성을 반영하기 위해 Cable요소의 그라우트 물성치를 적절하게 적용하는 것은 중요할 수 있다.
Cable요소의 그라우트 물성치는 록볼트 인발시험 데이터를 통해 산정할 수 있다(ITASCA, 2016). 이 산정법을 적용한 Cable요소로 전면접착형 록볼트를 모델링 하였을 때 거동 특성을 충분히 반영하는지, 또한 이 모델링 방법이 터널 거동에 미치는 영향을 분석한 연구는 현재까지 수행된 바가 없다.
본 연구에서는 전면접착형 록볼트의 거동 특성을 반영할 수 있는 합리적인 수치해석 방법을 제안하고자 Truss요소와 Cable요소를 대상으로 연구를 수행하였다. Cable요소의 그라우트 물성치에 따른 록볼트 거동 특성을 분석하기 위해, 그라우트 물성치를 록볼트 인발시험 데이터를 통해 산정하여 적용한 모델과 완전 접착을 가정하기 위해 임의로 크게 적용한 모델의 록볼트 거동을 비교하였다. 또한 동일한 터널 조건에서 전면접착형 록볼트를 Truss요소와 Cable요소로 각각 다르게 모델링하여 수치해석을 수행하였다. 이때 Cable요소는 인발시험 데이터를 활용한 모델링 방법과 완전 접착을 가정한 모델링 방법, 이 2가지 방법으로 달리 모델링하여 총 3가지 모델링 방법에 따른 터널 거동을 분석하였다. 연구결과들을 토대로 합리적인 전면접착형 록볼트 모델링 방법을 제시하고자 한다.
2. 이 론
2.1 NATM터널 수치해석
NATM터널의 수치해석에는 주로 유한요소법(Finite Element method, FEM), 유한차분법(Finite Difference method, FDM), 경계요소법 BEM (Boundary Element method), 불연속 거동을 고려할 시 개별요소법(Discrete Element method, DEM) 등이 사용된다. 터널 2차원 해석은 터널을 평면변형률 조건으로 가정하여 해석한다. 평면변형률 조건에서 종방향 아치효과와 숏크리트 경화시간을 고려하기 위해 굴착에 의하여 발생하는 총 하중을 굴착, 연성 숏크리트(Soft shotcrete), 강성 숏크리트(Hard shotcrete)의 3단계로 분배하는 방법인 하중분담율이 적용된다(Jeong et al., 2004). 터널 수치해석 결과는 터널 굴착에 따른 터널 및 주변지반 변위, 소성 발생영역, 지보재의 부재력 등이 있으며, 이를 허용치와 비교 및 검토하여 설계의 적정성을 판단한다.
2.2 전면접착형 록볼트 거동 특성
전면접착형 록볼트는 접착재를 통해 록볼트의 전면을 지반에 접착하는 방법이다. 접착재는 레진 혹은 시멘트 몰탈이 주로 쓰인다. 이 볼트는 터널 주위 지반의 변형으로 인해 하중이 록볼트에 전달되는 메커니즘을 갖는다. 하중의 주체가 지반변형이라는 관점에서 수동볼트(passive bolt)라고 부르기도 한다. 터널의 굴착에 따른 소성거동으로 인해 지반에 변형이 발생하면 지반과 록볼트에 상대변위가 발생한다. 상대변위가 0이 되는 중립점에서 최대 축력이 발생되며, 이 지점을 중심으로 왼쪽 구간, 오른쪽 구간을 각각 지지구간(pick-up length), 고정구간(anchor length)라고 한다. 지지구간은 터널 벽면 부근의 변형을 억제하기 위해 축력이 발현되는 구간이며, 고정구간은 볼트의 뿌리 역할을 하는 구간이다(Freeman, 1978). 지지구간은 지반 자체의 변위가 록볼트의 변위보다 더 크게 발생하며, 고정구간은 록볼트의 변위가 더 크게 나타난다. 록볼트를 충분히 길게 하여 탄성영역 내에 설치하게 되면 고정구간이 지지구간보다 더 길게 형성된다(Lee, 2016). 또한 선단고정판 유무에 따라 전면접착형 록볼트는 Fig. 1과 같이 거동한다(Hyett et al., 1996).
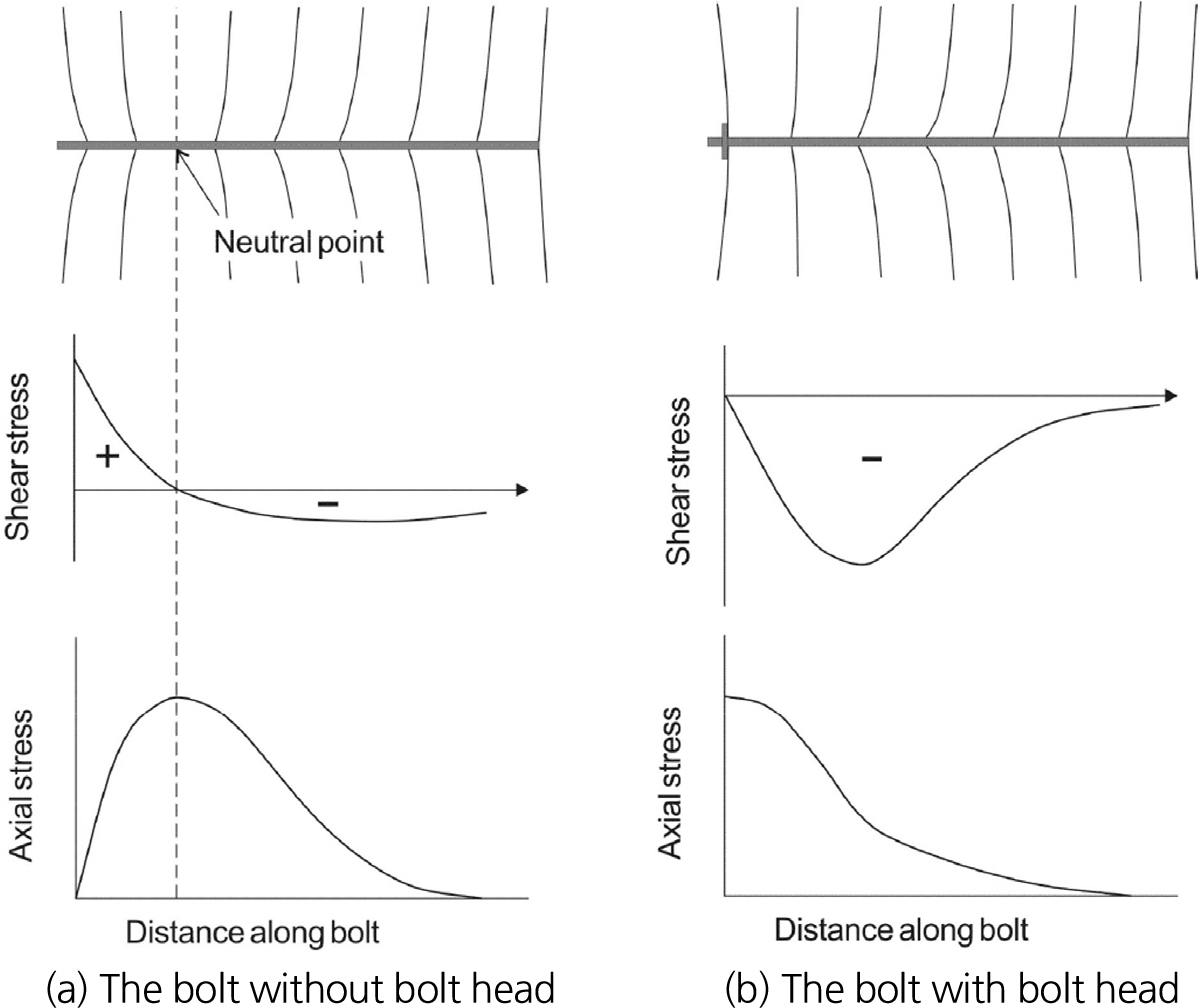
Fig. 1.
Distribution of axial and shear stresses along the bolt for two different condition (Hyett et al., 1996)
2.3 전면접착형 록볼트 모델링 방법
전면접착형 록볼트는 Truss요소와 Cable요소로 모델링할 수 있다. Truss요소는 록볼트가 통과하는 요소가 록볼트 그라우트로 보강되었다고 가정하여, 주변지반 요소의 노드 변위를 보간하여 통과요소 내 록볼트 변위를 구한다. 이를 임베디드 요소(embedded element)라 하며, 지반과 록볼트가 완전히 일체화되어 미끄러짐이 발생하지 않는 것으로 가정한다(Shin, 2020). Fig. 2는 Cable요소를 설명한다. Cable요소 또한 주변 지반 요소의 노드 변위를 보간하여 록볼트의 변위를 구한다. 반면 Cable요소는 Fig. 2(b)와 같이 축을 따라 Shear spring과 Shear slider가 형성되어 있다. 이를 통해 그라우트의 거동을 구현함으로써 록볼트와 지반 간 상대적인 거동을 고려할 수 있다. 즉, Truss요소와 달리 Cable요소는 그라우트의 거동을 구현할 수 있으므로 지반과 록볼트 간 미끄러짐의 발생을 고려할 수 있다.
3. 해석 조건
3.1 대상 터널의 단면 및 해석 조건
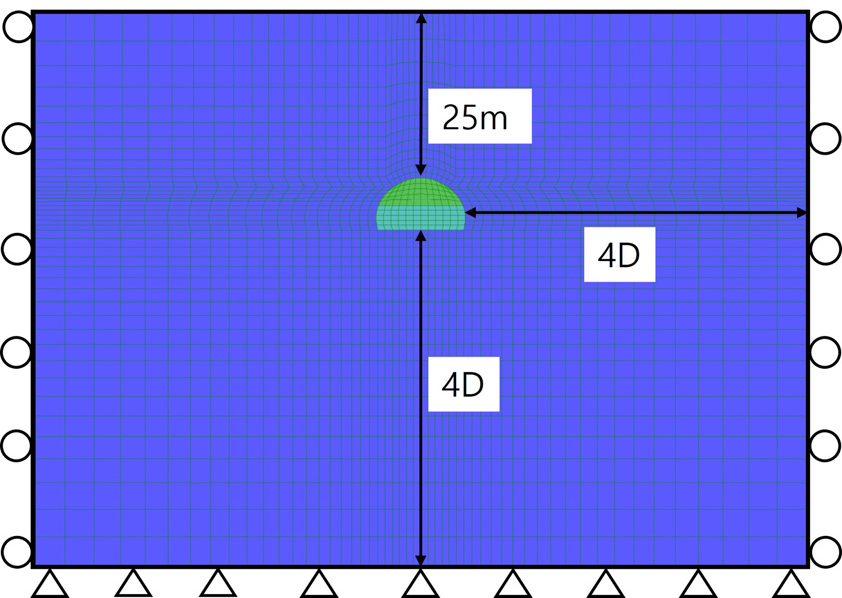
본 연구는 터널 2차원 수치해석을 수행하였다. 터널 단면은 고속국도 제400호선 양평~이천 간 건설공사 양평방향 터널의 설계도면을 참고하여 Fig. 3과 같이 모델링 하였다. 토피고는 25 m, 측부경계 및 하부경계는 4D를 적용하였다. 측부경계는 수평방향 변위를 구속하였고, 하부경계는 수평방향과 수직방향 변위를 구속하였다. 하중분담율은 2차원 터널해석에 주로 사용되는 굴착단계 40%, 연성 숏크리트 30%, 강성 숏크리트 30%을 적용하여 해석을 수행하였다(Kim and Shin, 2012). 또한 초기지압조건에 따른 터널 거동을 분석하기 위해 수평토압계수(K0)를 0.5, 1.0, 1.5로 각각 적용하여 해석을 수행하였다.
3.2 지반 물성 및 지보재 모델링
Table 1은 해석에 적용된 지보패턴이며, 지보패턴별 지반과 지보재 물성치는 각각 Table 2, Table 3에 나타내었다(Park et al., 2012). 본 연구에서는 전면접착형 록볼트 모델링 방법에 따른 터널 거동을 분석하기 위하여 보조공법은 고려하지 않고 주 지보재인 록볼트, 숏크리트, 강지보재만을 해석모델에 반영하였다. 록볼트의 선단고정판은 고려하지 않았으며, 숏크리트와 강지보재는 합성부재로 고려하였다. 합성부재의 등가 탄성계수는 단위 폭 또는 강지보재의 설치간격에 해당하는 임의 폭 당 포함되는 단면적비에 따라 식 (1)과 같이 구할 수 있다. 합성부재에 발생한 축력과 모멘트는 숏크리트와 강지보재가 분담한다. 이 때, 숏크리트에 작용하는 축력과 모멘트는 합성부재에 발생한 축력과 모멘트에 각각 식 (2)와 식 (3)으로 표현되는 분담율을 곱하여 구할 수 있다. 숏크리트에 작용하는 부재력을 이용하여 식 (4)로 응력을 계산할 수 있다.
여기서, 는 등가 탄성계수이다. 는 숏크리트의 탄성계수, 단면적, 단면 이차모멘트이며, 는 강지보재의 탄성계수, 단면적, 단면 이차모멘트이다. 는 숏크리트의 축력 분담율, 는 숏크리트의 휨모멘트 분담율이다.
여기서, 는 숏크리트의 휨 압축응력, 은 합성부재에 발생한 축력, 은 합성부재에 발생한 모멘트, 는 숏크리트에 분담된 축력는 숏크리트에 분담된 모멘트(), 는 숏크리트의 도심 거리이다(Kang et al., 2020).
Table 1.
Support patterns
Table 2.
Properties of support
Table 3.
Properties of rock mass
| P3 | P4 | P5 | |
| Unit weight (kN/m3) | 25 | 23 | 22 |
| Deformation coefficient (MPa) | 6,000 | 2,000 | 600 |
| Cohesion (kPa) | 100 | 40 | 10 |
| Friction angle (°) | 35.0 | 32.0 | 30.0 |
| Poisson’s ratio | 0.24 | 0.26 | 0.28 |
본 연구에서는 전면접착형 록볼트를 Truss요소와 Cable요소로 각각 다르게 모델링 한 뒤 터널 거동을 분석하는 것을 목적으로 하나, FDM은 Truss요소를 지원하지 않기 때문에 FEM을 활용하여 Truss요소 모델을 구축하였다. Cable요소는 프로그램 내에서 탄성-완전 소성거동을 기본으로 하지만, Truss요소는 재료모델을 직접 설정해주어야 한다. 따라서 Truss요소의 재료모델은 주로 금속재료를 모델링할 때 이용되며 탄성-완전 소성거동을 하는 Tresca모델을 적용하였다.
3.3 록볼트 인발시험 데이터를 활용한 그라우트 물성치 산정
록볼트 인발시험은 수도권 고속철도(◯◯)제 3-1공구 건설공사에서 시행되었다. 시험의 조건은 지보패턴 P3, P4, P5에서 수행되었으며, 각 패턴별로 터널 우측벽 10개소에서 시험이 수행되었다. 록볼트는 SD400/D25의 제원이 사용되었다. 인발시험은 충분한 정착효과가 얻어진 후에 실시하였으며, 인발하중의 재하속도는 1 ton/min 내외로 하였다. 지보패턴 P3, P4, P5에 대한 10개소에서의 인발시험 결과와 허용인발하중의 평균치를 Fig. 4에 나타내었다. Fig. 4의 점선과 실선은 각각 인발시험 결과의 형태와 허용인발하중 평균치의 시각화를 돕기 위해 도시하였다.
록볼트 인발시험 결과 중 허용인발하중은 설계치로 이용될 수 있다(Kim and Park, 2013). 따라서 Cable요소의 그라우트 전단강성(grout shear stiffness, )과 그라우트 전단강도(grout shear strength, )를 식 (5)와 식 (6)의 관계를 통해 계산하였다. 이 때, 10개소에서의 인발시험 결과가 상이하기 때문에 허용인발하중은 평균치를 적용하였다. Table 4는 지보패턴별 Cable요소의 그라우트 물성치이다.
Table 4.
Grout properties of cable element
| Support patterns | |||
| P3 | P4 | P5 | |
| Grout shear stiffness (N/m/m) | 6.751e6 | 4.133e6 | 3.515e6 |
| Grout shear strength (N/m) | 4.023e4 | 3.592e4 | 3.116e4 |
3.4 해석 Case
해석 Case는 Table 5에 나타내었다. Case 1-A와 Case 1-B는 각각 Truss요소와 Cable요소를 적용하지 않고, 숏크리트 및 강지보재만을 설치한 모델이다. 두 모델에 대하여 수치해석을 수행한 뒤 결과를 비교하여 록볼트 설치 전 두 모델의 수치해석 결과가 유사함을 확인한다. 이를 통해 전면접착형 록볼트를 Truss요소로 모델링하는 방법과 Cable요소로 모델링하는 방법, 이 두 가지 모델링 방법에 따른 터널 거동을 분석할 수 있음을 검증한다.
Table 5.
Case of numerical analysis
| Case 1 | Without rockbolt |
A (without truss) |
B (without cable) | ||
| Case 2 | With rockbolt |
A (truss) |
B (cable with stiff grouting properties) |
C (cable with pull-out test result) | |
Case 2의 세 가지 모델은 록볼트와 숏크리트 및 강지보재를 모두 설치한 모델이다. Case 2-A는 전면접착형 록볼트를 Truss요소로 모델링 하였고, Case 2-B와 Case 2-C는 Cable요소로 모델링하였다. 이 때, Case 2-B와 Case 2-C는 각각 그라우트 물성치를 지반과 록볼트 간 완전 접착을 가정하기 위해 임의로 크게 적용한 모델, 록볼트 인발시험 데이터를 통해 산정하여 적용한 모델이다. Case 2의 세 가지 모델을 통해 전면접착형 록볼트 모델링 방법에 따른 록볼트 및 터널 거동을 분석한다.
4. 해석 결과
4.1 록볼트 설치 전 터널 거동 분석
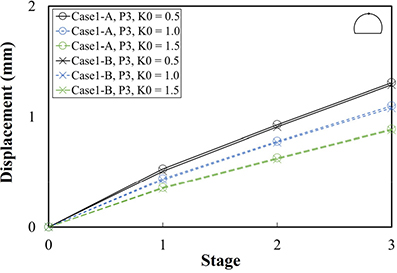
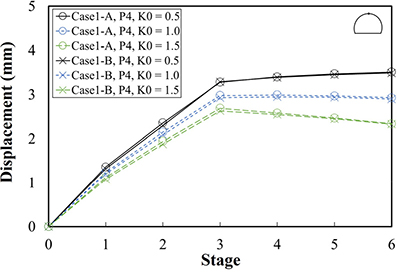
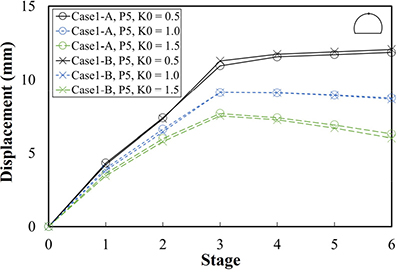
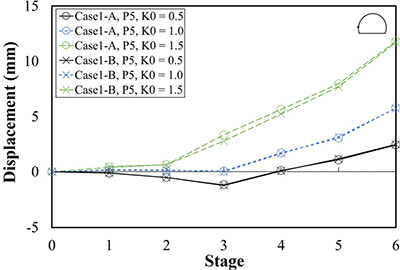
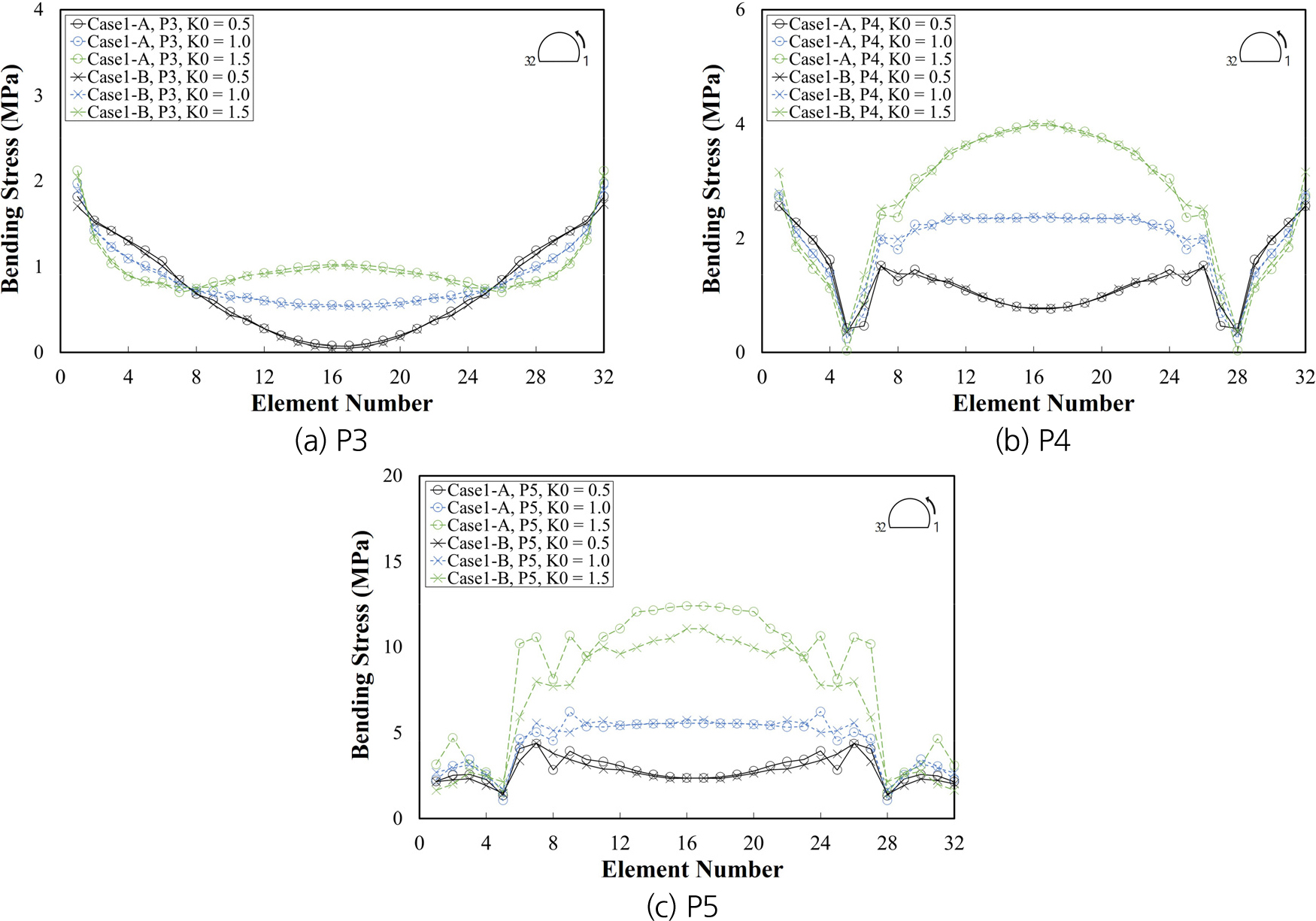
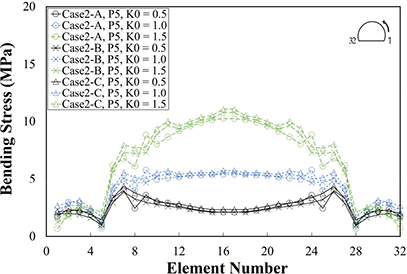
Table 6은 지보패턴별 해석 단계 및 하중분담율이다. P3은 전단면 굴착이 적용되며, P4와 P5는 상하반 분할 굴착이 적용된다. 따라서 P3, P4, P5의 해석 단계는 각각 3단계, 6단계, 6단계로 이루어진다. Table 7은 지보패턴 및 초기지압조건에 따른 Case 1-A와 Case 1-B의 변위, 숏크리트 응력이다. Table 8은 Case 1-A와 Case 1-B의 해석단계별 천단부 및 좌측벽부 변위이다. Fig. 5는 해석단면의 숏크리트 응력이며 마지막 시공단계(하반 숏크리트 경화단계)에서 계산된 숏크리트 응력이다. x축은 수치해석을 위해 작성된 해석단면에서 숏크리트의 부재번호를 나타내고 있다. 숏크리트 부재번호는 터널단면 우측하단에서 1로 시작하여 좌측하단에서 32로 끝난다.
Table 6.
Analysis stage & load distribution factor
Table 7.
Displacement and bending stress of shotcrete of Case 1
천단부 변위는 Case 1-A와 Case 1-B 모두 P5, P4 및 K0 = 0.5일 때는 해석단계가 진행됨에 따라 증가하였고, K0 = 1.0, 1.5일 때는 상반 굴착단계에서 증가하다가 하반 굴착 이후부터는 감소하였다. P3의 모든 초기 지압조건에서 천단부 변위는 Case 1-A와 Case 1-B 모두 해석단계가 진행됨에 따라 증가하였다. 좌측벽부 변위는 Case 1-A와 Case 1-B 모두 P5, P4 및 K0 = 1.5일 때는 해석단계가 진행됨에 따라 우측으로 발생하였고, K0 = 0.5, 1.0일 때는 상반을 굴착하는 단계에서 좌측으로 발생하다가 하반을 굴착하는 단계부터는 우측으로 발생하였다. P3의 모든 초기 지압조건에서 좌측벽부 변위는 Case 1-A와 Case 1-B 모두 해석단계가 진행됨에 따라 우측으로 발생하였다.
Case 1-A와 Case 1-B의 최대 변위차이는 P5 및 K0 = 1.5일 때 천단부와 좌측벽부에서 각각 Case 1-B가 Case 1-A보다 0.1 mm, 0.28 mm 크게 나타났으나, 그 차이는 미미한 것으로 판단된다. 이러한 결과들을 통해 Case 1-A와 Case 1-B의 변위 발생 경향이 유사하게 나타난 것으로 판단된다.
Case 1-A와 Case 1-B의 부재 번호에 따른 숏크리트 응력 발생 경향이 유사하게 나타남을 Fig. 5를 통해 확인할 수 있다. P5 및 K0 = 1.5일 때 Case 1-A가 Case 1-B보다 숏크리트 응력이 1.34 MPa 크게 발생하여 가장 큰 응력차이를 나타냈으나, Case 1-A와 Case 1-B 모두 천단부에 설치된 숏크리트에서 발생하였다.
본 절에서는 동일한 조건에서 록볼트를 설치하지 않은 모델인 Case 1-A와 Case 1-B의 터널 수치해석 결과를 비교하였다. 두 모델의 변위와 숏크리트 응력 발생경향이 유사하므로 서로 다른 록볼트 구조요소에 의한 터널 거동변화를 비교할 수 있는 것으로 판단할 수 있다.
4.2 Cable요소의 그라우트 물성치에 따른 전면접착형 록볼트 거동 분석
본 절에서는 동일한 조건에서 Case 2-B와 Case-C의 록볼트 거동을 비교하여 Cable요소의 그라우트 물성치에 따른 전면접착형 록볼트 거동을 분석하였다. Cable요소의 그라우트 물성치가 록볼트 거동에 미치는 영향을 검토하는 것이 목적이므로 지반조건이 가장 불량한 P5 및 K0 = 1.5일 때 만을 비교하였다. 이러한 조건에서 두 모델의 록볼트와 지반 간 상대변위, 록볼트의 중립점 위치, 축력 분포를 고찰하였다. Table 9는 두 모델의 Cable요소에 적용된 그라우트 물성치이다.
Table 9.
Grout properties of cable element
|
Case 2-B (cable element with stiff grouting properties) |
Case 2-C (cable element with pull-out test) | |
| Grout shear stiffness (N/m/m) | 1.5e10 | 3.515e6 |
| Grout shear strength (N/m) | 8.0e6 | 3.116e4 |
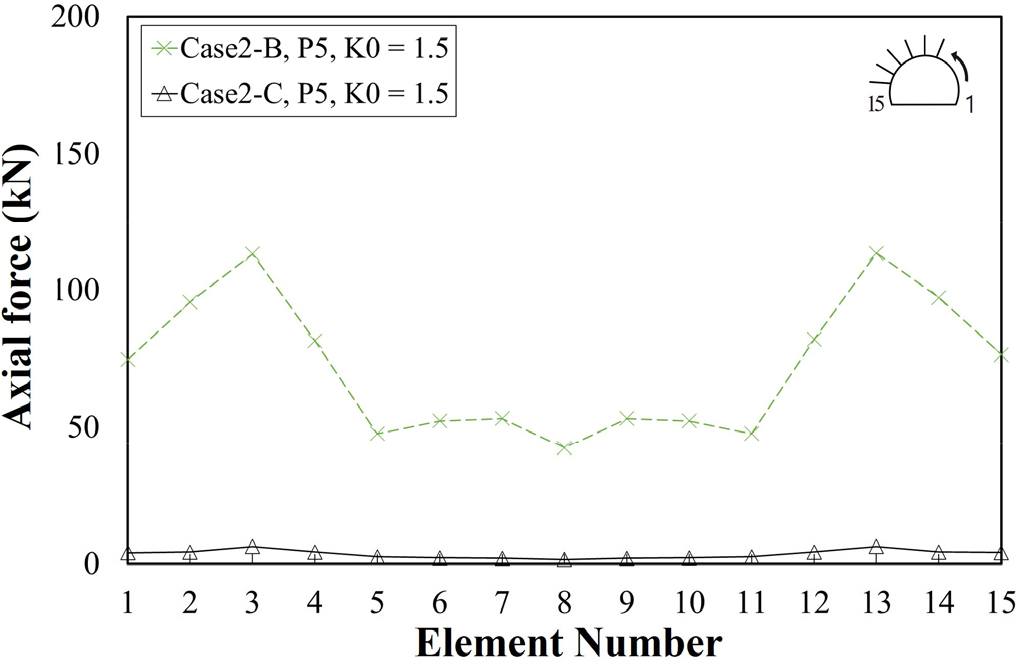
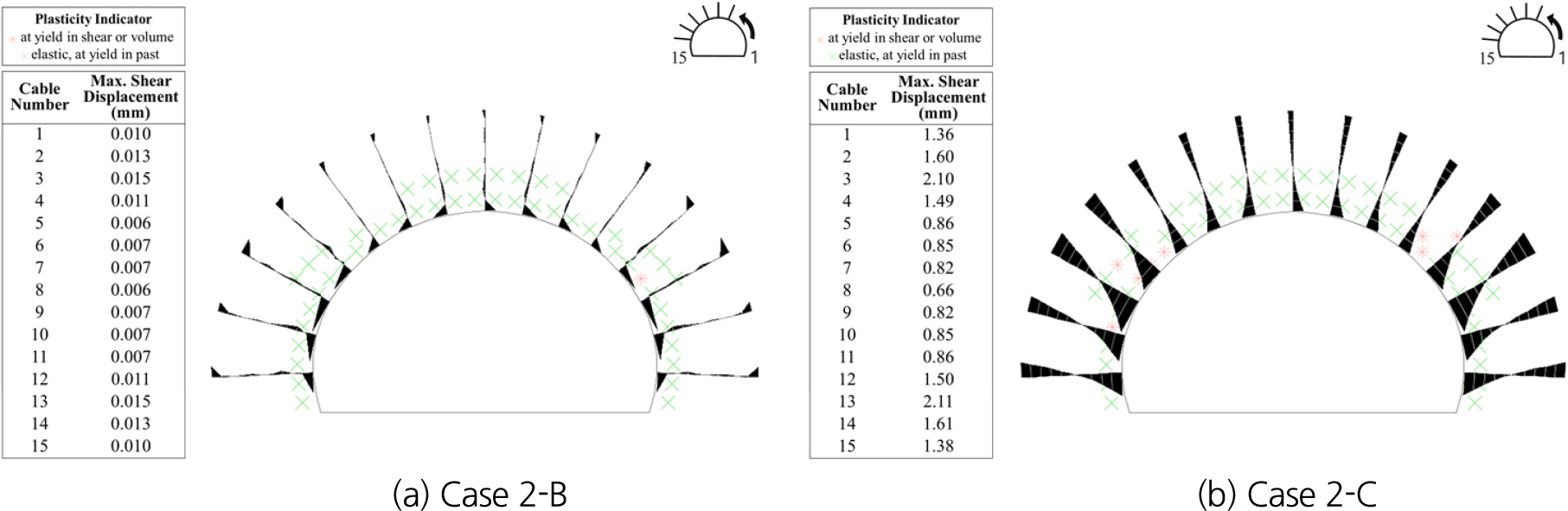
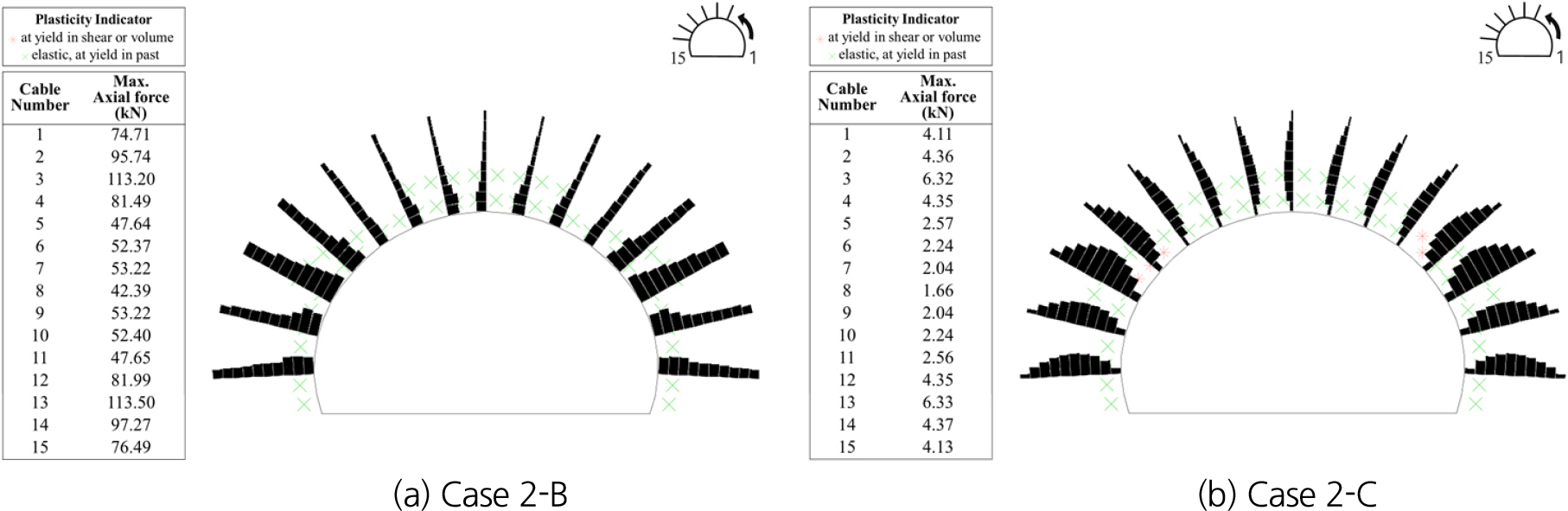
Fig. 6은 부재번호별 록볼트의 축력이다. 록볼트 부재번호는 터널 단면 우측 최하단에 설치된 록볼트를 1로 시작하여 좌측 최하단에 설치된 록볼트를 15로 끝난다. Fig. 7(a)와 Fig. 7(b)는 각각 Case 2-B와 Case 2-C의 록볼트의 상대변위 분포이고, Fig. 8(a)와 Fig. 8(b)는 각각 Case 2-B와 Case 2-C의 록볼트의 축력 분포이다.
Case 2-B와 Case 2-C의 록볼트 최대 축력은 13번 록볼트에서 각각 113.50 kN, 6.33 kN이 발생하는 것을 Fig. 6을 통해 확인할 수 있다. 이는 Case 2-B가 Case 2-C보다 록볼트 축력이 약 17.93배 더 크게 발생한 결과이다. Case 2-B와 Case 2-C의 록볼트와 지반 간 최대상대변위는 13번 록볼트의 지지구간에서 각각 0.015 mm, 2.11 mm가 발생하는 것을 Fig. 7을 통해 확인할 수 있다. Case 2-B의 록볼트는 상대변위 분포가 고르지 못하고 완전 접착에 가까운 거동을 하는 반면, Case 2-C의 록볼트는 상대변위 분포가 고른 형태로 나타났으며 상대변위를 어느정도 허용하는 결과를 나타내었다. 또한 Case 2-B의 록볼트 중립점은 터널 벽면 부근인 0~1 m에 위치하였고, Case 2-C의 록볼트 중립점은 중간지점 부근인 1~2 m에 위치하였다.
두 모델의 록볼트가 탄성영역까지 길게 설치되어 있음을 Fig. 8에서 확인할 수 있다. 이 결과와 더불어 본 연구에서는 선단 고정판을 고려하지 않았으므로 록볼트의 축력 분포는 2.2절의 Fig. 1(a)와 같이 형성되는 것이 적합하다. 두 모델의 록볼트 축력 분포를 비교하였을 때, 전체적으로 Case 2-C의 록볼트 축력 분포가 Case 2-B의 축력 분포보다 이론적으로 더 적합한 형태로 나타난 것으로 판단된다.
이러한 결과들을 종합하여 보았을 때, Case 2-C의 록볼트는 Case 2-B의 록볼트보다 전면접착형 록볼트의 거동 특성을 더 잘 반영하는 것으로 판단된다. 따라서 Cable요소로 전면접착형 록볼트를 모델링할 시 적절한 그라우트 물성치 적용은 중요한 것으로 판단되며, 거동 특성을 반영하기 위해 록볼트 인발시험 데이터를 활용하는 방법은 유효한 방법으로 판단된다.
4.3 전면접착형 록볼트 모델링 방법에 따른 터널 거동 분석
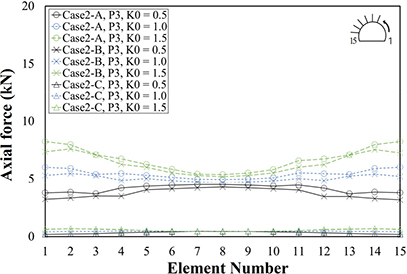
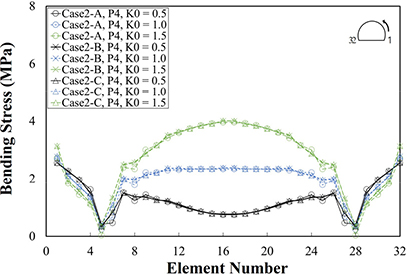
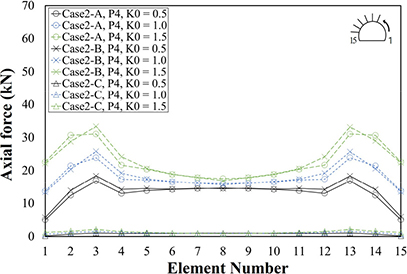
본 절에서는 3.4절에 언급된 3가지 전면접착형 록볼트 모델링 방법에 따른 변위, 숏크리트 응력, 록볼트 축력을 분석한다. Table 10은 지보패턴 및 초기지압조건에 따른 Case 2-A, Case 2-B, Case 2-C의 변위, 숏크리트 응력, 록볼트 축력이다. Table 11은 해석단면의 부재번호별 숏크리트 응력, 록볼트 축력이다. 그래프의 x축은 수치해석을 위해 작성된 부재번호를 나타낸다. 숏크리트 부재번호는 터널단면 우측하단에서 1로 시작하여 좌측하단에서 32로 끝나며, 록볼트 부재번호는 터널단면 우측 최하단에 설치된 록볼트를 1로 시작하여 좌측 최하단에 설치된 록볼트를 15로 끝난다.
Table 10.
Displacement and force of the supports of Case 1
Case 2-A과 Case 2-B의 천단부 최대 변위는 P5 및 K0 = 0.5일 때 각각 11.70 mm, 11.89 mm이 발생하였다. 이는 Case 2-A과 Case 2-B의 록볼트 설치 전 대비 각각 0.17 mm, 0.18 mm만큼의 변위를 억제하는 결과이다. Case 2-C의 천단부 최대 변위는 12.07 mm의 변위가 발생하였으며, 이는 록볼트 설치 전 대비 변위를 억제하지 못한 결과이다. Case 2-A, Case 2-B의 좌측벽부 최대 변위는 P5 및 K0 = 1.5조건에서 각각 11.45 mm, 11.37 mm로 발생하였다. 이는 록볼트 설치 전 대비 각각 0.36 mm, 0.34 mm만큼의 변위를 억제하는 결과이다. Case 2-C의 좌측벽부 최대변위는 11.71 mm로 천단부 변위와 마찬가지로 록볼트 설치 전 대비 변위를 억제하지 못하였다. P4와 P3 조건에서는 천단부 변위와 좌측벽부 변위가 모든 Case에서 록볼트 설치 전 대비 0.00~0.02 mm가 억제되었다.
록볼트 설치에 의한 변위 억제는 3가지 모델링 방법 모두 미미한 것으로 판단된다. 3가지 모델의 록볼트 설치에 의한 천단부 및 좌측벽부 변위 억제경향을 비교하였을 때, 지반조건이 불량한 P5에서는 Case 2-A와 Case 2-B는 록볼트가 터널의 변위를 미소하게 억제하였지만, Case 2-C는 그렇지 않았음을 확인할 수 있다. P4와 P3조건에서는 모든 Case에서 록볼트가 터널 변위 억제에 크게 관여하지 않았음을 확인할 수 있다.
Case 2-A와 Case 2-B의 숏크리트 최대 응력은 P5 및 K0 = 1.5일 때 천단부에 설치된 숏크리트에서 각각 10.24 MPa, 10.77 MPa 발생하였다. 이는 록볼트 설치 전 대비 각각 2.17 MPa, 0.30 MPa 감소한 결과이다. 특히 전면접착형 록볼트를 Truss요소로 모델링한 Case 2-A는 숏크리트 응력이 록볼트 설치에 의해 17.49% 감소한 결과이며, 이는 무시할 수 없는 결과로 판단된다. Case 2-C의 숏크리트 최대 응력은 P5 및 K0 = 1.5일 때 11.07 MPa로 록볼트 설치 전과 같은 결과를 나타내었다. P4와 P3조건에서는 모든 Case에서 숏크리트 응력이 록볼트 설치에 의해 0.00~0.02 MPa 감소하였다.
록볼트 설치에 의한 숏크리트 응력 감소는 P5에서 가장 크게 나타났다. P5는 지반조건이 불량하기 때문에 지보재에 작용하는 하중이 P4, P3보다 크다. 따라서 숏크리트와 록볼트가 지보재에 작용하는 하중을 분담하는 정도가 더욱 명확하게 나타난다. Case 2-A와 Case 2-B는 Case 2-C보다 숏크리트 응력을 더 크게 억제하였는데, 이는 지보재에 작용하는 하중을 숏크리트가 아닌 록볼트가 부담하는 정도가 Case 2-A와 Case 2-B가 Case 2-C보다 더 크기 때문에 발생된 경향으로 판단된다. 따라서 지반조건이 불량할 경우 전면접착형 록볼트를 정밀하게 모델링 하지 않으면, 즉, 거동 특성을 고려하지 않으면 숏크리트 응력이 과소평가될 가능성이 있는 것으로 판단된다.
Case 2-A와 Case 2-B의 록볼트 최대 축력은 P5 및 K0 = 1.5일 때 좌측벽부에 설치된 록볼트(부재번호 13번)에서 각각 124.38 kN, 113.50 kN이 발생하였고, Case 2-C의 록볼트 최대 축력은 P5 및 K0 = 1.5일 때 좌측벽부에 설치된 록볼트(부재번호 13번)에서 6.33 kN이 발생하였다. 즉, Case 2-C는 Case 2-A와 Case 2-B에 비해 록볼트 최대 축력이 각각 94.91%, 94.42% 적게 발생하였다. 또한 모든 지보패턴 및 초기 지압조건에서 Case 2-C의 록볼트의 축력은 Case 2-A과 Case 2-B에 비해 90% 이상 더 적게 발생하였다. 따라서 전면접착형 록볼트 모델링 시 거동 특성을 고려하지 않으면 록볼트의 축력이 과다하게 산정될 수 있다.
5. 결 론
터널 수치해석 시 전면접착형 록볼트는 거동 특성을 고려하지 않은 방법으로 모델링되는 경우가 많다. 이는 지보재의 부재력을 과소 혹은 과대평가하는 요인이 될 수 있다. 본 연구는 합리적인 전면접착형 모델링 방법을 제시하기 위해 Cable요소의 그라우트 물성치에 따른 록볼트 거동 특성을 분석하였고, 동일한 터널 조건에서 전면접착형 록볼트를 Truss요소와 Cable요소로 각각 다르게 모델링하여 수치해석을 수행한 뒤 해석결과를 비교하였다. 연구 결과를 바탕으로, 그라우트 거동 특성을 반영할 수 있는 전면접착형 록볼트 모델링 방법을 제시한다. 연구 결과는 다음과 같다.
1. Cable요소는 전면접착형 록볼트의 그라우트 거동 특성을 반영할 수 있다. 4.2절 결과를 통해 Cable요소로 전면접착형 록볼트를 모델링할 시 적절한 그라우트 물성치 적용은 중요한 것으로 판단되며, 거동 특성을 반영하기 위해 록볼트 인발시험 데이터를 활용하는 방법은 유효한 방법으로 판단된다.
2. 전면접착형 록볼트 모델링 방법에 따른 터널 거동을 분석하였다. Truss요소, 강한 그라우트 물성치를 적용한 Cable요소 및 인발시험 결과를 반영한 Cable요소를 이용한 모델링 방법에 따른 변위제어효과는 3가지 모델링 방법 모두 큰 차이가 없는 것으로 판단된다.
3. 지반조건이 불량할 경우 전면접착형 록볼트를 정밀하게 모델링 하지 않으면, 즉, 그라우트의 특성을 고려하지 않으면 숏크리트 응력이 과소평가될 가능성이 있는 것으로 판단된다. 특히 전면접착형 록볼트를 Truss요소로 모델링하는 경우 지반이 불량하고 수평토압계수가 클수록 숏크리트 응력이 과소평가되는 것으로 검토되었다.
4. 모든 지보패턴 및 초기지압조건에서 인발시험 결과를 반영한 그라우트 물성치를 적용한 Cable요소의 록볼트에서 90% 이상 축력이 작게 나타났다. Truss요소 및 강한 그라우트 물성치를 적용한 Cable요소로 록볼트를 모델링하는 경우 록볼트의 축력을 과대평가할 수 있는 것으로 검토되었다.
5. 이러한 연구결과들을 바탕으로 터널 수치해석 시 전면접착형 록볼트는 그라우트 거동을 표현할 수 있는 요소로 모델링하는 것이 바람직하며, 그라우트 물성치는 록볼트 인발시험 데이터를 통해 획득하여 적용하는 것이 합리적인 모델링 방법으로 판단된다.
본 연구는 전면접착형 록볼트 모델링 방법을 제시하는 과정에서 암반의 절리는 해석모델에 반영하지 않았다. 이는 실제 록볼트의 주된 보강효과인 절리의 봉합효과를 연구과정에서 고려하지 않았음을 뜻한다. 이후 수행될 연구는 록볼트 모델링 방법에 따른 절리의 봉합효과를 분석함으로써 본 연구가 지닌 한계를 보완할 수 있다.