A basic study on explosion pressure of hydrogen tank for hydrogen fueled vehicles in road tunnels

Ji-Oh Ryu; Sang-Ho Ahn; Hu-Yeong Lee

doi:10.9711/KTAJ.2021.23.6.517

Preview

Research Paper

Journal of Korean Tunnelling and Underground Space Association. 30 November 2021. 517-534
https://doi.org/10.9711/KTAJ.2021.23.6.517

A basic study on explosion pressure of hydrogen tank for hydrogen fueled vehicles in road tunnels

도로터널에서 수소 연료차 수소탱크 폭발시 폭발압력에 대한 기초적 연구

Ji-Oh Ryu¹^*

Sang-Ho Ahn²

Hu-Yeong Lee³

류 지오¹^*

안 상호²

이 후영³

¹Professor, Dept. of Mechanical and Automotive Engineering, Shinhan University

²Professor, Dept. of Mechanical and Automotive Engineering, Shinhan University

³Student, Dept. of ICT Mechanical Engineering, Shinhan University Graduate School

¹정회원, 신한대학교 기계자동차융합공학과 교수

²비회원, 신한대학교 기계자동차융합공학과 교수

³정회원, 신한대학교 대학원 ICT기계공학과 박사과정

^{*Corresponding Author}

ABSTRACT

Hydrogen fuel is emerging as an new energy source to replace fossil fuels in that it can solve environmental pollution problems and reduce energy imbalance and cost. Since hydrogen is eco-friendly but highly explosive, there is a high concern about fire and explosion accidents of hydrogen fueled vehicles. In particular, in semi-enclosed spaces such as tunnels, the risk is predicted to increase. Therefore, this study was conducted on the applicability of the equivalent TNT model and the numerical analysis method to evaluate the hydrogen explosion pressure in the tunnel. In comparison and review of the explosion pressure of 6 equivalent TNT models and Weyandt’s experimental results, the Henrych equation was found to be the closest with a deviation of 13.6%. As a result of examining the effect of hydrogen tank capacity (52, 72, 156 L) and tunnel cross-section (40.5, 54, 72, 95 m²) on the explosion pressure using numerical analysis, the explosion pressure wave in the tunnel initially it propagates in a hemispherical shape as in open space. Furthermore, when it passes the certain distance it is transformed a plane wave and propagates at a very gradual decay rate. The Henrych equation agrees well with the numerical analysis results in the section where the explosion pressure is rapidly decreasing, but it is significantly underestimated after the explosion pressure wave is transformed into a plane wave. In case of same hydrogen tank capacity, an explosion pressure decreases as the tunnel cross-sectional area increases, and in case of the same cross-sectional area, the explosion pressure increases by about 2.5 times if the hydrogen tank capacity increases from 52 L to 156 L. As a result of the evaluation of the limiting distance affecting the human body, when a 52 L hydrogen tank explodes, the limiting distance to death was estimated to be about 3 m, and the limiting distance to serious injury was estimated to be 28.5~35.8 m.

Keywords

TNT model

Hydrogen tank explosion

Explosion pressure

Hydrogen fueled vehicles

Plane wave

수소연료는 환경오염문제를 해소하고 에너지 불균형 및 비용을 절감할 수 있다는 점에서는 화석연료를 대체하는 에너지원으로 부각되고 있다. 수소는 친환경적이나 폭발성이 강하기 때문에 수소연료차의 화재, 폭발 사고에 대한 우려가 매우 높은 실정이다. 연구결과에서 수소사고는 일반적인 화재의 경우 비교적 안전하나, 폭발이 발생하면 매우 위험한 것으로 인식되고 있다. 특히, 터널과 같은 반밀폐공간에서는 위험도가 보다 증가할 것으로 예측되기에 이에 대한 예측방법 및 대책을 마련하기 위한 연구가 수행되고 있다. 이에 본 연구에서는 터널에서 수소폭발시 안전성을 평가하기 위해서 등가 TNT모델의 적용성과 수치해석 방법에 대한 검토를 수행하였다. 6개의 등가 TNT모델과 Weyandt의 실험결과의 폭발압력을 비교 ‧ 검토하여 모델의 적용성을 평가한 결과, Henrych식이 13.6%의 편차로 가장 근접하는 것으로 나타났다. 수치해석을 이용하여 수소탱크 용량(52, 72, 156 L)과 터널 단면적(40.5, 54, 72, 95 m²)이 폭발압력에 미치는 영향에 대한 검토한 결과, 터널에서 폭발 압력파는 초기에는 대기중에서와 마찬가지로 반구형 형태로 전파되나 벽체에 도달하면 반사파가 형성되며, 일정 거리 이상에서는 평면파로 변형되어 아주 완만한 감쇄율로 전파하는 것으로 나타났다. 등가 TNT모델인 Henrych식은 폭발압력이 급격하게 감소하는 구간에서는 수치해석 결과와 잘 일치하나 폭발압력파가 변형된 이후에는 큰 폭으로 과소평가하는 것으로 나타났다. 수소탱크용량이 동일한 경우에는 터널 단면적이 증가할수록 폭발압력이 감소하며, 단면적이 동일한 경우에는 수소탱크 용량이 52 L에서 156 L로 증가하면 폭발압력은 약 2.5배 정도 증가하는 것으로 나타났다. 인체에 영향을 미치는 한계거리에 대한 평가결과, 수소탱크용량이 52 L인 경우 사망에 이르는 한계거리는 약 3 m, 중상에 이르는 거리는 단면적별로 차이가 있으나 28.5~35.8 m로 나타났다.

키워드

TNT 모델

수소탱크 폭발

폭발 압력

수소연료차

평면파

MAIN

1. 서 론
2. TNT 등가 모델에 의한 폭발압력 분석
2.1 TNT 등가모델
2.2 폭발 압력계산식
2.3 폭발압력 비교
3. 수치해석에 의한 폭발압력 분석
3.1 해석모델의 검증
3.2 터널에서 수소탱크 폭발압력 해석모델
3.3 폭발 압력파 전파특성 고찰
3.4 폭발압력에 대한 단면적의 영향 분석
3.5 폭발압력에 대한 수소탱크용량의 영향 분석
3.6 인체영향에 따른 한계거리 분석
4. 결 론

1. 서 론

수소연료는 환경오염문제를 해소하고 에너지 불균형 및 비용을 절감할 수 있다는 점에서는 기존의 화석연료를 대체하는 에너지원으로 부각되고 있으며, 각국은 수소경제로의 전환을 위한 로드맵을 발표하고 있다. 산업통산자원부(MOTIE, 2019)에 따르면 국내 수소연료차 보급은 2040년까지 620만대를 보급하고 1,200개의 수소충전소를 확충하는 계획을 수립하고 있다. 이에 따라 향후 수소연료차의 보급이 급속도로 증가할 것으로 예상된다. 그러나 수소는 친환경적이나 폭발성이 강하기 때문에 수소연료차의 화재, 폭발 사고에 대한 우려가 매우 높은 실정이다. 이에 각국은 수소연료차의 안전성 확보의 일환으로 터널과 같은 반밀폐공간에서 수소 연료차의 폭발에 대비한 추가적인 대책의 필요성 등에 대한 많은 연구가 수행되고 있다(HyTunnel-CS, 2019).

Korea Research Institute of Standards and Science (2016)은 액화수소용기의 건전성 평가 및 안전기술 개발연구에서 수소와 관련된 국내 사고사례를 조사하였으며, 화재사고가 30.7%, 폭발사고 20%, 화재와 폭발을 동반한 사고 4%, 단순 누출사고 45.3%이고, 누출사고 시 폭발로 전개될 확률을 11.4%로 제시하고 있다. 또한 실내에서 시간당 수소 누출량을 0.17~0.68 g/s로 하여 FDS (Fire Dynamics Simulator)에 의해서 화재해석을 수행한 결과, 화재로 인한 인명피해는 발생하지 않으며, 폭발해석을 통해 폭발현상이 발생하면 공간 내 존재하는 모든 인명이 사망하는 것으로 예측하고 있다.

LaFleur et al. (2017)은 수소연료차의 수소누출, 제트화염, 화재폭발 등 다양한 위험요인에 대한 발생 가능성 및 위험을 분석하여 수소연료차 사고시나리오를 제시하고 있으며, 사고시나리오별 위험평가에 따르면 수소누출에 따른 일반화재나 제트화염은 비교적 위험이 높지 않으나, 수소가스의 폭발이 가장 위험한 것으로 보고하고 있다. Glover et al. (2020) 보고서에서는 도로터널에서 수소연료차의 위험평가를 위한 정량적인 위험 분석 시나리오를 통해 수소연료차 사고 시 폭발확률을 0.092%로 제시하고 있다.

이상에서 수소사고는 일반적인 화재 시에는 비교적 안전하나, 폭발이 발생하면 매우 위험한 것으로 인식되고 있음을 알 수 있다. 특히, 터널과 같은 반밀폐공간에서는 위험도가 보다 증가할 것으로 예측되기에 이에 대한 예측방법 및 대비책을 마련하기 위한 연구가 수행되고 있다.

수소 폭발 시 폭발압력(over pressure)을 예측하기 위한 연구는 일반적으로 실험적인 방법과 해석적인 방법을 통해 연구되고 있다. 해석적인 방법으로는 등가 TNT모델을 적용하는 방법과 수치해석적인 방법이 적용되고 있으며, 이에 대한 연구동향을 정리하면 다음과 같다.

Zalosh and Weyandt (2005)는 체적 72 L, 압력 34.3 MPa의 Type-II 수소탱크를 TPRD (Thermal Pressure Relief Device)를 제거한 채로 가열하여 탱크의 열화에 의해서 폭발시키고 폭발압력을 측정하는 실험을 실시하였다. 수소탱크는 약 370 kW로 가열한 후 6분 27초 만에 폭발하였으며, 폭발순간의 연료탱크의 내부 압력과 온도는 35.7 MPa, 39°C이고 지점별 최대 폭발압력은 300 (1.9 m), 83, 61 (4.2 m), 41 kPa (6.5 m)로 측정하고 있다.

또한 Southwest Research Institute’s (2006)는 34.5 MPa, 88 L의 수소탱크가 SUV차량에 장착된 채로 프로판에 의해서 가열하여 수소탱크 폭발실험을 수행한 결과, 가열 후 12분 18초에 폭발이 발생하며, 차량의 후미방향의 측정지점별 폭발압력을 140 (1.22 m), 56 (2.5 m), 30 (5 m), 14 (9.75 m), 5.5 kPa (24.38 m), 차량의 옆 방향에서는 측정지점별로 80 (2.5 m), 69 kPa (5.0 m)로 측정하고 있다. 위 두 실험은 Weyandt에 의해서 수행되었으며, 수소탱크가 차량에 장착된 채로 폭발하는 경우에는 2005년에 실험한 수소탱크만 가열할 때 폭발압력의 약 1/2 수준으로 감소하는 것으로 나타나고 있다. 차량에 장착된 경우에는 측정방향에 따라서 상당한 차이가 있는 것으로 나타나고 있다.

Yoon (2016)은 고체 및 기체의 폭발성 물질의 폭발에 따른 최대 과압과 충격량을 평가하기 위하여 TNT 등가법을 적용하였으며, 기존 실험에 의하여 발표된 최대과압-환산거리곡선과 환산충격량-환산거리 곡선을 폭발수율(0.01, 0.05, 0.1)조건에서 피팅하여 회기도식을 도출하고 Kingery-Bulmash 다항식과 비교하여 제시하였다.

Kwon and Park (2015)은 가스폭발에 따른 폭발에너지를 평가하기 위하여 TNT 등가량 환산방법에 대한 고찰을 수행하였으며, TNT 등가모델을 적용하여 보수적인 방법으로 폭발압을 예측하는 것이 가능한 것으로 보고하고 있다.

터널 내에서 수소폭발이 발생하는 경우에 폭발압력에 대한 예측은 Molkov and Kashkarov (2015), Shentsov et al. (2018), Molkov and Dery (2020)의 논문이 대표적이며, 등가 TNT모델 및 수치해석에 의한 결과를 실험결과와 비교하고 있다. 터널에서 폭발 압력파는 구조물에 도달하기 전까지는 대기중과 동일한 반구형 전파특성을 보이고 일정거리에 도달하면 평면파로 변형되는 것으로 보고하고 있으며, 평면파로 변형되기 전까지는 복잡한 양상을 보이는 것으로 보고하고 있다. 또한 시뮬레이션 결과를 정리하여 터널에서 폭발압력 예측을 위한 무차원 상관관계식을 제시하고 있다.

전술한 바와 같이 터널에서 폭발압력에 대한 예측은 터널의 단면의 형상 및 단면적에 영향을 크게 받으며, 등가 TNT모델을 적용하는 경우에도 수소가 갖는 에너지중에 폭발에너지로 변환되는 폭발수율에 영향을 크게 받는 것으로 알려져 있다.

따라서 본 연구에서는 현재 일반적으로 시공되고 있는 터널의 단면적과 상용 수소연료차의 수소탱크의 용량을 고려하여 터널 내에서 폭발압력을 예측하기 위한 방법론에 대한 고찰을 수행하고 수치해석적인 방법에 의해서 폭발압력을 해석하여 인체에 미치는 영향을 고려하기 위한 한계거리에 대한 검토를 수행하였다.

2. TNT 등가 모델에 의한 폭발압력 분석

등가 TNT모델은 TNT 폭발실험 결과를 바탕으로 하여 도출된 경험식으로 다른 폭발물의 등가 TNT질량을 구하여 폭발압력을 예측하는데 주로 사용되고 있다. 이에 본 장에서는 등가 TNT 모델에 대한 폭발압력을 분석하였다.

2.1 TNT 등가모델

등가 TNT모델은 식 (1)에 등가 TNT 질량( $M_{T N T}$ )을 구하고, 식 (2)에 의해서 환산거리( $Z_{e}$ ; Scale Distance)를 구하여 $Z_{e}$ 에 따른 폭발압력( $P_{E X}$ )를 경험식이나 선도에 의해서 구하게 된다.

(1)

M_{T N T} = \frac{E}{H_{T N T}}

(2)

Z_{e} = \frac{R}{\sqrt[3]{M_{T N T}}}

여기서, $E$ 는 폭발에너지(kJ)이며, $H_{T N T}$ 는 TNT의 연소열로 4,686 kJ/kg이다.

폭발에너지는 폭발물이 갖는 화학적 에너지( $E_{C H}$ ; kJ)와 기계적 에너지( $E_{M}$ ; kJ)중에 에너지 변환효율( $α, β$ )을 고려하여 식 (3)과 같이 결정한다.

(3)

E = α E_{M} + β E_{C H}

일반적으로 폭발 에너지가 화학반응에 의해서 발생하는 경우에는 $E_{C H}$ 를 폭발물의 총 연소열로 하고 여기에 변화효율을 고려하나, 고압의 수소연료탱크의 폭발의 경우에는 압력팽창에 의한 기계적 에너지가 폭발에너지로 변환되며 폭발압을 형성하고 연소는 그 이후에 일어나기 때문에 연소에너지가 폭발에너지에 기여하는 정도는 비교적 작은 것으로 평가된다.

본 연구에서는 Molkov가 제시한 식 (4)를 이용하여 기계적 에너지를 구하고 이를 폭발에너지로 고려하여 등가 TNT질량을 구하였다.

(4)

E_{M} = \frac{(P_{H_{2}} - P_{a t m}) (V_{H_{2}} - m_{H_{2}} \cdot b)}{γ - 1}

여기서, $P_{H_{2}}$ 와 $P_{a t m}$ 은 수소압력(Pa) 및 대기압(Pa), $V_{H_{2}}$ 는 수소의 체적(m³), $b$ 는 co-volume constant로 실제기체의 체적계산시 이상기체방정식을 보정하기 위한 상수로 7.69 × 10^-3 m³/kg이다.

수소의 질량( $m_{H_{2}}$ )은 식 (5)로 구한다.

(5)

m_{H_{2}} = (\frac{P_{H_{2}}}{P_{H_{2}} \cdot b + R \cdot T_{H_{2}} / M_{H_{2}}}) V_{H_{2}}

여기서, $R$ 은 기체상수(8.314 J/mol ‧ K), $T_{H_{2}}$ 은 수소탱크 내부온도(K), $M_{H_{2}}$ : 수소분자의 분자량(2.016 g/mol), $V_{H_{2}}$ 은 수소탱크의 체적(m³)이다.

2.2 폭발 압력계산식

2.2.1 Swisdak equation

Swisdak식은 Kingery-Bulmash식을 단순화한 것으로 식 (6)과 같다.

(6)

P_{E X} = e^{(A + B (l n Z_{e}) + C {(l n Z_{e})}^{2} + D {(l n Z_{e})}^{3} + E {(l n Z_{e})}^{4})}

여기서, $A$ ~ $E$ : 폭발유형, 규모거리범위에 따른 상수(Table 1)이다.

Table 1.

Constants for Swisdak equation

Z_e Constants	0.2~2.9	2.9~23.8	23.8~198.5
A	7.2106	7.5938	6.0536
B	-2.1069	-3.0523	-1.4066
C	-0.3229	0.4098	0
D	0.1117	0.0261	0
E	0.0685	-0.0127	0

2.2.2 Sadovskiy equation

Sadovskiy는 $Z_{e}$ 에 따른 최대압력을 식 (7)과 같이 제시하고 있다.

(7)

P_{E X} = \frac{0.085}{Z_{e}} + \frac{0.3}{Z_{e}^{2}} + \frac{0.8}{Z_{e}^{3}}

2.2.3 Henrych equation

Henrych는 $Z_{e}$ 에 따른 최대압력을 식 (8)과 같이 제시하고 있다.

(8a)

P_{E X} = \frac{14.0717}{Z_{e}} + \frac{5.5397}{Z_{e}^{2}} - \frac{0.3572}{Z_{e}^{3}} + \frac{0.00625}{Z_{e}^{4}} for 0.05 \leq Z_{e} \leq 0.3

(8b)

P_{E X} = \frac{6.1938}{Z_{e}} - \frac{0.3262}{Z_{e}^{2}} - \frac{2.1324}{Z_{e}^{3}} for 0.3 \leq Z_{e} \leq 1.0

(8c)

P_{E X} = \frac{0.661}{Z_{e}} - \frac{4.05}{Z_{e}^{2}} - \frac{3.288}{Z_{e}^{3}} for 1.0 \leq Z_{e} \leq 10

2.2.4 Brode equation

최대 압력은 식 (9)로 제시하고 있다.

(9a)

P_{E X} = \frac{0.975}{Z_{e}} - \frac{1.455}{Z_{e}^{2}} - \frac{5.85}{Z_{e}^{3}} - 0.019 for 10 bar \leq P_{EX} \leq 0.1 bar

(9b)

P_{E X} = \frac{6.7}{Z_{e}^{3}} + 1 for P_{E X} > 10 bar

2.2.5 Kinney & Graham equation

식 (10)은 공중에서 폭발이 발생하여 폭발파가 구형으로 전파되는 경우에 대한 예측식이다.

(10)

P_{E X} = \frac{808 [1 + {(\frac{Z_{e}}{4.5})}^{2}]}{\sqrt{1 + {(\frac{Z_{e}}{0.048})}^{2}} ∙ \sqrt{1 + {(\frac{Z_{e}}{0.32})}^{2}} ∙ \sqrt{1 + {(\frac{Z_{e}}{1.35})}^{2}}} ∙ P_{a t m}

2.2.6 Wei & Dharani equation

(11)

P_{E X} = P_{a t m} (\frac{0.696}{Z_{e}} + \frac{2.1}{Z_{e}^{2}} + \frac{4.13}{Z_{e}^{3}})

2.3 폭발압력 비교

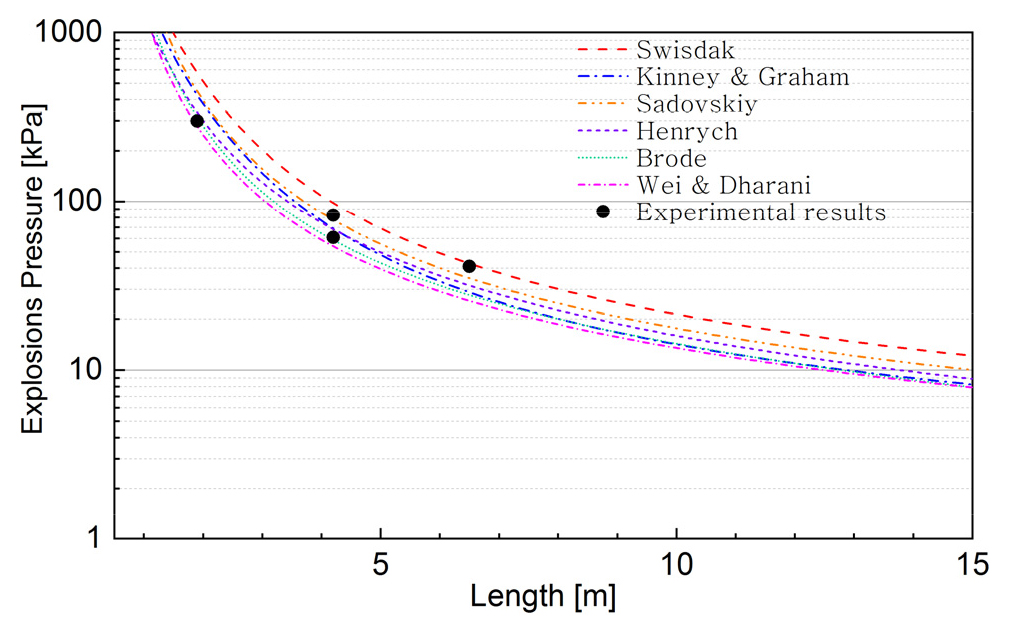
본 절에서는 수소탱크의 폭발 시 거리에 따른 폭발압력을 전술한 TNT 등가모델을 적용하여 계산한 결과와 Weyandt의 실험결과와 비교 검토하였다. 수소탱크 폭발 실험 시 수소탱크 제원은 Table 2와 같다.

Table 2.

Yield applied in studies on TNT equivalent mass

Tank pressure	34.3 MPa
Tank capacity	72.4 Liter
Tank temperature	27°C (300.15 K)
Hydrogen mass	1.654 kg
Mechanical energy	5.040 MJ
Equivalent TNT mass	2.151 kg

Fig. 1은 전술한 TNT 모델을 적용하여 거리에 따른 최대 폭발압력과 실험결과를 비교한 것이다. 그림에서 Wei & Dharani 식이 폭발압력을 가장 작게 평가하고 있으며, Swisdak 식이 가장 높게 평가하고 있다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F1.jpg

Fig. 1.

Length 15 m in TNT equations & explosion experimental

Table 3은 실험결과와 각 TNT 모델에 의한 폭발압력을 비교하여 나타낸 것이다. 거리가 1.9 m인 경우에는 모델에 의한 예측 값이 과대평가 되고 있으며, 거리가 6.5 m인 경우에는 대부분의 모델이 과소평가하고 있는 것으로 나타나고 있다. 편차를 비교하면 Henrych의 식이 실험결과와 비교적 잘 맞는 것으로 분석되었다.

Table 3.

Explosion pressure (kPa) at each point according to the TNT equivalent equation

Distance (m) Equation & Exp.	1.9	4.2	6.5
Experimental	300	61, 83 (72)	41
Swisdak	581.7 (93.9)	97.7 (35.6)	42.7 (4.2)
Sadovskiy	452.6 (50.9)	77.7 (7.9)	35.0 (-14.6)
Henrych	338.4 (12.8)	68.1 (-5.3)	31.7 (-22.7)
Brode	318.8 (6.3)	58.8 (-18.3)	27.8 (-32.2)
Kinney & Graham	428.5 (42.8)	69.0 (-4.2)	28.9 (-29.5)
Wei	280.5 (-6.5)	53.9 (-25.1)	25.7 (-37.3)

3. 수치해석에 의한 폭발압력 분석

3.1 해석모델의 검증

터널에서 차량의 충돌이나 화재 등으로 인해 수소연료차의 수소탱크가 폭발하는 경우에 폭발압력의 크기 및 전파특성을 분석하였다.

터널에서 수소탱크의 폭발압력을 해석하기 위해서 수치해석 방법을 검토하고 방법의 신뢰성을 확보하기 위해서 개방된 대기중에서 수소탱크 폭발 시 압력을 수치해석적인 방법으로 구하여 실험 데이터와 비교하여 검증하였다.

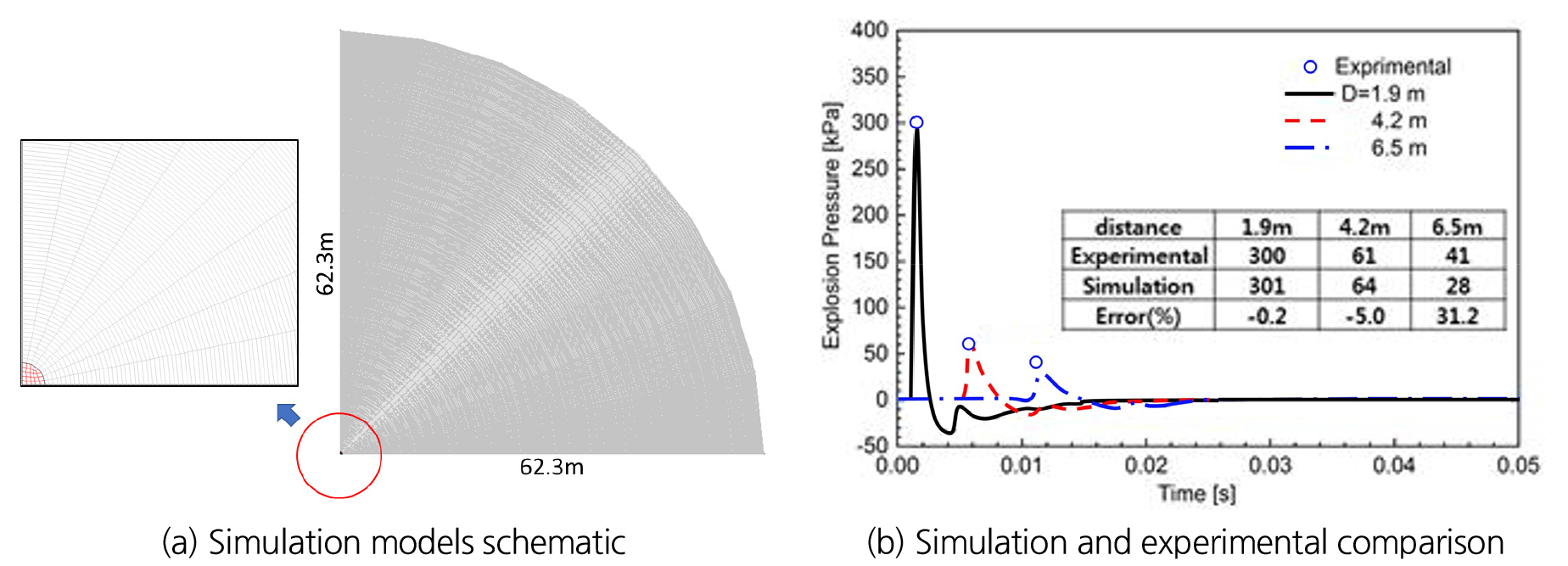
폭발압력을 해석하기 위한 수치해석 모델은 Fig. 2(a)에 보인 바와 같이 반구형 공간의 중앙에 수소탱크를 위치시키고 3D-axis-symmetric 조건으로 모델링하였다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F2.jpg

Fig. 2.

Open explosion experimental & simulation

반구의 직경은 124.6 m이며, 연료탱크는 직경이 0.576 m인 반구형으로 하였고, 체적은 Weyandt의 실험결과와 비교하기 위해서 72 L로 하였다. 연료탱크의 수소는 이상기체로 가정하였으며, 폭발직전의 압력과 온도는 Weyandt 실험 시 측정된 35.8 MPa, 312 K로 패치하고 시뮬레이션 시작과 동시에 방출하는 것으로 하였다.

시뮬레이션은 비정상상태로 수행하였으며, 시간간격은 2e-05s로 하였다.

Fig. 2(b)는 폭발지점에서 1.9, 4.2, 6.5 m 이격한 지점에서 시간경과에 따는 수치해석에 의한 폭발압력변화를 나타낸 것이다. 또한 그림에서 Experimental은 Weyandt의 실험결과를 나타낸 것이다.

그림에서 알 수 있는 바와 같이 각 지점에서 해석적으로 구한 최대폭발압력과 실험결과의 편차는 4.2 m 지점까지 0.2~5.0%로 거리가 증가하면 편차가 증가하는 것으로 나타나고 있으나, 6.5 m 지점에서는 31.2%로 나타났다.

3.2 터널에서 수소탱크 폭발압력 해석모델

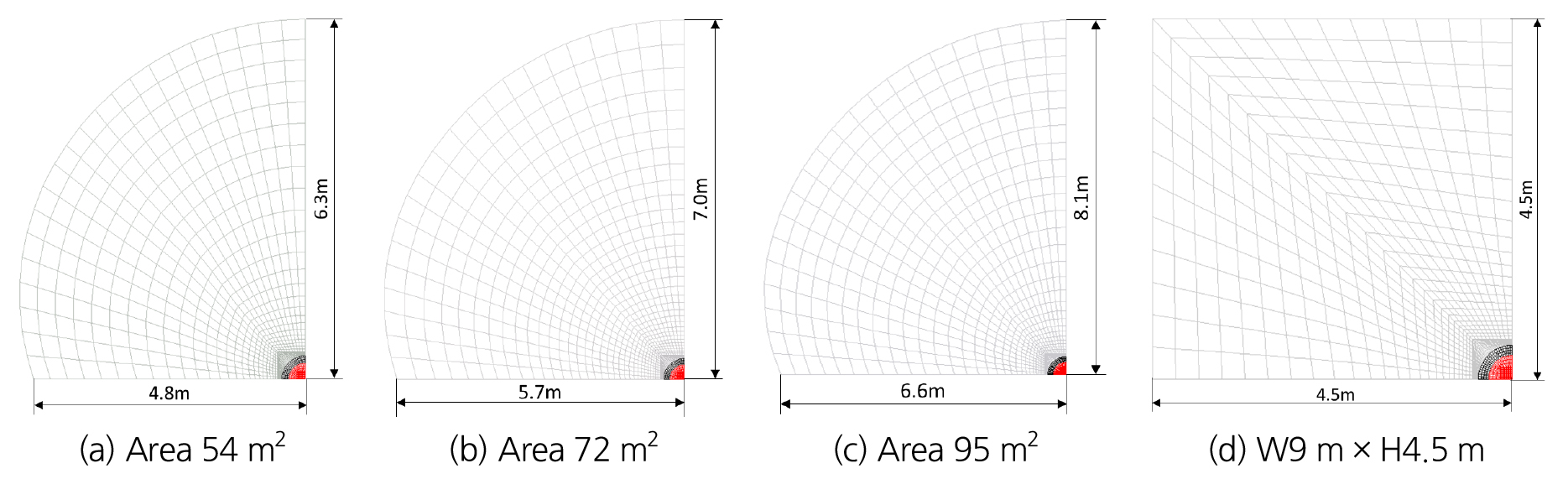
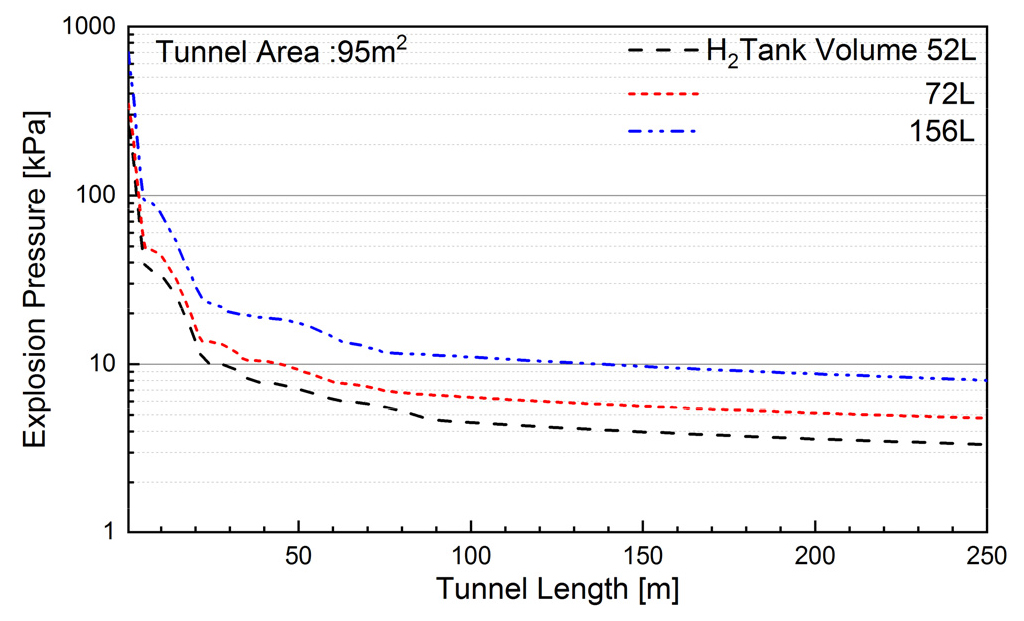
해석 터널의 연장은 500 m로 하였으며, 터널의 단면적은 마제형 터널은 54, 72, 95 m², 사각형 단면의 터널은 높이 4.5 m × 폭 9 m로 하였다. 수소탱크는 터널의 중앙에 위치하였으며, 탱크의 체적은 52, 72 156 리터로 하였다.

터널 내 공기의 초기온도와 압력은 300 K, 101,325 Pa로 하였으며, 폭발직전의 수소탱크의 수소는 완충된 상태로 초기온도와 압력은 395 K, 70 MPa로 하였다.

터널에서 수소탱크 폭발 시 압력파의 전파특성 및 폭발압력을 해석하기 위해서 터널의 단면적 및 수소탱크의 크기에 따른 폭발압력을 수치해석에 의해서 해석하였다. 해석모델은 Fig. 3에 나타낸 바와 같다. 해석모델은 터널을 좌우대칭 즉, 터널의 중심면을 symmetric면으로 하여 1/2만 모델링하였다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F3.jpg

Fig. 3.

Cross section mesh in tunnels

3.3 폭발 압력파 전파특성 고찰

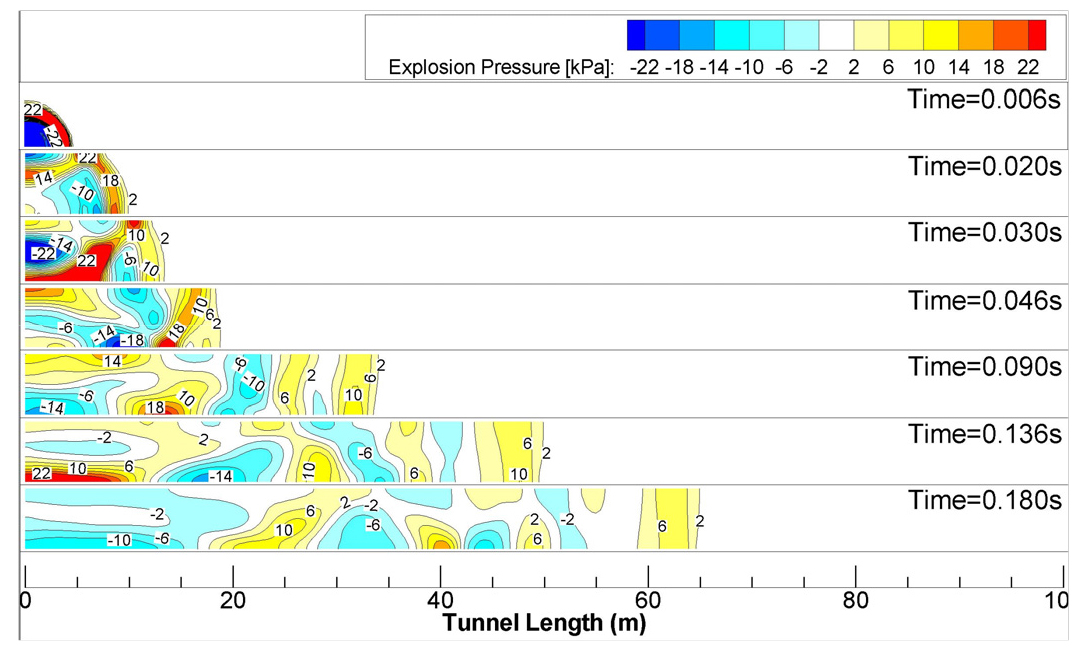
Fig. 4는 터널 단면적이 54 m²일 때 터널의 중심면에서 압력분포를 나타낸 것이다. 터널 내 폭발압력은 음속으로 전파되며, 압력파가 최초 벽면(또는 천장)에 도달하기 전까지는 개방된 공간에서 폭발과 같이 반구형으로 전파된다. 벽면 도달 후에 반사파가 생성되고 반사파는 선행하는 압력파와 중첩하여 복잡한 양상을 보이게 된다. 또한 거리가 일정거리 이상으로 증가하면 압력파는 평면파로 변형되며, 이후에는 터널을 따라 전파하게 된다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F4.jpg

Fig. 4.

Explosion pressure distribution in the tunnel

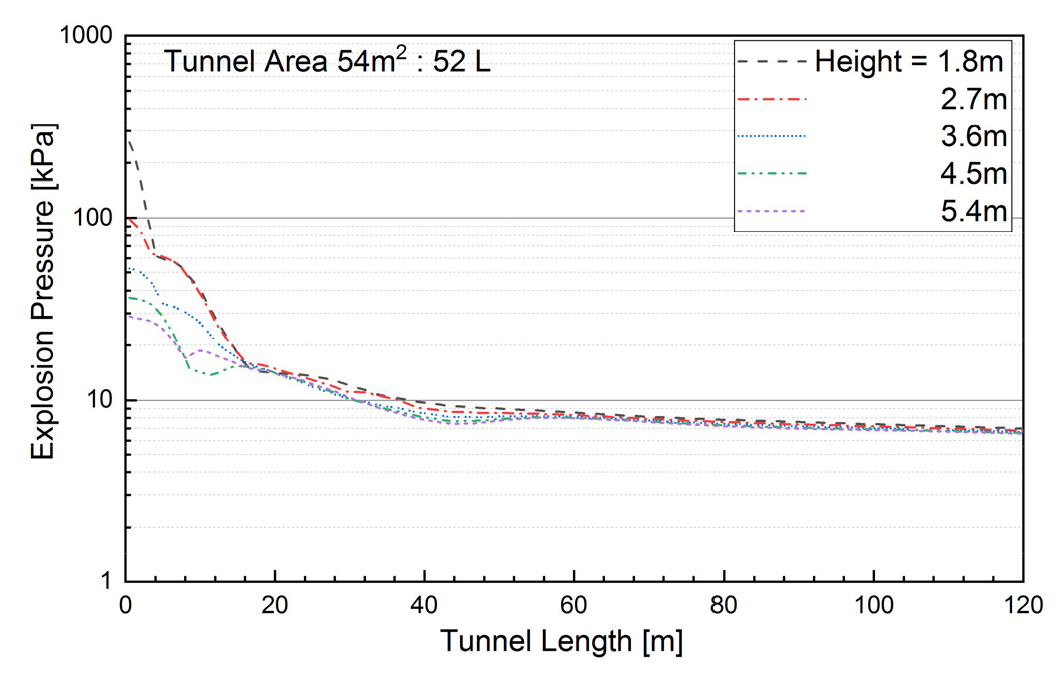
Fig. 5는 터널 단면적이 54 m²인 경우에 터널 중심면에서 높이별(1.8, 2.7, 3.6, 4.5, 5.4 m)의 5개 지점에서 최대폭발압력을 나타낸 것이다. 폭발압력은 폭발지점에서 멀어질수록 감소하며, 도로면에서부터 높이가 높을수록 최대 폭발압력은 낮아지는 것으로 나타나고 있다. 높이에 따른 폭발압력의 편차는 폭발지점에서 20 m까지는 평균 31.6%이며, 20~40 m에서는 23.0%, 평면파로 변화된다고 판단되는 약 60 m 이후에서는 평균 2.0%로 나타났다. 폭발압력은 거리가 증가함에 따라 지수감쇄하는 것으로 나타나고 있다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F5.jpg

Fig. 5.

Explosion pressure by tunnel height

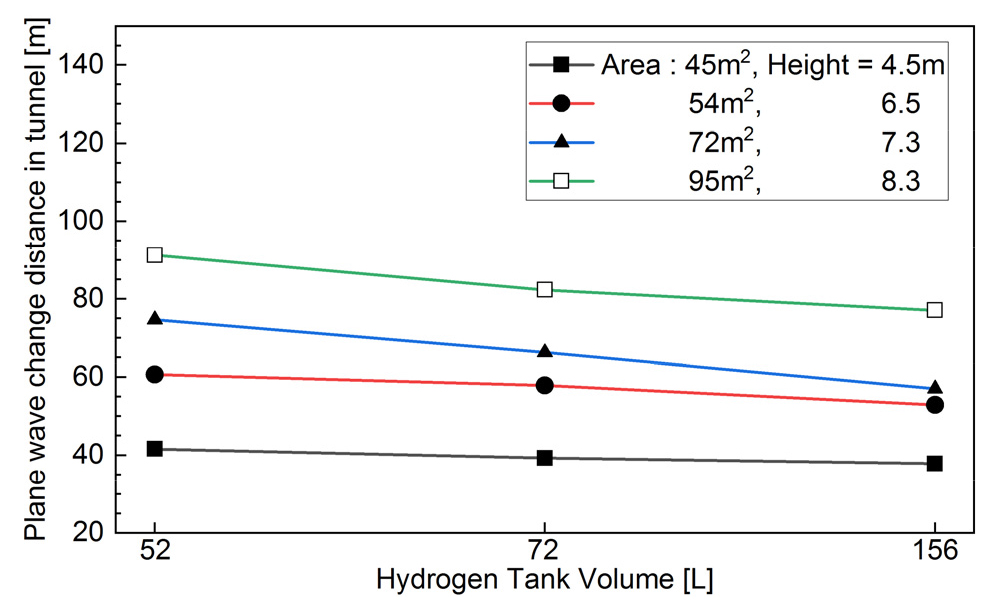
Fig. 6은 터널 단면적별 폭발압력이 평면파로 변형되는 거리를 검토한 것이다. 터널 단면적이 동일한 경우, 탱크용량이 증가할수록 평면파로 변형되는 거리가 감소하나, 본 해석조건에서는 약 20% 이내인 것으로 나타나고 있다. 그러나 터널단면적이 감소하는 경우에는 비교적 큰 차이가 발생하고 있어, 평면파로 변형되는 거리는 터널의 단면적에 보다 크게 영향을 받는 것으로 판단된다. 터널 단면적별로 평면파로 변형되는 거리는 터널높이의 8.8배(40.5 m²), 8.8배(54 m²), 9.1배(72 m²), 10.1배(95 m²)로 나타났다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F6.jpg

Fig. 6.

Transition distance to plane wave

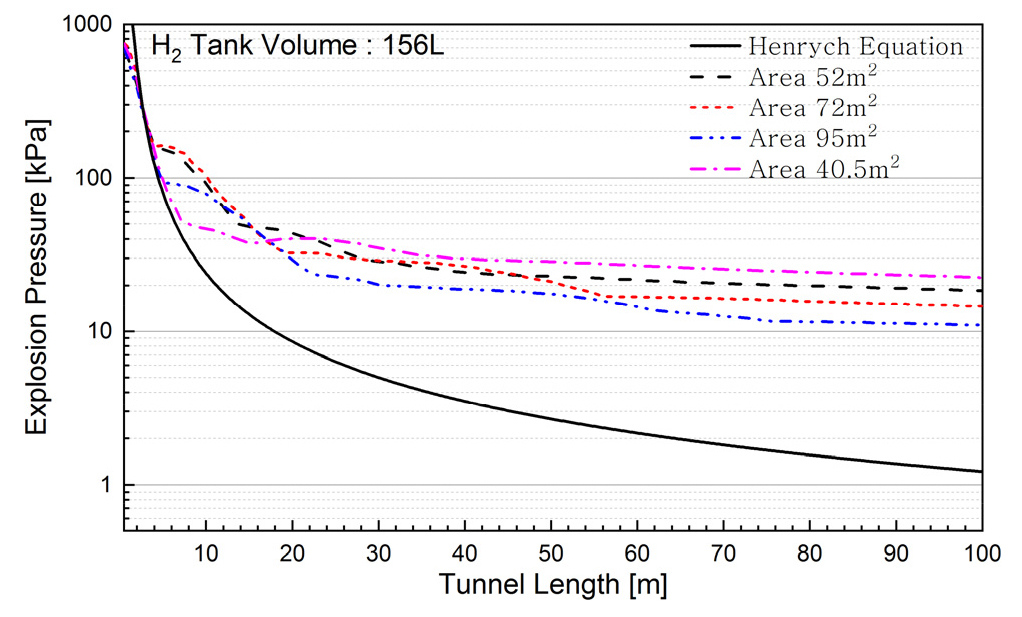
3.4 폭발압력에 대한 단면적의 영향 분석

Figs. 7, 8, 9는 수소탱크 용량별로 단면적에 따른 폭발압력을 높이 1.8 m에 대하여 나타낸 것이다.

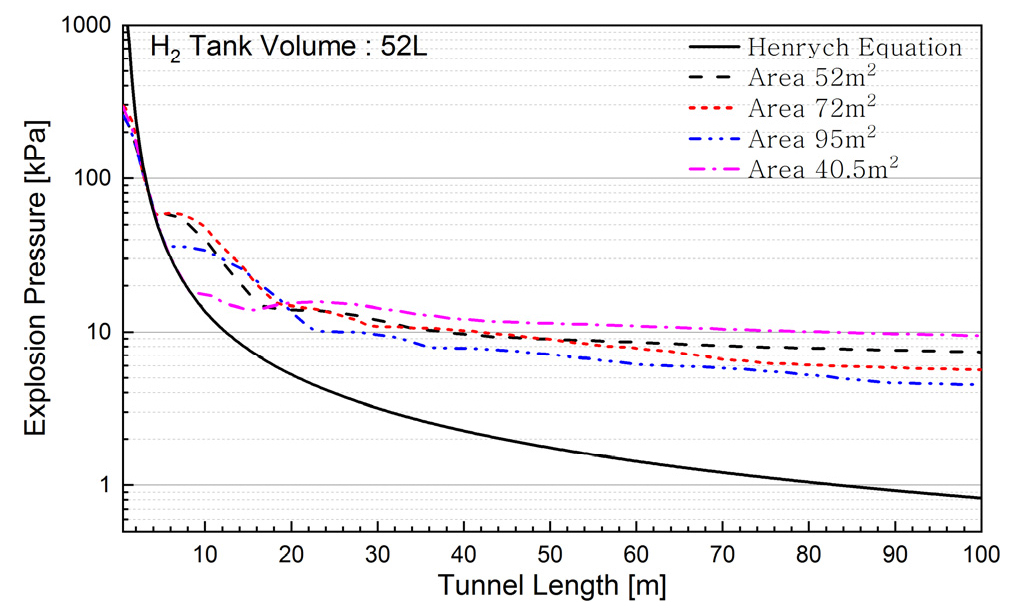
Fig. 7은 탱크 용량이 52 L인 경우에 단면적에 따른 각 지점에서 최대폭발압력을 나타낸 것이다. 단면적 별로 차이가 있으나, 반사파가 형성되기 이전에는 Henrych 방정식을 이용하여 구한 폭발압력과 3.0% 이내에서 잘 일치하고 있다. 그러나 거리가 증가할수록 개방공간에서 폭발압력을 예측하는 Henrych의 식에 의한 폭발압력과 편차가 증가하는 것으로 나타나고 있다. 따라서 터널에서 수소탱크의 폭발압력을 예측하기 위하여 개방공간에서 적용하는 등가 TNT모델을 적용하는 경우에는 반사파가 형성되기 이전까지의 거리에서 유효하나, 반사파가 형성된 이후에는 폭발압력이 큰 폭으로 과소평가될 것으로 판단된다. 또한 그림에서 약 20 m지점까지는 사각 단면의 터널의 폭발압력이 마제형 터널의 폭발압력보다 낮은 것으로 나타나고 있으며, 20 m 이후에는 단면적이 작을수록 폭발압력이 증대하는 것으로 나타나고 있다. 이는 폭발력이 동일하면 단면적이 작을수록 압력이 증가하기 때문으로 판단된다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F7.jpg

Fig. 7.

Explosion pressure according to tunnel area for 52 L tank

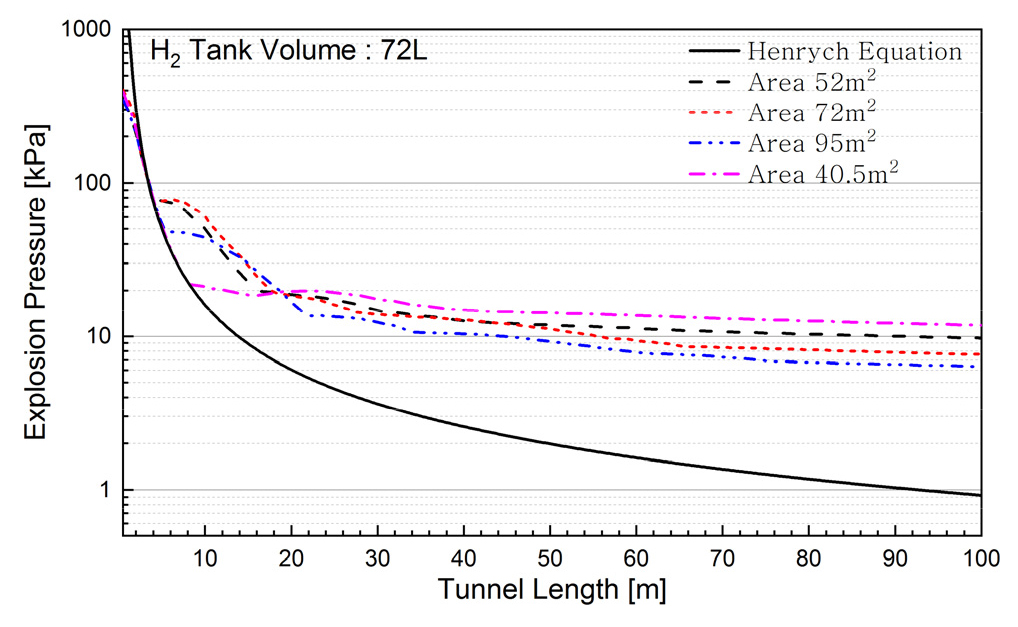
Fig. 8은 수소탱크 용량이 72 L인 경우에 단면적별 거리에 따른 폭발압력을 나타낸 것이다. 이 경우에도 10 m 이내의 짧은 거리에서는 등가 TNT모델 중 Henrych식과 0.4% 이내에서 잘 일치하고 있으나, 반사파로 변형된 이후에는 편차가 증대하는 것으로 나타나고 있다. 또한 폭파지점에서부터 거리가 20 m 이상이 되면 폭발압력의 감쇄율이 급격하게 감소하는 경향을 보이고 있으며, 이 범위에는 단면적이 클수록 폭발압력이 감소하고 있다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F8.jpg

Fig. 8.

Explosion pressure according to tunnel area for 72 L tank

Fig. 9는 탱크 용량이 156 L인 경우로 전술한 52 L와 72 L의 경우와 동일한 경향을 보이고 있다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F9.jpg

Fig. 9.

Explosion pressure according to tunnel area for 156 L tank

3.5 폭발압력에 대한 수소탱크용량의 영향 분석

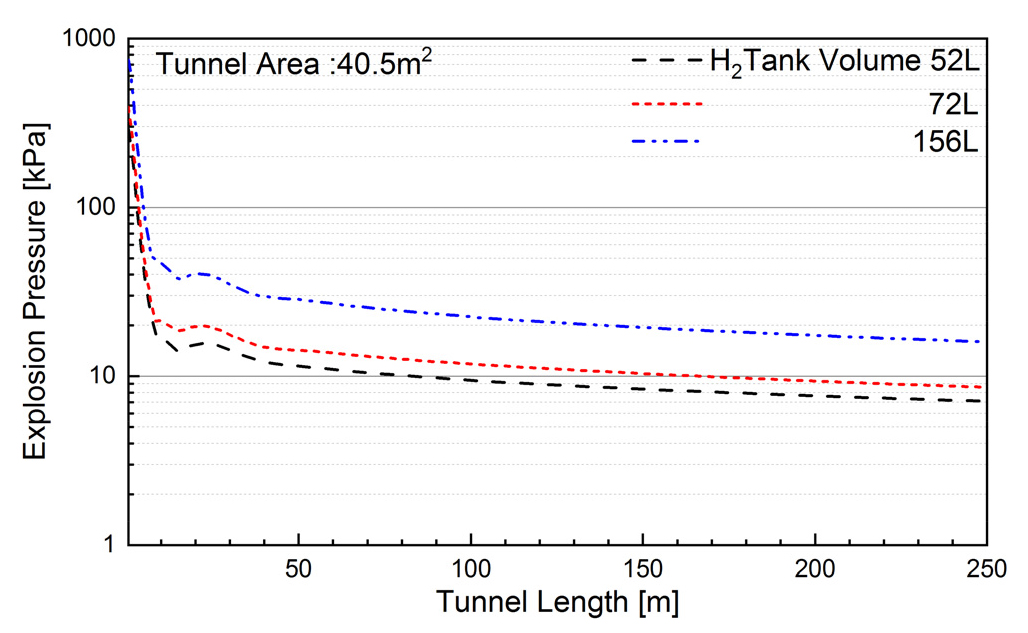
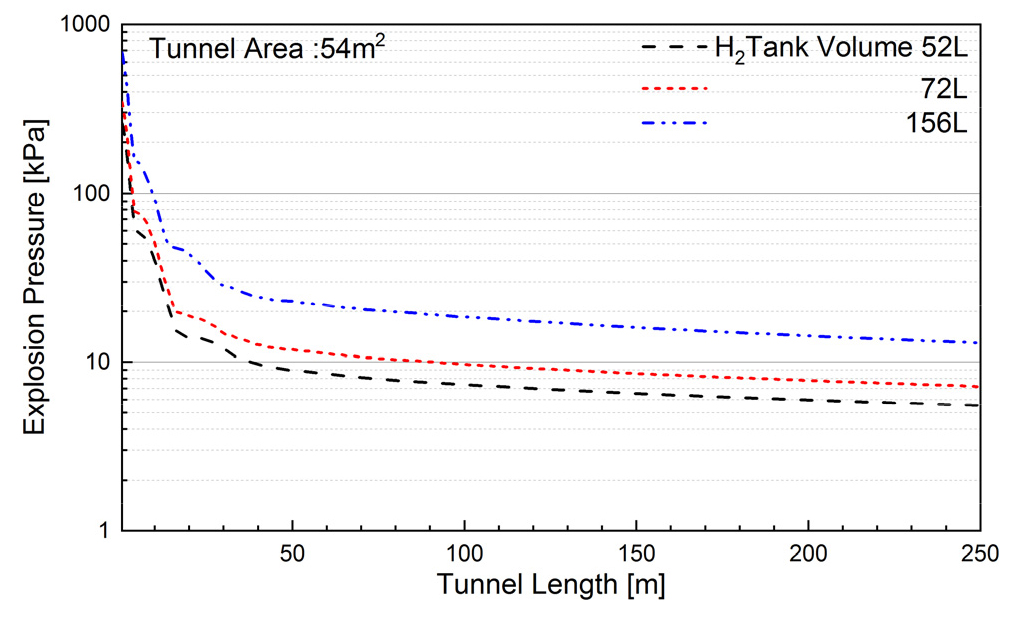
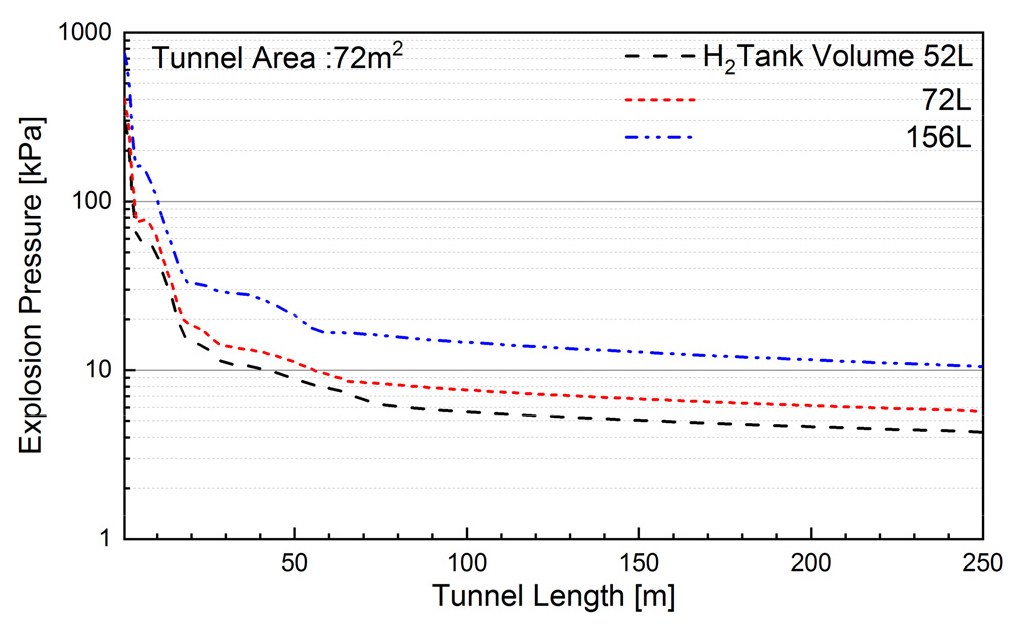
Figs. 10, 11, 12, 13은 단면적별로 수소탱크용량에 따른 1.8 m 높이에서 폭발압력을 나타낸 것이다.

Fig. 10은 사각터널(폭 9 m, 높이 4.5 m)에서 탱크용량에 따른 폭발압력이다. 연료탱크 용량이 52 L인 경우 8.0 m까지는 급격하게 감소하며, 8.0 m 이상에서는 비교적 완만하게 감소하는 경향을 보이고 있다. 8 m 지점에서 수소탱크 용량별 폭발압력은 19.0 kPa (52 L), 22.4 kPa (72 L), 50 kPa (156 L)로 분석되며, 수소탱크용량이 52 L에서 156 L로 3배 증가하면 폭발압력은 2.6배 증가하는 것으로 나타나고 있다. 거리가 8.0 m 이상에서 감소기울기는 거의 비슷한 값을 보이고 있으며, 250 m지점에서 수소탱크용량별 폭발압력은 7.1 kPa (52 L), 8.6 kPa (72 L), 16.0 kPa (156 L)로 나타나고 있다. 따라서 수소탱크용량이 52 L에서 156 L로 증가하는 경우, 폭발압력은 2.3배 증가하는 것으로 분석되었다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F10.jpg

Fig. 10.

Explosion pressures according to tank volume for tunnel area 40.5 m²

Fig. 11은 마제형 터널 중 단면적이 54 m²인 경우에 대한 폭발압력을 나타낸 것이다.

폭발압력은 약 16 m까지는 수소탱크용량별(52, 72 156 L)로 최대폭발압력(259 kPa, 348 kPa, 680 kPa)에서 부터 15.7 kPa, 20 kPa, 47.5 kPa로 급격하게 감소하는 것으로 나타났다. 거리가 16 m 이상 되는 지점에서 수소 탱크용량별 폭발압력의 감쇄율은 평균 -0.048 kPa/m로 분석된다. 또한, 지점별 폭발압력은 52 L를 기준으로 72 L는 1.3배, 152 L는 2.5배로 증가하는 것으로 나타나고 있다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F11.jpg

Fig. 11.

Explosion pressures according to tank volume for tunnel area 54 m²

Fig. 12는 단면적이 72 m²에 대한 폭발압력을 탱크용량에 따라 비교한 것이다. 72 m²의 터널의 경우도 약 18 m까지는 수소탱크 용량별로 최대폭발압력(52 L: 298 kPa, 72 L: 404 kPa, 152 L: 752 kPa)에서부터 16 kPa (52 L), 19.5 kPa (72 L), 35.4 kPa (152 L)로 급격하게 감소하며, 18 m이후에는 거의 동일한 기울기로 완만하게 감소하는 것으로 나타나고 있고, 평균감쇄율은 -0.035 kPa/m로 분석되었다. 또한 거리가 18 m 이상인 지점에서 수소탱크용량 증가에 따라 폭발압력은 52 L를 기준으로 72 L는 약 1.3배, 152 L는 약 2.5배 정도 높은 것으로 나타나고 있다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F12.jpg

Fig. 12.

Explosion pressures according to tank volume for tunnel area 72 m²

Fig. 13은 단면적이 95 m²인 경우로 전술한 단면적 54, 72 m인 경우와 거의 동일한 경향을 보이고 있으며, 수소탱크 용량별 최대 폭발압력은 258 kPa (52 L), 346 kPa (72 L), 701 kPa (156 L)이다. 이 경우에는 약 20 m지점에서 압력파 감쇄기울기가 완만해지기 시작하며, 폭발압력은 52 L를 기준으로 72 L인 경우에는 1.3배, 156 L의 경우에는 2.4배 정도 증가하는 것으로 나타나고 있다. 이 경우에 폭발압력의 감쇄율은 평균 -0.017 kPa/m로 분석되었다.

https://static.apub.kr/journalsite/sites/kta/2021-023-06/N0550230611/images/kta_23_06_11_F13.jpg

Fig. 13.

Explosion pressures according to tank volume for tunnel area 95 m²

수소탱크의 용량이 동일한 경우에 터널 단면적 변화에 따른 최고폭발압력의 편차는 -7.0~+8.3로 일정한 경향성을 보이지 않고 있다. 따라서 최고 폭발압력은 터널 단면적과는 무관한 것으로 판단되며, 수소탱크 용량이 52 L에서 156 L로 증가하면 폭발압력은 약 2.5배 정도 증가하는 것으로 분석되었다.

3.6 인체영향에 따른 한계거리 분석

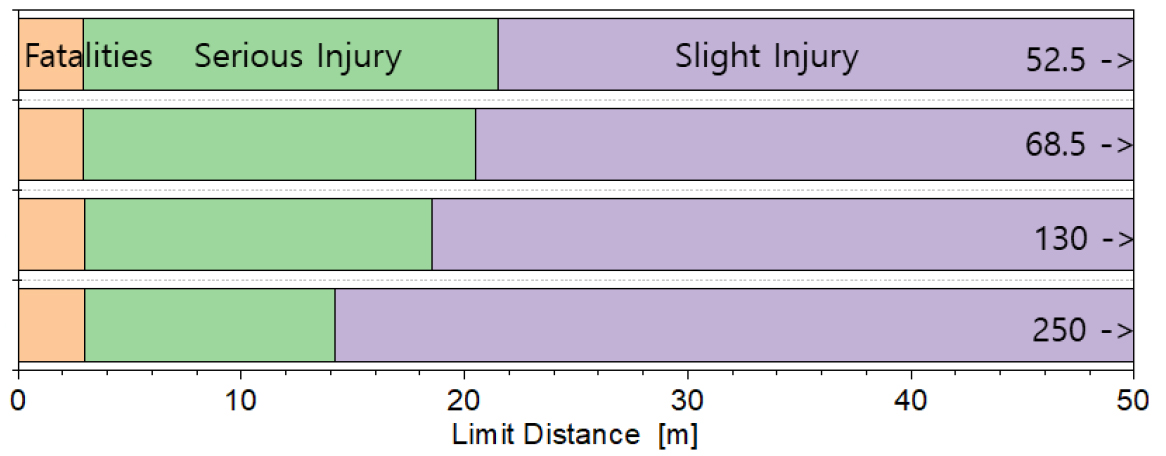
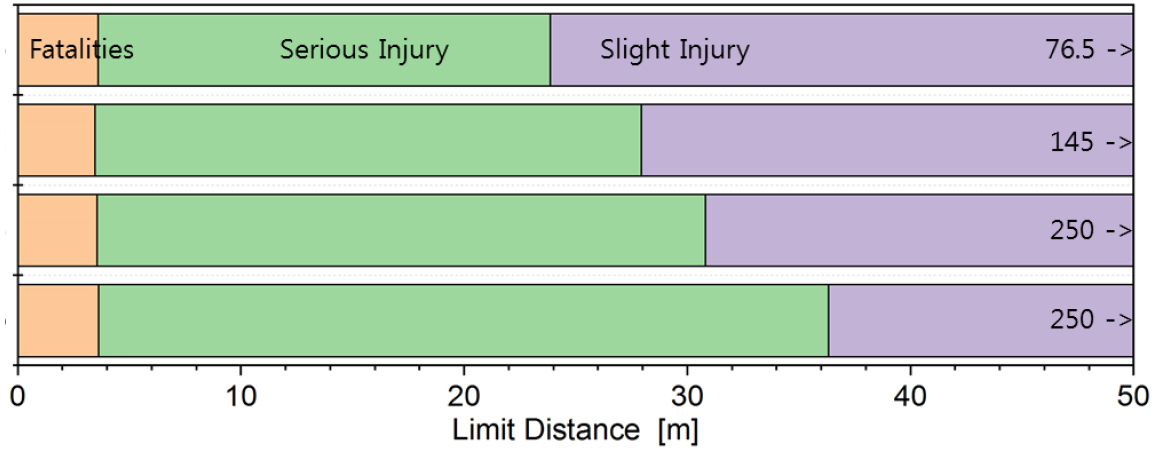
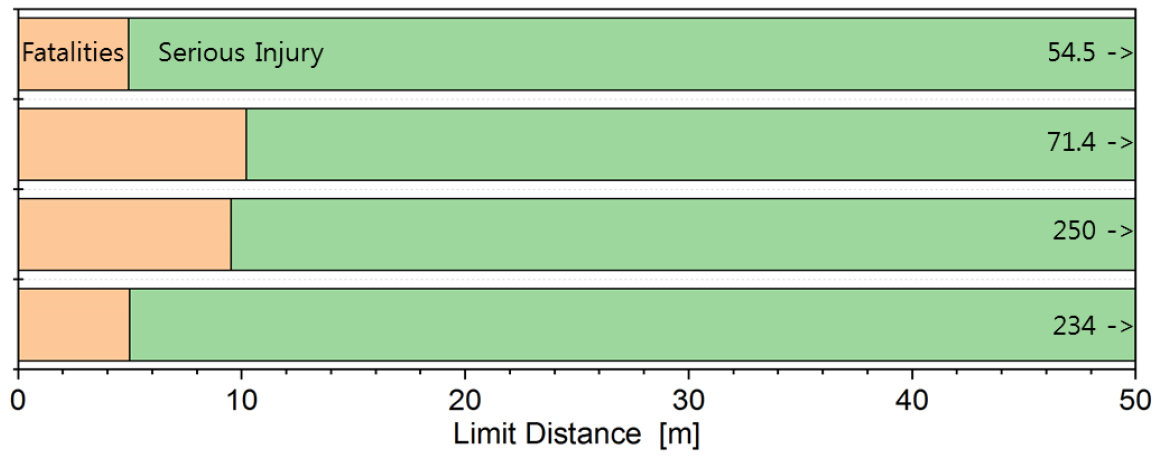
폭발압력이 인체에 미치는 영향의 조사 및 검토 보고서는 다수가 있으며, HyTunnel-CS (2019) 보고서에서는 노출정도에 따른 영향을 Table 4와 같이 3단계(사망: Fatality, 중상: Serious Injury, 경상: Slight Injury)로 구분하여 등가사망자수 산정기준에 의해 사망자를 산정하도록 제안하고 있다. 즉, 폭발압력이 100 kPa을 초과하는 범위에서는 노출인원이 1명이면 1명 사망, 100~16.5 kPa의 범위에서는 노출인원 10명이면 1명 사망, 16.5~1.35 kPa의 범위에 노출인원 100명을 1명 사망으로 정하고 있다. 그러나 본 연구에서는 경상의 하한이 1.35 kPa로 과도하게 평가되어 Argo and Sandstrom (2014)을 인용하여 6.89 kPa을 기준으로 하였다.

Table 4.

Equivalent fatalities, limit distance according to the effect on the human body

Pressure range (kPa)		≥100	100~16.5	16.5~1.35 (6.89)
Effect of humman		Fatality	Serious injury	Slight injury
Equivalent fatalities		1	1/10	1/100
Tank capacity	Tunnel area	Limit distance
52 L	95
	72
	54
	40.5

72 L	95
	72
	54
	40.5

156 L	95
	72
	54
	40.5

수소탱크 용량이 52 L인 경우에는 사망(Fatality)한계가 3 m 미만이고, 중상(Serious Injury)에 이르는 한계거리는 11~19 m정도이며, 단면적이 증가할수록 한계거리가 증가하는 경향을 보이고 있다. 이는 Fig. 7에서 보인 바와 같이 20 m 이내의 거리에서는 단면적이 작을수록 폭발압력이 감소하기 때문이다.

72 L의 수소탱크가 폭발하는 경우에 사망에 이르는 한계거리는 52 L의 수소탱크가 폭발하는 경우보다 약간 증가한 3.5 m정도로 분석되며, 단면적에 따른 차이는 거의 없는 것으로 나타났다. 또한, 중상에 이르는 한계거리는 20~33 m정도이며, 이 경우에도 단면적이 증가할수록 한계거리가 감소하고 있는데, 이는 반사파에 의한 교란이 심한 영역에서는 단면적이 클수록 폭발압력이 증가하기 때문으로 판단된다.

수소탱크용량이 156 L의 경우, 사망에 이르는 한계거리는 5~10 m정도이며 단면적별로 비교적 큰 편차가 발생하고 있고, 72 m²의 단면에서는 한계거리가 10 m정도이며 중상에 이르는 한계거리는 단면적이 54 m²보다 작은 경우에는 230 m를 초과하고, 단면적이 큰 72, 95 m의 경우에는 각각 71, 54 m로 분석되었다.

이상의 검토에서 현재 시판되고 있는 수소연료차량의 연료탱크 용량이 52 L이고 터널의 표준단면적이 70~75 m²인 점을 감안하면 수소탱크 폭발 시 중상에 이르게 되는 한계거리는 약 25 m정도로 파악된다.

4. 결 론

본 연구에서는 수소연료 전지차의 수소탱크가 폭발하는 경우에 폭발압력 예측을 위해서 등가 TNT 모델을 이용하는 폭발압력 예측식과 수치해석방안을 검토하였으며, Weyandt가 실시한 개방된 공간에서의 폭발압력 실측결과를 비교하여 수치해석 방안의 신뢰성을 검토하여 수치해석 방법을 도출하였다.

또한 터널 내에서 폭발압력파의 전파특성을 검토하고 터널의 단면적과 수소탱크용량에 따른 폭발압력의 크기를 수치해석적인 방법으로 검토하여, 다음과 같은 결과를 얻었다.

1. 등가 TNT 모델을 이용한 검토에서는 Weyandt의 실험결과에서 제시된 3개 지점에 대한 폭발압력을 비교한 결과, Henrych식을 적용하는 경우가 13.6%의 편차로 가장 근접하는 것으로 나타났다.

2. 터널에서 수소탱크가 폭발하는 경우에 폭발압력파가 벽체에 도달하기 전까지는 반구형으로 전파하나 벽체에 도달한 후에 반사파가 형성되면서 압력파의 전파형태는 복잡한 양상을 보이며, 거리가 어느 정도 증가하면 평면파로 변형되는 것으로 나타났다.

3. 평면파로 변형되는 거리는 터널높이의 약 9.2배 정도로 분석되며, 평면파로 전환된 후에 폭발압력은 감쇄율이 평균 -0.042 kPa/m로 감소한다.

4. 터널에서 거리에 따른 폭발압력은 급격하게 감쇄하는 구간에서는 Henrych식과 잘 일치하나 압력파가 변형된 이후에는 Henrych식은 폭발압력을 크게 과소평가하는 것으로 나타났다.

5. 수소연료 탱크의 크기가 동일한 경우에는 폭발압력은 압력파가 변형되기 전에는 단면적에 따른 경향성이 없으나, 변형된 이후에는 단면적이 증가할수록 감소하는 것으로 나타나고 있다.

6. 단면적이 동일한 경우에 수소탱크 용량이 52 L, 156 L로 증가하면 폭발압력은 약 2.5배 정도 증가하는 것으로 나타났다.

7. 인체에 영향을 미치는 한계거리는 수소탱크용량이 증가할수록 증가하며, 수소탱크용량이 52 L인 경우, 사망에 이르는 한계거리는 약 3 m, 중상에 이르는 거리는 단면적별로 차이가 있으나 28.5~35.8 m로 나타났다.

Acknowledgements

본 논문은 소방청의 ESS ‧ 수소시설 화재 안전기술 연구개발사업(20011645)의 지원을 받아 작성함.

저자 기여도

류지오 및 안상호는 연구개념, 자료분석, 해석모델링 검토, 원고 작성 및 검토를 수행하였으며, 이후영은 자료수집, 폭발압력 및 TNT등가 모델 데이터를 정리하고 원고를 작성하였다.

References

Argo, T., Sandstrom, E. (2014), Separation distances in NFPA codes and standards, Fire Protection Research Foundation, pp. 5-7.

HyTunnel-CS (2019), "Deliverable 1.2 Report on hydrogen hazards and risks in tunnels and similar confined spaces", Fuel Cells and Hydrogen Joint Undertaking (FCH JU), pp. 13-136.

Korea Research Institute of Standards and Science (2016), Development of safety and integrity evaluation technology for liquefied hydrogen storage vessels, pp. 246-252.

Kwon, S., Park, J.C. (2015), "A review of TNT equivalent method for evaluating explosion energy due to gas explosion", Journal of Korean Society of Explosives & Blasting Engineering, Explosives & Blasting, Vol. 33, No. 3, pp. 1-13.

Molkov, V., Dery, W. (2020), "The blast wave decay correlation for hydrogen tank rupture in a tunnel fire", International Journal of Hydrogen Energy, Vol. 45, No. 55, pp. 31289-31302. 10.1016/j.ijhydene.2020.08.062

Molkov, V., Kashkarov, S. (2015), "Blast wave from a high-pressure gas tank rupture in a fire: stand-alone and under-vehicle hydrogen tanks", International Journal of Hydrogen Energy, Vol. 40, No. 36, pp. 12581-12603. 10.1016/j.ijhydene.2015.07.001

MOTIE (2019), Future automotive industry development strategy -2030 national roadmap-, pp. 12-13.

LaFleur, C., Bran-Anleu, G., Muna, A.B., Ehrhart, B.D., Blaylock, M., Houf, W.G. (2017), Hydrogen fuel cell electric vehicle tunnel safety study, SAND2017-11157, Sandia National Laboratories, Albuquerque, New Mexico, pp. 36-71. 10.2172/1761273

Glover, A.M., Baird, A.R., LaFleur, C.B. (2020), Hydrogen fuel cell vehicles in tunnels, SAND2020-4507 R, Sandia National Laboratories, Albuquerque, New Mexico, pp. 54-59. 10.2172/1617268

Shentsov, V., Makarov, D., Molkov, V. (2018), "Blast wave after hydrogen storage tank rupture in a tunnel fire", Proceedings of the 8th International Symposium on Tunnel Safety and Security, Sweden, pp. 14-16.

Southwest Research Institute's (2006), Southwest Research Institute.

Yoon, Y.K. (2016), "Evaluation of peak overpressure and impulse induced by explosion", Journal of Korean Society of Explosives & Blasting Engineering, Explosives & Blasting, Vol. 34, No. 4, pp. 28-34.

Zalosh, R., Weyandt, N. (2005), Hydrogen fuel tank fire exposure burst test, SAE Technical Paper 2005-01-1886, pp. 1-6. 10.4271/2005-01-1886

Journal of Korean Tunnelling and Underground Space Association ISSN:2233-8292(Print) 2287-4747(Online) 한국터널지하공간학회 논문집

Preview

A basic study on explosion pressure of hydrogen tank for hydrogen fueled vehicles in road tunnels

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

Table 1.

Constants for Swisdak equation

(7)

(8a)

(8b)

(8c)

(9a)

(9b)

(10)

(11)

Table 2.

Yield applied in studies on TNT equivalent mass

Fig. 1.

Length 15 m in TNT equations & explosion experimental

Table 3.

Explosion pressure (kPa) at each point according to the TNT equivalent equation

Fig. 2.

Open explosion experimental & simulation

Fig. 3.

Cross section mesh in tunnels

Fig. 4.

Explosion pressure distribution in the tunnel

Fig. 5.

Explosion pressure by tunnel height

Fig. 6.

Transition distance to plane wave

Fig. 7.

Explosion pressure according to tunnel area for 52 L tank

Fig. 8.

Explosion pressure according to tunnel area for 72 L tank

Fig. 9.

Explosion pressure according to tunnel area for 156 L tank

Fig. 10.

Explosion pressures according to tank volume for tunnel area 40.5 m2

Fig. 11.

Explosion pressures according to tank volume for tunnel area 54 m2

Fig. 12.

Explosion pressures according to tank volume for tunnel area 72 m2

Fig. 13.

Explosion pressures according to tank volume for tunnel area 95 m2

Table 4.

Equivalent fatalities, limit distance according to the effect on the human body

Acknowledgements

References

Explosion pressures according to tank volume for tunnel area 40.5 m²

Explosion pressures according to tank volume for tunnel area 54 m²

Explosion pressures according to tank volume for tunnel area 72 m²

Explosion pressures according to tank volume for tunnel area 95 m²