1. 서 론
2. 시험 방법
2.1 구동형 언더커팅 절삭변수
2.2 언더커팅 절삭시험 시스템
2.3 시험편 및 절삭도구
2.4 시험조건
3. ADC 시험결과 분석 방법
4. ADC 시험 결과 및 토의
5. 결 론
1. 서 론
국내외 자원개발 및 터널공사에서 활용되는 기계화 암반굴착공법은 TBM (tunnel boring machine)과 로드헤더(roadheader)가 대표적이다. 과거 기계식 굴착장비에 대한 연구를 바탕으로 많은 분야에서 지속적인 발전을 이루어 왔으나, 기존의 암반 기계굴착공법은 암석을 절삭하는 메커니즘상 여전히 광범위한 조건에서 적용하는 데 한계점을 가지고 있다(Jeong et al., 2020). 전단면 굴착방식인 TBM의 경우 특수하게 제작되는 경우를 제외하면 굴착단면의 형상이 원형으로 제한되며, 이러한 특성상 터널 단면의 효율적인 활용 측면에서 한계점을 갖고 있다(Jeong et al., 2019). 반면 부분단면 굴착방식인 로드헤더는 절삭도구인 픽 커터(pick cutter)의 절삭성능 및 내 마모성의 한계로 주로 강도가 100 MPa 이하인 연암 및 보통암 조건에서 제한적인 적용이 가능한 것으로 파악되고 있다.
언더커팅(undercutting)은 이러한 전통적인 암반 기계굴착방식을 대체할 수 있는 공법 중 하나로 고려되고 있으며, 기존의 공법과 비교하여 생산성과 굴착효율을 향상시킬 수 있는 잠재성을 갖고 있는 것으로 평가된다(Jeong et al., 2020). 언더커팅은 암석을 절삭하는 메커니즘 특성상 직접적으로 인장균열을 생성시키기 때문에 적용가능한 암반의 강도가 연암에서부터 경암에 이르기까지 비교적 넓은 범위를 갖고, 기존의 디스크 커터 및 픽 커터에 비하여 커터의 궤적에 대한 자유도가 높기 때문에 굴착 가능한 단면 형상에 제한이 적다는 장점을 가진다.
해외에서는 유럽, 호주 등 일부 기술 선진국을 중심으로 언더커팅 방식에 대한 연구가 시작되었으며, 최근 호주를 중심으로 언더커팅에 의한 절삭메커니즘 정립과 절삭성능평가에 대한 연구가 활발히 진행되고 있다(Kovalyshen, 2015; Dehkhoda and Detournay, 2017; 2019; Dehkhoda and Hill, 2019). 본 연구는 언더커팅에 대한 기초연구로서 언더커팅에 의한 암석절삭변수들을 구현하기 위한 구동형 언더커팅(actuated undercutting disc, ADC)을 적용한 디스크커터와 이를 적용한 절삭시험시스템에 대해서 소개하였다. 언더커팅 절삭시험을 통해 획득되는 커터작용력을 이용하여 비에너지를 계산하기 위한 방법을 제시하고 언더커팅에 의한 암석절삭성능을 평가하기 위한 방법에 대하여 논하였다.
2. 시험 방법
2.1 구동형 언더커팅 절삭변수
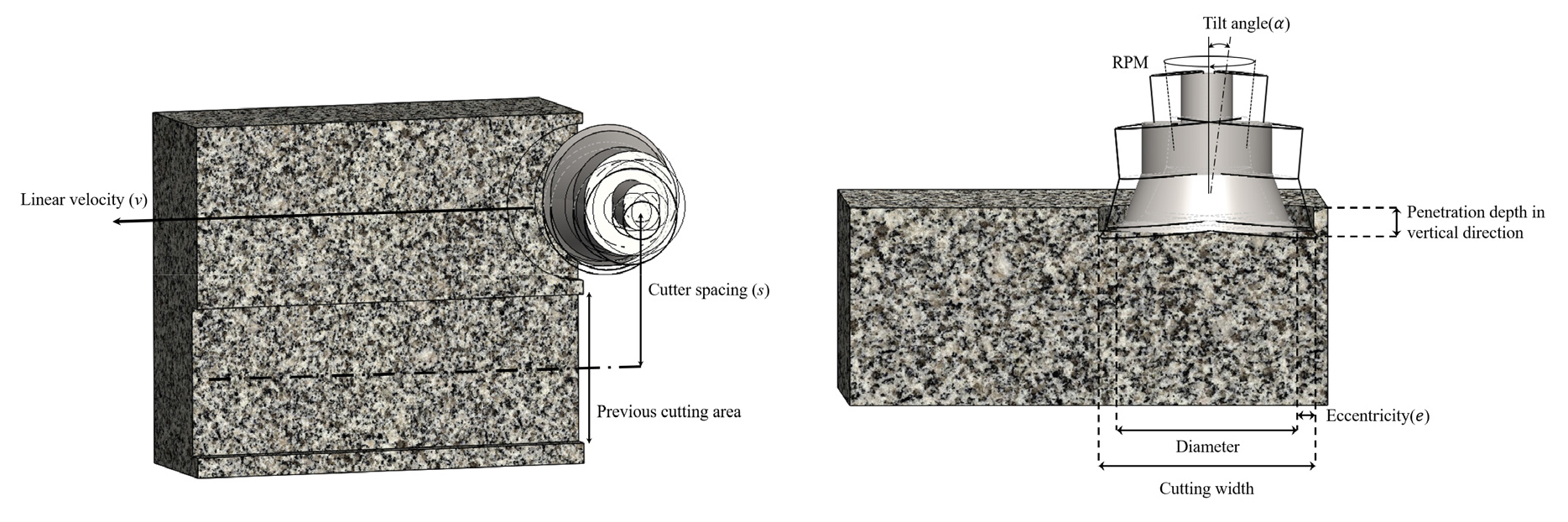
TBM 디스크커터와 픽 커터에 의한 암석의 절삭에서는 커터가 절삭면에 수직한 방향으로 암석에 관입하는 깊이와 인접한 커터 사이의 간격이 절삭성능에 영향을 미치는 중요한 절삭변수로 고려된다. 추가적으로 픽 커터의 경우에는 TBM 디스크커터와는 달리 3가지 절삭각도(attack, skew, tilt angle)가 절삭성능에 영향을 미치는 것으로 알려져 있다(Jeong and Jeon, 2018). 한편 본 연구에서 대상으로 하는 구동형 언더커팅을 이용한 암석절삭에서는 Fig. 1과 같이 여러 변수들이 추가적으로 정의된다. 선행연구(Jeong et al., 2020)에서 논의된 바와 같이, 압입깊이와 절삭간격 이외에도 커터의 선형이동속도, 절삭각도(tilt or clearance angle), 커터직경, 커터팁 각도, RPM, 편심(eccentricity)이 암석의 절삭성능에 관여한다. 여기서 압입깊이(p)는 커터가 절삭평면에 수직방향으로 관입한 깊이, 절삭간격(s)은 이전 절삭선과 현재 절삭선 중심 사이의 거리, 선형이동속도(v)는 커터의 절삭방향으로의 이동속도, 편심(e)은 커터축이 편심회전축으로부터 이격된 거리, RPM은 편심회전축을 중심으로 커터가 회전하는 속도, 커터기울임각(tilt angle, α)는 절삭평면으로부터 커터가 기울어진 각도로 정의된다.
2.2 언더커팅 절삭시험 시스템
본 연구에서 사용된 언더커팅 절삭시험시스템은 Fig. 2(a)에 나타낸 것과 같으며, Fig. 2(b)는 본 시험시스템을 이용하여 형성된 ADC에 의한 암석시편의 절삭면을 보여주고 있다. 서울대학교 암반공학연구실에서 구축한 이 언더커팅 선형절삭시험시스템은 3축 방향하중 20 tonf 용량의 로드셀이 장착되어 있고, ADC의 편심회전에 의한 암석절삭을 구현하기 위한 회전 전기모터(최대 토크 1,000 N ‧ m)가 설치되어 있는 것이 특징이다. 시험기에 연결된 컨트롤러를 통해 ADC의 시험조건을 구현할 수 있으며, RPM (최대 800), 선형이동속도(최대 100 mm/s), 압입깊이, 절삭거리 등을 입력하여 이들 변수를 자동으로 제어할 수 있다. 편심과 기울임각의 경우에는 수동으로 제어할 수 있도록 제작되어 있다.
2.3 시험편 및 절삭도구
앞서 소개한 시험기에 거치가능한 시험편의 최대 크기는 30 cm × 30 cm × 30 cm이다. 한편 언더커팅 방식을 적용한 실제 굴착장비에 장착되는 디스크커터의 직경은 500~550 mm로 실험실에서 가용할 수 있는 시험편의 크기가 제한됨에 따라 절삭시험에서의 커터의 크기를 축소시킬 필요가 있었다. Fig. 3은 축소된 스케일의 다양한 직경을 갖는 ADC의 모습을 보여주고 있다. 본 연구에서 사용된 커터는 직경 60 mm의 커터이며 실제 크기의 커터에 비해 8.3 (1/0.12)배 축소된 크기이다(500 mm 기준). 한편, 본 연구에서는 압축강도 20 MPa를 갖는 콘크리트로 유사 암석시험편을 제작하여 절삭시험을 수행하였다. 차원해석에 따라 본 시험편은 실스케일(강도축소비는 1/10.3)에서 약 220 MPa의 경암에 해당한다. Table 1에는 차원해석의 결과를 요약하였으며, 차원해석 시 콘크리트의 밀도는 2.1 g/cm3으로 측정되었고, 암석의 밀도는 2.6 g/cm3으로 가정하였다.
Table 1.
Scaled conditions used in the ADC cutting test
| Physical parameter | Dimension | Scale |
| Length | [L] | 0.12 |
| Gravity acceleration | [LT-2] | 1 |
| Time | [T] | 0.346 |
| Density | [ML-3] | 0.808 |
| Mass | [M] | 0.001 |
| Strength and stress | [ML-1 T-2] | 0.097 |
2.4 시험조건
본 연구에서 적용한 ADC의 절삭조건은 Table 2에 요약되었다. 다양한 ADC의 절삭조건 중 편심, 선형이동속도를 3단계로 변화시켜가며 시험을 수행하였다. 모든 시험조건에 대하여 압입깊이와 RPM은 각각 3 mm, 70으로 고정하였다. 각 케이스에 대하여 3방향 커터작용력을 획득하였고, 시험이 종료된 후 파쇄 된 암편을 회수하여 비에너지의 계산을 위한 절삭부피를 측정하였다.
3. ADC 시험결과 분석 방법
기계굴착에 의한 암석의 절삭효율을 평가하는 지수로는 비에너지(specific energy)가 일반적으로 사용되고 있으며, 디스크커터와 픽 커터의 비에너지는 식 (1)과 같이 단위 부피의 암석을 굴착하는 데 커터가 하는 일로 정의된다.
여기서, 는 비에너지, 는 절삭력(cutting force), 은 절삭거리, 은 절삭된 암석의 부피이다. 식 (1)에서와 같이 기존의 TBM 디스크커터와 픽 커터의 절삭에서는 절삭력의 방향과 커터가 일을 하는 방향이 서로 일치하고, 절삭 도중 커터의 이동방향은 선형궤적을 따라 일정하기 때문에 비에너지의 계산이 간단하게 이루어진다. 커터의 이동방향과 서로 직교하는 힘의 성분인 수직력과 측력이 커터가 하는 일에 미치는 기여분이 0이 되기 때문이다.
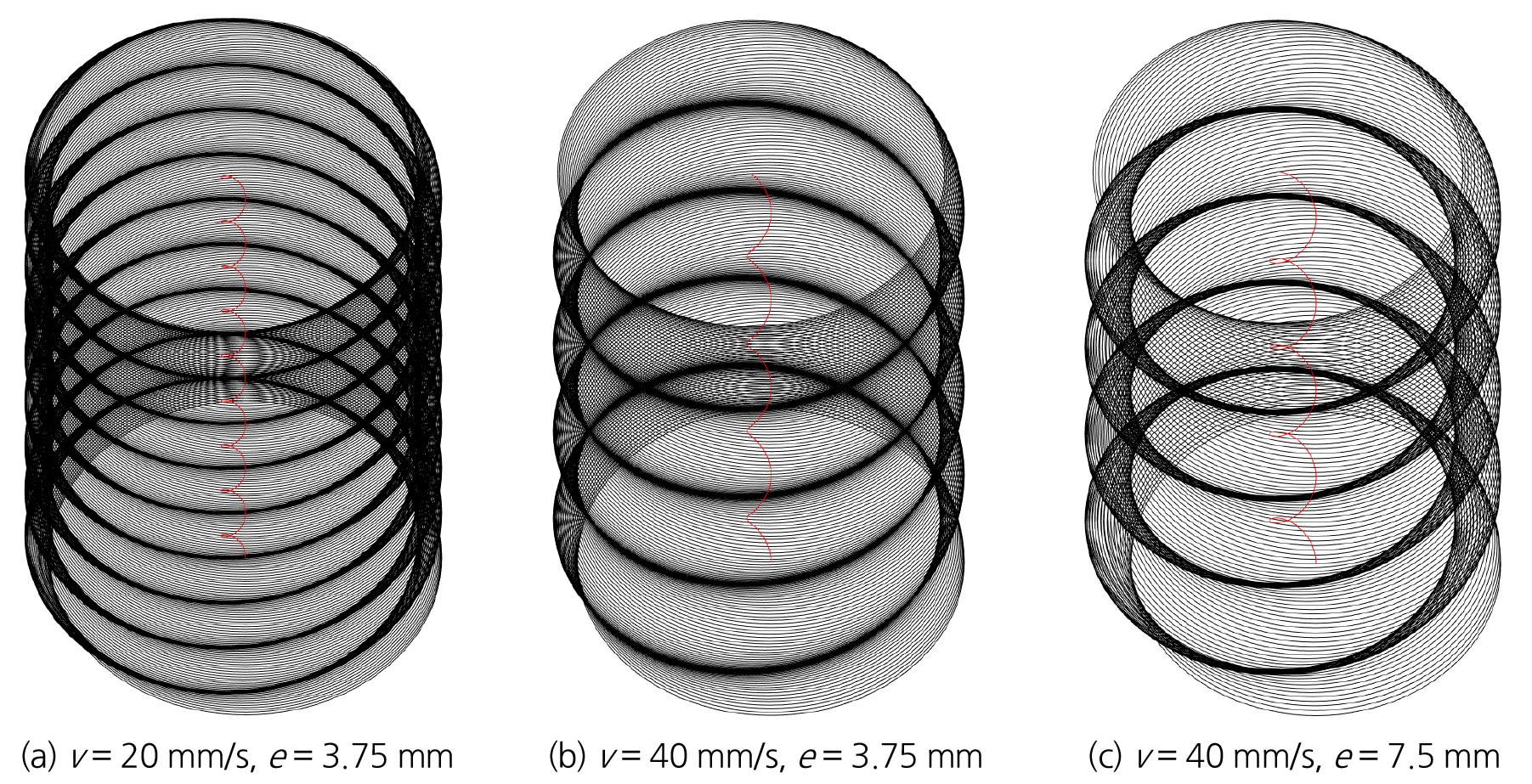
반면 ADC에 의한 암석절삭에서는 커터의 절삭궤적이 헬리컬궤적(helical trajectory)을 그리게 되며, Fig. 4는 본 연구에서 고려한 절삭조건에 따른 ADC의 궤적을 나타낸 그래프이다. 궤적의 형태는 선형이동속도, RPM, 편심, 커터직경에 따라 달라지게 된다. 선형이동속도가 작을 경우에는 ADC는 촘촘한 절삭궤적을 그리게 되며, 편심길이가 클 경우에는 커터의 좌우방향 움직임이 커지는 특성을 갖는다.
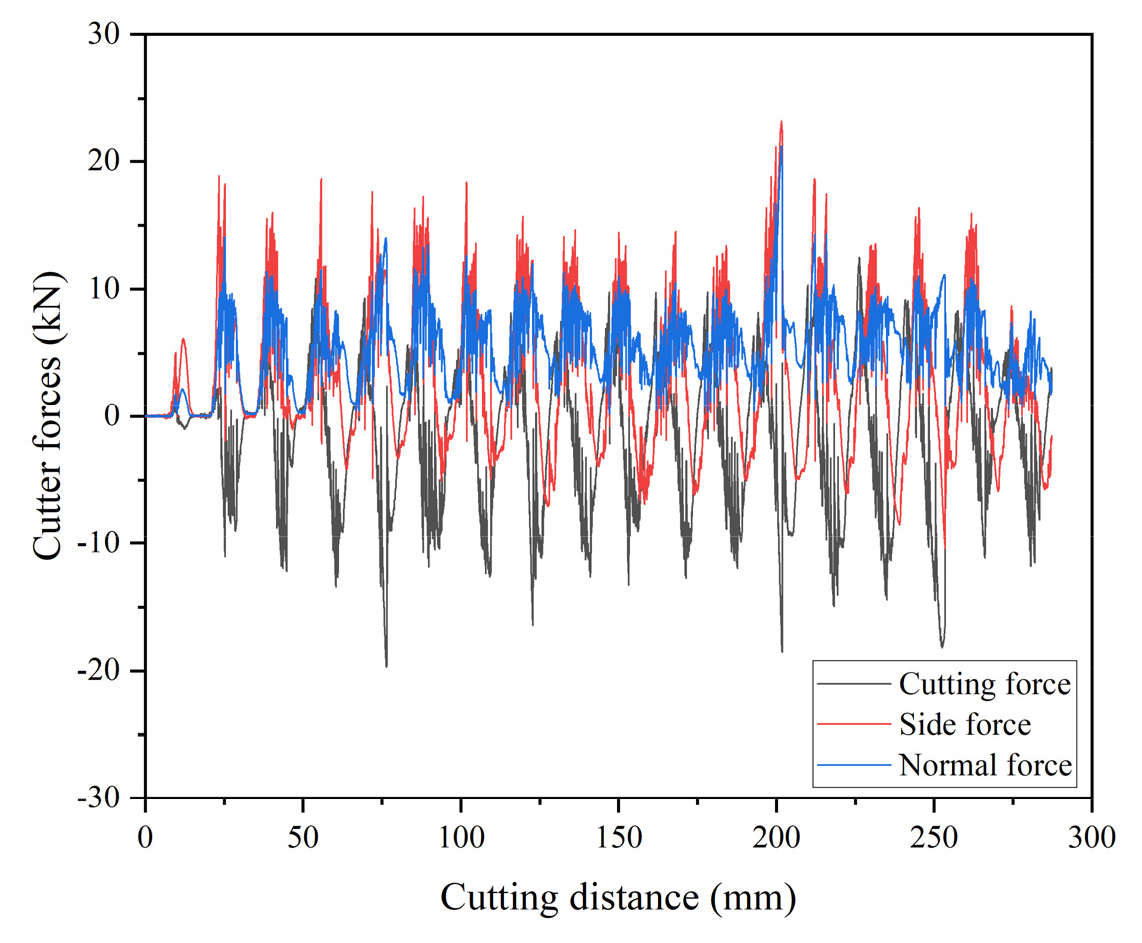
비에너지 계산식에서 커터가 하는 일은 본래 식 (2)와 같이 산출되어야 한다. 커터가 하는 일은 커터작용력의 합벡터와 이동거리 벡터의 내적 값이므로 두 벡터의 스칼라 값과 두 벡터 사이의 사잇각의 코사인 값을 곱하여 산출된다. 수직력은 커터의 이동궤적과 항상 수직이므로 기존의 커터들과 마찬가지로 커터가 암석을 절삭하는 데 소요되는 일은 0으로 계산된다. 하지만 ADC에서 일의 계산을 위해 적용되어야 하는 힘의 성분은 절삭력과 측력 성분 모두가 해당한다. TBM 디스크커터의 경우, 측력은 수직력, 회전력과 비교하여 그 크기가 작지만(1/10 이하), ADC에서는 측력의 비중이 수직력과 회전력과 유사하거나 혹은 커질 정도로 주요한 성분이 된다. Fig. 5에는 본 연구에서 획득한 커터작용력의 예시를 보여주고 있다. 절삭력(cutting force)는 선형이동방향으로의 힘을 의미하고, 측력(side force)은 절삭면에 평행하며 절삭력과 직교하는 축방향으로의 힘, 수직력(normal force)은 절삭평면에 수직한 방향으로의 힘이다. 앞서 설명한 바와 같이 세 방향의 커터작용력의 크기가 서로 유사한 수준으로 발생하는 것을 알 수 있으며, 선행연구(Jeong et al., 2020)에서 보고한 바와 같이 세 방향의 커터작용력은 주기적(periodic)이며, 특정한 수준의 최대값이 연속적으로 나타나는 것을 확인할 수 있다. 본 연구에서 소개한 절삭시험기에 설치된 3방향 로드셀은 고정된 세 개의 서로 직교하는 축에 대한 힘을 획득할 수 있으므로, 앞서 설명한 헬리컬궤적을 따라 이동하며 암석을 절삭하는 ADC의 비에너지 계산을 위해서는 실시간으로 변화하는 커터의 궤적을 고려하여 절삭력과 측력의 합벡터와 커터의 이동궤적벡터 사이의 각도를 지속적으로 계산해주어야 한다.
여기서, 는 ADC의 커터작용력 벡터,는 커터의 이동궤적 벡터, 은 커터작용력 벡터와 커터 이동궤적 벡터 사이의 각도이다. 본래 커터의 이동궤적을 따라 선적분을 하여 절삭이 이루어지는 동안 행해진 커터의 일의 총량을 산출하여야 하지만, 본 연구에서 사용된 로드셀에서는 초당 1,000개의 데이터를 실시간으로 획득할 수 있으므로 1/1,000초 동안 변화한 곡선궤적의 미소구간을 선형으로 근사하는 것이 합리적인 접근방식이 될 수 있다. 결국 ADC의 비에너지는 식 (3)과 같이 계산할 수 있게 된다.
여기서, , 는 각각 ADC의 절삭력, 측력 성분 벡터이며, 는 미소시간에 대한 곡선궤적길이, 는 절삭력과 측력의 합벡터와 커터 이동궤적 벡터 사이의 각도이다.
4. ADC 시험 결과 및 토의
Table 3에는 본 연구에서 수행한 ADC의 시험결과를 요약하였으며, 비에너지의 경우에는 3장에 서술한 방법을 이용하여 계산된 결과이다.
Table 3.
Results of ADC cutting test in this study
기존의 TBM 디스크커터와 픽 커터의 경우에는 잘 알려진 바와 같이 절삭간격과 압입깊이의 비로 표현되는 s/p비를 이용하여 최적절삭조건을 규명하는 것이 일반적이다. Fig. 6에 나타낸 바와 같이 비에너지는 절삭간격(s)과 압입깊이(p)에 영향을 받아 변화하며, 커터간격이 너무 좁게 설정된 경우에는 실제 암석을 파쇄시키기 위하여 필요한 양보다 과도한 에너지가 투입되어 과굴착이 발생하고, 반대로 커터간격이 넓게 설정된 경우에는 인접한 공간 상에 위치하는 암석을 효율적으로 치핑할 수 없게 된다. 또한 압입깊이가 증가함에 따라 비에너지의 값은 감소하는 경향을 보인다. 이러한 현상들은 기존의 TBM 디스크커터 혹은 픽 커터에 의한 암석 파쇄메커니즘에 기인한다. 커터의 관입에 의해 발생한 높은 수준의 압축응력으로부터 2차적으로 유도되는 반경방향으로의 인장균열에 의해 인접한 커터 사이의 암석이 치핑되므로 압축응력의 크기를 결정하는 커터의 압입깊이와 균열의 전파길이, 파쇄영역에 영향을 미치는 절삭간격이 비에너지에 영향을 미치는 주요한 인자가 된다.
반면 ADC 시험에서 관찰된 특징 중 하나는 언더커팅에서는 인접한 절삭선 사이의 상호작용이 거의 발생하지 않는다는 것이다. 이에 대한 원인은 언더커팅에서 발생하는 암석파쇄 메커니즘의 차이 때문인 것으로 판단된다. 선행연구(Jeong et al., 2020)에서 논의된 바와 같이, TBM 디스크 커터 혹은 픽커터에서는 압축파쇄에 의한 암석균열이 인장형 혹은 전단형으로 인접 절삭선으로 전파하는 반면, 언더커팅 디스크에서는 자유면을 향해 직접적으로 발생하는 인장균열에 의한 암석파쇄가 유도되므로 균열 영역이 비교적 크게 확장되지 않는 것으로 판단되며, 이에 대하서는 추가적인 연구가 필요하다.
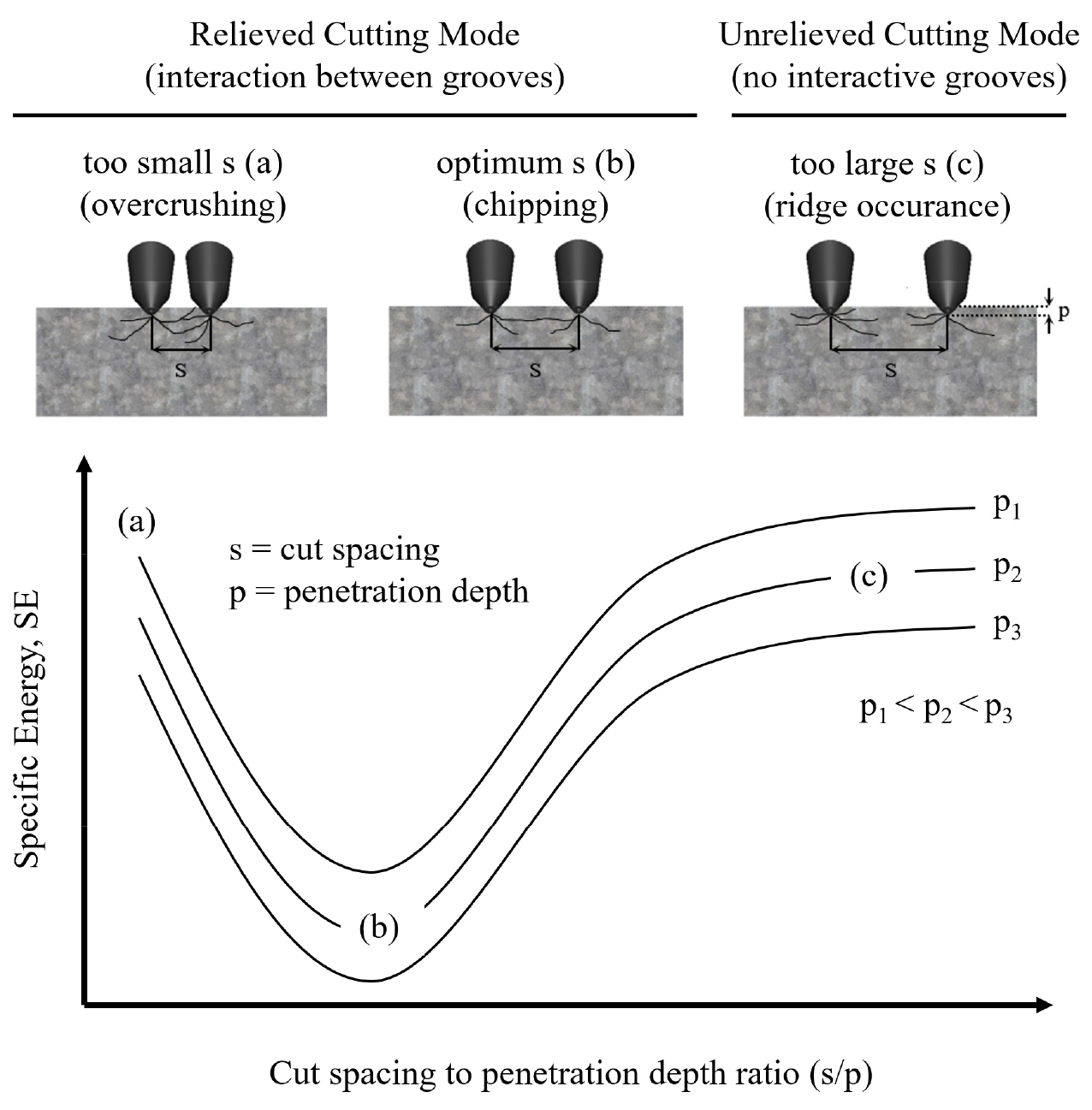
Fig. 6
Rock fragmentation patterns and specific energy according to the ratio of cut spacing to penetration depth in traditional rock cutting method (modified after Copur et al., 2017)
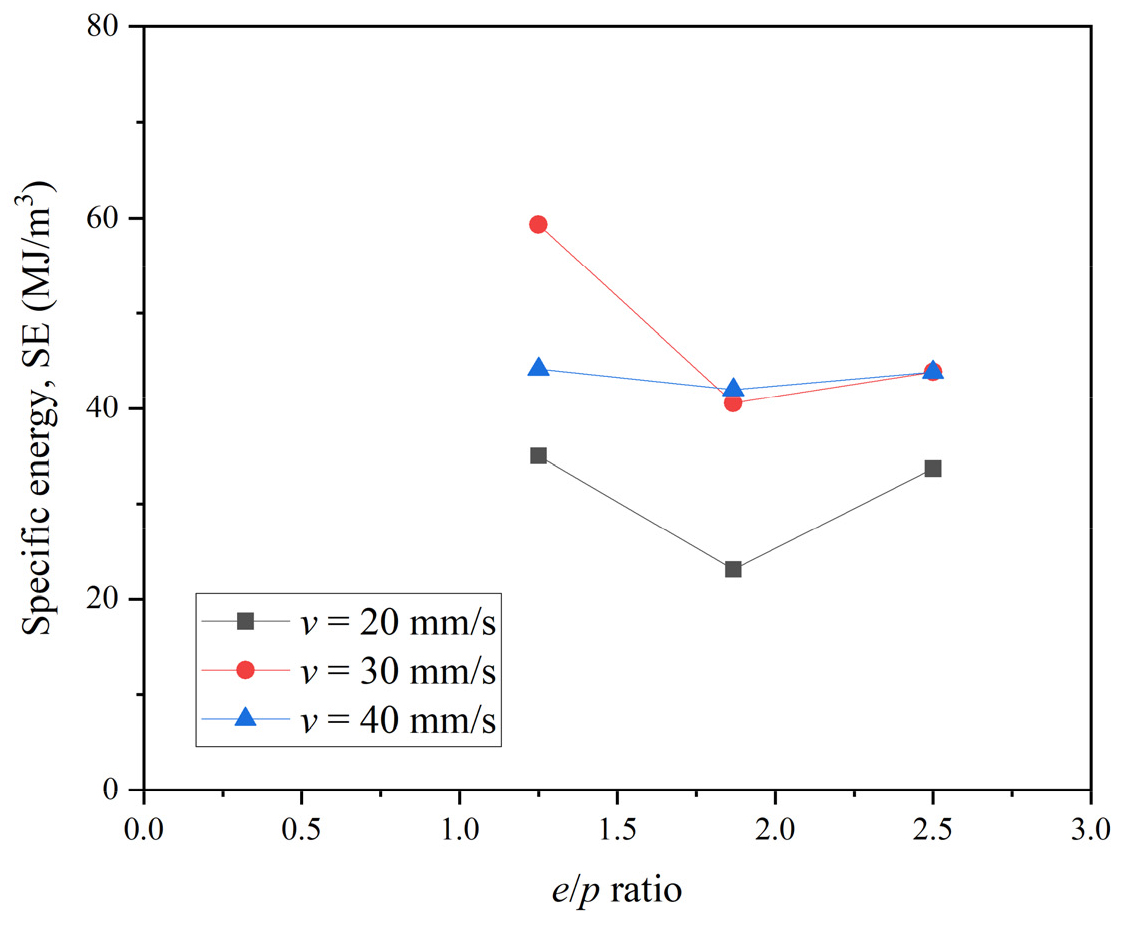
따라서 ADC의 암석절삭에서는 기존에 정의된 s/p비에 따라 최적절삭조건을 규명하는 것이 어렵고, 다양한 추가적인 변수들이 관여하기 때문에, 이 변수들의 조합에 따라 ADC가 최적의 절삭효율을 나타내는 절삭조건을 규명할 필요가 있다. Fig. 7은 본 연구에서 수행한 ADC 절삭시험에서 얻어진 비에너지를 e/p비(편심과 압입깊이 비)에 따라 도시한 그래프이며, e/p비가 변화함에 따라 최소의 비에너지 값을 보이는 지점이 나타나는 것을 확인할 수 있다. 비록 한정된 시험조건으로 인해 일부 조건에서는 명확하게 비에너지의 최소점이 명확하게 규명되지는 않았지만 이와 같은 분석을 통하여 ADC의 비에너지 최소점을 규명하는 것이 가능함을 보여주는 결과이다. 한편 Fig. 7에 나타난 바와 같이 ADC의 선형이동속도가 감소함에 따라 비에너지가 감소하는 경향을 보이고 있다. 선형이동속도가 증가하게 되면 평면상에서 커터가 편심회전에 따라 암석에 관입하는 깊이가 증가하게 되며, 이는 ADC의 절삭효율에 주요한 영향을 미치게 된다. 따라서 선형이동속도는 다른 절삭조건과의 조합에 따라 최적 값을 나타내는 지점이 존재할 것으로 판단되나, 본 연구에서는 한정된 시험조건으로 인하여 이를 명확하게 규명하기는 어려웠다.
5. 결 론
본 연구에서는 언더커팅에 대한 기초연구로서 구동형 언더커팅에 의한 절삭성능을 평가하기 위한 시험시스템을 소개하고 이를 활용한 절삭시험을 수행하였다. ADC의 다양한 절삭조건 중 편심과 선형이동속도를 변화시켜가며 시험을 수행하였으며, 시험결과를 분석하기 위한 방법론에 대하여 논하였다. 기존의 TBM 디스크커터 및 픽 커터와 ADC의 비에너지 계산에서의 차이점은 암석을 절삭하면서 발생하는 3방향 커터작용력 중 측력과 회전력을 모두 고려해주어야 한다는 점과, 절삭 도중 지속적으로 변화하는 커터작용력과 커터절삭궤적의 방향을 계산에 반영하여야 한다는 점이다. 본 연구에서는 이를 고려하여 ADC의 비에너지를 계산하기 위한 방법을 제시하였다. 또한 ADC는 기존의 TBM 디스크커터, 픽 커터와는 달리 절삭간격과 압입깊이의 비에 따라 최적 절삭조건을 규명하는 것이 불가능하며, 아직까지 절삭조건(편심, 압입깊이, RPM, 선형이동속도 등)이 비에너지에 미치는 영향이 규명되어 있지 않다. 편심과 선형이동속도를 변화시켜가며 ADC의 비에너지를 산출한 결과, 편심과 압입깊이 비(e/p ratio)에 따라 비에너지의 최소점이 나타나는 경향을 확인할 수 있었지만 한정된 시험조건으로 인해 그 영향을 명확하게 규명하는 것은 어려웠다. ADC에 의한 암석절삭에서는 본 논문에서 고정된 값으로 설정한 다양한 절삭조건(예: RPM, 압압깊이 등)들이 복합적으로 비에너지에 영향을 미칠 것으로 판단된다. 추후 연구에서는 ADC에서 고려되는 다양한 절삭조건을 변화시켜가며 절삭시험을 수행하고 이들이 비에너지에 미치는 영향을 규명할 예정이다.