1. 서 론

현대 사회는 지상공간의 부족으로 지상의 시설을 지하로 이전시키기 위한 지하공간의 개발이 활발히 이루어지고 있으며 이를 위한 다양한 연구가 진행 중이다. 일반적으로 지하구조물의 시공은 터널 공법을 확장하여 지반 내 대규모 공간을 굴착하고 내부에 신규 구조물을 타설하는 방식을 적용한다. 이러한 공법 중 원지반의 강도를 최대한 활용하는 지하공간 형성방법으로 격자형 지하공간 공법이 있다. 격자형 지하공간 공법은 주방식공법(Room-and-pillar method)과 유사한 공법으로 기존 광산에서 수평으로 매장되어 있는 광물을 효율적으로 채광 할 수 있는 공법으로 사용되어 왔다(Hartman and Mutmansky, 2002; Esterhuizen et al., 2011; Lee et al., 2015). 이러한 주방식 공법을 광산에 적용되던 방식 그대로 지하구조물의 설계 및 시공에 적용할 경우, 기존의 공법에 비해 안전성 측면에서 큰 차이가 발생(Chang et al., 2014; Lee et al., 2015)할 수 밖에 없으므로 주방식 공법의 적용은 제한된 지반조건에서만 적용이 가능하다. 그럼에도 주방식 공법을 통해 굴착공간을 크게 확보할 수 있다면 기존 공법에 비해 경제성의 향상(Lee et al., 2013a)을 기대할 수 있기 때문에 해외의 경우 시공되어 실제 운영이 이루어지고 있는 곳이 있으며, 국내의 경우도 토목구조물 건설에 적용하기 위한 활발한 연구들이 진행 중에 있다(Lee et al., 2013b; 2013c).

지하에 건설되는 격자형 지하공간 공법은 지반의 강도를 이용하여 안전성을 확보하므로 기둥의 역할을 하는 암주의 안전성이 대단히 중요하다. 암주의 안전성은 미국 NIOSH (National Institute for Occupational safety and Health)에서 제시하고 있는 암주 설계 가이드라인(Esterhuizen et al., 2011)과 암주 강도에 의한 추정으로 암주의 안전성을 검토하는 지류론(Chang et al., 2014)에 대한 연구를 참고할 수 있다. 그러나 지하공간의 안전성은 암주에 대한 안전성뿐만 아니라 실제 사용되는 공간(Room)에 대한 안전성 또한 확보되어야 하므로 암주와 동시에 공간(Room)에 대한 안정성이 평가되어야 하나, 이에 대한 연구는 이루어지지 않고 있는 실정이다.

따라서 본 연구에서는 격자형 지하공간에서 실제 사용되는 공간, 룸(Room)의 안전성에 대하여 암주의 안전성과 연계한 평가방안을 연구하였다.

2. 암주와 룸의 안전성 평가

2.1 암주의 안전성 평가

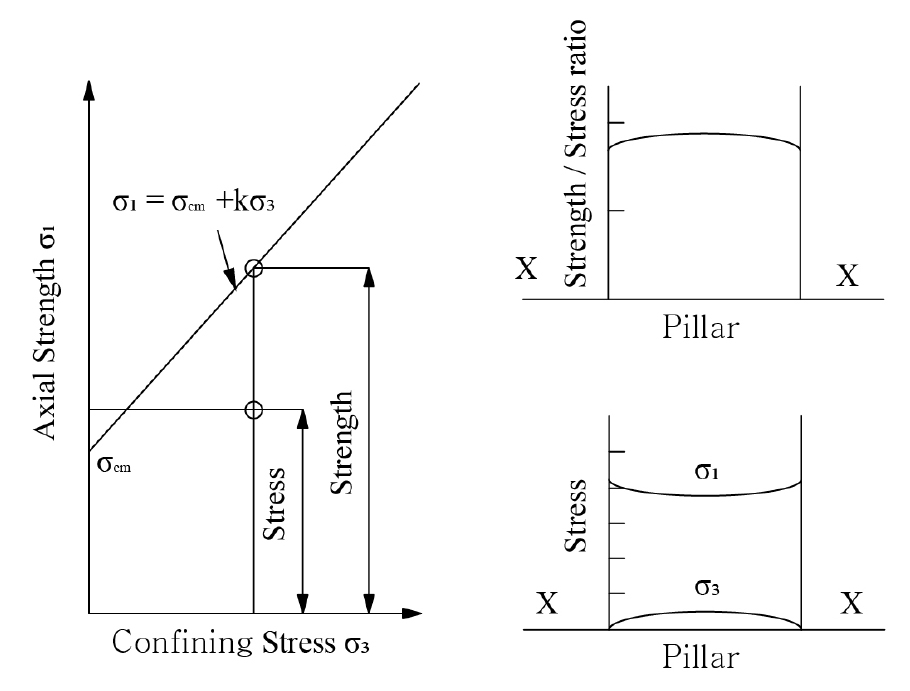
격자형 지하공간은 룸(Room)과 암주(Pillar)로 구성되어 룸에 작용하는 하중을 암주와 암주가 지지하는 것을 전제조건으로 한다. 암주에 하중이 작용한다는 점에서 2-Arch 터널의 필라부와 유사하나 이완하중 등의 아칭효과는 고려하지 않는다. 이러한 암주의 안전성은 암주에 작용하는 압축응력과 암주의 강도를 비교한 강도응력비를 통하여 평가할 수 있다(Fig. 1).

Fig. 1.

Curve of strength ratio (Hoek and Brown, 1980)

강도응력비는 구속압력 σ3에 대하여 소성파괴의 시작은 다음과 같이 표현될 수 있는 Mohr-Coulomb 파괴기준에 의해 규명된다고 가정하며, 식 (1)과 같다.

여기서, 암반의 일축압축강도 σcm은 식 (2)와 같이 정의된다.

또한, σ3에 대한 σ1의 선의 기울기 k는 식 (3)과 같으며, 필라에 대한 강도 응력비는 식 (4)와 같다.

2.2 룸의 안전성 평가

격자형 지하공간은 룸(Room)의 장기적인 안전성을 확보하기 위한 안전성을 평가해야 한다. 상재하중과 아칭효과를 고려하지 않는 조건으로 설계된 암주가 충분한 안전성을 확보하는 경우 룸은 낙반, 붕락, 균열 등 파괴가 수반되는 거동 뿐만 아니라 과도한 변형에 대해서도 충분히 안전해야 한다. 이러한 룸의 안전성을 평가하기 위한 방법으로 터널에 적용되고 있는 한계변형률(critical Strain)을 적용하여 안전성을 평가할 수 있다.

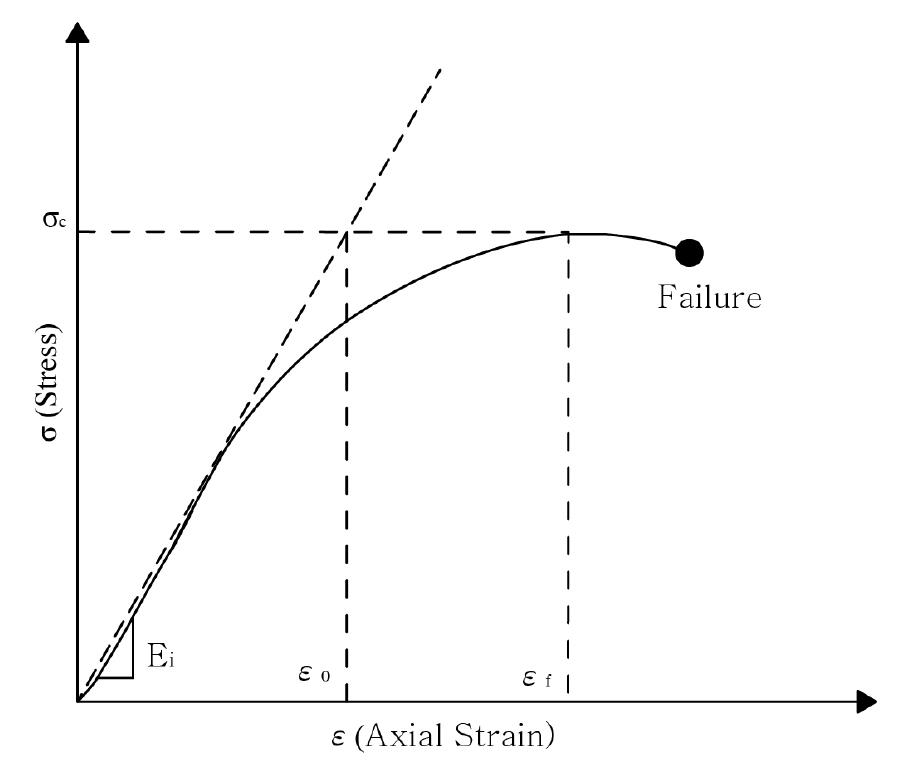
Sakurai (1982)에 의해 처음 제안된 한계변형률은 터널의 정량적 안정성 평가방법으로 제시되고 있다. 한계변형률은 토질 및 암석 시편에 대한 실내실험의 결과를 토대로 정립된 개념으로 일축압축강도시험 결과인 응력-변형률 관계로부터 구해지며 초기탄성영역의 거동특성과 파괴시의 일축압축강도를 이용하여 정의되고, 일반적으로 파괴변형률(εf)보다는 작은 값을 나타낸다(Fig. 2).

Fig. 2.

Strength/stress ratio at pillar (Sakurai, 1982)

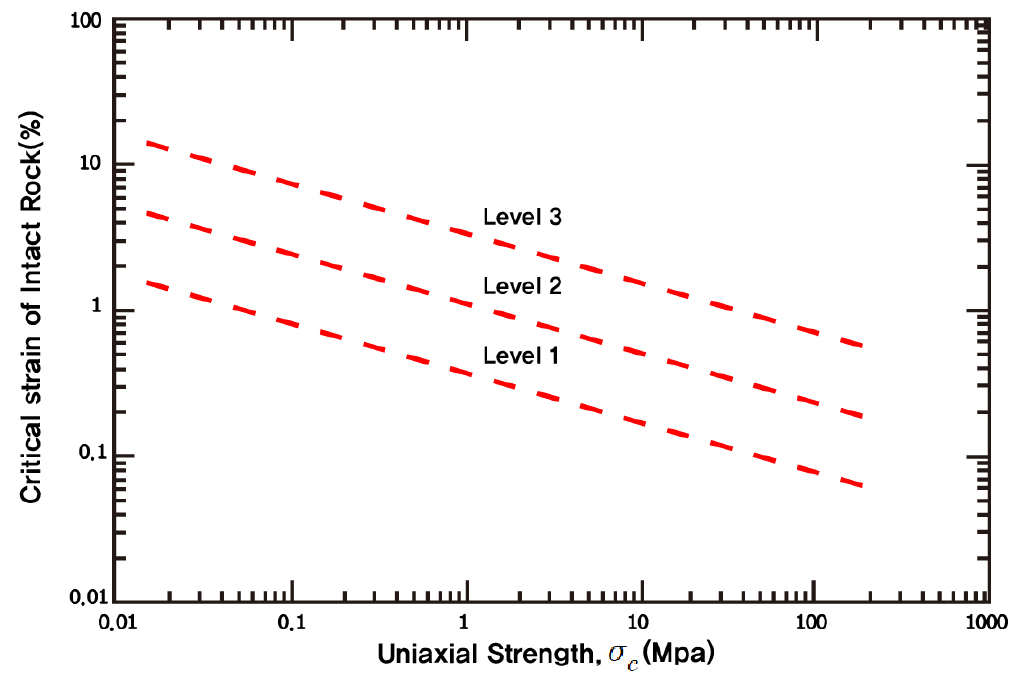
한계변형률을 적용하여 룸 천장부 안정성을 검토하기 위해서는 룸 주변지반의 한계변형률 평가가 필요하다. Sakurai는 한계변형률-지반변형계수(Sakurai et al., 1995)와 한계변형률-일축압축강도(Sakurai, 1997)에 대해 제안하였는데, 본 연구에서는 지반변형계수에 따른 한계변형률 기준을 적용하여 룸 천장부 안정성을 평가하였다.

위와 같은 한계변형률 기준에서 Level I은 지반이 안정 상태에 있지만 이완영역의 발생한계에 달하기 때문에 굴착에 주의를 요하는 단계이고, Level II는 이완영역이 발생하여 추가 지보시공이 이루어져야 하는 단계이며, Level III은 안전의 문제와 시공의 곤란이 예상되어 굴착을 정지하고 굴착방법 혹은 지보공법의 변경을 요하는 단계이다(Fig. 3).

Fig. 3.

Critical strain level (Sakurai, 1997)

3. 격자형 지하구조의 안전성 평가를 위한 수치해석

3.1 검토조건

본 연구에서는 도심지 지하공간 활용을 위한 격자형 지하공간 공법의 암주와 룸 변형률에 대하여 평가하기 위한 검토 조건을 설정하였다(Table 1).

격자형 지하공간 공법은 지반자체의 강도를 활용하여 암주를 형성하기 때문에 암반조건을 기본으로 하며, 룸의 높이 8 m, 룸 폭은 최대 4~48 m로 설정하여 사무용 공간부터 대형 플랜트를 설치하기 위한 공간까지 다양하게 시공될 수 있는 조건을 모사하였다.

수치해석은 미국 Itasca사의 FLAC 2D 유한차분법(FDM) 프로그램을 사용하였다. 해석모델은 Mohr-Coulomb 모델을 사용하였으며, 측압조건은 1.0, 토피고는 30 m를 기본 조건으로 설정하였으며, 굴착으로 인한 영향을 고려하여 좌우측 경계는 4.0H 이상 적용하였다(Fig. 4).

Fig. 4.

Analysis condition and model

격자형 지하공간이 시공되는 지반의 심도는 기존 지하시설물과 암반 출현 심도 등을 고려한 사례 조사를 통하여 지하 30 m로 설정하였고(Chang et al., 2014), 암주의 안전율은 Bullock (2011)과 미국 NIOSH의 가이드라인(Esterhuizen et al., 2011)에서 암주의 최소 안전율을 각각 2.0 및 1.8로 제시하고 있다는 점을 고려하여, 본 연구에서는 보수적인 평가를 위해 무지보 암주의 최소 안전율을 2.0으로 적용하였다.

3.2 암주 안전율에 대한 검토결과

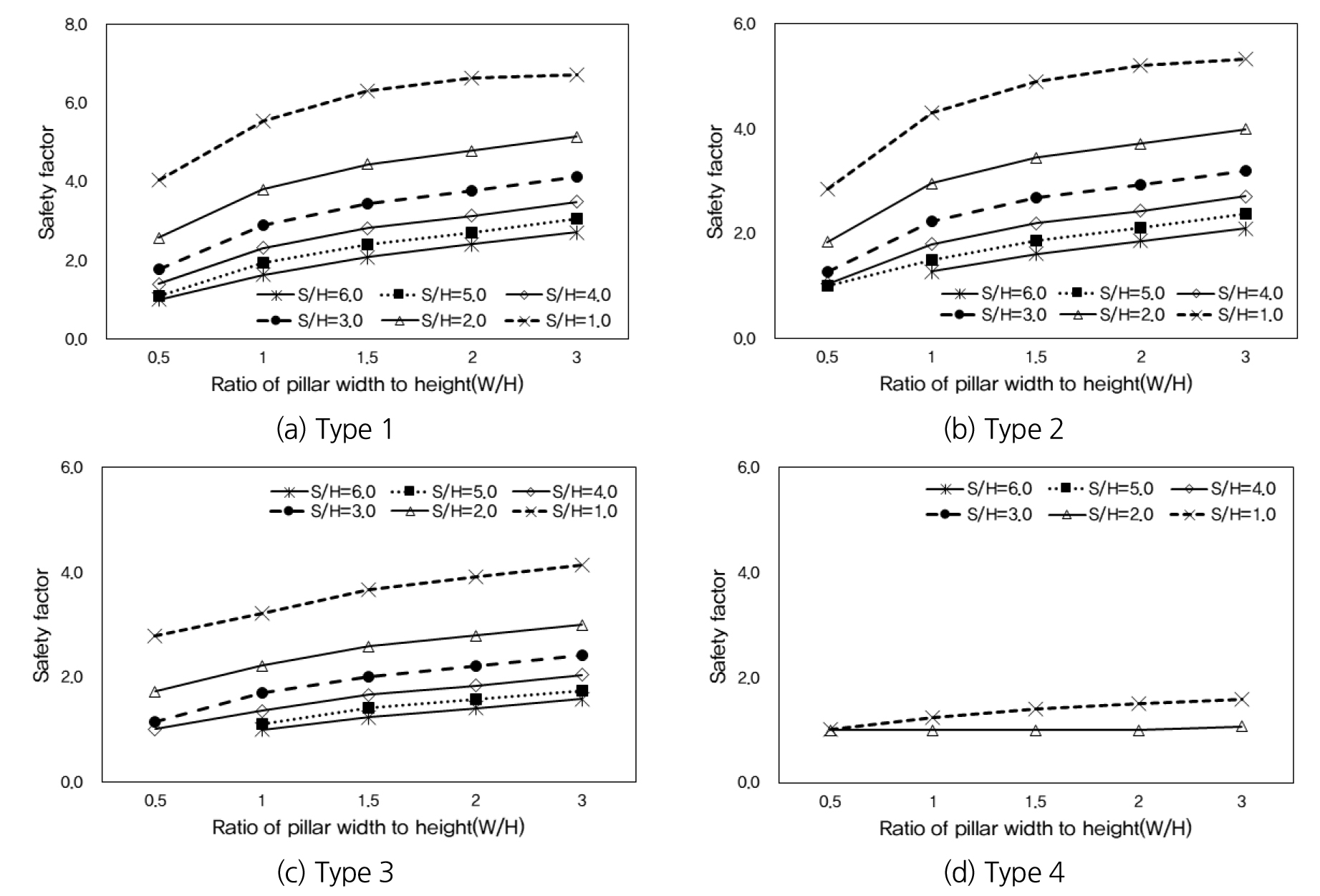
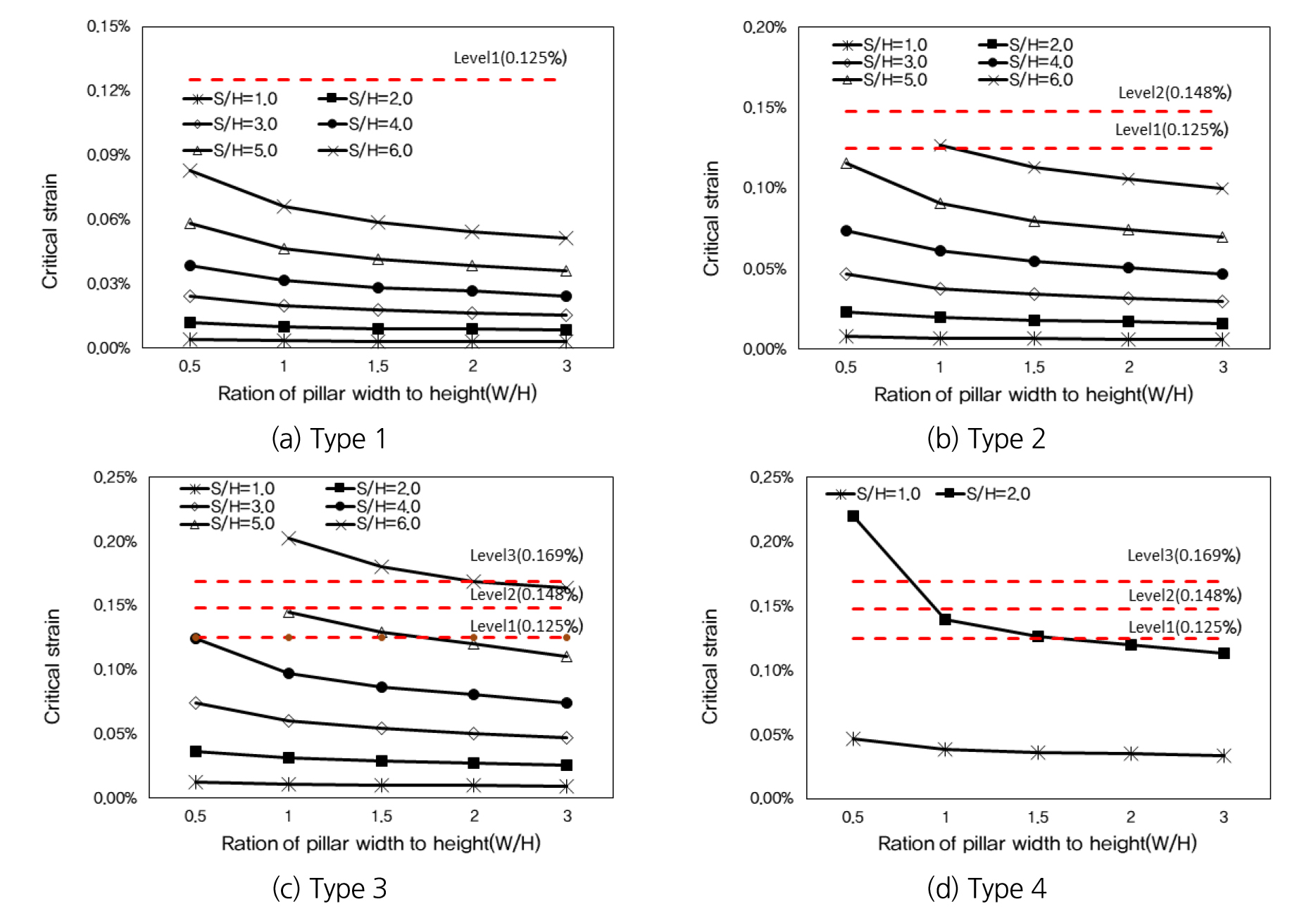
암주의 안전율은 강도응력비 평가방법을 사용하여 다음과 같이 변형계수 조건에 따라 암주의 안정성을 평가하였다(Fig. 5). Type 1 (E = 18,000 MPa)에 대한 암주 및 룸 형상에 따른 안전율 분석 결과, 암주의 폭이 좁아질수록 안전율이 감소하는 경향이 나타났으며 룸의 폭이 좁아질수록 안전율이 증가하는 경향을 보인다.

Fig. 5.

Safety of pillar

Type 2 (E = 9,000 MPa)에 대한 안전율 분석 결과는 Type 1 (E = 18,000 MPa)과 마찬가지로 암주의 폭이 좁아질수록 안전율이 감소하고 룸의 폭이 좁아질수록 안전율이 증가하는 경향이 나타났다. 안전율은 전체적으로 Type 1 (E = 18,000 MPa)보다 낮은 것으로 나타났으며 W/H = 0.5, S/H = 6.0에서 수렴하지 않는 결과를 보였다.

Type 3 (E = 5,400 MPa)에 대한 안전율 분석 결과에서도 Type 1 (E = 18,000 MPa)과 마찬가지로 암주의 폭이 좁아질수록 안전율이 감소하고 룸의 폭이 좁아질수록 안전율이 증가하는 경향을 보인다. 안전율은 전체적으로 Type 1 (E = 18,000 MPa)과 2 (E = 9,000 MPa)보다 낮은 것으로 나타났으며 W/H = 0.5의 S/H = 5.0, 6.0에서 수렴하지 못하는 결과를 보였다.

Type 4 (E = 1,800 MPa)에 대한 안전율 분석 결과에서도 Type 1 (E = 18,000 MPa)과 마찬가지로 암주의 폭이 좁아질수록 안전율이 감소하고 룸의 폭이 좁아질수록 안전율이 증가하는 경향이 나타났다. 안전율은 전체적으로 기준 안전율 2.0을 확보하지 못하는 것으로 나타났으며 W/H = 3.0 이상, S/H = 3.0 이상에서는 수렴하지 못하는 결과를 보였다.

암반의 강도에 따른 안전율 검토 결과 암반의 강도가 클수록 안전율이 크게 나타나며 암주의 폭이 넓어질수록 안전율이 증가하나 암주의 폭이 넓어짐에 따라 안전율의 증가 폭이 감소하여 수렴하는 경향을 보이는 것으로 나타났다. 또한 룸의 폭이 넓어질수록 안전율이 감소하고 암주의 폭과 마찬가지로 룸의 폭이 넓어짐에 따라 수렴하는 경향을 보이는 것으로 나타났다.

3.3 룸 변형률에 대한 검토결과

룸 변형률은 암주 높이와 암주폭의 비에 따른 변형률을 변형계수 조건에 따라 검토하였다(Fig. 6).

Fig. 6.

Critical strain of room

Type 1 (E = 18,000 MPa)에 대하여 룸 변형률을 분석한 결과, 모든 경우에서 Level 1 이내로 만족하는 것으로 나타났다. 룸 변형률은 암주의 폭이 좁아질수록 높게 나타났으며, 암주의 폭이 증가할수록 작아지는 경항을 보이고 룸의 폭이 좁아질수록 작게 발생하였다.

Type 2 (E = 9,000 MPa)에 대하여 룸 변형률을 분석한 결과, 수렴하지 않는 경우를 제외하고 S/H = 6.0, W/H = 1.0 구간에서 Level 1을 초과하였으며 나머지 케이스는 Level 1 이내로 모두 만족하였다. Type 1과 마찬가지로 룸 변형률은 암주의 폭이 좁아질수록 높게 나타났으며, 암주의 폭이 증가할수록, 룸의 폭이 좁아질수록 작게 발생하는 경향을 보인다.

Type 3 (E = 5,400 MPa)에 대하여 룸 변형률을 분석한 결과, 수렴하지 않는 경우를 제외하고 S/H = 5.0에서 W/H = 1.0, 1.5의 케이스가 Level 1을 초과하는 것으로 나타났으며 S/H = 6.0에서는 모두 Level 2를 초과하는 것으로 나타났다. Type 2와 마찬가지로 룸 변형률은 암주의 폭이 좁아질수록 높게 나타났으며, 암주의 폭이 증가할수록, 룸의 폭이 좁아질수록 작게 발생하는 경향을 보인다.

Type 4 (E = 1,800 MPa)에 대하여 룸 변형률을 분석한 결과, 룸 폭 S/H = 3.0 이상인 경우는 수렴하지 않았고, S/H = 1.0과 S/H = 2.0일 때 W/H = 2.0 이상인 경우만 Level 1 이내로 만족하였다. S/H = 2.0일 때 W/H = 1.5에서 1.0인 경우는 Level 2를 만족하였고, W/H = 0.5인 경우는 Level 3를 초과하는 결과가 나타났다.

3.4 암주 안전율과 룸 변형률에 대한 관계

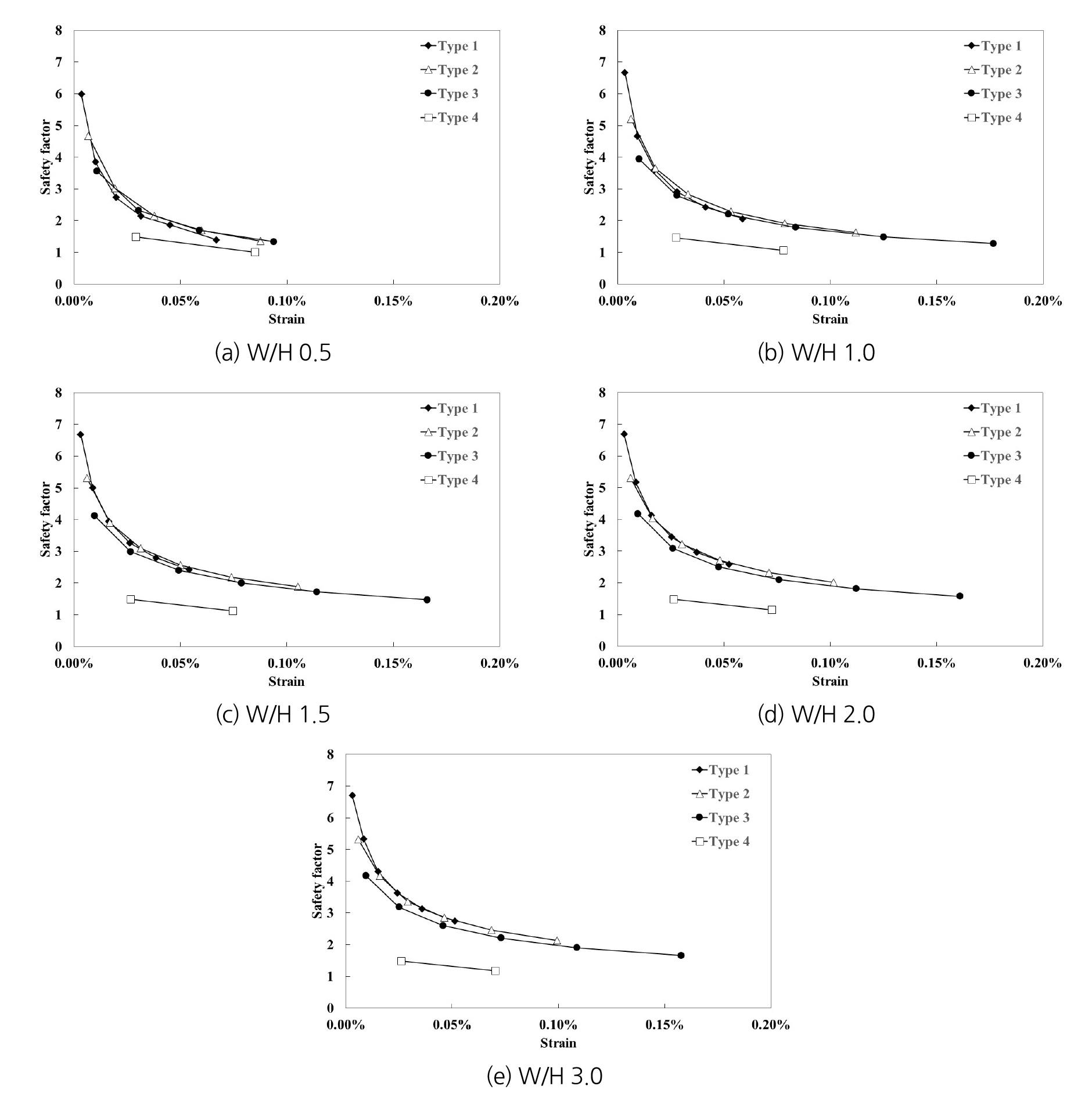
격자형 지하공간의 안전성을 평가하기 위해 3.2, 3.3절에서 검토된 암주 안전율과 룸 변형률에 대한 상관 관계를 분석하였다(Fig. 7). 암주의 형상비에 따라 지반조건별 암주 안전율과 룸 변형률의 연관성을 도시하면 아래 그림에 나타낸 바와 같이 암주 폭에 따라 일정한 분포를 나타낸다. 이를 활용하면 암주의 안전율 2.0을 기준으로 동일한 암주 폭에 대해서 허용 가능한 최대 룸 변형률을 확인할 수 있다.

Fig. 7.

Correlation between pillar safety factor and room critical strain

Table 2는 암주 기준 안전율 2.0에 대한 룸 변형률에 대해 표기하였다. 암주 형상비 W/H = 0.5 조건에서는 Type 4 조건을 제외하고 룸 변형률 0.0359%일 때 암주 안전율을 확보하는 것으로 나타났고 W/H = 1.0 조건에서는 Type 4 조건을 제외하고 룸 변형률 0.0600%일 때 암주 안전율을 확보하는 것으로 나타났다. W/H = 1.5 조건에서는 Type 4 조건을 제외하고 룸 변형률 0.0760%일 때 암주 안전율을 확보하는 것으로 나타났으며 W/H = 2.0 조건에서는 Type 4 조건을 제외하고 룸 변형률 0.0860%일 때 암주 안전율을 확보하는 것으로 나타났다. W/H = 3.0 조건에서는 Type 4 조건을 제외하고 룸 변형률 0.0930%일 때 암주 안전율이 확보되는 것으로 나타났다.

4. 결 론

본 연구에서는 격자형 지하공간에 대해서 지반조건, 암주 폭, 룸 폭을 변수로 하여 수치해석을 수행하여 그 결과를 확인하였으며, 그 결과에 의해 얻어진 결론은 다음과 같다.

1. 격자형 지하공간의 암주 안전율은 암반의 강도가 클수록 안전율이 크게 나타나며 암주의 폭이 넓어 질수록 안전율이 증가하나 암주의 폭이 넓어짐에 따라 안전율의 증가 폭이 감소하여 수렴하는 경향을 보이는 것으로 나타났다.

2. 격자형 지하공간의 룸 변형률은 지반조건이 변형계수 1,800 MPa 이하인 경우는 Level 1을 만족하지 못하여 안전성이 결여되므로 변형계수 5,400 MPa 이상의 암반에 룸 폭을 고려하여 시공되어야 할 것으로 판단된다.

3. 격자형 지하공간의 암주 안전율과 룸 변형률의 관계를 분석한 결과, 동일한 암주 폭에 대해서는 지반조건과 상관없이 일정한 상관관계가 나타나며, 이를 기준으로 암주 폭에 따른 룸 변형률의 상한값을 도출 할 수 있었다.