1. 서 론
터널 공사는 지반과 암반을 통과하는 복잡한 공정으로, 예기치 않은 붕괴 위험이 항상 존재한다. 이러한 위험은 인명 피해와 경제적 손실을 초래할 수 있으며, 공사 진행에 심각한 차질을 빚게 한다. 따라서 터널 붕괴 위험을 체계적으로 평가하고 예측하는 방법론의 개발은 터널 공사의 안전성과 효율성을 높이는 데 필수적이다.
기존의 터널 붕괴 위험도 평가 방법은 주로 정성적인 평가에 의존해 왔다. 그러나 이러한 방법은 평가자의 주관이 개입될 여지가 많아 객관적이고 신뢰성 있는 결과를 도출하는데 한계가 있다. 따라서 보다 객관적이고 정량적인 평가방법이 요구된다.
터널 붕괴 위험도 평가의 대표적인 방법은 RMR (rock mass rating, Bieniawski, 1989)과 Q-system (Barton et al., 1974)이다. RMR 시스템은 암반의 상태, 절리 특성, 지하수 상태 등을 종합적으로 평가하여 암반을 등급화하고, Q-system은 절리의 상태, 거칠기, 지하수 조건 등을 고려하여 암반의 안정성을 평가한다. 그러나 이러한 시스템들은 터널 붕괴의 복잡성을 충분히 반영하지 못하며, 특히 여러 영향 인자 간의 상호작용을 고려하는 데 한계가 있다.
터널 붕괴 위험도 평가에서의 불확실성을 고려하기 위한 방법론으로는 몬테카를로 시뮬레이션이 사용되고 있다. Ang and Tang (1975)은 구조물의 신뢰성 평가에 몬테카를로 시뮬레이션을 적용하여 다양한 불확실성을 고려한 구조물의 거동을 예측하는 방법을 제시하였다. 이 기법은 입력 변수의 확률분포를 기반으로 다수의 시나리오를 시뮬레이션하여 출력값의 통계적 특성을 분석하는 데 효과적이다. Meng et al. (2023)은 몬테카를로 시뮬레이션을 이용하여 터널 붕괴 위험성을 평가하고, 이를 통해 터널 건설의 실제 위험 평가에서 붕괴 확률을 예측하는 데 사용할 수 있음을 확인하였다. Zhou et al. (2020)은 베이지안 방법을 사용하여 터널 붕괴 위험을 분석하고, 터널 주변 암반의 변형을 관찰하여 구조물의 안정성을 평가 하였다. Huang et al. (2022) 베이지안 네트워크를 기반으로 한 터널 붕괴 위험 분석 방법을 제시하고, 복잡한 위험 요소 간의 상호작용을 정량적으로 분석하여 터널 붕괴 위험을 평가 하였다. He et al. (2021) 해석적 구조 모델링과 퍼지 베이지안 네트워크를 결합한 다기준 의사결정 방법을 제안하였다.
AHP는 복잡한 문제를 계층적으로 분석하여 각 요소의 중요도를 산정하는 데 사용된다. Saaty (1982)는 AHP를 통해 의사결정 문제를 구조화하고, 쌍대 비교를 통해 각 요소의 상대적 중요도를 평가하는 방법을 제안하였다. 이 기법은 터널 붕괴 위험도 평가에서 다양한 영향 인자의 중요도를 객관적으로 산정하는 데 유용하다. Kwon et al. (2022)은 AHP와 퍼지 이론을 결합하여 터널 리스크 평가 모델을 제안하였다. Li et al. (2022)은 엔트로피와 AHP를 결합한 가중치를 기반으로 한 터널 붕괴 위험 평가 방법을 제안하였다. Liu et al. (2023)은 터널 리스크 요인의 불확실한 정보를 종합적으로 고려하고, AHP와 엔트로피 가중치 방법을 통해 터널 리스크 요인의 종합 가중치를 계산하였다. Yu et al. (2022)은 퍼지-AHP 기반으로 터널 붕괴 위험을 평가 하였다.
본 연구는 터널 붕괴 위험도를 정량적으로 평가할 수 있는 새로운 지수인 터널 붕괴 위험도 지수를 개발하고자 한다. 먼저, AHP 기법을 활용하여 터널 붕괴에 영향을 미치는 주요 영향 인자의 중요도를 체계적으로 산정 하였다. 이를 통해 기존의 주관적 평가 방식을 보완하고, 각 인자의 상대적 중요도를 객관적으로 평가할 수 있다. 다음으로 몬테카를로 시뮬레이션 기법을 활용하여 터널 붕괴 위험도 지수를 산출 하였다. 이 기법은 다양한 입력변수의 확률분포를 고려하여 다수의 시나리오를 시뮬레이션 함으로써 불확실성을 반영한 평가 결과를 제공한다. 이를 통해 복잡한 터널 붕괴 위험 요소 간의 상호작용을 정량적으로 분석하였다.
2. 위험도 평가 방법
몬테카를로 시뮬레이션은 모의적 표본추출 방법(simulated sampling technique)으로, 통계적 방법을 통해 입력 변수의 확률분포(probability distribution) 값을 산출하고, 임의의 난수를 발생시켜 출력값에 대한 분포와 통계량을 통해 각 변수들의 발생 가능한 범위를 추정한다. 몬테카를로 시뮬레이션을 통해 얻은 결과는 확률분포로 나타나며, 임의적으로 산정된 결과 값이 전체 산정된 결과 값에서 차지하는 비율로 표현된다. 본 연구에서는 터널의 막장별 붕괴 위험도 평가를 위한 기준 지수를 산정하기 위해 몬테카를로 시뮬레이션을 수행하였다.
신뢰성 해석 문제는 종종 기본 랜덤 변수들로 이루어진 벡터 로 정식화 된다. 랜덤 변수들에 의해 한계 상태를 나타내는 한계 상태 함수 가 정의되며, 한계 상태는 설계 변수의 공간에서 안전과 파괴의 경계인 =0으로 정의된다. 본 연구에서 한계 상태 함수는 터널의 붕괴 위험도 지수와 그에 대한 붕괴 위험도 평가 기준 지수로 나타내며, 식 (1)과 같다.
여기서, Risk index는 터널의 붕괴 위험도 지수, Collapse risk index는 붕괴 위험도 평가 기준 지수, 는 각 인자의 가중치, 는 각 인자의 등급을 의미한다. 이때 붕괴 위험도 확률은 다음과 같이 표현되는 다차원 적분 식 (2)와 같이 정의된다.
여기서, 는 기본 랜덤 변수들 의 결합확률밀도함수(joint probability function)이며, 붕괴 위험도 영역에 대해 적분을 수행한다.
3. 붕괴 위험도 지수 평가
3.1 영향 인자 가중치 산정
본 연구에서는 문헌조사와 전문가 자문을 통해 터널 붕괴 위험도에 영향을 미치는 14개의 영향 인자에 대해(Kim et al., 2017) AHP를 활용하여 가중치를 산정하였다(Table 1). 구조화된 영향 인자의 쌍대 비교(pairwise comparison)를 통해 가중치를 설정하기 위해서는 각 영향 인자 간 상대적 중요도가 결정되어야 한다. 이를 위해 21명의 전문가를 대상으로 설문조사를 실시하여 각 영향 인자의 상대적 중요도와 우선순위를 조사하였다. 전문가 21인은 터널 설계 및 시공과 관련된 실제 프로젝트에 참여한 15년 이상의 경력이 있거나 관련 연구를 수행한 대학교수, 연구원 및 엔지니어 등을 선정하였다. 설문 조사에서 전문가들은 각 영향 인자의 상대적 중요도를 리커트 9점 척도를 이용하여 평가하였다.
Table 1.
Final compound weighting calculation on risk influence factors for tunnel collapse
설문조사 결과를 통해 상위 및 하위 계층 영향 인자의 가중치와 우선순위를 산정하였으며, 논리의 일관성 유지의 판단을 위하여 비일관성비율(inconsistency ratio)을 검증하였다(Saaty, 1982). 비일관성비율이 0.0이라는 것은 응답자가 완전한 일관성을 유지하며 쌍대 비교를 수행하였음을 의미한다. Saaty는 비일관성비율이 0.1 미만이면 쌍대 비교는 합리적인 일관성을 갖는 것으로 판단하고, 0.2 미만일 경우 용납할 수 있는 수준의 비일관성을 갖고 있는 것으로 판단한다. 비일관성 비율이 0.2 이상이면 일관성이 부족한 것으로 재평가가 필요하다고 제안하였다. 최종 복합가중치는 상위계층의 영향 인자에 대한 가중치와 종속된 하위계층의 영향 인자의 가중치를 곱하여 산정하였다.
각 계층의 가중치와 우선순위는 Table 1과 같다. 지보 및 보강조건의 가중치는 0.349로 우선순위 1위로 고려되었으며, 터널 기하학적 조건의 가중치는 0.058 우선순위 5위로 나타났다. 지반 및 물성의 형상, 지하수 조건, 굴착 조건에 대한 가중치는 각각 0.347, 0.155 및 0.091이며, 우선순위는 각각 2, 3 및 4순위로 나타났다. 전체 비일관성 비율은 0.00278로 분석되어 유의미한 것으로 나타났다.
3.2 영향 인자 정량적 평가
본 연구에서는 문헌 조사와 전문가 의견을 바탕으로 선정된 14개의 영향 인자에 대해, 위험도에 미치는 영향을 10점 범위 내에서 등급으로 구분하여 정량화 하였다. 제시된 등급화 가이드는 전문가들이 각 영향 인자에 점수를 부여할 때 획일적인 평가를 피하고, 주관적인 의견을 일정 범위 내에서 보다 구체적으로 표현할 수 있도록 구성하였다. 지반의 물성 및 형상의 평가 등급은 RMR (Bieniawski, 1989)의 내용을 토대로 암반의 절리면 상태, 절리면 간격, 절리방향에 대한 보정, 암반강도에 대한 등급화에 적용하였으며 Table 2와 같다. 지반 등급의 경우, 암반과 지반에 대해서 각각 RQD (rock quality designation)와 SPT (standard penetration test) N 값을 등급화에 적용하였다(Deere, 1964).
Table 2.
Grading guide on geotechnical properties and shape
터널 기하학적 조건의 평가 등급은 굴착 단면적과 심도비를 고려하여 분류하였으며 Table 3과 같다. 여기서 심도비는 지표로부터 터널의 천단부까지의 깊이를 나타낸 비율이다.
Table 3.
Grading guide on tunnel geometry conditions
지하수 조건의 평가 등급은 지하수 유입량과 지하수 수위로 RMR (Bieniawski, 1989)의 내용을 토대로 분류하였으며 Table 4와 같다. 지하수위가 막장보다 높게 위치할 경우, 지하수위에 의한 수압의 작용으로 막장에 가해지는 하중이 증가하며, 암반 내의 절리 등에 의한 지하수압의 증가로 인해 터널 막장의 위험도가 증가한다. 또한, 깊은 굴착 시 현장 주변 지반에 변위가 발생하여 터널 구조물 자체의 안정성에 영향을 받으며 막장 내 지하수 및 침투수는 터널 공사에 큰 영향을 준다.
Table 4.
Grading guide on groundwater conditions
굴착 조건에서 분할 굴착 공법은 터널의 안정성, 경제성, 공사 기간을 결정하는 중요한 요소이다. 분할 굴착 공법에 대한 평가 등급은 벤치의 길이와 수를 기준으로 범주화 하였다. 도로설계편람(MLTMA, 2012)에 따라 굴진장 등급 값과 함께 Table 5와 같이 등급화 하였다.
Table 5.
Grading guide on excavation conditions
지보 및 보강조건에 대해서는 도로 및 터널 설계 매뉴얼 및 RMR (Bieniawski, 1989; KICT, 2009; MLTMA, 2012) 기반으로 지보패턴수준, 보조공법, 지보 및 보강 시행시기로 평가 등급을 분류하였으며 Table 6과 같다.
Table 6.
Grading guide on support and reinforcement conditions
3.3 위험도 평가 기준 산정
실제 붕괴 사례 데이터를 수집하고, 본 연구에서 제시된 영향 인자별 등급지수를 산출하였으며, 붕괴 위험도를 비교할 수 있는 평가 기준을 마련하였다. 총 27개의 붕괴 사례 데이터를 수집하였으며, 수집한 27개 사례는 도로터널 44%, 도시철도 26%, 철도터널 19%, 전력구 및 여수로 터널이 각각 7%와 4%이다. 14개의 영향 인자의 가중치는 AHP를 통해 결정된 확정적 값을 활용하였고(Table 1), 각 영향 인자의 등급 점수는 등급화 가이드를 활용하였다(Tables 2, 3, 4, 5, 6). 27개의 붕괴 사례의 각 영향 인자별 해당되는 등급화 분류 체계의 중간 값을 점수로 적용하였다. 각 영향 인자별 총 27개의 사례에 대한 등급화 점수가 부여되고, 총 14개의 영향 인자가 존재하므로 수많은 난수 추출 경우의 수가 발생한다. 본 연구에서는 총 10,000회 실시하였다.
시뮬레이션 과정에서 추출된 각 영향 인자별 등급 점수는 해당 가중치와 곱해져서 해당 영향 인자의 지수가 산정된다. 이렇게 산정된 각 영향 인자 지수의 총합을 “터널 붕괴 위험도 지수”로 제안하였으며, 식 3과 같이 정의하였다.
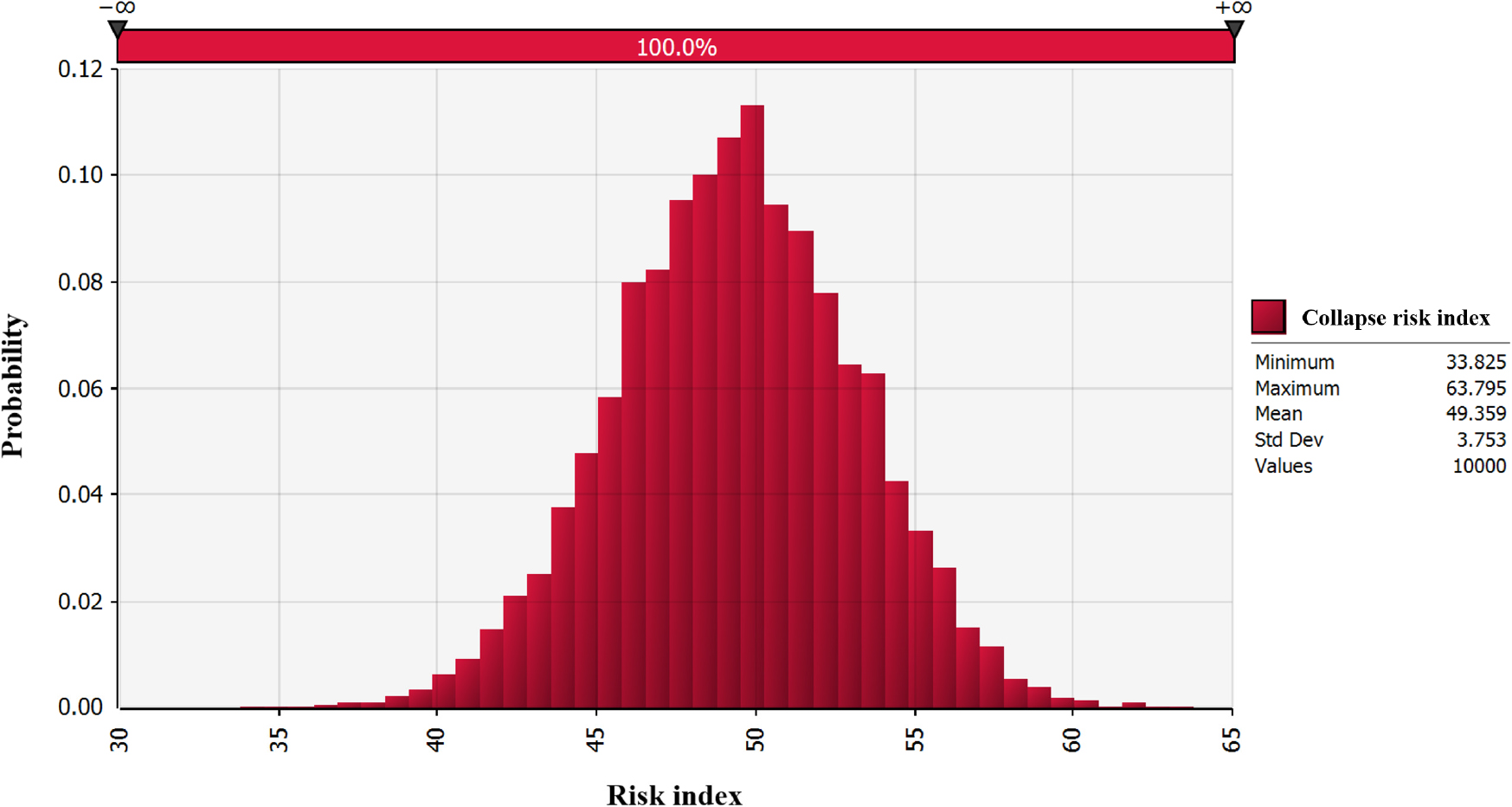
여기서, 는 각 인자의 가중치, 는 각 인자의 등급을 의미한다. 본 연구에서는 터널 붕괴 위험도 지수 산정에 확률분포 함수 중 삼각분포함수를 사용하였다. 각 분포의 특성은 14개 영향 인자별 등급 점수의 최소값, 최빈값, 최대값으로 표현하였다. 10,000회의 시뮬레이션이 수행되었으며, 총 10,000개의 결과값이 도출되었다. 도출된 결과값의 분포와 발생 확률을 정리하여 확률밀도함수로 제시하였고, PALISADE사의 @RISK 분석툴을 활용하여 산정하였다. 이러한 방법을 통해 붕괴 사례 데이터를 활용한 터널 붕괴 위험 지수를 도출하였으며 Fig. 1과 같다.
분석결과, 붕괴 위험도 지수의 최소값, 평균값 및 최대값은 각각 33.825점, 49.359점 및 63.795점이다. 붕괴 위험도 지수의 평균값인 49.359점은 터널 붕괴 위험도에 대한 막장별 평가 결과와 비교를 통해 해당 막장의 붕괴 위험도 수준을 평가 할 수 있다. Table 7는 각 영향 인자에 대한 붕괴 위험도 지수를 보여주며, 평균값은 붕괴 위험도가 높은 영향 인자를 파악하는데 활용하게 된다.
Table 7.
Collapse risk index analysis by influence factors
영향 인자별 분석된 지수를 살펴보면, 절리면 상태가 7.2747점으로 가장 높았고 심도비가 0.8223점으로 가장 낮게 나타났다. 이는 각 영향 인자별 가중치의 크기에 따른 결과로 판단된다. 가중치의 크기 대비 지수가 높게 산정된 영향 인자는 절리면 상태, 암반강도, 지반 등급(RQD/N), 절리면 간격, 절리방향에 대한 보정, 지하수위, 보조공법으로 분석되었다. 지반의 물성 및 형상, 지하수 조건에 관계된 인자가 붕괴 위험도와 민감도가 높았고, 지보 및 보강조건 중 보조공법도 매우 높게 분석되었다. 상대적으로 터널 기하학적 조건이 민감도가 낮게 나타났다. 본 연구의 터널 붕괴 위험도 지수는 향후 터널 붕괴 위험도에 대한 막장별 평가 결과와 비교를 통해 해당 막장의 붕괴 위험도가 낮은지 높은지 평가할 수 있다.
4. 결 론
본 연구에서는 터널 공사 중 발생할 수 있는 붕괴 위험을 체계적으로 평가하고 예측하기 위한 새로운 지수인 터널 붕괴 위험도 지수를 제안하였다. 터널 붕괴에 영향을 미치는 14개의 영향 인자에 대해서 AHP를 활용하여 각 인자의 가중치를 산정하였다. 각 영향 인자별 정량적인 등급화 기준을 마련하기 위하여 등급화 가이드를 작성하였다. 붕괴 위험도 평가 기준을 마련하기 위하여 27개의 붕괴 사례 데이터를 수집하여 몬테카를로 시뮬레이션을 통해 붕괴 위험도 지수를 산출하였다.
터널 붕괴 위험도 지수의 산정결과에 대한 확률분포를 살펴보면, 최소 33.825점, 최대값은 63.795점, 평균값은 49.359점으로 분석되었다. 이 평균값은 향후 터널 붕괴 위험도에 대한 막장별 평가결과와 비교를 통해 해당 막장의 붕괴 위험도가 낮은지 높은지 평가할 수 있다. 또한, 확률적 분석 결과를 활용한 신뢰성 해석에도 활용할 수 있다. 터널 붕괴 위험도 지수를 활용하면 붕괴 위험도가 높은 터널 구간을 사전에 예측할 수 있으며, 이를 통해 적절한 지보 및 보강 대책을 마련할 수 있다. 또한, 지반 조건, 설계 및 시공 고려사항 등 다양한 정보를 종합하여 터널 붕괴 위험도를 체계적으로 평가하는 방법론을 제공함으로써 터널 시공의 안전성과 효율성을 높일 수 있다. 터널 붕괴 위험도 지수 분석을 통해 각 영향 인자의 민감도를 평가한 결과, 절리면 상태, 암반강도, 지반 등급(RQD/N), 절리면 간격, 절리방향 보정, 지하수위 및 보조공법 등이 붕괴 위험도와 높은 민감도를 가지는 것으로 나타났다. 반면 터널 기하학적 조건은 상대적으로 민감도가 낮게 분석되었다.
본 연구에서 수행하는 터널 붕괴 위험도 지수는 구축된 붕괴 터널 현장자료를 통해 수행되므로, 붕괴 터널 현장 자료가 더욱 많아지고 자료 완성도가 높아짐에 따라 터널 붕괴 위험도 평가 기준의 신뢰도가 점진적으로 향상될 것으로 판단된다.