1. 서 론
2. 자유면 발파 선행연구
3. 시멘트 모르타르 시험체를 이용한 2, 3 자유면 발파실험
3.1 시멘트 모르타르 시험체 및 실험 조건
3.2 실험 결과
4. 2, 3 자유면 발파모델링
4.1 해석 모델
4.2 재료 모델
4.3 수치해석 결과
5. 결론 및 고찰
1. 서 론
터널 굴착 방법은 크게 기계굴착공법과 발파공법으로 분류할 수 있다. 기계굴착공법은 굴진율과 작업 안정성이 높고, 지반교란, 여굴량이 적으며 소음 및 진동에 의한 민원 발생의 우려가 없는 장점이 있으나 초기비용이 많이 들고 다양한 지질조건에 대응이 용이하지 않으므로 터널 길이가 짧거나 암질이 경암인 지질조건의 변화가 클 것으로 예상되는 경우 대부분 발파공법이 적용되고 있다(Ocak and Bilgin, 2010; Barton, 2012).
발파공법에서 비장약량과 굴진율은 발파효율을 결정하는 중요한 요소들이다. 비장약량은 단위부피의 암석을 파괴하는데 소요되는 폭약의 양으로 발파설계 시 주요한 인자로 사용된다. 적정 비장약량의 산정은 화약의 과소비 및 암반의 과발파를 줄여주고, 파괴불량 및 이로 인한 2차 발파의 필요성을 사전에 감소시키는 등 발파효율을 높이는 데 매우 중요한 역할을 하기 때문에 그동안 적정 비장약량을 산정하기 위한 연구가 많이 수행되어 왔다(Jong and Lee, 2004; Choi et al., 2009; Taiwo et al., 2023). 굴진율은 터널 발파에서 천공장 대비 굴진장의 비로 나타내며, 터널의 대단면화 및 장대화에 따른 장공발파로 인해 굴진율은 공사기간을 단축하는 데 큰 영향을 미치는 매우 중요한 요소가 되었다. 현재까지 터널의 굴진율을 개선하기 위해 장약밀도 변경, 발파패턴 변경, 전색재 개선, 전자뇌관 활용, 심빼기공법 개선 등 다양한 연구가 수행되어 왔다(No et al., 2006; Yoon et al., 2008; Kim et al., 2013; 2022; Ko, 2022).
심빼기 개선공법 중 선대구경수평보링공법은 굴진율 증대와 진동 감소에 크게 효과가 있는 것으로 알려져 있다(Beak et al., 2012). Kim et al. (2022)은 수치해석을 통해 burn-cut과 선대구경수평보링공법의 굴진율을 정량적으로 비교하였고, 선대구경수평보링공법의 굴진율 증대의 원인을 심발부에 자유면 형성과 이에 따른 인장파 영향의 확대로 설명하였다. 또한, Olofsson (1988)은 무장약공 직경, 천공장과 굴진율 간의 관계를 나타낸 도표를 제안했으며, 무장약공의 직경이 커질수록 굴진율이 증가함을 확인할 수 있다(Fig. 1).
그동안 자유면에 대한 연구는 자유면이 발파 진동과 파쇄도에 미치는 영향에 대해 주로 이루어졌으며, 많은 실험과 수치해석을 통해 정량적으로 평가되어 왔다(Oh et al., 2018; Zhang et al., 2020). 그러나 자유면의 수에 따른 굴진율 및 비장약량의 차이를 정량적으로 비교한 연구는 부족한 실정이다.
본 연구에서는 새로운 터널 발파패턴 개발을 위한 기초자료로 활용하고자 자유면 수가 비장약량과 굴진율에 미치는 영향을 실험과 수치해석을 통해 정량적으로 평가하였다. 동일 조건하에서 2, 3 자유면 발파에 대한 비장약량과 굴진율의 차이를 비교하였으며, 실험과 수치해석에서 모두 자유면 수의 증가가 굴진율 증대 및 비장약량 감소에 상당한 영향을 끼치는 것을 확인하였다.
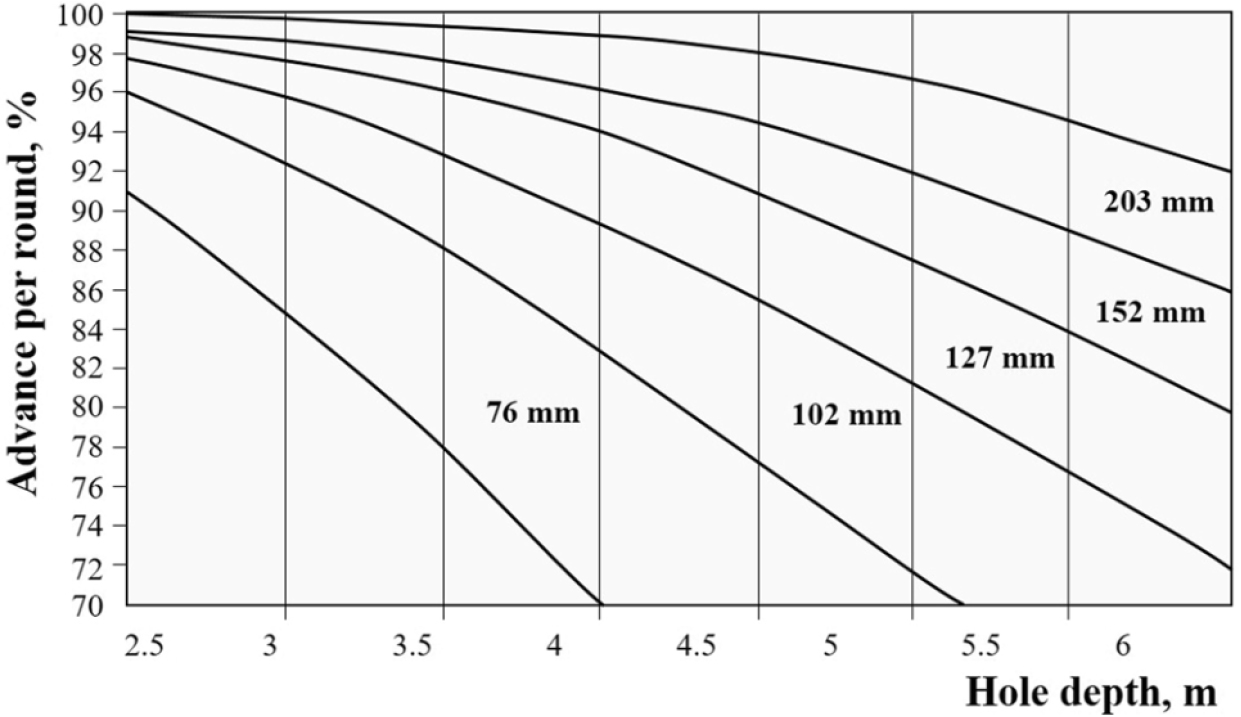
Fig. 1.
Relationship between hole depth and advance for various empty hole diameters (Olofsson, 1988)
2. 자유면 발파 선행연구
자유면이 발파에 미치는 영향을 분석하기 위해 많은 선행연구들이 수행되었으며, 이러한 연구들에서 자유면이 발파진동과 비장약량을 감소시키고, 파쇄도와 굴진율을 향상시키는 것으로 확인되었다. 이에 따라 자유면의 효과를 활용하기 위한 연구 또한 지속적으로 수행되고 있다. 이 장에서는 자유면의 발파효과에 대한 선행연구들을 간략히 소개하고, 본 연구의 목적을 설명하고자 한다.
Johansson and Ouchterlony (2013)와 Zhang et al. (2020)은 실험을 통해 자유면과 구속조건 차이에 따른 파쇄입도의 변화를 정량적으로 분석하였으며, 자유면의 수가 증가할수록 파쇄입도가 감소함을 보여주었다. Oh et al. (2018)은 콘크리트 시료에 인공 슬롯 자유면을 형성하여 발파실험을 수행하였으며, 인공 슬롯 자유면이 존재할 때 발파 진동과 파쇄입도가 감소하고 파쇄도가 보다 균질하며 인공 슬롯 자유면의 구조에 따라 파쇄체적 또한 비약적으로 증가할 수 있음을 보여주었다.
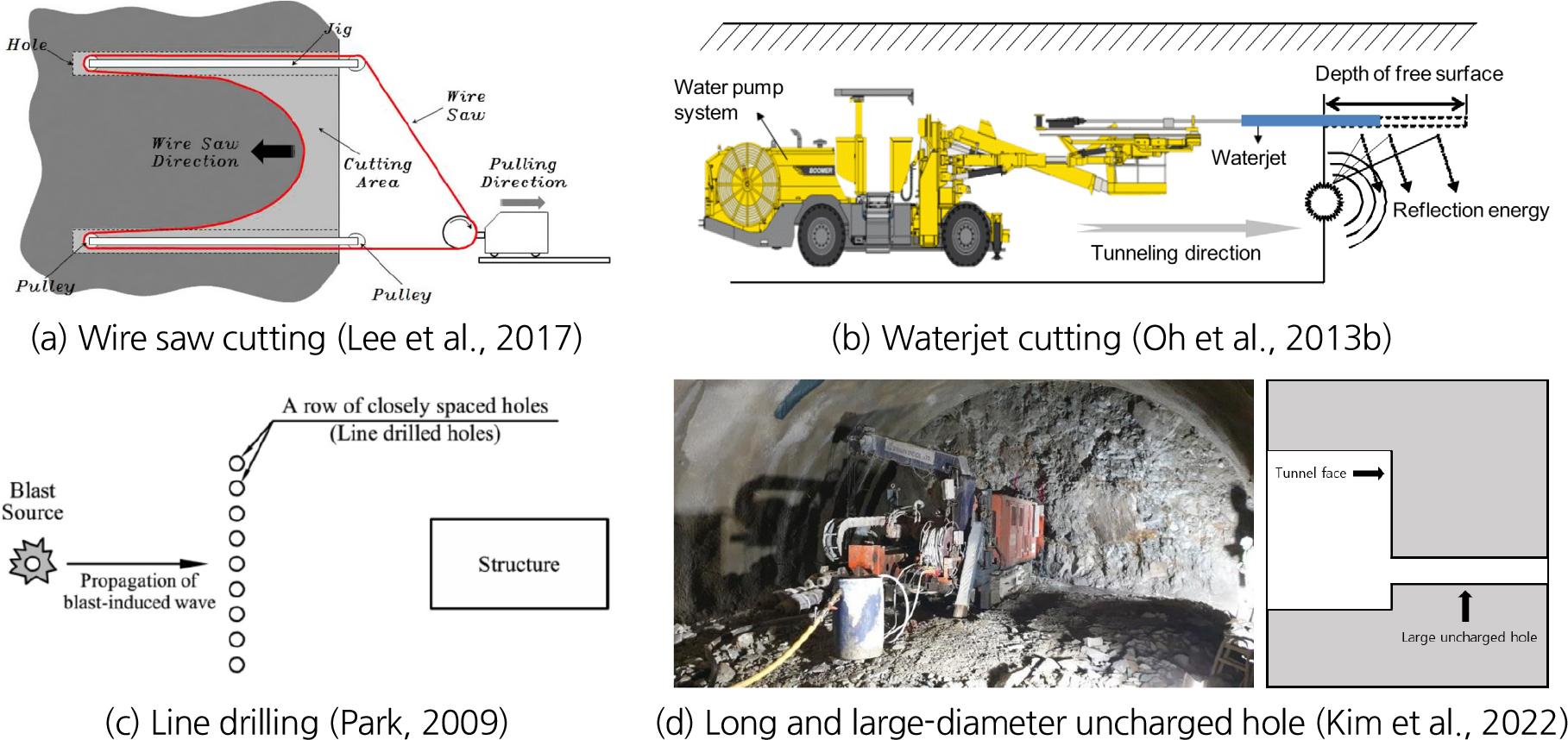
터널 발파 및 노천 발파에서 이러한 자유면 효과를 활용하기 위한 다양한 기술들이 개발되었는데, 이 중에서도 대표적인 기술로는 와이어쏘 절삭 인공자유면 발파, 라인드릴링공법, 워터젯 절삭 자유면 발파, 선대구경수평보링공법이 있다(Fig. 2).
와이어쏘 절삭 인공자유면 발파는 터널 심발부에 와이어쏘 절삭기술을 이용해 인공자유면을 형성한 후 발파하는 것으로 상대적으로 높은 진동이 발생하는 심발부의 발파진동 및 소음을 감소시키기 위해 사용된다(Lee et al., 2017). 라인드릴링 공법은 터널 발파와 노천 발파에서 활용되는 공법으로 목적하는 파단선을 따라 좁은 간격으로 다수의 무장약공을 천공하여 인공적인 파단면을 만드는 것으로 충격파의 전파를 차단해 발파 진동을 감소시키고 여굴 또는 암반의 손상을 완화시킨다(Park et al., 2009). 워터젯 절삭 자유면 발파는 연마재 워터젯을 이용해 막장 단면의 굴착 예정선에 일련의 자유면을 생성한 후 발파하는 것으로 라인드릴링공법과 비교하여 연속적인 자유면을 형성하여 발파 진동과 여굴을 보다 효과적으로 감소시키는 것으로 보고되었다(Oh et al., 2013a). 선대구경수평보링공법은 터널 심발부에 직경 250~1,000 mm의 무장약공을 10~60 m 정도 천공한 후 발파하는 것으로 대구경의 무장약공이 자유면 역할을 하여 발파진동 감소시키고 굴진율을 증가시키는 효과가 있다(Beak et al., 2012).
본 연구에서는 대형 물리 모형 시료를 활용하여 자유면의 수에 따른 굴진율과 비장약량의 차이를 정량적으로 비교하고, 이를 통해 자유면 발파의 메커니즘을 명확히 이해하고자 하였다.
3. 시멘트 모르타르 시험체를 이용한 2, 3 자유면 발파실험
3.1 시멘트 모르타르 시험체 및 실험 조건
현장 실험은 작업시간, 비용 등에서 제약이 있을 뿐만 아니라 암질의 변화, 암반의 불균질성, 불연속면 등으로 인해 자유면에 따른 파괴각도, 비장약량, 굴진율 등을 정량적으로 비교하기에는 한계가 있어 시멘트 모르타르 시험체를 제작해 축소모형 발파실험을 진행하였다. 시멘트 모르타르는 암석과 유사한 취성 파괴 거동을 보이는 것으로 잘 알려진 재료이다. 시멘트 모르타르 시험체는 직경 1,000 mm, 높이 600 mm의 다각기둥(28각형) 형태이다(Fig. 3). 시험체의 물성은 일축압축강도 50 MPa, 인장강도 3 MPa, 탄성계수 16 GPa, 포아송비 0.3으로 암석의 역학적 물성치와 유사한 범위에 속한다(Cheon et al., 2008).
실험에서 사용한 폭약 및 장약량은 에멀젼 폭약인 뉴마이트 플러스Ⅰ 2.0 g과 도폭선 5 cm (0.25 g)이며 뇌관은 MS (millisecond) 전기뇌관(PETN 0.73 g)을 사용하였다. 뉴마이트 플러스Ⅰ의 폭속은 5,700 m/sec, 비중은 1.2 g/cm3이며, 도폭선의 폭속은 7,000 m/sec이며, 심약량은 5 g/m이다. 전색재로는 모래를 사용하였다.
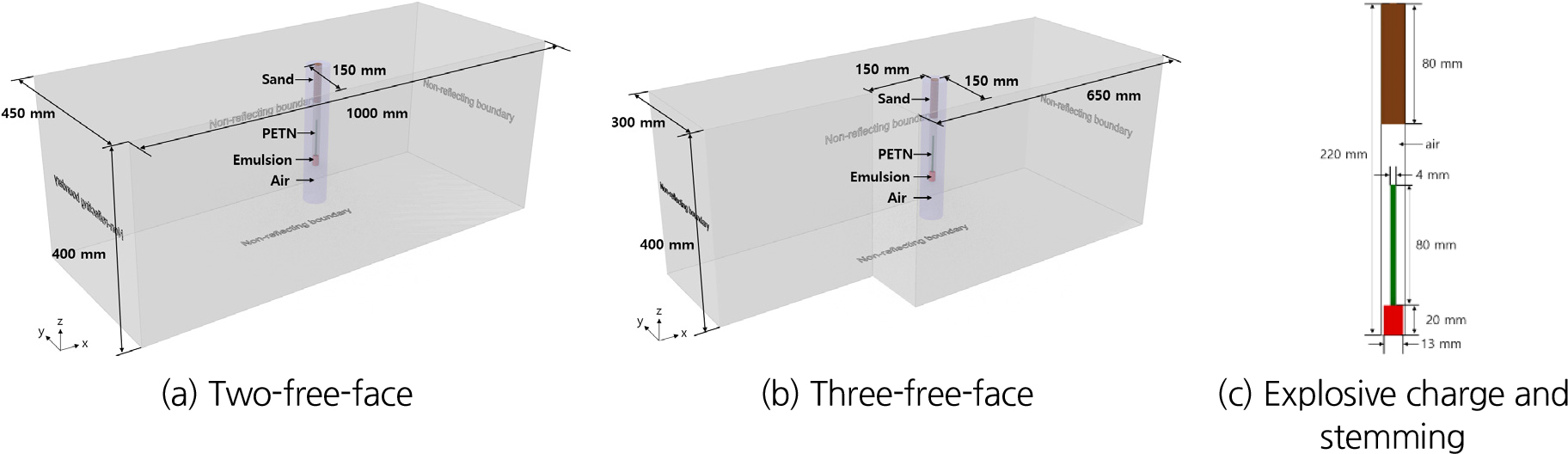
Fig. 4는 2자유면 및 3자유면 발파실험을 보여준다. 기본 실험조건은 최소저항선 150 mm, 천공경 16 mm, 천공장 220 mm, 장약장 70 mm이다.
3.2 실험 결과
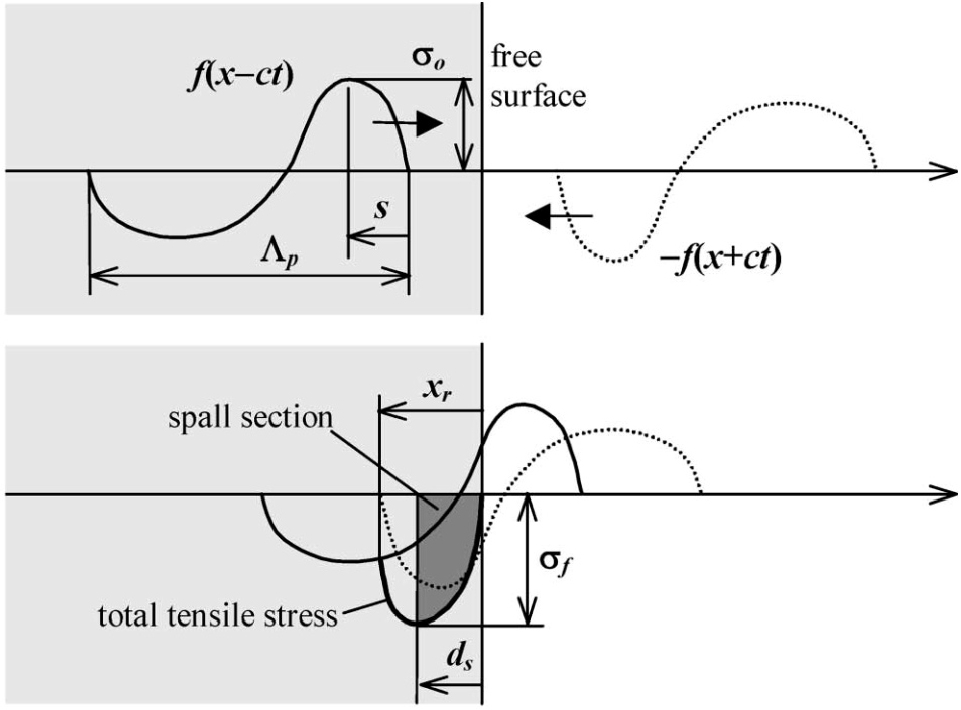
2자유면 발파 7회, 3자유면 발파 6회를 수행하였으며 2자유면 발파에서의 파괴각도는 천공장 바닥부에서 평균 120°, 3자유면 발파에서는 평균 150°로 측정되었다(Figs. 5 and 6). 파괴각도는 발파공 바닥부에서 발파공 입구에 가까워질수록 증가하였는데 이는 시험편 상단의 자유면에서 반사된 인장파로 인한 스폴링(spalling) 파괴의 결과로 판단된다. Fig. 7은 자유면에서 반사파에 의해 발생하는 스폴링 파괴 현상을 설명한 것으로 와 는 충격파 파형과 크기, 는 입사파, 는 반사파, 는 파괴 강도를 나타내는데, 자유면으로부터 만큼 떨어진 거리에서 입사파의 후행 인장 파형과 선행 압축 파형의 인장 반사파가 중첩되어 스폴링 파괴가 일어난 것을 보여준다.
본 연구에서 굴진장(advance length)은 발파로 인해 발생한 최대 파괴 길이로 정의하였으며(Fig. 8(c)), 굴진율은 천공장 대비 굴진장의 비로 정하여 2자유면과 3자유면의 발파에서의 굴진율 차이를 비교하였다. 2자유면 발파에서는 평균 346 mm, 3자유면 발파에서는 평균 385 mm의 굴진장이 측정되었다(Fig. 4). 실험에서 사용된 천공장은 220 mm로 2자유면 발파에서는 약 157%의 굴진율, 3자유면 발파에서는 약 175%의 굴진율을 보여주었는데 이는 자유면 수의 증가에 따른 반사파에 의한 영향 증대와 구속도의 감소로 인해 생긴 결과로 해석된다.
비장약량은 암석을 파괴하는데 사용되는 폭약의 양으로, kg/m3으로 표시한다. 본 실험에서 2자유면과 3자유면 발파에 사용된 폭약량은 동일하며, 파괴부피는 각각 14,368 cm3, 15,641 cm3로 측정되었다. 따라서 비장약량은 2자유면 발파에서 0.2074 kg/m3, 3자유면 발파에서 0.1905 kg/m3로 자유면 수가 증가함에 따라 비장약량이 감소하였다.
Table 1은 실험에서 측정한 자유면 수에 따른 파괴각도, 굴진율, 비장약량의 차이를 정리한 것이다.
4. 2, 3 자유면 발파모델링
4.1 해석 모델
본 연구에서는 LSTC (Livermore Software Technology Corporation)에서 개발한 상용 소프트웨어인 LS-DYNA를 사용하였다. LS-DYNA는 정적 및 동적 엔지니어링 문제를 해결하기 위한 일반적인 유한 요소 코드이며, 다양한 재료 모델과 상태방정식(EOS)을 제공하여 광범위한 종류의 재료 거동을 모사할 수 있다. 해석방법으로는 암시적 시간적분법(implicit time integration)과 명시적 시간적분법(explicit time integration)이 있다. 암시적 시간 적분법은 전체 강성 행렬(global stiffness matrix)을 계산하고, 그 역행렬을 구한 후, 이를 노드의 불균형 힘(nodal out-of-balance force)에 적용하여 변위 증분을 구하므로 사용자가 시간 간격(time step)의 크기를 선택할 수 있는 장점이 있으며 장시간이나 정적 해석을 수행하는데 적합하다. 명시적 시간 적분법은 각 노드 지점에서 내부 및 외부 힘이 합산된 후, 이 힘을 노드의 질량으로 나누어 가속도가 계산되며, 이 가속도를 시간에 대해 적분하여 해를 구하므로 충돌과 같은 동적 해석을 비교적 쉽게 처리할 수 있다(LSTC, 2007). 본 논문에서는 큰 비선형 변형과 극한 하중 조건(발파, 충돌)을 처리하는데 많이 사용되는 명시적 시간 적분법을 사용하여 발파 모델링을 수행하였다.
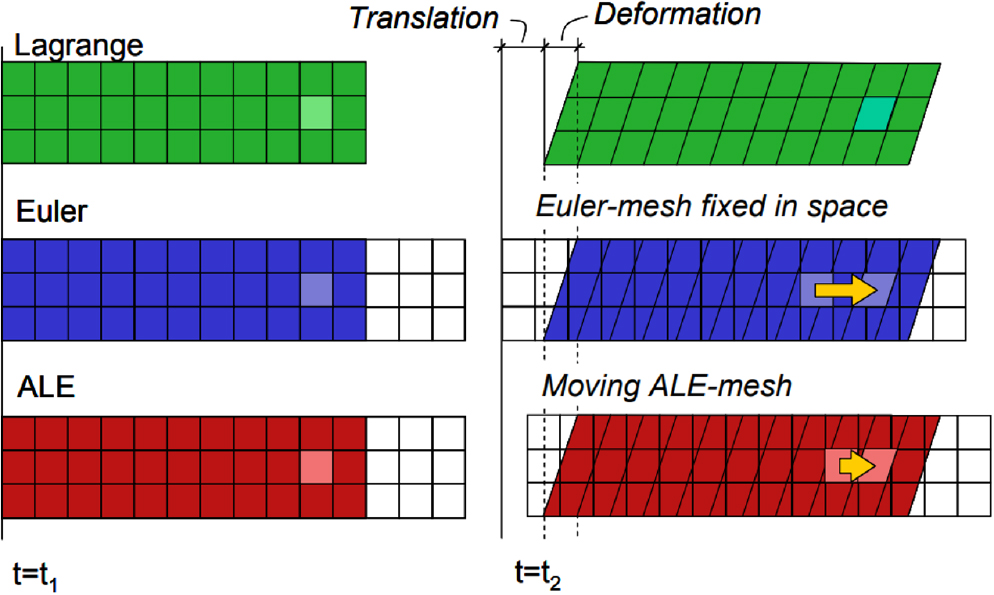
폭약의 폭굉과 이에 대한 콘크리트의 상호작용을 해석하기 위해 LS-DYNA의 ALE (Arbitrary Lagrangian-Eulerian)기법을 사용하였다. ALE 기법은 요소(element)는 고정되고 물질(material)이 요소를 통해 흐르는 오일러(Euler) 방식과 물질이 요소와 함께 움직이며 변형되는 라그랑주(Lagrange) 방식을 결합한 것으로 주로 유체로 인한 구조물 변형, 발파에 의한 구조물 파괴 등과 같은 유체와 구조물 간의 복잡한 상호작용을 해석할 때 사용되며, 이때 유체와 구조물 간의 상호작용(fluid-structure interaction, FSI)은 *CONSTRAINED_LAGRANGE _IN_SOLID 키워드를 통해 적용된다(Haufe et al., 2004). 발파모델링에서 ALE 기법의 적용은 폭약 요소의 대변형과 음의 부피와 같은 문제를 해결할 수 있다. Fig. 9는 라그랑주 기법, 오일러 기법, ALE 기법의 특징을 비교한 것이다. 라그랑주 기법에서는 메쉬가 물체의 변형을 따라가며, 각 요소는 하나의 재료를 포함하고 요소와 노드는 이동하며 변형한다. 오일러 기법에서는 메쉬가 고정되어 있고, 물질은 메쉬를 통해 흐르며 변형되며, 고정된 요소는 하나 이상의 재료를 포함한다. ALE 기법은 라그랑주와 오일러 요소 공식을 결합한 것으로 오일러 요소가 공간에서 이동할 수 있는 방법을 사용한다. 본 연구에서 콘크리트는 라그랑주 요소에 포함되었고, emulsion, PETN, 공기, 모래는 MM-ALE (multi-material ALE)로 그룹화되었다. 수치해석 모델의 구조는 Fig. 10과 같으며, 모델의 바닥부와 외곽부는 비반사경계조건(non-reflecting boundary)을 적용하였다. 요소의 개수는 총 1,985,772개이며, 요소의 평균 길이는 발파공 주변부가 0.4~4 mm이고, 외곽부는 4~10 mm이다.
4.2 재료 모델
본 연구에서 2, 3자유면 발파 모델링에 사용된 재료 모델은 콘크리트, 에멀젼, 도폭선(PETN), 공기, 모래 총 5가지로 구성되며 각 재료 모델은 다음과 같이 구성하였다.
4.2.1 RHT 모델
RHT (Riedel-Hiermaier-Thoma) 모델은 동적 하중조건에서 콘크리트나 암석과 같은 취성 재료의 거동을 모사하기 위해 개발된 모델이다(Riedel et al., 1999). 이 모델은 콘크리트의 다공성 압축을 설명하는 재료의 상태방정식과 재료의 강도와 관련된 세 가지 응력 한계면을 포함한 RHT 강도 모델을 결합한 것이다. 세 가지 응력 한계면은 각각 초기 탄성 항복면(initial elastic yield surface), 파괴면(failure surface), 파괴 후 잔류 마찰면(residual friction surface)이다. 이 응력 한계면은 변형 속도뿐만 아니라 각 응력 한계면을 따라 강도가 감소하는 것을 설명한다. Fig. 11은 일반적인 하중 시나리오를 보여준 것으로 응력이 초기 탄성 항복면에 도달할 때까지 모델은 탄성 거동을 보이며 이 항복면을 지나면 소성 변형이 발생하기 시작한다. 소성 변형과 콘크리트의 경화(hardening) 특성은 초기 탄성 항복면과 파괴면을 사이를 보간하여 유효 항복면을 형성한다. 응력이 파괴면에 도달하면 소성 변형에 의한 손상(damage)이 시작되며 파괴면과 잔류 마찰면 사이를 보간하여 파괴 후 응력 한계면을 정의한다. 완전히 손상된 재료의 경우(D = 1), 변형률 속도에 따른 영향이 없으며, 전단강도는 구속상태에서만 유지된다.
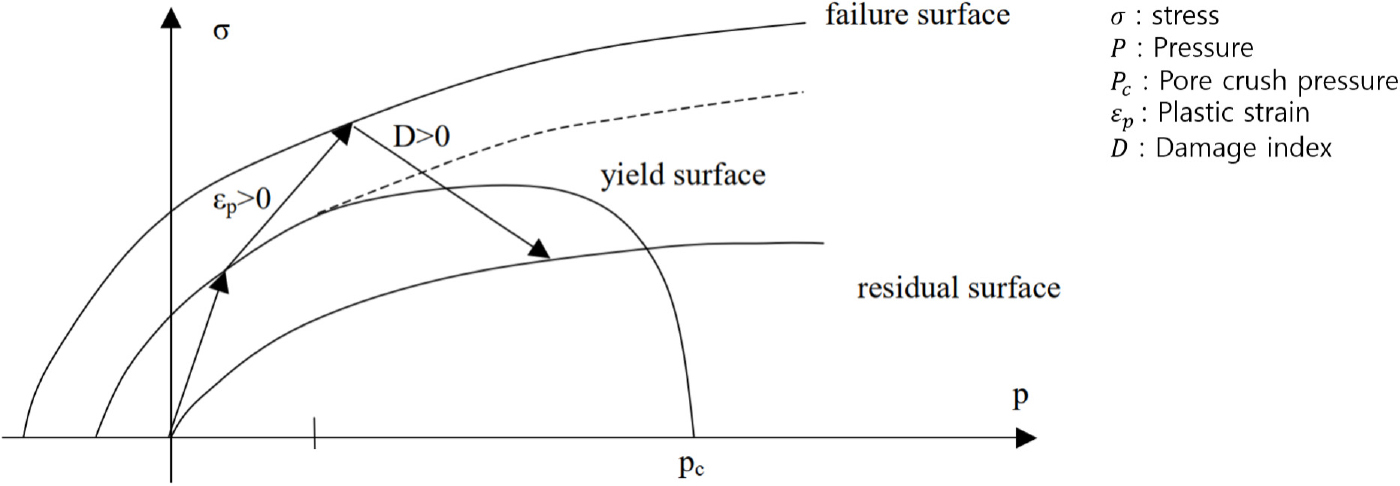
Fig. 11.
Stress limit surfaces and loading scenario in the RHT strength model (Borrvall and Riedel, 2011)
RHT 강도 모델의 파괴면, 탄성 항복면, 잔류 마찰면의 정의는 식 (1), (2), (3)과 같다.
는 주응력이 가 되는 조건에서 압력에 따른 재료의 거동 변화를 설명하는 압축 자오선(compressive meridian), 는 변형률 속도에 따른 강도 증가율을 나타내는 함수, 는 압축 자오선을 기준으로 값을 조정하는 무차원 함수로, 이며, 은 압력에 따라 재료의 탄성거동을 조정하는 탄성 조정 함수, 은 높은 압력에서 공극의 압축을 고려하여 탄성 항복면을 조정하는 함수, 탄성적 축차 응력을 제한하는 무차원 함수, 는 압축 강도로 정규화된 압력, B와 M은 잔류 파괴면의 상수와 지수이다(Riedel et al., 2009).
재료의 손상 지수는 식 (4)와 같이 정의되며, 범위는 로 손상 정도가 클수록 증가하며, =1은 재료가 완전히 파괴되었다는 것을 나타낸다.
는 손상 지수(damage index), 는 누적된 소성 변형률(accumulated plastic strain), 는 파괴 시 변형률(failure strain)이다.
RHT 모델은 총 38개의 매개변수로 이루어져 있으나 실험을 통해 요구되는 매개변수는 입방체 재료의 압축 강도이며 입방체 압축 강도에 따라 나머지 매개변수가 조정된다. 본 해석에서 적용된 콘크리트 입방체의 압축강도는 63 MPa이며, 나머지 매개변수의 값은 Table 2와 같다.
Table 2.
Input parameters for RHT model
4.2.2 폭약, 전색, 공기 재료 모델
본 절에서는 폭약의 팽창에 의해 생성된 폭발압력을 모델링하기 위해 *MAT_HIGH_EXPLOSIVE_BURN 재료모델과 Jones-Wilkins-Lee (JWL) 상태방정식을 사용하였다. JWL 상태방정식에서 폭발압력은 상대 부피와 내부에너지의 함수로 정의되며, 발파모델링에 널리 사용되어 왔다. 이 상태방정식은 식 (5)와 같이 정의된다.
는 폭발압력, 는 상대부피, 는 내부에너지, , , , , 𝜔는 입력 상수이다. 식 (5)에서 첫 번째 지수 항은 고압 상태에서 주된 항으로 작용하며, 두 번째 항은 중고압 상태, 세번째 항은 사실상 이상 기체의 상태방정식으로 저압 상태에서 주된 항으로 작용한다.
JWL 상태 방정식의 입력 상수값은 실린더 팽창 실험을 통해 결정되며, 에멀젼타입 폭약과 도폭선 및 뇌관의 PETN 폭약의 입력 상수값들은 Hansson (2009)과 Banadaki (2010)를 참고하였다(Table 3).
Table 3.
Parameters and properties of emulsion and PETN
전색재는 Krieg (1972)가 제안한 *MAT_SOIL_AND_FOAM 재료 모델을 사용하였다. 이 모델은 비교적 간단한 모델로서 전단 파괴 강도를 초과하면 재료가 점성 유체처럼 거동하게 되며, 재료의 체적 항복(volumetric yielding)은 표 형식의 압력과 체적 변형률의 관계로부터 결정된다(LSTC, 2006). Table 4와 Table 5는 본 연구에서 사용된 전색재의 입력 물성값을 나타낸다(Kulak and Bojanowski, 2011). 여기서 𝜌는 밀도, 는 전단 계수, 는 체적 계수, , , 는 항복 함수 상수, 은 인장 파괴에 대한 pressure cutoff이다.
Table 4.
Parameters of stemming (Kulak and Bojanowski, 2011)
| 𝜌 (g/cm3) | (MPa) | (MPa) | ||||
| 1.255 | 1.724 | 5.516 | 0 | 0 | 0.8702 | 0 |
Table 5.
Triaxial hydrostatic compression data for stemming material (Kulak and Bojanowski, 2011)
| True volumetric strain | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.33 |
| Pressure (MPa) | 0.02 | 0.05 | 0.07 | 0.12 | 0.2 | 0.34 | 0.5 |
공기는 *MAT_NULL과 *LINEAR_POLYNOMIAL 상태방정식을 사용하여 모델링하였으며, 압력은 식 (6)과 같이 계산된다.
, , , , , , 은 입력 상수이고, 는 현재 밀도와 초기 밀도의 비, 는 부피당 내부에너지이다. 이 선형 다항식 상태방정식은 감마 법칙 상태방정식을 따르는 이상 기체로 나타낼 수 있으며, 이때 C0, C1, C2, C3, C6는 0이고, C4와 C5는 γ - 1이다. 여기서 γ는 정압 비열과 정적 비열의 비율을 의미하며, 압력은 식 (8)과 같이 표현된다. Table 6은 입력 상수들의 값을 나타낸다.
4.3 수치해석 결과
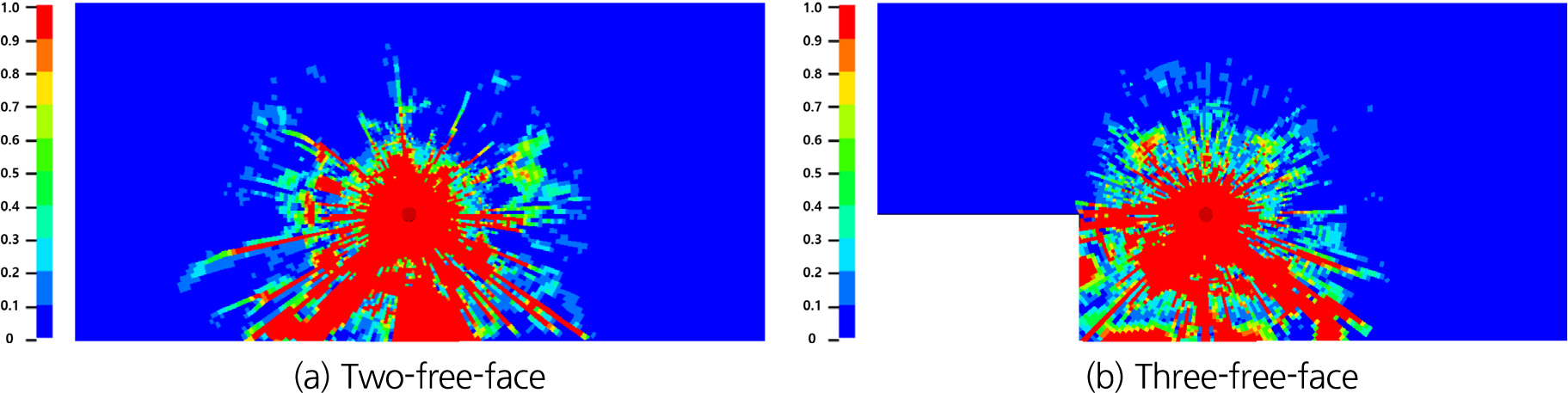
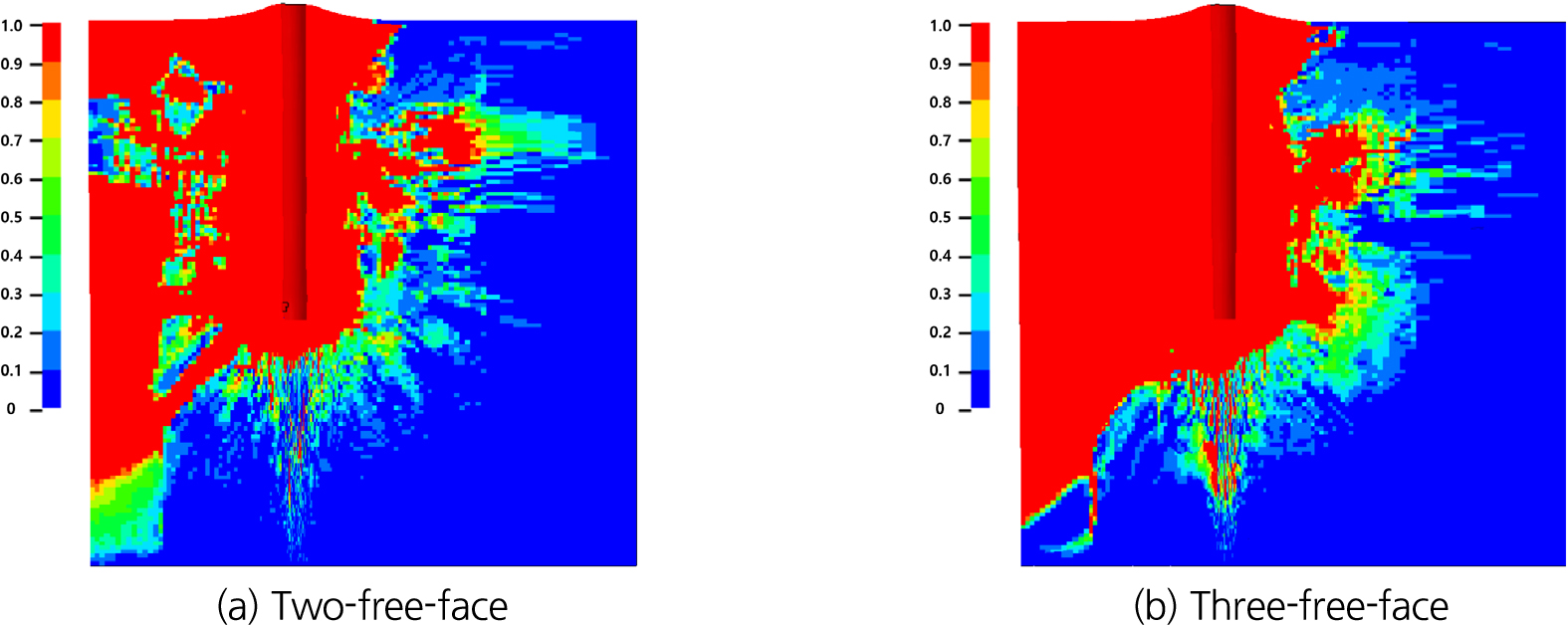
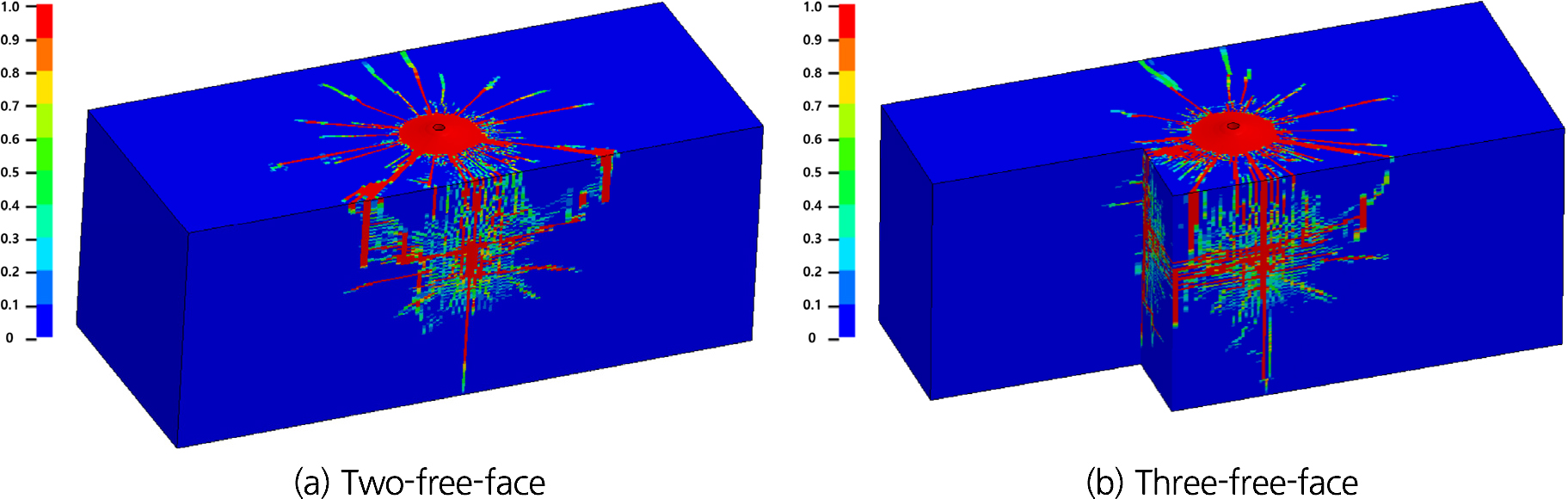
수치해석 결과는 식 (4)의 손상지수(damage index)를 통해 도식되었고, 이 손상지수는 0~1의 범위를 가지며 손상지수가 1이 되면 재료가 완전히 파괴되었다는 것을 나타낸다. 2자유면 발파에서의 파괴각도는 발파공 바닥부에서 110°, 3자유면 발파에서는 140°로 실험 결과값과 유사하였으며 자유면의 수가 증가함에 따라 파괴각도가 증가하였다(Fig. 12). 굴진장은 2자유면 발파에서 342 mm, 3자유면 발파에서 372 mm로 귤진율이 각각 155%, 169%가 되었다(Fig. 13). 굴진장 또한 실험 결과값와 유사하였으며 자유면의 수가 증가함에 따라 굴진율이 상승하였다. 파괴부피의 경우, 2자유면과 3자유면에서 각각 9,206 cm3, 12,537 cm3로 비장약량은 0.3237 kg/m3, 0.2377 kg/m3였다(Fig. 14). 실험 결과값과 비교하여 발파공 입구의 파괴 각도가 작아 파괴부피가 작게 모사되었으나 자유면 수가 증가함에 따라 파괴부피가 증가하고 비장약량이 감소하는 실험결과와 동일한 경향성을 보였다. 발파공 입구의 파괴 각도가 실제 실험에서 얻은 값보다 작은 이유로는 해석에서 사용한 메쉬 크기, 실험에서 사용한 폭약과 수치해석에서의 폭약 모델 매개변수 값의 차이, RHT 콘크리트 재료 모델의 불일치 가능성이 원인으로 생각되며, 메쉬 수 증가를 통한 조밀한 메쉬 구성, 실린더 팽창 실험을 통해 뉴마이트 플러스Ⅰ과 도폭선의 보다 정확한 JWL상태방정식 매개변수값 적용, RHT 콘크리트 재료 모델의 개선을 통해 해석의 정확도를 개선할 수 있을 것으로 판단된다.
Table 7은 수치해석에서 나타난 자유면 수에 따른 파괴각도, 굴진율, 비장약량의 차이를 정리한 것이다.
5. 결론 및 고찰
본 연구에서는 자유면의 수가 굴진율과 비장약량에 미치는 영향을 정량적으로 평가하기 위해 2자유면과 3자유면 발파 실험 및 수치해석을 수행하였다. 실험과 수치해석에서 모두 예상되는 바와 같이 자유면의 수가 증가함에 따라 굴진율은 향상되었고, 비장약량은 감소하였는데, 이는 자유면의 수가 증가하거나 자유면의 영역이 확대될 때 발파공 주변의 구속도는 줄어들게 되고, 인장파의 영향권은 확대되어 발생한 효과로 해석된다.
본 연구의 결과는 발파효율 증대를 위한 새로운 발파패턴 개발 연구에 기초자료로 활용이 가능하다. 이전 연구에서 보여주었듯 선대구경수평보링공법에서 심빼기 구간은 대구경 무장약공의 자유면 효과로 다른 심빼기 공법과 비교하여 높은 굴진율을 보여주기 때문에 심빼기 발파 후 이어지는 터널 확대부 발파 시에 상대적으로 굴진효율이 높고, 비장약량이 작은 3자유면 발파를 활용하면 심빼기 구간에서 얻은 굴진율 증대 효과를 확대부 구간까지 확장하여 터널의 전반적인 굴진율을 향상시킬 수 있을 것으로 기대된다.
또한, 자유면 수의 증가에 따른 비장약량의 감소는 동일한 화약량을 사용하였을 때 발파에 의해 제거된 파괴부피가 증가함을 의미하므로 3자유면 발파가 활용되는 확대부 구간에 화약량 및 천공 수를 감소시켜 발파현장에서의 경제성 향상을 기대할 수 있다.