1. 서 론
2. 지반침하 예측 모델 적용 기법
2.1 머신러닝 알고리즘: XGBoost (eXtreme Gradient Boosting)
2.2 하이퍼파라미터 최적화: 베이지안 최적화 기법
2.3 k겹 교차검증(k-fold cross-validation)
3. XGBoost 기반 지반침하 예측 모델
3.1 현장 개요
3.2 지반침하 계측 데이터
3.3 데이터세트 구성
3.4 지반침하 예측 모델 구성 및 성능 평가
4. 결과 및 논의
5. 결 론
1. 서 론
도시 집중화로 인한 교통량 증가는 도심지 내 교통 혼잡을 일으키고, 이에 따라 지하공간 활용에 대한 요구가 높아지면서 터널 시공 사례가 증가하고 있다. 기존 터널 시공 방법으로 적용된 NATM (new Austrian tunneling method) 공법은 지반 반응을 적극적으로 활용하는 방식으로 지반 조건에 대하여 유연하게 대응이 가능하나, 발파 과정에서 진동 ‧ 소음을 포함한 환경과 안전 문제를 비롯한 민원 발생 등으로 도심지에서 적용하는데 한계를 갖는다. 이러한 단점을 보완할 수 있는 기계화 굴착 공법 중 하나인 쉴드 TBM 공법은 굴진면에 토사나 이수를 통하여 막장압을 유지시켜 지반의 안정성을 확보하고 후방에서 세그먼트 장착과 테일 보이드(tail void)에 그라우트를 충전함으로써 지반 변형을 최소화하고 안정적인 시공을 가능케 하여 도심지 저토피 구간의 터널 공사에 적합한 대안으로 부각되고 있다(Broere, 2016). 그러나 실제 시공 현장에서는 쉴드 TBM 공법을 적용하더라도 지반침하를 완전히 억제하기 어려우며, 특히 저토피 조건에서 발생하는 침하 문제는 여전히 주요한 기술적 과제로 남아있다.
일반적인 터널 굴착 시 발생하는 지반침하 예측은 여러 현장의 계측자료 분석을 토대로 한 경험적 해석에 초점을 두었다. Peck (1969)는 터널 시공 중 계측한 지반침하 분석 결과 침하 특성을 가우스정규분포곡선(normal Gaussian distribution curve)과 같다고 제안하였고, O’Reilly and New (1982)는 지반침하와 터널 굴착 지반의 손실량에 대한 상관관계를 제시하였다. 이러한 경험적 침하예측 방법은 실제 고유 현장특성을 반영할 수 있으나 일반화에는 어려움이 있으며, 복합적인 영향요소들을 고려해야 하는 지반침하 예측에 한계가 있다. 쉴드 TBM 터널 굴착 시 발생하는 지반침하 예측과 관련된 수치해석 연구로서, Mori and Akagi (1985)는 테일 보이드로 인한 응력 해방 문제를 고려한 모델을 구축하고 유한요소해석을 통하여 지반침하량을 정량적으로 예측하였다. 또한 Kasali and Clough (1983)는 3차원 유한요소해석을 통해 다양한 지반조건 및 시공데이터를 고려한 지반침하 예측을 수행하였다. 그러나 3차원 유한요소해석을 활용한 지반침하 예측은 시간소모가 크고 복잡한 지반 특성과 쉴드 TBM 과정을 단순화하여 모델링을 수행하며 지반거동 지배방정식에 의하여 계산된다는 한계점이 존재한다. 이러한 한계점에도 불구하고, 도심지 얕은 심도에서의 쉴드 TBM 굴착 시 지반침하 예측은 경험적 ‧ 수치해석 기반 접근이 주를 이루어 왔으며, 저토피 조건에서는 굴착으로 인한 주변 지반의 변형 양상이 TBM 운전변수(예: 추진력, 막장압, 그라우팅량, 굴진속도)와 지반조건 간 복합적 상호작용으로 인해 발생하는 복잡한 거동을 정확히 반영하기 어렵다.
최근 TBM 시공이 증가함에 따라 장비에서 생성되는 기계 데이터가 축적되고 지반조건과 기계의 복합적인 요인들이 상호 간에 연결된 문제를 해결하기 위하여 기계데이터와 머신러닝(machine learning, ML) 기법을 활용한 쉴드 TBM 관련 연구가 활발히 진행되고 있다(Jung et al., 2019; Fu and Zhang, 2021; Kim et al., 2022c; 2024). ML 기반 예측 모델은 비선형적 특성과 다중 변수 간 상호작용을 효과적으로 반영할 수 있으며, 기존 경험식이나 수치해석적 접근이 갖는 한계를 보완하는 대안으로 주목받고 있다. ML 기반으로 쉴드 TBM 시공 중 지반침하 예측 연구는 SVM (support vector machine), RF (random forest), ANN (artificial neural network), XGBoost 등 다양한 머신러닝 알고리즘을 사용하여 여러 연구자들이 지반침하 예측 모델을 제안하였다(Suwansawat and Einstein, 2006; Samadi et al., 2021; Kim, 2022; Kim et al., 2022a; 2022b; Zhou et al., 2023). 최근에는 LSTM (long short-term memory)과 같은 딥러닝(deep learning) 모델을 활용하여 실시간(real-time) 또는 준실시간(near real-time)으로 지반침하를 예측하는 연구가 진행되고 있으며(Zhang et al., 2021; Chen et al., 2023; Lai et al., 2024; Yu et al., 2024), 이를 통해 시공 중 발생하는 복잡한 지반침하의 영향 요소를 반영하여 지반침하를 보다 정확하게 예측하는 방향으로 발전하고 있다. 특히 Kim et al. (2022a; 2022b)은 본 연구에 앞서 동일한 현장인 홍콩의 쉴드 TBM 지하철 터널의 시공 데이터 및 지반침하 계측 데이터 등을 이용해 데이터베이스를 구축하고 이를 이용한 지반침하 예측 연구를 수행하였는데, 해당 연구들에서 그들은 RF ML 알고리즘을 이용하여 지반침하 수준에 따른 분류모델을 개발하거나(Kim et al., 2022b), SVR (support vector regression), RF, XGBoost, GBM (gradient boosting machine), LGBM (light gradient boosting machine) 5가지 ML 알고리즘의 지반침하에 대한 예측 성능를 통해 XGBoost의 성능이 지반침하 예측에 가장 적합한 모델임을 보인 바 있다(Kim et al., 2022a).
그러나, 앞서 수행된 ML 모델을 이용한 쉴드 TBM 터널에 의한 지반침하 예측 연구는 대부분 기 시공된 현장에서 발생한 침하량 측정 데이터를 바탕으로 TBM 굴착 완료 후의 침하량, 즉 터널 후방의 지반 침하를 추정하는 데에 초점을 두고 있다. 그와 같은 지반침하량 예측 모델은 시공 완료 후 분석이나 피드백 제공에 유용하나, 실시간으로 수집되는 TBM 운전변수와 지반조건 정보를 활용하여 굴진 전방 구간의 침하 발생 가능성을 예측하고 그에 따라 선제적 대응책을 마련하는 데에는 한계가 존재한다. 따라서, 본 연구에서는 굴착 완료 후의 지반 침하(즉, 터널 후방 침하) 뿐만 아니라, TBM 미굴착 지점의 지반침하(즉, 터널 전방 침하) 및 TBM 굴진면 직상부에서 발생하는 지반 침하를 예측하고자 하였다. 이를 위해 도심지 쉴드 TBM 시공 현장에서 실시간으로 수집된 TBM 운영 데이터, 지반 조건, 터널 기하 조건 등 총 17개의 침하 영향인자를 기반으로 머신러닝 모델을 설계하였고, 17개의 주요 변수에 대해 각 변수 간의 상관관계를 분석하여 머신러닝 모델의 입력 변수로 적용하였으며, 계측된 지반침하 데이터를 활용하여 모델의 학습 및 검증을 수행하였다.
2. 지반침하 예측 모델 적용 기법
2.1 머신러닝 알고리즘: XGBoost (eXtreme Gradient Boosting)
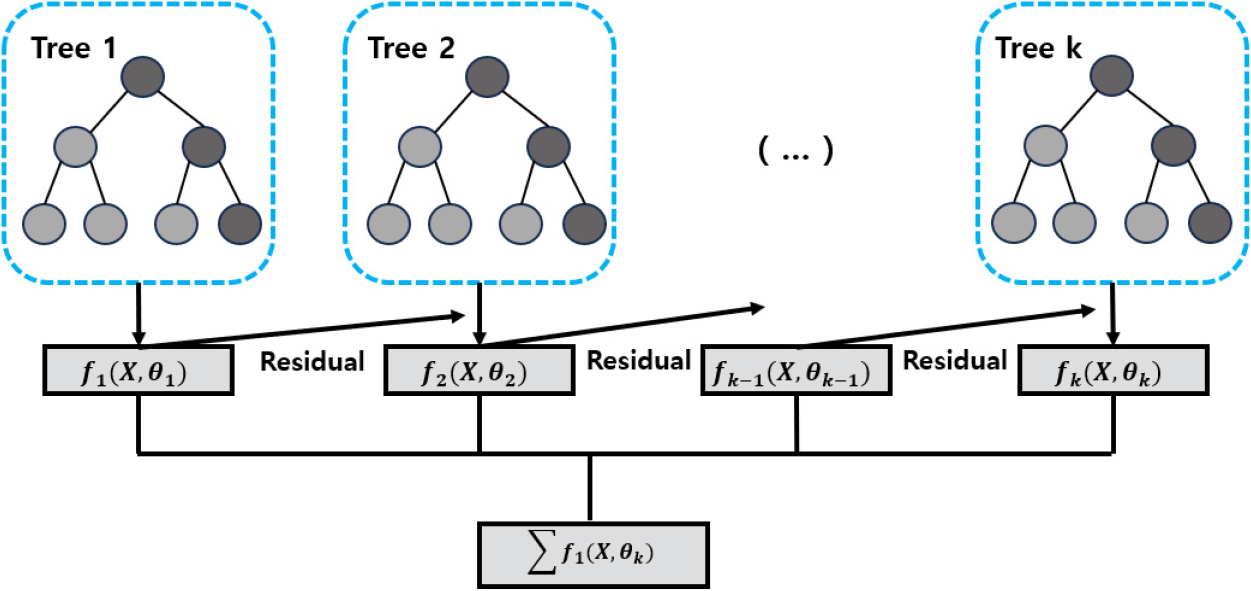
본 연구에서 지반침하 예측 모델에 활용한 XGBoost 알고리즘은 부스팅(boosting) 기법의 한 유형으로, 여러 약한 학습기(weak learner)를 결합하여 강력한 예측 모델을 구축하는 앙상블 기법이다. 부스팅 방식은 Fig. 1과 같이 초기 학습기(tree 1)가 데이터를 학습해 예측값을 생성하고, 그 결과와 실제 값 간의 잔차를 계산하는 것으로 시작된다. 이후 두 번째 학습기(tree 2)는 잔차를 학습하여 이전 학습기의 예측 오류를 보완하며, 이 과정은 k-번째 트리(tree k)까지 반복된다. 최종적으로 모든 학습기의 예측 결과는 선형적으로 결합되어 최종 예측값을 도출한다. XGBoost는 각 트리의 복잡도를 제어하기 위해 정규화 페널티를 도입하여 과적합을 방지하고, 높은 예측 정확도를 나타내며, 이는 데이터 패턴을 깊이 학습할 수 있는 강력한 도구로 평가받는다. 또한, 기존 부스팅 기법을 개선하여 계산 효율성을 높이고 학습 속도를 가속화하는 다양한 최적화 기법을 포함한다. 다만, XGBoost는 복잡한 하이퍼파라미터 튜닝이 필요하고, 이에 대한 연산을 수행하는데 오랜 시간이 요구된다는 단점이 있다. 그럼에도 불구하고, 뛰어난 예측 성능과 과적합 방지 특성 덕분에 XGBoost는 데이터 분석 및 예측 모델링에서 널리 활용되고 있다(Kim et al., 2022a; Zhou et al., 2023).
2.2 하이퍼파라미터 최적화: 베이지안 최적화 기법
ML모델 성능은 모델의 특성치(features)뿐만 아니라, 알고리즘 구조와 관련한 하이퍼파라미터(hyperparameters)에 의해 크게 좌우된다(Bergstra and Bengio, 2012). 적절한 하이퍼파라미터 선정은 과적합(overfitting) 또는 미비한 학습(underfitting)을 방지하고, 예측 성능 향상 및 모델 활용성을 극대화하는데 중요한 역할을 한다. 그리드 서치(grid search)나 랜덤 서치(random search)와 같은 단순한 탐색 전략을 제공하는 하이퍼파라미터 최적화 기법은 고차원 하이퍼파라미터 공간에서 낮은 탐색 효율성으로 인해 실제 적용 과정에서 한계를 보이며, 본 연구에서는 효율적 탐색 방법으로 제안된 베이지안 최적화 기법을 활용하여 최적화를 수행하였다(Bergstra and Bengio, 2012; Frazier, 2018). 베이지안 최적화는 이미 관측된 하이퍼파라미터-성능 관계를 바탕으로 사후분포(posterior distribution)를 형성하고, 대리모델(surrogate model) 및 획득 함수(acquisition function)를 활용하여 정보 가치가 높은 영역을 선별적으로 탐색한다(Snoek et al., 2012; Shahriari et al., 2016). 이러한 접근은 고차원 또는 복잡한 하이퍼파라미터 공간에서 불필요한 탐색을 최소화하며, 특히 학습 비용이 높은 상황에서보다 안정적이고 일반화 가능한 모델 성능 향상을 달성하는 데 효과적이다(Frazier, 2018).
2.3 k겹 교차검증(k-fold cross-validation)
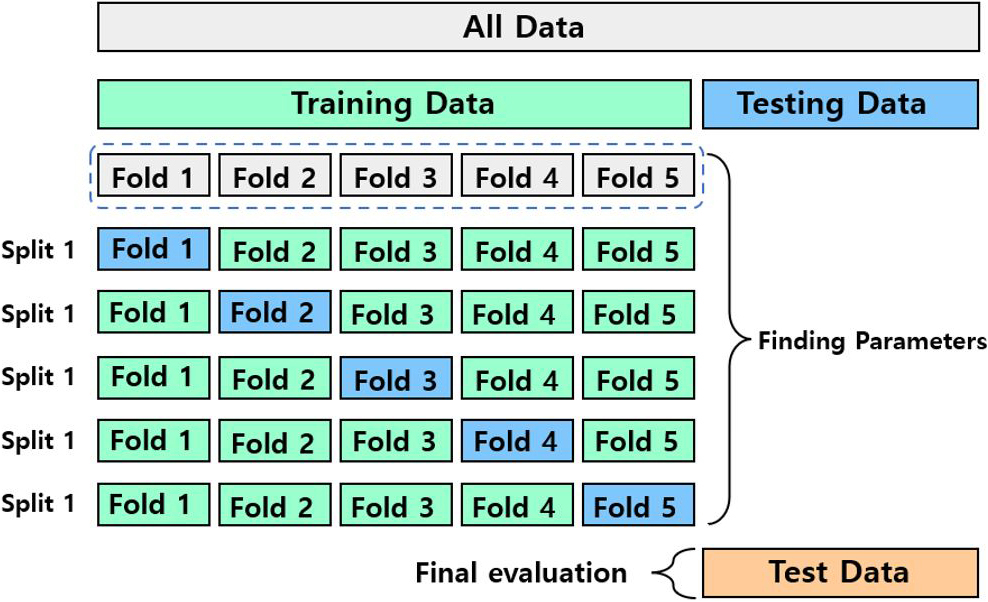
하이퍼파라미터 선정 후 모델 성능 검증 시 데이터 규모가 충분치 않을 경우 단일 검증세트 활용은 신뢰성 저하를 초래할 수 있다. 이를 보완하기 위해 k겹 교차검증을 적용하는데, 이 방법에서는 Fig. 2와 같이 전체 훈련자료를 k개 겹으로 균등 분할한 뒤 각 겹을 검증세트로 순환 활용함으로써 모든 데이터가 검증에 반영될 수 있도록 한다. 일반적으로 k 값은 데이터 특성에 따라 3~10 범위에서 선정되며, 계층적 샘플링(stratified sampling)을 사용하면 각 겹 내 클래스 비율을 유지하여 샘플링 편향을 줄일 수 있다. 마지막으로 각 겹에서 산출된 성능 결과를 평균함으로써 보다 안정적이고 일반화 가능한 모델 성능 추정치를 확보할 수 있다.
3. XGBoost 기반 지반침하 예측 모델
본 연구에서는 쉴드 TBM 굴착 시 지반침하 예측을 위하여 홍콩에서 기 시공된 쉴드 TBM 지하철 터널 현장으로부터 받은 쉴드 TBM 굴진 기계 데이터와 굴착 지반의 지반 특성, 터널 형상 등의 데이터들을 분석하고 지반침하에 영향을 주는 요인을 머신러닝 입력변수로 선정하였다. 여기서, 예측하고자 하는 지반침하의 위치에 따라 쉴드 TBM 본체를 기준으로 전방 예측 범위를 세그먼트 25링 전방(CASE 1), 중앙부를 TBM 본체 상부(CASE 2), 그리고 후방 예측 범위를 세그먼트 25링 후방(CASE 3)으로 각각 설정하였으며, 세 부분에 대한 지반침하를 예측하기 위하여 세 가지 데이터세트를 각각 구축하였다.
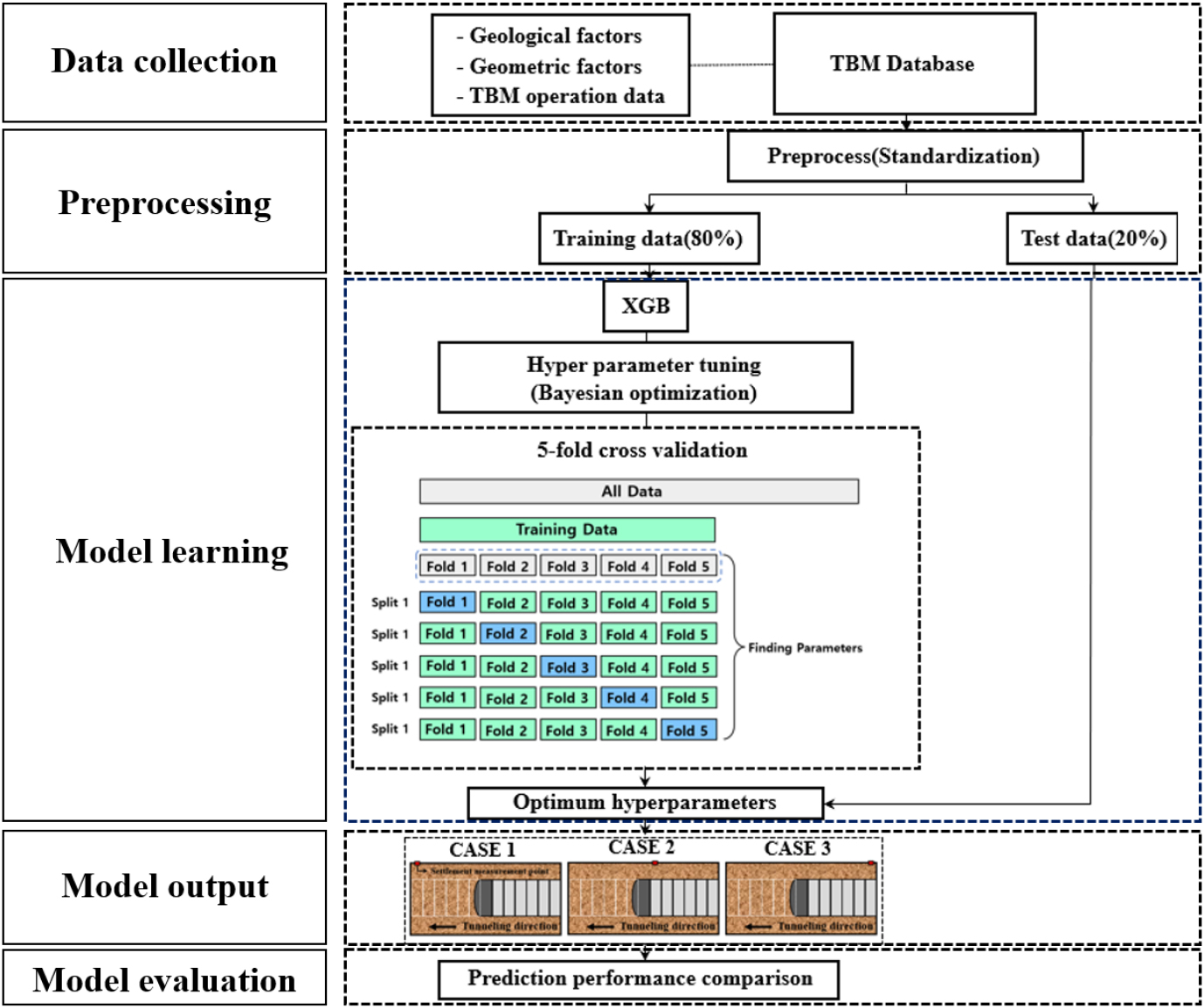
각 데이터세트는 훈련용(80%)과 검증용(20%)으로 분할하고, XGBoost 알고리즘을 적용하였다. 각 CASE에 대하여 베이지안 최적화 기법을 사용하여 최적 하이퍼파라미터를 탐색하였으며, 이를 k-겹 교차검증을 통하여 모델의 알반화 성능을 평가하고 데이터 편향 문제를 해결하였다. 도출된 모델의 성능 결과를 비교하여 지반침하 예측 정확도를 비교, 평가하였다. 쉴드 TBM 예측 모델 구현 절차는 Fig. 3에 도시하였다.
3.1 현장 개요
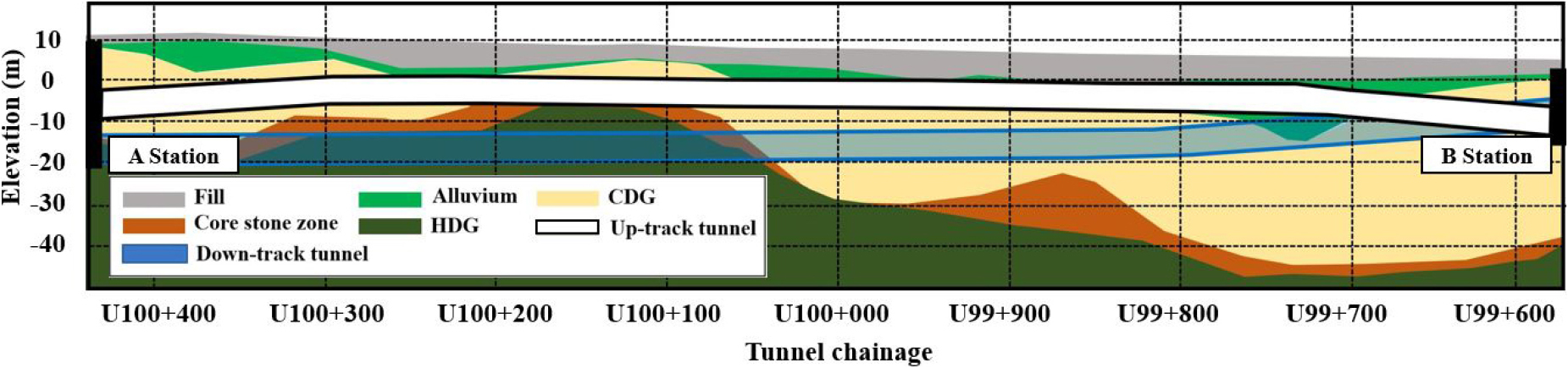
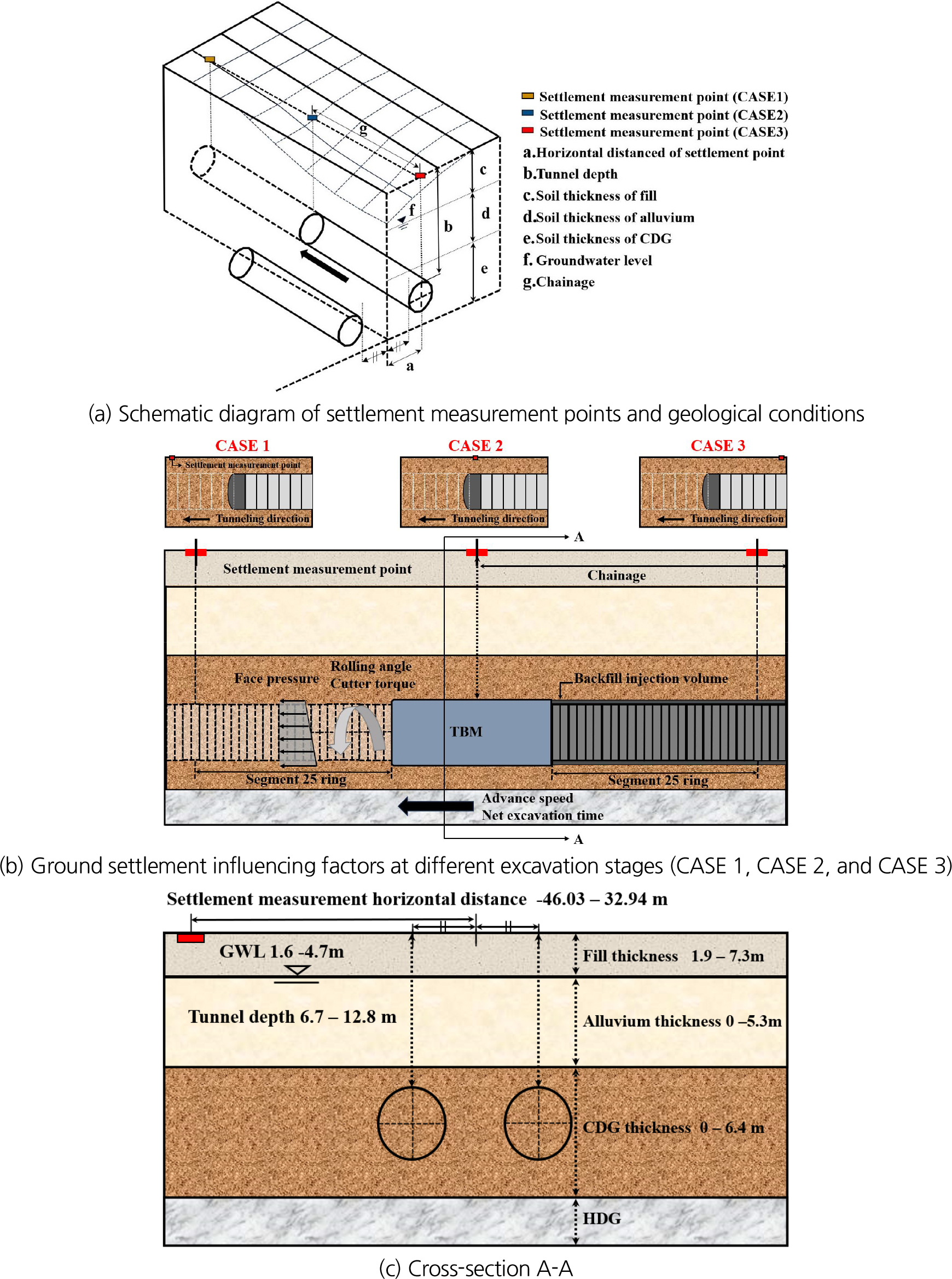
본 연구 대상은 홍콩에서 이수 가압식 쉴드 TBM 공법이 적용된 터널 시공 현장으로, 사용된 TBM 장비의 굴착 외경은 7.4 m, 쉴드 길이는 11 m이다. 해당 쉴드 TBM 장비 사양은 Table 1에 제시한 바와 같이 최대 추력 47,897 kN, 최대 토크 5 MN ‧ m였으며, 세그먼트 라이닝 외경은 7.1 m, 내경은 6.5 m, 길이는 1.5 m 규격으로 시공되었다. 연구대상 구간의 지층 분포는 설계 시 수행된 시추 조사와 CHI (cutter head intervention) 과정에서 기록된 데이터를 기반으로 분석되었다. 시추 조사를 통해 얻어진 지질 정보는 37개의 시추공 데이터를 포함하며, CHI를 통해 총 121개의 관측 데이터를 추가적으로 확보하였다. Fig. 4에 제시된 터널 구간의 지층 분포는 지표로부터 매립층(fill), 충적층(alluvium), CDG (completely decomposed granite), HDG (highly decomposed granite) 순으로 구성되어 있으며, 터널 중심축 기준으로 터널 심도는 상행선 터널이 약 15~22 m, 하행선 터널이 약 19~26 m에 분포하고 있다. 상행선 터널은 주로 CDG, HDG, 충적층 및 매립층을 지나는 복합지반을 통과하고, 하행선 터널은 충적층 아래 CDG 및 HDG로 이루어진 지반을 통과한다.
Table 1.
Specifications of utilized slurry shield TBM
| Description | Specification |
| TBM excavation diameter | 7.4 m |
| Maximum thrust force | 47,897 kN |
| Maximum torque | 5 MN ‧ m |
| Segment diameter |
7.1 m (outer diameter) 6.5 m (inner diameter) |
| Segment width | 1.5 m |
본 연구에서 상행선 터널 굴착 과정에서 발생하는 데이터를 활용하여 지반침하 예측을 수행하였으며, 이때 터널 노선을 따라 지하수위는 지표 아래 약 1.5~4.7 m 범위 내에 분포하였다. 한편, 상행선과 하행선 터널 굴착부에서 측정된 SPT (standard penetraion test)-N값은 각각 10~36, 27~200 범위이며, 해당 터널이 통과하는 토층 중 CDG는 0~19 m로 가장 두꺼운 분포를 보였고, 충적층과 매립층은 각각 0~8.6 m, 1.9~7.8 m 범위를 보였다. 핵석(corestone) 및 암반(rock)층은 거의 발견되지 않아 분석에서 제외하였으며, 각 지층 별 설계 지반 물성치는 Table 2에 나타내었다.
Table 2.
Ground properties
3.2 지반침하 계측 데이터
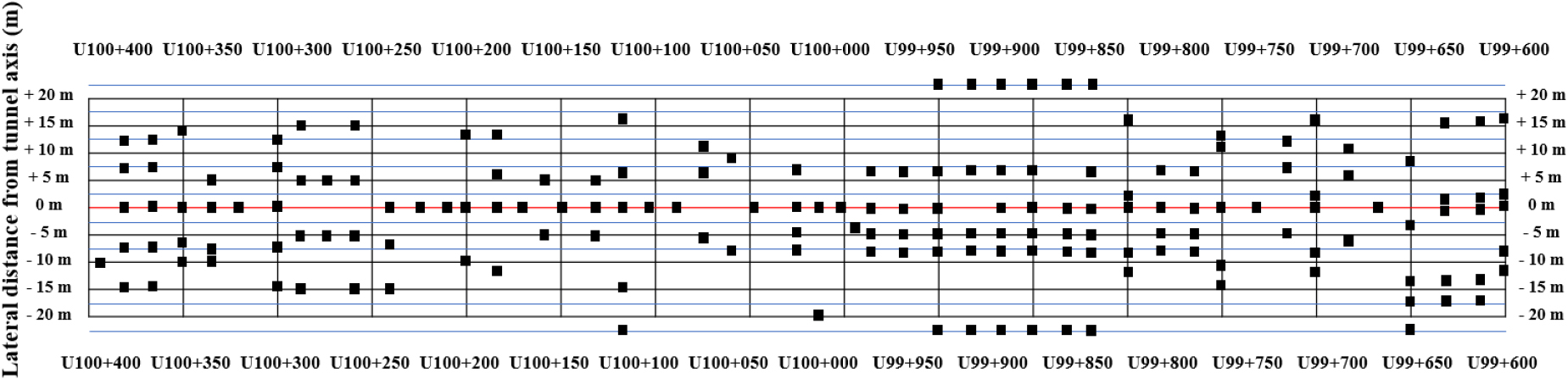
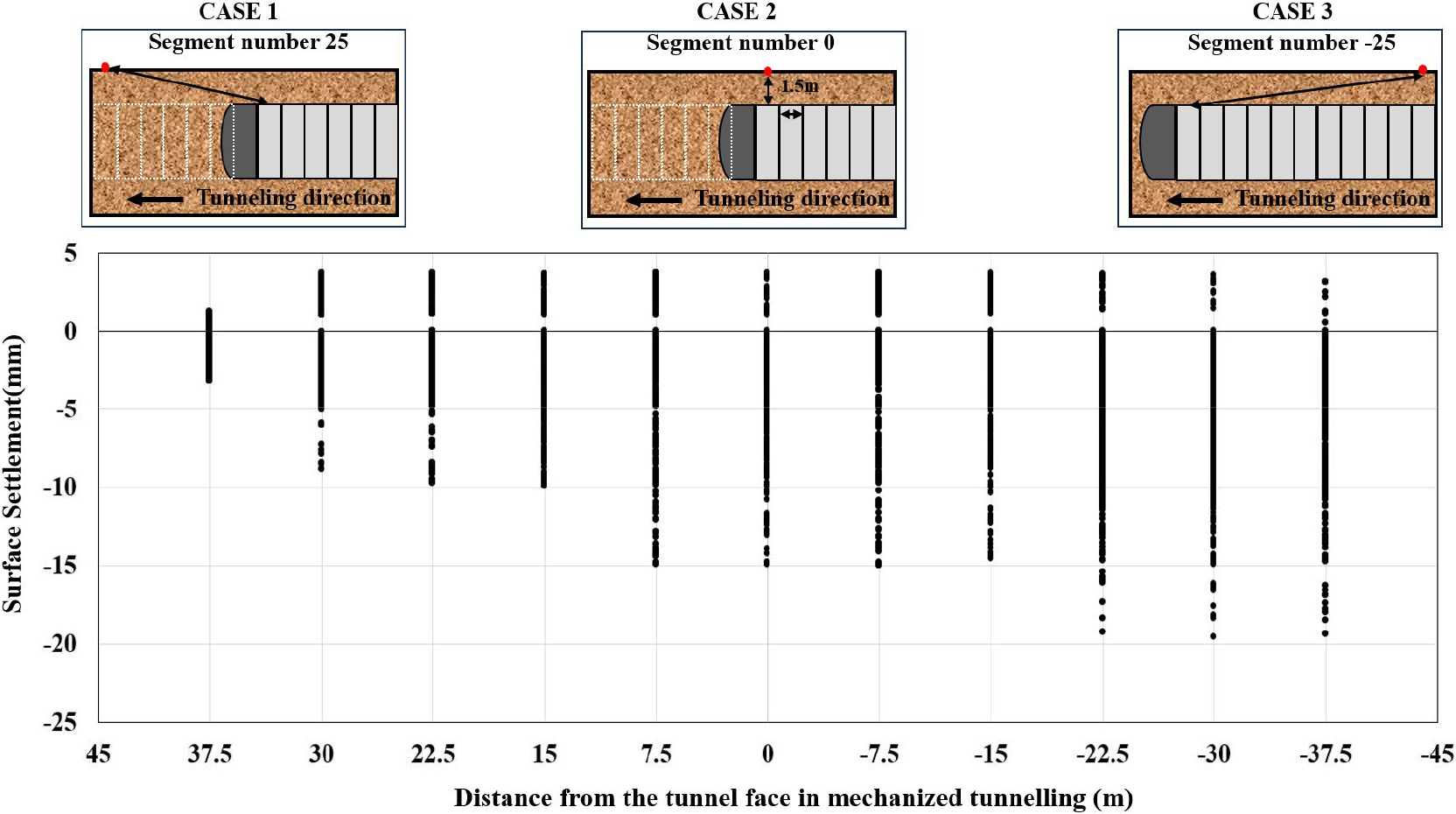
본 연구대상 구간에서 터널 굴착 시 지반침하 모니터링을 위해 노선에 따라 설치된 계측기 중 253개의 지반침하 계측기를 활용하였다. 터널 굴진 방향의 중심선으로부터 수평 방향(횡단면방향)으로 좌우로 각각 32 m에서 46 m까지 계측기가 배치되어 지반침하 계측데이터가 수집되었다(Fig. 5). 매일 계측되는 지반침하 데이터를 토대로 누적 침하량을 분석하였으며, 쉴드 TBM 막장면이 통과하는 시점에 침하 발생이 시작하는 것으로 확인하였다. Fig. 6은 굴진 중에 수집된 종단면의 지반침하량을 나타내며, 막장면으로부터 거리에 따라 나타내었다. 막장면 직상부를 기준으로 전방에서는 5 mm 내외의 침하 및 융기가 발생하고 막장면을 지나는 시점에서 침하의 크기가 커지면서 후방 22.5 m 까지 침하량이 커지고 이후로는 조금 회복되는 양상을 확인하였다.
3.3 데이터세트 구성
쉴드 TBM 굴진 중 복합적인 영향요인으로 인하여 지반침하가 발생되는데 이를 지반특성 요소, 쉴드 TBM 시공 인자 그리고 터널 기하학적 요인으로 구분할 수 있다. 본 연구에서는 지반침하에 영향을 미치는 요소라고 판단되는 5가지 지반특성요소, 8가지 쉴드 TBM 시공 인자, 그리고 4가지의 터널 기하 조건을 포함하여 총 17가지 지반침하 영향인자를 입력 데이터로 설정하고, 지반침하 계측기에서 측정된 6,831개의 침하량 데이터를 사용하여 XGBoost 머신러닝 학습을 위한 데이터세트를 구축하였다.
지반조건으로는 토피고, 지하수위, SPT의 N치, 각 지층 별 두께, 그리고 쉴드 TBM 운영 조건으로는 추력, 총 굴착소요시간, 막장압, 커터토크, 뒤채움 주입량, 굴진율, 상하 방향각도(피칭), 좌우 방향각도(롤링)를 입력데이터로 선정하였다. 더불어, 터널 기하 조건으로는 터널 축방향거리(chainage), 터널 심도, 지반 침하계 횡방향거리, 지반 침하계의 종방향 거리를 포함하였다. 전술한 17개의 특성(Fig. 7 참조) 및 지반침하 데이터의 통계량은 Table 3과 같다.
Table 3.
Statistical descriptions of the dataset
| Category | Features | Q1* | Q2* | Q3* | Max | COV | Unit |
| Geometry | Horizontal distanced of Settlement point | -16.00 | -4.33 | 8.00 | 32.94 | 4.11 | m |
| Vertical distance of Settlement point | 10.21 | 13.56 | 16.84 | 20.52 | 5.12 | m | |
| Tunnel depth | 7 | 7.4 | 8.7 | 12.8 | 1.33 | m | |
| Chainage | 114 | 276 | 475.5 | 793.5 | 226.80 | m | |
|
Geological condition | GWL | 2.43 | 2.77 | 3.00 | 4.73 | 0.67 | m |
| Standard penetration test | 15 | 16 | 22 | 36 | 6.42 | - | |
| Soil thickness of fill | 4.6 | 5.4 | 6.7 | 7.3 | 1.38 | m | |
| Soil thickness of alluvium | 0.6 | 1.6 | 2.7 | 5.3 | 1.41 | m | |
| Soil thickness of CDG | 0 | 0 | 0.7 | 6.4 | 0.89 | m | |
| Operation | Thrust force | 13.4 | 15.6 | 20.8 | 27.2 | 0.2 | MN |
| Advance speed | 25 | 33 | 38 | 48 | 9.33 | mm/m | |
| Face pressure | 1.49 | 0.6 | 2 | 2.45 | 0.30 | bar | |
| Cutter torque | 06 | 0.8 | 1.1 | 1.8 | 0.36 | MN ‧ m | |
| Backfill injection volume | 6.3 | 6.4 | 6.6 | 7.6 | 0.29 | m3 | |
| Net excavation time | 38.92 | 44.88 | 60.72 | 114.92 | 20.89 | min | |
| Pitching | -24 | 10 | 30 | 36 | 25.40 | mm | |
| Rolling | -4 | 2 | 3 | 11 | 5.52 | mm | |
| Settlement | CASE 1 | -1.25 | -0.44 | 0.33 | 1.12 | 0.91 | mm |
| CASE 2 | -6.8 | -2.4 | -0.7 | 3.2 | -1.2 | mm | |
| CASE 3 | -10.98 | -7.37 | -2.34 | 2.2 | 1.97 | mm |
지반침하 거동 특성을 종합적으로 파악하기 위해 토피 두께, 지하수위, 수평 거리 및 쉴드 TBM 운전 변수(추진력, 굴진속도, 커터 토크) 등을 대상으로 상관성 분석을 수행하였다.
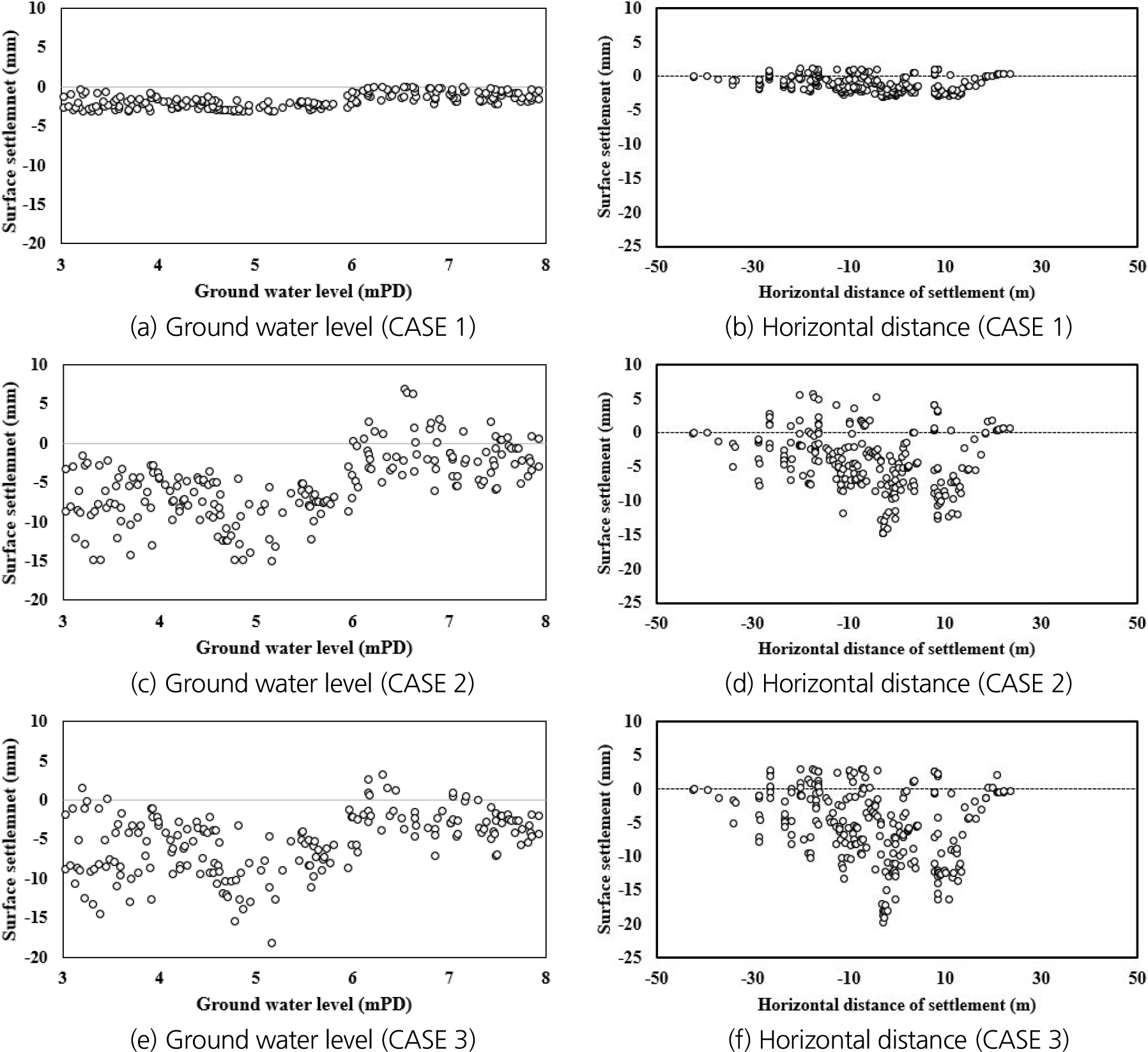
기존 연구인 Kim et al. (2020)에서는 쉴드 TBM 본체가 특정 구간을 통과한 후, 해당 위치에 설치된 지반침하 계측기에서 20일 동안 측정된 침하데이터를 활용하여 주요 변수 간의 상관관계를 분석하였으며, 이를 통해 해당 계측 지점에서 장기간 추적된 지반침하를 고려한 주요 변수 간의 상관관계를 도출하였다. 반면 본 연구에서는 쉴드 TBM 본체의 이동과 계측 지점 간의 관계를 고려하여 지반침하 데이터를 세 가지 CASE로 구분하여 분석하였다. 해당 CASE들에서 CASE 1은 TBM 본체 위치를 기준으로 미굴착 구간인 굴착 전방으로 37.5 m 떨어진 지점에서의 계측 데이터, 그리고 CASE 2는 TBM 본체가 계측기 위치를 통과하는 시점에서의 계측 데이터, 마지막 CASE 3은 TBM 본체로부터 후방으로 37.5 m 떨어진 지점에서의 계측 데이터를 가지고 각각 분석한 CASE를 의미한다. 여기서, 37.5 m는 약 25개의 세그먼트 링(ring) 길이이자 당 현장에서 평균 5일동안의 굴진거리에 해당하는 거리였다. 이러한 차이를 반영하여, 본 연구에서는 쉴드 TBM 굴착 과정에서 주요 변수와 지반침하 간의 상관관계를 분석하였으며, 특히 TBM 본체의 위치에 따른 지반침하 특성을 비교 분석하였다. 각 CASE별 상관관계 결과를 Fig. 8에 나타내었다.
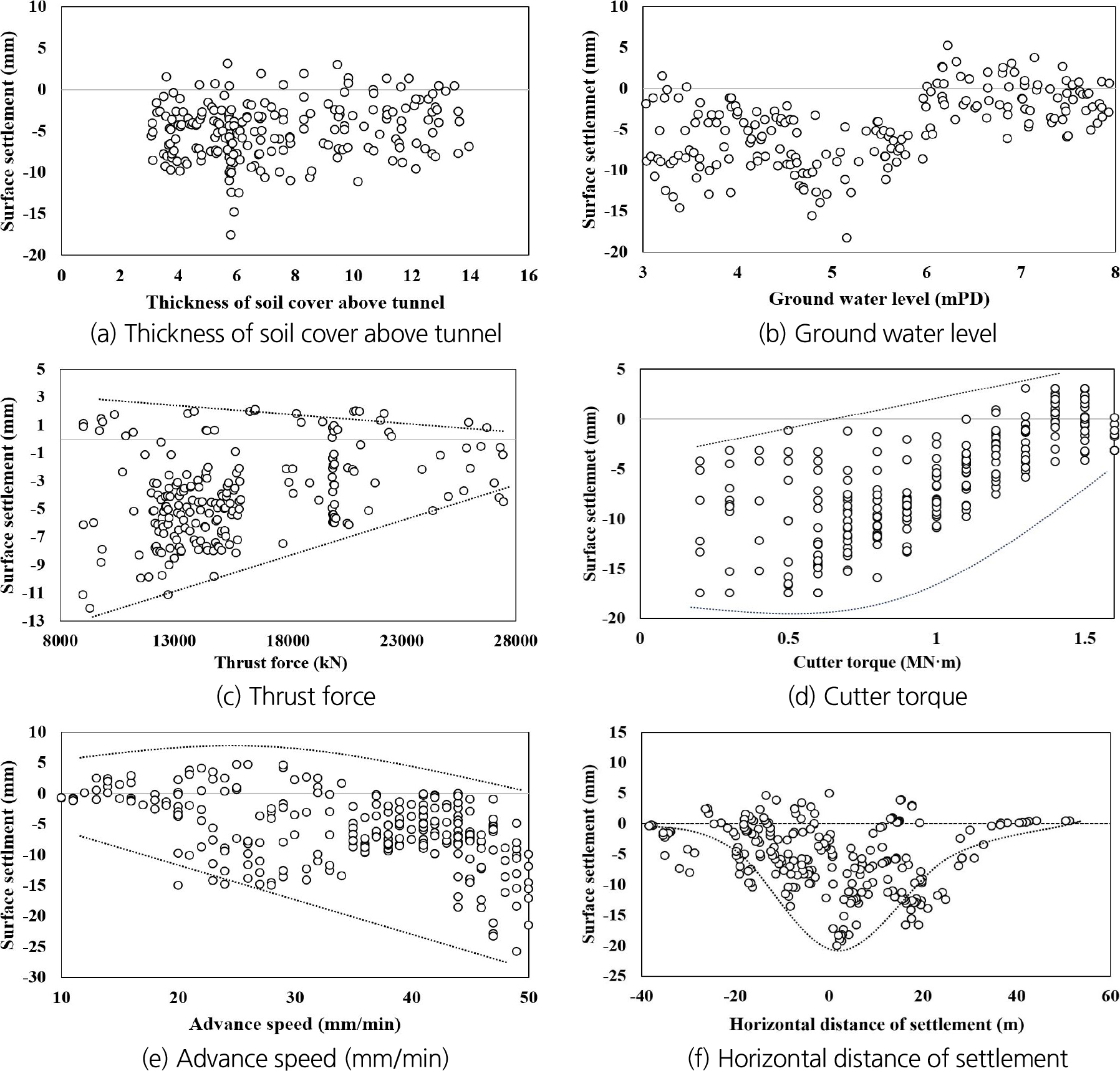
Fig. 8(a), (c) and (e)는 CASE 별 지하수위에 따른 지반침하 분포를 나타냈으며, Fig. 8(b), (d) and (f)는 터널 중심선을 기준으로 수평방향 지반침하 분포를 CASE별로 나타내었다. 지하수위, 수평방향의 CASE별 지반침하 CASE 1 (전방)에서는 명확한 상관관계가 확인되지 않으며 CASE 1 (전방)에서 CASE 3 (후방)으로 진행됨에 따라 지반침하와의 더 높은 상관관계를 보임을 확인하였다. 또한, 후방 침하량이 각 변수와 상관성이 높게 나타남을 확인함에 따라 지반침하의 주요 영향 요인을 도출하기 위해 CASE 3에 해당하는 후방 침하에 대한 상관성 분석 결과를 Fig. 9에 제시하였다. Fig. 9(a) and (b)는 터널 상부 토피 두께와 지하수위 변화에 따른 지반침하 분포를 나타내며, 분석 결과 마찬가지로 토피 두께와 침하량 간에는 명확한 상관관계가 확인되지 않았다. Fig. 9(c) and (d)는 쉴드 TBM 추력 및 커터 토크와 지반 침하량 간에 유의한 양(+)의 상관관계를, Fig. 8(e)는 굴진속도와 지반침하량 간에 음(-)의 상관관계를 보여준다. Fig. 9(f)는 터널 중심선을 기준으로 한 수평 방향 침하 분포를 나타내고 있으며, 이를 통해 침하량이 Gaussian 형태의 침하구배를 따름을 확인하였다. 이러한 결과는 지반 조건 및 TBM 운전변수가 복합적으로 작용하여 지반침하 거동을 좌우함을 시사하며, 향후 다변량 상관분석이나 보다 고도화된 인공지능 모델 예측을 통해 CASE 별로 주요 영향인자와 영향 정도의 분석이 필요하다.
3.4 지반침하 예측 모델 구성 및 성능 평가
본 연구에서는 17가지 지반침하 영향 인자를 입력데이터로 활용하여 TBM 시공 중 발생하는 지반침하를 예측하는 XGBoost 모델을 구현하였다. 데이터 전처리 과정을 거친 6,831개의 데이터를 80%는 학습에 나머지 20%는 시험에 활용하도록 구분하였다. 전술한 바와 같이 본 연구에서는 쉴드 TBM 굴진 과정에서 쉴드 TBM 본체 기준으로 전방, 상부, 후방으로 지반침하 예측 케이스를 구분하고 각각의 지반침하 예측 모델을 구축하였다. 여기서 ‘전방’ 구간은 막장면을 기준으로 세그먼트 링 25링(37.5 m) 전방에 해당하는 지점으로서 굴진 진행 방향 앞쪽에서 발생할 수 있는 지반침하 변화 양상을 예측하기 위한 구간이다. 그리고 ‘직상부’ 구간은 쉴드 TBM 본체 상부 중심부로서 굴착시점에 즉각적으로 발생하는 지반침하 거동을 추정하기 위하여 설정하였다. 마지막으로 ‘후방’ 구간은 쉴드 TBM 본체 기준 세그먼트 링 25링(37.5 m) 후방에 위치하는 구간으로, 굴진이 이미 지난 뒤 뒤따라 발생하는 지반침하 양상을 파악할 목적으로 설정하였다. 이와 같이 세 구간으로 구분하여 예측 모델을 구축하였으며, 각 모델의 최적화를 위하여 베이지안 최적화와 5겹 교차검증을 적용하여 예측 모델의 초매개변수(hyperparameters)를 계산하였다.
지반침하 예측 모델의 성능을 평가하기 위하여 평균제곱오차(mean square error, MSE), 평균절대오차(mean absolute error, MAE), 평균제곱근오차(root mean squared error, RMSE) 및 결정계수(R2)를 평가지표로 사용하였다.
평균제곱오차란 잔차의 제곱에 평균을 취한 값으로 개별 관측값들이 중심에서 얼마나 멀리 떨어져 있는지의 상대 척도를 나타내는데, 값이 작을수록 추정의 정확성이 높다. 평균제곱오차는 식 (1)과 같이 표현된다.
평균절대오차란 잔차에 절대값을 취하고 평균을 낸 것으로 직관적으로 확인할 수 있다는 장점이 있으며, 아래 식 (2)와 같이 표현된다.
평균제곱근오차는 잔차의 제곱에 대해 평균을 취한 값에 루트를 씌운 값으로 오류 지표를 실제값과 유사한 단위로 다시 변환하여 쉬운 해석을 지원한다. 평균제곱근오차는 식 (3)과 같이 표현된다.
회귀분석에서 독립변수가 종속변수를 얼마나 설명해주는지를 나타내는 결정계수, R2를 성능 검증 지표로 활용하였다. R2의 수식은 식 (4)와 같이 표현된다.
일반적으로 회귀모형에서 독립변수가 많은 회귀식에서는 수정된 결정계수(adjusted R2)를 사용하기도 하지만, 본 연구에서는 모델 간 상대적 비교를 목적으로 하여 독립변수 변동에 따른 보정이 필요하지 않다고 판단하였으므로 수정된 결정계수를 사용하지 않고 결정계수 R2 값으로 예측의 정확성을 비교 분석하였다.
4. 결과 및 논의
본 연구에서는 XGBoost 알고리즘을 적용하여 쉴드 TBM 터널 굴착 시 전방, 직상부, 후방의 지반침하를 예측하는 모델을 구축하였다. 모델 구축 과정은 데이터 수집부터 전처리, 훈련 세트와 테스트 세트의 분할, 학습 모델 생성, 결과 도출, 그리고 모델 성능 평가로 이루어진다. 데이터 전처리는 이상치 제거와 결측치 처리를 포함하고 정규화를 통하여 차원의 영향 제거와 모델에서 입력인자 훈련을 용이하게 하기 위하여 수행한다. 본 연구에서는 Standard Scaler 모듈을 사용하여 표준편차 표준화 방법으로 데이터를 정규화하였고, 80%의 데이터를 훈련 세트로, 나머지 20%를 테스트 세트로 무작위 구분하였다.
XGBoost 알고리즘을 적용한 전방(CASE 1), 직상부(CASE 2), 후방(CASE 3) 지반침하 예측 모델은 베이지안 최적화 방법을 사용하여 각 케이스별로 하이퍼파라미터를 최적화하였다. 도출된 최적의 하이퍼파라미터는 XGBoost 모델의 트리 구성을 위한 최대 깊이인 max_depth는 CASE 별로 모두 상이하며, 모델 학습 반복 횟수를 나타내는 nrounds는 CASE 1이 150회, 나머지 CASE 2와 CASE 3은 300회로 나타났다. 그 외 과적합 방지를 위한 스텝단계 축소값인 eta가 CASE 1가 0.3, 나머지는 0.2로 결정되었다. 트리를 생성할 때 샘플링되는 피처의 비율을 나타내는 colsample_bytree값은 CASE 2, 3은 동일한 0.7이며, CASE 1은 0.8로 나타났다. 그 외 하이퍼파라미터는 Default로 설정된 값을 유지하였다. CASE에 따른 XGBoost 알고리즘의 하이퍼파라미터는 Table 4에 나타내었다.
Table 4.
Search space of XGB hyperparameters
| Hyperparameter | CASE 1 | CASE 2 | CASE 3 |
| max_depth | 6 | 8 | 10 |
| learning_rate | 0.22 | 0.19 | 0.19 |
| eta | 0.3 | 0.2 | 0.2 |
| colsample_bytree | 0.8 | 0.7 | 0.7 |
| reg_alpha | 0 | 0.02 | 0.02 |
| subsample | 1 | 1 | 1 |
| nrounds | 150 | 300 | 300 |
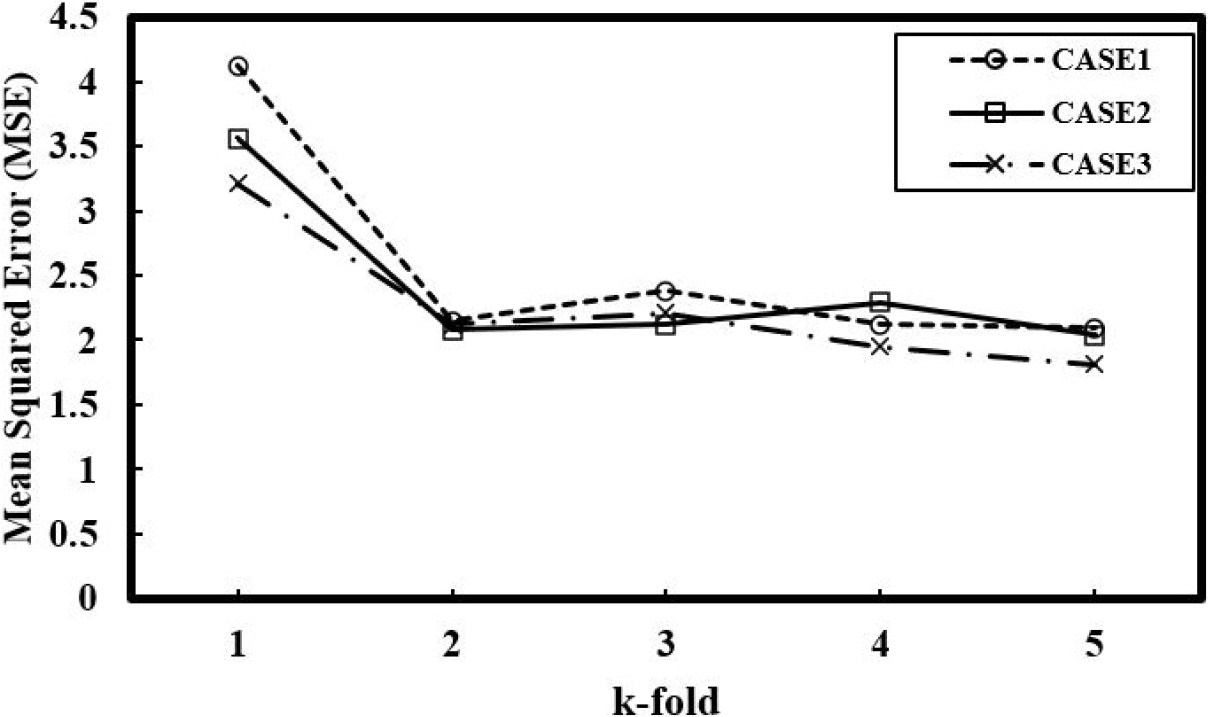
본 연구에서는 하이퍼파라미터 최적화 이후 k-fold 값에 따라 모델의 성능평가를 MSE로 실시하여 막장면 기준으로 다른 위치에서의 지반침하 예측 모델의 최적화를 수행하였다. Fig. 10은 각 케이스에 대하여 k-fold가 증가함에 따라 초기 고정된 훈련 ‧ 검증 분할 시보다 더 안정적이고 낮은 MSE를 보이는 경향을 나타낸다. 특히, k = 1에서 모든 CASE에 대해 상대적으로 높은 MSE를 보인 반면, k = 2 이후부터는 MSE가 유의미하게 감소하여 보다 견고한 모델 성능을 확보할 수 있음을 보여준다. 이후 k = 2 이상에서는 MSE의 변동 폭이 미미하며, 이는 추가적인 폴드 수 증가(k > 3)에 따른 일반화 성능의 개선 효과가 제한적임을 시사한다. 요컨대, 본 분석 결과 k-fold 교차검증에서 약 5 fold를 활용하면 모델의 성능이 안정적으로 수렴함을 확인하였다.
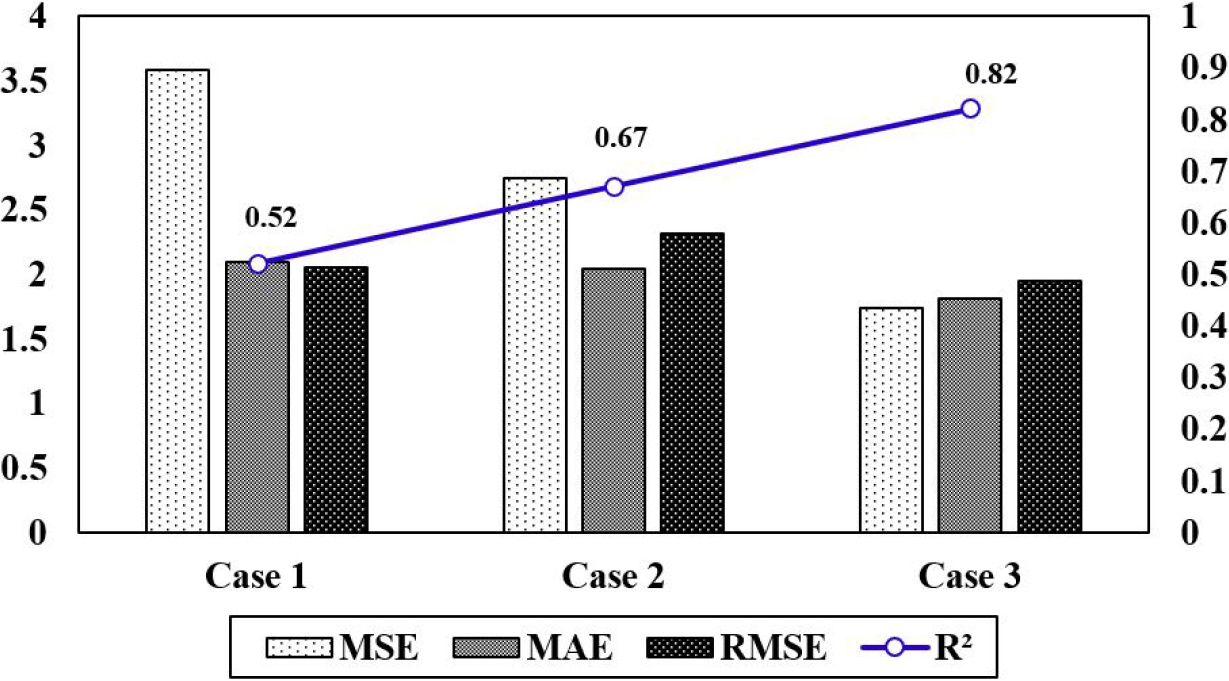
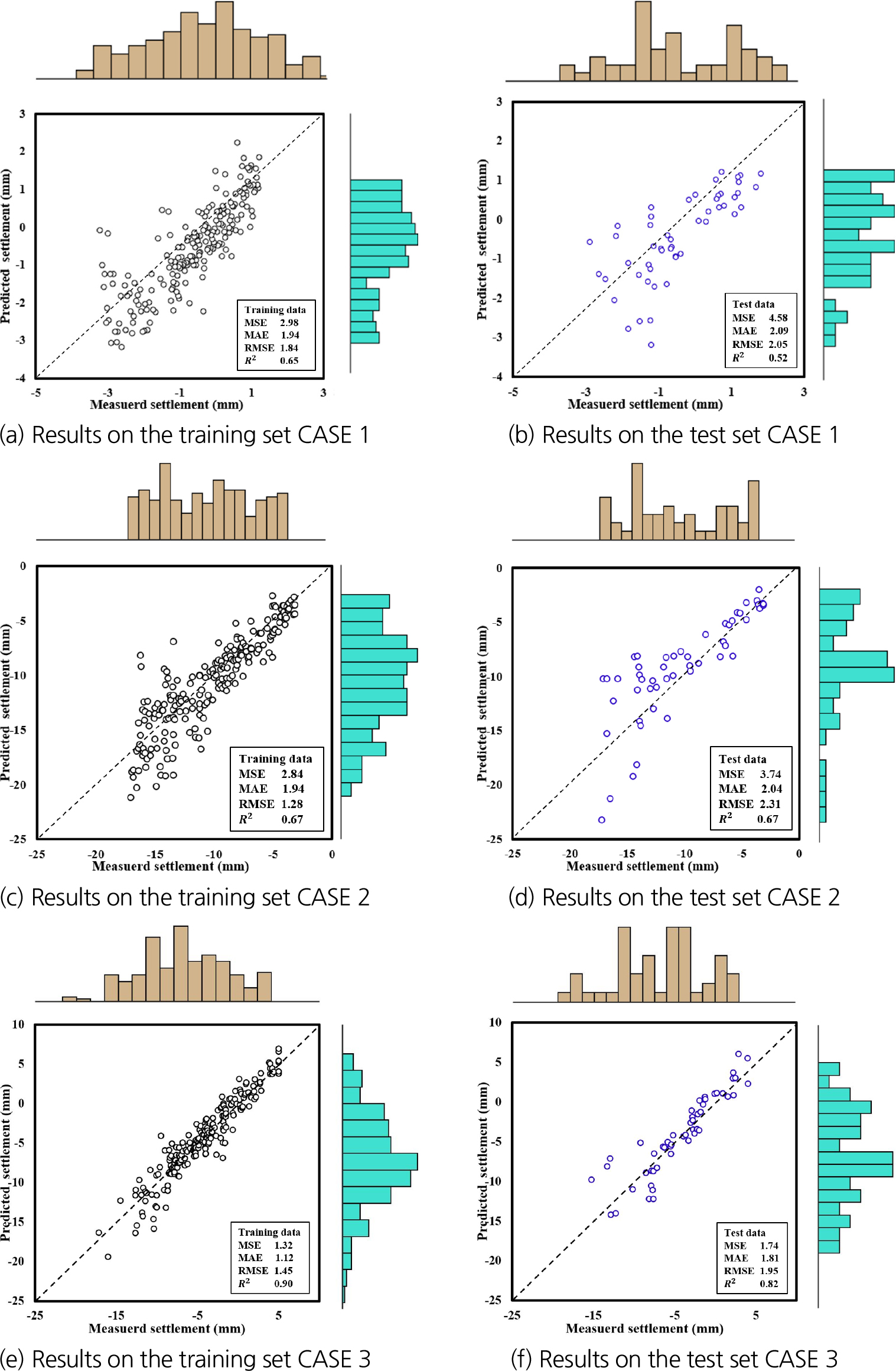
모델의 지반침하 예측 성능 평가는 MSE, MAE, RMSE, R2의 성능 지표를 통해 수행하였으며 결과는 Fig. 11에 정리하였다. Fig. 12는 각 케이스에 대한 지반침하에 대하여 각각 지반침하 예측 모델이 학습과 테스트 과정에서 측정된 지반침하량에 대한 예측 침하량 결과를 이상적인 일치선(Y = X)을 의미하는 대각선 점선과 함께 나타낸 것이며, 각 그래프 상단과 오른쪽에 있는 히스토그램은 각각의 측정 침하량과 예측 침하량의 분포를 시각화한 것이다.
CASE 1의 검증 데이터 결과는 MSE = 4.58, MAE = 2.09, RMSE = 2.05, R2 = 0.52로 나타나며, 측정값과 예측값의 편차가 큰 것을 확인하였다. CASE 2에서는 검증 데이터에 대해 MSE = 3.74, MAE = 2.04, RMSE = 2.31, R2 = 0.67로 CASE 1 대비 정확도가 다소 개선되었으나 여전히 측정값과 예측값 사이 오차를 확인하였다.
반면, CASE 3에서는 검증 데이터 기준으로 MSE = 1.74, MAE = 1.81, RMSE = 1.95, R2 = 0.82를 달성하여 두 케이스와 비교하면 모델 성능 지표 값이 향상되었음을 알 수 있다. 먼저, MSE 기준으로 CASE 3은 CASE 1 대비 약 38% 감소(4.58→1.74), CASE 2 대비 약 46% 감소(3.74→1.74)하였고, R2 역시 CASE 1 대비 약 58% (0.52→0.82), CASE 2 대비 약 22% (0.67→0.82) 향상되었다. 또한, MAE와 RMSE도 CASE 3에서 가장 낮은 값을 보여, 실제 측정된 침하량과 예측된 침하량 간의 차이가 다른 두 CASE에 비해 크게 줄어들었음을 의미한다. 이러한 성능 차이는 CASE 3에서 영향인자 간의 상관성이 보다 명확하게 나타난 결과로 해석된다. 특히, CASE 3에서는 모델 학습 데이터 내 변수 간 상호작용이 보다 효과적으로 반영되었으며, CASE 1과 CASE 2에서는 이러한 상관관계가 충분히 학습되지 않았거나, 데이터의 특성이 모델 학습 과정에서 비효율적으로 작용했을 것으로 판단된다. 향후 연구에서는 각 CASE에서의 변수 간 상호작용과 모델 학습 과정의 차이를 보다 상세히 분석할 필요가 있다.
5. 결 론
본 연구에서는 도심지 쉴드 TBM 터널의 시공 중 발생하는 지반침하를 예측할 목적으로 시공데이터와 지반정보를 활용하여 XGBoost 알고리즘을 적용한 머신러닝 기반 지반침하 예측 모델을 개발하고 그 성능을 평가하였다. 홍콩의 기 쉴드 TBM 현장에서 수집한 지반데이터, 시공데이터(터널 기하조건과 굴진데이터) 중 지반침하 영향인자라고 판단한 17가지 입력 특성을 활용하고 쉴드 TBM 본체 기준으로 세그먼트 25링 전방, TBM 본체 상부, 25링 후방으로 케이스를 구분하여 지반침하 예측 모델을 구축하였다. 베이지안 최적화 기법을 통해 케이스 별 XGBoost 모델의 하이퍼파라미터를 최적화하였으며, k-겹 교차검증을 통하여 데이터 편향 문제를 해결하였다. 최종적으로, 도출된 예측 결과를 비교분석하여 지반침하 예측의 정확도를 검토하였다. 본 연구의 주요 결과는 다음과 같다.
1. XGBoost 기반 지반침하 예측 모델의 성능 평가 결과, 쉴드 TBM 본체 기준으로 세그먼트 25링 후방(CASE 3)에 대한 지반침하 예측 성능의 결정계수는 0.82로 가장 우수한 예측 성능을 보였으며, 반면 막장면 기준으로 25링 전방에 대한 지반 침하 예측 성능의 결정계수는 0.52로 가장 낮은 성능을 나타내었다.
2. 전방 침하 예측 모델의 성능이 후방 침하 예측 모델에 비해 떨어지는 이유는 전방 침하 예측 시에는 미굴착 구간에 대한 지반 및 이를 반영한 굴착 변수의 불확실성이 상대적으로 높아지는데 기인한 것으로 판단된다. 반면, 후방 침하 예측 모델은 이미 발생한 침하 데이터를 기반으로 학습하기에 상대적으로 안정적인 예측 성능을 나타내었다.
3. 전방 지반침하 예측의 정확도를 높이기 위해서는 쉴드 TBM 막장면 기준으로 각 구간의 지반 침하에 영향을 미치는 주요 요인을 분석하는 것이 중요하다. 이를 위해 입력변수의 중요도를 체계적으로 파악하고, 해당 요인에 기반한 가중치 부여 전략 등을 적용하면 보다 정확한 예측이 가능할 것으로 기대된다. 이는 시공 중 발생하는 지반침하 영향인자를 명확히 파악하고, 지반침하량을 예측하여 선제적으로 대응할 수 있는 기반을 제공할 것으로 기대된다.