1. 서 론

세그먼트 터널에서 라이닝의 변형과 세그먼트 간 내력 전달에 이음부가 끼치는 영향을 이해하는 것은 아주 중요하다. 이런 이유로 많은 연구자들이 세그먼트 이음부의 특성을 설명하기 위해 모형 실험과 수치해석을 수행하였고 여러 이론을 제안하였다.

이음부의 영향을 고려하기 위해 Muir Wood (1975)는 라이닝의 전체 강성을 감소시키는 유효 휨강성을 제안하였고, 이 휨강성은 변위와 모멘트의 관계를 확인하거나(Morgan, 1961), 라이닝의 내력 분포와 변위를 추정하는 방법(Duddeck and Erdmann, 1982) 등과 같이 현재까지 설계 실무에서 자주 사용된다. Lee and Ge (2001)는 모멘트 감소계수를 적용하여 라이닝의 강성 및 지반반력의 관계를 연구하였다.

이음부의 강성에 대한 연구들도 있었다. Lee et al. (2001)은 휨, 축 및 전단강성을 갖는 이음부 강성 특성을 제안하고 전체 강성에 대한 이음부의 상대 강성으로 이음부 강성비(joint stiffness ratio)를 도입했다. 이음부의 거동을 실험과 비교하여 이음부의 휨강성이 상당히 가변적이며 이음부의 패킹(packing), 볼트의 특성에 영향을 받는다고 했다. El Naggar and Hinchberger (2008)는 균질한 등방성 토사 또는 암반에 매립된 터널 라이닝의 변위, 내력에 대한 이론식을 제안하고 이음부 강성계수(joint stiffness coefficient)를 도입하였다. 이론식과 수치해석을 비교해 일치된 결과를 얻도록 강성계수를 조정하여 제안된 방법을 검증하였다. Teachavorasinskun and Chub-uppakarn (2010)은 실험에서 구한 수직응력과 변위 관계를 수치해석과 비교하여 이음부를 Angular joint stiffness라는 스프링으로 표현하였다. 이 스프링 강성과 세그먼트 개수의 함수인 강성 감소계수를 도입하여 라이닝의 모멘트 전달 특성을 간단히 표현하였다.

세그먼트 이음부의 회전에 주목한 연구들도 있었다. Janssen (1983)은 세그먼트 이음부의 모멘트-회전 관계를 비선형 회전 스프링으로 설명하였다. Hordijk and Gijsbers (1996)는 네덜란드의 터널 실험을 통해 모멘트-회전 관계에 대한 볼트의 영향은 미미하며 이음부의 거동은 Janssen 모델에 의해 합리적으로 추정될 수 있다고 했다. Blom (2002a; 2002b)은 이중 선형 모델을 적용하여 이음부 회전강성에 소성 단계를 정의하였고, 일본의 기준(Japan Railway Technical Research Institute, 2003)도 이음부의 회전강성 산정에 대해 상세히 서술하고 있다.

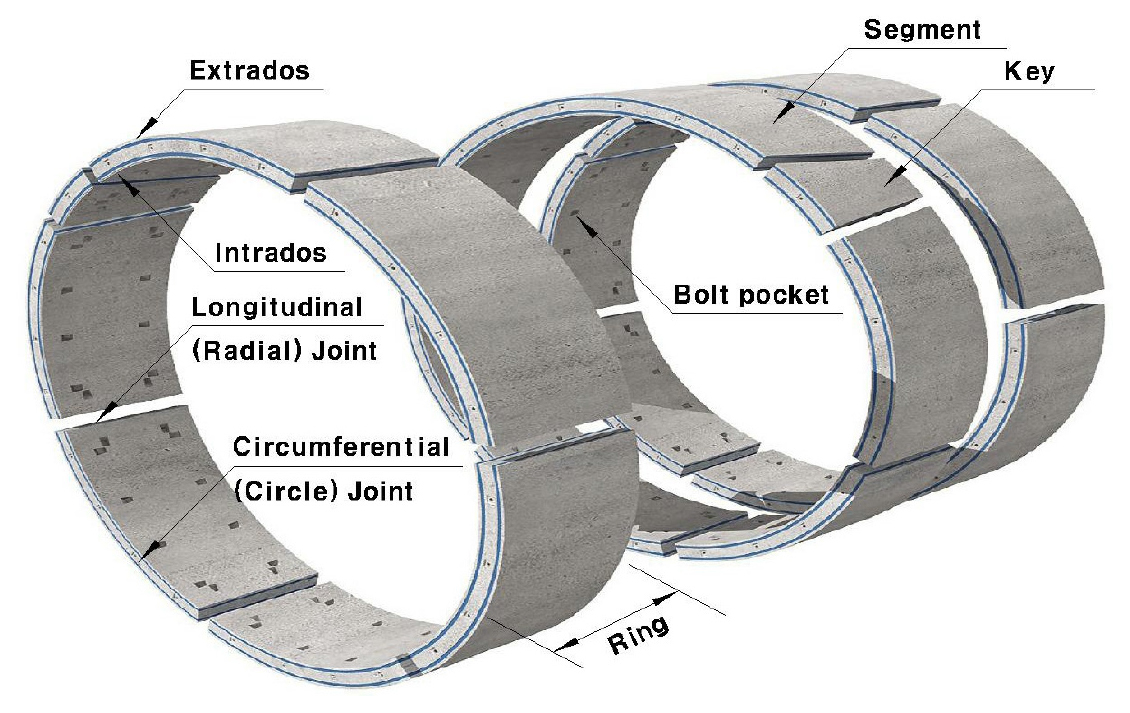
Fig. 1은 세그먼트 라이닝의 구성을 보여준다. 이 논문에서는 세그먼트와 세그먼트의 접촉면에 있는 이음부(longitudinal joint)를 세그먼트 이음부(segment joint)라 하였다. 다음 장에서 세그먼트 이음부에 대한 기존 모델들의 모멘트-회전 관계를 설명하고, 국내 기준에 맞는 지압강도 계산과 이음부의 모멘트-회전 관계를 추정하는 방법도 제시하였다. 2장의 모멘트-회전 관계를 이용하여 3장에서는 세그먼트 라이닝의 가상 설계를 수행하고, 그 결론을 4장에 수록하였다. 이 논문의 목표는 주어진 설계조건에서 세그먼트 이음부의 모델링을 통해 터널의 거동을 설명하고 그로 인한 영향을 이해하는 것이다.

Fig. 1

Segment lining configuration

2. 세그먼트 이음부의 모멘트-회전 관계

2.1 Janssen 모델과 Blom 모델

Leonhardt and Reimann (1965)은 실험을 통해 콘크리트 힌지의 거동을 조사해 설계 응력과 최대 허용 회전을 결정하고자 하였으며 수직력(N), 모멘트(M), 콘크리트 탄성계수(Ec), 종방향 길이(b) 및 이음부 폭(w)의 함수로 콘크리트 힌지의 회전(θ)을 식 (1)과 같이 제시하였다.

Janssen (1983)은 Leonhardt and Reimann의 모델을 기초로 하여 이음부의 회전을 아래와 같이 두 개의 부분으로 정리하였다.

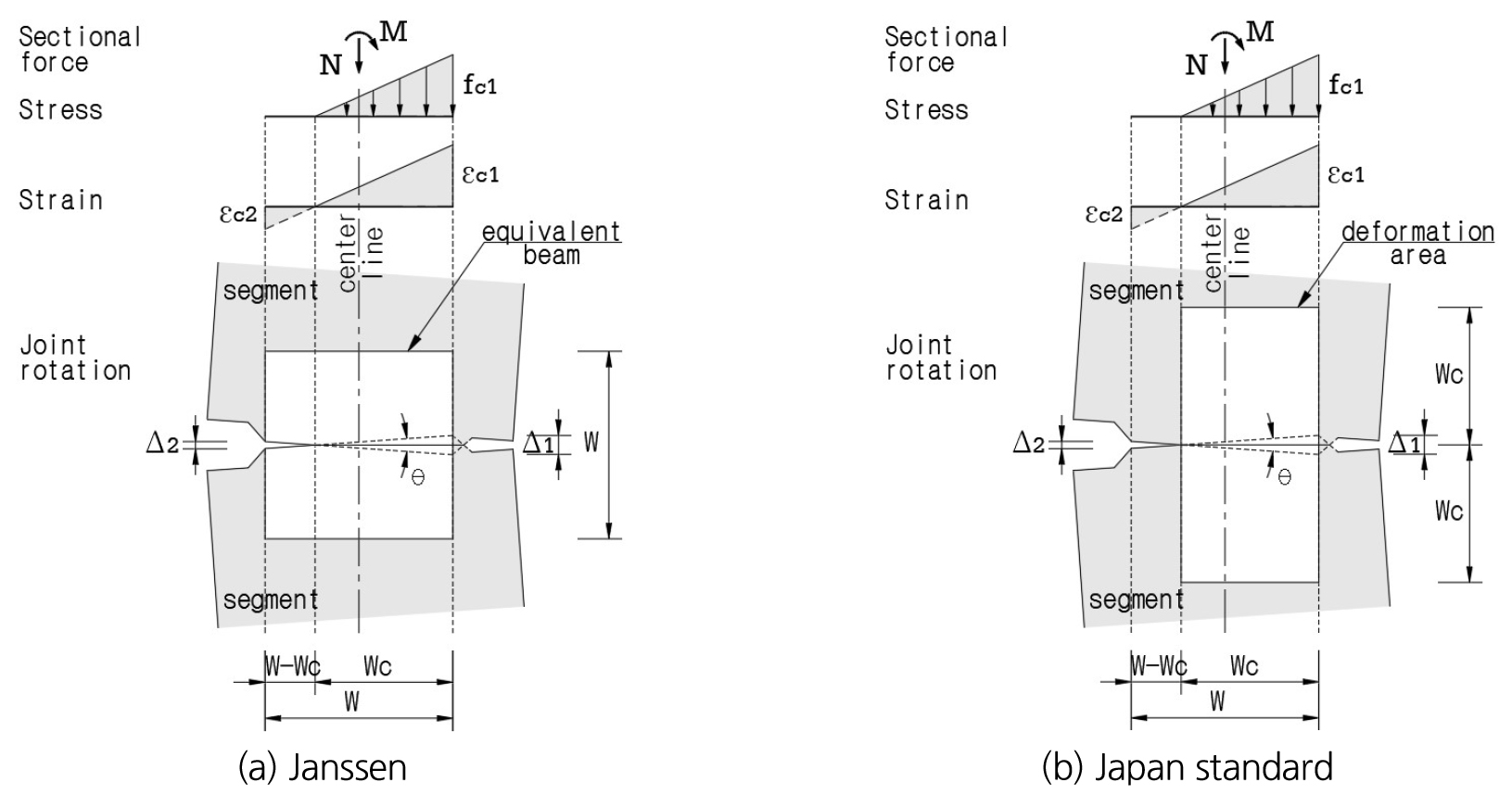
Fig. 2(a)를 참조하면 식 (2)는 이음부가 완전히 밀착된 경우(w=wc)를 설명한다. 이 때 모멘트가 증가하면 회전이 선형적으로 증가하고 편심 e(=M/N)와는 무관하다. 식 (3)은 식 (1)을 변형한 것으로 접촉면의 분리(wc<w)를 나타낸다. 이 경우 편심이 증가함에 따라 회전이 비선형적으로 증가하게 된다.

이 모델은 콘크리트의 선형 탄성 거동을 기반으로 이음부 폭(w)을 두 변으로 하는 정사각형 보(Fig. 2(a)의 equivalent beam)를 이음부의 변형 영역으로 가정한다. Janssen 모델의 이음부 변형 영역은 이음부의 폭(w)이 결정되면 회전과 무관하게 고유한 영역이다. 따라서 이음부의 회전에 관한 식 (2), (3)은 식 (4)로 나타낼 수 있다.

Fig. 2

Janssen’s approach and Japan standard

Blom (2002a; 2002b)은 이음부의 회전강성 산정에 이중 선형(bi-linear) 응력-변형률 관계를 적용했다. Blom은 Janssen 모델의 비선형 부분을 비선형과 소성 부분으로 구분한다. 이 모델의 회전 관계는 세 부분 -식 (2)에서 정의된 선형 부분, 응력-변형률 관계에서 최대응력에 도달하는 변형률까지는 식 (3)에서 정의된 비선형 부분, 그리고 극한변형률이 될 때까지의 소성 부분으로 구성된다. 두 모델의 모멘트-회전 관계는 Fig. 3에 도시하였다.

Fig. 3

Bending moment - rotation relations: comparison of the models studied (given N)

2.2 일본 설계 모델

이 모델은 국내 실무에서 가장 많이 적용되고 있다. 일본 철도구조물 등 설계표준 ‧ 동해설(Japan Railway Technical Research Institute, 2003)에는 회전강성을 아래와 같이 제시한다.

이 모델은 이음부 변형 영역에 대한 가정을 제외하면 Janssen 모델의 가정과 같다. 이음부 중심에서 모멘트 평형조건을 적용하여 식 (5)와 비교하면 변형률은 ε=θ/2=∆/(2wc)와 같다. 이음부 변형 영역은 Fig. 2(b)와 같이 압축을 받는 이음부의 폭(wc)을 두 변으로 하는 정사각형 보 2개를 쌓은 영역이 되며 이음부의 회전에 따라 이음부 변형 영역도 변하게 된다. 이음부의 회전은 식 (4)를 참조하면 식 (6), (7)과 같다.

식 (7)에서 이음부가 완전히 밀착된 경우(wc=w), 이 모델의 이음부 회전은 Janssen 모델의 두 배가 되고 선형 부분의 이음부 회전강성은 Janssen 모델의 절반이 된다. 그 후 차츰 이음부 회전이 증가하여 이음부의 반이 열릴 때(wc=w/2), Janssen 모델의 회전강성과 동일하게 된다. 이음부가 반 이상 열리게 되면(wc<w/2), Janssen 모델보다 큰 회전강성을 갖게 된다. 모멘트-회전 관계는 Fig. 3에 도시하였다.

2.3 지압강도와 제안 모델

부분 영역에 압축력이 작용하는 지압부에서 콘크리트의 설계지압강도(design bearing strength)는 KDS 14 20 20 (2016) 4.7절에서 식 (8)과 같이 주어진다.

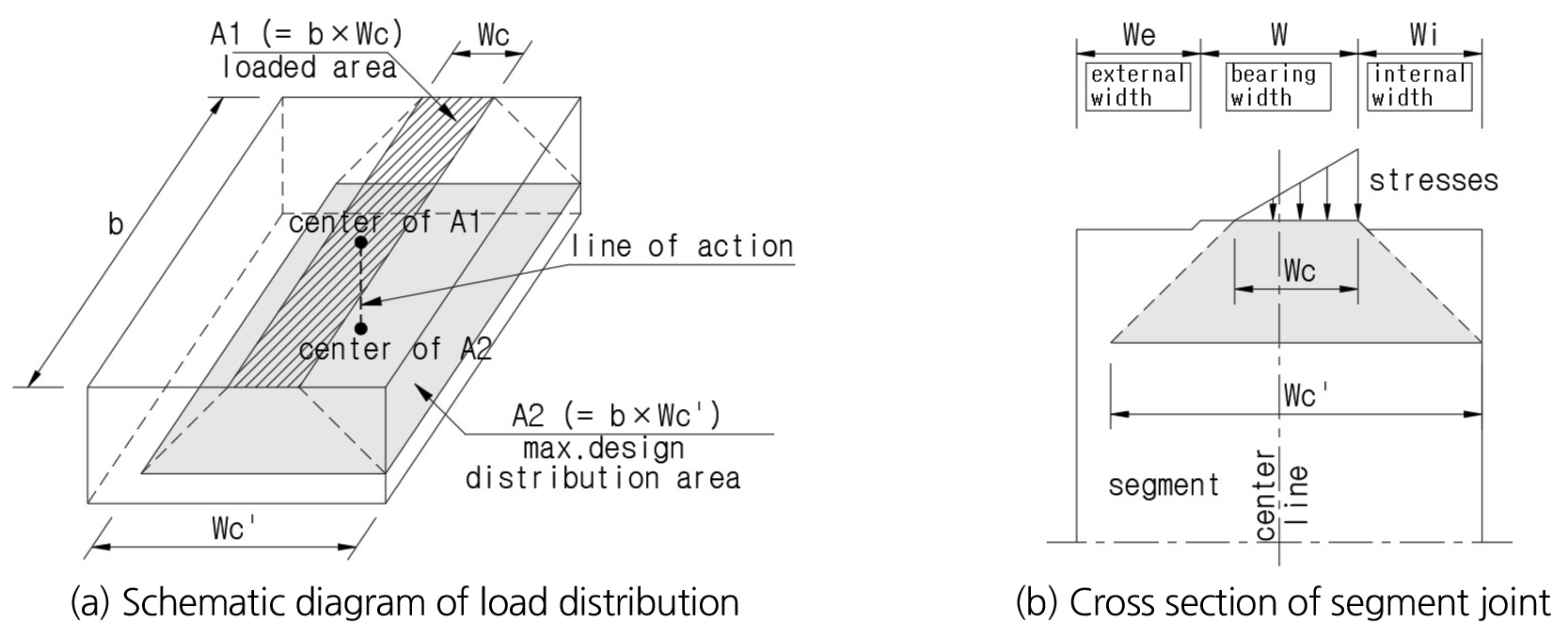
여기서, A1, A2는 지압력의 재하면적과 최대 설계 분포면적, fck는 콘크리트 기준압축강도, ∅는 KDS 14 20 10 (2016) 3.3절에서 주어진 강도감소계수로써 콘크리트 지압의 경우 0.65이다. 식 (8)이 유효하기 위해서는 Fig. 4(a)와 같이 A2의 중심이 A1의 중심을 지나는 작용선상에 있고 하중이 재하면에 균등(uniform)하게 재하되어야 한다. Fig. 4(b)와 같이 이음부의 회전에 의해 접촉면의 응력이 불균등(non-uniform)하고 모서리 쪽으로 갈수록 높은 접촉력을 받는 경우, KDS 24 14 21 (2019) 4.1.6절은 설계지압강도의 값을 감소시켜야 한다고 명시하고 있지만 그 감소값에 대한 기준은 명확하지 않다. 이런 이유로 세그먼트 이음부의 지압강도 계산법과 모멘트-회전 관계를 제시하고자 하며, 그 방법은 아래와 같다.

Fig. 4

Design distribution for partially loaded areas

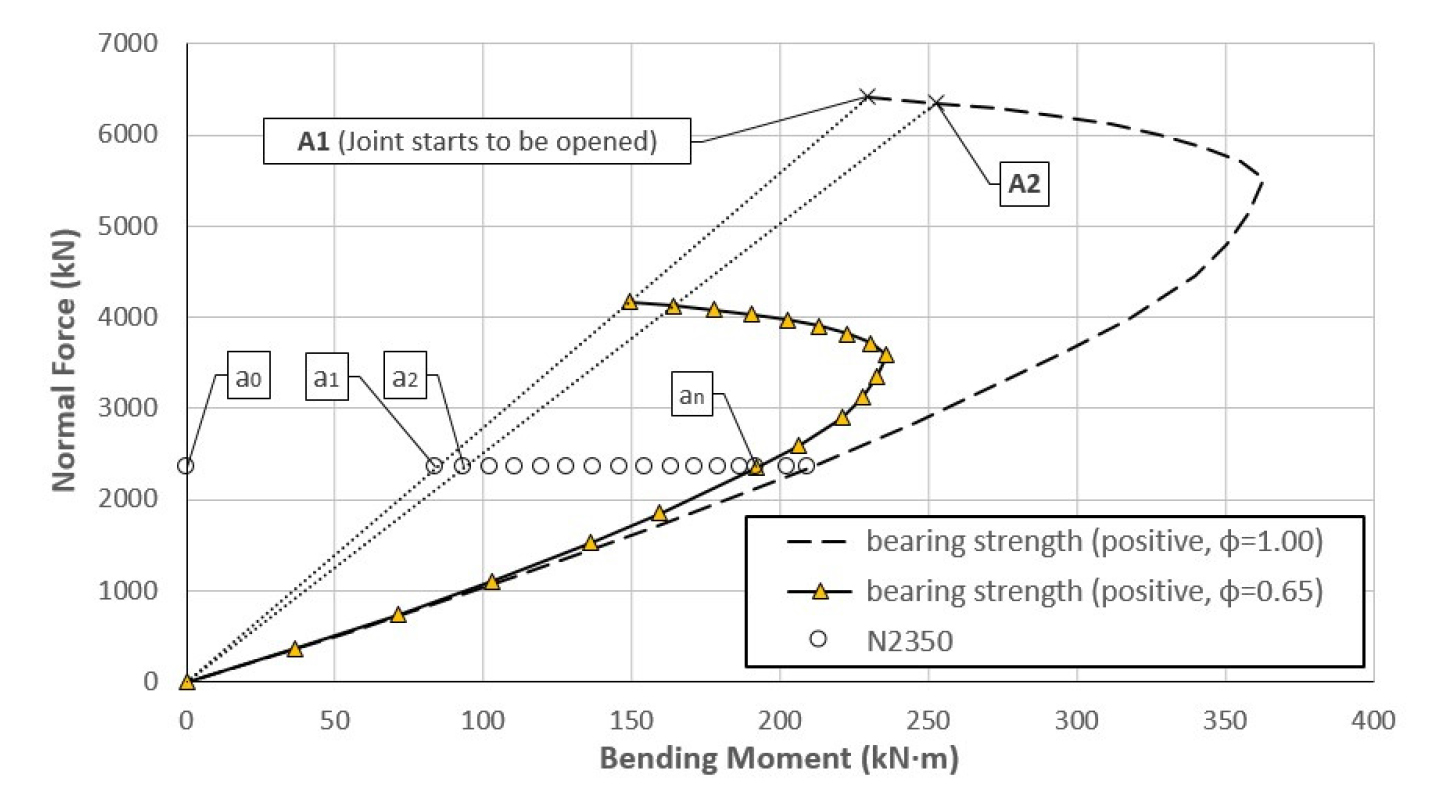
①식 (8)의 fckA2/A1를 구속 콘크리트 압축강도, fck,c로 표현하면 식 (9)가 된다. 콘크리트 압축응력의 분포와 변형률의 관계를 KDS 14 20 20 (2016) 4.1절에서 정의한 등가직사각형 응력블록으로 가정하면 등가압축영역에 0.85fck,c인 콘크리트 응력이 등분포하게 된다. 이음부의 회전에 따라 변하는 fck,c의 값을 고려해 수직력 및 모멘트를 구한 후, Fig. 5와 같이 상관도를 작성한다.

Fig. 5

Bearing strength for segment joint subjected to normal forces and moments

②이음부의 수직력(Fig. 5에서는 2,350 kN)을 가정하고, 수직력에 해당하는 점(A1에 대응되는 a1, A2에 대응되는 a2, …)들의 자취(a0,a1⋯an⋯)를 찾는다. 이음부 양단의 변형률을 εc1, εc2로 하는 선형 분포와 Janssen 모델의 이음부 변형 영역을 가정하면 이음부의 모멘트-회전 관계를 얻을 수 있다.

③모멘트-회전 관계를 이용하여 해석한 수직력이 가정한 수직력과 일치할 때까지 ②를 반복한다.

Fig. 5의 A1은 이음부가 분리되기 시작할 때이며 an은 주어진 수직력에 대한 지압강도의 최대점이 된다. 위 방법으로 구한 세그먼트 이음부의 모멘트-회전 관계는 Fig. 3에 도시하였다.

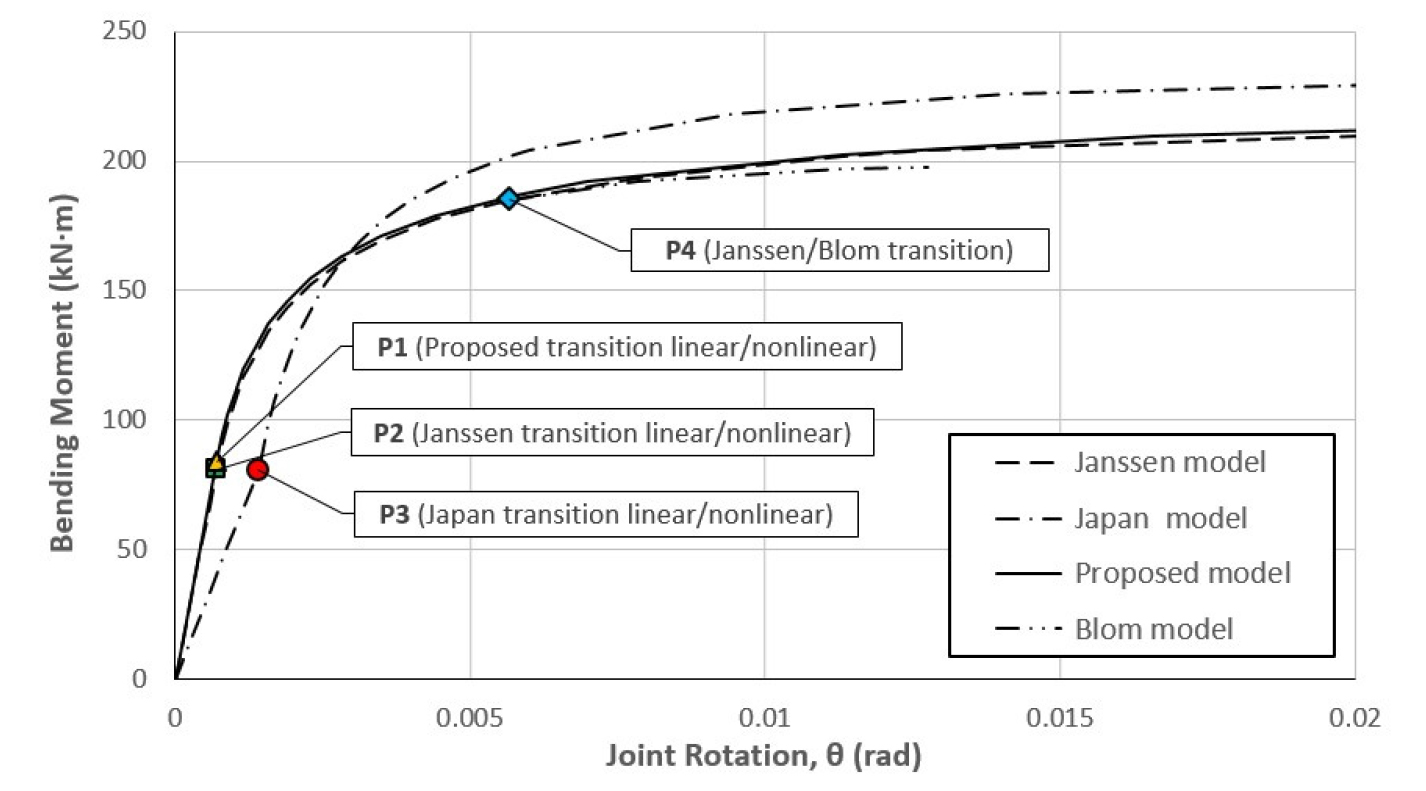
Fig. 3은 연구 모델들의 모멘트-회전 관계를 나타낸다. Janssen과 제안 모델은 거의 유사하나, 일본 모델의 모멘트-회전 관계는 2.2절의 설명처럼 상이한 관계를 보인다. P1, P2 및 P3는 각각 제안 모델, Janssen 및 일본 모델의 선형과 비선형 거동의 분기점이며, P4는 Blom 모델의 소성 단계가 시작하는 점이다.

3. 세그먼트 라이닝의 가상 설계

국내의 세그먼트 라이닝 설계에서는 대개 세그먼트 이음부의 선형 구간 회전강성만을 반영한다. 그러나 실제 이음부는 회전에 따라 강성이 비선형으로 변하므로 이를 고려하는 것이 라이닝의 실제 거동을 반영할 수 있다. 가상 설계를 통해 거동의 차이를 비교하고 지압강도에 대한 검토를 수행하였다.

해석 대상 라이닝의 단면 및 이음부의 위치는 Fig. 6(a)와 같다. 단면은 7개의 세그먼트, 7개의 이음부로 구성되며 이음부의 식별은 라이닝 하부에서 시작해 시계방향으로 번호를 부여하였다. 이음부의 상세는 Fig. 6(b)와 같다. 이음부는 평면 형태이며 콘크리트가 직접 접촉면을 형성한다. 수밀성을 위해 수팽창 지수재가 이음부의 외측에 배치되므로 세그먼트의 전체 두께보다 이음부의 두께는 상당히 줄어든다. 감소된 이음부를 관통하여 설치된 2개의 볼트로 인접한 세그먼트를 연결한다.

Fig. 6

Segment lining and joint detail

사용재료 및 주변 지반의 조건, 세그먼트 라이닝의 제원 등의 해석 입력값은 Table 1에 요약하였다. 구조해석 모델은 보요소인 세그먼트, 선형 및 비선형 회전강성을 갖는 이음부로 구성되며 주변 지반은 미공병단(USACE, 1997)의 공식을 이용하여 압축 전담 스프링으로 모델링하였다. 하중조합은 Korea Concrete Institute (2012)를 적용해 Case 1 (1.4×자중 + 1.4×수직토압 + 0.8×수평토압 + 1.6×수압)과 Case 2 (1.0×자중 + 1.0×수직토압 + 1.0×수평토압 + 1.0×수압)의 두 조합에 대해서 고려하였다. Case 1은 터널 라이닝에 가장 큰 곡률 변화를 야기하는 하중조합이 되며 라이닝의 변위는 Case 2에서 확인할 수 있다. 해석은 앞 장에서 제시된 세그먼트 이음부의 모멘트-회전 관계를 적용하되 이음부의 비선형 회전강성을 고려한 경우와 선형 회전강성만 고려한 경우에 대해 각각 수행하였다. 링 이음부의 상호작용도 중요한 요소이지만 세그먼트 이음부에 대한 이해를 위해 이 논문은 인접 링의 상대변위는 무시하고, 단일 링에 대해서 검토하였다. 해석 결과는 Table 2에 정리하였다.

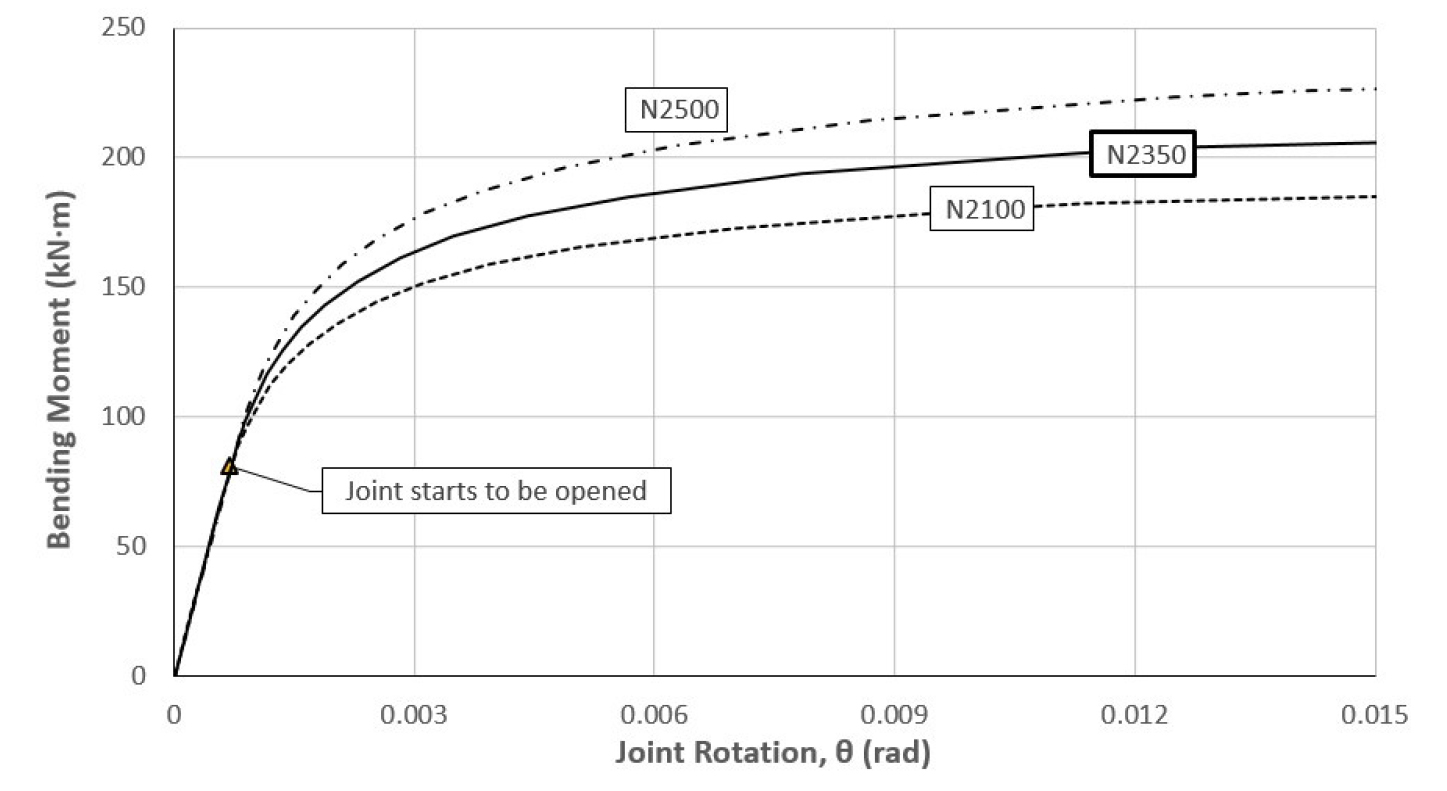
Table 2에는 각 모델들의 선형 및 비선형 해석 결과를 수록하였다. 단면에 유도되는 모멘트는 내측 인장이 발생할 경우 정모멘트(positive bending moment)이다. 해석결과, 이음부들의 수직력은 2,100~2,500 kN 사이에서 분포하였고 수직력의 크기에 따른 모멘트-회전 관계는 Fig. 7에 나타내었다. 수직력이 일정할 경우, 이음부의 회전이 증가함에 따라 더 큰 모멘트가 유도되고 이음부의 비선형 거동으로 회전강성이 점차 감소하게 된다. 더 큰 수직력이 작용하면, 비선형 구간의 회전강성은 증가하지만 선형 구간의 회전강성은 수직력의 크기와 무관하다. 실제 이음부 각각의 정확한 수직력을 적용해야 하지만, 이 논문에서는 쉬운 설명을 위해 평균값인 2,350 kN으로 모든 이음부의 모멘트-회전 관계를 설정하였다.

Fig. 7

Bending moment - rotation relations: comparison of different levels of normal force (Janssen)

Janssen과 제안 모델은 이음부의 회전과 모멘트가 거의 유사함을 Table 2에서 알 수 있다. 선형 거동을 하는 Joint 3에서 Janssen 모델의 회전강성은 약 114,000 kN ‧ m/rad (≒ 17.4 / 0.000152)이지만 일본 모델의 경우 절반에 해당하는 57,000 kN ‧ m/rad (≒ 21.485 / 0.000376)을 나타낸다. 비선형 거동을 하는 Joint 1을 보면 일본 모델의 모멘트와 회전이 더 크다. 이러한 모멘트-회전 관계의 특성은 2.2절에서 설명하였다.

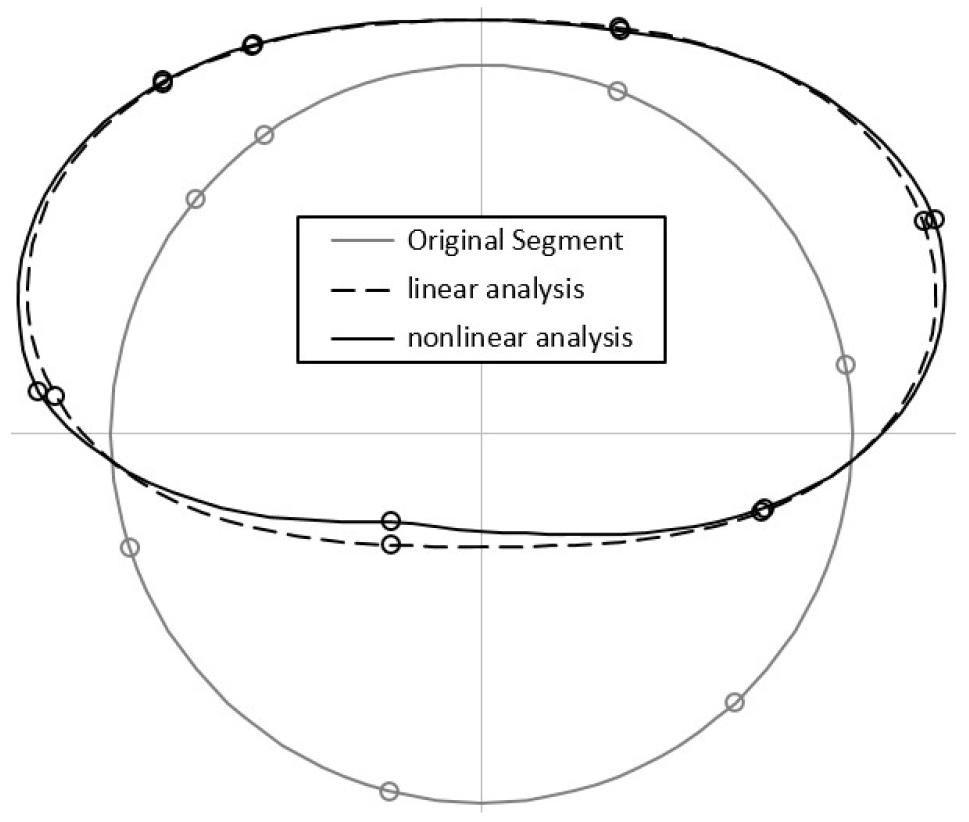
Fig. 8은 세그먼트 이음부의 선형 해석과 비선형 해석을 비교한 그림이다. 선형 해석의 경우 상당히 큰 모멘트가 발생하는데, 이는 회전에 따른 이음부의 강성 감소를 고려하지 않고 실제 강성보다 크게 평가하기 때문이다. 따라서 이음부 회전강성의 변화를 반영할 때 더욱 실질적인 결과를 얻을 수 있다.

Fig. 8

Bending moment - rotation relations: comparison of linear and non-linear analysis

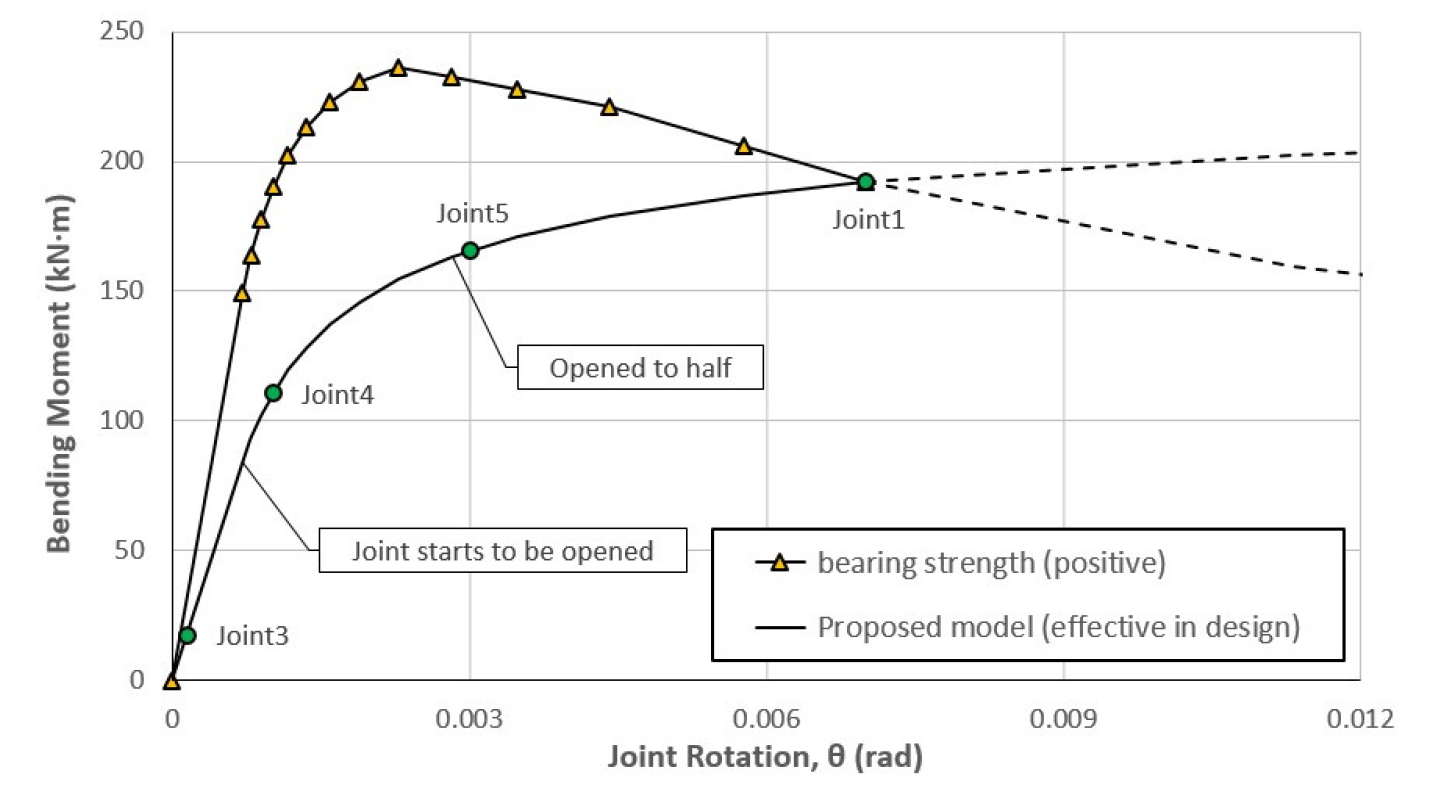
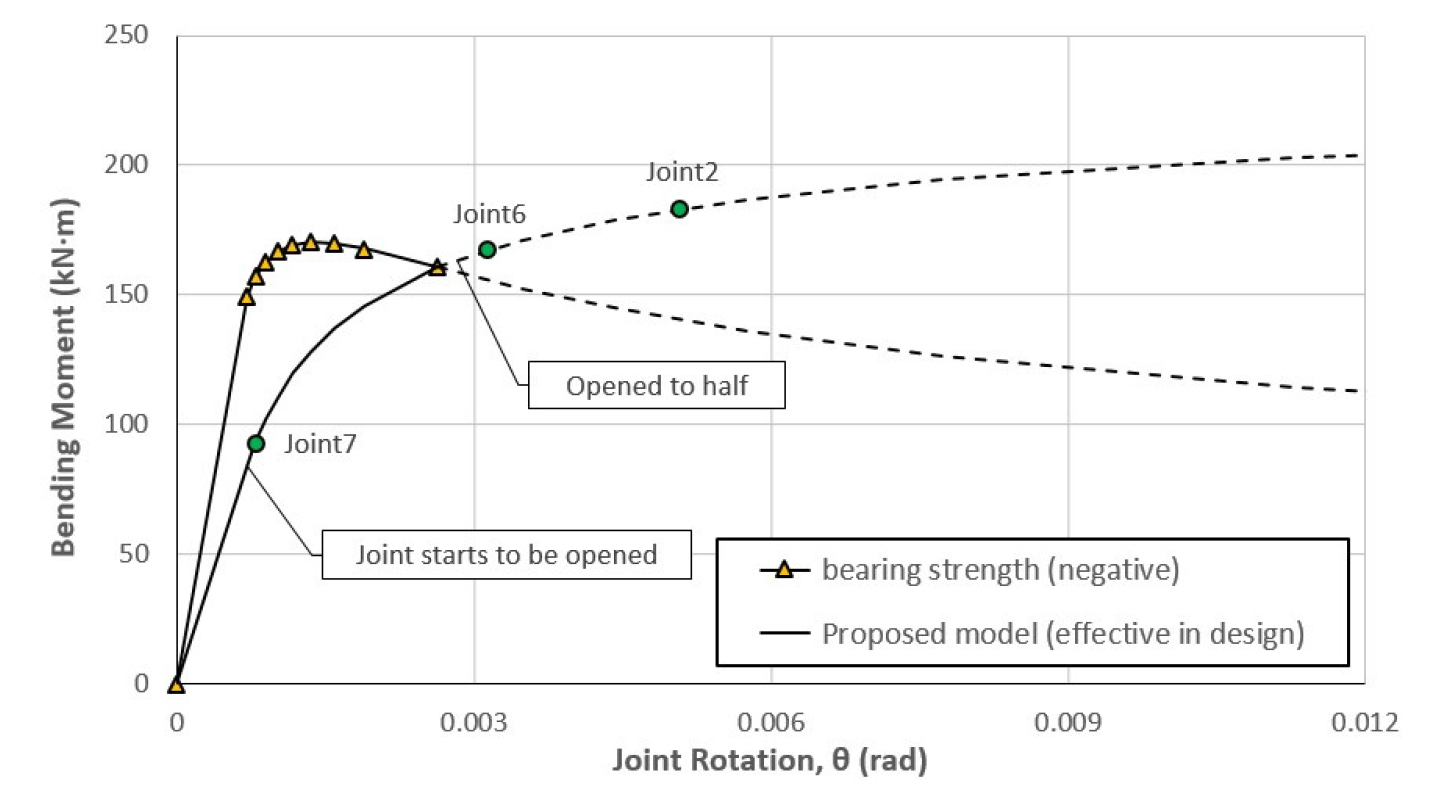
Fig. 9와 Fig. 10은 Fig. 5의 지압강도(∅ = 0.65) 곡선을 제안 모델의 모멘트-회전 관계와 중첩시켜 각각 정, 부모멘트부에 대해 표시한 그림으로 해당 이음부의 지압에 대한 안전을 쉽게 설명할 수 있다. Fig. 9의 정모멘트가 발생하는 Joint 1과 Joint 3~5는 지압에 대해 만족한다. Fig. 10의 부모멘트가 유도되는 Joint 2와 Joint 6은 Joint 1보다 더 작은 모멘트에도 불구하고 설계에 유효한 모멘트-회전 관계를 벗어난 곳에 위치하여 지압에 대해 만족하지 못한다. 그 이유는 Fig. 6(b)에서 보듯이 이음부 중심이 단면 중심에 비해 좀 더 내측에 위치하여 식 (9)의 fck,c가 내측 인장이 발생할 때 더 크기 때문이다. 이런 특성으로 인해 정모멘트부의 지압강도가 부모멘트부에 비해 더 크므로 단면을 결정할 때 반드시 검토가 필요하다.

Fig. 9

Bearing strength of segment joints (positive bending moment)

Fig. 10

Bearing strength of segment joints (negative bending moment)

Fig. 11은 선형 및 비선형 해석의 변위를 보여준다. 선형 해석의 변위는 전체 라이닝의 곡률 변화로 인해 발생하지만, 비선형 해석의 경우에는 이음부의 회전에 의한 변위가 추가로 발생된다. 따라서 이음부의 강성을 크게 평가하면 이음부의 회전을 무시하거나 과소 평가하게 된다. 이는 지반 조건 및 측압계수 등에 따라 세그먼트 라이닝 터널의 안전성에 큰 영향을 끼칠 수도 있다.

Fig. 11

Deformation: comparison of linear and non-linear analysis (scaled up)

4. 결 론

세그먼트 이음부의 회전은 선형 구간에서는 모멘트와 비례관계를 갖지만 회전이 증가함에 따라 수직력과 모멘트의 비선형 함수가 된다. 본 연구에서는 세그먼트 이음부의 모멘트-회전 관계를 반영하여 세그먼트 라이닝에 대한 해석을 수행하였다. 이음부를 선형 고유의 회전강성만 고려한 경우와 비선형 회전강성을 고려한 경우에 대해 비교하였으며, 이음부의 회전에 따른 지압강도 계산 방법을 제시하였다. 결론은 다음과 같다.

1. 세그먼트 이음부의 선형 회전강성만 고려한 해석과 및 비선형 회전강성을 포함한 해석을 비교하면, 선형 해석의 경우 상당히 큰 모멘트가 발생하게 된다. 이는 이음부의 강성 감소를 고려하지 않고 이음부를 실제 강성보다 크게 평가하기 때문이다. 따라서 이음부 회전강성의 변화를 반영할 때 보다 실질적인 결과를 얻을 수 있다.

2. 세그먼트 라이닝의 변위는 크게 라이닝 전체의 곡률 변화와 이음부의 회전에 기인한다. 이음부를 실제 강성보다 크게 평가하면 이음부의 회전 변위가 감소해 전체 변위를 과소평가할 수 있다. 이는 지반 조건과 측압계수에 따라 터널의 안전성에 큰 영향을 끼칠 수도 있다.

3. 이음부의 모멘트-회전 관계에 따르면 수직력이 일정할 경우, 이음부 회전의 증가에 따라 더 큰 모멘트가 유도되고 이음부의 비선형 거동으로 회전강성이 감소하게 된다. 수직력이 커지면, 이음부가 분리되는 구간(비선형구간)에서 수직력의 증가에 따라 회전강성이 증가하나 이음부가 완전히 접촉되는 구간(선형구간)의 회전강성은 수직력의 크기와 무관하고 일정하다.

4. Janssen과 일본 모델의 모멘트-회전 관계의 차이는 이음부 변형 영역의 가정에 기인한다. 이 가정으로 인해 이음부의 절반이 열리기 전까지 Janssen 모델의 회전강성이 크고, 이음부가 더 회전하게 되면 회전강성이 같거나 Janssen 모델의 회전강성이 작아지므로 라이닝의 내력과 변위를 구할 때 이 특성을 감안해야 한다. 이 논문에서 제시한 모멘트-회전 관계는 이음부의 지압강도를 계산하는 과정에서 구할 수 있으며 Janssen 모델의 가정을 기반으로 하여 Janssen 모델과 거의 유사한 결과를 얻을 수 있었다.

5. 일반적으로 방수재가 세그먼트 이음부의 외측에 배치되어 세그먼트의 전체 두께에 비해 이음부의 두께가 감소하게 되며 이음부의 중심은 단면중심보다 내측에 위치하게 된다. 이런 단면특성에 의해 이음부 지압강도는 정모멘트부(내측 인장)가 부모멘트부에 비해 더 크다. 이는 부모멘트부가 지압에서 더 위험할 수 있다는 의미이다. 따라서 이음부의 중심이 단면중심에 최대한 일치되도록 하여 정, 부모멘트부의 균형을 맞추는 것이 이음부의 지압성능에 유리하다.