1. 서 론
2. 머신러닝 알고리즘 개요
2.1 SVM (Support Vector Machine)
2.2 ANN (Artificial Neural Network)
2.3 PCA (Principal Component Analysis)
2.4 DT (Decision Tree)
2.5 Ensemble (Random Forest, XGBoost)
3. 데이터 준비
3.1 데이터 수집
3.2 데이터 처리
4. 결과분석 및 토론
5. 결 론
1. 서 론
최근 정부의 국가 균형발전 정책으로 인해 도로, 철도 등 각종 교통 인프라의 건설이 꾸준히 진행되고 있다. 국토의 70% 이상이 산악지대로 이루어진 우리나라의 지형적 특성상 교통 인프라 건설의 증가는 터널건설 수요의 증가로 이어진다. 이에 따라 2020년을 기준으로 국내의 도로 및 철도 터널은 총 3,526개소, 총연장은 3,062.3 km이 건설되었으며, 최근 10년간 연평균 131개소, 159.6 km의 도로 및 철도 터널이 준공되었다(MOLIT Statistics System, 2021a; 2021b).
터널 건설을 위해서는 먼저 시추조사, 전기비저항탐사 및 물리탐사 등과 같은 다양한 지반조사를 실시하고 이에 대한 결과를 종합적으로 분석하여 터널구간별 암반분류를 실시하는 것이 일반적이다. 이렇게 결정된 암반등급은 굴착공법, 발파패턴, 지보패턴 및 보조공법 결정에 중대한 영향을 미치게 되므로, 결과적으로 암반분류 결과는 터널의 구조적 안정성과 공사비용 및 기간을 좌우하는 가장 중요한 요인이 된다.
그러나 현재 적용되고 있는 RMR 또는 Q 값에 의한 암반분류결과는 현장 엔지니어의 주관적 판단에 따라 서로 상이한 결과가 나오는 경우가 많아서 일관된 암반분류를 위한 엔지니어를 대상으로 한 교육에 많은 노력이 요구되는 실정이다. Kim et al. (2015)은 사전 지반조사 물량의 적정성 및 지반상태 해석의 한계성으로 인하여 지반조사 결과의 신뢰성이 문제가 된다고 한 바 있으며, 마찬가지로 Kim et al. (2004)은 지반조사 시 내재된 지반의 불확실성을 지적한 바 있다. 이것은 터널구간별 암반등급이, 일부 몇 개의 지점에서만 이루어지는 시추조사 결과와 터널전체에 대해 암질의 상태를 파악하는 전기비저항탐사 등 몇 가지 탐사결과의 상관관계에 의해 결정되므로 시추조사가 이루어 지지 않은 터널구간의 암반등급이 실제와 많은 오차를 나타내는 경우가 많기 때문이다.
이러한 문제를 해결하기 위하여 암반분류와 탄성파 속도 간 상관관계에 대한 연구(You and Baek, 2003; Lee et al., 2018) 및 암반분류와 전기비저항 탐사결과 간의 상관관계 등에 대한 연구(Choi et al., 2003; Kwon et al., 2008; Lee et al., 2009; 2012; Ryu et al., 2013)가 다수 수행되었으며, 국내 화강암 지역을 대상으로 RMR, RQD 및 Q value 간 상관관계에 대한 연구가 이루어진 바 있다(Sunwoo et al., 2011). 이처럼 각각의 탐사 자료와 암반분류 간의 개별적인 관계에 대해서는 활발히 연구가 진행되었으나, 다양한 탐사 자료를 종합적으로 고려한 암반분류에 대한 연구는 아직 미미하다.
즉, 현장에서의 탐사자료 외에 암반등급에 영향을 미치는 다양한 지질적, 지형적 요인 그리고 해당현장과 유사한 지반특성을 나타내는 기존의 다른 현장에서의 설계 시 암반등급 결정결과와 시공 시 나타난 암반등급 등을 해당 현장의 설계 암반등급 결정에 활용한다면 보다 신뢰도 높은 암반등급 결과를 도출할 수 있지만, 결정을 위한 분석방법과 그 과정이 매우 복잡해진다. 이러한 경우 최근 그 활용도가 비약적으로 증가하고 있는 머신러닝 기법을 활용하면 복잡한 여러 인자들 간의 비선형적 관계를 효과적으로 분석하여 보다 신뢰도 높은 결과를 도출할 수 있다. 이와 관련하여 터널 심도, 탄성파 속도, 위치 정보 및 전기비저항 등의 탐사데이터와 인공신경망 알고리즘을 활용한 RMR예측에 관한 연구가 수행된 바 있으나(Han et al., 2002), 시추공 탐사 데이터를 추가로 활용하거나, ANN (artificial neural network) 외의 머신러닝 기법을 활용한 연구는 아직 수행된 바 없다. 머신러닝 기법은 ANN 외에도 SVM (support vector machine), DT (decision tree), RF (random forest), XGBoost, PCA (principal component analysis) 등 다양한 알고리즘이 존재하며, 데이터의 특성에 따라 알고리즘별 학습 효과가 달라질 수 있다.
따라서 본 논문에서는 지반조사 시 암반분류 결과의 신뢰도를 제고하기 위하여 상기 6개의 머신러닝 알고리즘을 활용한 암반분류 결과를 비교하였으며, 최상의 결과를 나타내는 알고리즘을 이용하여 터널 암반등급 예측 모델을 개발하였다. 이를 위해 기존 터널설계보고서 및 지반조사보고서에서 나타난 각종 물리 탐사 및 실내암석시험 자료를 정리하여 데이터 셋을 구축하였다.
2. 머신러닝 알고리즘 개요
머신러닝의 목적은 현재 보유하고 있는 정보를 기반으로 새로운 상황에서 원하는 결과값을 알아내는 것으로, 사용자가 활용하고자 하는 데이터의 특성을 가장 잘 반영할 수 있는 알고리즘 및 초매개변수(hyperparameter)를 결정해야 한다. 토목분야, 특히 암반공학분야에서 일반적으로 사용되는 머신러닝 알고리즘은 DT, SVM, ANN, PCA, RF 및 XGBoost 등이 있으며(Kim, 2021), 본 연구에서는 상기 6개의 머신러닝 기법을 모두 사용하고 각 기법의 초매개변수를 Tables 1, 2, 3, 4, 5, 6과 같이 변화시키며 각 경우의 암반분류 예측모델을 학습시켜 그 결과를 비교하였다.
Table 1.
Hyperparameters for SVM
2.1 SVM (Support Vector Machine)
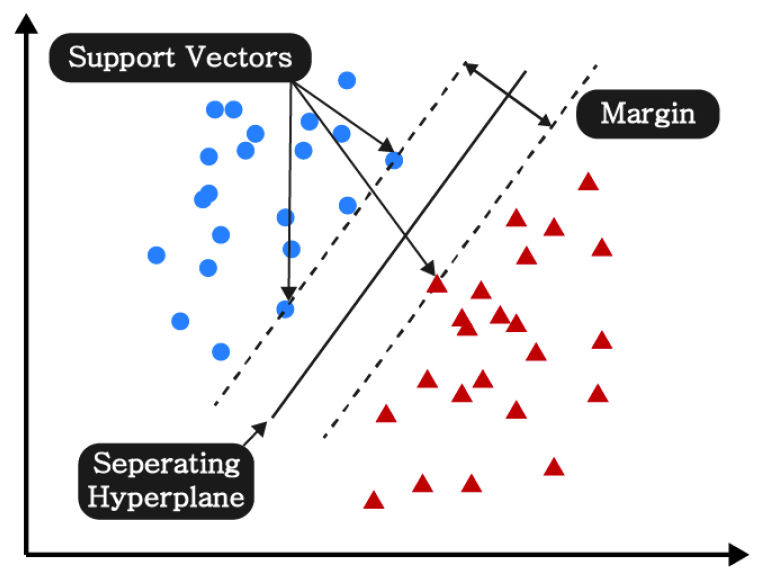
SVM은 데이터를 구분할 수 있는 선형 혹은 비선형 경계선과 서포트 벡터(support vector)를 생성하여 새로운 데이터가 경계의 어느 쪽에 해당하는지를 판별하는 기법이다(Fig. 1). 일반적으로 서포트 벡터를 이용하여 서로 다른 변수들을 구분하기 위한 목적으로 사용되지만, 반대로 서포트 벡터의 간격 안에 최대한 많은 데이터들이 들어가도록 학습할 경우 회귀 목적으로 사용될 수 있다. 본 연구에서는 생성되는 경계선의 간격(C) 및 데이터 구분을 위한 커널(kernel) 등을 Table 1과 같이 설정하였다.
2.2 ANN (Artificial Neural Network)
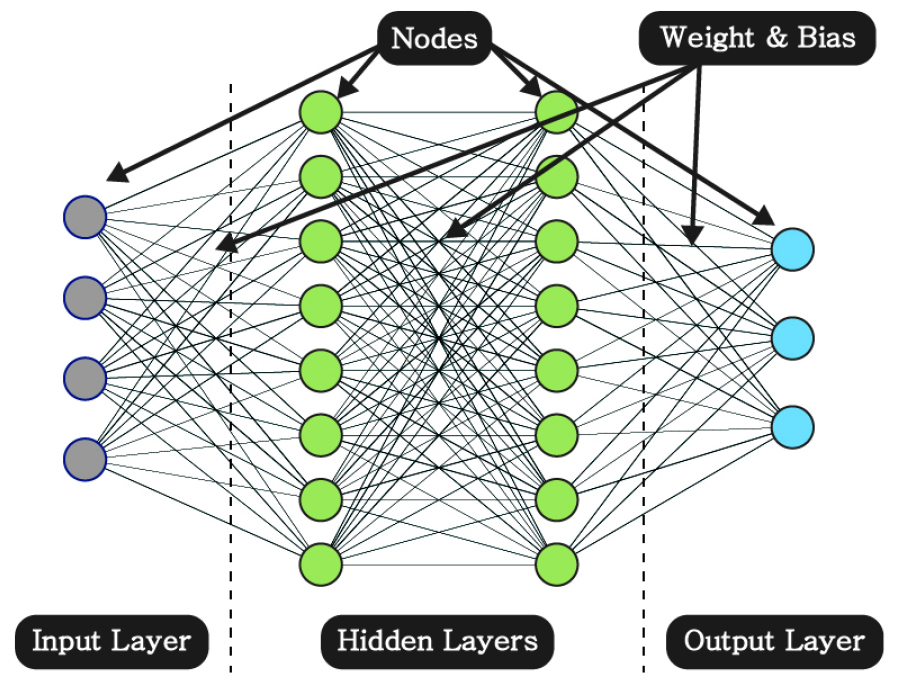
ANN은 생물체의 신경망을 모사한 퍼셉트론(노드)을 사용한다. ANN 모델은 입력층과 출력층 사이에 다수의 은닉층을 나열하고, 각각의 은닉층에 다수의 노드를 배치하여 구성하게 된다(Fig. 2). 이때, 모델 구조에 따라서도 학습효과의 차이가 발생하며, 본 연구에서는 은닉층의 개수(layer number), 각 은닉층별 노드의 개수(node number)와 같은 모델구조와 활성함수의 종류(activation function), 손실함수의 종류(loss function) 등을 Table 2와 같이 설정하였다.
Table 2.
Hyperparameters for ANN
2.3 PCA (Principal Component Analysis)
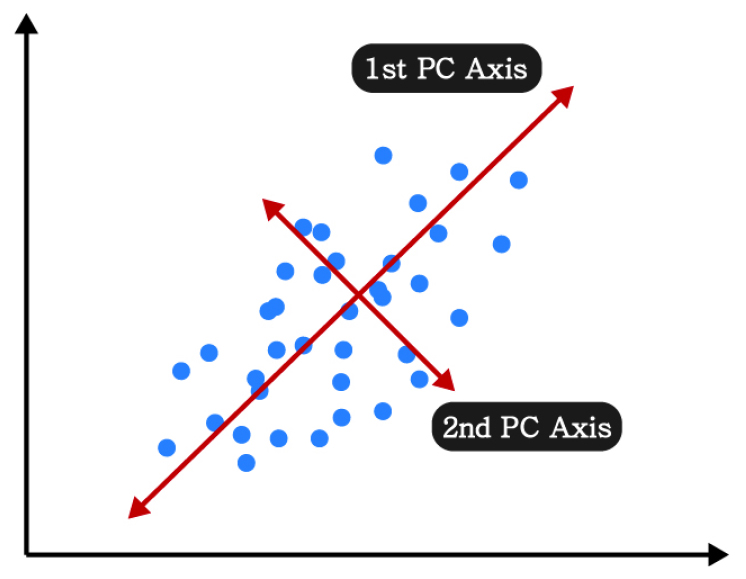
PCA는 고차원의 데이터를 대상으로 이를 잘 나타낼 수 있는 저차원 표현을 찾는 방법이다. 즉, 원래의 데이터 특성을 훼손하지 않도록 데이터들을 소수의 특정 벡터(주성분 벡터, principal component)로 정사영하여 표현하는 방법이다(Fig. 3). 주성분 벡터의 개수가 증가할수록 모델의 설명력은 증가하지만, 그만큼 모델의 복잡도 또한 증가하게 되며, 따라서 적정 수준의 설명력(PCA score)과 복잡도를 보이는 주성분의 개수를 찾는 것이 중요하다. 본 연구에서는 Table 3과 같이 PCA score를 설정하였으며, PCA의 효과는 단순히 데이터의 종류를 줄이는 것이기 때문에, PCA 결과 도출된 주성분을 ANN의 입력인자로 활용하여 RMR 예측 모델을 학습시켰다.
Table 3.
Hyperparameters for PCA
| Hyper-parameter | Description | Values |
| PCA score |
Minimum required model performance (The number of principal components that satisfy the PCA score will be selected automatically.) | 0.95 (95%) |
2.4 DT (Decision Tree)
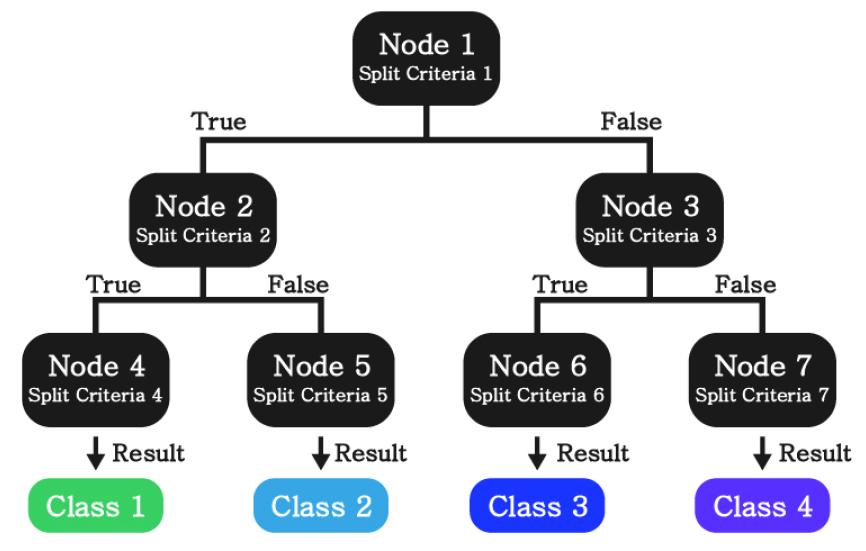
DT 모델은 마치 나뭇가지와 같이 데이터를 분류하기 위한 규칙으로 이루어진 분기점(노드)과, 분기점으로부터 뻗어 나가는 선택지(가지)로 이루어져 있으며(Fig. 4), 이 때 분기점이 많을수록 정확도는 올라가지만, 모델의 복잡성 및 계산시간이 증가하게 된다. 따라서 일반적으로 적정 수준에서 분기를 종료하여 효율적인 모델을 만들게 되는데, 이를 위해 최대 가지치기 횟수(max depth) 및 분기 종료 기준(min samples leaf) 등을 Table 4와 같이 설정하였다.
Table 4.
Hyperparameters for DT
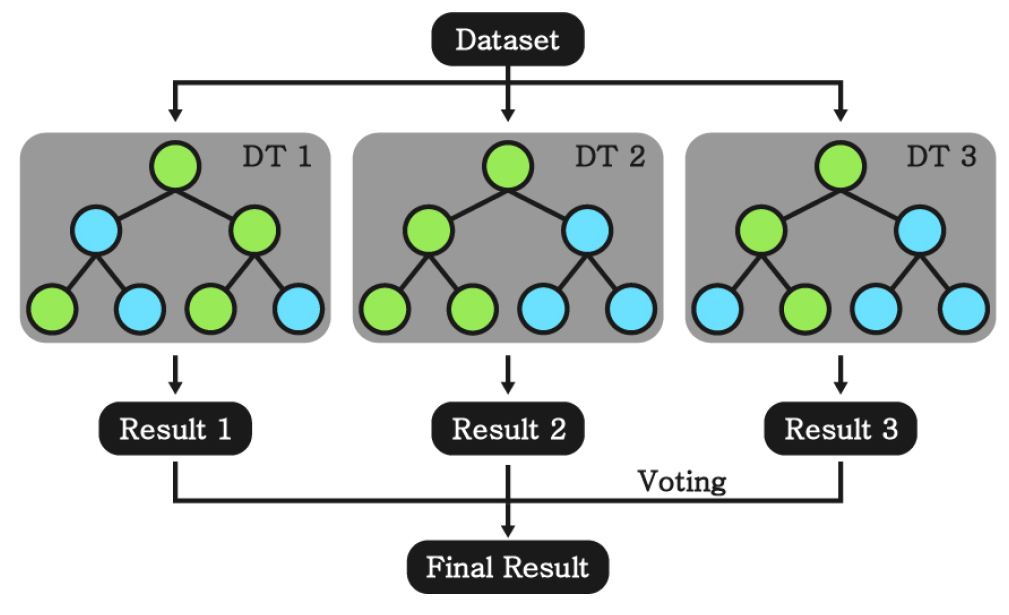
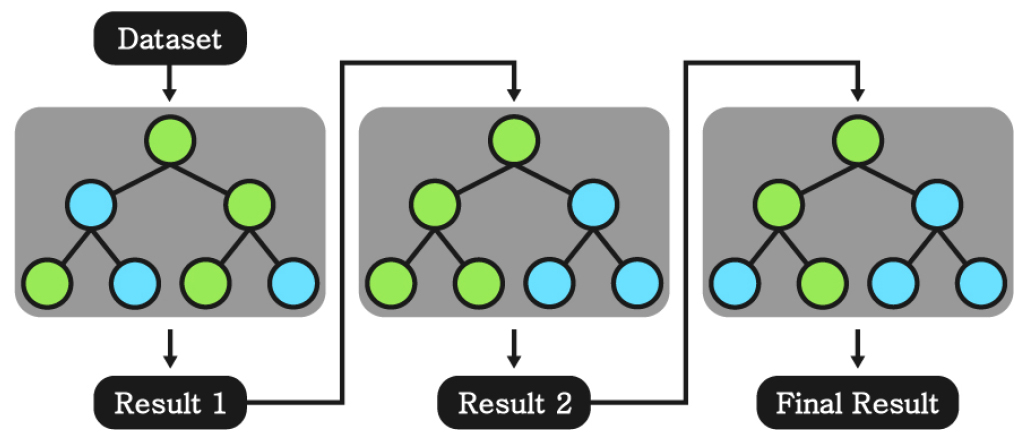
2.5 Ensemble (Random Forest, XGBoost)
머신러닝 모델은 학습 과정에서 과적합이 발생하게 된다. 각각의 모델은 과적합된 경향이 서로 다르다고 가정할 수 있으며, 다수의 모델을 생성하여 그 결과를 결합한다면 하나의 모델을 사용할 때보다 과적합의 영향을 감소시킬 수 있다. 이와 같이 다수의 모델을 학습시킨 뒤 결합하여 사용하는 방식을 앙상블(ensemble) 기법이라 한다. 앙상블 기법은 대표적으로 Fig. 5와 같은 RF (random forest)와 Fig. 6과 같은 XGBoost의 2개의 알고리즘이 존재한다. 이 두 알고리즘은 다수의 DT 모델을 결합하여 사용하므로 기본적인 초매개변수는 DT 알고리즘과 동일하며, 사용하는 모델의 개수(N estimators), 개별 모델 학습 시 사용하는 데이터의 수(subsample) 등과 같은 초매개변수는 Table 5 및 Table 6과 같이 설정하였다.
Table 5.
Hyperparameters for RF
| Hyper-parameter | Description | Values |
| N estimators | Number of DT model to create | 1~100 |
| Max depth | Maximum number of branching for each DT model | 1~14 |
| Max features | (Same with Table 4) | Auto, Sqrt, Log2 |
| Min samples leaf | (Same with Table 4) | 3, 4, 5, 6 |
Table 6.
Hyperparameters for XGBoost
3. 데이터 준비
3.1 데이터 수집
암반분류 예측모델의 학습을 위해 국내 철도 및 도로 터널을 대상으로 시추조사 데이터를 수집하였다. Table 7 및 Table 8과 같이 13개 터널, 총 73 km 구간에서 397개의 시추조사 자료를 대상으로 총 11 개의 학습인자를 선정하였다. 여기에는 시추심도(depth)와 심도별 RMR 및 암종(rock type) 외에, 무결암에 대한 역학적 특성을 나타내는 일축압축강도(uniaxial compressive strength, UCS), P파속도(Vp), S파속도(Vs), 영률(Young’s modulus, E), 단위중량(unit weight, UW), 포아송비(Poisson’s ratio, ν) 등 6개 물성치, 그리고 암반의 불연속성과 지하수에 의한 영향을 대표하는 시추심도에서의 전기비저항(electrical resistivity, ER) 탐사결과 및 RQD가 포함되며, RMR을 출력(output)인자로 그리고 기타 항목 10개를 입력(input) 인자로 설정하였다.
Table 7.
List of learning factor
| Data group | Collected factors |
| Input parameter | Depth, Rock type, RQD, Electric resistivity, Lab test (UCS, Vp, Vs, Young’s modulus, unit weight, Poisson’s ratio) |
| Output parameter | RMR |
Table 8.
List of tunnels used for data collection
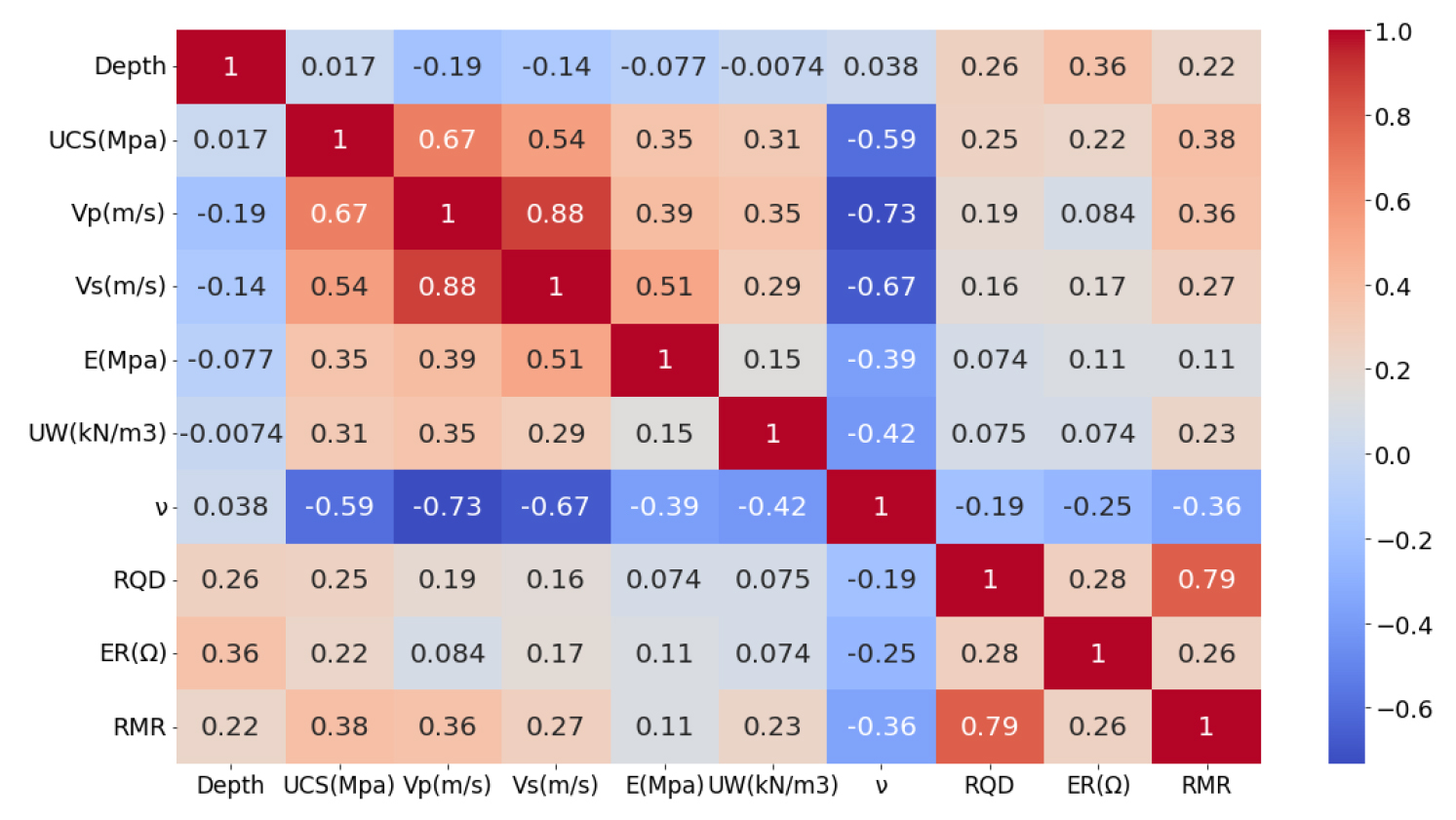
Fig. 7은 데이터의 각 변수들 간 상관관계를 나타낸 heatmap이다. UCS는 Vp 및 포아송비와, Vp는 Vs 및 포아송비와, Vs는 영률 및 포아송비와, RQD는 RMR과 0.5 이상의 상관계수를 보였다. 그 중에서도 특히 Vp와 Vs는 0.8 이상의 상관계수를 통해 높은 상관성을 확인할 수 있었다.
다중공선성은 개별적인 회귀계수(regression coefficient)의 값에는 영향을 미치지만, 모델의 전반적인 예측성능에는 큰 영향을 주지 않는다고 알려져 있다(Loo, 2003; Srisa-An, 2021). 본 연구에서는 모델의 예측성능에 대한 다중공선성의 실제 영향을 확인하기 위해서, 10개의 학습인자를 모두 포함하여 학습을 진행한 경우와 가장 강한 상관관계를 보이는 입력인자인 Vp와 Vs 중 Vs를 제외하고 학습을 진행한 경우를 각각 학습시켜 그 결과를 비교하였다.
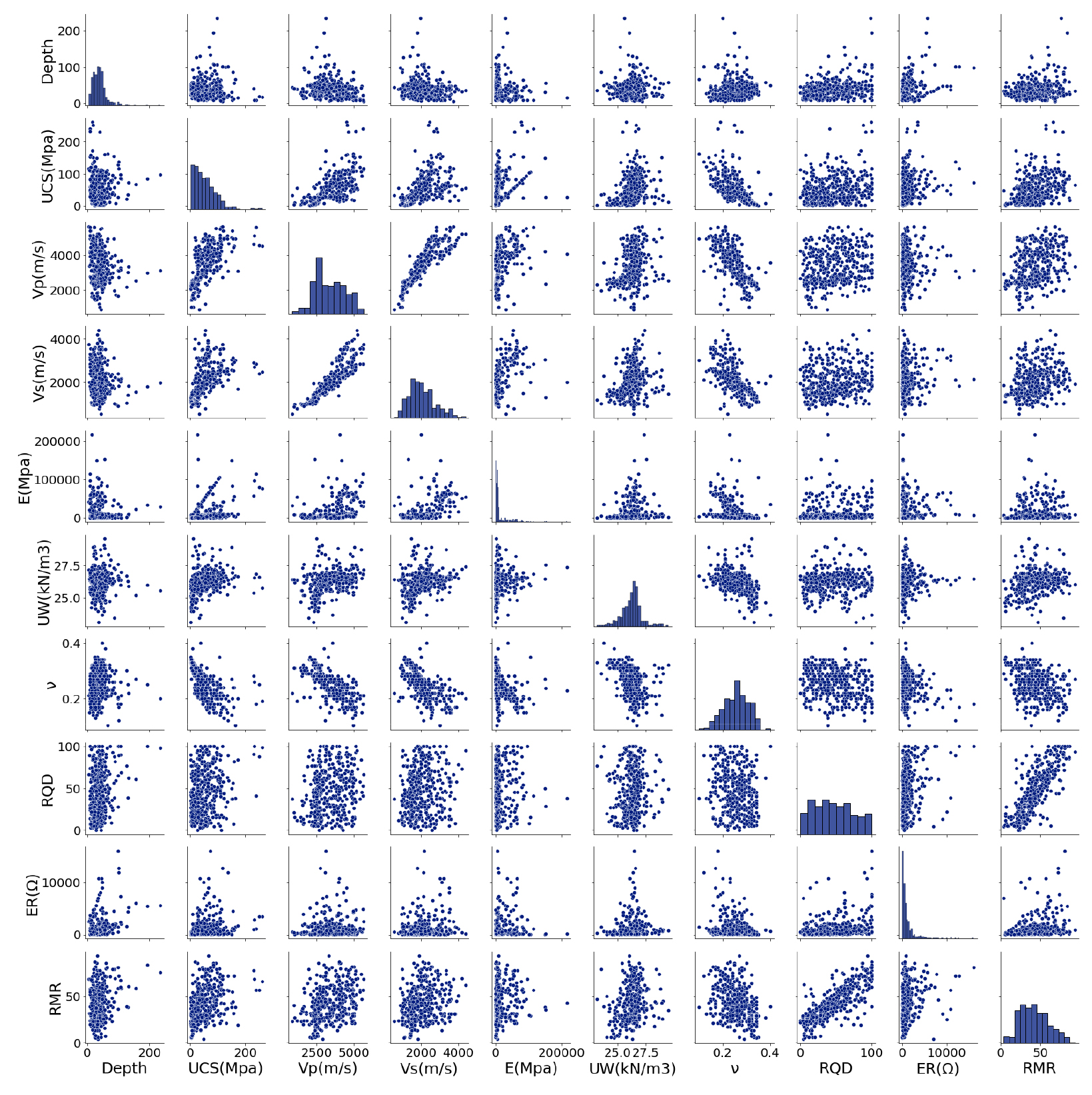
데이터 수집 과정에서 발생 가능한 각종 오류로 인한 이상치가 존재하는지 여부 및 상관관계를 파악하기 위해 Fig. 8과 같이 변수들 간 산포도를 파악해 본 결과, 큰 이상치는 발견되지 않았지만, 상관계수가 0.8에 근접하거나 그 이상의 값을 보이는 경우 변수간 뚜렷한 상관성을 확인할 수 있었다.
3.2 데이터 처리
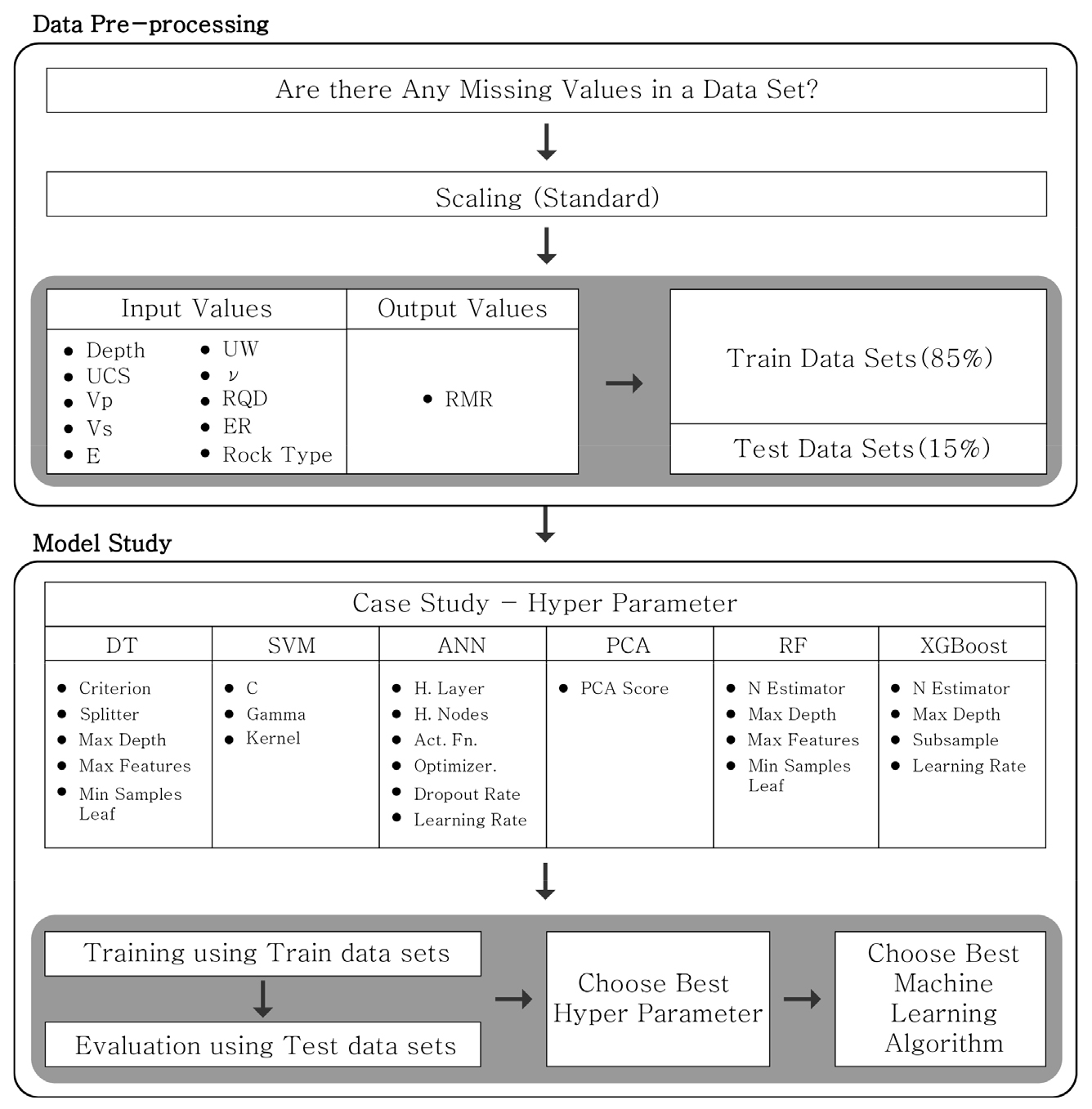
터널설계 특성마다 필요한 지반조사 데이터의 종류 및 세부적인 규격이 다를 수 있으므로 본 연구를 위한 머신러닝 수행과정은 Fig. 9와 같이 요약된다. 머신러닝 학습 이전에 데이터 전처리 과정(preprocessing)이 필수적이며, Fig. 9에 나타난 바와 같이 무결성 검사, scaling, 데이터셋 구성의 세 부분으로 나누어 수행하였다. 사람의 기록 오류, 기계의 오차 등 다양한 원인으로 발생한 데이터 결측치나 손실 여부를 판단하는 무결성 검사를 통해 결손 데이터를 모두 삭제하였다. 또한 단위 차이로 인한 학습의 왜곡을 방지하기 위해 모든 변수의 단위를 동일한 스케일로 변환하는 scaling을 수행하였으며, 각 변수 값의 범위를 평균 0, 분산 1인 분포로 표준화하는 standard scaling을 적용했다. 이렇게 전처리 된 데이터중 학습(train) 및 검증(validation) 데이터로 85%, 나머지 15%는 확정된 모델의 시험(test) 데이터로 사용하였다.
검증 데이터의 선정은 일정 비율에 따라 무작위로 이루어지므로, 경우에 따라서는 선정된 검증 데이터에 편향이 발생할 수 있으며 모델 평가의 신뢰성이 저하될 수 있다. 이러한 단점을 보완하고자 k-fold 교차 검증(cross validation)을 적용하였다. k-fold 교차 검증은 학습 및 검증 데이터 셋을 k개의 소 데이터셋으로 분할하고, 각각의 소 데이터셋들을 최소 한 번씩 돌아가면서 검증(validation) 데이터로 사용하는 방법이다. 각 경우의 검증데이터 마다 동일한 성능 평가지표를 사용한 모델을 평가하여 한 번의 학습 당 k개의 지표가 산출되며 이 값들의 평균을 이용하여 모델의 성능을 평가하게 된다. 본 연구에서는 k값을 3으로 하는 3-fold 교차 검증을 적용하였다.
4. 결과분석 및 토론
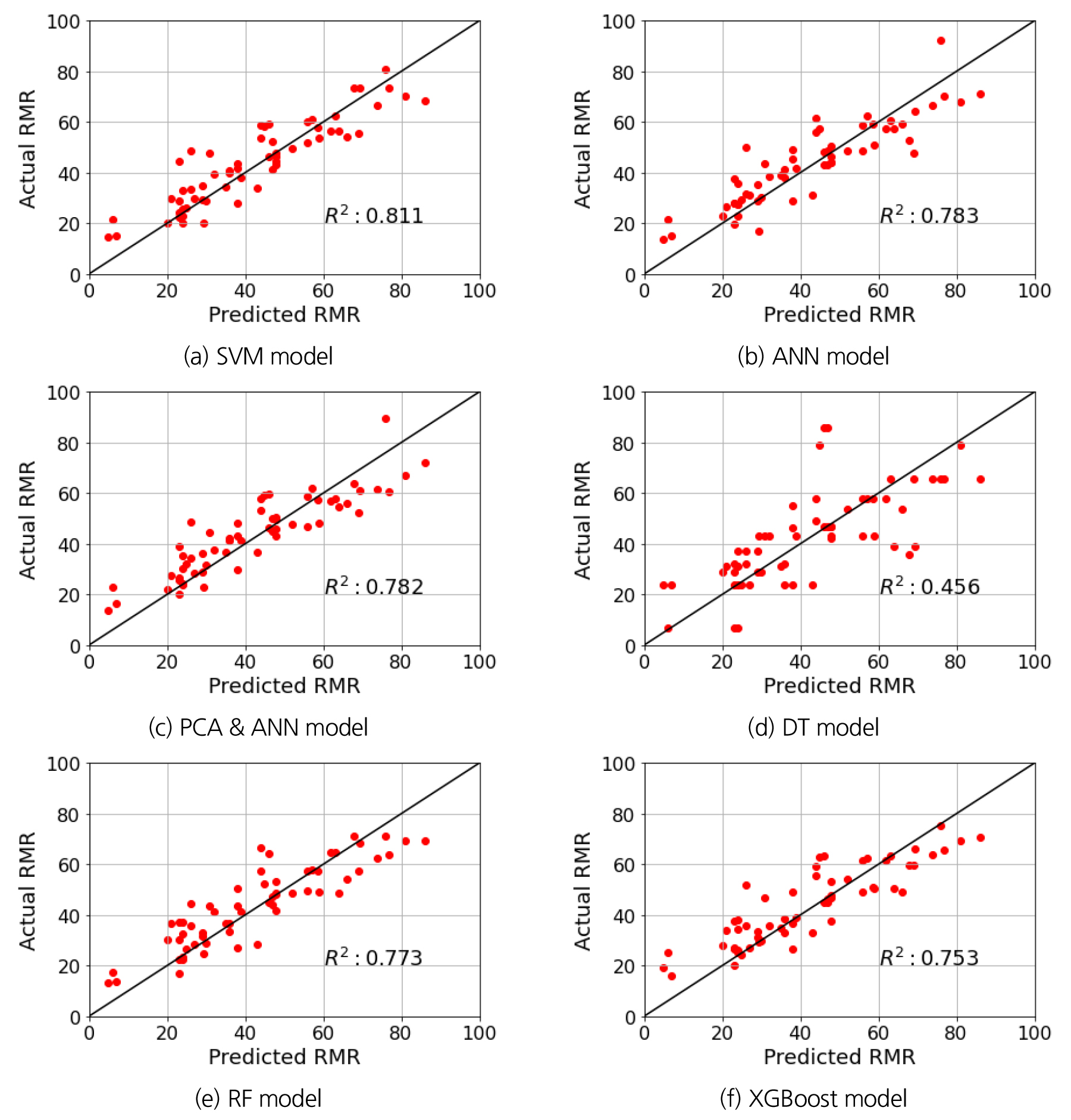
모델 생성 및 학습은 파이썬 환경에서 Scikit-learn, Tensorflow, Keras와 같은 라이브러리를 활용하여 수행하였으며, 각 머신러닝 알고리즘별 최적 초매개변수를 찾기 위해 전술한 Tables 1, 2, 3, 4, 5, 6에서 설정된 초매개변수의 변화에 따라 학습된 모델의 MAE (mean absolute error, 평균절대오차) 및 결정계수(R2)값을 산출하여 성능을 비교 및 분석하였다. Fig. 10과 Table 9는 그 결과를 나타낸 것으로, 10개의 입력인자와 1개의 출력인자를 사용했을 때 머신러닝 알고리즘별 최적의 초매개변수와 검증오차(validation error), 시험오차(test error) 및 결정계수 값을 나타낸 것이다. 가장 우수한 성능을 보이는 모델은 SVM이었으며, 최저성능을 나타낸 DT 모델을 제외한 4개 모델(ANN, PCA & ANN, RF, XGBoost)이 비슷한 성능을 보였다. SVM은 MAE 및 결정계수 값이 각각 6.43 및 0.81로 나타났는데, 이것은 본 연구에서 학습된 SVM 모델로 시추공 암석샘플에 대한 RMR값을 평가 시 실제 RMR값과의 오차가 6.4라는 의미이며, 예를 들어, 실제 RMR값이 50이라면 본 SVM 모델로 예측 시 RMR값이 약 43~57 사이에서 결정된다고 할 수 있다. RMR에 의한 암반등급이 20점 간격 또는 상황에 따라 10점 간격으로 구분된다는 것을 고려할 때, DT 모델을 제외한 SVM 등의 여타 모델의 암반등급 평가 정확도는 일반적으로 수용할 만한 수준인 것으로 사료된다. 또한 SVM의 이러한 성능은 MAE 및 결정계수 값이 10.28 및 0.46인 DT에 비해 향상된 것으로(MAE 37% 감소, 결정계수 56% 증가) 분석되었다. 한편 MAE를 기준으로 판단할 경우 중간 성능을 나타낸 4개의 모델 중 RF 모델이 가장 양호한 결과를 보였으며, 결정계수를 기준으로 판단할 경우 상기 4개 모델 중 ANN이 가장 우수한 결과를 보였다.
Table 9.
RMR prediction performances and optimal hyperparameter by machine learning models (with Vs as an input parameter)
Fig. 10은 학습된 모델에 시험(test) 데이터를 사용하여 예측된 RMR (predicted RMR)값과 실제 RMR (actual RMR)값을 비교하여 산포도를 도시하고, y = x 직선을 기준으로 결정계수 값을 산출하여 나타낸 것이다. 최저 성능을 보이는 DT 모델을 제외한 나머지 5개 모델의 산포도가 y = x에 모여 있으며, 이러한 경향은 결정계수 값이 1에 가까워질수록 더욱 두드러짐을 확인할 수 있다.
오차는 여러 원인에 의해 발생할 수 있는데, 본 연구에서 가장 주요한 원인으로는 다음과 같이 2개를 고려해볼 수 있다. 첫 번째는 입력인자의 적정성이다. 사용된 입력인자들이 출력인자인 RMR을 예측하기에 충분한 정보를 내재하지 못한 경우 학습 효과가 감소할 수 있다. RMR은 RQD, UCS, 불연속면 간격, 불연속면 상태, 지하수 상태, 불연속면의 상대적 방향에 의해 결정되는데, 이 중 RQD 및 UCS는 입력인자로 포함되어 있다. 그러나 불연속면의 상태나 지하수에 대한 정보를 반영할 수 있을 만한 입력항목은 전기비저항 탐사자료 밖에 포함되지 않았기 때문에 오차의 중요한 원인이 될 수 있으며, 향후 탄성파탐사 결과 등을 추가로 확보한다면 보다 양호한 결과가 도출되리라 판단된다.
두 번째 원인은 데이터의 다양성이다. 머신러닝 모델은 학습된 데이터를 기반으로 하여 예측을 하기 때문에 다양한 조건 및 상황에서 획득한 데이터가 골고루 존재할수록 모델의 예측력이 향상되지만, 반대의 경우에는 예측 성능이 감소하며, 과적합 및 편향성이 증가하게 된다. 본 연구에서 활용한 데이터의 84.9%는 편마암 지역에서 수집되었으며, 9.6%는 화강암, 3.5%는 안산암 지역에서 수집되었다. 따라서 본 연구의 결과는 편마암 지역에서의 암반분류에는 적합하지만, 이외의 암종에 대해서는 예측력이 감소할 수 있다. 향후 다양한 암종에 대한 데이터 수집이 이루어진다면 보다 포괄적이고 신뢰성 있는 RMR 예측이 가능할 것으로 기대된다.
학습데이터의 과적합 여부를 판단하기 위해, 검증 데이터에 대한 MAE와 시험 데이터에 대한 MAE 비율을 검토하였는데, SVM이 1.042로 가장 낮고, PCA & ANN, ANN, XGBoost, RF, DT 순으로 MAE 비율이 점차 증가하였다. 따라서 SVM과 ANN 기반의 모델들이 상대적으로 DT 기반의 모델보다 과적합의 위험이 낮다고 판단된다.
높은 상관성을 보이는 Vp 및 Vs 중 Vs를 입력인자에서 제외하고 학습한 경우, Table 9의 결과와 비교했을 때 DT 모델을 제외한 나머지 5개 모델의 시험오차 및 결정계수 값에서 평균적으로 1~3%의 차이가 발생했으며, 전반적으로 비슷하거나 더 저조한 성능을 보였다. 따라서 본 연구에서 사용한 데이터를 대상으로 SVM, ANN, PCA & ANN, RF, XGBoost와 같은 머신러닝 알고리즘을 활용한 학습 시 다중공선성이 모델의 예측 성능에 큰 영향을 미치지 않는다는 것을 확인할 수 있다.
5. 결 론
본 연구에서는 시추조사 데이터를 종합적으로 고려하여 RMR 평가를 보다 신뢰성 있게 할 수 있는 머신러닝 예측 모델을 개발하였다. 이를 위해 13개 터널 현장에서 총 397개의 암반분류 데이터셋을 6개의 머신러닝 알고리즘으로 분석하여 그 결과를 비교하였다. 이러한 과정을 통해 도출된 주요 결론은 다음과 같이 요약할 수 있다.
최적의 암반분류 예측 모델을 개발하기 위해 Decision Tree (DT), SVM, ANN, PCA & ANN, Random forest (RF), XGBoost 등 총 6개의 머신러닝 알고리즘을 적용하여 시험데이터에 대한 MAE (평균절대오차)를 비교한 결과, SVM 모델이 6.43, 결정계수는 0.81로 최고의 학습 성능을 나타냈다.
DT 모델을 제외한 나머지 5개 머신러닝 모델 간 시험오차의 범위가 7.1~7.3으로 그 차이가 1 미만이며, SVM과의 차이도 크지 않기 때문에, 향후 다양한 지반조건에서 탄성파 탐사자료 및 현장 시험결과가 추가된다면 오차를 더 감소시킬 수 있으며, 그에 따라 최상의 모델도 변경될 수 있다고 판단된다.
최근 국토교통부 등 정부기관에서는 건설사업데이터 기반의 새로운 비즈니스 창출과 관련산업 활성화를 지원하기 위해 각 기관에서 생성 또는 취득한 공공데이터를 공개하고는 있지만, 현장별로 정보의 형태(그림, 문서, 도면 등), 포함된 정보의 종류 및 정리 방식에 많은 차이가 있어서 이를 활용하기 위해서는 많은 시간과 노력이 필요한 실정이다. 특히 시공현장에서 작성되는 자료 중 막장관찰도 등과 같은 수기자료는 현장에 따라 대외공개를 꺼리는 경향이 있어, 이러한 사항이 개선된다면 보다 정밀하고 향상된 연구결과가 도출될 수 있으리라 사료된다.
본 연구의 결과는 암반분류 시 전문가의 판단을 보조하기 위해서 사용될 수 있으며, 향후 시추조사, 탄성파 탐사, 전기비저항 탐사 등과 같은 데이터에 더하여 해당 현장의 실제 막장 RMR 평가 결과도 추가적으로 확보하여 미시추 구간의 암반등급 산정, 지보패턴 산정, 발파패턴 산정 및 보조공법 적용 여부 등을 자동화하거나 자동화에 도움을 줄 수 있는 기초 후속 연구를 진행할 계획이다.