A preliminary study for numerical and analytical evaluation of surface settlement due to EPB shield TBM excavation

Jun-Beom An; Seok-Jun Kang; Jung Joo Kim; Kyoung Yul Kim; Gye-Chun Cho

doi:10.9711/KTAJ.2021.23.3.183

Preview

Research Paper

Journal of Korean Tunnelling and Underground Space Association. 31 May 2021. 183-198
https://doi.org/10.9711/KTAJ.2021.23.3.183

A preliminary study for numerical and analytical evaluation of surface settlement due to EPB shield TBM excavation

토압식 쉴드 TBM 굴착에 따른 지반침하 거동 평가에 관한 해석적 기초연구

Jun-Beom An¹

Seok-Jun Kang¹

Jung Joo Kim²

Kyoung Yul Kim³

Gye-Chun Cho⁴^*

안 준범¹

강 석준¹

김 정주²

김 경열³

조 계춘⁴^*

¹Ph.D. Student, Dept. of Civil and Environmental Engineering, KAIST

²Researcher, Next Generation Transmission & Substation Laboratory, KEPCO Research Institute, KEPCO

³Chief Researcher, Next Generation Transmission & Substation Laboratory, KEPCO Research Institute, KEPCO

⁴Professor, Dept. of Civil and Environmental Engineering, KAIST

¹학생회원, 한국과학기술원 건설및환경공학과 박사과정

²정회원, 한전 전력연구원 차세대송변전연구소 일반연구원

³정회원, 한전 전력연구원 차세대송변전연구소 수석연구원

⁴정회원, 한국과학기술원 건설및환경공학과 교수

^{*Corresponding Author}

ABSTRACT

The EPB (Earth Pressure Balanced) shield TBM method restrains the ground deformation through continuous excavation and support. Still, the significant surface settlement occurs due to the ground conditions, tunnel dimensions, and construction conditions. Therefore, it is necessary to clarify the settlement behavior with its influence factors and evaluate the possible settlement during construction. In this study, the analytical model of surface settlement based on the influence factors and their mechanisms were proposed. Then, the parametric study for controllable factors during excavation was conducted by numerical method. Through the numerical analysis, the settlement behavior according to the construction conditions was quantitatively derived. Then, the qualitative trend according to the ground conditions was visualized by coupling the numerical results with the analytical model of settlement. Based on the results of this study, it is expected to contribute to the derivation of the settlement prediction algorithm for EPB shield TBM excavation.

Keywords

EPB shield TBM

Surface settlement

Face pressure

Tail void backfill

Injection pressure

토압식 쉴드 TBM 공법은 커터헤드 후면 챔버에 버력을 채워 막장 안정성을 확보하는 공법으로, 연속적인 굴착 및 지보를 통해 지반 변형을 억제하는 것으로 알려져 있다. 하지만 여전히 지반 조건, 터널 크기, 그리고 시공 조건에 의해 무시할 수 없는 지반 침하가 발생하는 실정이다. 따라서 지반침하 영향인자에 의한 침하 거동을 명확하게 이해하고 이를 기반으로 시공 중 발생 가능한 지반침하를 평가할 필요가 있다. 본 연구에서는 토압식 쉴드 TBM 시공 시의 지반침하 주요 영향인자들과 침하 발생 메커니즘이 반영된 해석 모델(analytical model)을 제시하였고, 시공 중 조절 가능한 인자들에 대한 매개변수 해석을 수치해석 기법을 통해 수행하였다. 수치해석 결과를 통해 시공 조건에 의한 침하 거동을 정량적으로 도출하였으며, 침하 해석 모델과의 연계를 통해 지반 조건에 따른 정성적인 경향성을 도시하였다. 본 연구 결과를 통해 토압식 쉴드 TBM 굴착에 의한 침하예측모델 도출에 기여할 것으로 기대된다.

키워드

토압식 쉴드 TBM

지반침하

막장압

테일 보이드 뒷채움

뒷채움 주입압력

MAIN

1. 서 론
2. 토압식 쉴드 TBM 굴착에 의한 지반침하 메커니즘
3. 수치해석을 통한 토압식 쉴드 TBM 굴착 모사
3.1 토압식 쉴드 TBM 굴착 모델링
3.2 수치해석 수행 및 결과 분석
4. 수치해석 결과 기반 침하 모델 검토
5. 결 론

1. 서 론

기존의 발파를 통한 터널 굴착과 비교하여 TBM (Tunnel Boring Machine) 공법은 기계적으로 직접 지반을 파쇄하여 상대적으로 소음과 진동이 적게 발생하여 안전하며 여굴이 적고 균등한 굴착 단면을 획득할 수 있어 효율적인 것으로 알려져 있다. 또한 NATM 공법과 비교하여 굴착과 버력 반출, 그리고 지보 작업이 연속적으로 수행되기 때문에 경제적인 시공이 가능하다. TBM 공법은 주면 지보 수행 여부에 따라 개방형 TBM과 쉴드 TBM으로 나뉘며, 쉴드 TBM은 굴진면 지보 수행 여부와 추진을 위한 반력의 획득 방식에 따라 다양하게 분류된다(ITA WG Mechanized Tunneling, 2000). 이 중 토압식(Earth Pressure Balanced, EPB) 쉴드 TBM은 추진 잭을 통해 전진하며, 쉴드를 통한 주변 지보에 추가로 커터헤드 후면의 챔버에 굴착 버력을 채워 막장면의 안정성을 확보하는 공법으로, 국내 쉴드 TBM 시공 사례의 주를 이룬다(Lee et al., 2011).

토압식 쉴드 TBM 공법은 연속적이고 효율적인 굴착을 통해 지반의 변형을 최소화하는 것으로 알려져 있지만, 다양한 요인에 의해 지반침하가 발생하는 실정이며, 이로 인한 지상구조물과 지중매설물의 손상으로 인해 경제적 손실과 민원이 발생한다. 토압식 쉴드 TBM 굴착에 의한 지반침하의 영향인자는 터널의 직경과 깊이(Melis et al., 2002; Chakeri et al., 2013), 지반 종류(Selby, 1988), 막장압(Lambrughi et al., 2012; Comodromos et al., 2014), 테일 보이드 뒷채움 주입압력과 주입시점(Suwansawat and Einstein, 2007) 등 그 종류가 다양하게 제시된 바 있다. 따라서 토압식 쉴드 TBM 굴착에 의한 지반침하 메커니즘을 이해하여 주요 영향인자를 규명하고, 각각에 의한 침하 거동을 이해할 필요가 있다. 본 연구에서는 토압식 쉴드 TBM 굴착에 의한 지반침하 모사를 위한 해석적 해(analytical solution)을 제시하고, 각 인자들의 침하 영향을 정량적으로 파악하기 위해 수치해석을 통한 매개변수 해석을 수행함으로써 침하 거동을 정량적으로 평가하고자 하였다.

2. 토압식 쉴드 TBM 굴착에 의한 지반침하 메커니즘

터널 굴착을 수행하게 되면 대상 지반은 그 종류에 따라 세부적인 양상은 다르나 기본적으로 응력 재분배에 의해 점진적인 변형을 겪는다(Kirsch, 1898; Terzaghi, 1943). 이에 따라 재래식 터널 굴착 공법은 지반의 변형이 과도하게 발생하기 전에 굴진면 및 터널 주면에 지보재를 설치하여 지반 변위를 제어하도록 설계된다. 따라서 일반적인 터널 굴착 시 지반침하는 설계 오류 혹은 시공 오류에 의해 굴착이 과도하게 발생하는 경우, 그리고 지보 수행이 미흡하거나 지연되는 경우에 발생하게 되며, 달리 말하면 터널 지보와 지반 사이에 시간적, 공간적 관점에서 간극(gap)이 발생하는 경우 지반침하가 발생한다고 할 수 있다. 쉴드 TBM 굴착 역시 동일한 지반 변형 메커니즘을 따르며, 실제 굴착 직경과 터널 단면간의 시간적, 공간적 간극을 Gap parameter로 정의하고 이로 인해 야기된 지반의 탄성 및 소성 변형을 지반 손실(ground loss)로 정의하여 이론적으로 분석되었다(Lo and Rowe, 1982; Rowe et al., 1983). 쉴드 TBM 시공에 의해 발생하는 지반 손실은 세 가지 경우로 구분할 수 있다(Lee et al., 1992). 우선 막장 지보가 적절하며 TBM과 벽체의 배열이 선형인 경우 쉴드 TBM의 테이퍼링(tapering)과 커터헤드의 여굴(over-excavation), 그리고 후방 세그먼트(segment lining) 벽체의 테일 보이드(tail void)에서 필연적으로 발생하는 지반손실과, 막장 지보가 부적절한 경우 지반이 갱내에 초과 인입하여 발생하는 지반손실, 그리고 TBM과 벽체 배열이 연약 지반 등의 이유로 선형을 이루지 못한 경우 발생하는 과도한 굴착에 의한 지반손실이 존재한다. 정리하자면, 쉴드 TBM 시공에 의한 지반침하의 주요 영향인자는 대상 지반의 물성 및 강도특성, 터널의 직경과 깊이, 막장면 지보 특성, 뒷채움 지보 특성, 그리고 과도한 굴착 및 지하수 유출 등의 설계 외 사고와 같이 총 다섯 가지로 정리할 수 있다.

지중 터널 굴진방향과 직교하는 횡단면에서 지표면의 지반침하 형상은 침하 트라프(settlement trough)로 정의되며, 이는 가우시안 분포 곡선(Gaussian distribution curve)을 따르는 것으로 알려져 있다(Peck, 1969; O’Reilly and New, 1982). 가우시안 분포 곡선으로부터 침하 트라프의 형상( $S$ )을 다음과 같이 나타낼 수 있으며, 이를 적분하여 침하 트라프의 단위체적( $V_{S}$ )을 아래와 같이 구한다.

(1)

S = S_{m a x} ∙ \exp (- y^{2} / 2 i^{2})

(2)

V_{S} = \sqrt{2 π} i S_{\max}

이때 $S_{m a x}$ 는 해당 지점의 최대 침하량, $y$ 는 터널 중심으로부터 거리, $i$ 는 터널 중심으로부터 침하 트라프 변곡점의 거리를 의미한다. 침하 트라프의 변곡점( $i$ )은 일반적으로 아래와 같은 관계를 갖는 것으로 알려져 있다(O’Reilly and New, 1982).

(3)

i = K z_{0}

이때 $z_{0}$ 는 터널의 굴착 깊이, $K$ 는 침하 트라프 변수(trough width parameter)이며, 침하 트라프 변수는 지반의 종류에 따라 결정되며 점성토에서 0.5, 사질토와 자갈에서 0.25의 값을 갖는 것으로 제안되었다(O’Reilly and New, 1982). 이후 현장계측 및 실험을 통해 평균적으로 점성토에서 0.5, 사질토 및 자갈에서 0.35의 값을 갖는 것으로 확인된 바 있다(Mair and Taylor, 1997). 이로부터 굴착 시 발생한 지반침하를 정량적으로 평가하기 위하여 침하 트라프의 횡단면 단위체적과 설계 터널 면적의 비를 체적 손실( $V_{L}$ ; volume loss)로 정의하여 설계 및 시공 단계에서 활용되고 있다.

(4)

V_{L} = V_{S} / (\frac{π D^{2}}{4})

이때 $D$ 는 터널의 직경을 의미한다. 터널 종단면 침하 트라프는 쉴드 TBM이 굴진함에 따라 점차 누적되어 이론적으로 누적 가우시안 분포 곡선 형태를 따르는 것으로 알려져 있다(Attewell and Woodman, 1982). 하지만 종단면 침하 곡선은 쉴드 TBM 굴착 공정단계별로 직접적인 영향을 받기 때문에 정형화한 형태로 파악하기 어려운 한계를 갖는다. 일반적으로 쉴드 TBM 굴착에 의해 발생하는 종방향 지반침하는 전방침하, 막장침하, 쉴드침하, 후방침하, 장기침하로 분류할 수 있다(Sugiyama et al., 1999).

앞서 터널 설계단면을 기준으로 Gap parameter에 의해 발생하는 지반의 변형을 지반 손실로 정의하였다. 이로부터 각 시공 단계별 지반손실의 총합( $G_{L}$ )을 횡방향 침하 트라프의 단위체적( $V_{S}$ )과 같다고 가정하였다. 이때 굴착 위치로부터 멀리 떨어진 곳에서 발생하는 전방침하와 쉴드의 형상에 의한 스티어링 갭(steering gap)에 의해 발생하는 쉴드침하는 그 영향이 상대적으로 작기 때문에 본 연구에서는 고려하지 않았으며, 굴착 중 교란에 의해 장기간에 걸쳐 발생하는 장기침하는 상대적으로 발생량이 적을 뿐만 아니라 점성토의 압밀에 의해 한정적으로 발생하기 때문에 마찬가지로 고려하지 않았다. 결과적으로, 아래의 식과 같이 막장면 지반손실( $G_{f}$ )과 후방 지반손실( $G_{t v}$ )로부터 최대 침하량( $S_{m a x}$ )을 도출하였으며, 이론적으로 반영하기 어려운 각 단계별 지반손실간의 의존성과 교란에 의한 체적 변동을 반영하기 위해 보정 계수( $α, β$ )를 도입하였다.

(5)

V_{S} = V_{L} \frac{π D^{2}}{4} = \sqrt{2 π} i S_{\max} ≅ [α G_{f} + β G_{t v}]

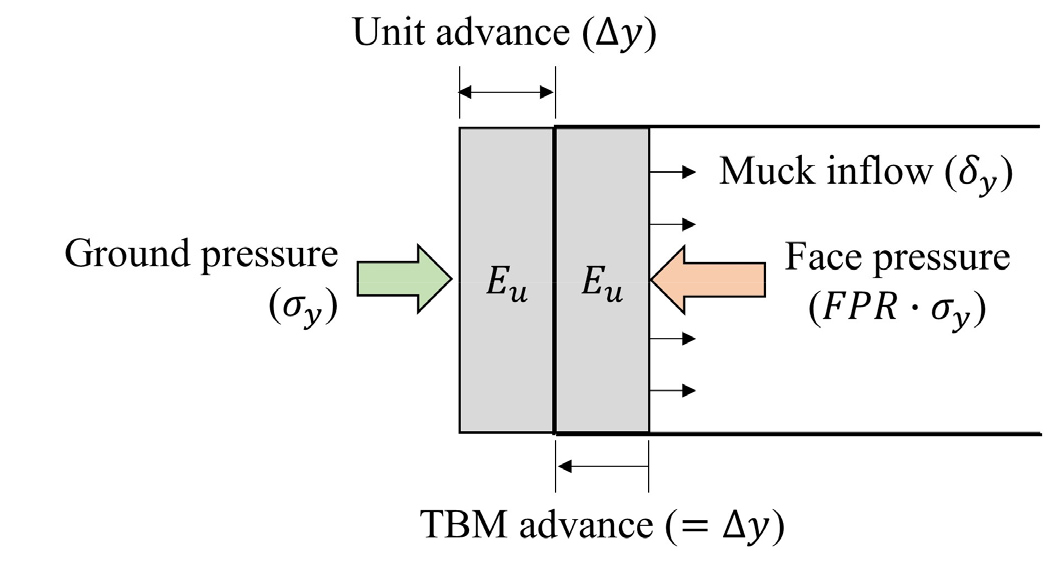
막장면 지반손실은 쉴드 TBM 막장면 전방 지반의 굴진 축방향 변형률과 굴착 면적의 곱에 해당한다(Lee et al., 1992). 쉴드 TBM이 굴진하는 동안 막장 전방의 단위 굴진거리( $∆ y$ , m)에 해당하는 지반은 막장압(face pressure, kPa)과 외부 토압( $σ_{y}$ , kPa) 사이의 응력 평형과 무관하게 굴착이 수행된다. 막장압이 토압보다 작게 설정되어 응력 평형이 유지되지 않으면 단위 굴진 거리만큼 굴진하는 동안 전방의 다음 단위 굴진거리에 해당하는 지반이 압축에 의해 이번 굴진 단계에서 추가로 인입하게 된다. 반면 막장압이 토압보다 크게 설정되는 경우 단위 굴진거리만큼 굴진하는 동안 현재 단위 굴진거리에 해당하는 지반이 압축되어 버력이 적게 발생한다. 이때 굴착 버력 유입은 굴착 면적에 대해 균등하게 발생하는 것으로 가정하였다. 마찬가지로 유입된 버력의 체적을 굴착 면적으로 나누어 지반 인입량( $δ_{y}$ , m)으로 정의하였고 이를 단위 굴진거리에 대응하여 막장면에서의 지반 변형률을 도출하였다(Fig. 1).

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F1.jpg

Fig. 1

Schematic diagram of ground loss due to excavation face instability

토압식 쉴드 TBM은 전응력(total stress)을 기준으로 막장압을 재하하며 지반을 통째로 굴착하기 때문에 지반의 비배수 탄성계수( $E_{u}$ , kPa)를 사용하였다. 이를 통해 시공 불량에 의한 누수와 구분하여 시공 중 막장면에서의 지반 손실을 아래 식과 같이 유도할 수 있다.

(6)

δ_{y} = ∆ y + ∆ y ∙ (\frac{σ_{y} - F a c e p r e s s u r e}{E_{u}}) = ∆ y ∙ \{1 + \frac{(1 - F P R) σ_{y}}{E_{u}}\}

(7)

G_{f} = (π a^{2}) ∙ \frac{δ_{y}}{∆ y} = (π a^{2}) ∙ \{1 + \frac{(1 - F P R) σ_{y}}{E_{u}}\}

이때 $π a^{2}$ 는 굴착 면적에 해당하여 쉴드 TBM의 반지름( $a$ , m)을 사용하였다. 그리고 막장압과 토압의 비를 $F P R$ (-)로 나타내어 식을 단순화시키고자 하였다.

후방 지반손실은 테일 보이드 뒷채움 그라우팅재의 주입 면적과 주면 방향 변형률의 곱으로 설정하였다. 또한 적용의 편의를 위해 뒷채움재는 등방성으로 압축된다고 가정하였다.

(8)

G_{t v} = π [a^{2} - (a - d_{t v})^{2}] \times \frac{σ_{z} - σ_{g r t}}{M_{g r t}}

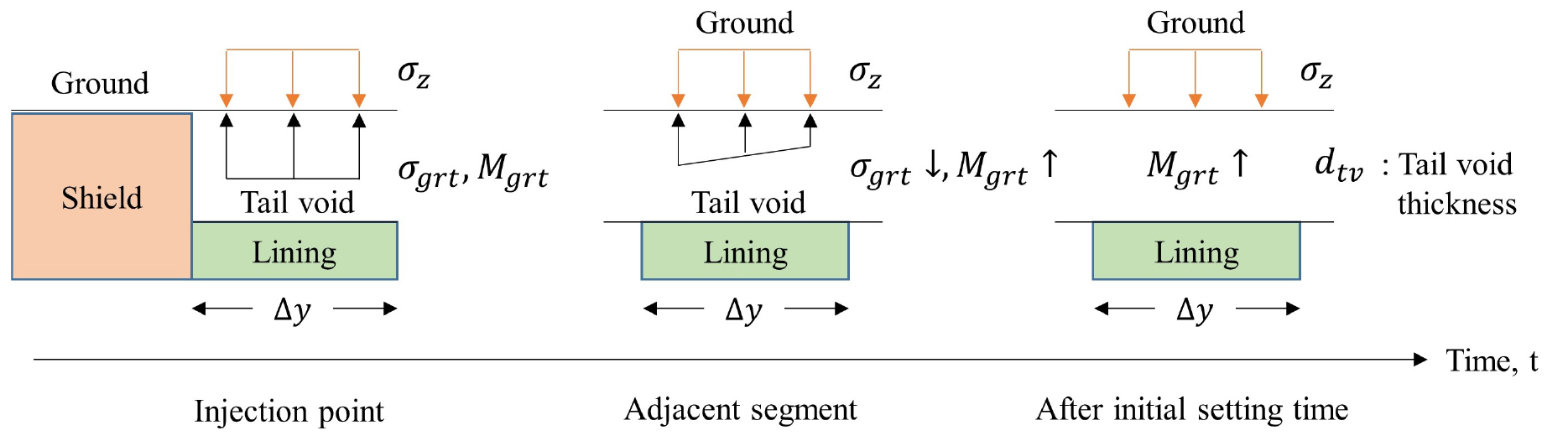
이때 $d_{t v}$ 는 테일 보이드의 두께(m)에 해당하며 $σ_{z}$ 는 지반의 연직방향 전응력(kPa)을 의미한다. 실제 시공 시 뒷채움재는 이론적인 테일 보이드의 체적보다 약 20% 이상 초과하여 주입하도록 권장되고 있으나(Suwansawat and Einstein, 2007; GEO Report No. 298, 2014), 지반과의 교반을 고려하지 않고 테일 보이드 부피의 변형을 나타내기 위하여 테일 보이드의 두께를 그대로 사용하였다. Fig. 2와 같이 그라우팅재의 주입압력( $σ_{g r t}$ , kPa)과 구속탄성계수( $M_{g r t}$ , kPa)는 주입 이후 시간에 따라 변화하지만, 각 현장마다 다르게 설계되는 그라우팅재의 물성과 거동을 정확하게 모사할 수 없는 한계를 갖는다.

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F2.jpg

Fig. 2

Schematic diagram of tail void backfill grouting properties transition

따라서 이러한 비정상 상태(transient state)를 직접 모사하는 대신 보수적인 관점에서 그라우팅재의 구속탄성계수는 초기 경화 시(initial setting time)의 값을 적용하도록 설정하였다. 보다 정확한 적용을 위하여 테일 보이드 뒷채움 특성을 고려한 수치적(numerical) 이해가 동반될 필요가 있다.

결과적으로 식 (5), 식 (7), 식 (8)로부터 쉴드 TBM 굴착에 따른 터널 중심축에서의 최대 침하량( $S_{m a x}$ )을 아래 식과 같이 나타낼 수 있다. 이때 1,000은 최대 침하량의 단위를 mm로 맞추기 위해 추가되었다.

(9)

S_{\max} ≅ \frac{1000}{\sqrt{2 π} ∙ K z_{0}} \times [α ∙ (π a^{2}) ∙ \{1 + \frac{(1 - F P R) σ_{y}}{E_{u}}\} + β ∙ π [a^{2} - (a - d_{t v})^{2}] \times \frac{σ_{z} - σ_{g r t}}{M_{g r t}}]

주요 영향 변수로는 터널 설계조건에 해당하는 터널의 중심깊이( $z_{0}$ , m), 쉴드 TBM의 굴착직경( $2 a$ , m)과 지반 조건에 해당하는 침하 트라프 변수( $K$ ), 비배수 탄성계수( $E_{u}$ , kPa), 그리고 굴착 조건에 해당하는 단위 굴진거리( $∆ y$ , m), 막장압 비( $F P R$ ), 뒷채움재 주입압력( $σ_{g r t}$ , kPa) 및 초기 경화시점의 구속탄성계수( $M_{g r t}$ , kPa), 테일 보이드 두께( $d_{t v}$ , m)가 고려되었다. 또한 지반의 연직 전응력( $σ_{z}$ , kPa)과 수평 전응력( $σ_{y}$ , kPa)은 지반의 단위중량과 굴착 깊이에 해당하는 지층의 내부 마찰각을 통해 도출할 수 있다.

3. 수치해석을 통한 토압식 쉴드 TBM 굴착 모사

앞서 토압식 쉴드 TBM 굴착에 의해 발생 가능한 지반침하의 메커니즘을 이해하고 주요 영향인자에 따른 침하 발생 거동에 대한 해석적 해를 도출하였다. 도출된 모델의 활용을 위해서는 보정계수( $α, β$ )가 굴착 조건에 따라 어떻게 변화하는 지를 파악할 필요가 있다. 따라서 수치해석을 수행하여 보정계수를 정량적으로 도출하고, 굴착에 의한 침하 거동을 보다 정밀하게 평가하고자 하였다.

3.1 토압식 쉴드 TBM 굴착 모델링

수치해석은 굴착 과정을 단계별로 모사하기 용이한 FDM 기반 상용 프로그램인 Itasca 사의 FLAC3D를 사용하였다. 수치해석 모델링의 검증을 위해 토압식 쉴드 TBM을 사용한 테헤란 지하철 7호선 공사의 시공 데이터를 활용하였다(Chakeri et al., 2013). 본 지반은 지하수가 존재하지 않고 점토와 실트, 자갈 등이 혼재된 네 개의 지층으로 구성되어 있다. 각각의 물성은 Table 1에 도시하였다.

Table 1.

Ground properties of target site (Chakeri et al., 2013)

Ground layer	Classification (BSCS)	Thickness (m)	Unit weight (kg/m³)	Cohesion (kPa)	Internal friction angle (degree)	Elastic modulus (MPa)	Poisson's ratio
Layer 1	Filling	1.2	1,900	29	35	15	0.30
Layer 2	ML, CL	8		40	27	30	0.35
Layer 3	GML, GCL	11.6		30	35	80	0.27
Layer 4	GWM, GML	Base		20	38	100	0.27

ML: Silt, CL: Clay, GML: Silt with gravel, GCL: Clay with gravel, GWM: Well graded silty gravel

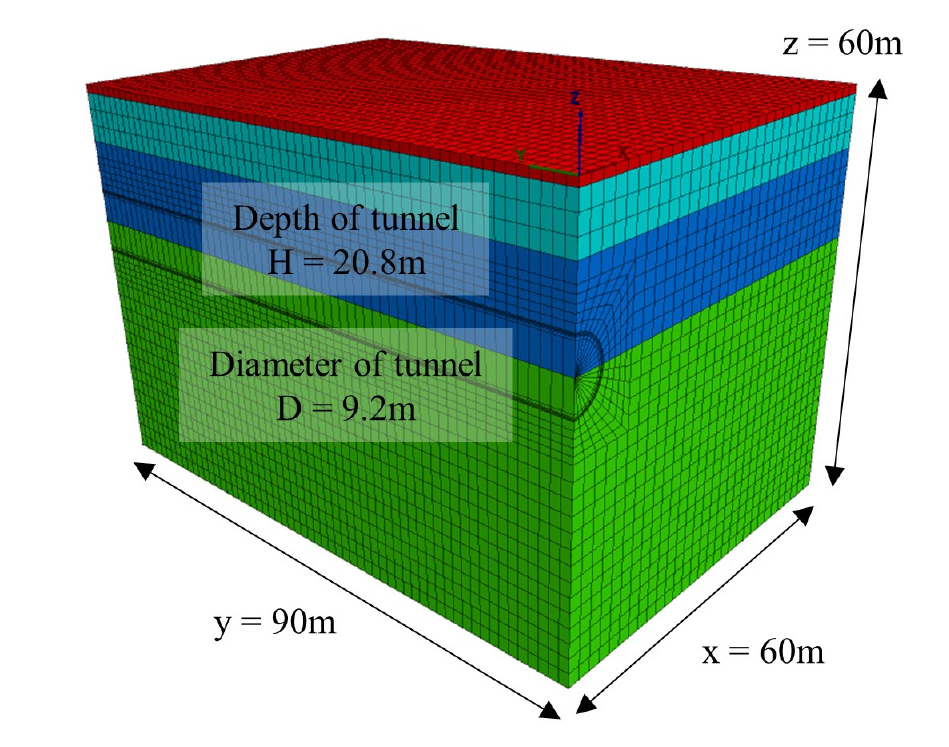
지반은 동질성(homogeneous), 등방성(isotropic), 탄소성(elasto-plastic) 거동을 보이는 것으로 보고 모어-쿨롬 모델(Mohr-Coulomb criterion)을 통해 모사하였다. 무한히 넓은 지반을 가정하기 위하여 굴착 직경(D)과 굴착 중심깊이(H)로부터 터널 굴착 축방향(y-axis)으로 90 m (>H+3D), 굴착 횡방향(x-axis)으로 60 m (~3H), 그리고 지반의 총 높이(z-axis)를 60 m (>H+4D)로 각각 설정하였다(Rodríguez, 2000; Lambrughi et al., 2012). 경계면의 노드는 모두 경계면과 직교하는 방향으로 고정되었다. 상기 사항을 적용하여 구성한 지반 모델은 Fig. 3에 도시하였다.

본 현장에 적용된 토압식 쉴드 TBM은 굴착 직경이 9.2 m, 쉴드의 길이가 9.0 m이며, 사용된 세그먼트 벽체는 외경 8.85 m, 길이(span) 1.5 m, 두께 0.35 m의 크기를 갖는다. 본 연구에서는 메쉬 설정의 편의를 위해 세그먼트 외경을 8.90 m로 적용하였다. 쉴드와 세그먼트, 그리고 테일 보이드 뒷채움 그라우트재의 물성은 Table 2에 도시하였다.

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F3.jpg

Fig. 3

Sketches of an adopted mesh: only half is shown based on x = 0

Table 2.

Input properties of structures (Chakeri et al., 2013)

	Elastic modulus (GPa)	Poisson's ratio	Unit weight (kg/m³)	Shear modulus (GPa)	Thickness (m)
Shield	200	0.25	7,840	80	0.50
Segment	27	0.2	2,400	11.25	0.35
Grouts	1	0.25	1,200	0.4	0.15

세 가지 구조물은 모두 Shell 요소로 구현되었으며(Chakeri et al., 2013; Comodromos et al., 2014), 세그먼트와 그라우트재는 두께방향 변형을 확인하기 위해 Shell 요소에 일반적인 Zone 요소를 중첩하였다. 구조물에 해당하는 Zone은 탄성 거동(Elastic model)을 적용하였다.

토압식 쉴드 TBM의 굴착의 모사는 막장압 재하와 테일 보이드 뒷채움의 두 가지가 반영되어야 한다. 우선 막장압은 막장압 비( $F P R$ ) 개념을 도입하여 터널 중심에서의 초기 수평토압을 기준으로 막장압 크기를 조절하였고(Lambrughi et al., 2012), 굴착 단면 전체에 대해 균등하게 직교하도록 재하하였다. 이 과정에서 초기 수평토압( $σ_{y}$ , kPa)은 지반의 유효연직응력( $σ_{z}^{'}$ , kPa)과 간극수압( $u$ , kPa), 그리고 내부 마찰각( $\emptyset'$ , degree)으로부터 도출된 정규압밀 토사의 정지토압계수( $K_{o}$ )를 통해 산출하였다(Jaky, 1944).

(10)

막장압 = F P R \times (K_{o} \times σ_{z}^{'} + u) = F P R \times [\{\frac{1 + 2 / 3 \sin \emptyset'}{1 + \sin \emptyset'} ∙ (1 - \sin \emptyset')\} \times σ_{z}^{'} + u]

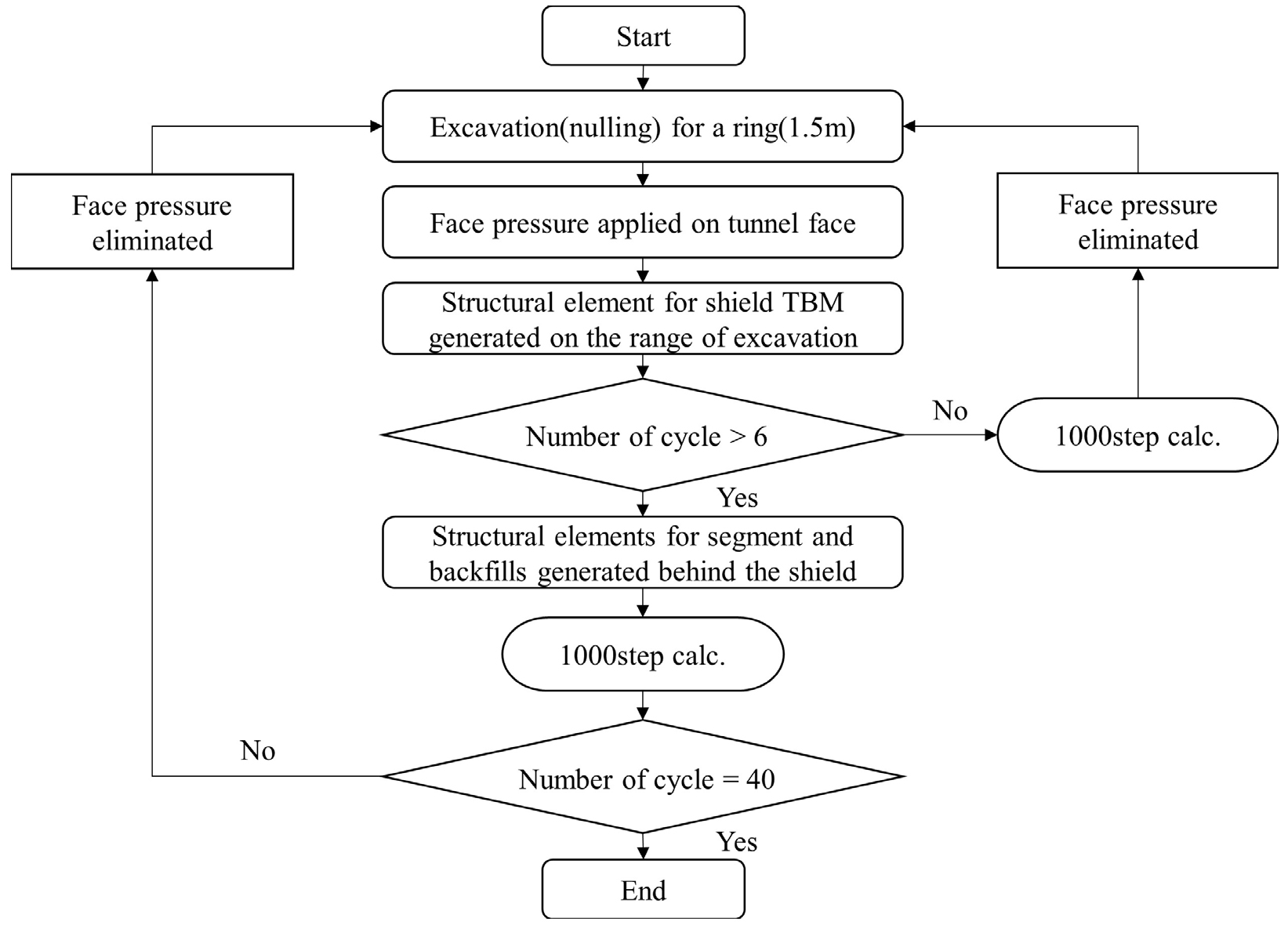
테일 보이드 뒷채움은 시간에 따라 증가하는 그라우트재의 탄성계수를 이산적으로 적용하였다. 이를 위해 평균 일일 굴진율을 세그먼트 10링으로 가정하고 5개 링 마다 탄성계수를 달리하였다. 그리고 그라우트재의 초기 경화시간은 현장마다 편차가 존재하지만 약 12시간 정도로 알려져 있으므로(Shirlaw et al., 2004), 주입 후 5개 링에서만 주입 압력을 굴착 외주면에 균등하게 직교하도록 가하였다. 결과적으로 주입 후 5개 링 마다 최종 경화 시의 탄성계수를 기준으로 2, 3, 20, 40, 55, 65, 72, 80, 83, 86, 89, 100%를 차례로 적용하였다(Lambrughi et al., 2012; Comodromos et al., 2014). 토압식 쉴드 TBM의 굴착은 밀폐형 시공(Closed mode)을 가정하여 Fig. 4와 같이 굴착과 막장압 재하, 세그먼트 벽체 생성(ring building), 뒷채움 수행의 공정을 반복하여 모사하였다. 이때 단위 굴진거리는 세그먼트 링 길이인 1.5 m에 해당하며, 쉴드 TBM의 길이 9.0 m에 해당하는 6회 반복 이후부터 벽체 생성과 뒷채움(동시주입)이 수행되었다. 각각의 굴진은 1,000 step만큼 계산이 수행되었다.

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F4.jpg

Fig. 4

Designed sequences for simulating EPB shield TBM excavation in numerical modelling

3.2 수치해석 수행 및 결과 분석

해석 수행 조건은 문헌의 테헤란 지하철 7호선 시공을 기준으로 지반 조건과 터널 설계 조건을 고정하고 토압식 쉴드 TBM의 시공 조건을 조절하도록 하였다. 우선 막장압의 범위를 설정하기 위하여 TBM 시공 및 설계 시 활용되는 막장압 산정방법을 상대적으로 단순하고 범용성이 높은 일본 지반공학회의 방법을 따라 최소 막장압( $F P_{m i n}$ )은 Rankine의 주동토압과 간극수압으로, 최대 막장압( $F P_{m a x}$ )은 정지토압과 간극수압으로 설정하였다(Jun and Kim, 2016). 즉, 최대 막장압은 $F P R$ 이 1인 경우에 해당하며, 최소 막장압은 터널 굴착 깊이에 해당하는 지반의 내부 마찰각으로부터 $F P R$ 이 약 0.6인 경우에 해당한다. 뒷채움 주입압력은 막장압과 마찬가지로 뒷채움 주입압력과 토압의 비를 주입압 비( $B P R$ )로 정의하여 조절하였다. 뒷채움 주입압력은 막장압으로 인한 후방의 과도한 교란을 방지하고 그라우트재를 충분히 주입할 수 있도록 최소 막장압에 준하는 압력을 가하도록 권장되며, 국내에서는 막장압보다 0.1~0.2 MPa 크게 주입하도록 제안되고 있다(KDS 27 25 00, 2016). 따라서 본 지반에서는 막장압보다 약 80 kPa 이상 높은 응력으로 뒷채움을 수행하기 위해 $B P R$ 을 $F P R$ 보다 0.5만큼 더 크게 설정하였다. 마지막으로 뒷채움 주입 시점은 대단면 터널에서 동시주입을 원칙으로 하며 소단면의 경우 현장 여건에 맞게 설계하도록 권장된다(KDS 27 25 00, 2016). 수치해석 수행 조건은 Table 3에 도시하였으며, 모든 해석 조건에서 뒷채움은 동시주입으로 수행되었다.

Table 3.

Numerical test conditions

Conditions	Cases	Reference
(1) BPR = FPR + 0.5, E_grt = 1.0 GPa	FPR = 0.4, 0.6, 0.7, 0.8, 0.9, 1.0, 1.2	This study
(2) FPR = 0.8, E_grt = 1.0 GPa	BPR = 0.3, 0.8, (1.3), 1.8	This study
(3) FPR = 0.8, E_grt = 2.8 GPa	BPR = 0.3, 0.8, 1.3, 1.8	This study
(4) BPR = FPR + 0.1, E_grt = 1.0 GPa	FPR = 0.6, 0.7, 0.8, 0.9, 1.0	An et al. (2021)
(5) FPR = 0.8, E_grt = 1.0 GPa	BPR = 0.6, 0.7, (0.8), (0.9), 1.0	An et al. (2021)

FPR: Face Pressure Ratio, BPR: Backfill injection Pressure Ratio

Duplicated data were put in brackets

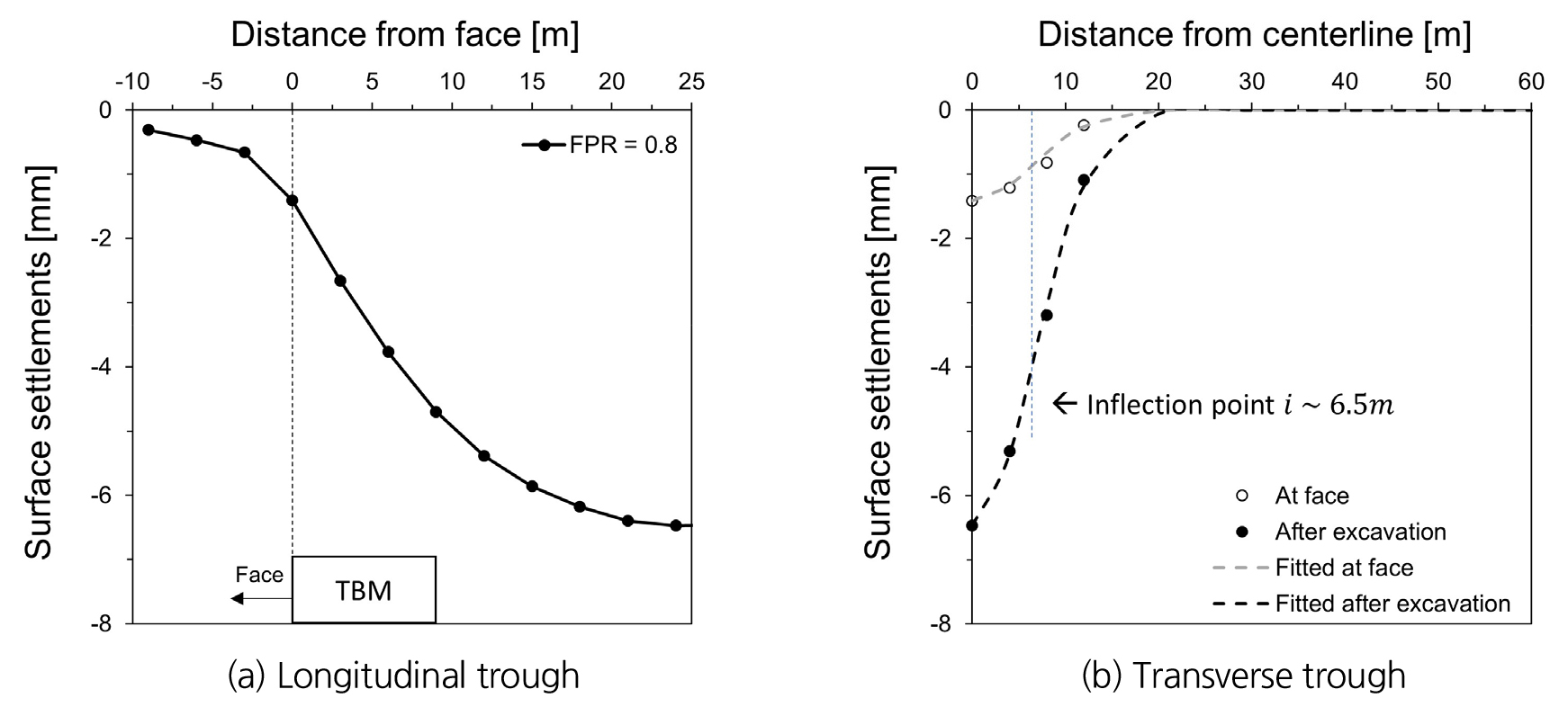
대조군에 해당하는 테헤란 지하철 7호선 시공의 경우 실제 현장에서 사용된 막장압의 수치가 불분명하나, Chakeri et al. (2013)은 막장압의 영향을 확인하기 위한 수치해석에서 최대 88 kPa의 낮은 막장압을 사용하였다. 이에 따라 본 연구의 수치해석 모델링의 검증은 최소 막장압에 해당하는 $F P R$ 이 0.6, $B P R$ 이 1.1인 경우와 실제 현장에서 계측된 최대 침하량 값을 비교하여 수행되었다. Fig. 5의 종단면 침하 트라프로부터 굴착에 의해 지표침하가 누적되어 수렴하는 양상을 확인하였다. 그리고 횡단면 침하 트라프의 형태가 가우시안 분포 곡선을 따르는 것을 확인하였고, 변곡점은 중심으로부터 6.5 m 떨어진 곳에 위치하며 침하 트라프 변수 $K$ 는 약 0.31의 값을 갖는다. 침하 트라프 변수의 값은 기존 문헌에서 밝혀진 자갈층의 값 0.35에 가까우며 대상 지반이 점토와 자갈이 혼합된 지반인 것을 고려할 때 적합한 것으로 판단된다. 수치해석을 통해 얻어진 최대 침하량은 6.95 mm로 나타나며, 현장에서 실제 계측된 최대 침하량은 6.9~7.1 mm로 거의 일치하는 것을 확인하였다. 이를 통해 본 수치해석 모델링이 유효하다고 판단된다.

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F5.jpg

Fig. 5

Settlement trough formation at control group (FPR = 0.6, BPR = 1.1)

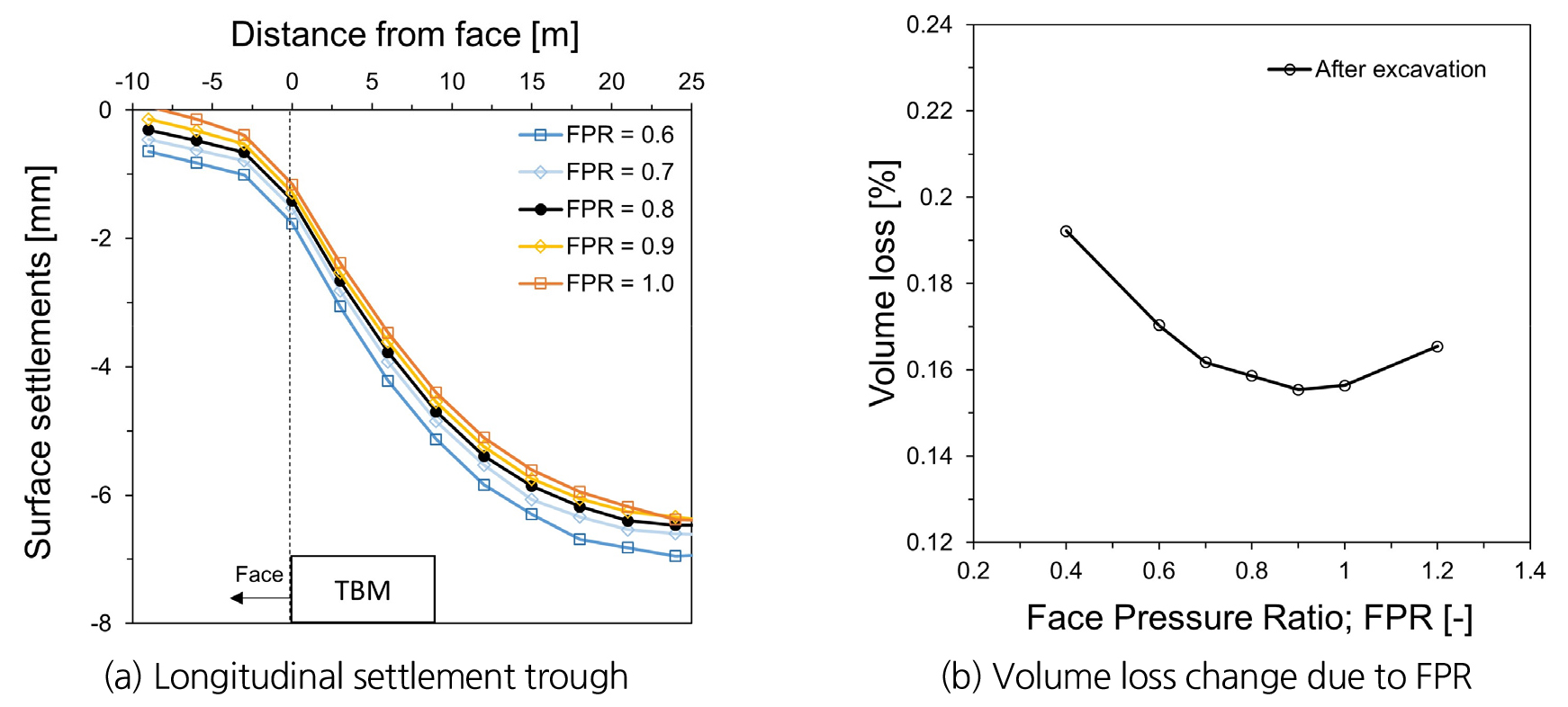
막장압을 조절하는 경우 Fig. 6과 같이 최대 막장압 이하의 범위에서 막장압이 강할수록 침하를 더 많이 보상하는 것을 확인하였다. 하지만 최대 막장압을 가하였을 때 막장면 전방 지반에서 일시적인 융기가 발생하는 것을 확인하였고 시공 중에도 이를 고려할 필요가 있다. 각각의 침하 트라프에서 산출된 체적 손실로부터 최소 막장압보다 낮은 막장압을 가할 때 침하량이 크게 증가하는 것을 확인할 수 있으며, 최대 막장압보다 큰 막장압을 가하는 경우 지반의 교란이 과도하게 발생하여 전방 지반의 침하는 보상되지만 최종 침하량이 오히려 증가하는 효과를 나타내는 것을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F6.jpg

Fig. 6

Effect of FPR on surface settlement development

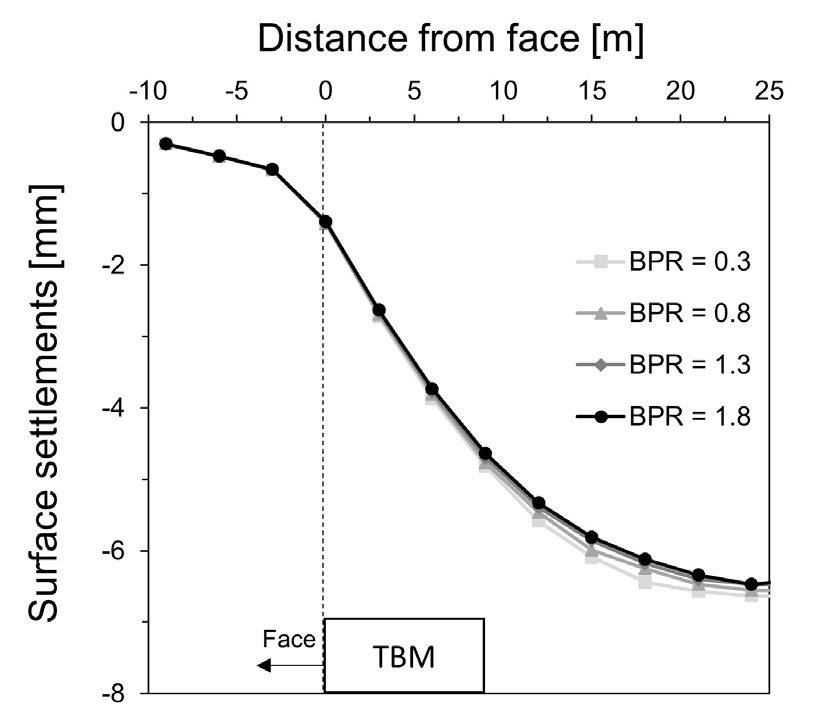
뒷채움 주입압력을 조절할 때 Fig. 7과 같이 주입압력이 증가할수록 최대 침하량이 감소하는 것을 확인할 수 있다. 주입압의 편차에 의한 침하 보상보다 막장압의 편차에 의한 침하 보상이 더 크게 나타나며, 이는 뒷채움 그라우트재의 주입압력이 그라우트재가 유동성을 지니며 상대적으로 낮은 강성을 지닐 때 작용하기 때문으로 판단된다. 변곡점과 침하 트라프 변수는 지반의 특성에 의존적이며 막장압 및 뒷채움 주입압과는 무관하다.

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F7.jpg

Fig. 7

Effect of BPR on longitudinal settlement trough

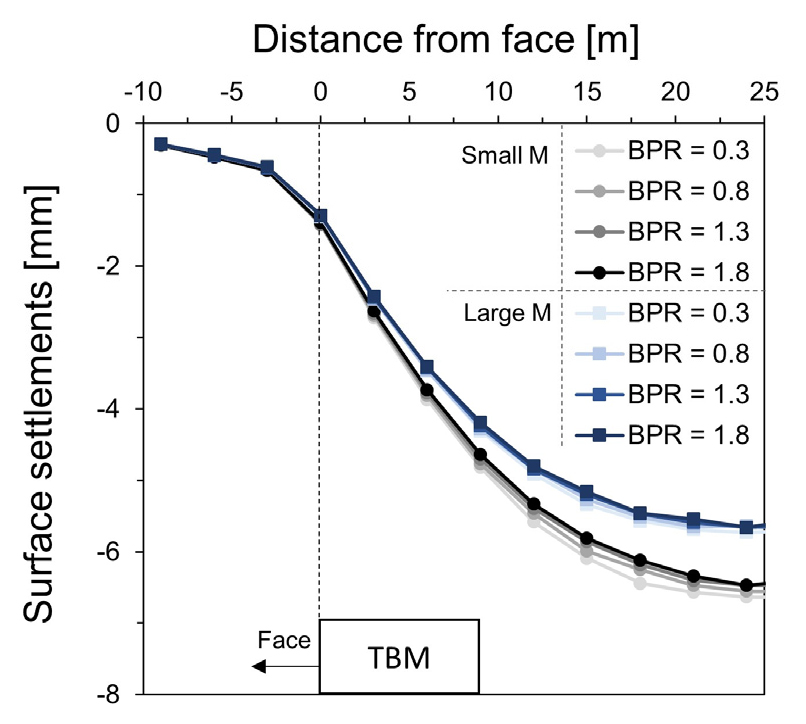
뒷채움 그라우트재의 탄성계수가 증가할 때 Fig. 8에서 나타난 바와 같이 지표 침하량은 보다 감소하지만 주입 압력에 의한 편차 역시 감소한다. 이를 통해 뒷채움 그라우트재의 주입압력보다 그라우트재의 탄성계수가 침하 보상에 보다 중요한 인자임을 확인할 수 있다. 실제 현장에서는 주입 성능을 고려하여 유동성과 초기경화시간을 설계하게 되므로 주입압력과 탄성계수를 적절하게 선정할 필요가 있다.

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F8.jpg

Fig. 8

Effect of BPR and constrained modulus of grout on settlement

4. 수치해석 결과 기반 침하 모델 검토

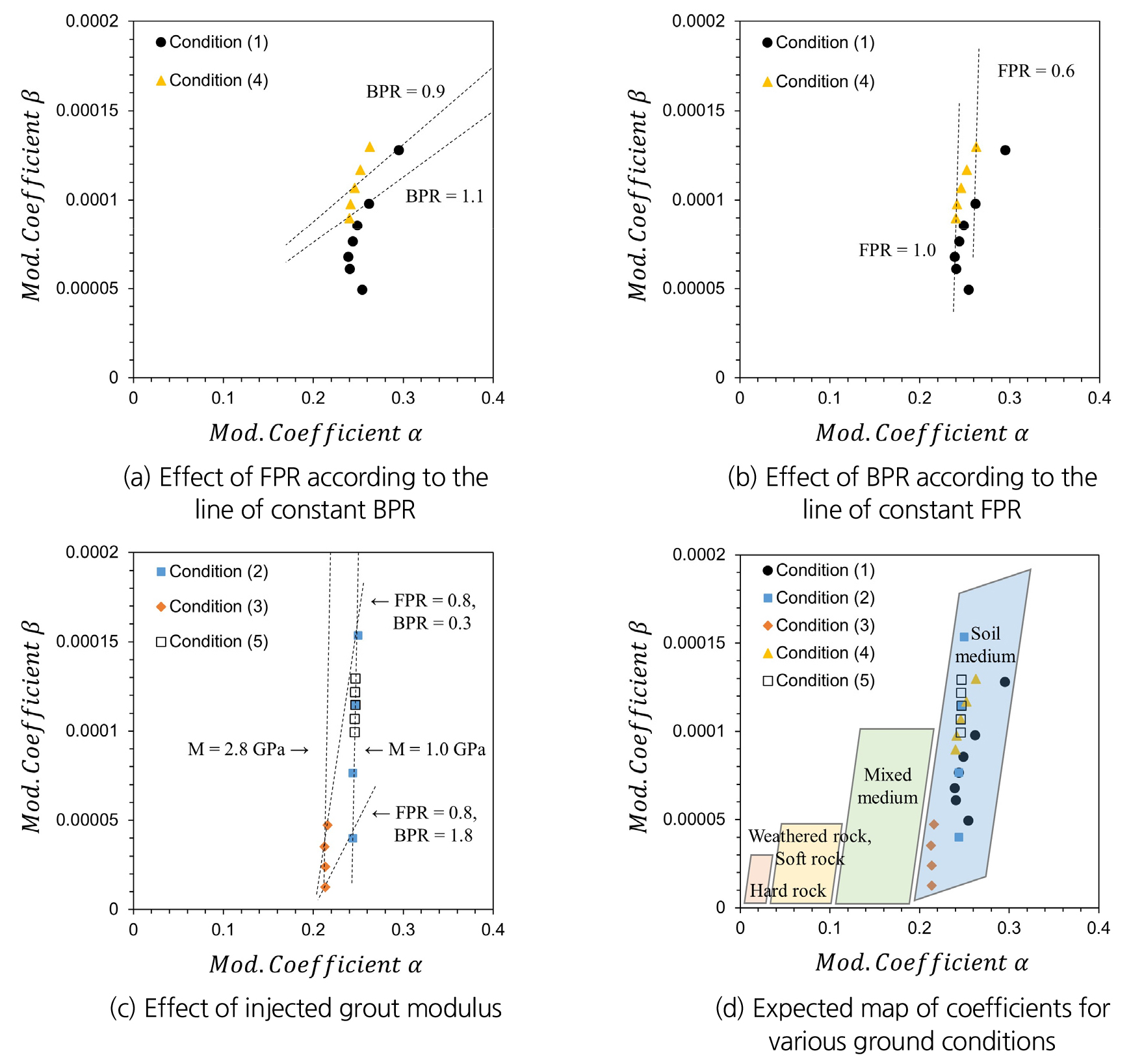
매개변수 수치해석 결과를 앞서 구축한 해석 모델에 적용하였다. 이를 기반으로 토압식 쉴드 TBM 시공 조건과 터널 설계 조건에 의해 특정 지반 조건에서 가능한 보정계수( $α, β$ )의 범위를 도출할 수 있다. 침하 트라프의 변곡점으로 보정계수를 나누어 수정 보정계수(modified coefficient)를 Fig. 9에 도시하였다. 이때 Table 3에서 분류한 해석 조건 (1)~(5)을 각각 도시하였다.

Fig. 9(a)에서 같은 뒷채움 주입압력에서 막장압이 다르게 적용되는 경우를 점선으로 연결하였을 때 보정계수 $α$ 와 $β$ 가 동시에 변화하며, 이를 통해 막장압이 지반의 교란과 변형에 가장 주요한 역할을 수행하고 있음을 알 수 있다. Fig. 9(b)에서 같은 막장압에서 뒷채움 주입압력이 변화하는 경우를 점선으로 연결하였을 때, 보정계수 $α$ 는 거의 변화하지 않으며 뒷채움 주입압력은 막장압보다 덜 주요한 역할을 수행하는 것을 확인하였다. 반면, Fig. 9(c)에서 막장압과 뒷채움 주입압력이 같을 때 뒷채움 그라우트재의 탄성계수가 다른 경우를 점선으로 연결하였을 때 주입압력보다 보다 확연한 침하 보상을 획득하는 것을 확인하였다. 보정계수 간의 상관관계를 통해 시공 조건에 따른 중요도와 경향성을 평가할 수 있었다. 본 연구에서는 침하예측모델에 적용된 보정계수를 도출할 때 테헤란 지하철 7호선 지반에서만 수치해석이 수행되었으므로 이와 같은 전단면 토사조건에서만 유효하다. 다만, 이러한 경향성을 기반으로 추후 다양한 지반 조건을 고려하게 되면 Fig. 9(d)와 같이 지반 조건에 따라 보정계수의 범위를 사전에 설정하고 예상되는 지반 침하량을 도출할 수 있을 것으로 사료된다.

https://static.apub.kr/journalsite/sites/kta/2021-023-03/N0550230304/images/kta_23_03_04_F9.jpg

Fig. 9

Correlations between analytical model coefficients based on numerical results

5. 결 론

본 연구에서는 토압식 쉴드 TBM 굴착으로 인해 발생하는 지반침하의 거동을 이해하고 주요 영향인자를 선정하여 각 인자별 영향 정도를 이해하고자 하였다. 그리고 정량적인 침하 평가를 위해 수치해석을 통한 매개변수 해석을 수행하였다. 이를 통해 얻어진 결론은 다음과 같다.

1. 토압식 쉴드 TBM 시공에 의해 발생 가능한 지반침하의 주요 영향인자는 지반 조건과 터널 크기, 그리고 굴착 조건의 세 가지로 분류할 수 있으며, 이 중 굴착 조건만이 시공 중 조절이 가능하다. 굴착 조건에 의해 발생하는 지반침하 요인으로는 막장압과 토압의 균형 여부에 따른 막장면 지반손실과 테일 보이드 뒷채움의 주입압력 및 강성에 따른 후방 지반손실이 존재하며, 이를 기반으로 최대 침하량을 산출하는 해석적 해를 도출하였다.

2. 주요 침하 영향인자에 대한 매개변수 해석을 수행하기 위해 FLAC3D 프로그램을 활용하여 수치해석을 수행하였으며, 막장압, 뒷채움 그라우트재 주입압 및 탄성계수가 지반침하에 어떠한 영향을 끼치는지 정량적으로 도출하였다. 이를 기반으로 최대 침하량의 해석적 해에 각각의 해석 조건을 대입함으로써 각 요인들의 침하 영향을 평가하였다. 추후 연구를 통해 굴착 조건 외에도 다양한 지반 조건에 따른 매개변수 해석을 수행하게 되면 침하 모델에 사용된 보정계수의 범위를 시공 이전에 파악하고 범용성을 지닌 침하예측모델을 구축하여 보다 정확한 침하량을 예측할 수 있을 것으로 판단된다.

3. 본 연구에서 구축한 해석적 해는 쉴드 TBM 굴착 중 오퍼레이터가 조절할 수 있는 변수들에 한해 산정한 것으로, 실제 주의가 요구되는 지반침하는 정지상태에서 과도하게 굴착 및 배토가 발생하거나 막장면 및 주면에서 지하수가 갱내로 유입되는 경우와 같이 사고에 준하는 위험상황에서 발생한다. 따라서 추후 연구를 통해 과도한 굴착 및 누수가 발생할 때의 지반침하 모델을 구축하여 실질적인 지반침하 위험도를 평가할 필요가 있다.

Acknowledgements

본 연구는 한국전력공사 자체연구개발 과제(R19SA02) ‘전력구 터널 지반 위험예측 기술 개발’의 지원으로 수행되었습니다. 연구 지원에 감사드립니다.

이 논문은 국토교통부의 스마트시티 혁신인재육성사업으로 지원되었습니다.

저자 기여도

안준범은 연구 설계, 데이터 수집 및 분석, 원고 작성을 하였고, 강석준은 데이터 수집 및 원고 작성을 하였고 김정주와 김경열은 연구 설계 및 원고 검토를 하였고 조계춘은 데이터 해석 및 원고 검토를 하였다.

References

An, J.B., Park, J., Cho, G.C. (2021), “Numerical evaluation of surface settlement due to shield TBM excavation conditions”, Proceedings of the Korean Tunnelling and Underground Space Association Annual Spring Conference, Seoul, pp. 103-104.

Attewell, P.B., Woodman, J.P. (1982), “Predicting the dynamics of ground settlement and its derivitives caused by tunnelling in soil”, Ground Engineering, Vol. 15, No. 8, pp. 13-22.

Chakeri, H., Ozcelik, Y., Unver, B. (2013), “Effects of important factors on surface settlement prediction for metro tunnel excavated by EPB”, Tunnelling and Underground Space Technology, Vol. 36, pp. 14-23. 10.1016/j.tust.2013.02.002

Comodromos, E.M., Papadopoulou, M.C., Konstantinidis, G.K. (2014), “Numerical assessment of subsidence and adjacent building movements induced by TBM-EPB tunneling”, Journal of Geotechnical and Geoenvironmental Engineering, Vol. 140, No. 11, 04014061. 10.1061/(ASCE)GT.1943-5606.0001166

GEO Report No. 298 (2014), Ground control for EPB TBM tunnelling, Geotechnical Engineering Office, Hong Kong.

ITA WG Mechanized Tunneling (2000), Recommendations and guidelines for tunnel boring machines (TBMs), pp. І-22~І-34.

Jaky, J. (1944), “The coefficient of earth pressure at rest. In Hungarian (A nyugalmi nyomas tenyezoje)”, Journal of the Society of Hungarian Architects and Engineering, Vol. 78, No. 22, pp. 355-358.

Jun, G.C., Kim, D.H. (2016), “A Intercomparison on the estimating shield TBM tunnel face pressure through analytical and numerical analysis”, Journal of Korean Tunnelling and Underground Space Association, Vol. 18, No. 3, pp. 273-282. 10.9711/KTAJ.2016.18.3.273

KDS 27 25 00 (2016), TBM (in Korean).

Kirsch, C. (1898), “Die theorie der elastizitat und die bedurfnisse der festigkeitslehre (The theory of elasticity and its application to the strength of materials)”, Zeitschrift des Vereines Deutscher Ingenieure, Vol. 42, pp. 797-807.

Lambrughi, A., Rodríguez, L.M., Castellanza, R. (2012), “Development and validation of a 3D numerical model for TBM-EPB mechanised excavations”, Computers and Geotechnics, Vol. 40, pp. 97-113. 10.1016/j.compgeo.2011.10.004

Lee, K.M., Rowe, R.K., Lo, K.Y. (1992), “Subsidence owing to tunnelling. I. Estimating the gap parameter”, Canadian Geotechnical Journal, Vol. 29, No. 6, pp. 929-940. 10.1139/t92-104

Lee, S.W., Jang, S.H., Choe, S.U. (2011), “Prediction of future demand for domestic TBM tunnels”, Geotechnical Engineering, Vol. 27, No. 2, pp. 18-26.

Lo, K., Rowe, R.K. (1982), Prediction of ground subsidence due to tunnelling in clays: research report GEOT-10-82, Faculty of Engineering Science, University of Western Ontario.

Mair, R.J., Taylor, R.N. (1997), “Theme lecture: Bored tunnelling in the urban environment”, Proceedings of the Fourteenth International Conference on Soil Mechanics and Foundation Engineering, Rotterdam, pp. 2353-2385.

Melis, M., Medina, L., Rodríguez, J.M. (2002), “Prediction and analysis of subsidence induced by shield tunnelling in the Madrid Metro extension”, Canadian Geotechnical Journal, Vol. 39, No. 6, pp. 1273-1287. 10.1139/t02-073

O'Reilly, M.P., New, B.M. (1982), “Settlements above tunnels in the United Kingdom-their magnitude and prediction”, Proceedings of the Tunnelling'82, London, pp. 173-181.

Peck, R.B. (1969), “Deep excavations and tunneling in soft ground”, Proceedings of the 7th ICSMFE, Mexico City, pp. 225-290.

Rodríguez, L.M. (2000), Estudio de los movimientos originados por la excavación de túneles con escudos de presión de tierras en los suelos de Madrid (Study of the movements caused by the excavation of tunnels with earth pressure shields in the soils of Madrid), Doctoral Dissertation, University of A Coruña.

Rowe, R.K., Lo, K.Y., Kack, G.J. (1983), “A method of estimating surface settlement above tunnels constructed in soft ground”, Canadian Geotechnical Journal, Vol. 20, No. 1, pp. 11-22. 10.1139/t83-002

Selby, A.R. (1988), “Surface movements caused by tunnelling in two-layer soil”, Geological Society, London, Engineering Geology Special Publications, Vol. 5, No. 1, pp. 71-77. 10.1144/GSL.ENG.1988.005.01.05

Shirlaw, J.N., Richards, D.P., Ramond, P., Longchamp, P. (2004), “Recent experience in automatic tail void grouting with soft ground tunnel boring machines”, Proceedings of the ITA-AITES World Tunnel Congress, Singapore, pp. 22-27.

Sugiyama, T., Hagiwara, T., Nomoto, T., Nomoto, M., Ano, Y., Mair, R.J., Bolton, M.D., Soga, K. (1999), “Observations of ground movements during tunnel construction by slurry shield method at the Docklands Light Railway Lewisham Extension-East London”, Soils and Foundations, Vol. 39, No. 3, pp. 99-112. 10.3208/sandf.39.3_99

Suwansawat, S., Einstein, H.H. (2007), “Describing settlement troughs over twin tunnels using a superposition technique”, Journal of Geotechnical and Geoenvironmental Engineering, Vol. 133, No. 4, pp. 445-468. 10.1061/(ASCE)1090-0241(2007)133:4(445)

Terzaghi, K. (1943), Theoretical soil mechanics, John Wiley & Sons, New York, pp. 11-15. 10.1002/9780470172766

Journal of Korean Tunnelling and Underground Space AssociationISSN:2233-8292(Print) 2287-4747(Online)한국터널지하공간학회

Preview

A preliminary study for numerical and analytical evaluation of surface settlement due to EPB shield TBM excavation

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

Fig. 1

Schematic diagram of ground loss due to excavation face instability

(6)

(7)

(8)

Fig. 2

Schematic diagram of tail void backfill grouting properties transition

(9)

Table 1.

Ground properties of target site (Chakeri et al., 2013)

Fig. 3

Sketches of an adopted mesh: only half is shown based on x = 0

Table 2.

Input properties of structures (Chakeri et al., 2013)

(10)

Fig. 4

Designed sequences for simulating EPB shield TBM excavation in numerical modelling

Table 3.

Numerical test conditions

Fig. 5

Settlement trough formation at control group (FPR = 0.6, BPR = 1.1)

Fig. 6

Effect of FPR on surface settlement development

Fig. 7

Effect of BPR on longitudinal settlement trough

Fig. 8

Effect of BPR and constrained modulus of grout on settlement

Fig. 9

Correlations between analytical model coefficients based on numerical results

Acknowledgements

References