1. 서 론
2. 굴착손상영역(EDZ)
3. 대변형 유한요소 수치해석
3.1 CEL 기법
3.2 Auto-remeshing (AR) 기법
3.3 TBM 굴진 모사 및 의사정적 해석
4. 해석 결과 및 분석
4.1 굴착손상영역 범위
4.2 터널 굴진면 안정성 분석
5. 결론 및 향후 활용방안
1. 서 론
대변형 해석 기법의 발전은 컴퓨터 전산 용량의 증가와 함께 이루어졌다. 대변형 해석 기법은 말뚝, 앵커링, 토석류와 산사태 등 지반공학 분야 전반에 적용되었다. Coupled Eulerian Lagrangian (CEL), remeshing, 그리고 efficient arbitrary Lagrangian-Eulerian (EALE) 기법 등이 주로 활용되었고, 많은 연구와 사례를 통해 그 효용성과 정확도가 검증되었다(Hu and Randolph, 1998; Kim and Jeong, 2021).
전 세계의 도시화율이 높아짐에 따라 인구가 밀집되는 도심지의 교통 환경 개선과 지하공간활용의 극대화를 위한 터널 굴착 프로젝트가 빈번해지고 있다. 이러한 터널 굴착 시에는 소음, 진동 및 분진의 발생뿐만 아니라 인접 구조물과 주변 지반에 대한 부정적인 영향 등에 의해 New Austrian Tunnelling Method (NATM)과 같은 기존 발파공법의 적용은 많은 문제점을 내포하고 있다. 그러한 이유로 최근에는 Tunnel Boring Machine (TBM) 등을 활용한 기계화 굴착의 비중이 증가하고 있는 추세이다.
기계화 터널 굴착에 의한 주변 지반 손상과 지반 물성치의 변화에 관한 연구는 캐나다(Underground Research Laboratory, URL), 스웨덴(Swedish Nuclear Fuel and Waste Management Corporation, SKB) 등의 국가에서 연구가 진행되었고, 국내에서는 한국원자력연구원 등에서 연구가 수행되었다. 캐나다 URL에서는 발파공법뿐만 아니라 기계화 터널 굴착에 대한 모형시험을 수행하여 굴착면을 따라 형성되는 균열 형성에 관한 연구를 진행하였다(Martini et al., 1997; Read et al., 1998). 스웨덴의 SKB에서는 발파공법과 기계화 터널 굴착으로 인한 굴착손상영역(Excavation damage zone, EDZ)의 범위와 그 범위 내 지반 물성치의 변화를 비교 분석하였다(Bauer et al., 1996; Emsley et al., 1997). 한국의 원자력연구원에서는 암반 굴착으로 인한 지반의 거동과 물성치의 변화를 실험적으로 확인하였다(Kwon et al., 2009). 터널 굴착 중 굴착손상영역의 형성은 터널의 시공 중 및 사용 중 구조적 안정성을 저해하고, 주변 지반의 물성치를 약화시키는 것으로 밝혀졌고, 그 형성 범위는 터널의 구조적 단면뿐만 아니라 굴착 중 발생하는 동적 하중(진동)의 영향을 받는 것으로 확인되었다(Fairhurst and Damjanac, 1996; Winberg, 1991; Aglawe, 1999; Stepansson et al., 2008; Arson and Gatmiri, 2012; Siren, 2015). 이는 기존의 발파공법뿐만 아니라 TBM 등을 활용하는 기계화 공법에도 해당하는 것으로 나타났다(Siren, 2015).
하지만 터널 굴착 중 형성되는 굴착손상영역에 대한 연구는 대부분 기존의 발파공법을 대상으로 이루어졌고, 상대적으로 적은 진동이 발생하고 TBM 등의 기계로 인하여 굴착면으로의 접근 및 현장 계측이 어려운 기계화 터널에 대한 연구 및 계측은 미흡한 것으로 드러났다(Read et al., 1998; Carbonell et al., 2010; Xu and Arson, 2014; Lee et al., 2016). 더욱이 기계화 터널에 대한 수치해석 연구 또한 지반의 대변형 거동 고려, 연속적인 굴착 과정 및 동적 하중 모사의 어려움으로 인하여 연구가 미비하였다.
본 연구에서는 CEL과 Remeshing 기법을 적용하여 TBM 굴착 과정을 모사하고 이에 따른 주변 지반에 미치는 영향과 지반의 거동을 분석하였다. 본 논문에서는 1) 터널 굴착의 대변형 거동을 모사함에 있어 두 해석 기법의 이론적인 기초와 특성과 2) 현장의 TBM 굴진속도와 커터헤드 회전속도를 고려한 두 해석 기법의 적용에 대한 상세한 내용을 기술하고자 하였다(Hoek and Bieniawski, 1965; Chang et al., 2006; Cho et al., 2010; Hammerer, 2013). 이를 통하여 3) 두 해석 기법을 통해 도출된 결과를 기반으로 TBM 굴착으로 인한 굴착손상영역의 범위를 제안하고, RMR, 터널 심도, 터널 직경 등의 영향인자에 대한 분석도 수행하였다. 제안된 굴착손상영역의 범위는 관련 시험 및 계측 결과를 통해 검증을 수행하였다. 그리고 최종적으로는 굴착손상영역의 형성과 터널의 구조적인 안정성에 대한 상관관계를 분석하였다.
2. 굴착손상영역(EDZ)
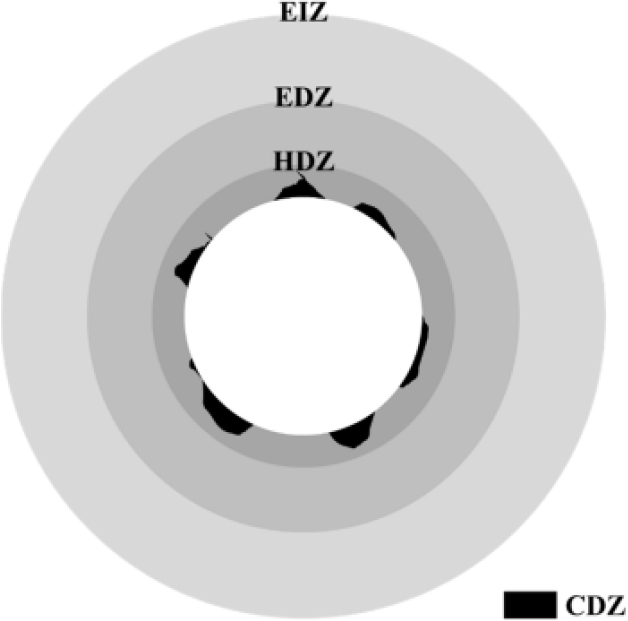
터널 굴착은 지반과 암반 내 응력의 변화를 유발하고, 이로 인해 균열이 발생하기도 한다. 굴착에 의한 손상의 개념은 손상의 원인에 대한 이해와 그에 따른 지반 및 암반 내 물성치의 변화에 대한 연구가 진전됨에 따라 발전되어 왔다. 일반적으로 굴착으로 인한 지반의 교란 및 손상영역은 Fig. 1과 같이 나타낼 수 있다(Perras and Diederichs, 2016). Harrison and Hudson (2000)은 굴착면에 바로 인접하여 극심한 손상을 입은 영역은 구조적 손상영역(construction damage zone, CDZ)이라고 정의하였다. 이러한 구조적 손상영역은 대부분의 경우 매우 좁은 영역으로 나타나 시공과 사용 중에 고려하지 않는 경향이 있다. 고도 손상영역(highly damaged zone, HDZ)은 비가역적인 손상이 고도로 발생하는 영역으로, 일반적으로 연결된 균열의 망으로 관찰된다. 고도 손상영역 바로 밖은 굴착손상영역(excavation damage zone, EDZ)으로, 굴착으로 인한 지반 또는 암반 내 응력의 변화가 탄성영역을 초과하여 새로운 균열이 발생하는 영역으로 정의된다. 굴착손상영역은 비가역적인 손상이 발생하고 실제 지반 물성치의 확연한 변화가 계측되고 구조적인 안정성의 저하가 발생하는 영역이다(Martino et al., 2007; Jonsson et al., 2009). Siren (2015)은 굴착손상영역 밖 영역을 굴착교란영역(excavation influence zone, EIZ, excavation disturbed zone, EDZ)으로 정의하고, 탄성영역 내 응력 변화가 발생하여 가역적인 교란만이 발생하고, 새로운 균열의 발생, 지반 물성치의 저하 또는 강도 약화가 발생하지 않은 영역이다.
Hoek and Bieniawski (1965)는 암반이나 시멘트 같은 취성 재료의 균열 발생에 관한 실험 연구를 진행하였다. 압축하중이 가해지는 조건에서는 재료의 최대인장력의 800%의 압축력이 작용하였을 때 최초의 균열이 발생하는 것으로 나타났다. Martin (1993)과 Martin et al. (2001)은 암반의 균열발생과 항복 단계를 통한 터널 굴착으로 인한 굴착손상영역을 정의하였으며, Diederichs et al. (2004)은 다양한 암반의 최초 균열발생 응력을 산정하기 위한 현장응력비(field stress ratio, FSR)을 실험적으로 Table 1과 같이 도출하였다.
Table 1.
Field stress ratio of brittle materials (Diederichs et al., 2004)
Saiang (2004)은 현장에서 계측한 결과를 바탕으로 터널 주변의 굴착손상영역을 산정하는 모델을 제안하고, 여러 영향인자에 대한 연구를 진행하였다. 스웨덴에서는 “실험을 통한 굴착으로 인한 교란 영역(ZEDEX)” 프로젝트를 통해 기존 발파공법뿐만 아니라 기계화 굴착으로 인해 발생하는 굴착손상영역에 대한 연구를 진행하였고, 암반에 미치는 영향 등을 실험과 현장 계측을 통해 비교 및 분석하였다(Emsley et al., 1997). NATM과 TBM 터널 굴착 시 발생하는 굴착손상영역의 크기와 형성 모양에 대한 분석과 두 공법 적용시 발생하는 지반 또는 암반의 물성치의 변화에 대한 현장 데이터 기반 연구도 진행되었다(Siren, 2015). Carbonell et al. (2010)은 수치해석을 활용한 연구를 진행하였는데, 입자유한요소(particle finite element method, PFEM) 해석기법을 활용하여 기계화 터널 굴착 시 암반의 손상을 입자 단위 미세균열의 발생과 연계하여 구현하고 추정하였다. 이러한 연구에도 불구하고, 터널과 굴착손상영역 관련 연구는 주로 기존 발파공법에 한정되어 있거나 터널 시공이 완료된 후 생성된 손상의 계측 위주로 이루어지고 있는 실정이다. 반면에, 기계화 터널 시공 중 발생하는 굴착손상영역의 범위, 주변 지반에 대한 영향, 또는 터널의 안정성에 관한 연구는 미흡하다. 이에 터널 시공 전 또는 시공 중 적용이 가능하며 굴착손상영역 범위와 터널의 안정성을 예측할 수 있는 대변형 수치해석 모델 구축을 위한 상세한 연구가 필요하다.
3. 대변형 유한요소 수치해석
터널 굴착은 지반과 암반 내 대변형이 발생하고 이에 따른 응력의 변화 및 균열이 발생하기도 한다. 따라서 굴착이 진행됨에 따라 발생하는 대변형에 의한 응력 변화량의 크기와 범위를 산정하기 위해 본 연구에서는 지반공학 분야에서 광범위하게 활용되는 대변형 해석기법인 coupled Eulerian-Lagrangian (CEL) 기법과 remeshing 기법을 적용하여 수치해석을 수행하였다.
3.1 CEL 기법
Coupled Eulerian-Lagrangian (CEL) 기법은 유체와 같은 거동을 관장하는 Eulerian 요소와 강체와 같은 거동을 관장하는 Lagrangian 요소를 결합하여 해석을 수행하는 기법이다. 지반공학 분야에서는 사질토(유체거동 요소)에 설치되는 타입말뚝(강체거동 요소)의 해석에 주로 활용된 기법으로 폐색효과 등을 정확하게 예측하는 것으로 검증되었다(Ko, 2015). 본 연구에서는 굴착 대상인 지반을 Eulerian 요소로, TBM의 커터헤드와 본체를 Lagrangian 요소로 모델링하여 해석을 수행하였다. Fig. 2(a)는 지반을 모델링한 유한요소망을 나타낸 것이고, Fig. 2(b)는 TBM 커터헤드와 본체를 모델링한 것이다. 지반은 Eulerian 요소(EC3D8R)로 설정되었고, 유한요소망의 크기는 터널 직경(D)을 기준으로 상하, 좌후로 5D의 크기로 모델링하여 경계층 효과(boundary effect)가 발생하지 않도록 하였다. 또 해석 소요시간의 단축을 위해 반단면으로 모델링하였고, 각 유한요소망 크기(mesh size)는 터널 굴진면 기준 1D 이내는 조밀(fine)하게, 그 밖의 영역은 상대적으로 크게(coarse) 설정하여 터널 굴진면 주변에서 높은 정확도를 보이도록 모델링하였다. TBM 커터헤드와 본체는 8-node Lagrangian 요소(C3D8R)로 모델링 되었고, 재료는 강체 거동을 하는 선형-탄성체로 가정하였다. 커터헤드와 지반 사이의 인터페이스 값(Rint)은 일반적으로 구조물-지반 사이의 값인 0.7보다 높은 0.9로 모델링하여 커터헤드의 거칠기를 모사하였다. TBM 요소에 적용된 물성치는 Table 2와 같다.
Table 2.
Material properties of lining and cutterhead
|
Model (element) | (MPa) | 𝜐 | 𝛾 | |
| Lining |
Linear elastic (C3D8R) | 23,000 | 0.15 | 24.0 |
| Cutterhead | 200,000 | 0.30 | 82.5 |
3.2 Auto-remeshing (AR) 기법
Remeshing 기법은 일정 거리 굴착 후 유한요소망을 재구성하여 각각의 요소망의 과도한 변형이나 찢어짐을 방지하도록 하는 대변형 해석 기법이다. CEL 기법과 비교하였을 때, 실제 TBM 커터헤드의 회전이나 TBM 본체의 전진 등을 실시간으로 모사할 수는 없지만, 새로운 유한요소망이 재구성 되면서 앞선 유한요소망에서 발생한 응력이나 변형을 승계하여 대변형 해석을 가능하게 하는 기법으로 지반의 시추 또는 굴진 해석에 널리 활용되어 왔다(Hu and Randolph, 1998; Tian et al., 2014; Wang et al., 2015).
본 연구에서는 약 300단계에 걸쳐 수행할 유한요소망 재구성 대변형 해석을 위해 컴퓨터 프로그래밍 언어인 PYTHON을 이용하여 해석 과정을 자동화하였다. PYTHON 언어를 이용하여, 요소의 구성/배열, 요소, 경계면 조건, 단위 굴진 거리 등을 확정하여 첫 번째 해석 단계에 적용하도록 하였다. 그 후 다음과 같은 명령어를 삽입하여 첫 번째 해석 단계에서 발생한 응력, 변형, 유한요소망의 조건 변화 등을 재구성될 유한요소망에 승계하도록 하였다.
Mdb.Model(name=newmodel, objectToCopy=mdb.models[oldmodel])
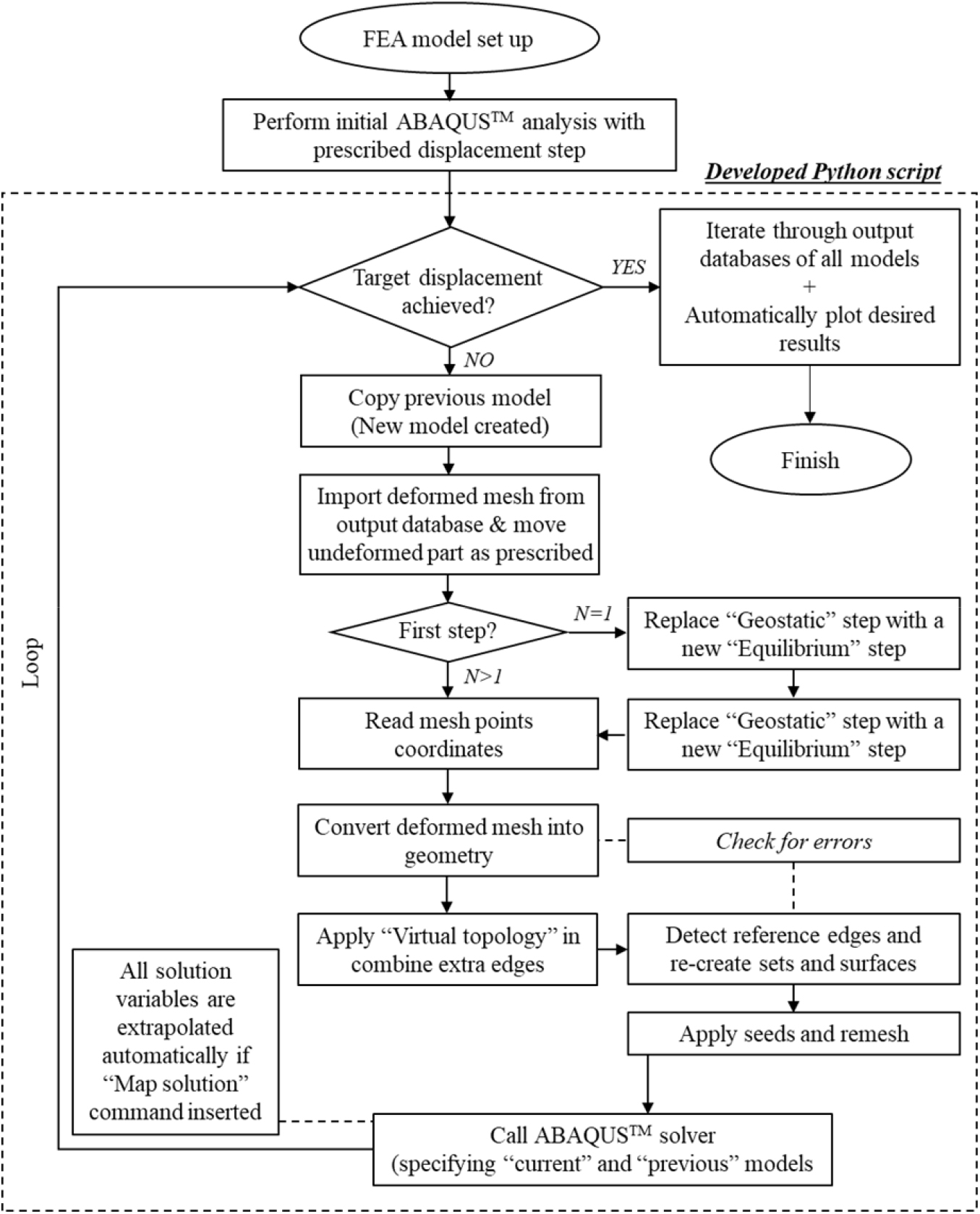
여기서, oldmodel은 일정 거리의 굴진이 모사된 i번째 유한요소망, newmodel은 전 단계 유한요소망의 응력상태, 변형, 경계면 조건 등이 승계된 해석 단계가 (i+1)번째인 재구성 유한요소망을 나타낸다. 이러한 과정은 최종적으로 설정된 목표 굴진 거리 또는 굴진 해석 단계까지 자동으로 진행되도록 프로그래밍 되었다. 이러한 자동화 과정은 Fig. 3에 나타나 있다(Orazalin, 2017).
3.3 TBM 굴진 모사 및 의사정적 해석
보다 정확한 TBM 굴진 모사를 위해 본 연구에서는 실제 TBM 굴진 과정을 모델링할 수 있는 CEL 해석기법을 적용함과 더불어 실제 현장과 기존 연구의 내용들을 반영하여 TBM 굴진속도와 커터헤드 회전속도를 각각 1.8 m/h, 6 rad/s (또는 1 RPM)로 설정하였다(ITA, 2000; Lee et al., 2016; Kim, 2021). 하지만 이러한 조건 하에 동적 해석을 수행하면 해석 시간이 과도하게 길어지기 때문에 의사정적(quasi-static) 해석을 수행하였다.
터널을 비롯한 대부분의 지하 구조물은 주변 지반에 완전히 둘러싸여 있어 자유 진동이 불가능하므로 구조물의 거동은 지반 운동을 따르게 된다. 따라서 지중 터널에서는 1차원 지반응답에 의해 계산된 변위와 응력을 적용한 의사정적 해석이 널리 사용되고 있다(Hashash et al., 2001; 2005; Kim, 2021). 지하 구조물과 지반의 상호 작용을 모사하기 위한 동적 해석 역시 광범위하게 적용되고 있다. Hashash et al. (2010)은 지중 터널 구조물의 유사정적 방법과 동적 해석법의 결과를 비교하였는데, 그 차이가 최대 25% 이내로 발생하는 것으로 확인하였다. Argyroudis and Pitilakis (2012)가 수행한 유사한 연구에서도 유사정적 기법과 동적 해석에 의한 결과 간 차이가 미미한 것으로 나타나 지하 터널 구조물의 응답 계산에는 의사정적 해석만으로도 충분한 정확도의 확보가 가능하다는 것을 검증하였다(Park et al., 2016; Kim and Jeong; 2021; Kim, 2021).
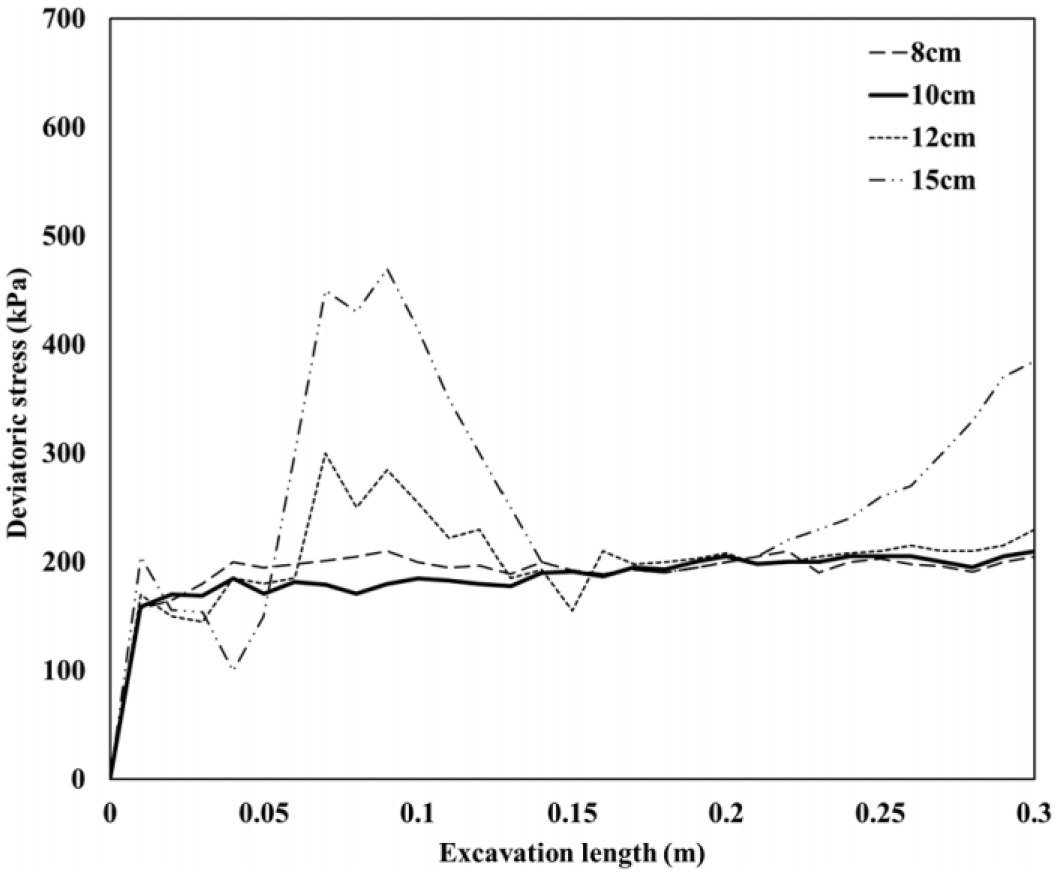
유한요소해석 바탕으로 의사정적 해석을 수행함에 있어서 각각의 유한요소망 내 단일 요소(mesh) 크기가 해석 결과에 영향을 미친다. 따라서 본 해석에서는 예비해석을 수행하여 높은 정확성뿐만 아니라, 적절한 해석 소요 시간을 도출할 수 있도록 하였다. Fig. 4는 유한요소망 내 각각의 요소 크기에 따라 도출되는 축차응력 결과를 도시한 것이다. 요소의 크기를 가장 적게(fine, 요소 직경 8 cm) 설정한 조건 하의 결과는 굴진 거리와 무관하게 축차응력이 안정적으로 산정되는 것으로 나타난 반면, 요소의 크기가 커져서(coarse) 12 cm를 넘어서게 되면 해석 소요 시간은 약 33%로 감소하지만 축차응력 결과에 산발적인 값이 나타나는 것으로 확인되었다. 따라서 본 연구에서는 해석을 수행함에 있어 유한요소망 요소의 최대 크기를 10 cm로 설정하여 진행하였다.
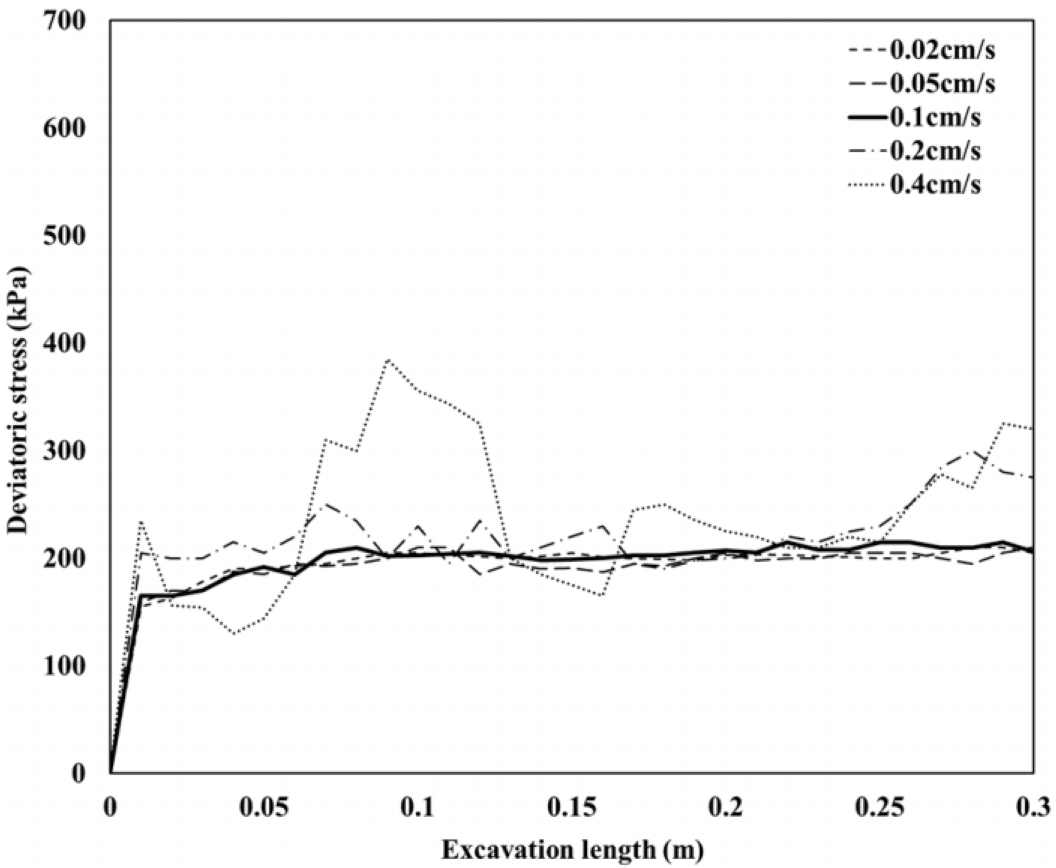
의사정적 해석을 진행함에 있어 TBM 굴진 속도 또한 해석 결과에 큰 영향을 미치는 것으로 확인되었다. Fig. 5는 TBM 굴진 속도에 따른 지반 내 축차응력 값을 나타낸 것이다. 예비 해석 결과, TBM의 굴진 속도를 0.02 cm/s로 설정할 경우 굴진으로 인한 축차응력이 일정한 값으로 수렴하고 안정적으로 도출되는 것으로 확인되었지만, 해석에 많은 시간이 소요되는 것으로 나타났다. 굴진 속도를 0.1 cm/s로 설정한 경우 해석 시간은 약 70% 감소하면서도 안정적인 해석이 가능한 것으로 확인되었다. 굴진 속도를 그 이상으로 설정하게 되면 해석 값이 수렴하지 않고 불안정하여 적용할 수 없는 것으로 나타났다.
따라서 본 연구에서는 TBM 굴진에 의한 지반 내 동적 거동을 모사함에 있어서 과도한 해석 소요 시간을 방지하고 정확한 축차응력 계산을 통한 굴착손상영역을 도출할 수 있도록 유한요소망의 단일 요소 크기를 10 cm, TBM 굴진 속도는 0.1 cm/s로 설정, 의사정적 조건 하에서 위와 같은 조건으로 해석을 수행하여 달라진 굴진속도가 해석 결과에 영향을 미치지 않도록 하였다.
4. 해석 결과 및 분석
본 연구에서는 가장 널리 활용되고 있는 두 가지 대변형 해석 기법을 적용하여 TBM 굴착으로 인한 지반 내 굴착손상영역의 형성 범위와 터널의 구조적 안정성을 분석하였다. 수행한 해석 케이스(총 54 케이스)와 적용된 암반 물성치(Jeong et al., 2014)는 각각 Table 3과 Table 4에 요약하였다.
Table 3.
Summary of numerical analysis case
| Diameter | Depth | RMR rating (rock type) | |
| 1 | 2.5 m | 15 m | 1st grade (hard rock) |
| 2 | 3.5 m | 30 m | 3rd grade (soft rock) |
| 3 | 4.5 m | 60 m | Weathered rock |
Table 4.
Index properties of jointed rock mass (Jeong et al., 2014; Kim, 2021)
| Group | RMR | (MPa) |
𝛾 (kN/m3) | 𝜐 |
𝜙 (°) | (kPa) |
UCS (MPa) |
| Hard rock | 80~100 | 20,000 | 27 | 0.20 | 45 | 4,000 | 75 |
| Soft rock | 41~60 | 600 | 25 | 0.24 | 35 | 1,000 | 30 |
|
Weathered rock | - | 200 | 21 | 0.30 | 32 | 50 | 2 |
4.1 굴착손상영역 범위
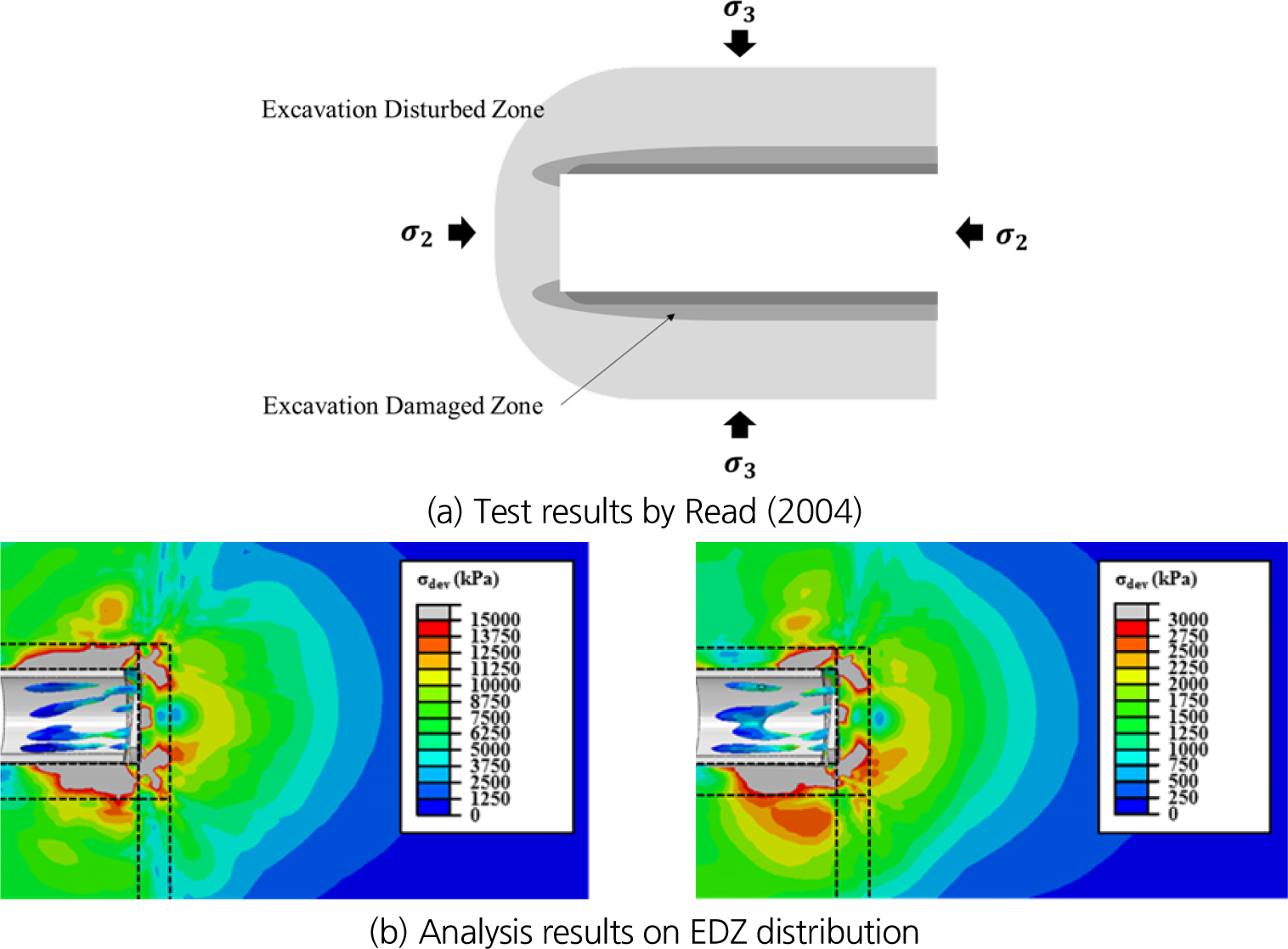
Table 5는 CEL과 AR 기법을 통해 도출된 터널 중심으로부터 굴착손상영역의 최외곽 요소 사이의 거리를 터널 직경으로 정규화(굴진면에서 최외곽 요소까지의 거리(m) / 터널 직경(m))한 수치를 정리한 것이다. 해석상 굴착손상영역의 정의는 현장응력비(field stress ratio, FSR) 이론은 근거로, 굴착으로 인해 발생한 축차응력이 원지반 일축압축강도의 30%를 초과한 영역으로 정의하였다. Fig. 6(a)에서는 기존 연구에서 진행한 모형 시험을 통해 측정된 굴착손상영역을 나타낸 것이고(Read, 2004), Fig. 6(b)는 본 연구에서 수행한 수치해석 결과 예시를 나타낸 것이다. 이 둘의 비교를 통해 본 연구에서 진행한 수치해석은 실제 굴착으로 확인된 굴착손상영역의 경향을 비교적 정확하게 나타낼 수 있는 것으로 검증되었다. 그뿐만 아니라, 두 해석 기법으로부터 계산된 값을 분석한 결과 TBM 굴착으로 인한 굴착손상영역의 형성 경향과 그 범위가 매우 흡사한 것으로 나타났다. 두 가지 결과를 종합하면 일반적으로 굴진 방향 전면 방향으로의 굴착손상영역 범위보다 굴진 방향 기준 수직 방향 - 특히 아래 방향 - 으로 형성되는 굴착손상영역이 상대적으로 큰 것으로 나타났다. 이러한 경향은 국내외에서 수행한 축소 모형 시험 결과와 현장 TBM 운영 중 실측에 의한 데이터를 통해서도 확인이 가능하다(Martini et al., 1997; Diederichs et al., 2004; Read, 2004).
Table 5.
Numerical results on EDZ range (vertical / horizontal; normalized)
터널 심도에 따른 굴착손상영역 범위를 분석한 결과, 심도가 깊어짐에 따라 굴착하는 암반의 일축압축강도가 높아지고, 이에 따라 굴착에 의한 축차응력이 높아진 일축압축강도의 30%를 초과하지 못하여 굴착손상영역이 더 좁게 형성되는 것으로 확인되었다. 이는 실제로 터널 심도 깊어짐에 따라 구속압이 높아지고, 굴착손상영역의 판단 기준인 균열이 폐쇄되는 경향과도 일치한다.
굴착 되는 암반의 RMR 등급 또한 굴착손상영역의 형성 범위와 밀접한 관계가 있는 것으로 드러났다. RMR 등급이 높고 양호한 암일수록 굴착에 의한 손상영역이 더 광범위하게 형성되는 것으로 나타났다. 이는 강성이 높고, 탄성계수가 높을수록 동적 하중과 진동이 더 광범위하고 빨리 전파한다는 것과 연관 지어 검증이 가능하다. 하지만 이는 단순히 굴착으로 인한 축차응력의 변화가 기준 이상으로 발생한 영역을 바탕으로 산정한 영역으로 실제 터널 및 굴진면의 안정과는 별개인 것으로 나타났다. 이에 대해서는 다음 절에서 더 자세하게 다루었다
수치적으로 산정된 굴착손상영역의 형성 과정을 보면 AR 기법은 굴착 과정 전반에 걸쳐 꾸준하게 범위가 확장되어 가는 모습을 보였지만, CEL 기법의 경우 굴착 과정 초반(300번의 굴착 모사 과정 중 첫 50번)에 가파르게 확장되다가 수렴하는 모습을 보였다. 이는 AR 기법은 자동으로 유한요소망을 갱신하여 요소의 과도한 변형이나 응력의 집중을 방지하지만, CEL 기법은 Lagrangian 요소로 모델링 된 TBM이 Eulerian 요소로 이루어진 지반을 실제로 관통하면서 진행하기 때문에 초반에 지반이 열리기까지 과도한 응력이 발생하는 데에서 기인하는 것으로 분석된다. 마지막으로, 형성된 굴착손상영역의 범위는 터널의 직경과 정비례하는 것으로 굴착손상영역의 범위를 터널의 직경으로 정규화 한 결과 나타났다.
4.2 터널 굴진면 안정성 분석
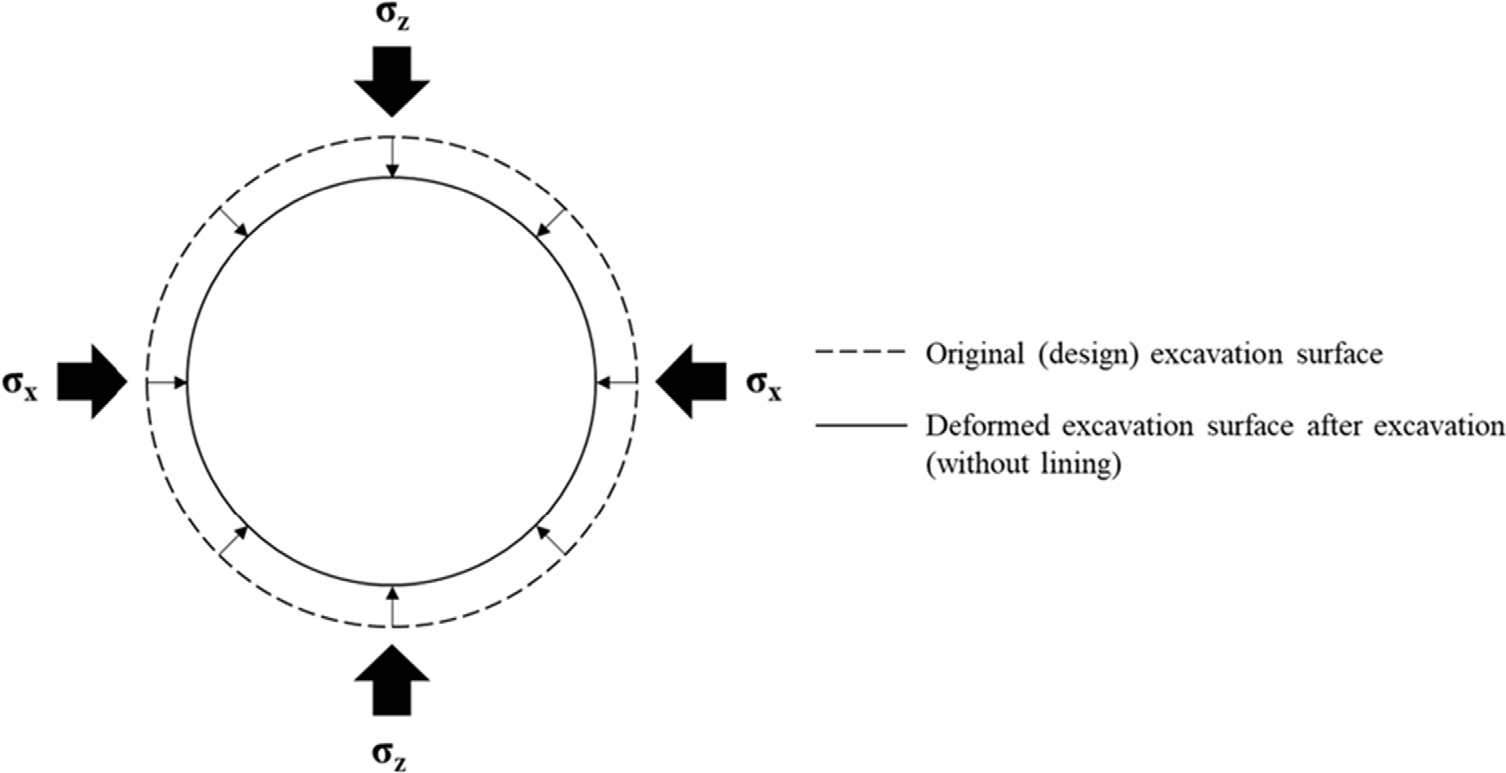
TBM 굴착으로 인한 터널 굴진면의 구조적 안정성은 터널 굴진면의 단면적 변화와 터널 굴진면에서 발생하는 최대 변위를 기준으로 분석하였다. 터널 굴진면의 안정성은 Fig. 7에 나타난 바와 같이 터널 직경을 기준으로 산정된 초기 터널 단면적과 TBM 굴착 후 라이닝을 제거한 조건에서 터널 변형으로 인한 단면적 변화율과 터널 굴진면을 따라 발생한 최대 변위 두 가지 결과를 기초로 분석하였다. 터널 굴진면 안정성에 대한 기준은 Sakurai (1984)와 Chern et al. (1998)이 현장 계측을 통해 도출한 결과를 바탕으로, 설계 터널 굴진면 기준 1% 이상의 변위 또는 변형이 생겼을 경우 구조적인 안정성에 문제가 발생했다고 가정하여 분석을 수행하였다.
Table 6은 TBM 굴진에 따른 터널 단면적의 변형을 나타낸 것이고, Table 7은 TBM 굴진 중 터널 굴진면에서 발생한 최대 변위를 요약 정리한 것이다. 터널 단면적을 기준으로 안정성을 분석한 결과 RMR 3등급 이상으로 양호한 암반에서는 대부분 1% 이내의 변형이 생겨서 안정성이 유지되는 것으로 확인되었다. 반면에 풍화암에서는 TBM 본체 기준으로 최대 약 17%까지 단면적의 변형이 생기는 것으로 계산되어 구조적으로 불안정해진 것으로 나타났다.
Table 6.
Deformation of tunnel sectional area due to TBM excavation (D = 2.5 m / 3.5 m / 4.5 m)
Table 7.
Maximum deformation on excavation surface due to TBM excavation (D = 2.5 m / 3.5 m / 4.5 m)
굴진면에서 발생하는 최대 변위를 기준으로 안정성을 분석한 결과, RMR 1등급의 양호한 암반에서는 60 m 이상의 심층 터널 조건을 제외하고는 1% 이하의 변위가 발생해 매우 구조적으로 매우 안정적인 것으로 확인되었다. RMR 3등급 조건에서도 최대 발생 변위는 2% 내외로 제한되어 비교적 안정적인 것으로 나타났으나, 풍화암에서는 최대 약 24%까지 변위가 생기는 지점이 확인되었다.
대변형 수치해석을 통해 도출된 터널 굴진면의 변형을 기준으로 분석한 구조적 안정성은 TBM 굴착으로 인해 발생하는 굴착손상영역의 범위와는 대체로 반비례하는 것으로 확인되었다. 이는 양호한 암반일수록 진동의 전파가 더 광범위하게 이루어져 굴착으로 인해 새로운 균열이 더 광범위하게 발생할 수 있지만 그 변화가 반드시 구조적인 안정성과 직결되지 않을 수도 있다는 분석이 가능하다. 하지만 이는 암반파열 현상(rockburst)와는 별개로 굴착 중 암반 내에 축적된 변형에너지의 급작스러운 방출로 인해 구조적인 안정성이 급격히 감소할 수도 있다.
5. 결론 및 향후 활용방안
본 연구에서는 가장 널리 활용되는 두 가지 대변형 해석 기법을 적용하여 TBM 굴착으로 인해 암반 내에 발생하는 굴착손상영역(excavation damage zone)의 범위를 도출하고 터널 굴진면의 안정성을 분석하였다. 대변형 해석에는 coupled Eulerian-Lagrangian (CEL) 기법과 Auto-remeshing (AR) 기법이 적용되었으며, TBM 굴진 과정에서 발생하는 굴착손상영역과 그에 따른 굴진면의 변형을 도출하였다.
1. TBM 굴진으로 인해 지반 내에서는 응력의 변화가 생기고 이 응력의 변화에 의해 균열이 발생하기도 하는데, 이러한 균열이 발생하는 범위를 굴착손상영역이라고 정의하였다. 암반 내 균열이 발생하였기에 비가역적인 손상이 발생하였고, 기존 연구 및 계측을 통해 굴착손상영역 내에서는 투수계수, 열전도도 등에서 유의미한 변화가 관찰되었다. 대변형 해석 결과, TBM 굴진 과정에서 발생하는 굴착손상영역은 RMR 등급이 높을수록(양호한 암반일수록) 더 광범위하게 형성되는 것으로 확인되었다. 이는 진동의 전파가 탄성계수가 높고 양호한 암반일수록 더 광범위하게, 빨리 전파되는 것과 연관이 있는 것으로 나타났다.
2. 굴착손상영역의 범위와는 별개로 터널 굴진면의 구조적 안정성을 터널 단면적과 터널 굴진면에서 발생하는 최대 변위를 기준으로 분석하였다. 수치해석 결과, 굴착손상영역의 형성 범위와 터널의 안정성과는 대체로 반비례 관계인 것으로 나타났다. 이는 암반의 강도가 높아짐(i.e. 탄성계수 증가)에 따라 굴착손상영역 형성 범위는 증가하였지만, 암반 자체의 강도가 높아져 터널 굴착 후에도 굴진면의 자립이 가능하기 때문인 것으로 분석되었다. 이는 터널의 굴진 단면적과 굴진면 내 최대 변위를 기준 모두에 해당되는 것으로 확인되었다.
3. 본 연구에서 도출된 결과는 단순히 TBM 터널 굴진 시 암반의 반응을 확인하는 연구뿐만 아니라, 지하공간 활용의 중요성이 높아지고 있는 도시 및 도로계획 수립에도 기여를 할 수 있을 것으로 기대된다. 기존 주로 경제적, 사회적인 요소를 기초로 수립되었던 도시 및 도시계획에 본 연구에서 수행된 연구 과정 및 결과를 반영하여 지반(암반)공학적인 측면에서 실현 가능한 지하공간 및 도로의 후보지 또는 후보 경로를 도출할 수 있을 것으로 보인다.