1. 서 론
2. 터널의 안정성 평가에 대한 기존 연구
3. 측압계수의 터널 응력에 미치는 영향
4. 등가물성치 산정
5. 유한차분법에 의한 수치해석 모델링
6. 수치해석 결과 정리 및 분석
6.1 터널의 안정성 분석
6.2 터널의 내공변위 비교 ‧ 분석
6.3 지보재 휨응력 비교 ‧ 분석
6.4 터널 주변 지반의 소성영역 분석
7. 결 론
1. 서 론
최근 도로 주행 성능의 향상을 위해 2019년 12월 기준 매년 7.6%씩 터널 개소의 증가 및 1,102 km 이상 길이가 연장되어 우리나라의 도로건설이 가속화되는 추세이다(Ministry of Land, Infrastructure and Transport, 2020). 이에 터널 시공 건수가 증가되는 만큼 터널의 붕락 또는 융기사고도 마찬가지로 증가할 것으로 예상된다. 터널 시공 중 붕괴 또는 붕락에 의한 사고가 빈번하여 이와 관련된 연구가 주로 진행되어 많은 대책 방안을 찾았으나, 터널 바닥부 융기에 의한 사고는 상대적으로 적게 발생하여 연구 및 대책방안이 부족한 실정이다.
이에 Cho (2020)는 연약한 지반에 시공 중인 도로 터널을 대상으로 터널 바닥부 융기 발생 구간에 대한 거동특성을 분석 및 효율적인 보강방안을 제시하고자 하였다. 또한, 유한차분해석에 근거한 수치해석 프로그램인 FLAC 2D 5.0 (Itasca Consulting Group, Inc., 2005)을 이용하여 연약지반에서 터널 바닥부 곡률에 의한 효과를 분석하였다. 이를 위해 터널 바닥부 곡률의 크기를 달리하여 바닥부 중앙에서의 최대 깊이를 0, 50, 100 cm로 설정하고 터널의 내공변위, 안전율, 소성영역을 분석하여 터널의 안정성을 평가하였다. 한편, 굴착면과 지표면까지의 높이인 토피고를 일부 영역을 제외하고 상재하중으로 처리하여 해석의 효율성을 고려하였다.
연구 결과, 바닥부(floor, invert)의 곡률이 커질수록 터널의 내공변위는 감소하고 안전율은 증가하였으며 터널 주변 지반의 소성영역도 줄어들어 터널의 안정성이 확보되는 것을 확인하였다. 다만, 지반조건, 지보재, 측압계수를 한 가지 경우로 고정하여 보다 다각적인 해석이 필요할 것으로 판단된다.
Kim (2021)은 기존 Cho (2020)가 수행한 터널 바닥부 곡률에 의한 효과를 해석하고자 하였다. 이를 위해 FLAC 2D 5.0을 이용하여 모델링을 하고 터널 바닥부 곡률의 크기를 5가지로 세분화하였고 지반조건 및 지보재의 조건도 각각 3가지 및 2가지로 확장하였다. Cho (2020)와 마찬가지로 해석의 효율성을 위해 터널 상부지반을 상재하중으로 처리하고 해석영역을 줄여 해석의 효율성을 고려하였다. 해당 파라미터를 통해 안전율, 내공변위, 지보재 휨응력, 소성영역을 다각도로 비교 ‧ 분석하여 바닥부 깊이가 깊어질수록 터널의 안정성이 증대되는 것을 확인하였다. 기존 해석에서 바닥부 곡률의 크기, 지반조건, 지보재 조건을 추가로 고려하여 터널의 안정성이 확보되는 것에 대해 신뢰성을 높였으나, 측압계수 영향을 고려하지 않았고, 터널 상부지반의 일부를 상재하중으로 처리하여 해석하였는 바, 여전히 이에 대한 검증이 필요할 것으로 판단된다.
따라서 본 연구에서는 지반 범용 해석프로그램인 FLAC 2D 5.0을 활용하여 응회암 변질대에 위치한 터널 바닥부 곡률의 보강효과에 대해 수치해석적 민감도 분석을 수행하여 터널의 안정성을 평가하고자 하였다. Cho (2020) 및 Kim (2021)에서 진행된 연구와 마찬가지로 일반적인 왕복 2차선 도로 터널을 대상으로 상 ‧ 하 분할 굴착과정을 모델링하였으며 바닥부 깊이 5가지(0, 25, 50, 75, 100 cm), 지반조건 3가지(응회암 변질대 3, 4, 5등급), 지보재 두께 2가지(25, 40 cm)를 고려하였다. 특히 측압계수 및 터널 상부 해석영역의 높이의 영향을 조사하기 위해, 각각 4가지(0.5, 1.0, 1.5, 2.0) 및 3가지(10, 20, 40 m)로 변화시켜가며 터널 바닥부 곡률의 보강효과를 분석하였다. 즉, 360가지의 경우에 대해 민감도 분석을 수행하였다.
2. 터널의 안정성 평가에 대한 기존 연구
Park (2003)은 2차선 마제형 터널을 대상으로 측압계수 및 암반등급이 터널의 안정성에 미치는 영향을 평가하였다. 이를 위해 Zienkiewicz et al. (1975), Naylor (1982), Donald and Giam (1988) 및 You et al. (2000)이 언급한 전단강도감소기법에 기초하여 터널의 안전율을 측압계수(0.5 및 2.0) 및 암반등급별로 Table 1과 같이 안전율을 산정하였다. 결과적으로 지반의 강도가 높고 측압계수가 낮을수록 안전율이 더 크게 나타남을 확인했다.
Table 1.
Tunnel factor of safety according to K0 and rock grade (Park, 2003)
Rock grade K0 | I | II | III | IV | V | VI |
| 0.5 | 6.23 | 3.97 | 2.69 | 1.79 | 1.23 | 1.13 |
| 2.0 | 6.41 | 3.81 | 1.97 | 1.23 | 1.07 | 1.01 |
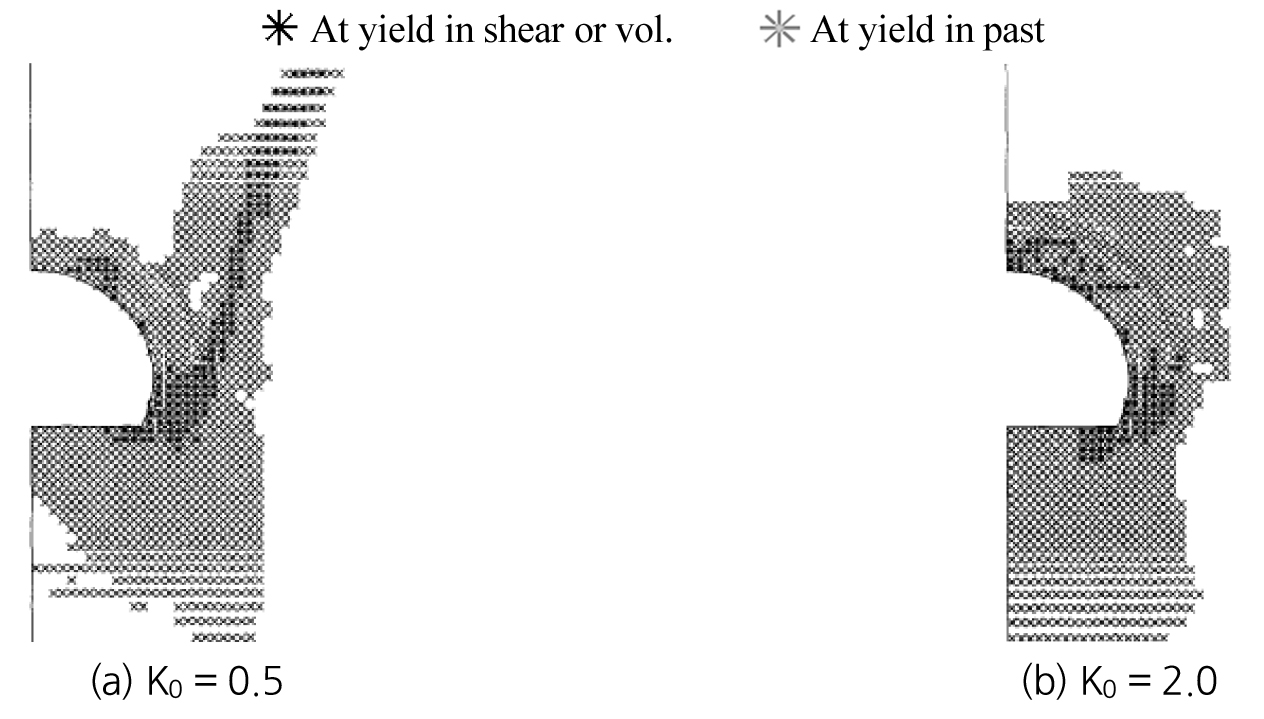
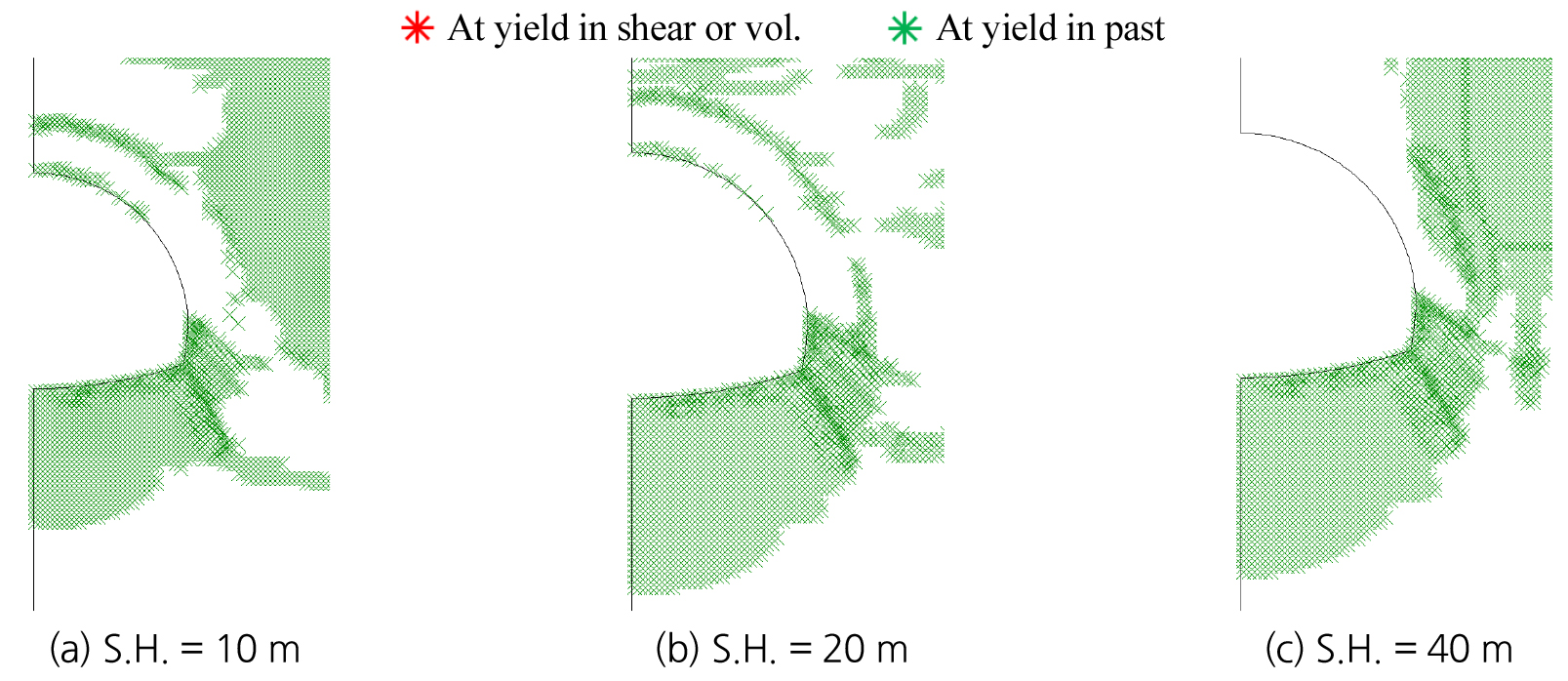
소성영역은 Fig. 1과 같이, 측압계수 0.5의 경우 주로 터널의 측벽부에서 발생하였으며, 암반등급이 낮아질수록 분포가 확장되었고 부분적으로 활동성 전단파괴영역도 나타났다. 측압계수 2.0의 경우 터널의 천단부 및 바닥부에 주로 소성영역이 발생하였다. 측압계수 0.5와 같이 암반등급이 저하될수록 소성영역의 분포가 확장되었으며 일부 영역에서 활동성 전단파괴영역이 발생하였다. 즉, 측압계수가 0.5인 경우 연직응력이 수평응력보다 영향이 크므로 터널의 측벽부에 주로 파괴가 발생하고 측압계수가 2.0인 경우 반대로 수평응력이 연직응력보다 영향이 크므로 터널의 천단부 및 바닥부에서 소성영역이 발생하는 결과가 나타났다. 이는 측압계수에 따라 터널의 측벽 또는 천단 및 바닥부에 작용하기 때문으로 판단하였다.
3. 측압계수의 터널 응력에 미치는 영향
등방 탄성 암반 내에 놓인 원형터널에서의 측압계수의 영향은 Kirsch가 제안한 해(Solution)를 통해 알 수 있다(Goodman, 1989). Fig. 2(a)와 같이 수평 및 연직 방향의 초기지중응력이 각각 및 가 작용할 때, 터널 굴착 후의 반경방향 및 접선방향 응력(, )은 측압계수()를 사용하여 각각 식 (1)과 식 (2)를 이용하여 구할 수 있다.
여기서, 는 반경 인 원형터널 중심에서부터의 거리, 는 수평축으로부터 반시계방향으로 잰 각도(radian)이다. Fig. 2(b)는 터널 측벽과 바닥으로부터 방사거리별 초기연직응력과 접선응력의 비의 분포를 보여준다. 따라서 측압계수()는 초기연직응력과 함께 굴착 후의 응력에 영향을 주는 것을 알 수 있다.
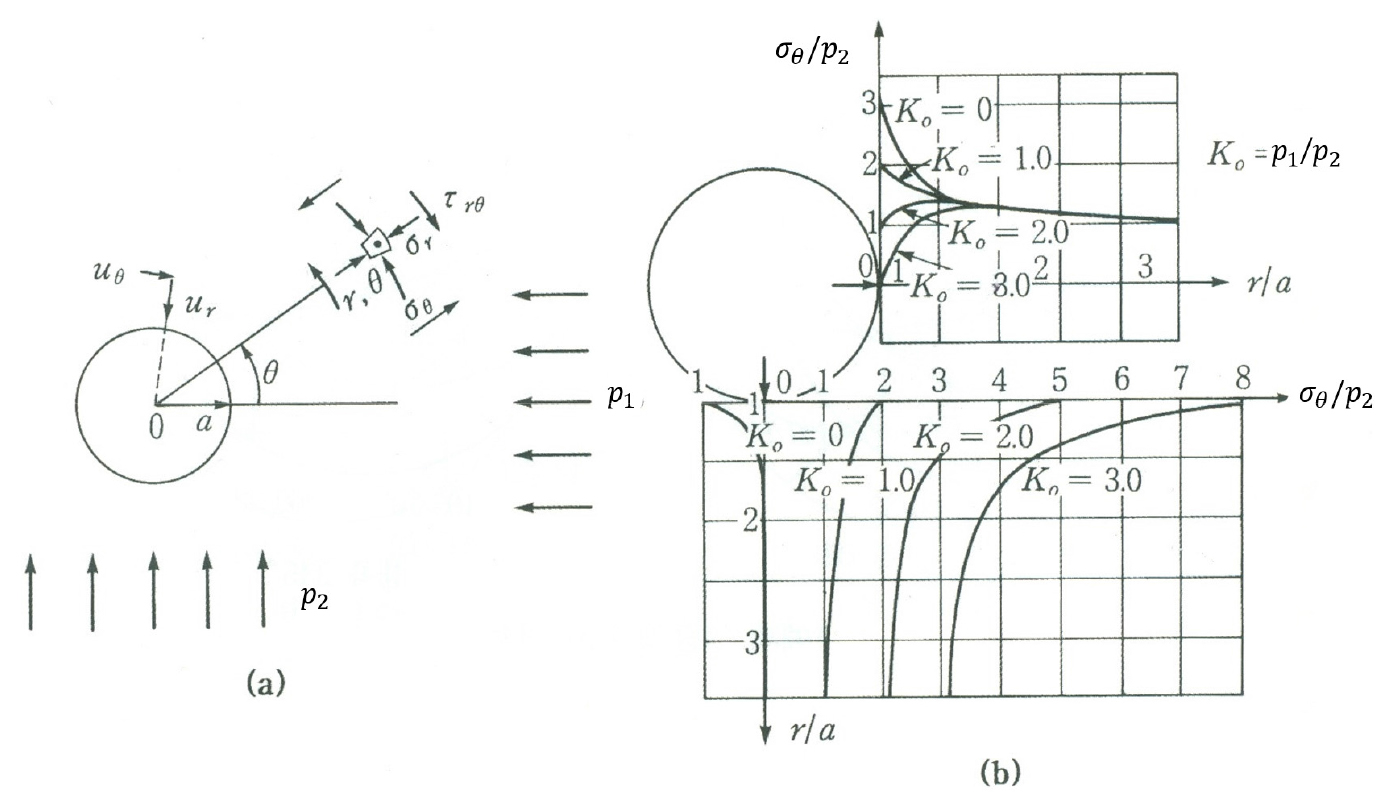
Fig. 2
Stresses around a circular tunnel in an isotropic, linearly elastic, homogeneous continuum (Goodman, 1989)
한편 Fig. 3과 같은 타원형 터널에서 굴착 후의 측벽 A와 천단부 B에서의 접선응력, 및 는 각각 식 (3)과 식 (4)를 이용해 구할 수 있다(Brady and Brown, 1985).
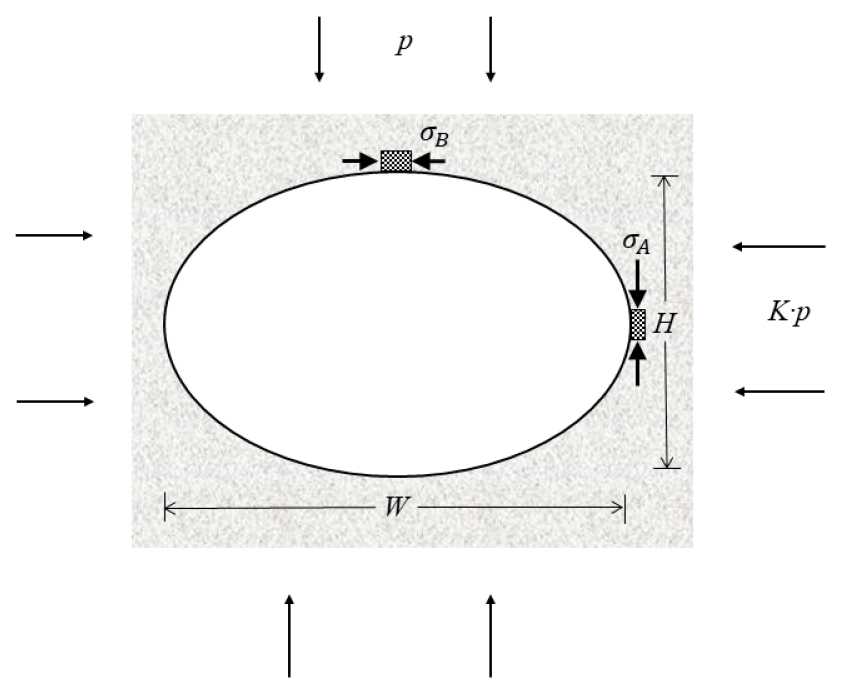
Fig. 3
Definition of nomenclature for an elliptical excavation with axes parallel to the field stresses (Brady and Brown, 1985)
여기서, 와 는 A점과 B점에서의 곡률반경이고, 이다.
따라서 타원형체 터널에서의 측압계수()는 타원의 장반경과 단반경의 비()와 더불어 터널의 경계면의 접선응력에 영향을 주는 것을 알 수 있다.
4. 등가물성치 산정
Song and Cho (2006)는 구근(bulb)과 강관(steel)이 하나의 복합체로 거동할 경우 식 (5)와 같이 등가탄성계수()를 결정하는 방법을 제시하였다.
여기서, 및 는 구군 및 강관의 탄성계수, 및 는 구군 및 강관의 면적이다.
따라서 터널에서 강지보가 숏크리트와 복합체로 거동하거나, 강관다단그라우팅이 지반과 복합체로 거동한다는 가정하는 경우, 식 (5)의 구군과 강관 대신 각각 2가지 다른 매질을 대입하여 적용함으로서 등가물성치를 산정할 수 있다.
5. 유한차분법에 의한 수치해석 모델링
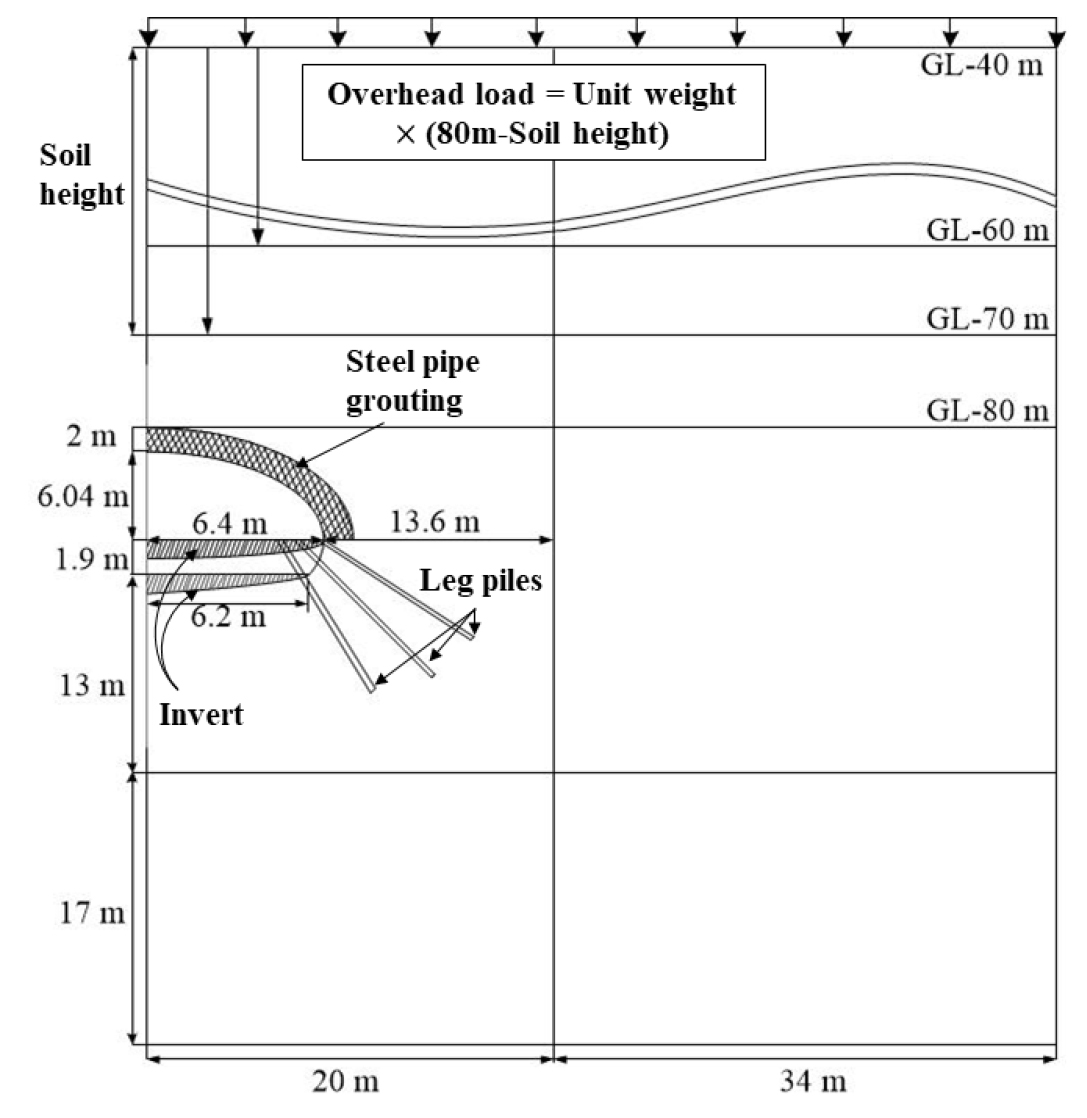
본 연구에서는 연약지반(응회암 변질대)에 위치한 터널 바닥부 곡률의 보강효과에 대해 수치해석적으로 민감도 분석을 수행하고자 하였다. 이를 위해 FLAC 2D 5.0 (Itasca Consulting Group, Inc., 2005)을 이용하여 일반적인 왕복 2차선 도로 터널을 상 ‧ 하부 반단면 분할굴착할 경우에 대해 Fig. 4와 같이 모델링 하였다. 이때, 해석 효율성을 위해 터널의 대칭성을 반영하여 반단면(half-section) 해석을 수행하였다. 또한, 터널 천단부부터 지표면까지의 토피고가 82 m인 상부지반에 대해 GL-40 m, 60 m, 70 m까지를 상재하중으로 처리하였다. 즉, 터널 상부 해석영역의 높이(Soil Height, S.H.)는 각각 40 m, 20 m, 10 m가 되도록 하였다. 한편, 전체 지반영역은 단일층으로 구성된 응회암 변질대(tuff deterioration)로 가정하여 적용하였다.
해석영역은 터널 측벽에서부터 우측으로 약 4D, 바닥에서부터 아래로 약 2.5D만큼으로 설정하였다. 경계조건을 위해 좌 ‧ 우측 및 하단 경계부에서 수평 및 수직변위를 각각 구속하였다. 요소망 크기는 굴진면에서 수직 및 수평 방향으로 1D만큼 인접한 구역은 20 cm로 세밀하게 하고, 외곽으로 갈수록 점진적으로 증가하도록 하여 해석의 효율성과 신뢰도를 높였다. 한편, 지반조건이 연약하여 터널 상부에 대구경 강관 그라우팅 보강을 180°로 적용하였다.
지반, 지보재 및 보강재 물성치는 Table 2와 Table 3과 같이, 응회암 변질대(tuff deterioration, T.D.) 3, 4, 5등급, 숏크리트와 강지보 및 강관다단(steel pipe)과 레그파일(leg pile) 보강영역의 물성치를 Cho (2020) 및 Kim (2021)이 사용한 값을 참고하여 적용하였다. 단, 강지보 및 숏크리트는 보요소로 일체로 거동하는 것으로 가정하여 등가면적을 계산하고, 레그파일은 파괴가 되지는 않는 탄성체 지반요소로 구성하였다. 참고로 Table 3에서 ‘C.T.C.’ 용어는 강지보재와 강관의 종방향 중심간 간격(Center to Center)을 의미한다.
Table 2.
Properties of ground
Table 3.
Properties of supports and supporting materials
Table 4는 지보재인 숏크리트와 강지보재의 물성치를 근거로 계산된 등가 탄성계수를 정리한 것이다. 숏크리트 두께가 0.4 m 경우는 강성을 증가시키기 위해 H-형강의 규격을 H-300으로 상향시켜 해당 물성치를 적용하였다. 또한, 등가 물성값 중에서 단면 2차 모멘트는 강지보재의 값이 매우 작으므로 숏크리트의 값을 그대로 적용하였다.
Table 4.
Equivalent properties of shotcrete and steel rib
6. 수치해석 결과 정리 및 분석
6.1 터널의 안정성 분석
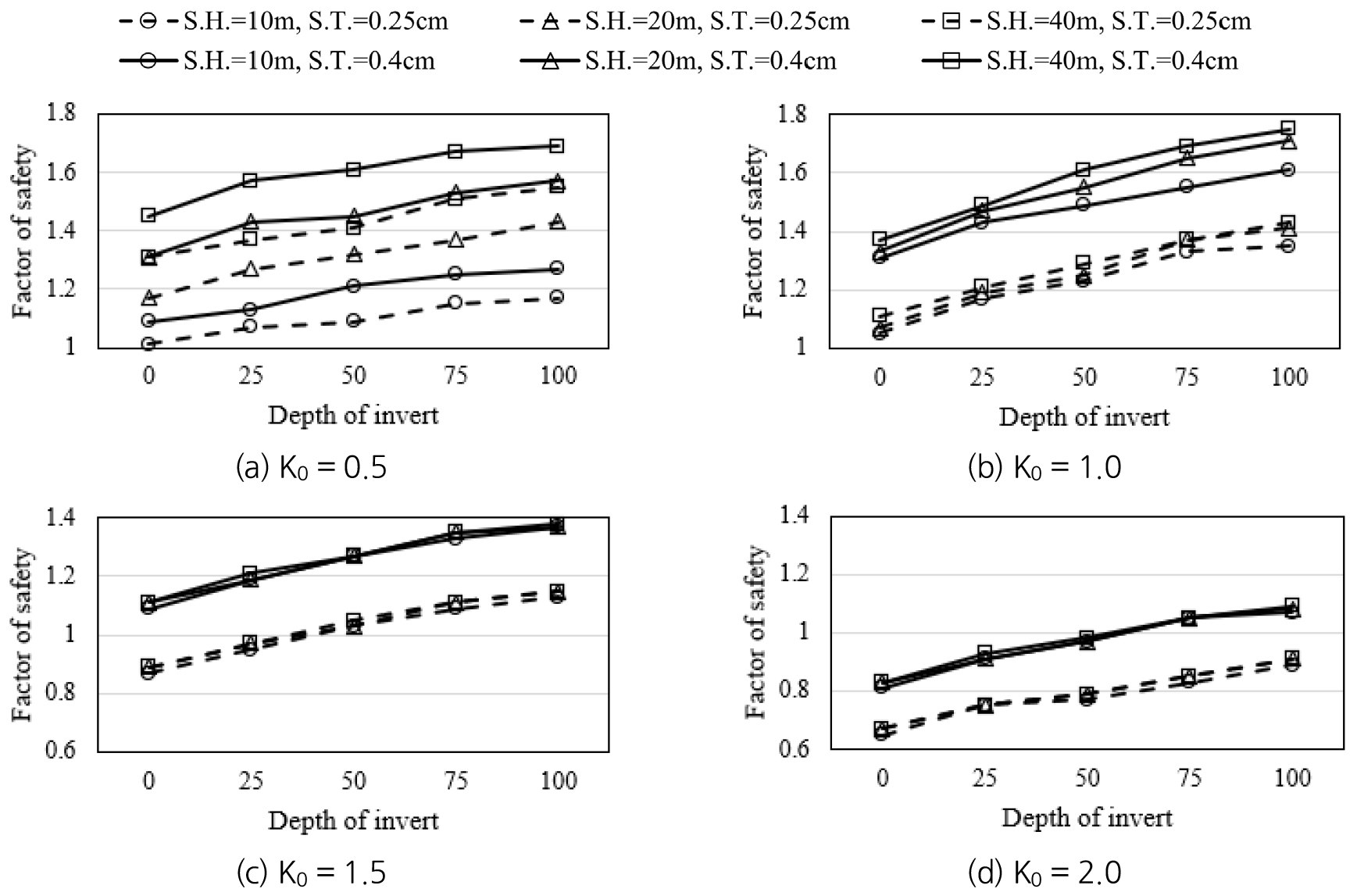
터널 천단에서부터 지표면까지의 상부 지반영역을 상재하중으로 모델링 시 터널의 안정성에 미치는 영향을 정량적으로 확인하기 위해 상부 지반영역, 지보재 두께, 측압계수 및 바닥부 깊이를 달리하여 Table 5와 같이 안전율을 정리하였다. 또한, 측압계수 및 터널 상부지반 해석영역의 높이(Soil Height, S.H.)별로 산출된 안전율의 경향을 Fig. 5와 같이 그래프로 도시하였다.
Table 5.
Factor of safety by depth of invert and soil height (T.D.-5)
해석 결과 전반적으로 바닥부 깊이가 깊어질수록, 터널 상부 해석영역 높이를 크게 모델링할수록 안전율이 크게 산출되는 것으로 나타났다. 특히, K0 = 0.5에서 상부 해석영역을 40 m 높이로 모델링 한 경우가 10 m로 한 경우보다 안전율이 최대 25.1%까지 증가하는 것으로 나타났다. 반면 K0 = 1.5에서 최대 2.2%까지만 증가하는 것으로 나타나, 상부 해석영역의 높이가 안전율에 미치는 영향이 거의 없음을 알 수 있었다. 따라서 측압계수가 작을수록 상부 해석영역이 높을수록 안전율이 커지는 것을 알 수 있었다. 이는 해석영역의 높이가 증가할수록, 측압계수가 켜질수록 각각 활동면의 길이와 수직응력이 증가하여 결과적으로 터널 상부의 파괴활동면에 작용하는 전단응력이 증가하기 때문으로 판단된다.
6.2 터널의 내공변위 비교 ‧ 분석
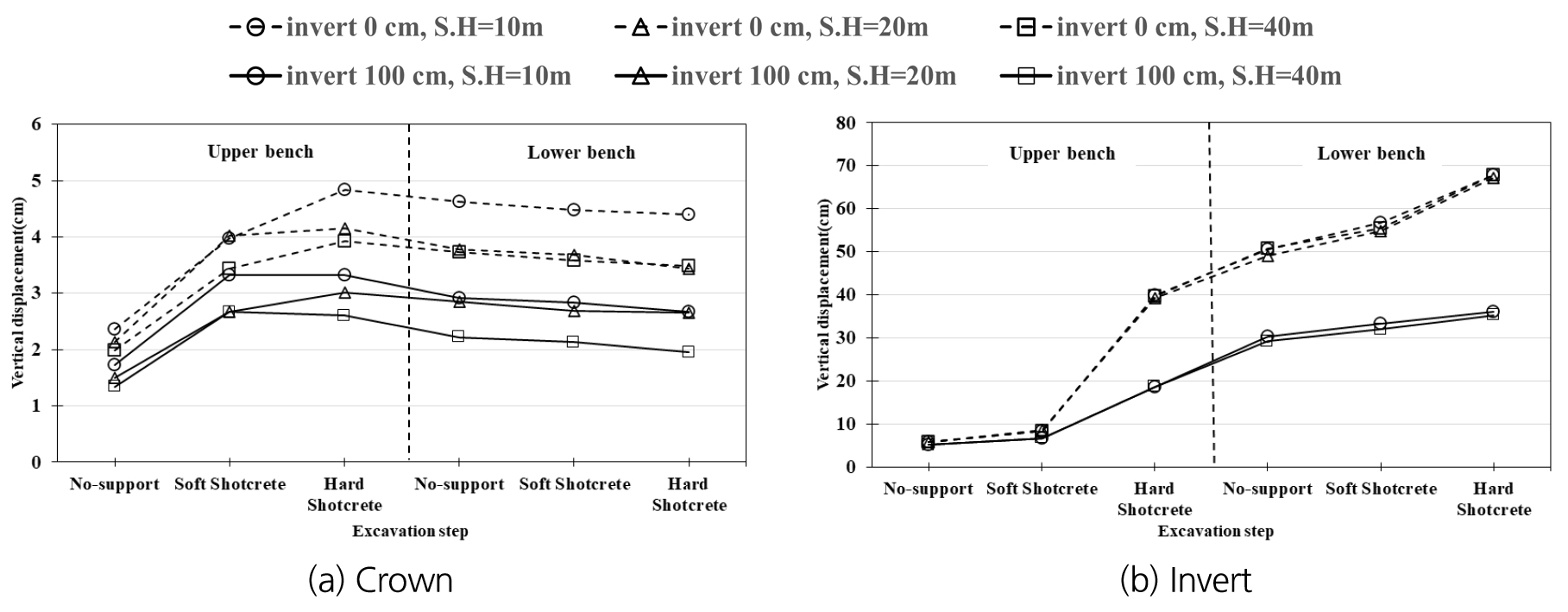
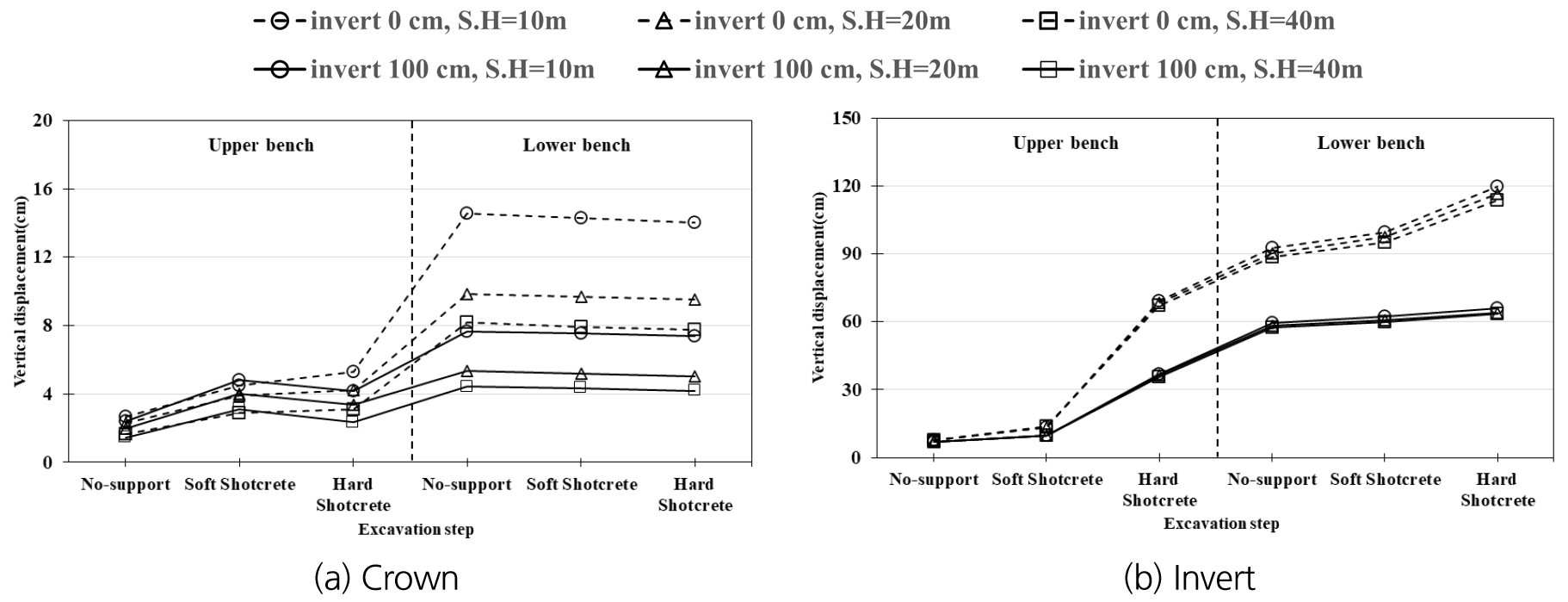
터널 바닥부 깊이 및 상부 해석영역의 높이를 달리해가며 수치해석을 수행하고, 발생된 터널의 내공변위를 분석하였다. 응회암 변질대 지반(T.D.-) 3등급 및 5등급의 경우에, 터널의 바닥부에서 발생된 수직변위를 시공단계별로 각각 Table 6 및 Table 7에 정리하고, Fig. 6 및 Fig. 7과 같이 그래프로 도시하고 경향을 분석하였다. 이때, K0 = 1.5, 지보재 두께는 25 cm로 고정하고 터널의 천단 및 바닥부 변위는 터널 내부방향으로 발생한 변위를 (+)로 나타내었다.
Table 6.
Tunnel vertical displacements by soil height at excavation step (T.D.-3, K0 = 1.5, S.T. = 25 cm) (unit: cm)
Table 7.
Tunnel vertical displacements by soil height at excavation step (T.D.-5, K0 = 1.5, S.T. = 25 cm) (unit: cm)
해석 결과 천단부는 지반 5등급의 경우(Fig. 7(a)), 터널 하부 굴착단계에서 변위가 크게 발생한 반면, 3등급(Fig. 6(a))에서는 상부 경성 숏크리트 단계 이후로 변위가 증가하지 않고 다소 감소하는 것으로 나타났다. 바닥부의 경우 지반조건과 상관없이 상부 연성 숏크리트 단계 이후로 수직변위가 급격하게 크게 발생하는 경향이 나타났다. 터널 상부지반을 더 많이 상재하중으로 처리할수록 천단부에서는 지반 3 및 5등급의 경우, 각각 최대 35.9% 및 47.7%만큼 변위가 증가하였다. 반면 바닥부에서는 지반 3 및 5등급의 경우 각각 최대 2.7% 및 3.3%의 차이를 보여, 터널 상부 해석영역의 높이와 관계없이 거의 유사하게 수직변위가 발생하였다. 이러한 현상은 터널의 토피가 작을수록 천단변위가 크게 발생하는 것과 같은 이유로 설명될 수 있다. 한편, 바닥부 깊이가 0 cm에서 100 cm로 증가할 경우, 지반 3등급에서 천단 및 바닥부의 최대 수직변위가 각각 43.5% 및 48.0%만큼 감소하고, 지반 5등급의 경우 각각 46.9% 및 47.4%만큼 감소하여 바닥부 곡률의 보강효과가 확인되었다.
6.3 지보재 휨응력 비교 ‧ 분석
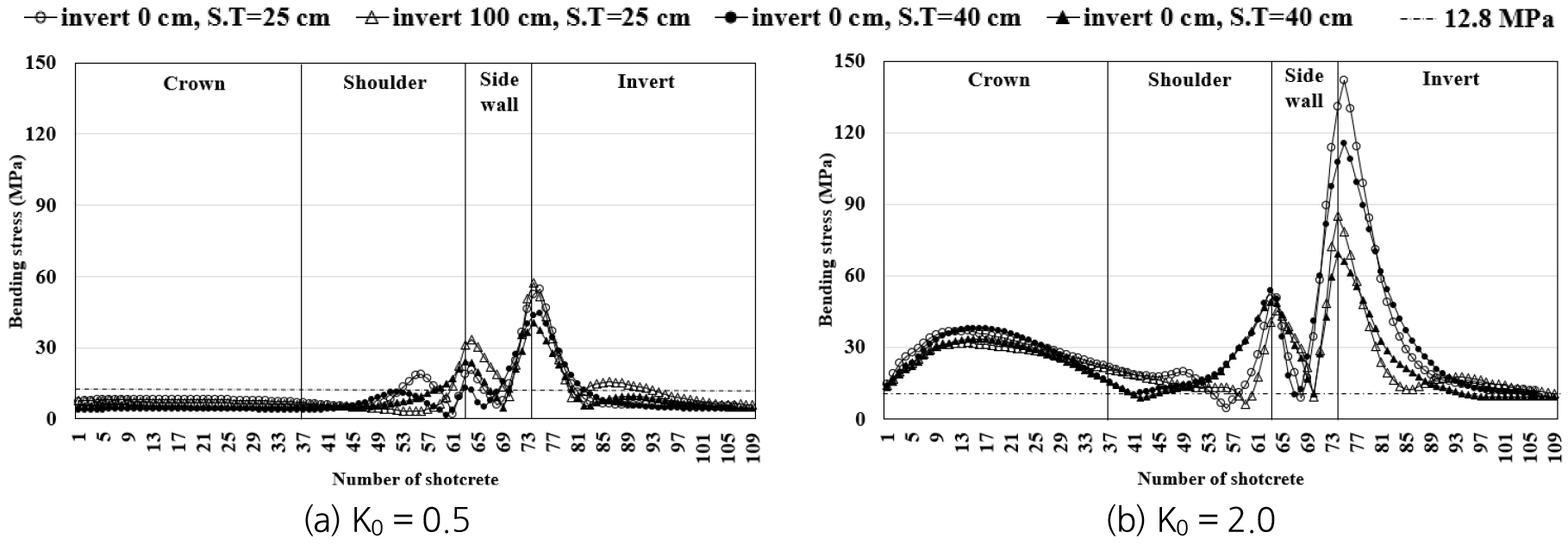
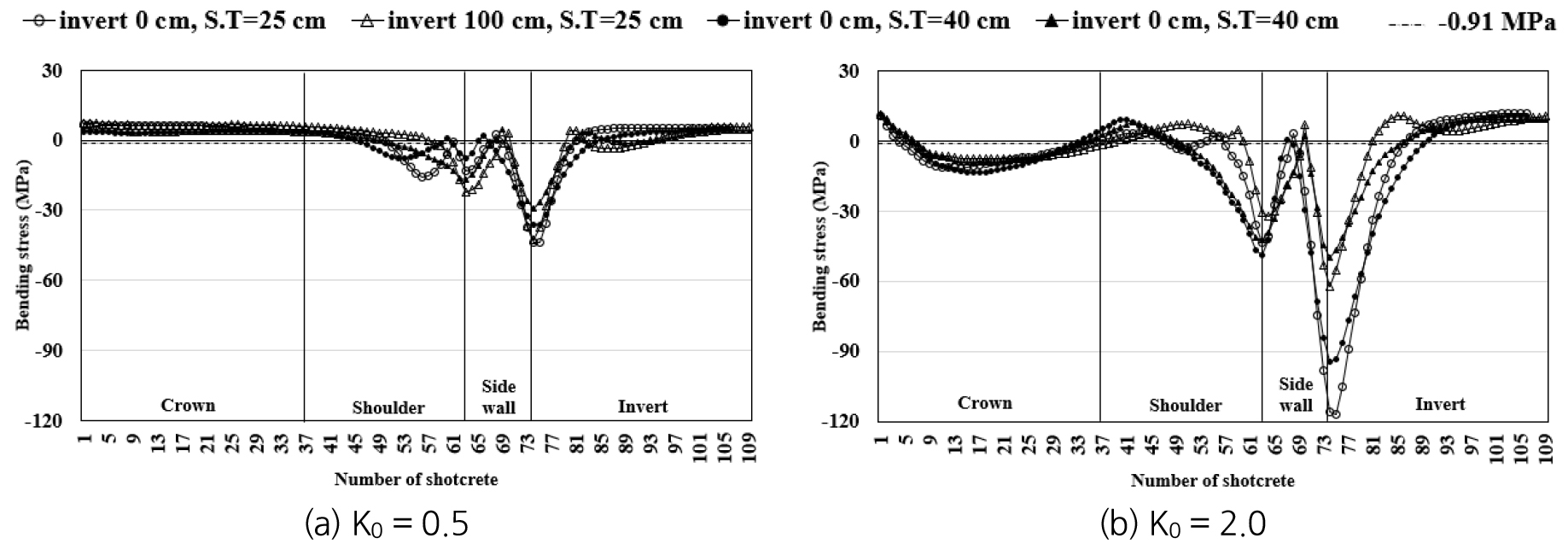
바닥부 곡률을 보강한 터널 및 지보재에 작용하는 응력을 분석하고자 Table 8과 같이 숏크리트 두께 및 측압계수(K0)를 변화시켜가며 바닥부 깊이별로 해석을 수행하였다. 이때 지반조건은 5등급으로 해석영역은 40 m로 고정하였다. 한편 지보재의 파괴영역도 확인하고자 일반적으로 적용되는 허용 휨압축응력 는 12.8 MPa 및 휨인장응력 는 -0.91 MPa를 초과할 경우 파괴된 것으로 판단하였고 파괴 시 잔류강도는 허용 휨압축응력의 절반인 6.4 MPa를 적용하였다.
Table 8.
Maximum bending stresses of shotcrete by depth of invert (T.D.-5, S.H. = 40 m) (unit: MPa)
Fig. 8과 Fig. 9에서 보는 바와 같이, 모든 경우에서 어깨부와 측벽부의 경계부 및 측벽부와 바닥부의 경계 부근에서 허용 휨압축 및 인장응력을 모두 초과하여 파괴가 발생하였다. 특히, 측압계수가 증가할수록 휨응력이 증가하였는데, 2.0일 때 최대휨응력이 압축의 경우 142.0 MPa, 인장의 경우 -116.9 MPa 만큼 크게 발생하였다. 한편, 지보재의 내면부에 작용하는 휨압축응력의 경우 측압계수 0.5를 제외하고 천단부에서 허용 휨압축응력을 초과하였고 지보재 두께를 보강하지 않을 시 어깨부까지 파괴가 발생하였다. 지보재의 배면부에 작용하는 휨인장응력의 경우 내면부와는 다르게 측압계수가 2.0인 경우에 천단부에서 파괴가 발생하였다.
전반적으로 지보재 두께가 두꺼울수록, 바닥부 곡률이 커질수록 최대 휨압축 ‧ 인장응력이 감소하였다. 지보재 두께를 보강할 경우 휨압축 및 인장응력 모두는 최대 31% 정도 감소하였다. 마찬가지로 바닥부 곡률이 커질수록 휨압축 및 인장응력이 최대 40.1% 및 47.4%만큼 감소하여 터널의 안정성이 확보되는 것을 확인하였다.
6.4 터널 주변 지반의 소성영역 분석
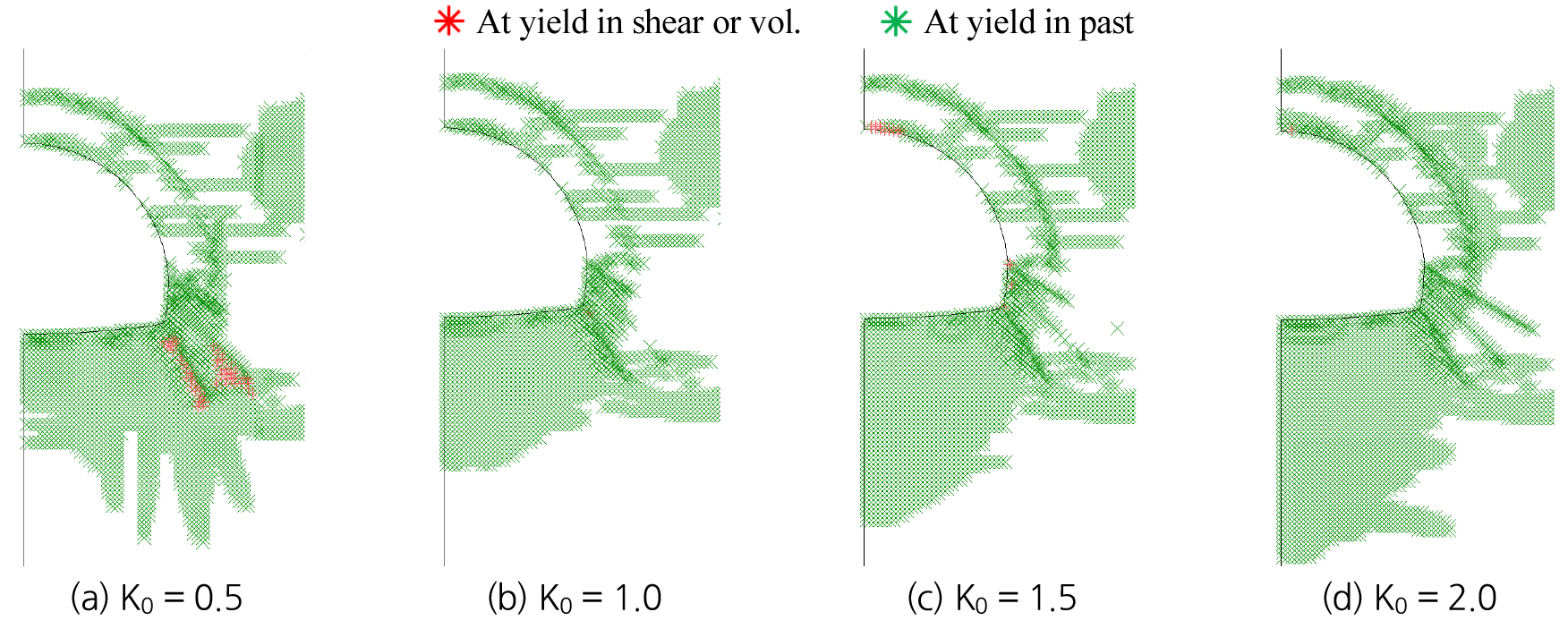
대상 터널 주변 지반의 소성영역을 분석하기 위해 측압계수 및 상부지반영역을 달리하여 터널 주변 지반의 소성영역을 각각 Fig. 10과 Fig. 11에 도시하였다. 이때, 지반조건은 3등급 및 지보재 두께는 25 cm로 고정하였다.
해석 결과 Fig. 10과 같이 측압계수가 커질수록 전반적으로 터널 주변 지반의 소성영역이 확장되는 경향이 나타났다. 특히, 측압계수가 1.5 이상으로 커질 때 터널 바닥부의 소성영역이 약 4 m 깊이 만큼 확장되어 하부 지반이 취약해진 것을 확인하였다.
상부 해석영역 높이별 터널 주변 지반의 소성영역 분포를 Fig. 11과 같이 도시하였다. 터널 바닥부의 소성영역은 변화가 거의 없었으나, 상부 해석 높이를 40 m로 모사한 경우가 10 m 및 20 m로 한 경우와는 다르게 천단부에서 소성영역이 발생하지 않았다. 이는 터널의 토피가 증가한 효과와 같은 이유 때문인 것으로 판단된다.
7. 결 론
본 연구에서는 응회암 변질대에 위치한 터널 바닥부 곡률의 보강효과를 조사하기 위해, 측압계수(0.5, 1.0, 1.5, 2.0) 및 터널 상부 해석영역의 높이(10, 20, 40 m) 등을 변화시켜가며 FLAC 2D ver.5.0을 이용하여 수치해석적 민감도 분석을 수행하였고, 다음과 같은 결론을 도출하였다.
1. 터널 바닥부 곡률이 커질수록 깊어질수록, 터널 상부 해석영역 높이를 크게 모델링할수록, 측압계수가 작을수록 안전율이 크게 산출되는 것으로 나타났다. 이는 해석영역의 높이가 증가할수록, 측압계수가 켜질수록 각각 활동면의 길이와 수직응력이 증가하여 결과적으로 터널 상부의 파괴활동면에 작용하는 전단응력이 증가하기 때문으로 판단된다.
2. 터널 상부의 더 많은 영역을 상재하중으로 처리하면 할수록 천단부의 내공변위가 크게(최대 47.7%) 증가하나, 바닥부의 경우는 큰 차이가 없었다. 이는 터널의 토피가 줄어드는 효과와 같기 때문으로 판단된다.
3. 바닥부 곡률이 켜질수록 천단 및 바닥부에서 발생한 수직변위가 최대 47% 정도 감소하고, 휨응력도 최대 (40~47)% 정도 감소하는 것으로 나타나 터널의 안정성 확보에 도움이 되는 것을 알 수 있었다. 또한, 숏크리트에 작용하는 휨응력은 두께가 감소하고, 측압계수가 증가할수록 켜지는 것을 확인할 수 있었다.
4. 측압계수가 커질수록 전반적으로 터널 주변 지반의 소성영역이 확장되는 경향을 확인하였다. 또한, 터널 상부 해석영역의 높이를 증가시켜 상재하중을 줄일수록 천단부의 소성영역이 줄어들었는데 이는 터널 토피가 증가하는 효과와 같다고 판단된다.
결과적으로 지반조건, 측압계수, 터널 상부 해석영역의 높이와 상관없이 터널 바닥부의 곡률이 커질수록, 지보재 두께가 두꺼울수록 터널의 안정성이 확보되는 것으로 나타났다. 하지만, 본 연구와 같이 토피가 80 m 정도의 연약지반(응회암 변질대)에 위치한 깊은 터널의 경우는 측압계수 및 터널 상부 해석영역의 높이에 따라 해석 결과가 다를 수 있다. 하지만, 본 연구 결과는 2차원 수치해석에 기초한 것으로서 3차원 거동을 하는 실제 터널 현장에 적용하는 데에는 한계가 있을 수 있다. 또한, 큰 응력이 작용하는 대심도의 암반 터널의 경우에도 굴착 시 굴착면의 응력 수준(stress level)이 바뀌어, 본 연구 결과를 활용하는 데에는 무리일 수 있습니다. 한편, 본 연구 결과는 수치해석에 의한 개념적인 결과로서 향후 실제 현장에서의 거동특성이 반영된 계측결과 등을 활용한 추가적인 검증 연구가 필요할 것으로 판단됩니다.