1. 서 론
2. 운용 중 세그먼트에 작용하는 토압산정 방법
3. 현장계측을 통한 세그먼트 작용 하중상태 변화고찰
3.1 Case 1 : ○○선 쉴드터널 계측결과 분석
3.2 Case 2 : 도쿄 ○○선 쉴드터널 계측결과 분석
3.3 Case 3 : ○○지구 공동구 쉴드터널 계측결과 분석
4. 결 론
1. 서 론
국내를 비롯하여 터널 선진국이라 할 수 있는 유럽, 일본 등에서는 기존의 재래식 터널 공법인 NATM 외에 기계화 시공(mechanized tunnelling method) 방식인 TBM 공법 적용이 계속적으로 증가 또는 보편화되고 있다. 이러한 이유는 기존의 NATM 공법 대비 TBM 공법은 터널시공이 어려운 연약지반 조건에서도 시공이 가능하며, 발파공해가 없어 친환경적이고, 천층터널 조건에서 인접구조물의 침하영향을 최소화하여 민원발생 소지가 적다. 추가적으로 공사기간이 단축된다는 점에서 적용사례 증가사유를 찾을 수 있다. 특히 최근 국가철도 공단에서는 쉴드 TBM의 활성화를 위한 기술적 ‧ 제도적 개선사항을 수립하기 위한 여러 가지 노력이 지속되고 있다.
국내의 경우 쉴드 TBM 공사가 마무리 된 이후 “시설물의 안전 및 유지관리에 관한 특별법”에 따른 구조물 유지관리에만 초점을 맞추고 있어 쉴드 TBM 터널의 안정성 변화여부 파악이 불가한 상황이다. 그러나 일본의 경우 시공완료 이후 다양한 쉴드 TBM 계측관리를 통해 안정성 변화유무를 파악하는 연구자료가 다수 보고되고 있다(Lee et al., 2012; 2017). 이를 통하여 설계단계에서 예측한 세그먼트 라이닝의 작용하중 상태가 운용 중 어떠한 형태 및 크기로 작용하는 지를 파악할 수 있다.
직경 7.5 m 이상의 지하철 쉴드 TBM 터널의 경우 전체 공사비 중 약 25~40%로 가장 큰 비중을 차지하는 세그먼트 공사비의 절감을 위하여 합리적인 세그먼트 설계기법 및 신재료의 적용을 위해서는 쉴드 TBM 터널의 운영 중 안정성 변화추이 파악이 많은 도움이 된다(Lee et al., 2017).
따라서 본 논문에서는 쉴드 TBM 시공경험 및 관련연구가 풍부한 일본 쉴드 TBM 터널의 계측결과 분석을 통해 터널 시공 및 운용 중 외부하중 조건 등의 변화추이를 고찰하고 설계 시 예상치와 계측값의 차이를 분석함으로서 경제성 확보를 위한 설계 개선사항을 연구하고자 하였다.
2. 운용 중 세그먼트에 작용하는 토압산정 방법
세그먼트 라이닝은 지반하중과 수압을 지지하는 지하구조물로써의 기능과 함께 시공 중 쉴드기의 추진을 위한 반력대 기능도 함께 수행하여야 하며 공장에서 제작되어 적치, 운반 후 쉴드장비 내에서 설치되므로 세그먼트는 다양한 하중조건에 노출되게 된다. 따라서 시공 및 운용 중 세그먼트에 작용하는 다양한 하중조건을 고려한 안정성 검토가 필요하다(Kim et al., 2017).
본 논문은 운용 중에 시행한 계측자료 분석을 통한 세그먼트 라이닝 응력 및 변위 상태가 설계단계와 상이한 특성을 보이는지 여부를 파악하기 위한 것에 초점을 맞추고 있음에 따라 설계 시 지반조건에 따른 이완하중에 대한 산정방법을 고찰하였다.
토사지반을 대상으로 한 지반 이완토압의 기본식은 Terzaghi의 이완 토압 산정식인 Fig. 1을 따른다. 토피고가 얕거나 지반조건이 매우 불량한 경우는 터널 토피고 전체를 적용하여 연직토압을 산정하지만 보통의 조건에서는 굴착에 따른 지반이완을 고려한 연직토압을 산정한다. 이완하중 산정방법으로는 여러 가지 방법이 있으나 지반의 전단강도와 토피고를 고려할 수 있으며 보수적인 값을 보이는 Terzaghi 이완하중 산정방법이 주로 사용된다.
수평토압은 세그먼트가 설치되는 지반조건(점성토 및 사질토)에 따라 산정방향을 달리한다. 점성토 지반의 경우 토압과 수압이 일체로 작용하는 반면(토수일체), 사질토 지반에서는 토압과 수압이 분리해서 작용(토수분리)한다는 가정 하에 토압을 산정하게 된다(Table 1 참조).
Table 1.
Calculation of vertical and horizontal loads
| Clay | Sand | ||
 |  |  |  |
| Consider water and earth pressure together | Consider water and earth pressure separately | ||
지하수위 하부에 터널이 시공되는 경우 토압과 수압을 모두 고려하여야 한다. 사질토에서는 토압과 수압을 분리하는 토수분리 방법을 적용하여야 하며, 이 경우의 이완토압은 다음과 같이 산정한다.
여기서, : 지하수위면에서의 이완 토압(kPa)
: 링 정상부에 작용하는 이완 토압(kPa)
: 수평 토압과 연직 토압의 비
𝜙 : 흙의 내부마찰각(°)
: 흙의 점착력(kPa)
𝛾 : 흙의 단위체적중량(kN/m3)
𝛾′ : 흙의 수중 단위체적중량(kN/m3)
2 : 링 정상부의 이완폭(m)
: 상재하중(kPa)
: 토피 두께(m)
: 지하수위면까지의 토피 두께(m)
: 세그먼트 도심선의 직경(m)
점성토 지반의 경우 점착력 C≠0, 𝜙 = 0이라는 특성을 고려하여 다음의 식으로 산정한다.
다층지반의 경우에는 상부의 층부터 차례로 층 경계에서의 (n번째의 층 경계)을 계산하고, 이후 이 층의 경계를 지표면으로 하여 을 상재하중으로서, 그 아래층 경계에 대한 을 계산하고, 끝으로 터널 정상부에서의 를 구하며, 다음의 식을 따른다.
여기서, : 층 경계에서의 이완 토압(kPa)
: 링 정상부의 이완 토압(kPa)
: 수평 토압과 연직 토압의 비
, : 제 1, 2층의 토피 두께(m)
, : 제 1, 2층의 흙의 내부마찰각(°)
, : 제 1, 2층의 흙의 점착력(kPa)
, : 제 1, 2층의 흙의 단위체적중량(kN/m3)
2 : 링 정상부의 이완폭(m)
: 상재하중(kPa)
: 세그먼트 도심선의 직경(m)
3. 현장계측을 통한 세그먼트 작용 하중상태 변화고찰
3.1 Case 1 : ○○선 쉴드터널 계측결과 분석
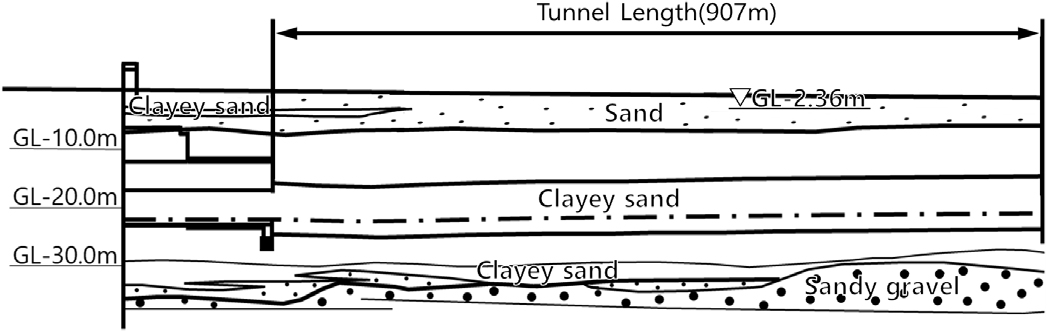
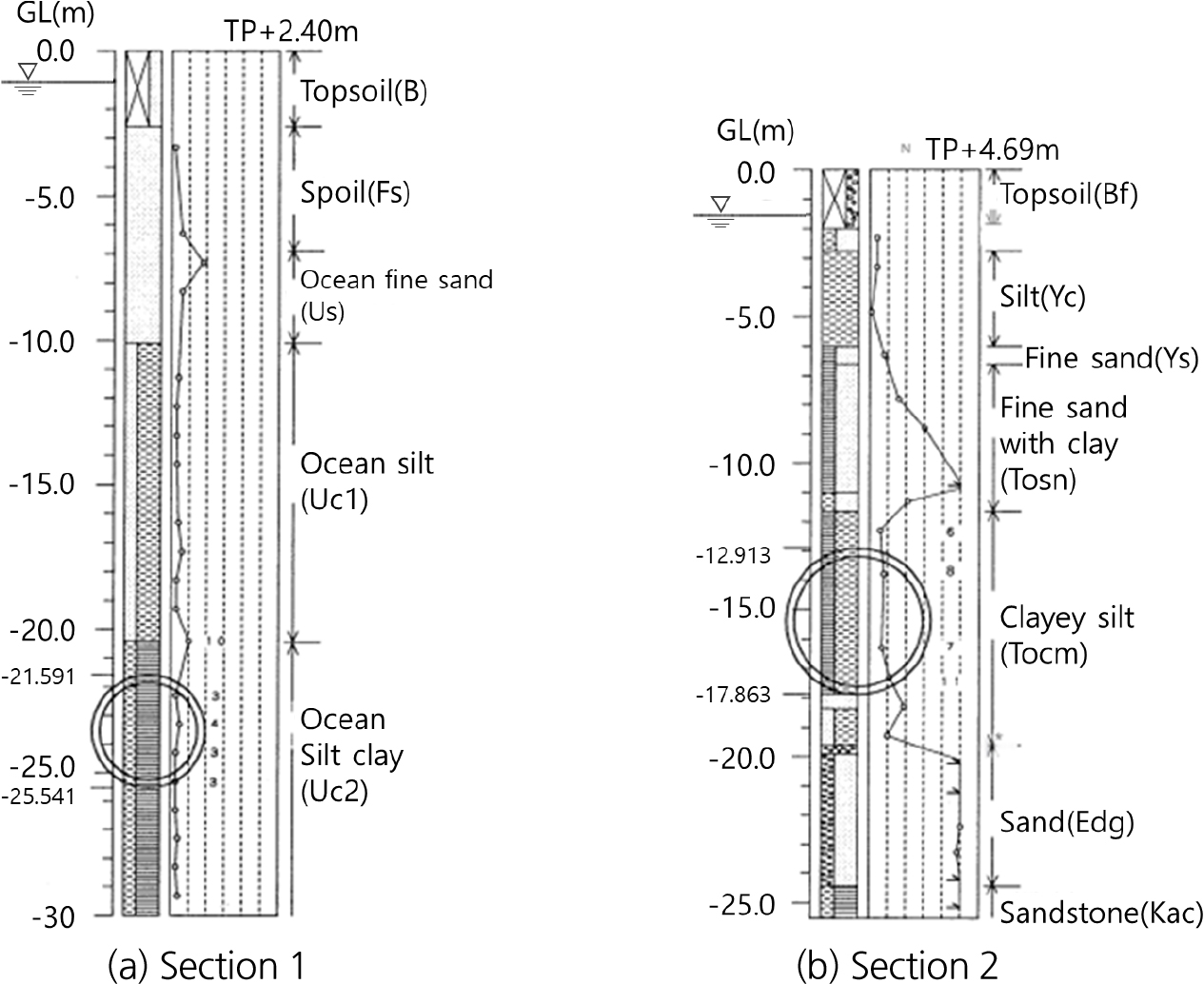
본 현장은 지하철 ○○선 쉴드터널 현장으로써 이토압식 쉴드공법을 이용하여 총연장 907 m의 지하철 터널을 시공하였다(Ariizumi et al., 1998). 세그먼트는 외경은 9.4 m에 두께는 440 mm인 RC세그먼트가 사용되었으며 터널 통과구간의 지반조건은 N치 0~4타의 연약한 충적 점성토층이다. 터널 종단 및 형상은 각각 Fig. 2 및 Table 2와 같다.
Table 2.
Overview of ○○ line tunnel layout
| Tunnel length | 907 m | 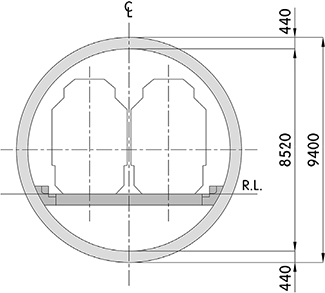 | |
| Shield external diameter | 𝜙 9,600 mm | ||
| Average depth | 13.7~15.4 m | ||
| Segment | Type | RC segment | |
| External diameter | 𝜙 9,400 mm | ||
| Thickness | 440 mm | ||
| Width | 1,500 mm | ||
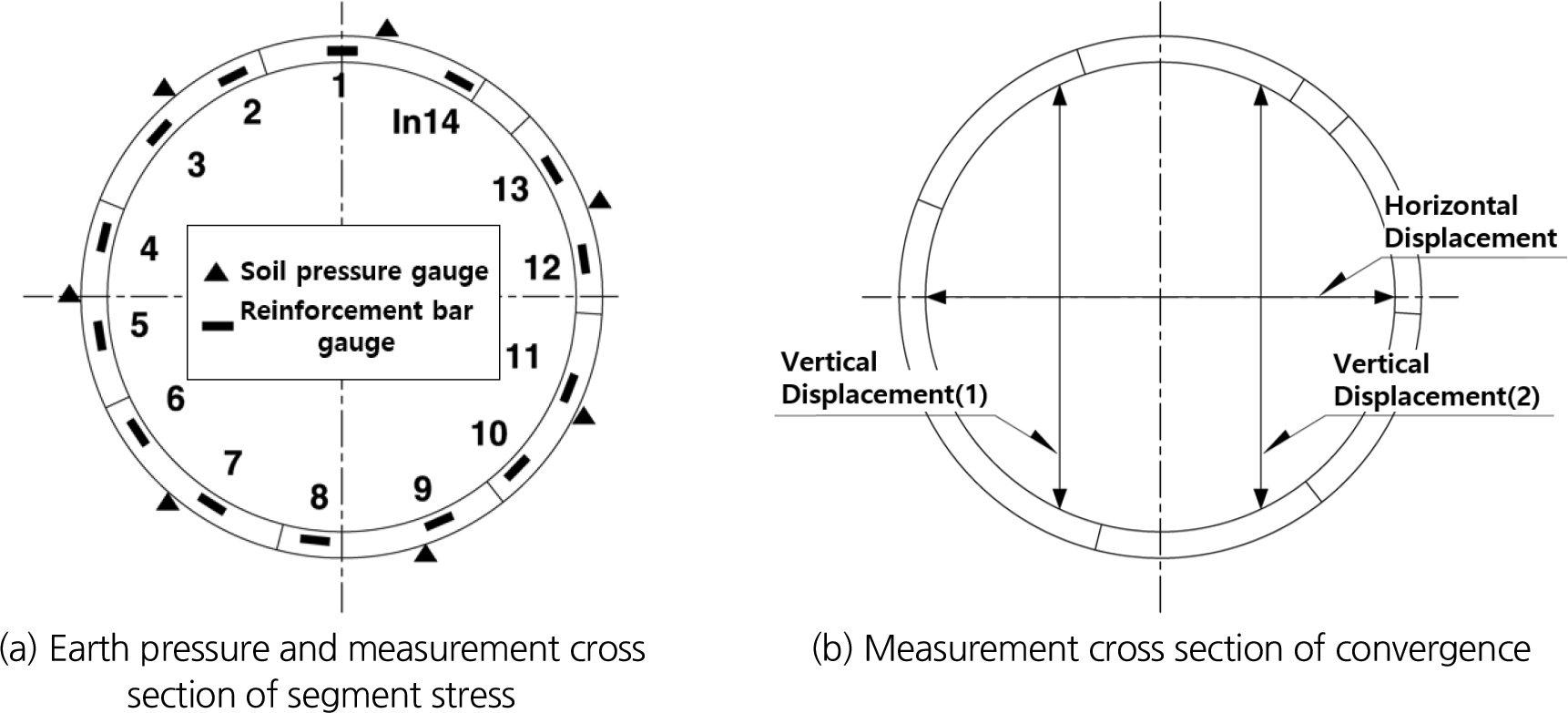
세그먼트에 작용하는 토압 및 휨모멘트, 축력 등을 계측하여 시공 중 및 운용 중 세그먼트 거동을 파악하기 위하여 터널 내 2개소에서 변위 및 세그먼트 응력 계측을 측정하였다. 주요 계측기기 배치상황은 Fig. 3과 같으며 계측기간은 장기적인 세그먼트 거동파악을 위하여 세그먼트 조립직후부터 8개월간 계측을 시행하였다.
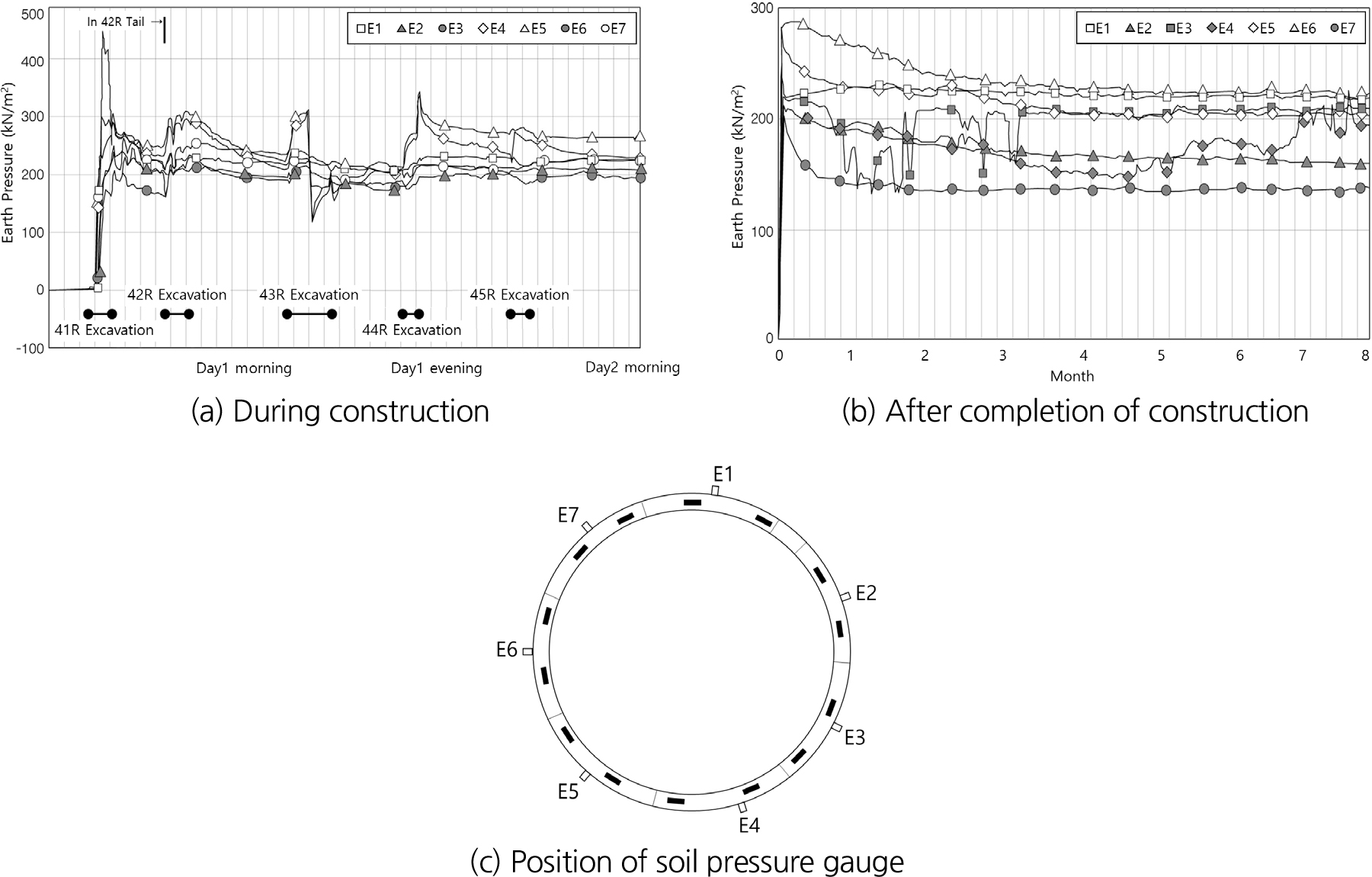
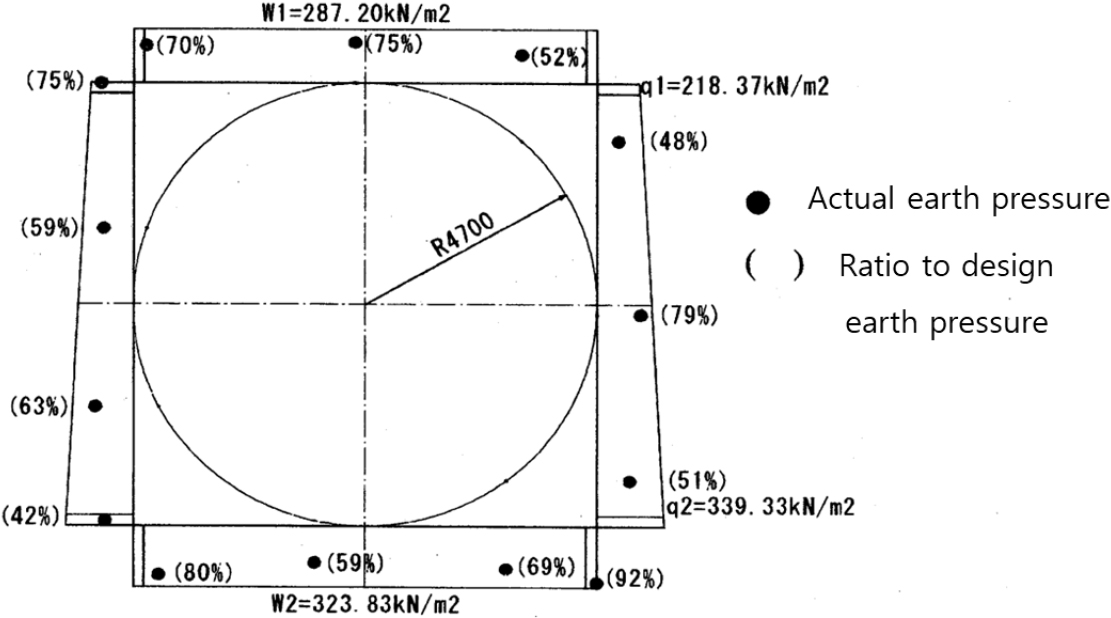
시공 중 세그먼트에 작용하는 하중은 굴진 및 세그먼트 조립을 할 때마다 큰 압력 변화를 보인다. 세그먼트 조립 직후에는 터널 벽면과 tail seal의 접촉으로 인해 약 170~280 kN/m2이나 뒤채움재 주입압(3.58 kN/m2)으로 인해 최대 320 kN/m2까지 상승했다가 4링을 굴진한 약 1일 경과 후 뒤채움재가 경화됨에 따라 약 200~290 kN/m2으로 안정화된 경향을 보인다(Fig. 4). 세그먼트의 초기 하중이후, 시간 경과에 따라 서서히 감소하는 경향을 보이며 3개월 경과 후에는 감소량이 거의 없어지면서 6개월가량 경과하면서 일정한 값에 수렴하였다. 세그먼트 계측값이 안정됐다고 판단한 8개월 후의 설계 시 예상하중과 비교해보면, 설계하중에 연직하중은 52%~75%, 수평하중은 48~79% 보이는데(Fig. 5 참조) 이는 뒤채움재 경화에 따른 뒤채움압의 소산과 굴착에 따른 토압이 주변 지반 및 세그먼트 구조물에 재분배되면서 결과적으로 세그먼트에 작용하는 하중이 보다 작은 값으로 보이는 것으로 추정된다.
3.2 Case 2 : 도쿄 ○○선 쉴드터널 계측결과 분석
당 현장은 도쿄대학에서 발진하여 코라쿠엔역에 도달하는 총연장 1,064 m의 ○○선 ○○공구로써 이수식 쉴드공법을 이용하여 복선쉴드터널을 건설하였다(Yahagi et al., 2004). 쉴드외경은 10.0 m이며 세그먼트 외경은 9.8 m이고 RC 세그먼트 2종류 및 ductile 세그먼트 3종류가 사용되었다. 세그먼트 라이닝 설치 후 두께 150~200 mm의 2차 라이닝콘크리트 및 인버트 콘크리트를 타설하였다. 상세한 계측현장 개요 및 터널단면은 Table 3과 같다.
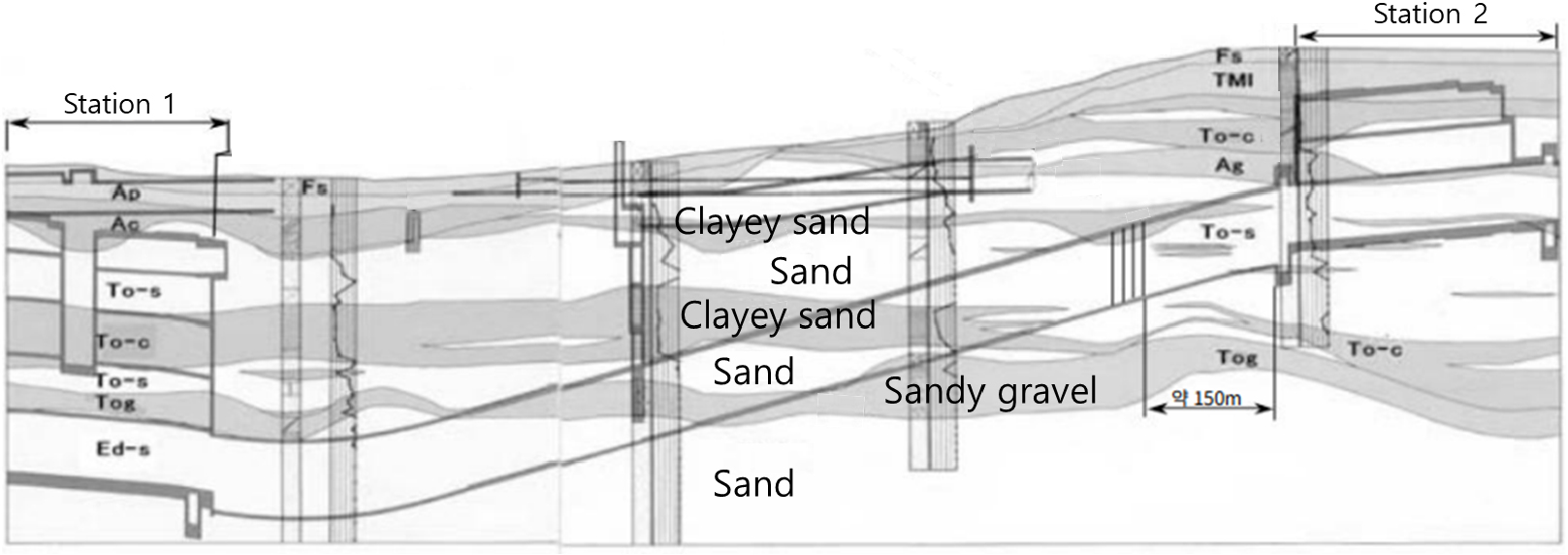
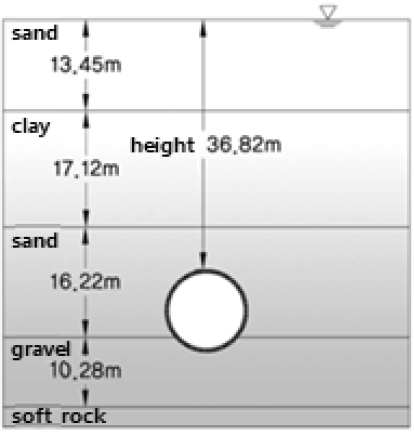
터널 관통부의 지반조건은 Fig. 6과 같이 도쿄층의 사질토 및 점성토, 역암층 및 제4기 홍적세층이 존재하며 대부분의 구간에서 N치 40 이상의 양호한 도쿄 사질토층을 통과하고 있다.
Table 3.
Overview of ○○ line tunnel layout
| Tunnel length | 1,064 m | 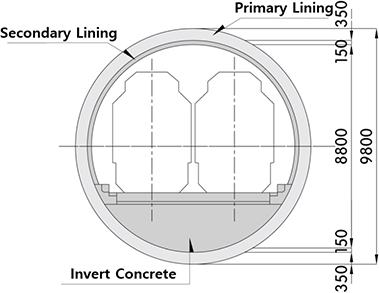 | |
| Shield external diameter | 𝜙 10,000 mm | ||
| Average depth | 17.5 m | ||
| Segment | Type | RC segment, Ductile segment | |
| External diameter | 𝜙 9,800 mm | ||
| Thickness | 350 mm | ||
| Width | 1,000 mm | ||
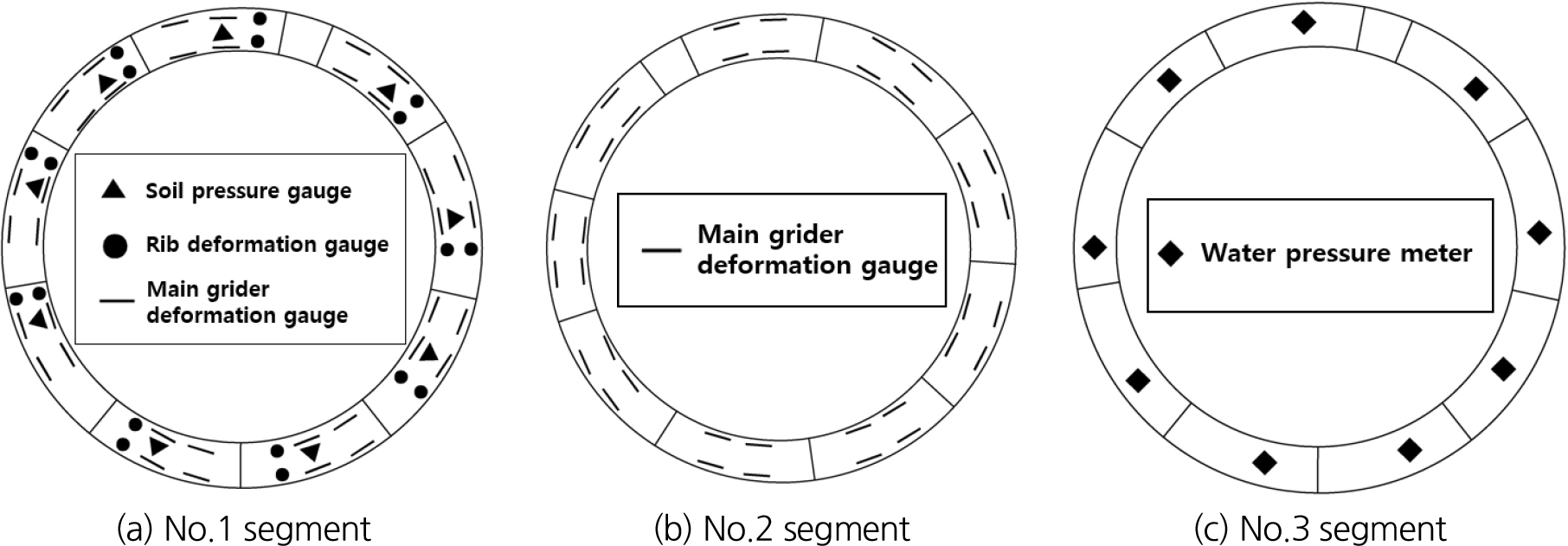
세그먼트에 작용하는 하중(토압 및 수압)과 세그먼트 응력에 대하여 계측을 실시하였으며 계측기기는 Fig. 7과 같이 3링에 연속적으로 배치하여 No.1링에서는 토압계와 변형계를 설치하였고 No.2링에는 변형계, No.3링에는 수압계를 설치하였다. 계측기간은 장기간동안의 세그먼트 작용하중 변화를 확인하기 위하여 세그먼트 조립직후인 1993년 7월에 시작하여 3,832일(약10년)후인 2004년 1월까지 실시하였다.
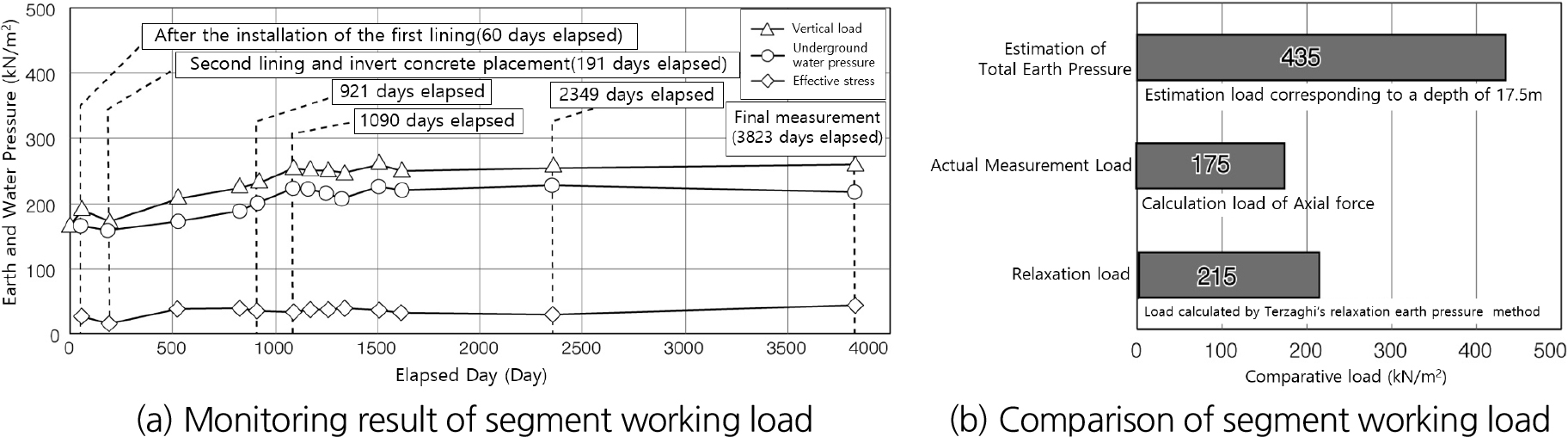
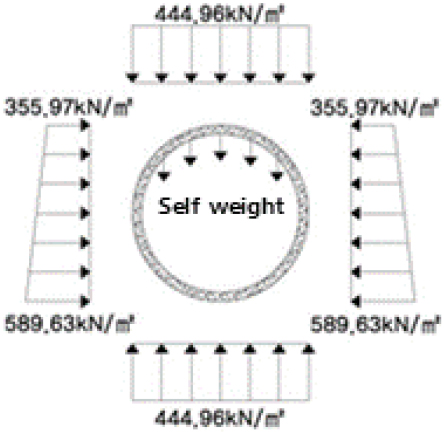
시공 중 세그먼트에 작용하는 하중은 굴착으로 인한 수압변화가 안정된 후에는 완만한 변화를 보이다가 2차라이닝 및 인버트 콘크리트가 타설된 후 다시 변화를 보이고 안정화되기까지 약 1,000일간이 소요되었다(Yahagi et al., 2004). 2차라이닝 및 인버트 콘크리트 자중 및 건조수축의 영향으로 인한 연직하중 증가는 약 84 kN/m2, 인버트 콘크리트가 시공되고 있는 하부 측면하중 증가는 약 270 kN/m2가량으로 이는 기존 작용하중의 약 30% 이상인 값으로써 이로 인해 터널에 작용하는 하중형태에 큰 변화가 발생하였으므로 2차라이닝 및 인버트 콘크리트가 세그먼트의 응력상태에 미치는 영향을 작용하중으로 환산하면 무시할 수 없는 것이라고 할 수 있다. 본 터널은 열차 하중 등도 고려할 필요가 있지만, 주변의 지반조건 및 뒤채움 주입의 경화 등을 생각하면 하중이 누적되어 있다고 보기는 어렵다. 이 때문에, 인버트 콘크리트에 의한 건조수축에 의한 영향이 큰 것으로 판단했다. 반면 운영 중 터널 내 열차운행에 따른 하중증가는 미소한 것으로 나타났는데 이는 뒤채움재의 경화, 주변지반조건 변화 등으로 인한 것으로 판단된다. 터널에 작용하는 하중이 안정화된 후 터널에 작용하는 연직하중을 추정해보면 정수압(259 kN/m2)과 2차라이닝 및 인버트 콘크리트 하중(84 kN/m2)을 제외한 순수토압은 175 kN/m2가량이 되어 1차 라이닝의 안정기로부터의 토압의 변화는 거의 없고, 수압의 상승 등에 의한 수압의 변화라고 판단된다. 이는 전체토피하중 435 kN/m2의 40% 이하 값이며 Terzaghi 이완토압 산정방법에 의한 하중값 215 kN/m2의 값의 약 81% 수준으로 약간 작게 나타났다(Fig. 8). 따라서, 본 터널을 구성하고 있는 홍적지반은 비교적 자립성이 높았던 것으로 보인다.
3.3 Case 3 : ○○지구 공동구 쉴드터널 계측결과 분석
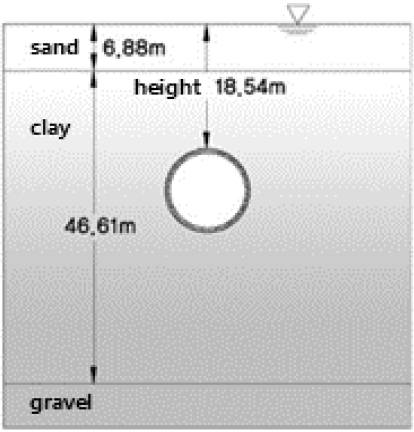
본 계측현장은 ○○시 전력구 쉴드터널 현장으로 이수식 쉴드공법을 이용하여 총연장 1,866 m의 터널을 시공하였다(Yahagi et al., 2002). 세그먼트 외경은 3.95 m이며 두께는 275 mm, 폭은 1,200 mm인 RC세그먼트가 사용되었다. 터널 통과부의 지반조건은 Fig. 9와 같이 토피고 21.6 m의 충적층 실트질 점토지반으로 N치 3~4타인 연약한 지층조건을 보인다. 상세한 계측현장 개요 및 터널단면은 Table 4와 같다.
Table 4.
Overview of measurement site
| Tunnel length | 1,866 m | 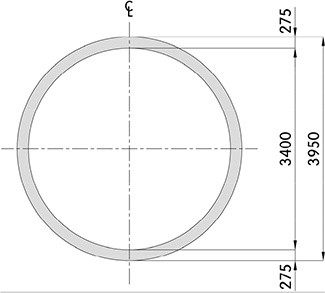 | |
| Average depth | 21.6 m | ||
| Segment | Type | RC segment | |
| External diameter | 𝜙 3,950 mm | ||
| Thickness | 275 mm | ||
| Width | 1,200 mm | ||
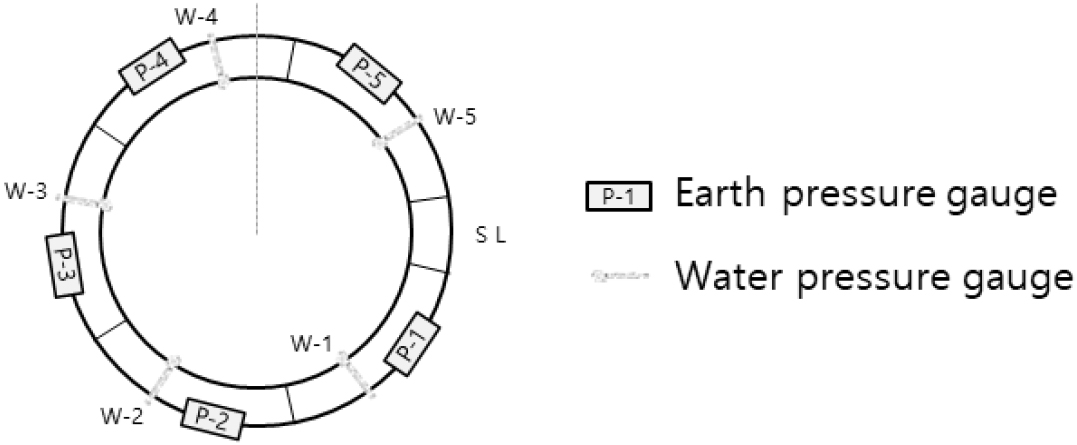
세그먼트에 작용하는 하중(토압 및 수압)과 세그먼트 응력을 계측하기 위해 토압계 및 간극수압계, 세그먼트 변형계를 Fig. 10과 같이 설치하였으며, 계측기간은 세그먼트 조립직후부터 약 1년 후까지 실시하였다.
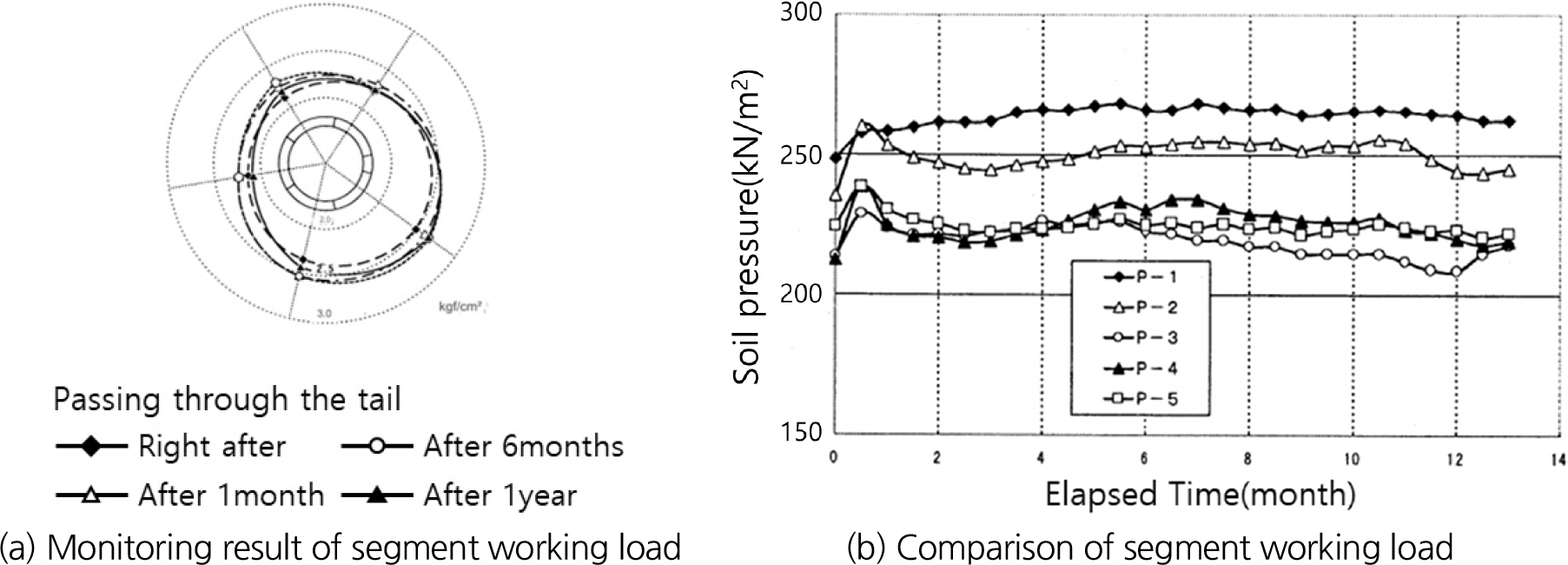
Fig. 11은 세그먼트 설치 이후 0.5개월 간격으로 측정한 토압의 변화를 계측기 설치위치별로 나타낸 것이다. 터널 단면상에서 위치별 토압분포는 비대칭형상을 보임에 따라 우측하단(P-1) 및 바닥부(P-2)에 위치한 토압계에서 최대토압은 약 250~270 kN/m2을 보이며, 다른 위치(P-3~P-5)에서는 약 225 kN/m2 정도의 토압이 1년여 동안 일정하게 발생하는 것을 알 수 있다.
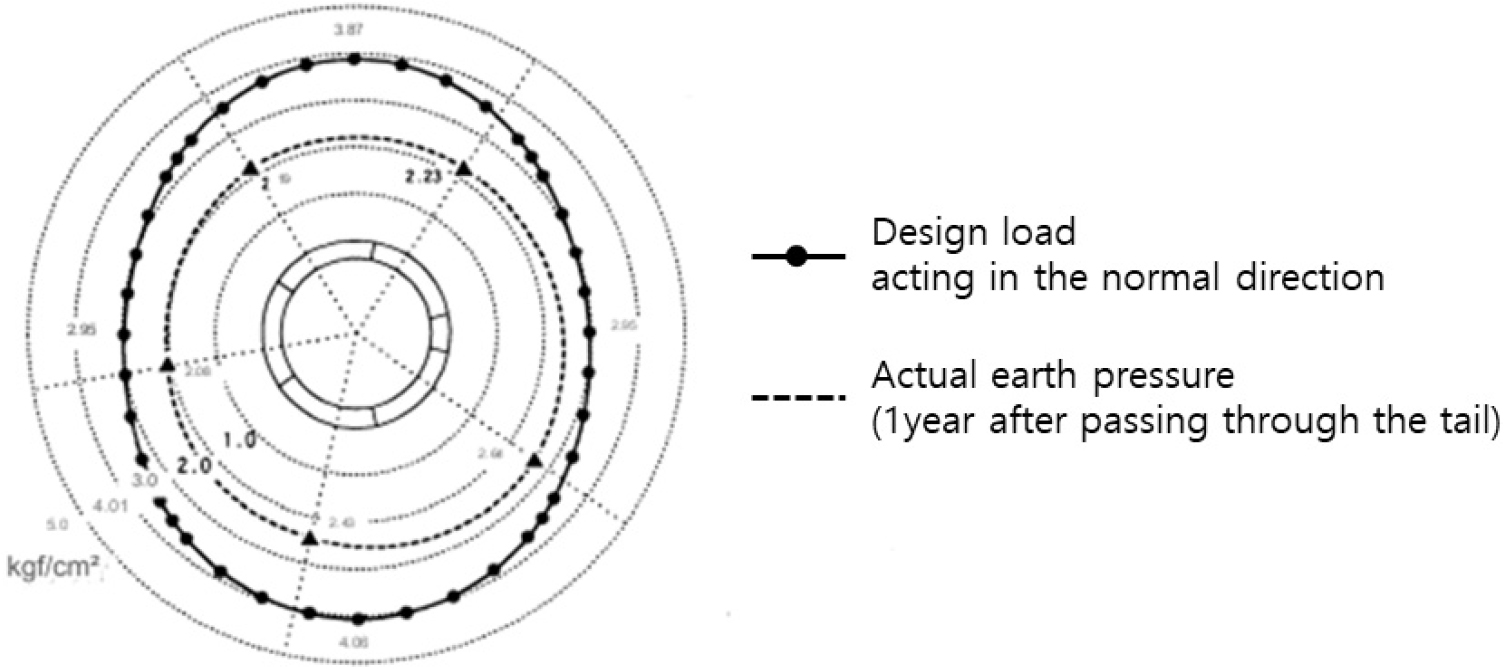
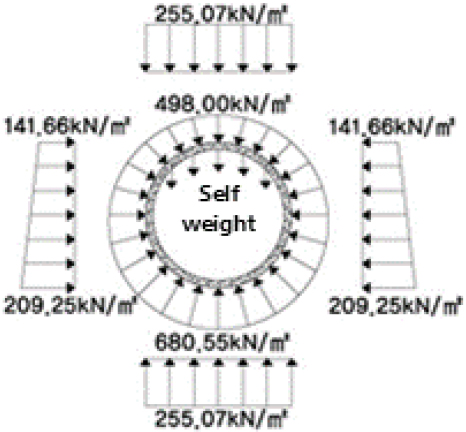
토압계로 계측되는 토압은 세그먼트 원주면에 수직인, 즉 법선 방향의 전체 토압을 계측하는 것이다. 즉, 접선방향의 하중은 계측이 불가하다. 따라서 간접적으로 Terzaghi 계산법에 의한 연직하중과 수평하중의 합력을 이용하여 접선방향 성분 대비 측정된 토압을 Fig. 12와 같이 도시하였다. 천정부의 연직하중은 설계치가 약 368 kN/m2이며, 실측된 토압은 220 kN/m2로서 설계값이 약 67% 높은 값을 보이고 있다. 이는 바닥부의 토압분포도 유사한 경향을 보이고 있다.
4. 결 론
국내에서는 쉴드 TBM에 실제로 작용하는 운용 중 토압분포에 대한 계측자료가 전무하다. 일본의 경우 국내대비 많은 쉴드 TBM 공사실적이 있으며, 운용 중 세그먼트에 작용하는 토압관련 계측결과 분석에 대한 연구가 다수 진행되었다. 본 고에서는 운용 중 세그먼트에 작용하는 토압에 대하여 설계 대비 실측치를 상호비교함으로서 설계단계에 사용하는 토압에 대한 대소여부를 판단하고자 하였으며, 주요 결과는 다음과 같다.
1. 토사지반에 시공되는 쉴드 TBM 설계의 경우 운용 중 작용 토압은 Terzaghi의 이완토압을 기본식으로 하며, 분포하는 대상지반 조건에 따라 점토지반의 경우 토수일체, 사질토 지반의 경우 토수분리 개념을 이용한 이완토압을 산정하여 설계하고 있다.
2. 총 3개 Case의 운용 중 세그먼트에 작용하는 토압 계측결과를 분석하였다. 분석결과 모든 Case에서 설계 시 토압은 운용 중 작용 토압 대비 작은 값을 보였으며, 대부분의 경우 최소 40%~최대 60%에 해당하는 토압이 실제로 작용하고 있는 것으로 분석되었다. 수압의 경우 설계 시 값과 유사한 값을 보였다.
3. 세그먼트에 작용하는 하중은 시공 중 하중(적재하중, 뒤채움 하중 등)과 함께 운용 중 하중(토압, 수압 등)을 모두 고려한 설계를 수행한다. Case 1의 경우 뒤채움 공종 시 운영 중 토압하중 대비 높은 값을 보이며, 이를 고려하여 설계 시 뒤채움 압력에 대한 안정성 검토를 수행함이 바람직하다 판단된다.
4. 운영 중 토압은 설계 시 예상 토압보다 작은 값을 보임에 따라 전체 공사비의 약 30~40%를 차지하는 세그먼트의 경제적 설계가 가능하다는 것을 보여주는 상황이다. 따라서 설계 시 최악 조건 또는 최대 단면력이 발생되는 위치의 철근 보강량을 전구간에 적용하는 비경제적 설계임에 따라 지층조건에 따른 철근보강량 차등 적용의 방안 수립이 가능할 것으로 판단된다.
5. 세그먼트 설계를 위한 이완하중은 Terzaghi 이완하중을 이용하게 되나, 이는 과도한 안전측 설계를 유도하는 경향이 있다고 알려져 있다. 따라서 국내에서도 세그먼트 이완하중의 운용 중 계측 자료 획득을 통하여, 토사 및 암반구간의 설계 대비 시공 중 이완하중 비교연구가 필요하다 판단된다.