1. 서 론
그라우팅은 지반의 고결화를 통해 역학적 물성을 변화시켜 강도 및 지지력을 증가시키고 대상지반의 투수성을 감소시키는 것을 목적으로 그라우트(grout)를 지반에 주입하는 공법을 의미한다(Bezuijen et al., 2011; Seo et al., 2016). 터널 굴착 시에는 주변지반의 전단강성이 확보되지 못하거나 단층 파쇄대 및 지하수 유입이 우려되는 경우 막장 전방 및 터널 천단부에 그라우팅을 수행한다. 특히 NATM 공법을 통한 터널 시공 시 국내에서는 주로 강관보강그라우팅이 활발히 적용되어왔다(Park and Im, 2004; Shin et al., 2021). 강관보강그라우팅은 터널 천단부에 천공 후 구조용 강관을 일정간격으로 설치하고, 그라우트를 주입하여 지반과 강관이 일체가 되게 함으로써 보강 및 차수를 수행하는 공법이다. 강관보강그라우팅은 공통적으로 강관 삽입 및 주입구 코킹(caulking)에 의해 강관을 고정한 후, 주입 조건 및 공정의 차이에 의해 분류할 수 있다. 이 중, 보어홀 내벽과 강관 외벽 사이에 씰재(seal)를 주입하여 주입재의 역류를 방지하고, 강관 내부에 이동식 패커(packer)를 이용하여 구획별로 순차적으로 그라우트를 가압해 침투 주입을 유도하는 강관다단그라우팅이 가장 보편적으로 활용되었다. 하지만 씰재의 경화시간(gelation time)이 24시간 이상 요구되었기 때문에 공기지연 및 공비 증가가 불가피하였고, 이에 대응하기 위해 최근 다양한 무실링 공법이 제안되었다. 공법의 세부사항에 대해서는 시공사마다 차이를 보이지만, 크게 강관동시주입과 외부 패커를 이용한 강관다단주입의 두 가지로 분류할 수 있다. 우선 강관동시주입의 경우 강관 내부에 사장용 패커와 주입호스를 통해 1~4개의 분할된 구간을 나누어 동시에 주입하여 역류와 무관하게 시공 효과를 얻을 수 있는 공법이다. 시공 시에 한 번에 많은 펌프를 요구하거나 복잡한 주입계통을 필요로 하지만 보어홀 하나를 주입하는 데 있어서 짧은 주입시간을 통해 공기 절감이 가능하다고 알려져 있다. 한편 외부 패커를 이용한 강관다단주입은 강관 외벽과 보어홀 내벽 사이에 외부패커를 설치하여 주입재의 역류를 방지하고, 이를 통해 기존과 같이 다단주입을 수행하는 공법이다. 기존의 일반적인 다단주입과 같이 단순한 주입계통으로 효율적인 시공이 가능하며, 이를 통해 주입재의 교차를 통한 급결(quick-setting) 그라우팅이 용이하다고 알려져 있다.
그라우트의 주입 범위는 그라우트의 물성과 주입 시 시공자의 변수, 그리고 주입 공법에 따라 다르게 나타난다. 실내 실험을 통해 그라우트 자체의 주입성을 측정하고자 하는 다양한 연구가 수행되었으며(Axelsson et al., 2009; Markou et al., 2015), 주입 시 지반조건에 의한 압력과 유량 등의 영향 역시 다양하게 분석된 바 있다(Mitchell, 1981; Kim et al., 2009; 2021; Celik, 2019). 또한 유변학적 특성을 반영한 다양한 유체의 주입 범위가 분석되었으며(Bouchelaghem, 2009; Yoon and El Mohtar, 2015), 연구를 통해 제안된 그라우트의 주입 범위는 실험 및 수치해석을 통해 검증되었다(Chupin et al., 2009; Kim and Whittle, 2009). 그럼에도 불구하고 주입공법 자체에 대한 이해를 바탕으로 공법의 효용성을 정량적으로 평가하기 위한 연구는 다소 부족한 실정이다. 따라서 본 연구에서는 강관보강그라우팅 주입 조건에 따른 그라우트 확산 범위를 수치해석적으로 평가하고자 하였다. 변수가 되는 주입 조건은 무실링 강관동시주입과 외부 패커를 사용한 강관다단주입을 모사하여 단일 주입공에 할당된 주입 구간의 길이를 달리 적용하였다. 또한 지반의 투수계수와 공극률을 두 가지씩 부여하여 느슨한 지반과 조밀한 지반을 상정하였고, 시멘트 밀크와 급결 그라우트의 두 가지 주입재를 적용하였다. 그라우트 모사를 위해 요구되는 물성을 간단한 실내 실험을 통해 획득하였고, 전산 유체 역학(computational fluid dynamics, CFD) 상용 프로그램을 사용하여 수치해석을 구동하였다. 이를 통해 주입 조건에 따른 시공 효율성을 설비 및 시공환경 외에도 지반공학적 측면에서 평가할 수 있을 것으로 예상된다.
2. 그라우트 특성
강관보강그라우팅은 주로 침투 주입에 의해 수행되며, 지반종류에 따라 일부 맥상주입이 동반된다고 알려져 있다. 침투 그라우팅(permeation grouting) 혹은 약액 그라우팅은 그라우팅 방법의 일종으로 침투 확산(permeation diffusion)을 통해 지반 구조의 변형을 야기하지 않고 공극 내에 그라우트를 주입하며, 큰 공극을 갖는 사질토 및 풍화토 지반이나 절리를 갖는 풍화암 지반에서 주로 활용되고 있다(Baek et al., 2020; Zhang et al., 2022). 그라우트는 시멘트성 그라우트와 화학 그라우트로 분류할 수 있다(Chun et al., 2006). 강관보강그라우팅에서는 두 종류의 그라우트가 모두 사용 가능하다. 주로 시멘트와 물을 혼합한 시멘트 현탁액 그라우팅을 주재료(A액)로 사용하며, 다양한 물시멘트비를 갖는다. 시멘트 현탁액은 주입시간동안 낮은 점성도를 유지하므로 지질 조건에 따라 적절한 보강영역을 형성하지 못하고 유실될 수 있다. 따라서 현장에서 상황에 맞게 LW (labiles waterglass) 그라우팅을 수행한다. LW 그라우팅은 물유리계(규산소다) 용액(B액)과 시멘트 현탁액을 혼합한 그라우트를 주입하는 공법으로, 국외에서는 주로 cement-sodium silicate grout와 같이 풀어서 설명된다(Zhang et al., 2018; Zhu et al., 2021). 강관보강그라우팅에서 LW 그라우팅은 경화 시간을 조절하여 주입재 이탈을 방지하고 영향범위를 확보하는 용도로 사용된다. 경화 시간은 일반적으로 시멘트성 그라우트는 수 시간 내, 화학 그라우트는 수 분 내로 알려져 있다(Benmokrane et al., 1995; Powers et al., 2007).
수치해석을 통해 그라우트의 유동을 확인하기 위해서는 유체의 점도(viscosity)를 평가할 필요가 있다. 정지상태의 유체를 흐르게 하기 위해서는 전단응력(shear stress)을 유체에 가하여야 하며, 이로 인해 발생한 유체의 속도는 전단율(shear rate)에 의해 표현할 수 있다. 유체의 점도는 전단응력과 전단율의 비에 해당하므로 이를 통해 유체 유동의 원인과 결과를 표현할 수 있다. 따라서 본 장에서는 시멘트 현탁액(A액)과 LW 그라우트(A액+B액)의 점도를 정의하고 계측하여 수치해석에 적용하고자 한다.
전단응력의 변화에 대해 전단율이 정비례하는 유체를 뉴턴 유체(Newtonian fluid)라고 하며, 그렇지 않은 유체를 비뉴턴 유체(non-Newtonian fluid)라고 한다. 즉 뉴턴 유체란 전단율의 변화에도 일정한 점도 값을 갖는 유체를 의미한다. 물이나 물유리계 약액(B액)은 뉴턴 유체로 분류되며, 시멘트 현탁액(A액)과 LW 그라우트(A액과 B액의 혼합물)는 비뉴턴 유체로 분류할 수 있다. 특히 시멘트 현탁액은 주입 후 안정화되면 경화되는 빙햄 소성 유체(Bingham plastic fluid)로 분류된다. 빙햄 소성 유체란 유체의 유동이 시작되기 위해 요구되는 항복 응력(yield stress)을 가지며, 유동이 발생하면 전단응력과 전단율이 선형으로 비례하는 유체를 의미한다. 따라서 항복응력 이상의 응력이 가해졌을 때 전단율에 따른 점도 변화가 발생하지 않으며, 일반적인 점도계(viscometer)를 사용하여 계측 가능하다. 하지만 LW 그라우트의 경우 급격한 수화(hydration) 반응으로 상전이 시간(phase transition time)이 수초에 불과하므로 일반적인 시멘트 현탁액과 상이한 유변학적 특성을 갖는다(Nguyen et al., 2011; Liu et al., 2019). 전단율을 점진적으로 증가시켜 전단응력을 측정하는 레오미터(rheometer) 역시 LW 그라우트와 같이 급결하는 경우 전단율 변화에 따른 안정적인 측정치를 확보할 수 없다(Wang et al., 2021). 이를 해결하고자 Lianzhen et al. (2023)은 레오미터를 사용하여 전단율을 바꾸어가며 시간에 따른 전단응력 변화를 계측하고, 구성된 데이터 셋을 역산하여 각 시점별 전단율-전단응력 그래프를 도출하는 방법을 제안하였다. 하지만 연구의 목적이 수치해석적으로 그라우트 침투 확산 범위를 평가하는 것에 있기 때문에 정교한 유변학적 특성의 계측보다는 점도계를 통해 시간에 따른 점도를 계측하는 것을 목표로 하였다(Li et al., 2021).
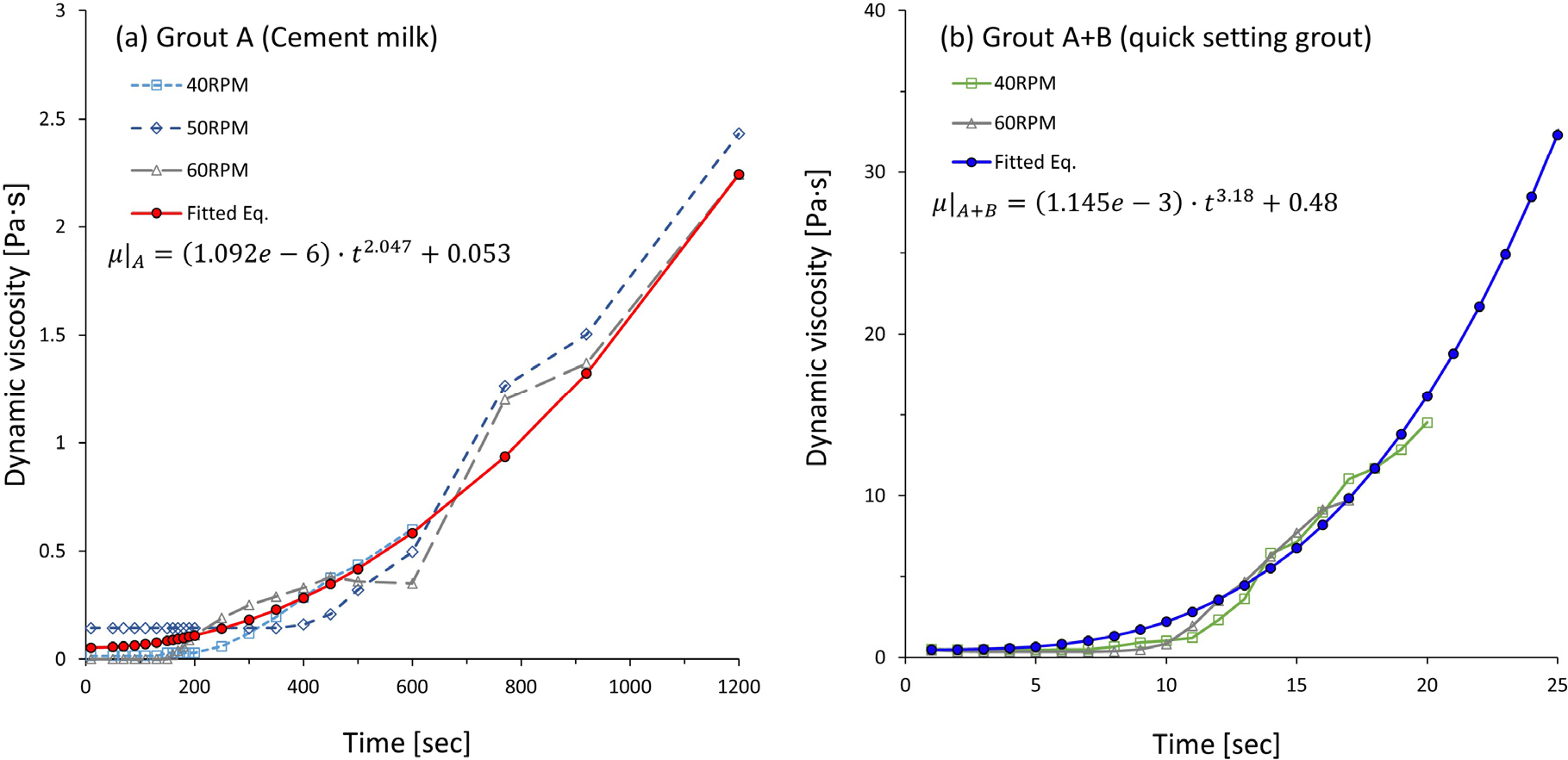
점도의 측정은 회전식 점도계를 사용하였다. 점도는 전단응력 외에도 온도와 압력에 의존적인 성질을 가지나 본 연구에서는 온도 영향을 무시하고 상온에서 계측 및 수치해석을 수행하였다. 계측을 위한 스핀들(spindle)은 대상이 되는 유체의 점도 범위에 따라 달라지며 본 연구에서는 1,000~2,000,000 mPa ‧ s의 측정 범위를 갖는 LV-4 스핀들을 사용하였다. 계측은 물시멘트비 135%로 배합된 시멘트 현탁액(A액)을 40, 50, 60 RPM을 적용하여 시간에 따른 점도를 계측하였고, 규산소다와 물을 부피비 1대1로 섞은 물유리계 약액(B액)을 A액과 부피비 3대1 (A:B = 3:1)로 혼합한 급결 그라우트를 40, 60 RPM을 적용하여 계측하였다. A액은 빙햄 소성 유체이기 때문에, 급결 그라우트는 시간에 대한 의존성이 매우 강하기 때문에 각각 Fig. 1과 같이 대표적인 시간에 따른 점도 값을 도출할 수 있었다. 급결 그라우트는 전단율에 따라 최대 점도값과 상전이 시간이 다르게 나타나지만 현장에서의 급결 그라우트 적용이 매우 짧은 시간 내에 수행되므로, 전단율에 따른 차이가 거의 발생하지 않은 초기 구간에 대해서는 도출된 대표값을 신뢰할 수 있다고 판단된다.
3. 수치해석 모델링
수치해석은 FEM (finite element method) 기반의 COMSOL Multiphysics를 사용하였으며, 본 연구에서는 이차원 축대칭(2D axisymmetric) 지오메트리를 구성하여 삼차원 거동을 모사하고자 하였다. 또한 그라우팅 조건 및 그라우트 물성에 의한 수리학적 거동만을 대상으로 하며 지반 보강에 대한 역학적인 검토는 수행하지 않았다.
현장에서 강관보강그라우팅을 수행할 때 사용되는 펌프는 흔히 실내 실험이나 수치해석에서 모사하는 바와 같이 등압 조건으로 그라우트를 주입할 수 없다. 실제로 현장에서는 펌프의 주입 속도를 최대 10 L/min으로 주입하며 이 과정에서 계측된 주입압력, 즉 초기압력에 추가로 걸리는 압력이 최대 1.5 MPa를 넘지 않도록 규정하고 있다(Korea National Railway, 2018). 이러한 거동을 실제와 같이 모사하기 위해서 펌프로부터 그라우트가 등적으로 유입되어 강관 및 보어홀 내부를 따라 흐르는 거동과, 그 결과로 지반으로 침투된 그라우트의 확산을 모사하기 위한 거동을 각각 모사하여 서로 결합(coupled)하였다.
3.1 지배방정식
보어홀 내에서 그라우트가 흐르는 과정은 층류(laminar flow)를 통해 모사되었다. 앞서 짧은 시간에 한해서 뉴턴 유체 거동을 따른다고 간주할 수 있음을 실험적으로 확인하였기 때문에 단상(single-phase) 유동은 식 (1) 비압축성 연속방정식(continuity equation)과 식 (2) 나비에-스토크스 방정식(Navier-Stokes equations)에 의한 운동량 방정식(momentum equation)을 지배방정식(governing equation)으로 갖는다.
여기서, 𝜌는 유체 밀도, 는 시간, 는 유속장(flow velocity vector field), 는 미분자(gradient), 𝜇는 유체 점도(dynamic viscosity), 는 유체 압력, 는 외력에 해당한다. 온도 변화에 대한 에너지 방정식은 본 연구에서 다루지 않는다.
시멘트 그라우트의 침투 확산 과정은 공극 내 지하수의 유동과 간극수압에 의해 쉽게 영향을 받는다(Zhang et al., 2022). 본 연구는 주입 조건에 따른 그라우트 확산 범위의 평가를 목적으로 하기 때문에 변수에 따른 결과가 확연한 차이를 보이도록 그라우팅이 상대적으로 수월하지 못한 포화된 지반을 대상으로 한다. 이를 위해 수리학적 지배방정식으로 2상 다르시의 법칙(two-phase Darcy’s law)을 사용하였다. 이 법칙은 서로 다른 밀도와 점성도를 갖는 두 유체의 유동을 모사할 수 있다. 일반적인 다르시의 법칙과 마찬가지로 2상 다르시의 법칙 하의 유속장은 식 (3)과 같이 정의된다.
여기서, 𝜅는 다공 매질의 투수성, 즉 고유투과계수(intrinsic permeability)에 해당한다. 또한 유체는 계에 들어오는 유체의 질량이 계에서 나가는 유체 질량과 계에 축적되는 유체 질량의 합과 같다는 연속방정식을 만족한다고 가정된다. 식 (4)와 같이 연속방정식을 표현할 수 있으며 비압축성 유체의 경우 유체 밀도가 상수이므로 식 (1)과 같이 표현된다.
식 (4)에 식 (3)을 대입하면 아래 식 (5)와 같은 형태의 지배 방정식을 획득할 수 있다.
여기서, 는 매질의 공극률(porosity)에 해당한다. 이를 통해 두 유체의 평균밀도와 평균 점성도는 다음 식 (6)과 같은 관계를 갖는다(Brooks and Corey, 1966; Van Genuchten, 1980; Chen et al., 2006).
이때, 는 각 유체의 포화도, 는 각 유체의 상대투수율(relative permeability)에 해당한다. 즉, 2상 다르시 법칙은 단상 다르시 법칙과 같이 지반재료를 통과하는 유체 유속장을 총 수두경사와 다공 매질의 구조에 의해 결정하며, 유체의 평균 밀도와 점성도는 각각의 포화도 및 고유 물성에 의해 도출된다. 결과적으로 2상 다르시 법칙을 지배방정식으로 활용하면 그라우트의 침투 거동과 유효 범위를 상대적으로 단순하게 거시적으로 도출할 수 있는 장점을 가지나, 공극 내 유체에 실제로 걸리는 압력과 유체 고유의 항복 응력 등을 고려한 미시적인 주입범위 분석은 수행할 수 없는 한계를 지닌다. 하지만 앞서 설명한 바와 같이 전단율에 의한 변화보다 시간에 의존적인 유변학적 특성을 갖는 급결 그라우트의 주입을 검토하고자 할 때는 충분히 유의미한 결과를 빠르고 정확하게 도출할 수 있을 것으로 사료된다.
3.2 모델링 방법 및 조건
본 연구에서 구축한 이차원 축대칭 수치해석 모델의 지오메트리(geometry)는 Fig. 2와 같다. 수치해석적 연구는 매개변수 연구를 위해 단일 보어홀에 대해서만 수행되었다. 메쉬는 유체역학에 대해 사전에 지정된 느슨한(coarse) 메쉬를 사용하였다(Fig. 2(a)). 강관보강그라우팅이 보어홀 축방향을 따라 전방으로는 수행되지 않는다고 가정되었으며, 이에 따라 지반은 반경 1.5 m, 길이 12 m의 원통형태로 모사되었다. 지반 내에서의 수리학적 거동 모사를 위해 요구되는 주된 물성은 앞서 확인한 바와 같이 공극률 과 고유투과계수 𝜅에 해당하며, 본 연구에서는 대조를 위해 느슨한 지반( = 0.4, 𝜅 = 10-9 m2)과 조밀한 지반( = 0.2, 𝜅 = 10-11 m2)의 두 가지 지반물성이 설정되었다. 그라우팅의 기대효과가 클 것으로 예상되는 범위 내에서 지반 물성을 설정하고자 하였으며, 느슨한 지반은 자갈섞인 모래지반을, 조밀한 지반은 조밀한 모래지반을 상정하였다(Bear, 1972). 보어홀은 일반적인 강관보강그라우팅 시공방법에 근거하여 축의 원점으로부터 반경 0.05 m, 길이 12 m로 설정되었으며, 내부에 강관 및 패커는 직접 모사하지 않았다. 지반은 공통적으로 200 kPa의 수압이 걸려있도록 초기 조건이 설정되었다.
강관보강그라우팅은 총 연장 12 m 중 하나의 펌프가 그라우트를 주입하는 거리를 12 m, 6 m, 3 m로 갖는 동시주입 공법과 3 m씩 4회에 걸쳐 수행되는 다단주입 공법을 Fig. 2(b) and (c)와 같이 모사하였다.
동시주입 공법의 주입거리가 12 m인 경우 전체 지오메트리가 구분되지 않고 유니온(union) 형태로 형성되었다. 동시주입 공법에서 주입거리 6 m와 3 m의 경우 각 보어홀 구획이 맞닿는 지점이 패커에 의해 통과하지 못하는 벽체(wall)로 기능해야 하며 동시에 다음 구획의 주입구(inlet)로도 기능해야 한다. 이를 위해 각 구획 별로 유니온을 형성한 후 구획끼리 어셈블리(assembly) 형태로 접합시킨 지오메트리를 구성하였다. 지반에 부여된 어셈블리 경계면은 두 경계면(boundary)에 연속성(continuity)을 따로 지정하여 해석을 수행하였다. 이 때, 어셈블리 경계면에서 노드가 서로 일치하여야 한다.
보어홀 내에서의 그라우트 층류는 현장 주입 조건에 근거하여 펌프로부터 지속적으로 새로운 유체가 10 L/min으로 공급되는 것으로 간주하고 주입 후 1초가 지난 시점의 점성계수를 적용하였다. 따라서 A액(시멘트 밀크)을 주입하는 경우 점도는 0.05 Pa ‧ s, 주입율(mass flow rate)은 0.267 kg/s를 적용하였고, A+B액(급결 그라우트)을 주입하는 경우 점도는 0.48 Pa ‧ s, 주입율은 0.233 kg/s를 적용하였다. 주입구와 배출구를 제외한 벽체는 유속을 0으로 갖는 no slip wall 조건을 부여하였다. 배출구에서의 유속장은 연산 결과에 해당하며, 도출된 유속장을 지반의 이상 다르시 법칙에 대입하여 두 물리법칙을 결합하였다. 지반에 부여되는 유체 진입의 경우 앞서 확인한 바와 같이 시간에 따라 비선형으로 증가하는 점도를 적용하여 수치해석을 구동하였다. 현상을 엄밀히 모사하기 위해서는 선행 주입된 유체와 이후에 주입된 유체가 서로 다른 점도를 가져야 하지만, 본 연구에서는 그라우트의 항복 응력이 규명 및 부여되지 않았으므로 유체 전체의 성질이 한 번에 변화하는 것으로 설정하였다. 이러한 모사 방식은 주입 조건에 따른 주입 범위의 변화를 확인하기 위한 본 연구의 목적에는 부합한다고 판단된다. 지반의 상대 투수율에 대해서는 Brooks and Corey (1966) 모델을 사용하였고, 모세관 진입 압력(entry capillary pressure) 10 kPa와 입도분포지수(pore size distribution index) 2를 적용하여 주입 조건에 의한 거동을 보기 위해 상대적으로 단순하게 구성하였다. Table 1과 같이 수치해석 모델링의 주요 물성을 정리하였다.
Table 1.
Properties of numerical modeling
현장에서 전 주입재를 동일 믹서에 미리 규정배합으로 혼합하여 교반시킨 후 1대의 펌프로 주입하는 방식을 1액 1계통식(1.0 shot), 그리고 A액과 B액의 두 유체를 각각 별도의 믹서와 펌프로 교반, 압송하여 주입관 두부에서 혼합해 주입하는 방식을 2액 1계통식(1.5 shot)이라고 한다. 기본적으로 1액 1계통식이 활용되므로 모든 동시주입, 다단주입 조건에 대해 A액(시멘트 현탁액)을 주입하는 수치해석을 구동하였다. 또한 급결 그라우트를 주입하는 경우와 2액 1계통식으로 시멘트 현탁액을 선행 주입 후 급결 그라우트를 주입하는 경우를 각각 모사하였다. 시멘트 현탁액과 급결 그라우트의 교차 시에는 보어홀에 급결 그라우트의 물성을 부여하고 지반 내 공극에 시멘트 현탁액의 물성을 부여하여 선행 주입된 유체가 밀려나는 거동을 확인하였다.
수치해석 구동 케이스는 Table 2와 같다. 지반조건과 유체 물성에 따라 수렴성이 다르게 나타나므로 Fully coupled 연산에서 최대 반복연산 횟수(maximum number of iterations)를 25회, tolerance factor를 0.01로 고정하고 minimum damping factor를 10-4에서 10-8 범위에서 바꾸어가면서 수렴성을 증진시켰다.
4. 수치해석 결과 및 분석
수치해석을 통해 그라우트 주입 범위의 형상과 유효 반경, 그리고 그라우트의 포화도를 확인하였으며, 대표적으로 Fig. 3과 같이 주입방법에 따른 주입재의 포화도 등고선을 도출할 수 있다.
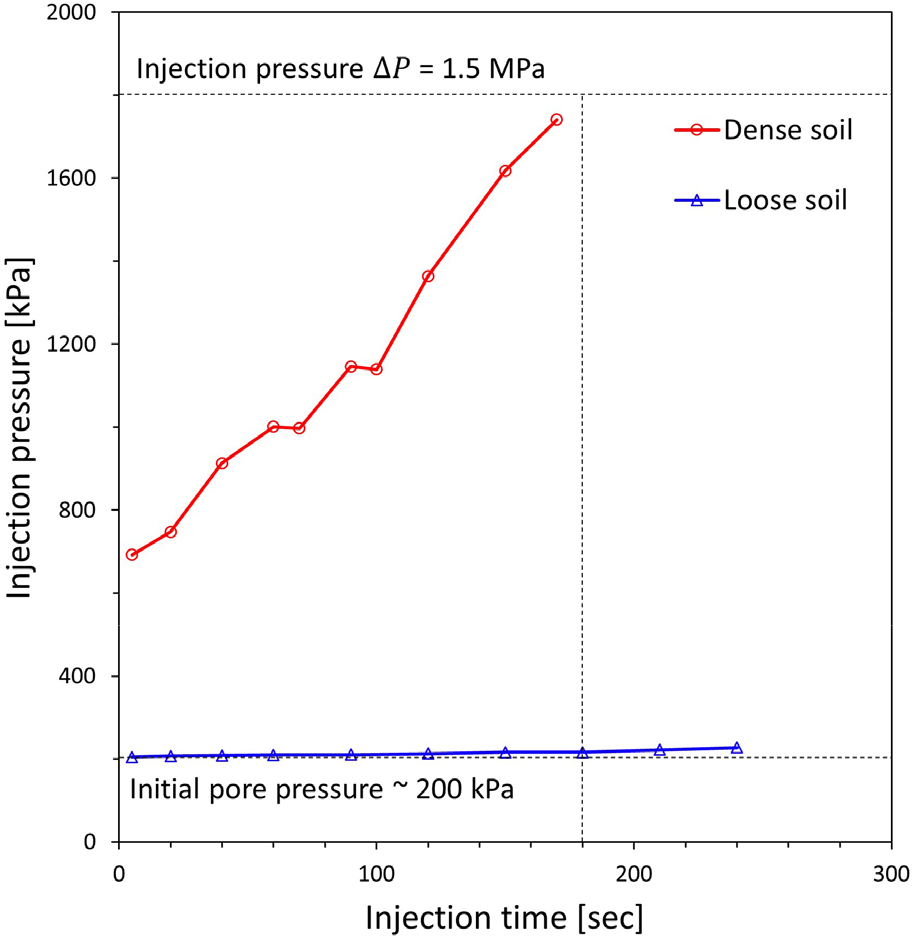
유효 반경은 지반 공극 내 그라우트의 포화도 값에 따라 나타내었다. 지반 개량의 목적에 따라 그라우트 주입 범위가 다르게 평가되어야 하므로, 본 연구에서는 그라우트 포화도 10%, 50%, 90%의 등고선을 각각 추출하여 표시하였다. 시멘트 밀크를 사용하였을 때, Fig. 4와 같이 느슨한 지반에서는 주입 압력이 크게 증가하지 않고 지속적인 주입이 가능하였으며, 조밀한 지반에서는 약 180초가 지난 시점에서 초기 압력과 주입 압력의 차이가 1.5 MPa를 초과하였다. 따라서 본 연구에서는 공통적으로 주입 이후 180초가 지난 시점에서의 그라우트 주입 범위를 도시하였다.
우선 느슨한 지반과 조밀한 지반에서의 차이를 확인하기 위해 한 구획을 12 m로 갖는 동시주입 조건에서 그라우트 주입 범위를 도시하였다. Fig. 5(a)에서와 같이, 느슨한 지반의 경우 주입공 근처에서 다소 넓은 주입 범위를 갖지만 전반적으로 균질한 범위를 형성하고 있다. 반면, 조밀한 지반의 경우 주입공 근처에서만 넓은 주입 범위를 갖고 주입공으로부터 일정 거리 이상 떨어진 경우에 주입 범위가 크게 감소하는 것을 확인하였다. 이는 주입공으로부터 멀수록 펌프의 압력이 온전히 전달되지 못하고 감소하므로, 투수계수와 공극률이 작은 조밀한 지반에서는 그라우트를 주입, 확산시키는데 요구되는 압력을 일정 거리 너머에서 충족시킬 수 없기 때문에 나타나는 현상으로 판단된다. 또한 Fig. 5(b)에 나타난 바와 같이 조밀한 지반에서 시간 경과에 따른 주입 범위의 확산을 확인한 결과, 그라우트 주입 범위가 보어홀 길이방향으로 성장하였음을 확인할 수 있다. 이는 선행 주입된 그라우트가 공극 내에서 계속해서 확산되지 못하므로 아직 주입이 안 되어 있는 방향으로 주입 압력이 작용함에 따라 발생한 현상으로 판단됩니다.
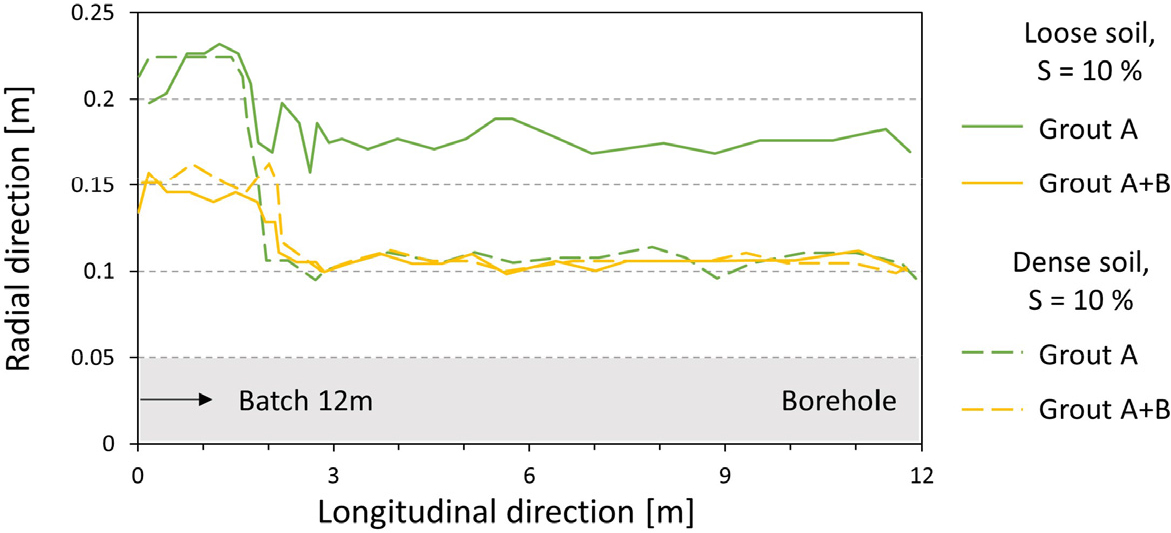
A액(시멘트 현탁액)과 A+B액(급결 그라우트)의 차이를 확인하기 위해 한 구획을 12 m로 갖는 동시주입 조건에서 그라우트 주입 범위를 도시하였다(Fig. 6). A+B액의 경우 그라우트 포화도 50%와 90% 범위가 매우 좁게 형성되었으므로 비교를 위해 포화도 10% 범위만을 도시하였다. A+B액은 점도가 빠르게 증가하기 때문에 느슨한 지반에 주입할 때도 조밀한 지반에 주입할 때와 같이 주입공 인접구간에 집중된 주입 범위를 갖는다.
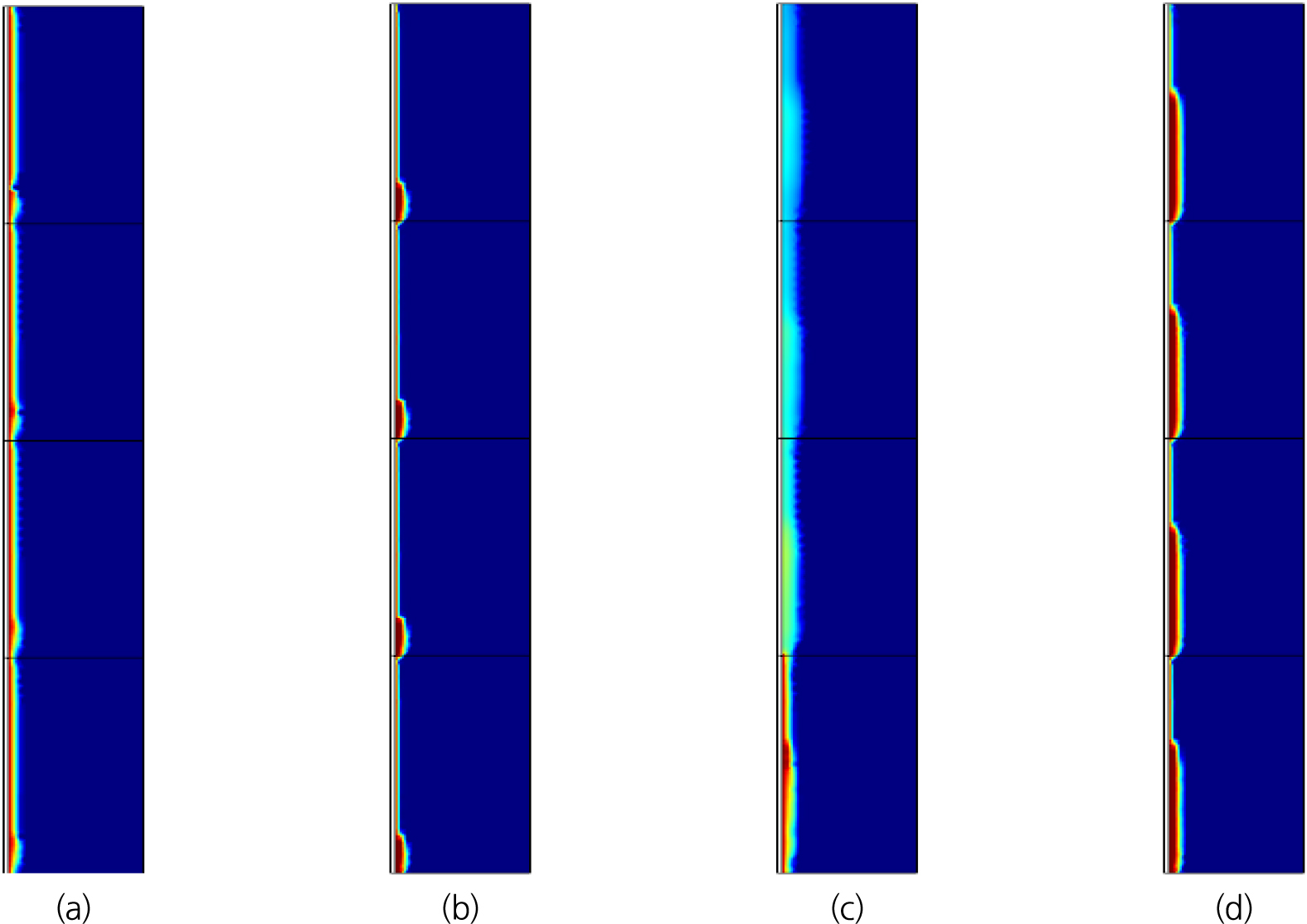
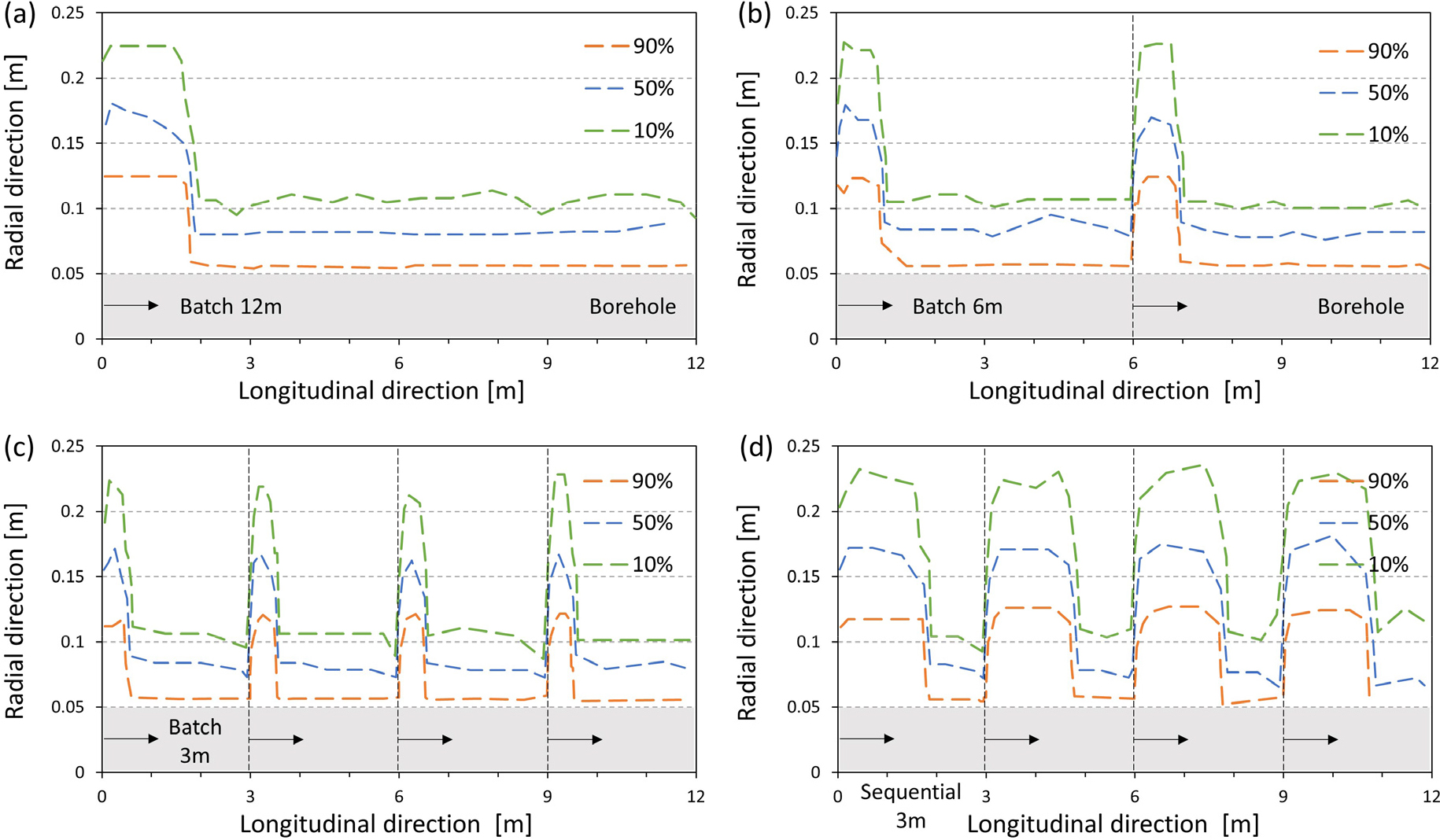
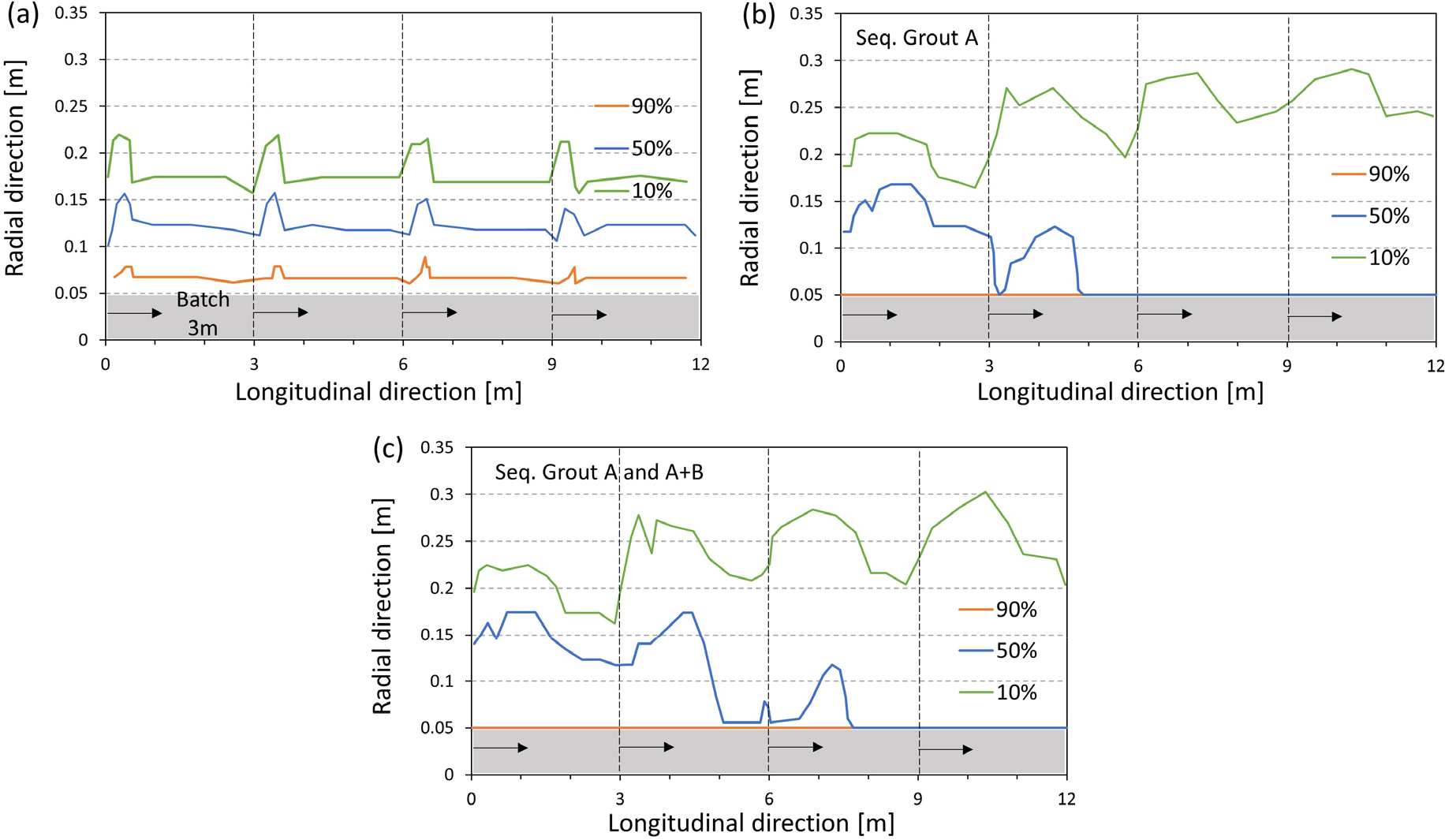
주입 방법의 차이를 확인하기 위해 조밀한 지반에서 A액을 주입하였을 때 각 주입 방법에 따른 주입 범위를 Fig. 7과 같이 나타내었다. 앞서 확인한 바와 같이, 공통적으로 주입공 근처에서 그라우팅 범위를 형성하였다. 동시 주입 시 구획의 개수가 증가할수록 주입공 근처에 형성된 넓은 그라우팅 범위가 점차 좁고 짧아지는 것을 확인할 수 있다. 주입구 인근에서 방사방향으로 멀리 주입된 부분을 서로 비교할 때, 12 m 동시 주입은 길이방향으로 약 1.8 m 주입되었으나, 6 m와 3 m 주입 조건에서는 각각 약 1.0 m와 0.6 m로 감소하였으며, 다단 주입 수행 시 12 m 동시 주입과 유사하게 1.8 m의 주입 길이를 갖는다. 이는 인접한 주입공에서 가해진 압력에 의해 매질의 압력이 증가하므로 주입 압력과의 차이가 줄어들기 때문으로 판단된다. 따라서 다단 주입 공법에서는 한 구획씩 주입이 수행되기 때문에 12 m 구획에 동시 주입하였을 때 형성된 그라우팅 주입 범위와 유사한 주입 범위가 각 구획 별로 형성되는 것을 확인할 수 있다. 이를 통해 주입 범위를 확보하기 위해 동시 주입보다 다단 주입이 효과적임을 확인하였다.
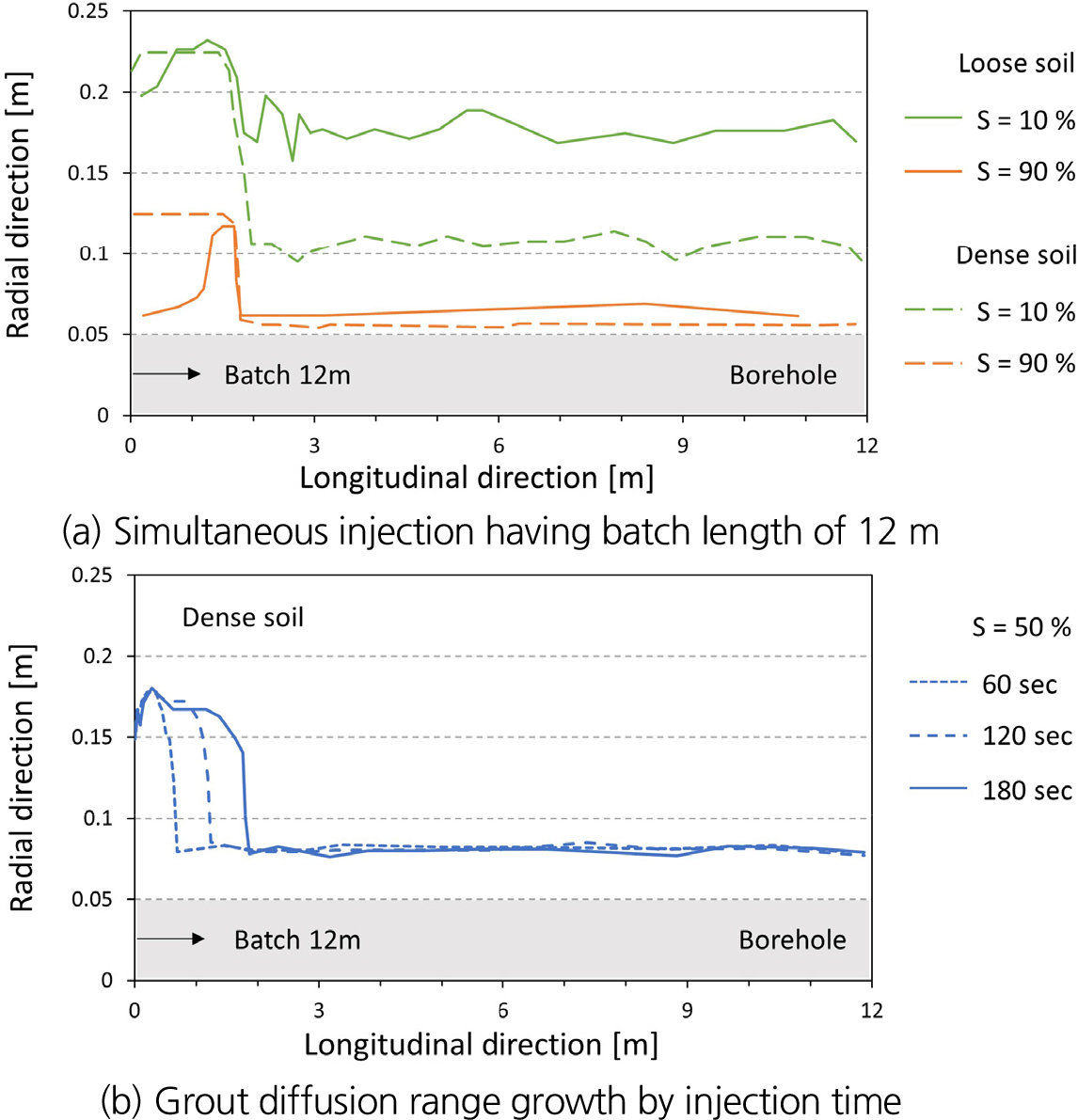
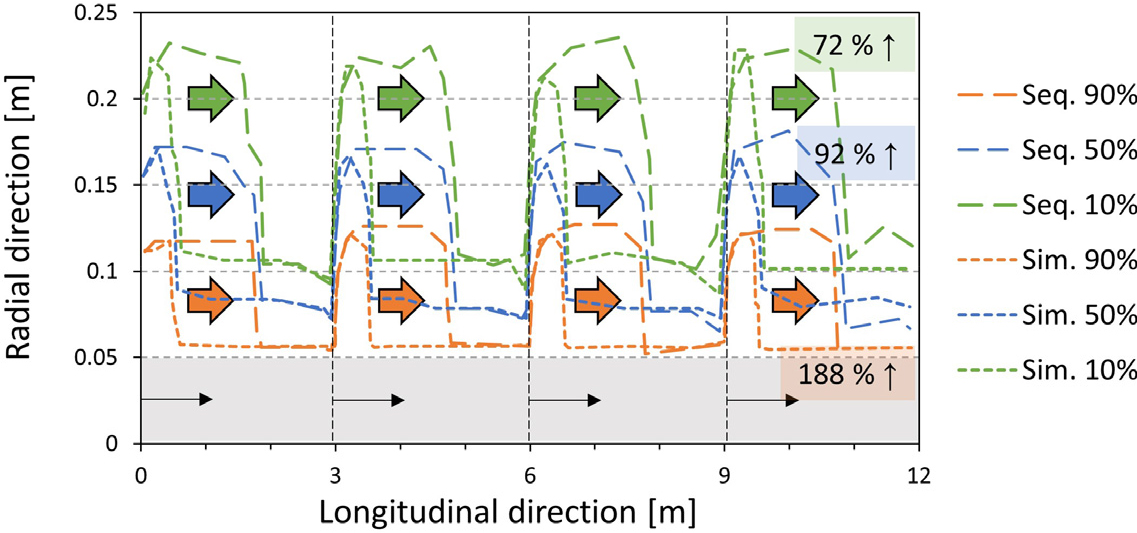
정량적인 검토를 위해 3 m씩 동시 주입한 경우와 다단 주입한 경우를 Fig. 8에 함께 나타내었다. 각 구획 별로 방사방향으로는 주입 범위의 차이가 거의 발생하지 않았으나 길이방향으로는 크게 증가하는 것을 확인하였다. 주입구 인근에서 방사방향으로 멀리 주입된 부분을 서로 비교할 때, 포화도 90%의 경우 길이방향으로 약 0.5 m에서 약 1.8 m로 증가하여 균질한 공극 분포를 가정할 때 전체 주입 범위(면적)가 약 188% 증가하였고, 포화도 10%의 경우 길이방향으로 약 0.6 m에서 약 1.9 m로 증가하여 전체 주입 범위(면적)가 약 72% 증가하였다. 그리고 포화도 50%의 경우 유사한 거동을 보이며 전체 주입 범위(면적)가 약 92% 증가하였다. 그라우트 주입범위(면적)에 지반의 공극률과 포화도를 곱하여 그라우트 주입량을 산출할 수 있으므로 주입량 역시 동시주입보다 다단주입에서 크게 증가하는 것을 알 수 있다.
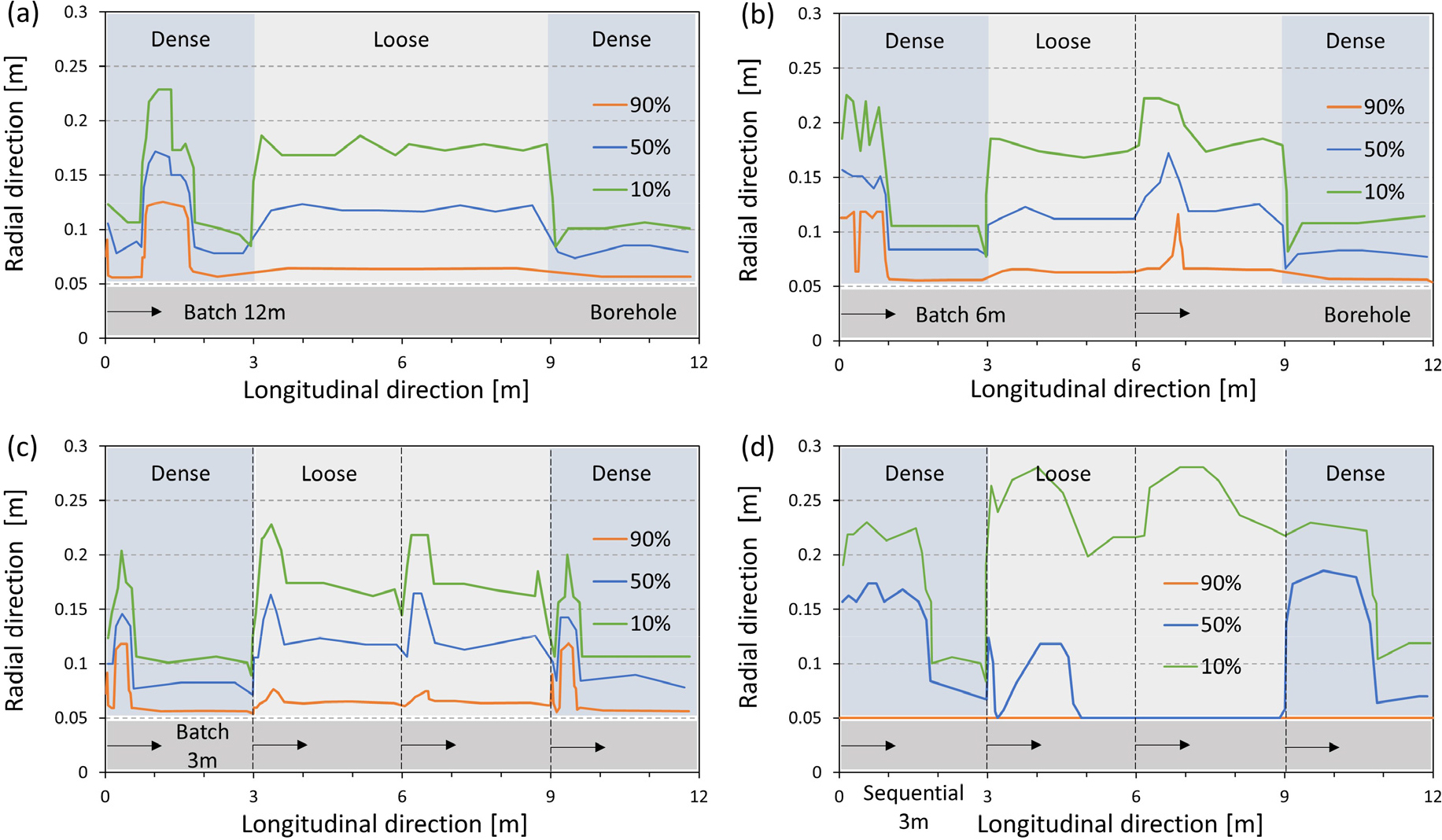
마찬가지로 주입 방법에 따른 차이를 확인하기 위해, 비균질한 지반에서 A액을 주입하였을 때의 주입 범위를 Fig. 9와 같이 나타내었다. 비균질한 지반은 3 m씩 조밀, 느슨, 느슨, 조밀한 지반의 순서로 모사되었다. 앞서 Fig. 7에서 확인한 바와 같이, 공통적으로 주입공 근처에서 주입 범위가 주변보다 넓게 형성되었다. 또한, Fig. 9(a) and (b)에서와 같이 구획이 길어져 주입공에서의 거리가 먼 곳에 조밀한 지반이 존재하는 경우 거의 주입이 수행되지 않는 반면 Fig. 9(c) and (d)와 같이 많은 구획으로 동시 주입을 수행하거나 다단 주입을 수행하는 경우 각각의 지반에 충분히 그라우트가 주입되었음을 확인할 수 있다. 하지만 다단 주입의 경우 주입이 반복되어 시간이 소요되는 동안 느슨한 지반에 주입된 그라우트가 이후 주입과정에서의 주입 압력에 의해 보어홀로부터 더 멀리 주입되며 그 농도가 옅어지는 것으로 나타난다. 이러한 이유로 Fig. 9(d)에서 주입공에서 먼 쪽부터 4회에 걸쳐 다단주입을 수행한 이후 90%의 포화도를 보이는 구간이 지반 내에 존재하지 않으며, 보어홀 경계면에 표현되었다. 마지막으로 Fig. 10을 통해 느슨한 지반에서 3 m 구획을 갖는 동시 주입과 다단 주입, 그리고 다단 주입 시 A액과 A+B액의 교차 주입을 각각 비교하였다. A액과 A+B액을 교차하는 경우 A액을 150초 주입한 후 A+B액을 30초간 추가로 주입하였다. 그 결과 급결 그라우트와의 교차 주입의 경우 지반이 느슨하더라도 막장면에 가까운 쪽에 한해서는 상대적으로 더 넓은 주입 범위를 안정적으로 확보할 수 있음을 확인하였다.
즉, 주입 범위의 확보에 있어서는 다단주입이 동시주입보다 적합하다고 판단되며, 이는 2액 1계통 교차 주입이 가능한 경우 더 극명하게 나타날 것으로 여겨진다. 또한 동시 주입의 경우 보어홀 하나당 요구되는 펌프와 주입계통의 수가 많은 대신 짧은 시간 내에 시공이 가능하다고 알려져 있으나, 현장에서 여러 개의 보어홀에서 동시에 시공하는 경우에 어떤 공법이 더 효율적인 지에 대해서는 해당 현장의 시공 상황에 의존적일 것으로 추정된다. 따라서 주입계통 설비와 공사 기간 등의 실무적인 면에 대해서는 별도의 검토가 필요하다.
5. 결 론
본 연구에서는 강관보강그라우팅 주입 조건에 따른 그라우트 확산 범위를 실내 실험을 통해 측정한 그라우트의 점도를 반영하여 수치해석적으로 평가하였다. 지반이 조밀할수록 주입공과 가까운 쪽에서 주입이 집중되는 것으로 나타나며, 주입 영역은 시간에 따라 증가하였다. 그라우트의 점도가 클수록 주입 영역이 확연히 감소하며 지반 종류보다 더 지배적인 역할을 수행한다. 강관동시그라우팅은 주입 구획이 잘게 나뉠수록 시공 효율성이 증가하지만 실제 주입 범위는 다소 감소하는 것으로 나타난다. 또한 조밀한 지반일수록 주입공으로부터 먼 곳의 주입이 확연히 적게 발생한다. 반면 강관다단그라우팅은 하나의 보어홀에 소요되는 시간은 길지만 그라우트 확산 범위 확보 측면에서 상대적으로 우수한 것을 확인하였다. 강관다단그라우팅이 느슨한 지반에 적용된 경우 그라우트가 안정적으로 유지되지 못하고 포화도가 옅어지는 한계를 확인하였으나 시멘트 현탁액과 급결 그라우트의 교차 주입이 수행될 수 있다면 충분히 효과적일 것으로 기대된다. 본 연구에서 확인한 주입 방법과 지반 종류, 그리고 그라우트 종류에 따른 주입 범위에 추가로, 실대형 및 현장시험을 통해 주입 절차와 주입계통의 영향을 정량적으로 평가한다면 더 효과적인 주입공법을 제안할 수 있을 것으로 기대된다.