1. 서 론
2. 연구동향
3. 현장 실험에 사용된 강관과 계측기
3.1 현장 실험에 적용된 강관
3.2 현장 계측개요
4. 현장 계측결과 분석
4.1 굴착초기 형상변위계 계측결과
4.2 터널 굴착에 따른 형상변위계 계측결과 분석
4.3 터널 굴착에 따른 변형률계 계측결과 분석
5. 결 론
1. 서 론
터널 형성의 이론에서 지반의 아칭효과는 매우 잘 알려진 이론이다. 터널을 굴착함에 따라 굴착부에 이완하중이 발생된다. 발생된 이완하중은 지반의 아칭효과로 인해 응력분배가 발생되어 굴착된 터널의 안정화가 가능한 것이라는 많은 연구결과가 Terzaghi (1936) 이후 많은 연구결과가 나타나 있다. 또한, 터널의 안정성을 증대시키기 위해 실무에서 많이 활용하는 강관보강 그라우팅 시 터널의 거동 특성에 대한 연구도 2000년 초반부터 매우 활발히 진행되었다. 그러나 최종 목적의 터널 구조물의 안정성에 관심이 집중되어 정작 강관 보강재에 대한 거동 메커니즘에 대해서는 그 동안 정성적인 보강설계가 되었던 것은 사실이다. 이러한 결과로 아직 강관보강 그라우팅의 적절한 설계법도 정립되지 않은 실정이다.
현장 실무에서는 일반적으로 강관 보강 그라우팅에 대한 설계를 수행함에 있어 강관의 거동 특성을 고려한 설계법이 없어 강관과 주면으로 침투된 그라우트체와 원지반을 단순한 복합지반으로 보고 수치해석을 통한 검증을 하여 적용하는 경우가 많다. 하지만 수치해석에 사용되는 지반 물성치가 다소 정성적이고, 실제로는 불균질한 지반이 때문에 해석결과와 실제와는 차이가 발생하게 된다. 원지반으로 침투되는 그라우트가 맥상주입이나 할열주입과 같은 현상으로 주변지반으로 고르게 주입되어 강관으로 보강된 주변지반이 전체적으로 전단강도가 증가된다고 보기에는 무리가 있다. 이로 인해 매우 많은 현장에서 강관보강 그라우팅을 적용하지만, 보강을 하였음에도 굴착 시 붕락이 발생되는 사례도 많아지고 있다. 따라서 본 연구에서는 강관보강 그라우팅의 거동 특성을 연구하기 위해 실제 강관 보강이 이루어지는 현장에서 강관에 형상변위계와 변형률계를 설치하여 굴착에 따른 강관 보강재의 거동 특성을 분석해 보았다.
2. 연구동향
강관보강 그라우팅에 대한 연구는 오랜 동안 국내외에서 매우 활발한 연구가 수행되고 있다. 주로 보강 효과에 대한 연구가 대부분으로 강관 보강 그라우팅에 따른 터널의 거동 특성이나 강관과 그라우트재가 주입된 복합 영역에 대한 등가 물성의 산정법 등에 대한 연구가 그 대표적인 사례이다.
먼저 보강 효과에 대한 연구사례는 수치해석을 통한 매개변수에 대한 연구와 현장 계측을 통해 터널과 주변지반의 거동 특성을 분석하고, 강관보강 그라우팅의 보강 효과를 확인하는 연구가 대부분을 이루고 있다. Barisone et al. (1982), Pelizza and Peila (1993), Choi et al. (1997)의 연구에서는 강관보강 그라우팅 적용 시 터널 굴착면의 안정효과와 터널 주변지반의 개량효과를 분석하였다. 터널 굴착면의 안정성을 증대시키고 지반침하 억제, 지하수 유입 차단 등에 매우 우수하다고 평가하였다. Yoo et al. (1995)은 보강영역의 강성, 횡방향 보강범위, 경사도에 대한 매개변수 변환 연구를 3차원 수치해석을 통해 연구하였다. 연구결과 UAM (Umbrella Arch Method) 공법은 지표침하보다는 천단침하 억제에 더욱 효과적이며, 강관의 경사도가 작을수록 하중경감 효과가 증대하고, 종방향 및 횡방향 아칭효과로 터널 주변의 접선응력과 토압이 현저히 감소하여 터널 안정성이 증대되는 것으로 연구결과가 도출되었다. 또한, Choi et al. (1997)은 보강효과 확인을 위해 보강 전후에 대한 수압시험과 지시약 반응시험, 빔 아치 형성에 의한 상부 토압 경감효과, 굴착 시 암괴 낙반현상에 따른 육안관찰에 의한 효과를 확인하여 터널의 안정성을 증대시킨 것으로 평가하였다. 한편, Kim (1995)은 지하철 터널을 모델로 2, 3차원 수치해석을 통해 주변 지반의 거동 억제효과, 지표침하 및 심도별 지층 변위 등을 비교, 분석하여 수직방향은 터널 천단부로부터 2D (D: 터널 직경)까지, 수평방향을 터널 중심에서 2D 영역까지 변위 억제 효과의 범위가 있는 것으로 평가하였다. Kim and Moon (2002)은 탄성계수와 지층두께에 대한 수치해석에 의한 매개변수 변환 연구를 수행하여 UAM의 보강효과를 천단변위에 대해 회귀분석을 실시하여 굴착면의 천단침하량(S0)과 수렴 후의 최대침하량(Smax)으로 표현되는 지수함수 형태의 천단침하량 예측식을 제안하였다.
한편, Bae et al. (1997)은 서울 지하철 5-A 공구에 대표 계측구간을 설정하여 여러 지반조사 방법에 의한 본 공법의 시공효과 확인을 수행하여 시공 후 개량지반의 탄성계수가 약 4배 정도 증가한다는 결론을 제시하였다. Song and Cho (2006)는 보강영역의 물성치 결정에 있어 거시적 접근법의 개념을 기반으로 미시적 접근법을 적용한 등가 물성치를 결정하는 기법(5가지)을 제시하였다. 3차원 수치해석을 통해 제시한 기법의 적정성을 평가한 결과 강관과 구근의 직렬강성 시스템이 실제와 거의 유사한 거동을 나타내는 것으로 나타났다. 그러나 수치해석 시 소요시간 과다 및 높은 난이도가 요구되므로 강관과 구근의 병렬연결 강성이 원지반과 직렬로 연결되는 보강지반의 직병렬 시스템으로부터 구한 등가 물성치를 이용한 해석법을 추천하였다. 최근 실무에서는 위 연구에서 제시한 등가 물성치 결정에 의한 기법이 많이 사용되고 있다.
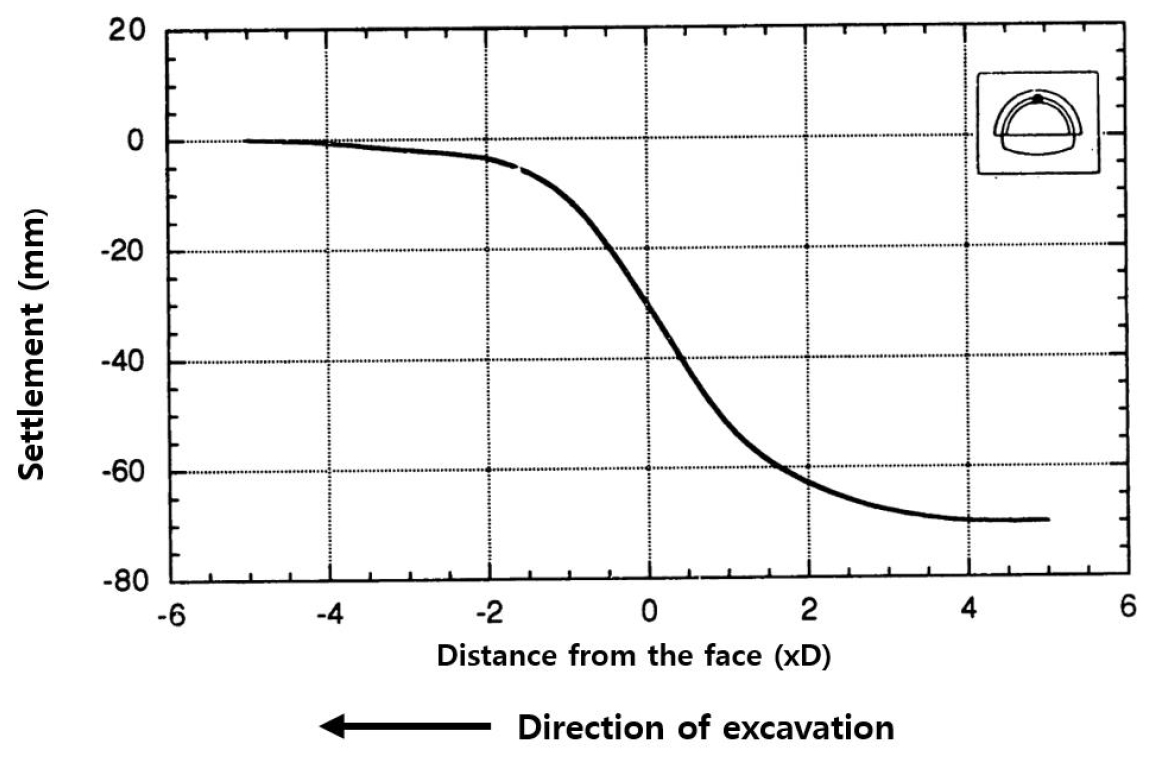
강관 보강의 거동 메커니즘의 연구사례 중 아칭효과를 고려한 거동 특성을 연구한 사례가 있다. Muraki (1997)는 굴착면 전방으로부터 특정한 위치, 즉 굴착면에 도달하게 되면, Fig. 1과 같이 전체 지반 침하의 30~40%의 침하가 발생하게 된다. 이것은 터널 굴착이 이루어진 영역에서 적용된 어떤 대책도, 굴착면 앞의 지반에서 발생하는 침하를 억제할 수 없다는 것을 의미한다고 했다. 따라서 터널 굴착에 있어서 굴착면 보다 전방에 대한 보강이 그 면 앞의 지반 침하를 줄이는 데 효과적이라고 판단했다.
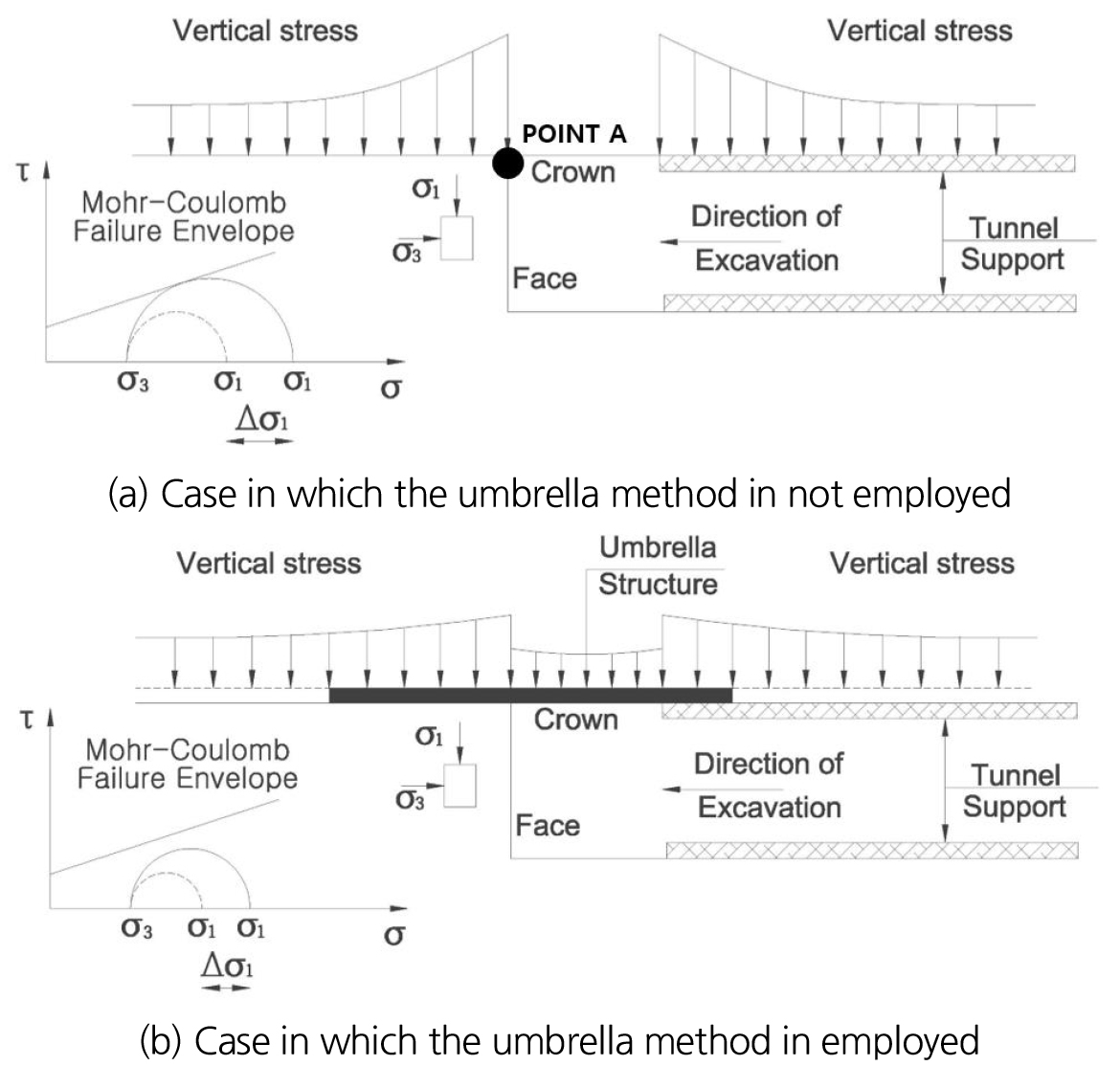
특히, 터널을 굴착하게 되면, Fig. 2(a)에서 보여주듯이 굴착면 직전에 응력집중이 생기고 굴착면(point A)에서 수직 응력이 ‘0’으로 급격하게 감소한다. 터널 지보가 굴착면 일정 거리 뒤에서 설치되어진다고 가정하면, 터널의 무보강 구간 단면을 따라 응력은 ‘0’이 된다. Fig. 2(b)와 같이 강관 보강 그라우팅 방법을 적용하면 터널의 무지보 단면이 강관으로 보강되어 결과적으로 구조물이 상재하중을 부담한다. 이로 인해 굴착면 직전 및 직후의 응력 집중이 비슷하다는 것을 알 수 있었다.
Geo-Fronte Research Association (1994)에서는 강관 보강의 메커니즘은 Fig. 3과 같이 터널 주면 아치형태의 보강영역에 의해 터널의 종단 및 횡단 방향에서 굴착면을 안정화시키는 것으로 평가하였다. Fig. 3(a)에서 보여주는 횡단 방향에서 안정화와 관련하여 아치 같은 보강 영역이 지반 하중을 부담한다. 종단 방향에서의 안정화에 관련해서는 Fig. 3(b)에서 보여주는 바와 같이, 방금 굴착된 위치의 지반 하중을, 한쪽은 터널 지보에, 다른 한쪽은 지반에 의해 지지되는 빔에 의해 지지하는 것을 연구하였다.
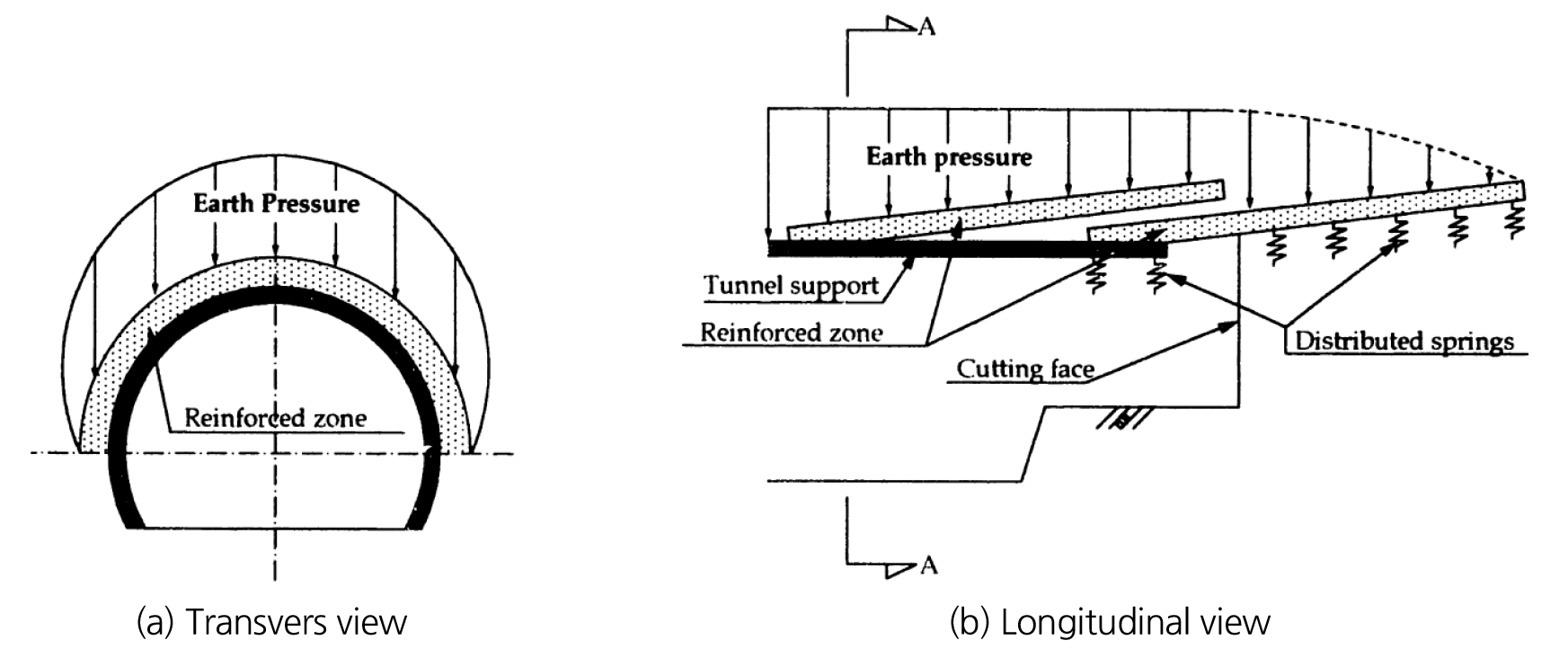
Fig. 3
Schematic description of the steel pipe reinforcement mechanism (Geo-Fronte Research Association, 1994)
3. 현장 실험에 사용된 강관과 계측기
강관 보강에 대한 이론적인 연구 사례에 근거하여 터널 굴착이 진행됨에 따라 실제 터널 전면에 보강된 강관의 거동 특성을 파악하기 위해 실제 보강이 계획된 터널 단면 중 모멘트가 크게 발생하는 어깨부 위치에 SGT275강관과 SGT550강관에 형상변위계와 응력계를 부착하여 시공하였다.
3.1 현장 실험에 적용된 강관
본 실험에서는 SGT275강관과 SGT550강관을 이용하여 연구를 수행하였다. SGT550 강관은 고강도 강관으로 항복강도가 550 MPa 이상으로 기존의 일반 강관(SGT275)보다 항복강도가 2배가량 크고, 인장강도도 690 MPa로 일반 강관의 410 MPa보다 훨씬 큰 강관이다. 고강도 강관(SGT550)과 일반 강관(SGT275)의 기계적, 화학적 성질은 Table 1과 같다.
Table 1.
Comparison of mechanical properties and chemical composition of steel pipes
강관 보강 그라우팅에 적용되는 고강도 강관(SGT550)의 제원은 가급적 기존 강관보강 그라우팅에 적용되는 일반 강관(SGT275)의 파일 부재력과 유사하도록 선정하였으며, 고강도 강관의 경우 직경과 두께를 모두 줄여 강관의 부재력은 기존 강관과 유사하되 동일한 천공경 내에서 충분한 그라우트 주입이 될 수 있도록 하였다. 강관 보강 그라우팅에 적용되는 강관의 제원은 Table 2와 같다.
Table 2.
Specifications of steel pipe
| Kinds | Diameter (mm) | Thickness (mm) | Area (mm2) | Unit weight (N/m) | Member forces (kN) |
| SGT275 | 60.5 | 4.0 | 710.0 | 55.7 | 195.2 |
| SGT550 | 54.0 | 2.9 | 465.6 | 34.4 | 256.1 |
3.2 현장 계측개요
강관의 보강효과를 검증하기 위해 실제 심층 풍화대 구간의 강관보강 그라우팅이 적용되는 구간에 일반 소구경 강관(SGT275 (D60.5 × 4t))과 고강도 대구경 강관(SGT550 (D54.0 × 2.9t))에 형상변위계와 변형율계를 부착하여 터널 좌, 우측에 대해 각 1공씩 설치하고 계측을 시행하였다.
현장 계측구간에 대한 시공 및 계측의 개략적인 개요는 Fig. 4와 같다.
Fig. 4(a)의 지반조건을 보면 터널 상반 굴착부는 파쇄가 심한 풍화대가 존재하고, 하반 굴착부는 연암에 위치하여 굴착 시 터널 천단 및 어깨부의 안정성 확보가 필요하다. 이를 고려하여 설계 시 소구경 강관보강 그라우팅이 적용되어 있다. Fig. 4(b)는 해당 구간의 지보패턴을 나타낸다. 소구경 강관은 어깨부 끝단의 좌측부에는 SGT550을 우측부에는 SGT275 강관을 설치하였고, 이를 Fig. 4(c)에서 확인할 수 있으며, 또한 Fig. 4(d)와 같이 해당 강관에 형상변위계와 변형율계를 부착하였고, 터널 천단과 어깨부에는 터널 변위측정을 위해 변위 타켓을 부착하였다.
특히, 굴착 시 터널 거동을 파악하기 위해 천단 및 내공변위계를 설치하였고, 강관에는 형상변위계(1 m 간격)와 변형율계(2 m 간격)를 설치하였다.
형상변위계는 강관에 1 m 간격으로 12개씩 총 24개를 설치하였고, 변형율계는 2 m 간격으로 총 12개소를 설치하였고 Table 3과 같고 계측기 설치 전경은 Fig. 5와 같다.
Table 3.
Number of measuring instruments installed and initial date
| Kinds | SGT275 | SGT550 | Interval | Installed date | Initial date |
| Shape displacement meter | 12 EA | 1 m | 2018. 11. 21 |
Same as installation date | |
| Strain guage | 6 EA | 2 m | |||
형상변위계는 MEMS Type으로 측정범위 ±30°, 정확도는 ±1.5 mm의 성능을 가지는 제품을 사용하였고, 변형률계는 진동현식으로 측정범위는 3,600 microstrain, 정확도는 0.1% FSR의 성능을 가지는 제품을 사용하였고 Fig. 6에 나타내었다.
4. 현장 계측결과 분석
계측은 초기치가 설정된 2018년 11월 21일부터 7 m의 굴착이 진행된 2018년 11월 25일까지 수행하였다. 강관의 거동에 초점을 형상변위계와 변형율계를 이용하였고, 설치 초기의 강관의 거동여부를 확인하기 위해 1 m 굴착 후 시간별 계측결과도 수록하였다.
4.1 굴착초기 형상변위계 계측결과
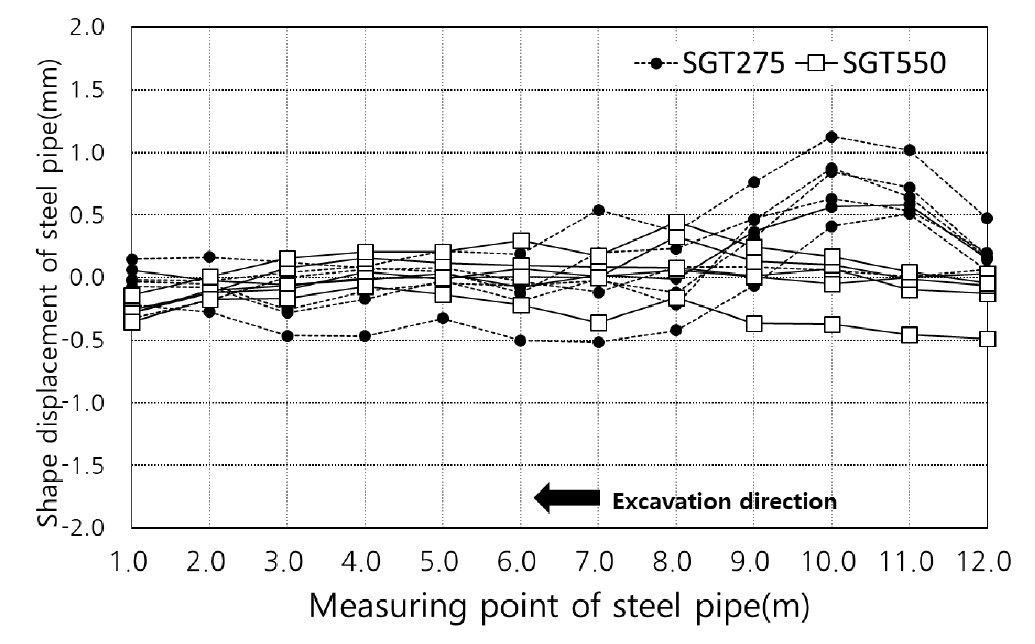
강관 설치 초기(11/21, 01:00)부터 상반 굴착 직후(11/21, 07:00)까지 계측 결과 중, 형상변위 계측결과를 분석한 결과 SGT275 강관이 설치된 우측 터널 어깨부의 변위는 최대 0.515~1.125 mm로 발생된 반면, SGT550 강관이 설치된 좌측 터널 어깨부의 경우 0.255~0.490 mm의 범위로 변위가 발생하였다. 즉 이 결과에서 보면 SGT550 강관이 SGT275 강관 대비 43~50%수준의 터널 내공변위 저감을 보였다. Table 4와 Table 5는 강관의 형상변위계 계측결과로 그래프로 나타내면 Fig. 6과 같다. 계측결과를 보면 SGT550 강관의 변위가 SGT275 강관보다 작게 발생하는 것을 명확하게 보여주고 있다.
Table 4.
SGT275 steel pipe shape displacement meter measurement result (1 m after excavation)
Table 5.
SGT550 steel pipe shape displacement meter measurement result (1 m after excavation)
Fig. 7에서 보면 SGT275 강관보다 SGT550 강관이 더욱 강관의 변형량이 작으며, 거동이 SGT275보다 상대적으로 발생되지 않고 있음을 알 수 있다. 즉, 1 m 굴착 후 SGT275강관은 굴착 전방에 처짐이 발생하지만 SGT550강관의 경우 상대적으로 변형이 거의 없는 것으로 나타난다. Fig. 8에서는 터널에 대한 초기 굴착 후 추가 굴착이 발생되기 전까지를 시간대 별로 구분하여 나타낸 것이다. 즉, Fig. 7을 시간대별로 구체적으로 나타낸 것이다. 강관의 형상변위계를 보면 지속적으로 변형이 발생되고 있는 것을 알 수 있다. 이는 굴착 초기에 발생되는 굴착 이완하중에 대해 지반의 평형상태를 이루기 위한 아칭효과로 시간대별로 계속적인 응력수렴이 발생되고 있음을 나타내며 지반 내 응력의 재분배가 발생되면서 이에 대한 응력이 강관부에 변형으로 나타내고 있음을 알 수 있다.
각 시간대별 강관의 형상변위에 대한 계측결과 그래프(Fig. 8)에서 보면 굴착 1시간 후부터 굴착 7시간까지 강관의 형상변위가 SGT275 강관의 경우 굴착 영향구간에서 이완하중이 가해지면서 시간이 경과함에 따라 아칭효과에 의해 지중 속에 삽입된 강관의 위치에서도 (+), (-)의 변형이 반복되고 있는 것을 알 수 있다. SGT550의 경우에도 큰 변형은 발생되지 않으나 경시 변화에 따라 지속적으로 변형이 발생되고 있는 것으로 계측되었다. 이는 굴착 이완하중에 따른 주변지반의 응력변화에 대응하는 아칭현상에 따라 응력 분배가 안정화 상태까지 계속 강관에 영향을 미치는 것으로 판단된다.
4.2 터널 굴착에 따른 형상변위계 계측결과 분석
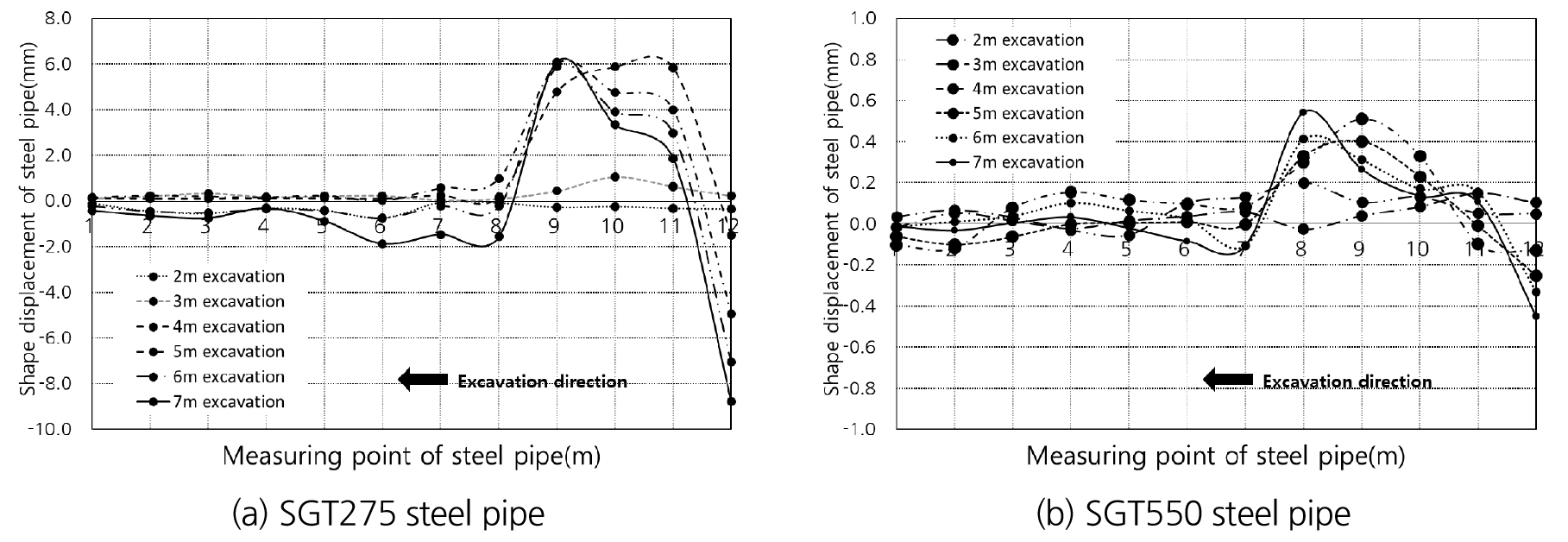
계측기가 설치된 후, 5일 동안에 6 m를 굴진하였다. 형상변위계의 경우 굴착 초기의 변위양상과 다른 경향을 보이는데, 지중 속에 삽입되어 있는 강관의 변형은 굴착이 진행된 구간보다 적게 발생되며, 굴착이 진행됨에 따라 발생되는 변위 경향이 변화하게 된다. Fig. 9는 SGT275 강관과 SGT550 강관의 형상변위 계측결과값을 나타낸다.
우선 Fig. 9(a)의 SGT275 강관에 대한 형상변위 그래프에서 보면 굴착 연장이 2~3 m일 경우 강관의 형상 변형이 크게 발생되지 않았으나 4~6 m까지 굴착된 경우 점차 변형값이 크게 발생되었고, 굴착 거리에 따라 큰 변화가 나타나고 있다. 이러한 경향은 Fig. 9(b)의 고강도 강관의 경우에서도 유사하게 나타나고 있다. 한가지 특이한 사항은 6~7 m까지 굴착하였을 경우 6~7 m 지점으로 처짐 변위가 발생되지 않는다는 것이다. 이러한 사유는 굴착이 진행됨에 따라 이완하중은 더욱 커져가므로 이에 따라 아칭현상이 발생되어 주변지반의 응력 재분배가 발생하고, 강관보강 그라우팅의 저항능력로 인해 최대 이완하중이 발생되는 6~7 m 지점에서는 (-)의 변형값을 보이고, 4~5 m 지점에서는 (+)의 변형값을 나타내고 있다. 즉, 이러한 거동은 터널 굴착에 따라 발생되는 굴착 이완하중에 대응하기 위해 아칭현상이 발생된다. 이런 아칭현상으로 터널 굴착면을 따라 응력 분배가 발생되고, 아칭효과에 의해 지반 내에 삽입된 강관도 이와 동일한 거동특성을 나타낸다고 할 수 있다.
특히, 본 그래프에서 한 가지 특이한 점은 굴착이 발생되지 않고 삽입되어 있는 8~12 m 구간의 형상변위계의 경향을 보면 굴착에 따라 지속적으로 변형이 발생되고 있다. 즉, 굴착에 따른 이완하중이 발생됨에 따라 미굴착 구간에 삽입된 강관도 이완하중에 대응하는 것을 의미한다. 굴착 거리에 따른 강관의 형상변위 그래프는 Fig. 10과 같다.
4.3 터널 굴착에 따른 변형률계 계측결과 분석
변형률계를 통한 응력변화 경향을 살펴보면 형상 변위의 경향에서 유추되는 응력변화가 합리적인 것으로 판단된다. 굴착이완하중이 가장 크게 발생되는 굴착 초기 위치에서 가장 큰 응력이 발생되고, 그에 따른 응력 재분배에 따라 강관의 위치별 응력 변화가 Fig. 11에서 나타나고 있는 걸 확인할 수 있다. 강관의 처짐이 발생된 위치에서는 양(+)의 응력값이 나타나고, 상향변위가 발생된 위치에서는 음(-)의 응력값을 나타내고 있다. 특히 굴착되지 않은 전방 지반에 설치되어 있는 강관 위치에서도 응력이 발생되고 있어 강관도 아칭현상에 의한 거동을 나타내고 있고, 이로 인해 강관은 휨을 지지하는 구조체로서 역할을 하고 있는 것이다.
SGT550 강관의 경우에도 이와 유사한 경향을 나타내고 있으나 SGT275 강관보다 작은 값을 나타내는 것이 특이하다. 이러한 특성으로 강관의 강도가 클수록 실제 발생응력에 대한 저항능력이 크므로 강관에 발생되는 응력도 감소되어 강관의 구조 안전성 측면에서 유리하게 나타난다.
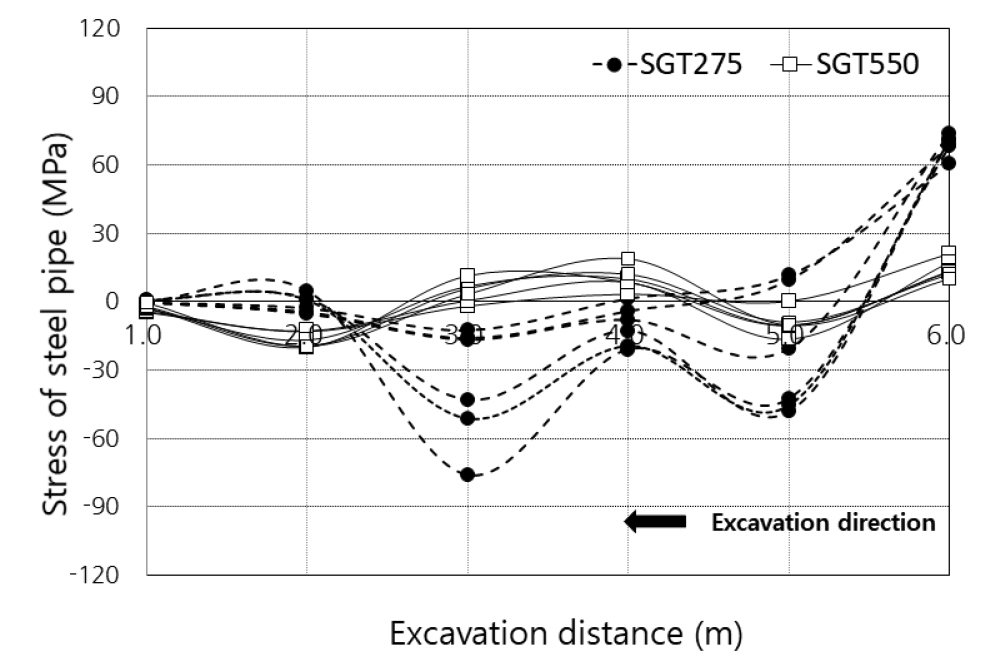
Fig. 12에서 나타난 바와 같이 강관의 발생응력의 분포가 하중의 발생과 유사하게 양과 음의 응력이 동시에 발생되고 있음을 알 수 있다. 즉, 지중 내에 삽입된 구간의 강관에서도 강관의 길이의 연속적인 응력의 변화가 발생되고 있음을 나타낸다. SGT275 강관의 경우 -75 MPa~70 MPa까지의 응력이 길이별로 나타나며, SGT550 강관의 경우 -25 MPa~27 MPa의 값을 나타내고 있다. 2 m 간격으로 설치된 변형율계가 압축으로 휘어지는 경우 (+)의 값이, 인장으로 늘어나거나 휘어지는 경우 (-)값이 나타나므로 강관의 길이방향으로 아칭효과로 인해 압축과 인장의 응력이 강관에 미치고 있음을 나타낸다.
한편, Fig. 12의 굴착 단계별 강관의 응력 변화를 보면 형상변위계의 굴착 거리별 변화경향과 매우 유사한 것을 알 수 있다. 변위가 크게 발생되거나 변화되는 변곡점에서 응력이 발생되고 있다. 특히 지반 내에 삽입되어 있는 구간에서도 강관에 발생하는 응력의 변화치가 변위발생량보다 상대적으로 큰 경향을 보이고 있다. 이는 굴착에 따른 아칭효과에 의한 응력 재분배에 대응하는 강관의 강도와 연관이 있는 것으로 판단된다.
또한, SGT275와 SGT550 강관의 응력 발생량 차이가 4 m 굴착 시 SGT강관의 경우 27 MPa, SGT550 강관의 경우 70 MPa로 약 2.6배 이상 발생하여 고강도 강관일수록 주변 지반의 이완응력에 저항 성능이 우수함을 확인할 수 있다.
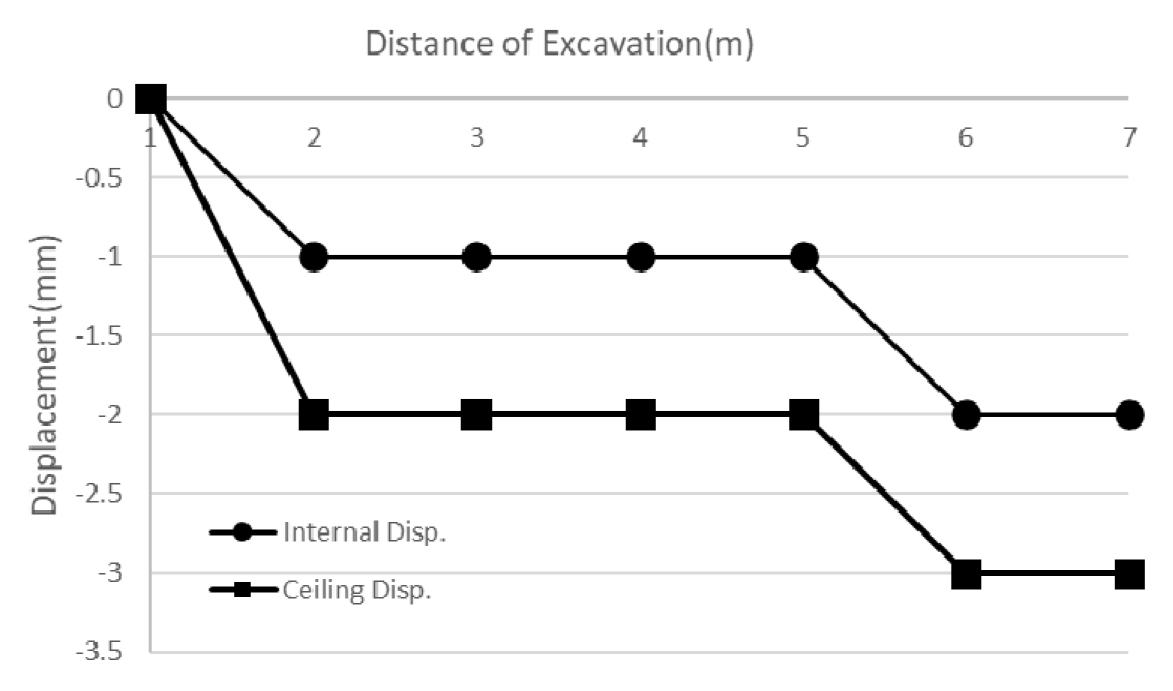
Fig. 13은 터널 굴착에 따른 터널 천단부와 내공변위를 나타내고 있다. 굴착 초기 1 mm가 발생되었으나 7 m까지 굴착 완료시에는 2~3 mm 정도로 변위가 발생되고 있다. 굴착에 따라 터널의 안정성은 확보되고 있는 것으로 계측결과 나타났다.
5. 결 론
그 동안 강관 보강 그라우팅과 관련된 연구는 강관 보강에 따른 터널의 보강 효과 혹은 안정성 연구 등을 활발히 연구되었으나 강관 보강 그라우팅의 거동 메커니즘에 대한 연구는 미비하였다. 따라서 본 연구에서는 강관 보강 그라우팅의 거동이 지반의 아칭효과에 따라 거동한다는 기존 연구사례를 근거하여 실제 거동 특성을 파악하기 위해 실제 현장실험을 시행하였다. 강관에 형상변위계와 변형률계를 부착하여 초기 1 m 굴착 후 다음 굴착을 시작하기 전까지와 1 m씩 총 7 m의 굴착이 진행됨에 따라 발생된 강관의 변형과 응력 경향을 통해 강관 보강 그라우팅의 거동을 분석하였다.
본 연구를 통해 얻어진 결론은 다음과 같다.
1. 터널 강관보강의 거동 특성을 파악하기 위해 현장 계측결과를 통해 강관 보강 그라우팅의 거동 메커니즘에 대한 연구를 수행하였다. 강관 보강 그라우팅을 설치한 다음 터널 1 m를 굴착한 후 강관에 부착된 형상변위계를 통해 강관의 변형을 검토한 결과 굴착 후 발생한 이완 하중에 의해 지반의 응력재분배가 지속적으로 발생하는 것으로 확인되었다.
2. 굴착된 1 m 구간은 강관의 처짐이 발생되고 그에 따라 강관은 지중에 삽입된 구간까지 처짐과 상승의 곡선형태로 변형이 발생되는 것을 확인할 수 있었다. 7 m까지 터널을 굴착한 결과 4 m 굴착 시부터 강관의 변형이 크게 증가하였다. 2~3 m 굴착 시 1 mm 이하였던 변위가 4 m 굴착 시부터 6 mm까지 급격히 증가하였고, 특히, 6 m 굴착 시에는 최대 변형량은 6 mm로 동일하나 최대 변형량의 발생위치가 굴착방향으로 전이되는 것을 확인할 수 있었다.
3. 강관의 응력계측 결과에서는 굴착 직후부터 굴착이 진행됨에 따라 굴착 길이방향으로 응력이 양(+)과 음(-)의 응력이 반복되는 경향을 나타낸다. 이러한 거동은 이완하중에 따라 주변 지반의 아칭효과로 인해 강관에 휨 응력이 발생하는 것으로 판단된다. 특히, 4~5 m 굴착 시 지중에 삽입되어 있는 구간에서도 70 MPa까지 발생됨을 확인할 수 있었다.
4. 한편, SGT275 강관과 SGT550 강관의 거동 특성을 비교할 때 경향은 상호 거동이 유사한 것으로 나타났지만 변형량의 경우 최대 18배 정도, 응력은 최대 12배 정도의 차이를 보였다. 즉, 고강도 강관일수록 강관에 변형과 응력에 저항하는데 유리한 것으로 사료된다.
5. 현장 계측 결과를 비추어 볼 때 터널 굴착에 따른 이완하중은 아칭효과에 의해 응력 재분배가 지속적으로 발생하게 된다. 보강되어 있는 강관의 경우에도 이러한 이완하중에 대응한 거동이 발생하는 것을 알 수 있었다. 즉, 원지반과 상대적인 강성이 큰 강관은 지반 내에서 터널 굴착에 따라 발생되는 이완하중의 아칭현상에 대응하면서 거동이 발생하는 메커니즘을 지니는 것으로 판단된다.