1. 서 론
2. 모터 그레이더 소개
2.1 모터 그레이더 완성차
2.2 블레이드 모듈
3. 해석방법
3.1 동해석 기법
3.2 골재 DEM 모델링
3.3 해석 시나리오
4. 실험계획 및 해석결과
4.1 설계인자 및 실험계획
4.2 해석 결과
5. 설계 최적화
5.1 점진적 2차 반응표면법(Progressive Quadratic Response Surface Method)
5.2 설계문제 정식화
5.3 설계 최적화 결과
6. 결 론
1. 서 론
모터 그레이더는 도로공사에서 골재 및 토사 평탄화 작업에 주로 사용되는 토질작업용 건설기계이다. 선진국에서는 도로기초용 평탄화 작업뿐만 아니라 아스팔트 혼합, 트렌치 굴착, 경사면 절삭, 제설작업 등 다양한 작업에 활용되고 있다. 모터 그레이더의 여러 장치중 블레이드는 배토판(mold board)으로 불리기도 하는데, 골재를 직접 절삭, 산포하는 핵심적인 역할을 수행한다.
모터 그레이더는 도로공사에서 골재 및 토사 평탄화 작업에 주로 사용되는 토질작업용 건설기계이다. 선진국에서는 도로기초용 평탄화 작업뿐만 아니라 아스팔트 혼합, 트렌치 굴착, 경사면 절삭, 제설작업 등 다양한 작업에 활용되고 있다. 모터 그레이더의 여러 장치중 블레이드는 배토판(mold board)으로 불리기도 하는데, 골재를 직접 절삭, 산포하는 핵심적인 역할을 수행한다.
도로시공을 효율을 높이기 위해서 시공목적에 맞게 블레이드를 적절히 제어하면서 운용하는 것이 매우 중요하다. 굴착기와 같은 일반 건설기계는 국내 생산이 활발하므로 생산, 검사, 유지보수, 부품교체와 같은 서비스 및 현장지원도 비교적 수월한 편이다. 반면, 모터 그레이더와 같은 특수장비는 주로 해외수입에 의존하므로, 교육 프로그램과 시공매뉴얼이 충분히 구비되어 있지 않고, 작업자 개인의 경험과 직관에 의존하여 운용되는 실정이다. 이 때문에 부품고장이 발생하는 경우, 부품의 수급이 어려워 보수 및 교체에 시간이 소요되는 경우가 많다. 최근 국내 건설산업에서 시공자동화, 자율운전 등 스마트 건설기술이 적용되면서 모터 그레이더의 자동제어, 자율운전, 운영 최적화에 대한 관심이 증가하고 있는 추세이다(Yukihisa, 2002; Kononov et al., 2019; Galitskov et al., 2020). 따라서 모터 그레이더와 같은 특수목적형 건설기계 부품의 국산화 및 매뉴얼 확립이 시급한 시점이다.
현재까지 모터 그레이더와 같은 특수장비에 대한 연구로는 작동효율 향상을 위한 부품 구조 안정성, 동력-유압시스템 분석, 장비 거동해석과 같은 기초적인 연구사례가 많이 보고되어 있다(Heikkilä and Jaakkola, 2002; Carmen and Nastac, 2012; Ruiying and Xin, 2012; Klets et al., 2017; Lee et al., 2021). 반면, 부품 및 모듈 설계 및 제조기술은 선진사의 고유한 지식재산으로 외부에 공개되지 않기 때문에 국내업체의 접근이 제한적인 경우가 많다. 따라서 장비의 고장시 부품 교체에 많은 시간이 소요되고, 고장부품의 수리와 신규 제작에 애로점이 빈번히 발생하고 있다.
모터 그레이더 핵심 부품인 블레이드의 설계 및 운영기술에 대한 국내 연구사례는 거의 보고된바 없기 때문에 기초 설계기술을 확보하기 위한 목적으로 연구가 수행되었다. 모터 그레이더 완성차의 사용 목적과 블레이드 부품의 제어방법에 대해서 간략히 설명하였다. 이 후 블레이드의 현재 설계기술을 분석하고, 이를 보완, 개선하기 위한 설계인자를 선정하였다. 설계인자를 바탕으로 실험계획을 구성하였다. 이후 블레이드의 골재 절삭 및 평탄화작업을 동해석 코드로 모사하여 설계인자의 민감도를 수치해석적으로 분석하였다. 이후 최적화 과정을 수행하여, 각 인자의 최적 설계값을 도출하고자 하였다.
2. 모터 그레이더 소개
2.1 모터 그레이더 완성차
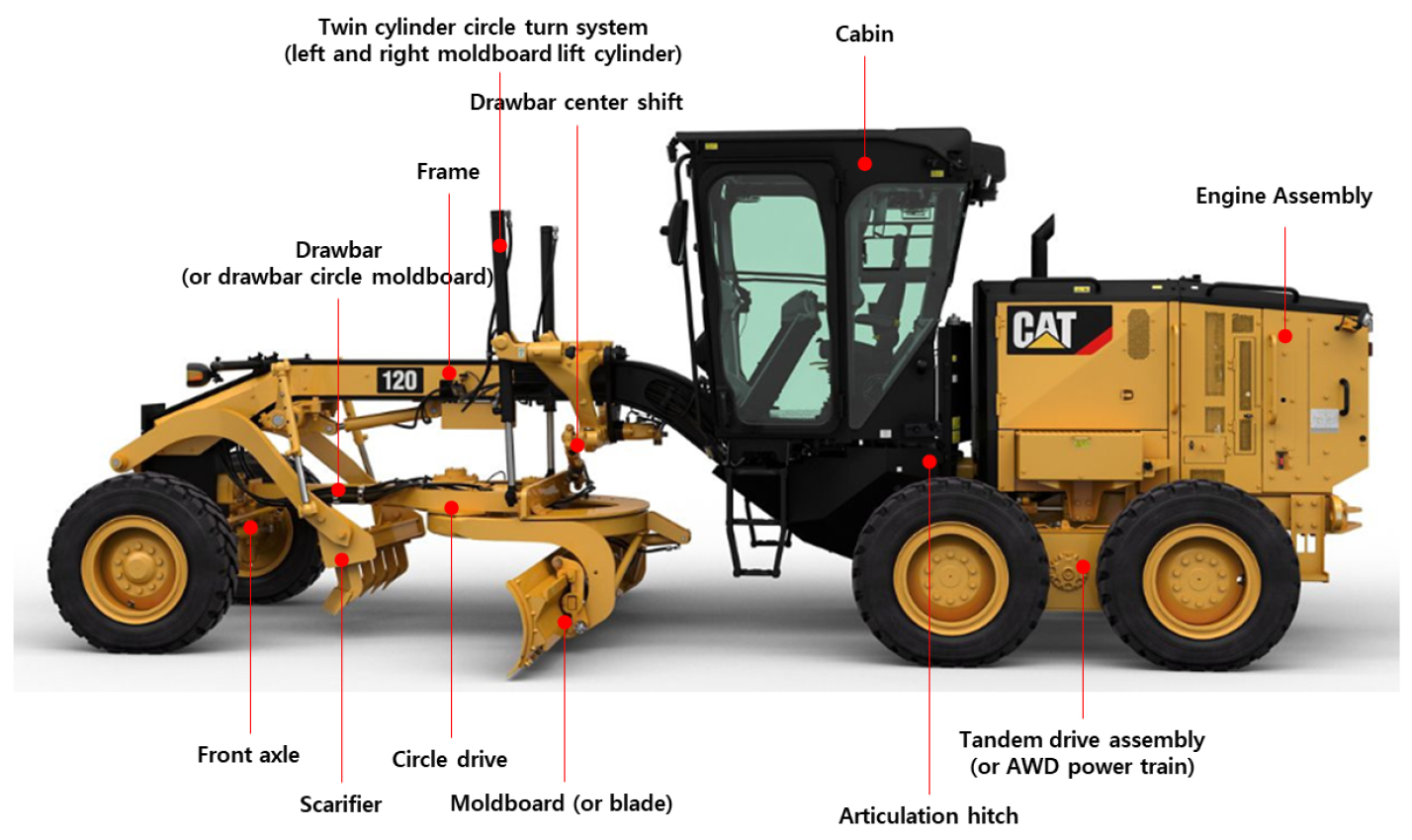
모터 그레이더는 도로 및 토질사면의 표면을 절삭하거나 평탄화하는 용도로 사용되는 건설기계 완성차이다. Fig. 1에서 보는 바와 같이 운전석을 중심으로 기능이 구분되어 있다. 앞은 지표면을 고르는 블레이드 및 이를 제어하고 차체를 조종하는 제어모듈로 구성되어 있다. 운전석 후방은 엔진과 이의 동력을 주행체에 전달하는 파워트레인이 탑재되어 있다. 모터 그레이더는 정지 장치를 가진 자주식 건설기계로 정의되며, 장비 등급은 블레이드의 길이로 분류된다.
모터 그레이더의 작업량은 TBM과 유사하게 시간당 부피의 단위(m3/h)로 표현되며 표준 작업량(Q)은 식 (1)과 같이 계산된다.
여기서, Q : 운전시간당 작업량(m3/h), L : 블레이드의 유효폭(m), D : 1회의 편도 작업거리(m), H : 굴착심도 또는 포설 두께(m), f : 토량 환산계수, E : 작업효율, Cm : 사이클 타임(min.)이다.
2.2 블레이드 모듈
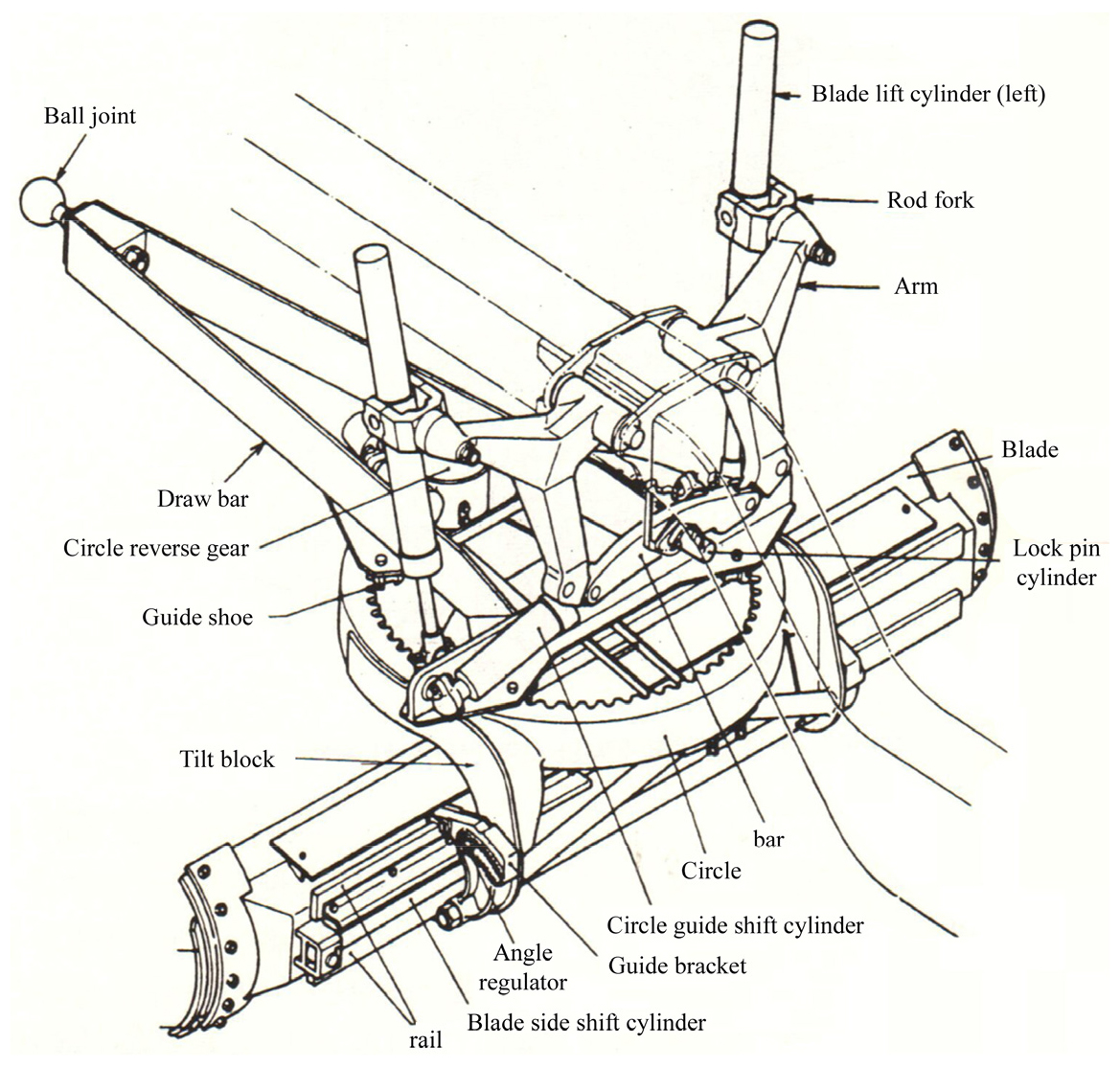
블레이드 모듈은 Fig. 2와 같이 구성된다. 블레이드는 3방향 직선운동(x, y, z)과 3방향 회전운동(pitch, roll, yaw)의 6 자유도 조절이 가능하다. 블레이드의 상하 높이와 롤 제어는 볼 조인트를 중심으로 리프트 실린더를 통해 조절이 가능하며 리프트 실린더를 동시에 조절하면 상하 높이를 제어할 수 있고, 개별로 조절하면 롤 제어가 가능하다. 블레이드의 측동은 사이드 쉬프트 실린더와 서클센터 시프트 실린더를 통해 조절이 가능하다. 피치 제어는 첵과 가이드 브래킷이 담당하고, 요 제어는 서클의 유압 모터가 담당한다. 특히, 서클은 스캐리 파이어를 제거하면 360도 회전이 가능하다.
3. 해석방법
3.1 동해석 기법
본 연구에서는 블레이드와 골재 사이의 접촉, 충돌을 해석하기 위해 동해석 코드인 LS-dyna (Livermore Software Technology, 2012)를 사용하였다. Ls-dyna는 물체간의 접촉, 충돌을 모사하는 기능을 지원하는 상용 프로그램이다. 본 연구의 목적은 블레이드의 변형 혹은 안정성 분석이 아니라 토사 평탄화 작업성능 개선하는 데에 있다. 따라서 블레이드 파트를 강체로 모델링하여 골재와 블레이드의 접촉 상호작용을 주로 분석하고자 하였다. 골재와 블레이드의 상호작용은 “DEFINE_DE_TO_SURFACE_COUPLING” 조건을 적용하여 모델링하였으며, 전처리 작업은 LS-PrePost을 사용하였다.
3.2 골재 DEM 모델링
골재 파트는 개별요소법(DEM)을 이용하여 직경 20 mm의 개별입자 그룹으로 모사하였다. 이를 통해 블레이드에 의해 접촉, 절삭, 산포되는 일련의 과정이 실제와 유사하게 구현되도록 구성하였다. 골재 모델의 개별입자의 기본 물성은 밀도 3.1e-9 ton/mm3, 포와송비 0.3이며, 접촉물성은 마찰계수 0.3, 댐핑계수 0.8을 사용하였다.
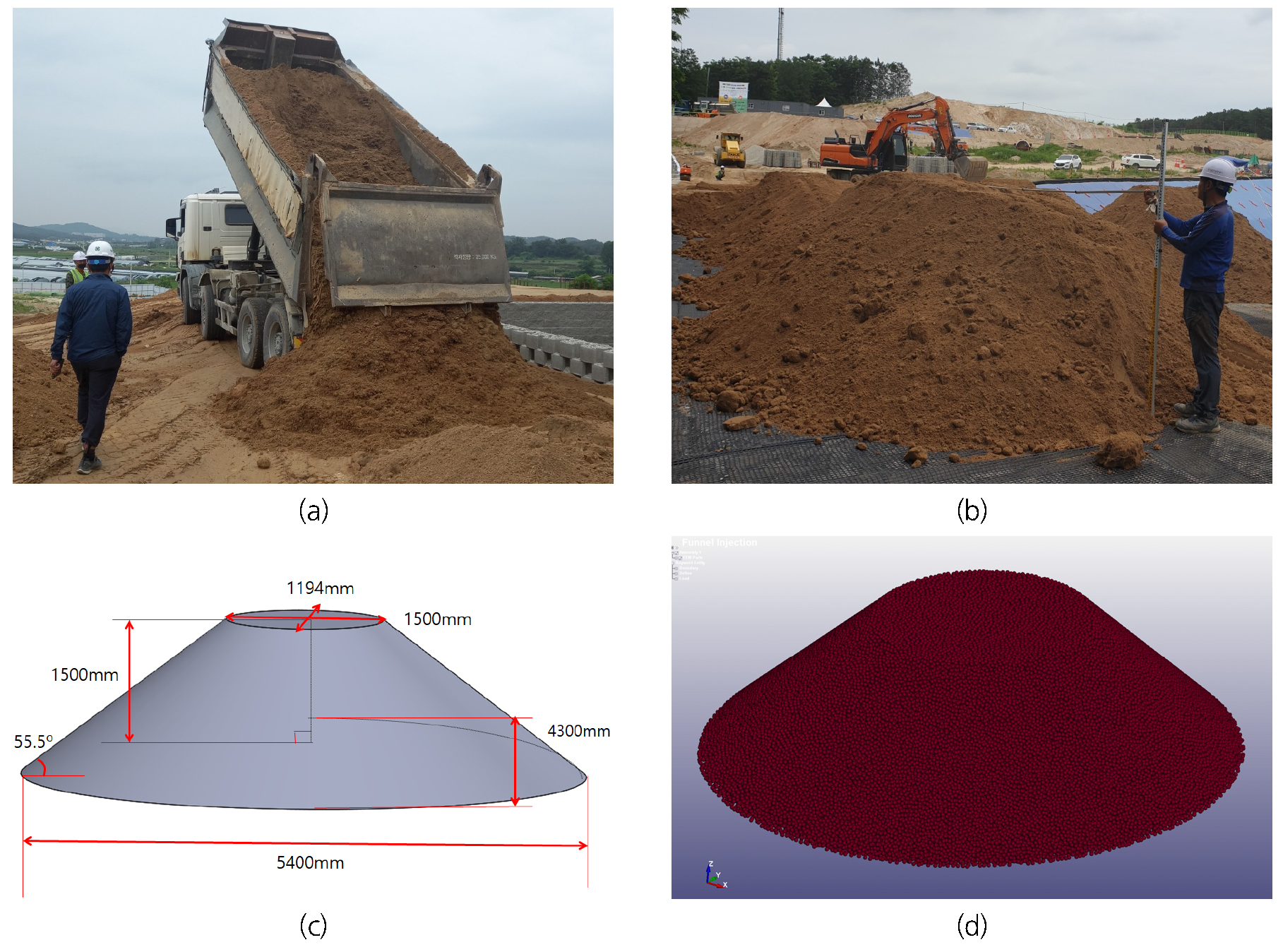
도로 하부 시공용 골재 및 토사의 치수를 전산해석에 반영하기 위하여 건설현장의 지원을 받아 25톤 덤프트럭의 하차작업시 적치되는 골재의 치수를 측정하였다(Fig. 3(a), 3(b)). 측정 결과는 Fig. 3(c)와 같다. 밑면의 최대폭은 5.4 m, 윗면의 최대폭은 1.5 m로 조사되었고, 하차하는 트럭의 진행방향으로 약간 더 긴 형태의 타원형 원뿔이 형성되었다. 측정된 치수를 기준으로 골재 DEM의 초기 모델링에 형상으로 적용하였다(Fig. 3(d)).
3.3 해석 시나리오
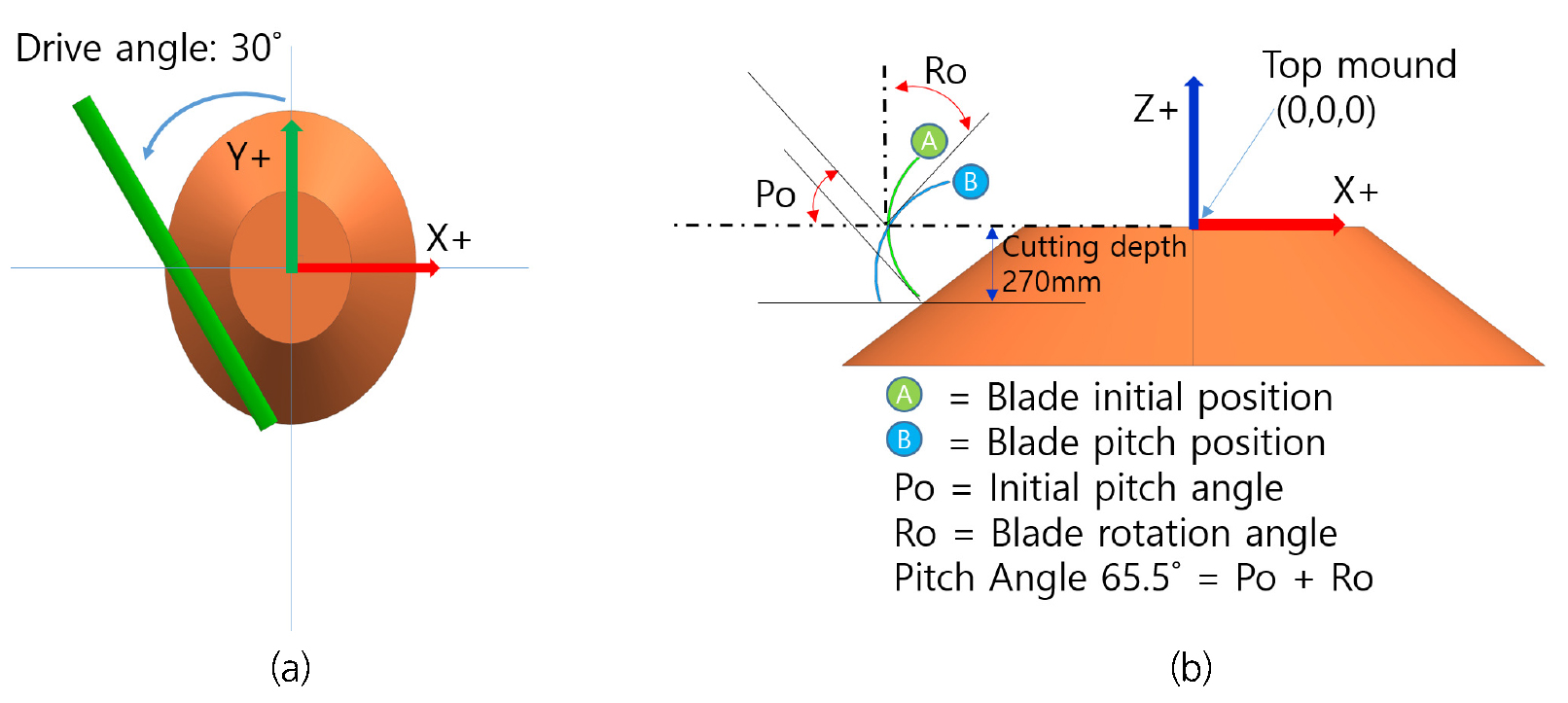
블레이드의 평탄작업중 최초 1회를 동해석으로 구현하였다. 타원의 단축방향(+x방향)으로 블레이드 추진방향을 설정하였다(Fig. 4(a)). 블레이드의 추진각도(drive angle)와 절삭각도(pitch angel)는 산포작업 기본각도인 30°, 65.5°로 각각 설정하였다(Fig. 4(b)). 산포작업은 블레이드 하단부의 접촉이 끝나는 지점까지 진행한 후 각 해석을 종료하였다.
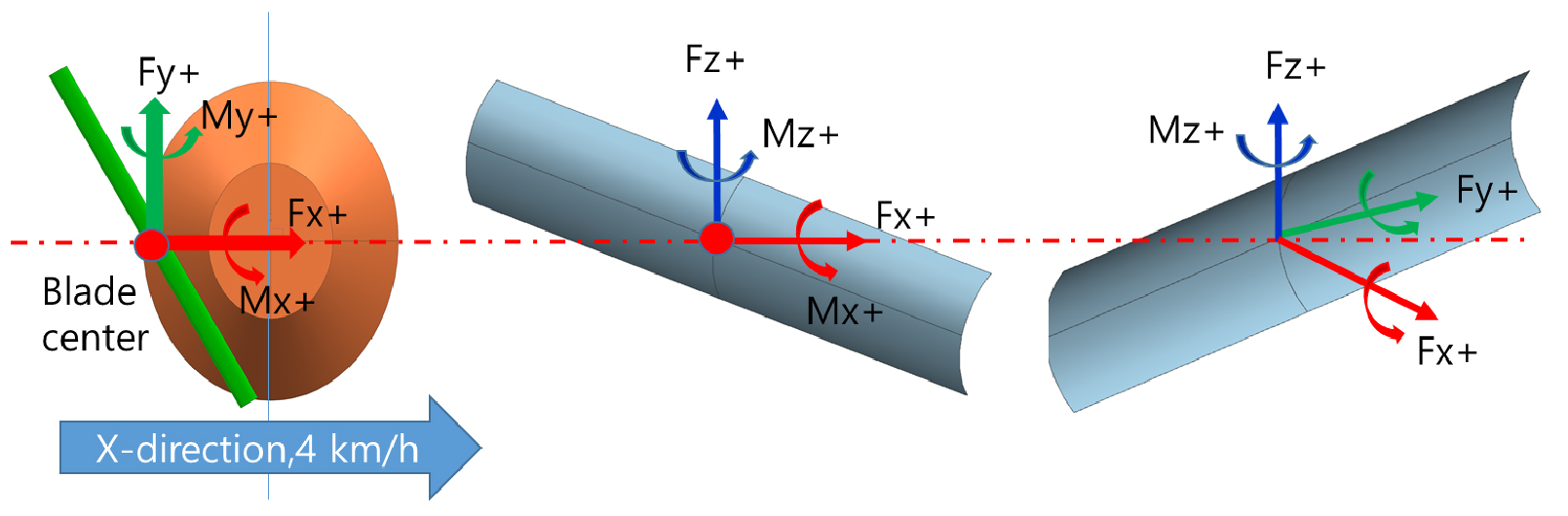
모터 그레이더는 블레이드 추진시 반력과 회전저항성이 낮을수록 블레이드 제어에 유리하고, 1회 작업에서 최대한 골재를 넓게 산포시켜야 작업 효율성이 높다. 따라서 블레이드에 작용한 3방향 반력, 모멘트, 산포면적을 출력값으로 기록하였다. 블레이드 추진시 기록되는 힘과 모멘트는 블레이드의 중심점(center)을 기준으로 계산하였고, 각 성분은 Fig. 5에 정의하였다.
4. 실험계획 및 해석결과
4.1 설계인자 및 실험계획
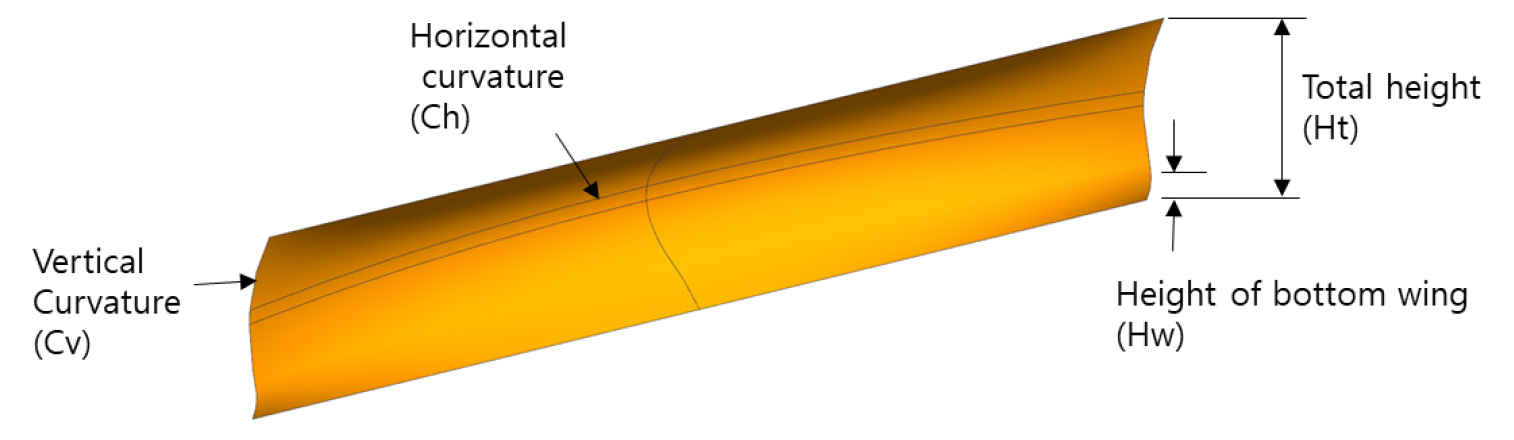
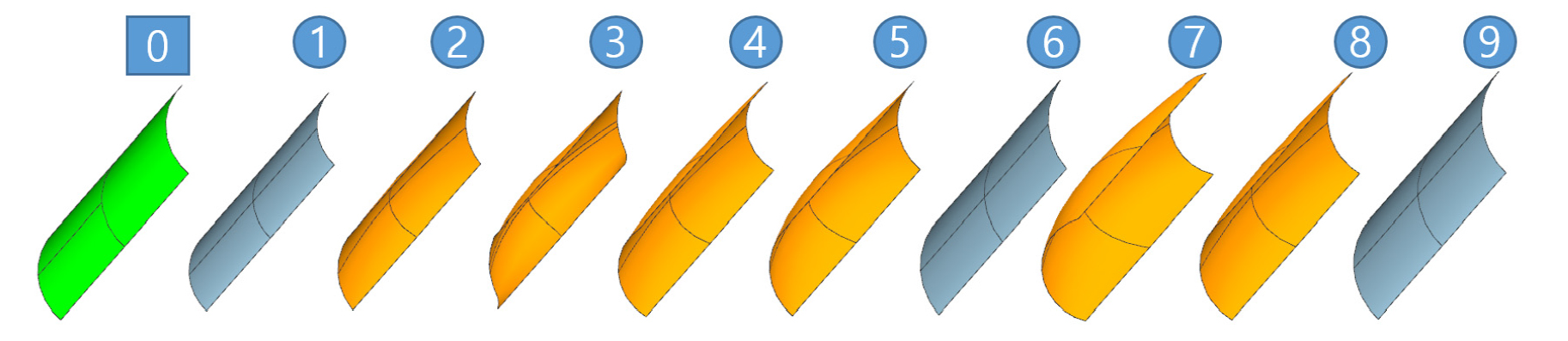
블레이드의 치수는 수직 높이, 좌우 폭, 수직방향 곡률이 기본적으로 설정되어 있다. 이 중 좌우 폭은 모터 그레이더 등급에 따라 고정된 설계값이므로, 설계자가 변경할 수 있는 치수는 수직 높이와 수직방향 곡률 2가지 인자이다. 수평곡률과 하단 날개의 높이를 신규 설계인자로 고안하였다(Fig. 6). 최종적으로 실험계획의 설계인자로 높이, 수직곡률, 수평곡률, 하단날개 높이 4가지를 설정하였다. 또한 설계인자의 영향력 판단을 위한 초기 실험점은 4인자 3수준의 L9(34) 직교배열법을 이용하였다(Table 1). 이 배열법은 블레이드 형상 설계에 중요한 설계인자들의 상호작용을 고려하고, 이외의 상호작용을 희생시켜 실험 횟수를 감소할 수 있는 것으로 보고된 바 있다(Kim et al., 2019). 또한, 통계적인 분석방법으로는 분산분석(ANOVA)를 채택하여 설계인자의 영향성을 판단하였다. 현재모델을 포함해 총 10개의 전산모델을 수립하였다. Fig. 7은 10개 설계인자의 수준 조합에 따른 모델의 평면도를 보여준다.
Table 1.
DOE (design of experiment) for blade design parameters (unit: mm)
4.2 해석 결과
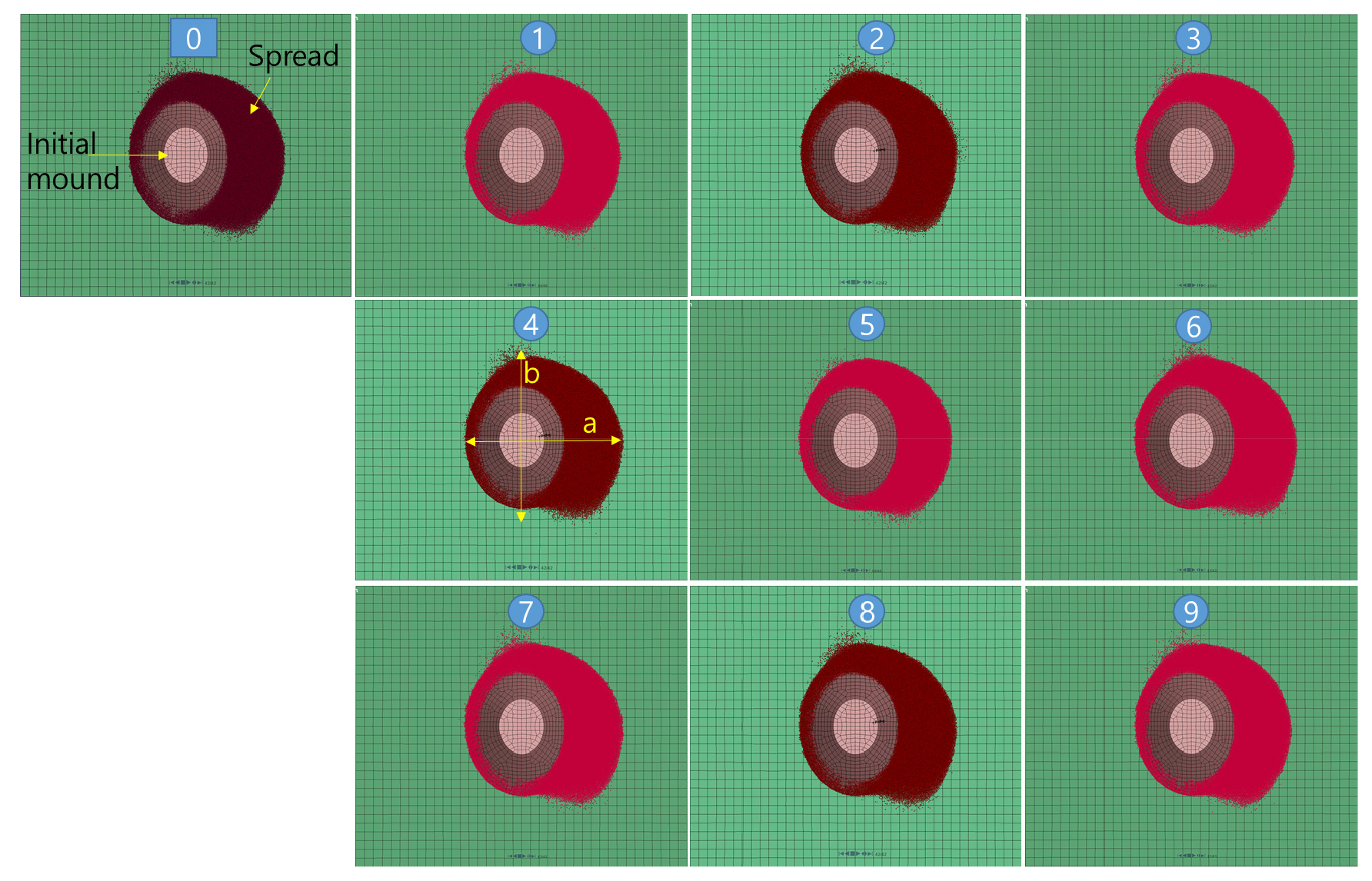
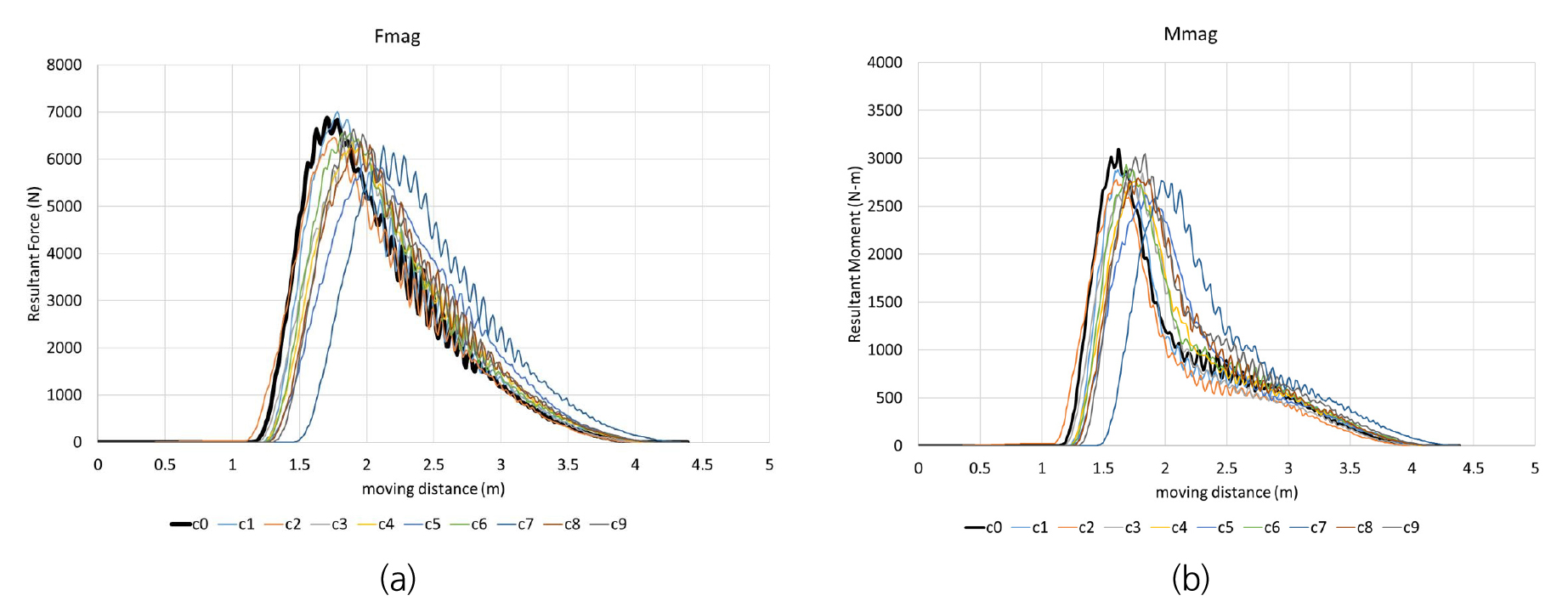
실험계획에 의한 개별요소법 해석은 Table 1의 직교배열표 상 설계인자의 조합에 따라 총 9번 수행하였으며, 최초 설계안과 개선모델의 작업성능을 비교하였다(Table 2). 초기의 골재가 블레이드에 의해 산포되는 해석결과 그림은 Fig. 8과 같다. 블레이드가 왼쪽에서 오른쪽으로 골재를 산포하기 전과 후의 영상을 각각 표현하였다. 앞서 Fig. 5에서 설명한 바와 같이, 반시계 방향으로 추진각도를 설정했기 때문에 추진방향의 우측면 방향에서 산포가 더 진행된 결과를 보여주고 있다. 산포결과는 격자를 이용하여 조건별 산포면적(As: spread area)을 계산하였고, 블레이드 추진 중 습득한 3방향 반력과 모멘트를 추출하였다(Fig. 9).
Table 2.
DEM analysis result according to design combination
해석으로부터 도출된 3가지 결과데이터(반력, 모멘트, 산포면적)과 4가지 입력변수의 관계에 대하여 분산분석을 실시하였고, 그 결과를 Table 3에 제시하였다. 또한 분산분석의 결과로 계산된 각 인자의 민감도를 Table 4에 정리하였다. 이때, 각 인자의 민감도는 식 (2)와 같이 제곱합(Seq SS)을 바탕으로 계산되었다.
Table 3.
Analysis of variance results of design factors
Table 4.
Sensitivity analysis results of four design factors
설계인자별 가장 큰 영향력을 가지는 값을 회색으로 표시하였다. 블레이드 높이(Ht)는 수직방향 모멘트(My)에 가장 큰 영향력을 가졌다. 수직곡률(Cv)은 산포면적(As)에, 수평곡률은 3방향 반력(Fx, Fy, Fz)과 추진시 수평회전 모멘트(Mz)에 가장 큰 영향력을 끼쳤다. 연구진이 추가로 설정한 인자중 하나인 하단 날개 높이(Hw)는 대부분의 출력값에 유의한 영향력을 보여주지 못했다.
기존에 알려진 설계인자인 블레이드의 높이와 수직곡률은 유의한 인자임을 재확인하였다(Ko et al., 2005). 여기에 수평곡률이 블레이드의 작업효율을 증대하는 데에 중요하다는 사실을 본 해석과정을 통하여 새롭게 발견하게 되었다. 이 결과를 기준으로 3가지 인자(높이, 수직곡률, 수평곡률)를 핵심 설계인자로 설정하여 최적화 기법을 적용하고자 하였다
5. 설계 최적화
5.1 점진적 2차 반응표면법(Progressive Quadratic Response Surface Method)
본 연구에서는 분산분석을 통해 계산된 각 인자의 민감도의 결과를 바탕으로 블레이드의 구조 최적화를 진행하였다. 최적화 알고리즘으로는 점진적 2차 반응표면법(PQRSM), 근사모델(meta-model)은 크리깅(kriging) 모델을 채택하였다. 근사모델은 설계공간 내에서 반응값과 변수의 관계를 근사화 하며, 근사모델 중 하나인 크리깅 모델은 대표적인 보간 모델로 설계변수가 많고 비선형성이 강한 최적화 문제에서 우수한 예측성능을 보이는 것으로 보고된 바 있다(Park et al., 2011). 점진적 2차 반응표면법은 설정한 설계공간 내에서 목적함수와 구속조건을 2차 함수로 근사화한다. 이후 탐색 과정에서 최적점이 존재할 것으로 기대되는 신뢰영역을 근사모델 관리 기법(반응값과 변수관계 갱신)과 제약조건을 만족하는 설계공간(Design space)에서 점진적으로 최적화를 수행하는 방법이다. 최적점 탐색은 Fig. 10과 같이 첫 번째 반복단계 설계점(x01)에서 각 설계변수 축(x1, x2)에서 2개씩, 중심점에서 1개씩 모두 2n+1개의 표본점(sampling points)을 선택함으로 2n+1번의 함수계산을 통해 2차항까지 구성된 근사함수를 생성하여 최적화를 수행하고 새로운 설계점(x*1)을 탐색한다(Park and Choi, 2004, Kim et al., 2019). 또한 기존의 반응표면법 보다 적은 실험점을 요구하기 때문에 효율적이며, 회귀계수를 정확하게 계산할 수 있어 근사함수를 구성하는데 적합하며 수치적인 노이즈를 포함하는 CAE Solver를 이용해야 하는 설계 문제를 해결하는 데에 효과인 것으로 보고된 바 있다(Kim et al., 2019).
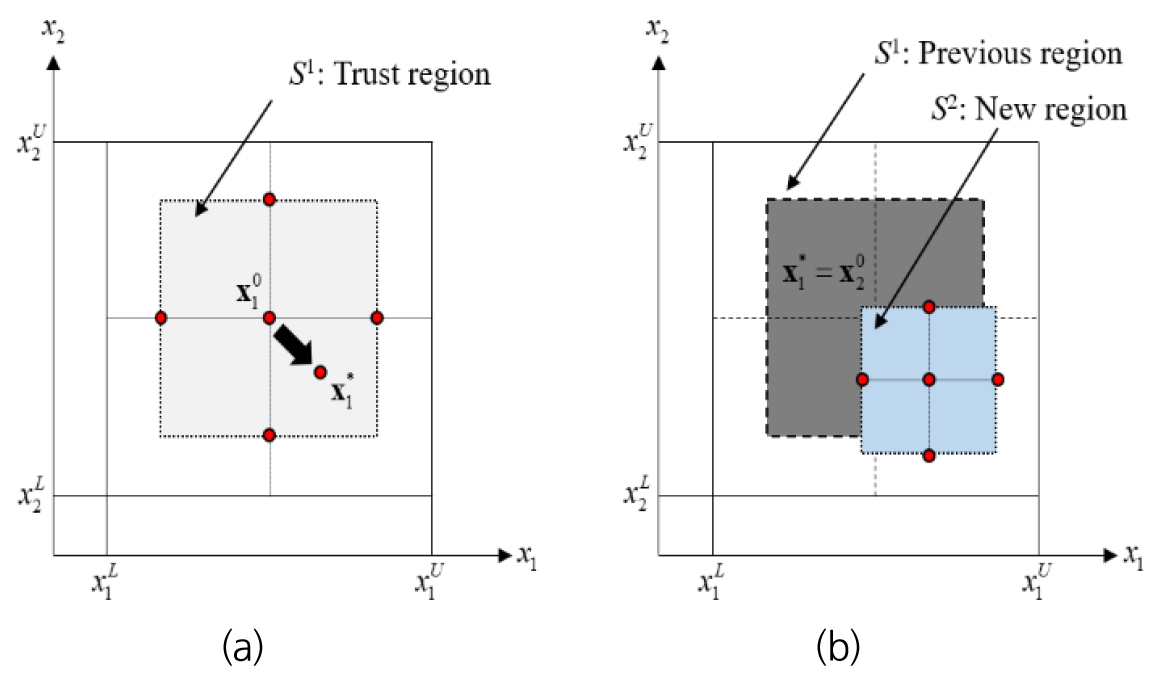
Fig. 10.
Design points sampling at first and two iterations; (a) at the first iteration, (b) at the second iteration (Park and Choi, 2004; Kim et al., 2019)
5.2 설계문제 정식화
본 연구의 블레이드 형상 최적화를 위해 고려한 주요 성능인자는 블레이드에 작용하는 반력으로 결정하였다. 작용되는 반력의 최소화는 산포면적의 최대화, 장비 운용의 안정성을 기대할 수 있기 때문이다. 따라서 블레이드의 반력의 최소화를 목적함수로 설정하였으며, 설계 제약조건은 10번의 개별요소법의 해석결과를 토대로 기존보다 높은 산포면적을 적용하여 반력 최소화 동시에 기존 이상의 산포면적 기대할 수 있도록 설계문제를 정식화하였다. 아래 문구는 최적화 조건에 대한 명령식이며, 최적화는 상용 PIDO (process integration and design optimization) 프로그램인 PIAnO를 사용하였다(PIDOTECH Inc., 2015).
- Find : Ht, Cv and Ch
- To minimize : Fm and Mm
- Constraint : 9.79 < As < 10.37
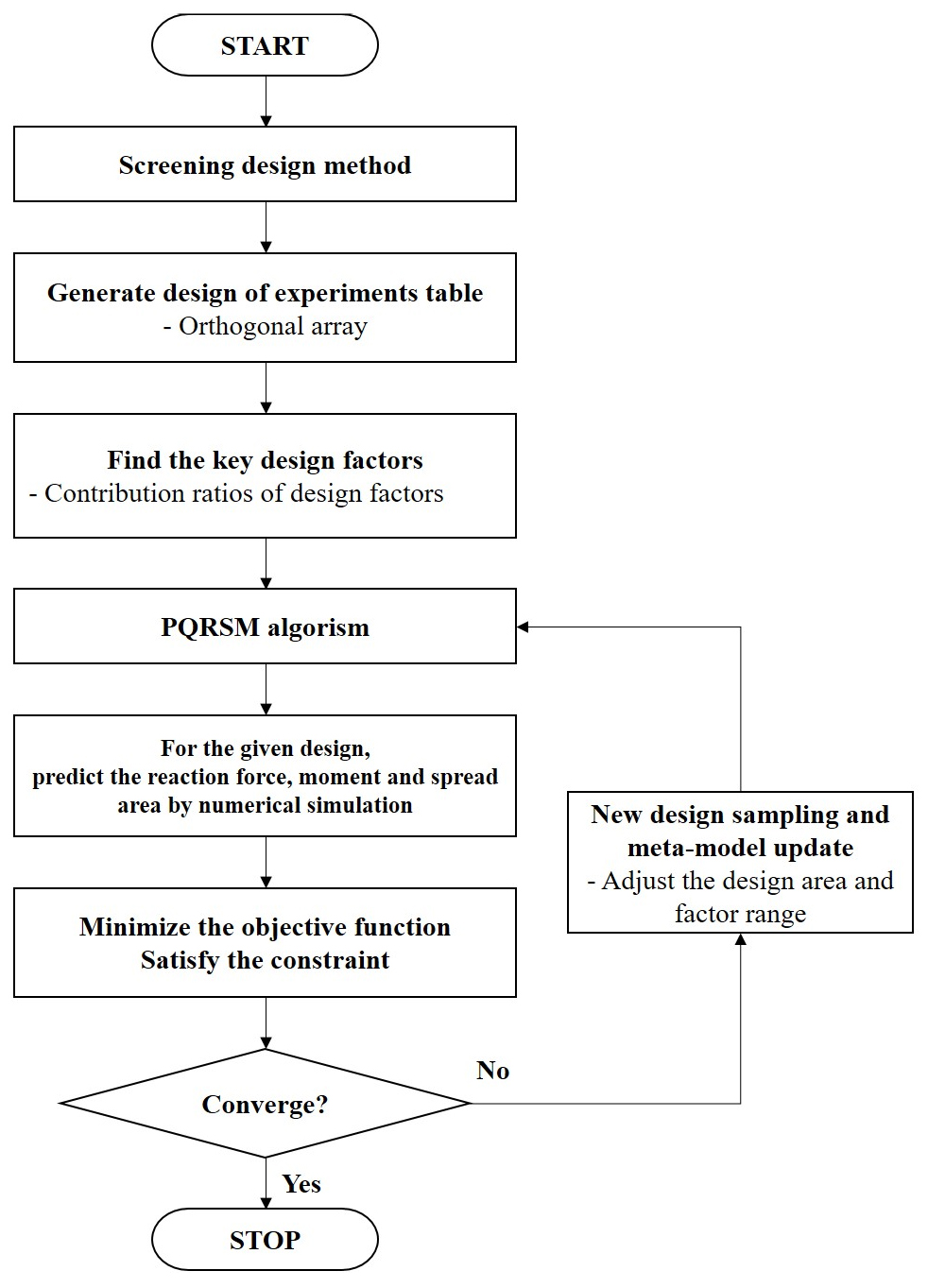
블레이드 형상 최적화의 수렴조건은 3회 반복과정(iteration) 이상 설계 제약조건을 만족하면서 목적함수의 개선이 없을 경우 수렴하도록 정의하였다(Kim et al., 2014). Table 5에 최적화에 적용된 설계인자 및 수준을 정리하였으며, 최적화 수행절차는 Fig. 11에 제시하였다.
Table 5.
Level of design factors
| Design factors | Level 1 | Level 2 | Level 3 | |
| Total height (mm) | Ht | 500 | 610 | 700 |
| Vertical curvature (mm) | Cv | 360 | 413 | 500 |
| Horizontal curvature (mm) | Ch | 0 | 10,000 | 20,000 |
5.3 설계 최적화 결과
점진적 2차 반응표면법과 근사모델을 이용하여 블레이드 반력 최소화를 위한 최적화 과정을 수행하였다. 최적화 수행 결과, 3번째 반복과정 이후 3회 이상의 반복과정 동안 구속조건을 만족하면서 목적함수의 개선이 되지 않았다. 따라서 3번째 반복과정을 최종 결과로 결정하였다(Table 6).
Table 6.
Convergence results of design factors for blade reaction force, moment, and spread area
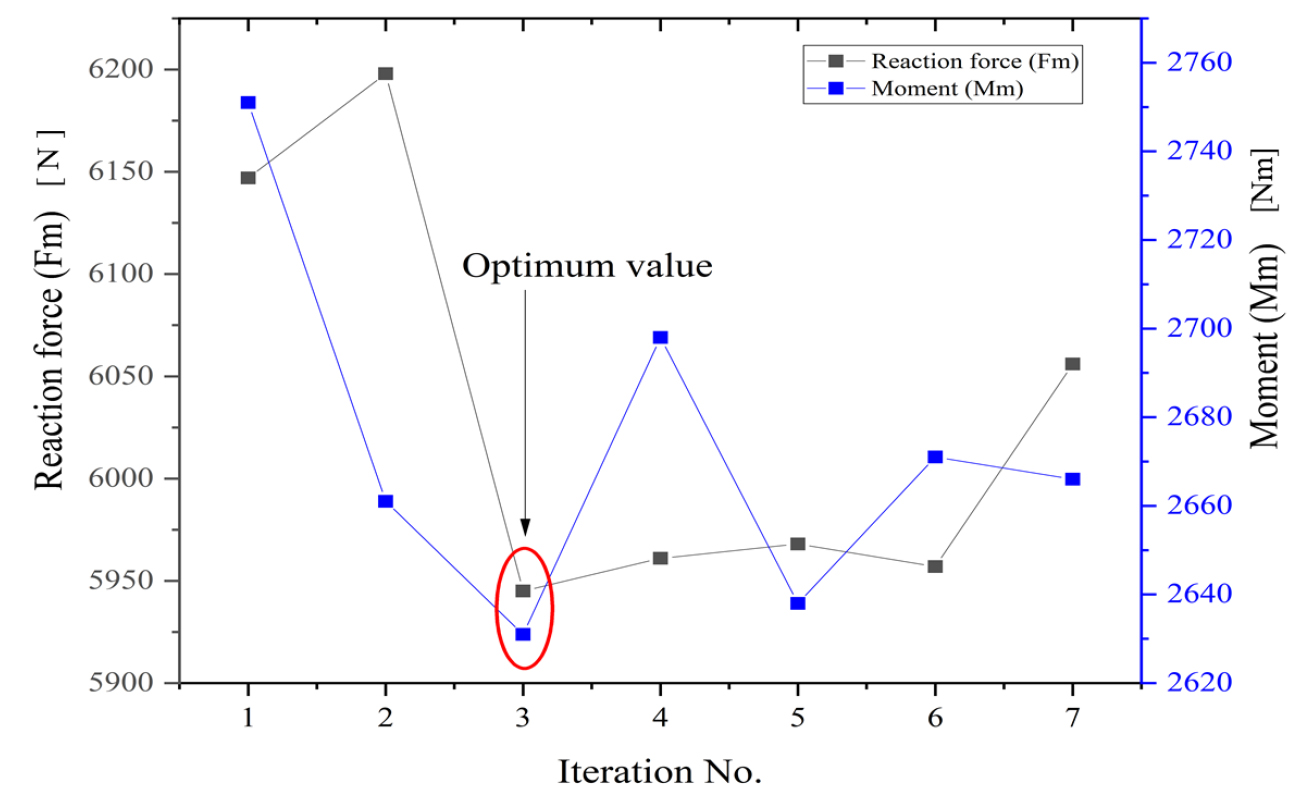
목적함수 즉, 블레이드 반력은 3번째 반복과정에서 Fm은 6,888 N에서 5,945 N으로 14%, Mm은 3,094 N ‧ m에서 2,631 N ‧ m로 15% 감소하였으며, 산포면적의 경우 9.79 m2에서 10.28 m2으로 기존 모델 대비 5% 증가하였다(Fig. 12). 블레이드의 최적 설계모델을 활용하면, 모터 그레이더의 구동 에너지를 10%이상 절감할 수 있을 것으로 예상된다.
Table 7에 최적화 수행으로 도출된 설계인자들의 초기값과 최적값을 비교하였다. 결과적으로 블레이드의 효율적인 작업을 위해서는 블레이드 높이는 577 mm, 수직곡률은 417 mm, 수평곡률은 10,250 mm에서 최적의 평탄화 작업이 가능할 것으로 판단되었다. 기존 블레이드 설계에 높이 및 수직곡률은 적용되었지만, 고려되지 않았던 수평곡률 적용한다면 블레이드 작업성능을 추가적으로 향상시킬 수 있을 것으로 판단된다.
6. 결 론
본 연구에서는 모터 그레이더의 블레이드 모듈의 기술 자립화를 위한 기초 설계연구를 수행하였다. 4가지 주요 설계인자를 고안한 후 실험계획을 수립하였다. 블레이드의 제작 및 실험비용을 절감하기 위하여 DEM 기법을 도입한 동해석을 수행하였다. 이후 분산분석을 통한 민감도 분석을 실시하여 핵심 설계인자에 대한 최적화를 진행하였다. 일련의 과정을 통해 얻어진 결론은 다음과 같다.
1. 초기 실험계획에 따른 동해석을 수행한 결과, 블레이드 높이는 수직방향 모멘트에, 수직곡률은 산포면적에, 수평곡률은 회전 모멘트에 가장 큰 영향력을 가진다.
2. 블레이드의 높이 및 수직곡률은 기존에 알려진 주요 설계인자였으나, 수평곡률이 블레이드의 작업효율을 증대하는 데에 중요한 인자라는 사실을 발견하였다.
3. 최적화 기법을 도입하여 추가 동해석을 수행하였고, 이를 통해서 3가지 주요인자인 블레이드 높이, 수직곡률, 수평곡률에 대한 설계 최적치를 제안하였다. 설계 최적치를 사용하여 작업시 에너지 효율일 약 10% 이상 향상될 것으로 기대된다.
본 결론은 골재직경 20 mm를 기준으로 수행한 동해석 결과를 바탕으로 획득된 것이므로, 이를 검증하기 위한 실증시험이 필요하다. 또한, 다른 직경분포를 갖는 골재에 대한 블레이드 설계치는 다른 값을 가질 수 있다.