1. 서 론
2. 머신러닝 기법 개요
2.1 K-최근접 이웃(K-Nearest Neighbors, KNN)
2.2 서포트 벡터 머신(Support Vector Machine, SVM)
2.3 랜덤 포레스트(Random Forest, RF)
2.4 XGB (eXtreme Gradient Boosting)
3. 데이터 분석 및 머신러닝 적용
3.1 현장개요 및 쉴드TBM 장비 제원
3.2 데이터 세트
3.3 모델 구현
4. 결과 및 해석
4.1 예측모델 비교 평가
4.2 특성 중요도
5. 결 론
1. 서 론
도심지 지상 공간이 포화되고 인구집중 현상이 심화되면서, 지하 인프라 시설의 수요가 증가하여 지하공간 및 터널 개발의 중요성이 부각되고 있다(Sharafat et al., 2021). 쉴드TBM 공법은 쉴드로 지반을 지지하며, 챔버 내부를 굴착토 또는 이수로 채워 추력으로 가압한 후 막장에 작용하는 토압과 수압에 대응하면서 굴진하는 터널시공공법이다. 최근 국내외에서 친환경, 안정성, 시공성에 대한 요구의 증가로 쉴드TBM 공법의 수요가 지속적으로 증가하고 있는 추세이다(Hyun et al., 2015; Zhang et al., 2022).
도심지와 같이 연약지반을 굴진하는 쉴드TBM의 경우에는 막장의 안정성 확보와 막장 변형의 제어를 위해 막장면에 적절한 지지 압력을 가하는 것이 매우 중요하다(Broere, 2001; Mollon et al., 2013). 하지만, 현장 및 지반조건, TBM 운영조건 등에 따라 소요 지지 압력이 상이하기 때문에 TBM 굴진 중 가해야 할 지지 압력을 결정하는 것은 매우 어렵다. 실제 TBM 적용 현장에서는 막장 지지 압력 관리 범위를 설정하여 이 범위 내에서 유지되도록 관리한다. 이때, 최소 막장 지지 압력의 결정이 매우 중요하며, 이에 따라 최소 막장 지지 압력 산정을 위한 이론적(Davis et al., 1980; Leca and Dormieux, 1990; Anagnostou and Kovari, 1996), 경험적(Broms and Bennermark, 1967), 수치해석적(Kirsch, 2010) 연구가 꾸준히 진행되어 왔다. 이러한 관리범위는 실제 지반 및 굴진 조건, 침하계측치와 연계하여 적정여부를 확인해야 하고, 필요시 수정 및 보완되어야 한다.
최근 급속히 발전되는 인공지능 기술을 토목공학분야에 적용하고자 하는 시도가 많고, 특히 머신러닝 기법 적용 사례가 증가하고 있다(Gao et al., 2021). 머신러닝 기법은 터널 시공 현장에서 계측된 데이터의 고차원, 비선형적 특성에 대한 고려가 가능하여, 터널 전방 지반조건 예측(Jung et al., 2019; Kim et al., 2021), TBM 성능 예측(Grima et al., 2000; Benardos and Kaliampakos, 2004), 지표침하량 예측(Santos and Celestino, 2008; Kim et al., 2022) 등의 연구에 적용되었다. Gao et al. (2019)은 RNN에 기반한 머신러닝 기법을 이용하여 위치별 챔버압(좌측 상부, 좌측 하부, 우측 하부)을 각각 예측하였지만, 해당 연구에서는 터널 시공 현장의 지반조건을 고려하지 않고, 입력특성이 다양하여 일반화가 불가능하다는 한계점이 존재한다.
본 연구에서는 머신러닝 기법을 통해 국내 토압식 쉴드TBM 터널 시공 현장의 대표적인 지반조건 및 굴진특성 데이터를 분석하여, 토압식 쉴드TBM 막장압 예측모델을 제안하였다. 이때, 토압식 쉴드TBM에서 막장에 실제로 가해지는 압력의 측정이 어려우므로 본 연구에서는 챔버압을 막장압으로 가정하였다. 수집된 지반조건 및 굴진특성 데이터로 데이터 세트를 구성하고, KNN (K-Nearest Neighbors), SVM (Support Vector Machine), RF (Random Forest), XGB (eXtreme Gradient Boosting) 머신러닝 기법을 통해 데이터를 학습하여 머신러닝 기법별 예측모델을 구축하였다. 각 예측모델의 학습과정에서 격자 탐색(Grid search)을 수행하였고, 교차검증을 통해 해당 학습성능을 확인하였다. 시험 데이터 세트에 대한 각 예측모델의 시험성능을 비교함으로써 최적의 토압식 쉴드TBM 막장압 예측모델을 선정하는 연구를 수행하였다.
2. 머신러닝 기법 개요
2.1 K-최근접 이웃(K-Nearest Neighbors, KNN)
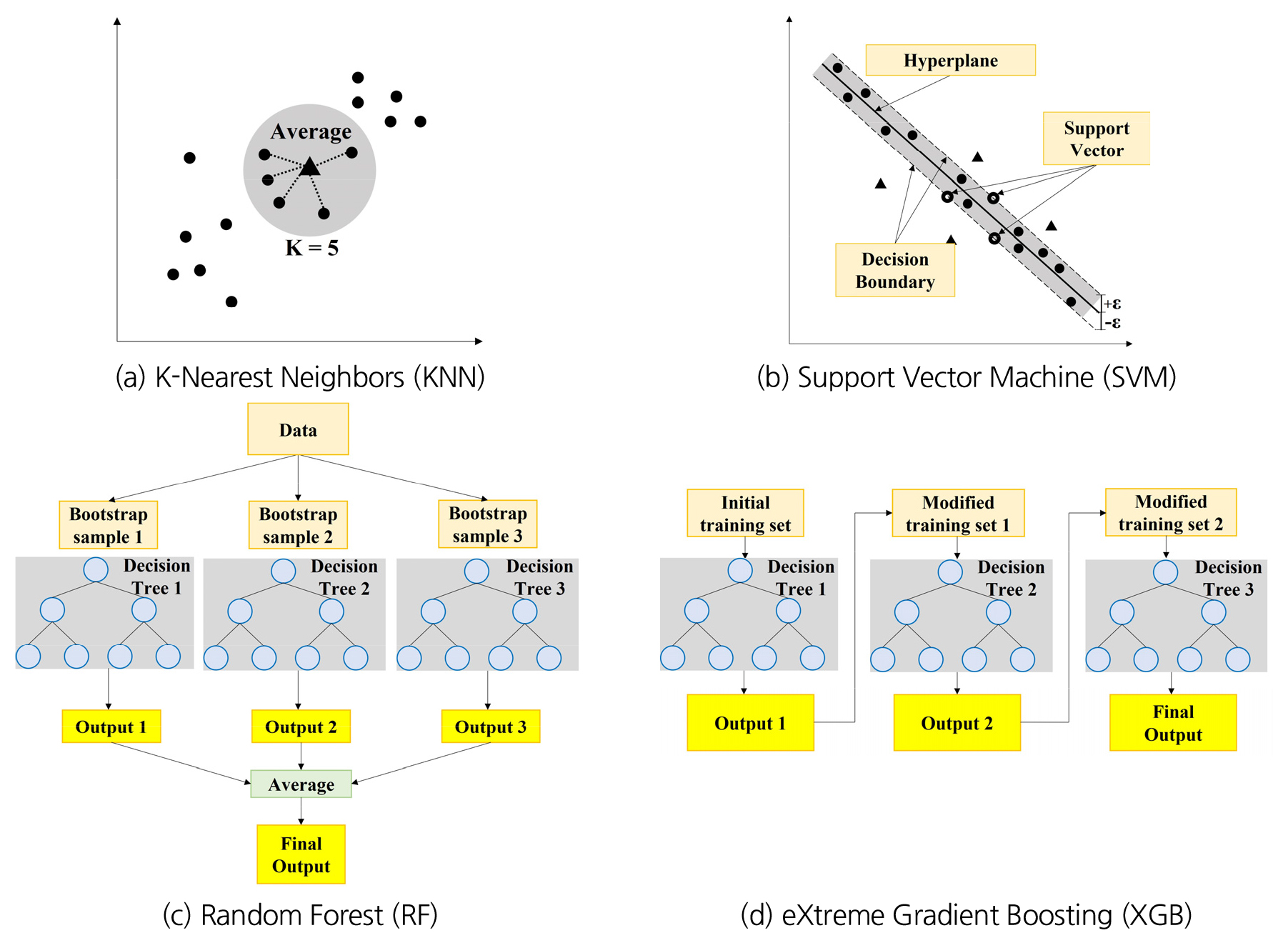
K-최근접 이웃 기법은 새로운 데이터와 유사성이 가장 높은 K개의 기존 데이터 특성을 이용하여 새로운 데이터의 값을 도출하는 기법이다(Fig. 1(a)). 새로운 데이터와 기존 데이터 간 거리를 산정한 후, 새로운 데이터와 가장 근접한 기존 데이터 K개의 평균으로 새로운 데이터의 값을 산출한다. K-최근접 이웃 기법은 간단한 기법으로서 구현이 용이하고 효율적인 데이터 분석이 가능하다는 장점이 있지만, 고차원 데이터 분석 시 상당한 연산 시간이 소모되고 변수 간 거리가 증가하여 성능이 감소한다는 단점이 있다.
2.2 서포트 벡터 머신(Support Vector Machine, SVM)
서포트 벡터 머신 기법은 데이터가 사상(Mapping)된 공간에 서포트 벡터(Support vector)를 생성하여 최적의 의사결정 영역(Decision boundary)과 초평면(Hyperplane)을 도출하는 기법이다(Fig. 1(b)). 데이터를 공간에 사상하여 초평면을 생성한 뒤, 해당 초평면의 상하로 ε만큼의 범위를 가진 의사결정 영역을 생성한다. 이때, 의사결정 영역 내에 최대한 많은 데이터가 포함되도록 하는 초평면을 도출한다. 최종적으로 서포트 벡터 머신 기법은 해당 초평면을 통하여 새로운 데이터의 값을 산출하는 기법이다. 서포트 벡터 머신 기법은 저차원 및 고차원 데이터 분석에 모두 용이하다는 장점이 있지만, 많은 연산 시간과 메모리 양이 소비되고 데이터 전처리와 예측 결과 해석이 용이하지 않다는 단점이 있다.
2.3 랜덤 포레스트(Random Forest, RF)
랜덤 포레스트 기법은 다수의 결정 트리 모델로 구성된 앙상블(Ensemble) 기법 중 배깅(Bagging) 유형 기법이다(Fig. 1(c)). 배깅은 과적합(Overfitting)을 방지하기 위하여 데이터 세트에서 무작위 복원 추출을 통해 임의의 개수로 구성된 부트스트랩 샘플(Bootstrap sample)을 생성하고 샘플별로 각 결정 트리 모델을 학습하여 결과를 집계하는 기법이다. 랜덤 포레스트 기법의 최종 결과값은 모든 결정 트리 모델의 출력 값을 평균 집계하여 산출된다. 랜덤 포레스트 기법은 대용량 데이터 처리에 효과적이고 과적합을 방지하며 특성 중요도 분석이 가능하고 예측 결과 해석이 용이하다는 장점이 있지만, 메모리 소모가 크다는 단점이 있다.
2.4 XGB (eXtreme Gradient Boosting)
XGB 기법은 예측력이 약한 학습기(Weak learner)의 결합으로 예측력이 강한 학습기를 생성하는 앙상블 기법 중 부스팅(Boosting) 유형 기법이다(Fig. 1(d)). 부스팅은 학습기를 병렬적으로 생성한 뒤, 이전 학습기에서 발생한 오차를 감소시키도록 가중치를 수정한 데이터를 다음 학습기에 적용하여 오차를 재산정하는 기법이다. 이를 모든 학습기에 대해 순차적으로 수행함으로써 오차가 감소되도록 데이터의 가중치를 수정한다. 이때, XGB 기법은 학습기로 랜덤 포레스트 기법과 동일하게 결정 트리 구조를 사용하고, 학습기의 복잡도가 증가할수록 페널티를 주어 과적합을 방지하는 기법이다. XGB 기법은 예측 성능이 우수하고 과적합을 방지하는 데 용이하다는 장점이 있지만, 많은 연산 시간이 소모되며 하이퍼파라미터(Hyperparameter) 설정이 용이하지 않다는 단점이 있다.
3. 데이터 분석 및 머신러닝 적용
3.1 현장개요 및 쉴드TBM 장비 제원
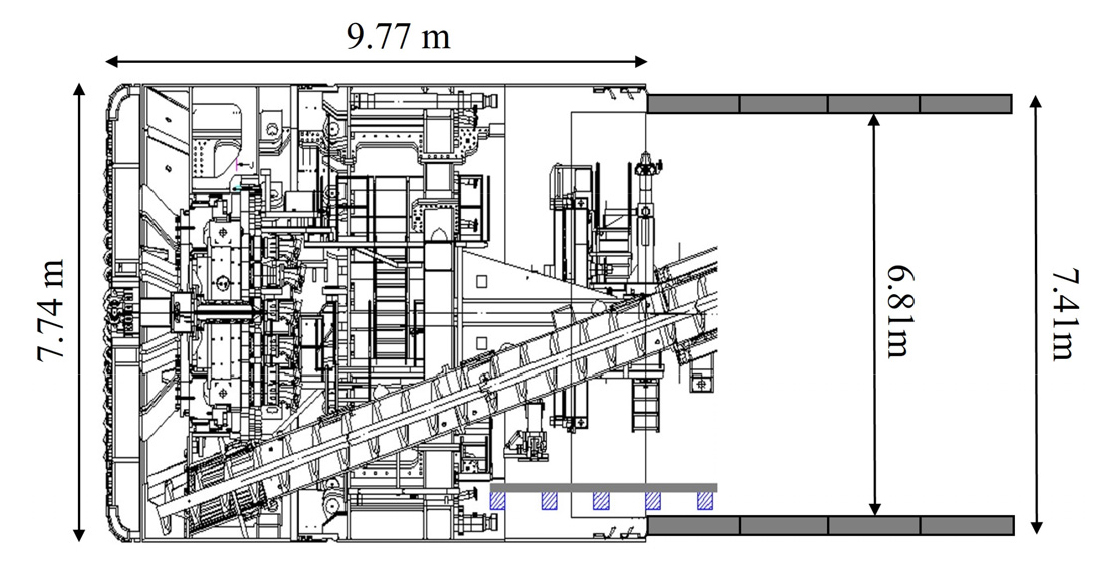
본 연구의 적용대상 현장은 국내 유틸리티 터널 시공 현장이며, 총 터널 연장 중 쉴드TBM 구간은 2,205 m이다. 사용된 토압식 쉴드TBM의 굴착직경과 길이는 각각 7.74 m, 9.77 m이며, 최대 가용 추력과 토크는 각각 54,978 kN, 10,366 kN ‧ m이다. 세그먼트 라이닝은 외경 7.41 m, 내경 6.81 m, 길이 1.5 m의 제원을 갖는다. 현장에서 사용된 토압식 쉴드TBM 장비의 형상 및 장비 제원은 각각 Fig. 2 및 Table 1에 나타냈다.
Table 1.
Summary of EPB TBM specification
| Type | Description |
| TBM excavation diameter | 7.74 m |
| TBM length | 9.77 m |
| Maximum thrust force | 54,978 kN |
| Maximum torque | 10,366 kN ‧ m |
| Segment diameter | 7.41 m (OD), 6.81 m (ID) |
| Segment width | 1.5 m |
3.2 데이터 세트
본 연구에서는 259~1,400번 세그먼트 링 데이터를 수집하여 데이터 세트를 구성하였다. 그 중 기록이 누락된 세그먼트 링(838번, 1,086번)의 데이터를 제외한 총 1,140개 세그먼트 링 설치 위치에서의 지반조건 및 굴진특성 데이터 세트를 구성하였다. 지반조건으로는 비배수 전단강도, 토피고, 지하수위 깊이(지표면에서 지하수위까지의 거리), 수압을 수집하였고, 굴진특성으로는 추력, 토크, 순 굴진율, 막장압을 수집하였다.
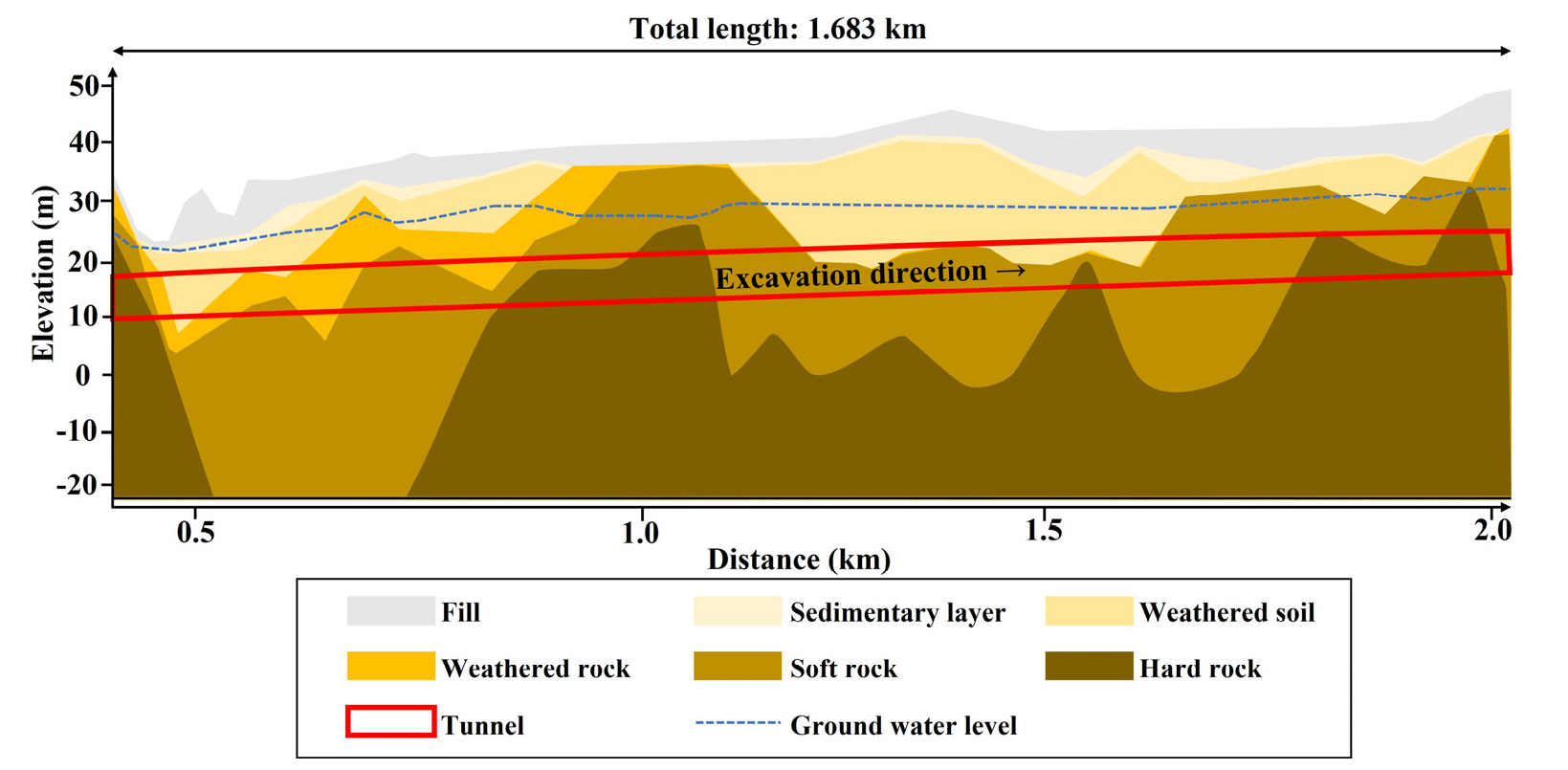
총 터널 연장 중 본 연구 범위(259~1,400번 세그먼트 링)에 해당하는 종단면도를 Fig. 3에 도시하였다. 쉴드TBM 터널은 0.5%의 상방향 구배로 풍화토, 풍화암, 연암, 경암을 통과하며, 터널 굴착 중 조우한 풍화토, 풍화암, 연암, 경암 지반의 비율은 각각 10%, 37%, 39%, 14%이다. 비배수 전단강도는 지반 종류별로 현장에서 채취한 비교란시료에 대한 일축압축강도시험을 통해 산정되었다. 풍화토, 풍화암, 연암, 경암의 평균 비배수 전단강도는 각각 28.9 kPa, 55.3 kPa, 282.1 kPa, 2,050.3 kPa로 산정되었다.
터널 상부 토피고는 5.84~23.50 m의 범위에 존재하고, 이 구간 중 토피고가 2.0D 이하인 약 160 m의 저토피 구간 이후에는 토피고가 약 19 m로 유지되었다. 지하수위 깊이는 1.29~10.47 m의 범위를 보이며, 지하수위는 Fig. 3에 보인 바와 같이 전 구간에서 쉴드TBM 굴착 구간 상부에 존재하고 변동폭이 적었다. 지반에서 쉴드TBM으로 가해지는 수압은 토피고와 지하수위 깊이를 고려하여 산정하였으며, 굴착 방향에 따라 지속적으로 상승하는 경향을 보였다. 굴진 초반부인 312번 세그먼트 링 인근에서는 수압이 35.57 kPa로 비교적 작게 산정되었으나, 후반부인 1,371번 세그먼트 링에서는 계측된 수압이 185.60 kPa로 5배 이상 증가함을 확인하였다.
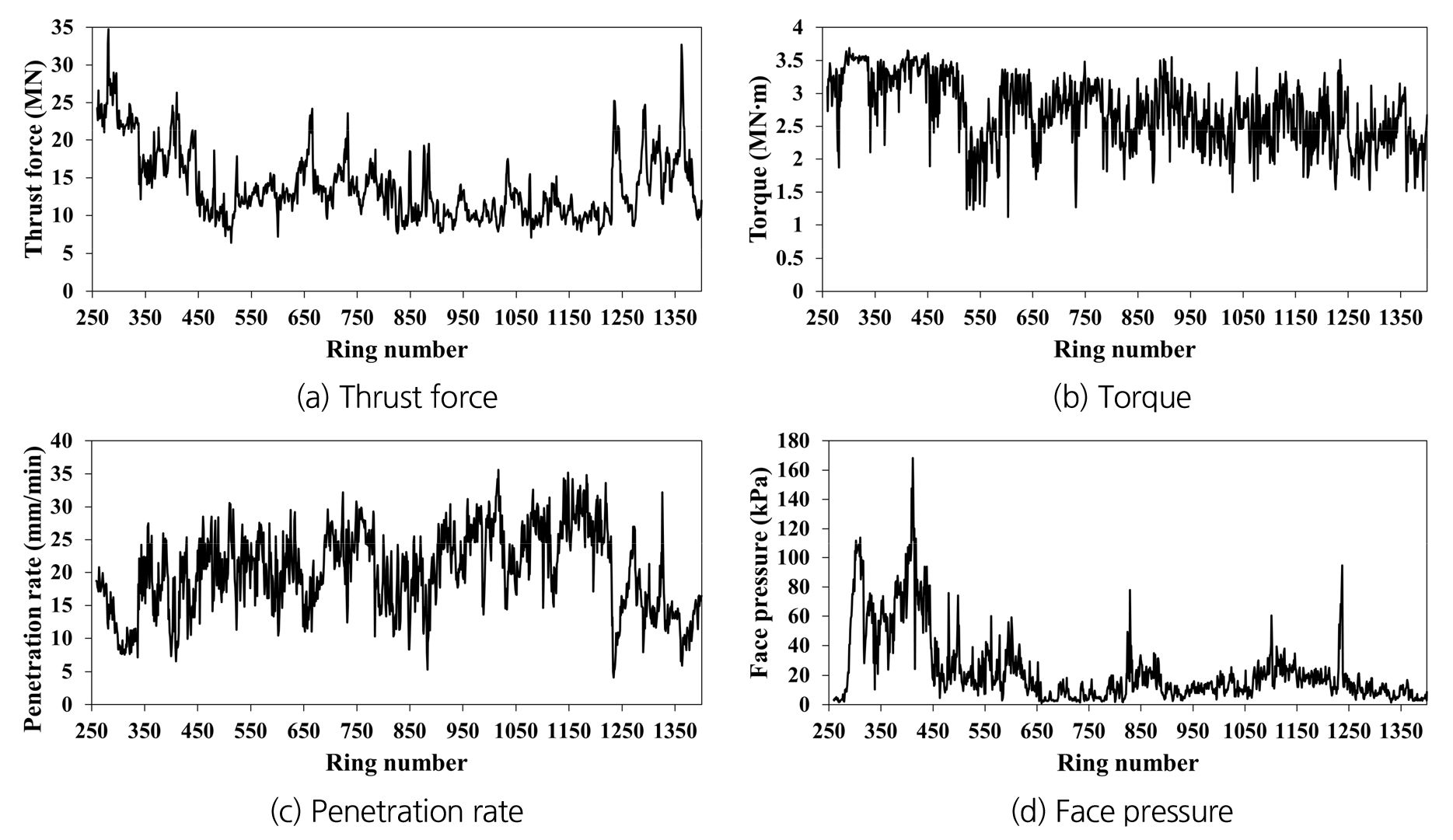
굴진특성 데이터는 지반조건 데이터와 동일하게 총 1,140개의 세그먼트 링 설치 위치에 해당하는 토압식 쉴드TBM 기계데이터(추력(Thrust force), 토크(Torque), 순 굴진율(Penetration rate), 막장압(Face pressure))로 구성하였다. TBM 터널 굴착에 따른 굴진특성 데이터의 분포를 확인하기 위하여 추력, 토크, 순 굴진율, 막장압의 4가지 굴진특성의 데이터를 Fig. 4에 도시하였다.
추력은 전반적으로 10~20 MN의 범위 내에 존재하였지만, 일부 세그먼트 링 구간(259~335번, 1,360~1,367번)에서 상대적으로 높은 추력이 측정되었다. 이는 경암 지반에서 원활한 굴착을 위한 TBM 추력의 증가에 따른 것으로 판단된다. 토크는 2~3.5 MN ‧ m의 범위 내에서 변동하며 지속적으로 감소하는 경향을 보였다. 순 굴진율은 대체적으로 약 20 mm/min 전후 범위 내에 존재하나, 일부 세그먼트 링 구간(300~335번, 400~415번, 848~850번, 882~884번, 1,230~1,245번, 1,360~1,380번)에서 다른 구간에 비해 상대적으로 낮은 순 굴진율을 보였다. 이는 저토피 구간 통과 시 막장 안정 및 지반침하 방지를 위한 지지 압력의 상승, 경암 지반에서의 낮은 절삭 효율로 인한 굴진 속도 저하 등에 의한 것으로 판단된다. 막장압은 275~440번 세그먼트 링 구간에서 높게 측정되었으나, 이후 약 20 kPa 전후로 안정적으로 관리되었다. 이는 저토피 구간 통과 시 막장 안정 및 지반침하 방지를 위한 지지 압력의 상승에 따른 것으로 판단된다. 추가적으로, 수집된 지반조건 및 굴진특성 데이터의 통계치(최소값, 평균, 최대값, 표준편차)를 Table 2에 정리하였다.
Table 2.
Statistical descriptions of field data
3.3 모델 구현
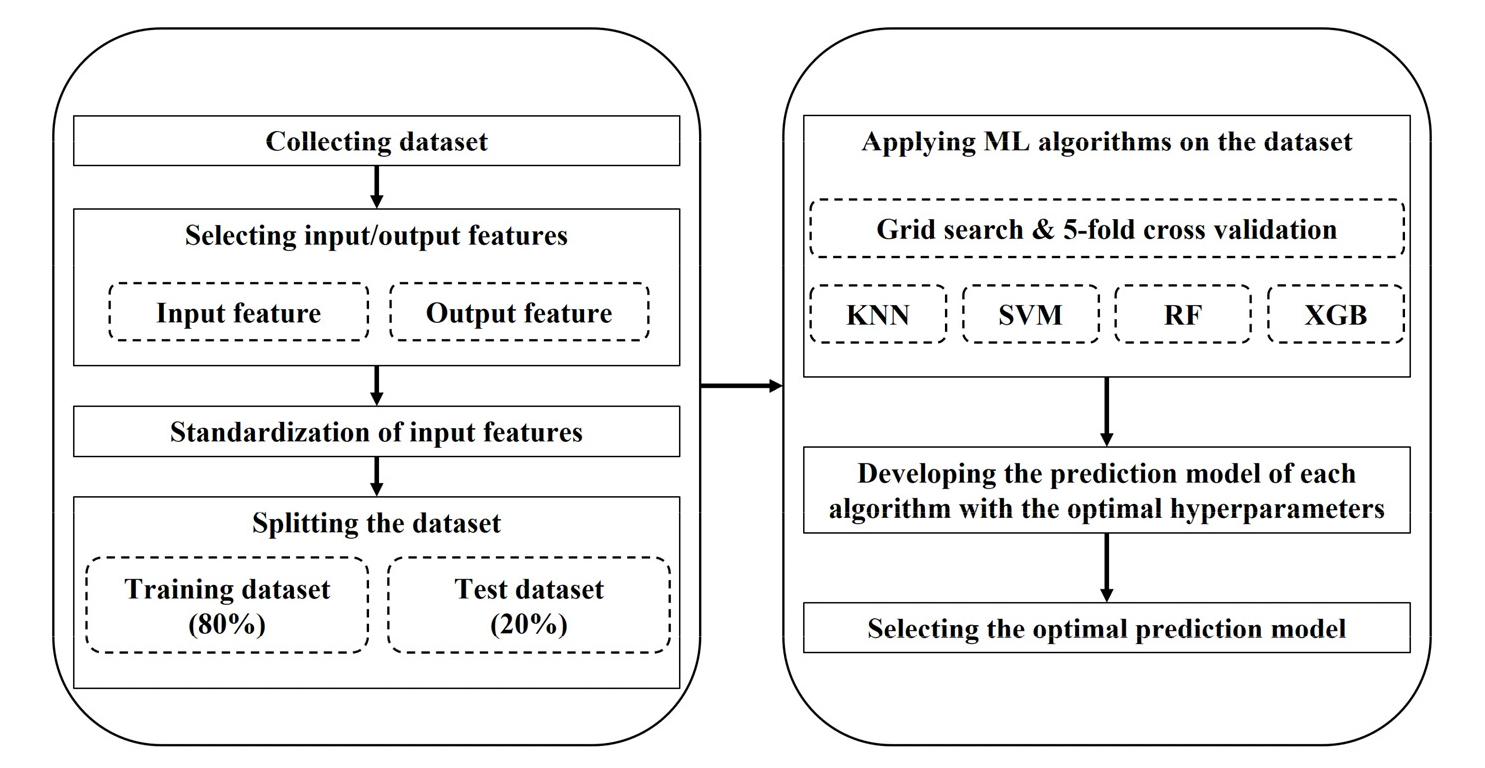
현장에서 수집된 지반조건 및 굴진특성 데이터 세트를 이용한 토압식 쉴드TBM 막장압 예측모델을 Fig. 5와 같은 흐름으로 구현하였다. 이는 데이터 세트 수집, 입력 및 출력특성 구분, 표준화(Standardization), 머신러닝 기법 적용, 최적 모델 선정 등으로 구성된다.
먼저, 수집된 데이터 세트 내에서 입력 및 출력특성을 구분하였다. 비배수 전단강도, 토피고, 지하수위 깊이, 수압, 추력, 토크, 순 굴진율은 입력특성으로, 막장압은 출력특성으로 선정하였다. 지반조건 및 굴진특성을 입력과 출력특성으로 구분한 이후에 입력특성에 대하여 데이터 스케일링(Scaling)을 수행하였다. 데이터 스케일링이란 서로 다른 특성의 데이터 범위를 일정하게 조절하는 과정을 의미한다. 값이 매우 크거나 작은 데이터를 데이터 스케일링 없이 머신러닝에 적용할 경우, 모델 학습과정에서 0으로 수렴하거나 무한으로 발산하여 머신러닝 성능이 저하될 수 있다. 본 연구에서는 데이터 스케일링 기법 중 각 입력특성 데이터의 평균을 0, 분산을 1로 조정하여 입력특성별로 정규분포를 따르도록 하는 표준화를 수행하였다.
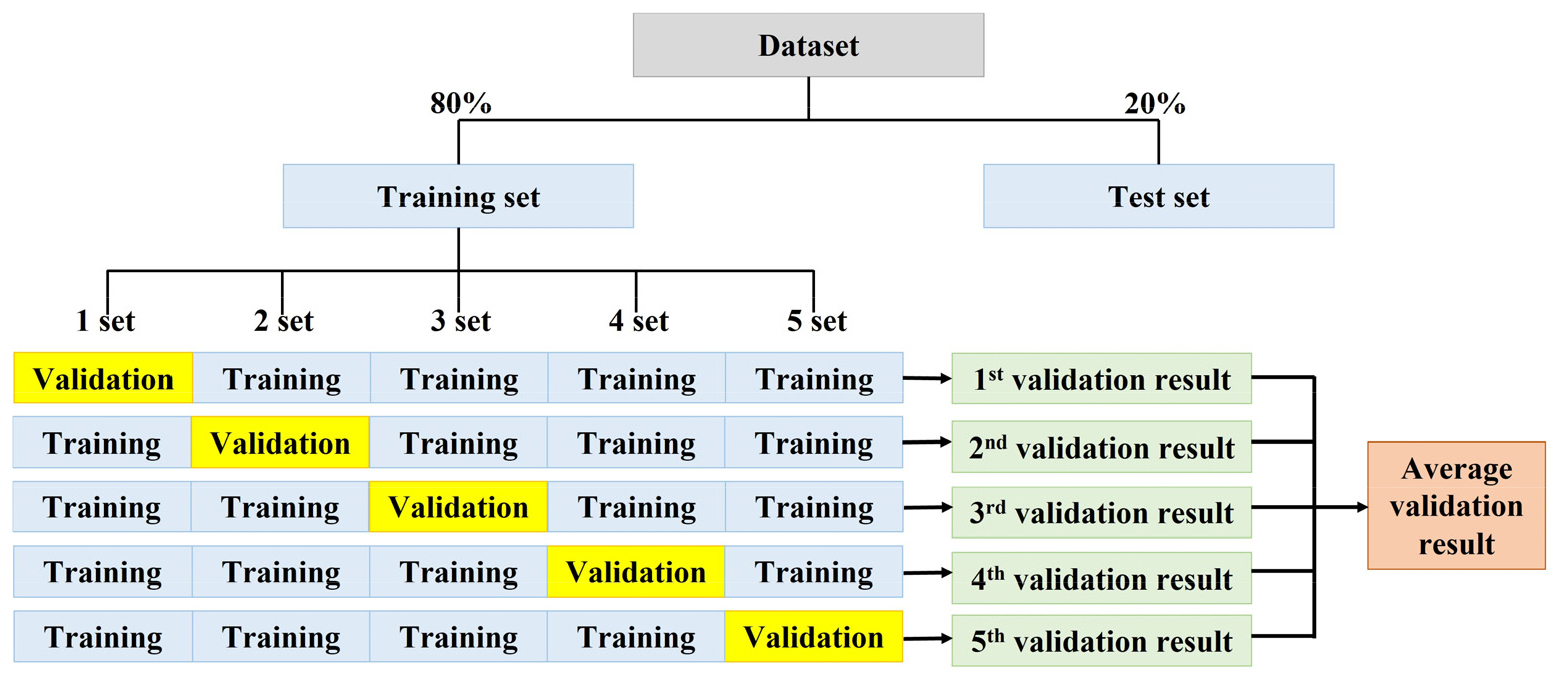
데이터 세트를 학습 데이터 세트(Training data set)와 시험 데이터 세트(Test data set)로 구분하고, 머신러닝 기법(KNN, SVM, RF, XGB)을 데이터 세트에 적용하여 머신러닝 기법별로 토압식 쉴드TBM 막장압 예측모델을 구축하였다. 데이터 세트 중 80%는 학습 데이터 세트로, 나머지 20%는 시험 데이터 세트로 활용하여, 912개의 학습 데이터 세트와 228개의 시험 데이터 세트로 구분하였다. 학습과정에서 격자 탐색(Grid search)과 교차검증을 수행하여 머신러닝 기법별로 막장압 예측모델을 구축하였다. 격자 탐색이란 모든 하이퍼파라미터의 조합을 시행하여 가장 우수한 성능을 도출하는 조합을 탐색하는 최적화기법을 지칭한다. 또한, 본 연구에서는 교차검증으로 5겹 교차검증을 적용하였다. 이는 Fig. 6과 같이 학습 데이터 세트를 5개의 소 데이터 세트로 분할한 후, 각각의 소 데이터 세트를 1회씩 돌아가면서 검증 데이터로 사용하여 성능을 평가하고, 성능지표의 5회 평균값으로 모델의 학습성능을 최종적으로 평가하는 기법이다.
본 연구에서는 성능지표로 평균 제곱근 오차(Root Mean Square Error, RMSE)를 적용하였다. 평균 제곱근 오차는 식 (1)과 같이 표현되며, 낮은 값이 산출될수록 모델의 성능이 우수함을 의미한다. 식 (1)에서 은 예측 데이터의 수를 의미하며, 와 는 각각 실제 막장압과 예측 막장압을 의미한다. RMSE를 막장압 예측모델의 시험성능지표로 선정하여 4가지 머신러닝 모델의 예측 성능을 비교한 후, 최적 토압식 쉴드TBM 막장압 예측모델을 선정하였다.
4. 결과 및 해석
4.1 예측모델 비교 평가
학습 데이터 세트와 격자 탐색을 이용하여 최적화된 각 머신러닝 모델(KNN, SVM, RF, XGB)의 학습성능을 5겹 교차검증을 통해 비교하였다. 예측모델의 학습성능을 비교한 결과, KNN, SVM, RF, XGB 모델의 평균 제곱근 오차가 각각 11.01 kPa, 10.56 kPa, 9.69 kPa, 9.44 kPa로 산출되었다. 머신러닝 기법별 예측모델의 학습성능과 최적 하이퍼파라미터를 Table 3에 정리하였다.
Table 3.
Face pressure prediction performance and optimal hyperparameter of the models
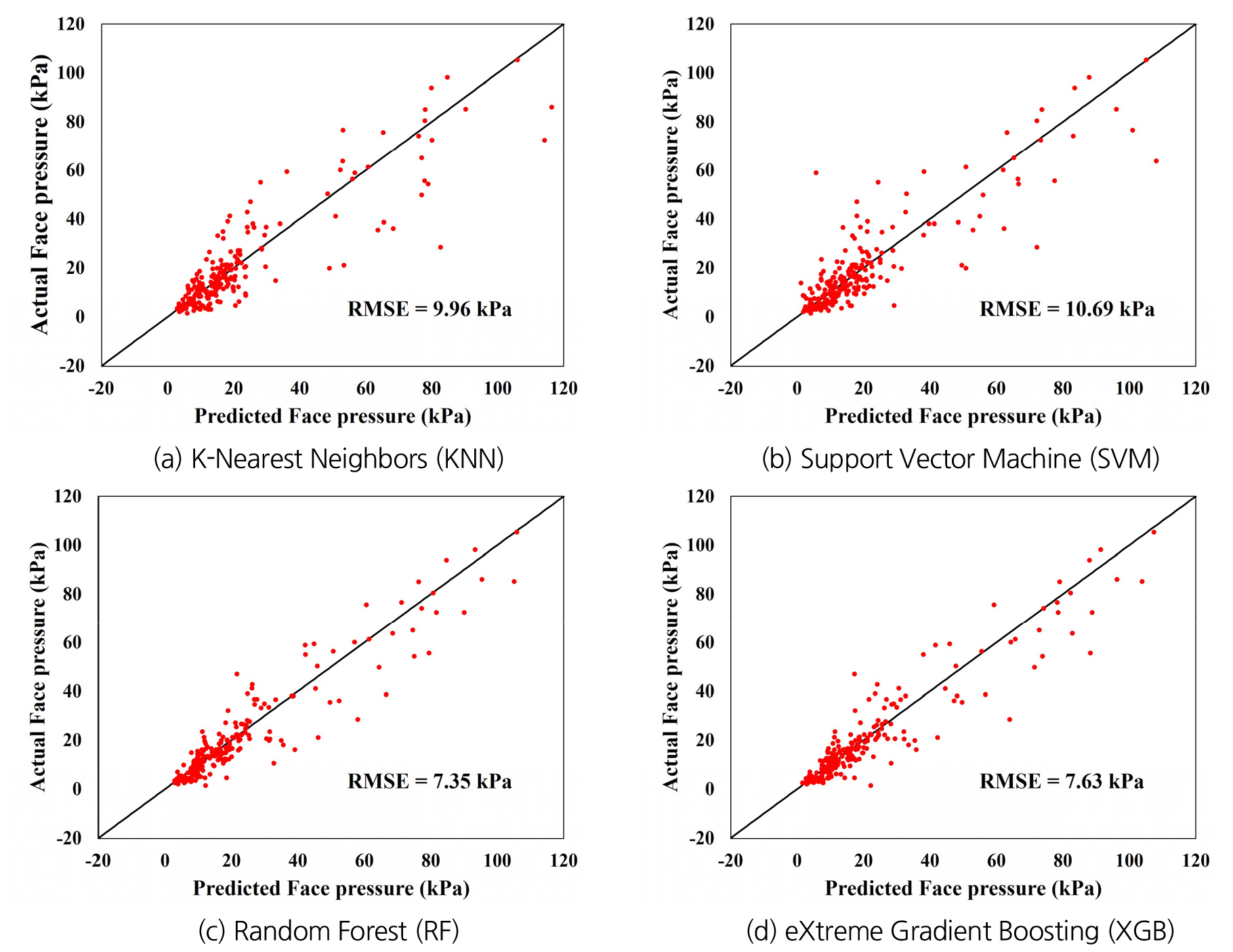
최적 토압식 쉴드TBM 막장압 예측모델을 선정하기 위하여 머신러닝 기법별 예측모델의 시험성능을 비교하였다. 머신러닝 기법별 예측모델의 시험성능을 Table 3에 정리하였고, 실제 막장압과 머신러닝 기법별 예측모델을 통하여 예측된 막장압의 비교 결과를 Fig. 7에 도시하였다.
Fig. 7을 통해 30 kPa 이하의 막장압에 대한 예측성능은 모든 모델에서 비교적 우수하나, 그 이상의 막장압에 대한 예측성능은 모델별로 상이함을 알 수 있다. RF, XGB 모델의 경우, 30 kPa 이상의 막장압에 대해서는 KNN, SVM 모델에 비해 비교적 예측도가 우수함을 알 수 있다. 따라서 결정 트리 기반 모델(RF, XGB 모델)의 경우, 본 연구에서 적용한 현장의 막장압 예측성능이 우수함을 알 수 있다. 또한, 예측모델의 시험성능지표를 비교한 결과, KNN, SVM, RF, XGB 모델의 평균 제곱근 오차가 각각 9.96 kPa, 10.69 kPa, 7.35 kPa, 7.63 kPa로 산출되어 RF 모델을 최적 토압식 쉴드TBM 막장압 예측모델로 선정하였다.
4.2 특성 중요도
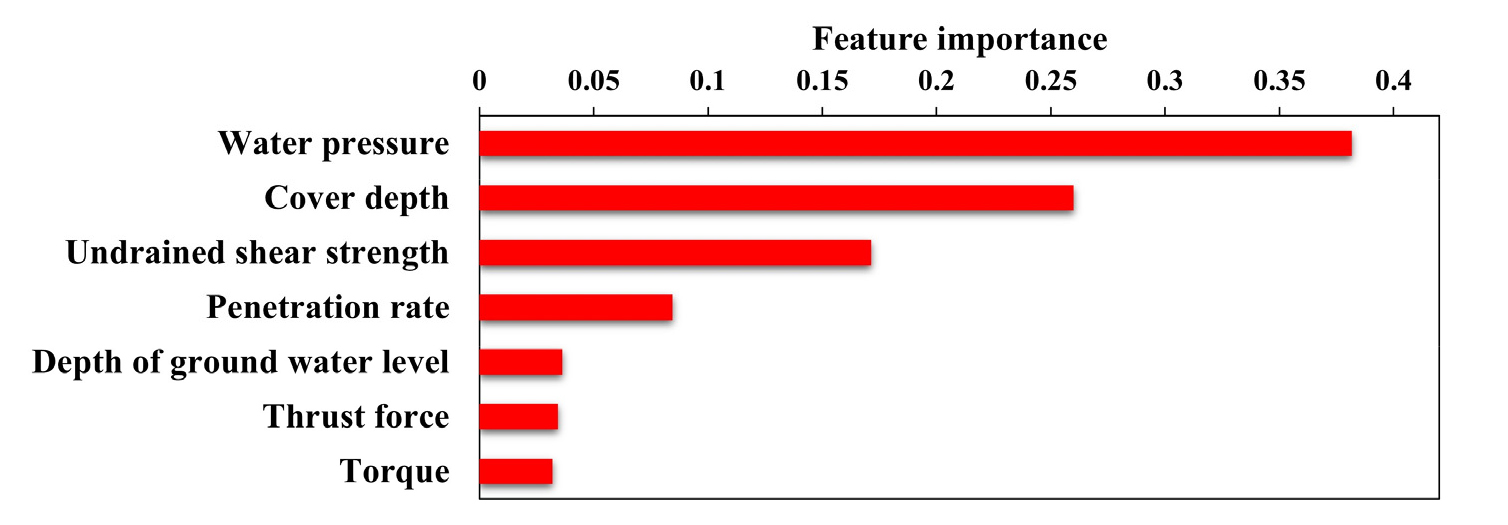
본 연구에서는 토압식 쉴드TBM 막장압 예측을 위하여 비배수 전단강도, 토피고, 지하수위 깊이, 수압, 추력, 토크, 순 굴진율의 총 7가지 특성이 사용되었다. 이때, 7가지 특성이 최종적으로 학습된 머신러닝 모델의 막장압 예측에 관여하는 비중은 상이하므로, 토압식 쉴드TBM 터널 시공 시 각 특성이 막장압에 미치는 영향도를 고려하여 막장압을 관리하게 되면 쉴드TBM을 효율적으로 운영할 수 있다. 따라서 본 연구에서는 최적 토압식 쉴드TBM 막장압 예측모델인 RF 모델의 특성 중요도를 산출하였고, 이를 Fig. 8에 도시하였다.
특성 중요도를 분석한 결과, 수압의 중요도가 0.38로 가장 높게 평가되었다. 따라서 해당 현장에서 수집된 지반조건 및 굴진특성 데이터를 바탕으로 선정된 최적 토압식 쉴드TBM 막장압 예측모델을 분석한 결과, 해당 현장에서는 수압이 막장압을 결정하는 데 가장 영향도가 높다고 판단된다. 일반적으로 TBM 터널 시공 중에 굴착면의 토압과 수압에 대응하기 위하여 그에 상응하는 막장압을 지반에 가하므로 막장압과 수압의 연관성이 깊다. 또한, 해당 현장의 굴진 방향에 따른 수압이 35.57~185.60 kPa로 전반적으로 크게 작용하고 있으므로 수압의 영향도가 높은 것으로 판단된다. 추가적으로, 7개의 특성 중 지반조건의 특성 중요도(수압: 0.38, 토피고: 0.26, 비배수 전단강도: 0.17, 지표면과 지하수위 거리: 0.04)가 굴진특성의 특성 중요도(순 굴진율: 0.08, 추력: 0.03, 토크: 0.03)에 비해 전반적으로 높음을 확인하였다. 이는 적용대상 현장의 지반조건이 양호하여, 응력해방을 일부 허용함으로써 지반의 지지능력이 활성화되었기 때문으로 판단된다.
5. 결 론
본 연구에서는 국내 유틸리티 터널 시공 현장의 지반조건 및 굴진특성 데이터를 4가지 머신러닝 기법에 적용하여 머신러닝 기법별 토압식 쉴드TBM 막장압 예측모델을 구축하고, 각 예측모델의 시험성능을 비교하여 최적 토압식 쉴드TBM 막장압 예측모델을 선정하였다. 이를 통해 도출된 결론은 다음과 같다.
1. 비배수 전단강도, 토피고, 지하수위 깊이, 수압, 추력, 토크, 순 굴진율을 입력특성으로, 막장압을 출력특성으로 선정하고, 4가지 머신러닝 기법(KNN, SVM, RF, XGB) 기반 토압식 쉴드TBM 막장압 예측모델의 성능을 비교한 결과, RF 모델의 시험성능이 상대적으로 우수함을 확인하였다. 따라서 본 연구에서는 RF 모델을 최적 토압식 쉴드TBM 막장압 예측모델로 선정하였다.
2. 7가지 입력특성이 각각 막장압에 관여하는 영향도를 분석하기 위하여 선정된 최적 모델인 RF 모델의 특성 중요도를 산출하였다. 입력특성 중 수압이 가장 높은 특성 중요도가 도출되었고, 지반조건이 굴진특성에 비해 특성 중요도가 전반적으로 높음을 확인하였다. 이는 적용대상 현장의 지반조건이 양호하여, 응력해방을 일부 허용함으로써 지반의 지지능력이 활성화되었기 때문이다. 반면, 점토층과 같은 연약지반 굴진 시에는 변위를 최대한 구속해야 하기 때문에 굴진특성의 영향도가 증가할 것으로 판단된다.
3. 현장 엔지니어는 지반조건 및 지반침하 데이터 등을 분석하고 기존 경험을 활용하여 쉴드TBM의 막장압을 관리하므로, 현장 엔지니어의 작업부하강도가 크다. 본 연구에서 선정한 최적 토압식 쉴드TBM 막장압 예측모델은 머신러닝 기법으로 지반조건(비배수 전단강도, 토피고, 지하수위 깊이, 수압)에 따라 굴진특성(추력, 토크, 순 굴진율)을 적절하게 조절하여 적정 관리 범위 내의 막장압 유지를 가능하게 하여, 쉴드TBM 운영의 안정성 향상과 현장 엔지니어의 작업부하강도 저하에 기여할 수 있다. 추후 머신러닝 기법을 통한 커터 교체 시기 예측, 커터 폐색 여부 예측 등으로 연구범위를 확장함으로써 쉴드TBM 내 인력 개입 비율 최소화에 이바지할 수 있다.