Enhancing machine learning-based anomaly detection for TBM penetration rate with imbalanced data manipulation

Kibeom Kwon; Byeonghyun Hwang; Hyeontae Park; Ju-Young Oh; Hangseok Choi

doi:10.9711/KTAJ.2024.26.5.519

Preview

Research Paper

Journal of Korean Tunnelling and Underground Space Association. 30 September 2024. 519-532
https://doi.org/10.9711/KTAJ.2024.26.5.519

Enhancing machine learning-based anomaly detection for TBM penetration rate with imbalanced data manipulation

불균형 데이터 처리를 통한 머신러닝 기반 TBM 굴진율 이상탐지 개선

Kibeom Kwon¹

Byeonghyun Hwang¹

Hyeontae Park²

Ju-Young Oh³

Hangseok Choi⁴^*

권 기범¹

황 병현¹

박 현태²

오 주영³

최 항석⁴^*

¹Ph.D. Candidate, Dept. of Civil, Environmental and Architectural Engineering, Korea University

²Master Student, Dept. of Civil, Environmental and Architectural Engineering, Korea University

³Ph.D., Construction Technology Team, Samsung C&T

⁴Professor, School of Civil, Environmental and Architectural Engineering, Korea University

¹정회원, 고려대학교 건축사회환경공학과 박사과정

²정회원, 고려대학교 건축사회환경공학과 석사과정

³정회원, 삼성물산 건설부문 기반기술팀 공학박사

⁴정회원, 고려대학교 건축사회환경공학부 교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Anomaly detection for the penetration rate of tunnel boring machines (TBMs) is crucial for effective risk management in TBM tunnel projects. However, previous machine learning models for predicting the penetration rate have struggled with imbalanced data between normal and abnormal penetration rates. This study aims to enhance the performance of machine learning-based anomaly detection for the penetration rate by utilizing a data augmentation technique to address this data imbalance. Initially, six input features were selected through correlation analysis. The lowest and highest 10% of the penetration rates were designated as abnormal classes, while the remaining penetration rates were categorized as a normal class. Two prediction models were developed, each trained on an original training set and an oversampled training set constructed using SMOTE (synthetic minority oversampling technique): an XGB (extreme gradient boosting) model and an XGB-SMOTE model. The prediction results showed that the XGB model performed poorly for the abnormal classes, despite performing well for the normal class. In contrast, the XGB-SMOTE model consistently exhibited superior performance across all classes. These findings can be attributed to the data augmentation for the abnormal penetration rates using SMOTE, which enhances the model’s ability to learn patterns between geological and operational factors that contribute to abnormal penetration rates. Consequently, this study demonstrates the effectiveness of employing data augmentation to manage imbalanced data in anomaly detection for TBM penetration rates.

Keywords

Imbalanced data

Machine learning

Penetration rate

Synthetic minority oversampling technique

Tunnel boring machine

TBM (tunnel boring machine) 터널 프로젝트의 리스크 관리 측면에서 굴진율 예측은 중요하며, 이를 위한 머신러닝 기반 TBM 굴진율 예측 연구가 지속적으로 진행되어 왔다. 그러나, 기존 연구의 머신러닝 예측 모델은 정상 굴진율과 이상 굴진율 간의 불균형 데이터를 고려하는 데 한계가 있다. 본 연구에서는 데이터 증강 기법을 통해 불균형 데이터를 처리하여 머신러닝 기반 TBM 굴진율 이상탐지 성능을 개선하였다. 먼저, 상관관계 분석을 통해 유사 변수를 제거하여 6가지 입력특성을 선정하였다. 또한, 하위 10%와 상위 10%의 굴진율을 각각 이상 등급으로, 그 외 범위의 굴진율을 정상 등급으로 굴진율 등급을 구분하였다. 기존 학습 데이터와 SMOTE (synthetic minority oversampling technique)를 통해 증강된 학습 데이터를 각각 XGB (extreme gradient boosting)에 적용한 XGB 모델과 XGB-SMOTE 모델을 구축하였다. 굴진율 등급 예측 성능을 비교한 결과, XGB 모델은 정상 굴진율에 대한 예측 성능은 우수하나 이상 굴진율 예측 성능은 상대적으로 낮게 도출되었다. 반면, XGB-SMOTE 모델은 모든 굴진율 등급에서 일관되게 우수한 예측 성능을 보였다. 이는 SMOTE를 통한 이상 굴진율 데이터의 증강이 이상 굴진율을 유발하는 지반조건과 TBM 운영인자 간의 패턴 학습 수준을 향상시켰기 때문으로 판단된다. 결론적으로, 본 연구는 머신러닝 기반 TBM 굴진율 이상탐지 시 데이터 증강 기법을 활용한 불균형 데이터 처리가 효과적임을 보여준다.

키워드

불균형 데이터

머신러닝

굴진율

SMOTE

TBM

MAIN

1. 서 론
2. 관련기법 개요
2.1 XGB (extreme gradient boosting)
2.2 SMOTE (synthetic minority oversampling technique)
3. 머신러닝 예측 모델 개발
3.1 현장 개요
3.2 데이터세트 구성
3.3 예측 모델 구현
4. 결과 및 논의
5. 결 론

1. 서 론

최근, 도심지 인구밀집 현상이 가속화되고 교통혼잡비용이 증가함에 따라 터널 시공의 중요성이 더욱 부각되고 있다(Broere, 2016). 다양한 터널 시공 기법 중 친환경성, 안정성, 시공성 측면으로 우수한 TBM (tunnel boring machine)의 적용이 국내외적으로 확대되고 있다(Hyun et al., 2015). 터널 프로젝트의 공사비 및 공사기간의 적절한 관리를 위해 TBM 성능에 대한 정확한 예측이 중요하다(Yang et al., 2022). 일반적으로, TBM 성능 관리는 지연시간(downtime)을 제외한 순 굴착시간에 대한 굴착거리의 비율을 의미하는 굴진율을 기반으로 수행되고 있으며(Yagiz et al., 2009), 이는 파악하기 어려운 다양한 요인에 의한 지연시간을 성능 관리 분석에서 배제하기 위함이다(Farrokh, 2018). 이때, 지연시간은 커터 점검 및 교체, 세그먼트 설치, 과다 배토 등으로 인해 TBM이 정지된 시간을 의미한다(Kwon et al., 2024a).

TBM 굴진율 관리 시, 리스크 관리 측면에서 사전에 위험상황을 예측하여 방지하고 이에 대한 적절한 대응 방안을 수립하여 효율적으로 TBM을 굴진하기 위해서는 사전에 설계된 정상 범위를 벗어난 이상 굴진율의 탐지가 필수적이다(Moharrami et al., 2022). 예를 들어, 점착성 지반에서 발생하는 커터헤드 폐색 등 불리한 지반조건으로 인해 리스크 사건이 발생할 경우 굴진율이 저하될 수 있다(Vergara and Saroglou, 2017). 또한, 암반 구간 혹은 복합지반을 과도하게 높은 굴진율로 통과할 시, 디스크 커터에 가해지는 진동 및 하중이 증가하여 디스크 커터의 마모량 증가 혹은 비정상 마모가 유발될 수 있다(Tóth et al., 2013; Agrawal et al., 2022).

이러한 TBM 굴진율 관리의 중요성과 굴진율 영향인자들 사이의 비선형적 관계로 인해 머신러닝 기반 굴진율 예측 연구가 꾸준히 수행되어 왔다(Benardos and Kaliampakos, 2004; Yagiz et al., 2009; Mahdevari et al., 2014; Armaghani et al., 2017; Xu et al., 2019; Gao et al., 2021; Zhou et al., 2021; Yang et al., 2022; Ghorbani and Yagiz, 2024). 그러나, 기존 연구는 이상 굴진율의 낮은 발생빈도로 인한 정상과 이상 굴진율 간의 불균형 데이터를 고려하는 데 한계가 있다. 불균형 데이터를 효과적으로 고려하지 못하는 경우, 머신러닝 예측 모델이 정상 굴진율 예측에 편향되어 이상 굴진율에 대한 탐지 성능이 저하될 수 있다(Rezapour, 2021; Bae et al., 2022).

본 연구에서는 불균형 데이터를 효율적으로 처리하여 머신러닝 기반 TBM 굴진율 이상탐지 성능을 개선하였다. SMOTE (synthetic minority oversampling technique) 기반 데이터 증강을 통해 정상과 이상 굴진율 간의 불균형 데이터를 처리하였다. 이후, 데이터 증강을 적용한 경우와 그렇지 않은 경우에 개발된 예측 모델의 굴진율 등급 분류성능을 비교 평가하였다. 본 연구의 결과는 TBM 시공 중 위험 상황에 대한 조기 경보 시스템 구축에 기여하여, TBM 시공의 안전성과 경제성을 향상시킬 것으로 판단된다.

2. 관련기법 개요

2.1 XGB (extreme gradient boosting)

XGB 기법은 결정 트리와 같은 약한 학습기를 순차적으로 결합하여 강한 학습기를 생성하는 gradient boosting 유형의 앙상블 기법으로, Chen and Guestrin (2016)에 의해 제안되었다. Gradient boosting은 이전 학습기에서 발생한 잔차를 다음 학습기가 학습하여 점진적으로 잔차를 감소시키고, 최종적으로 모든 학습기의 예측을 결합하여 최종 예측 결과를 도출하는 기법이다. 특히, XGB 기법은 학습기의 복잡도가 증가할수록 페널티를 부과하는 정규화된 손실 함수(regularized loss function)를 사용하여 과적합을 방지하는 특징이 있어 활용 빈도가 높다(Kim et al., 2022; Kwon et al., 2022; 2024c; Pham et al., 2023).

2.2 SMOTE (synthetic minority oversampling technique)

SMOTE는 소수 등급의 데이터를 증강하여 학습 세트의 불균형 등급 분포를 균등하게 조정하는 데이터 증강 기법이다(Chawla et al., 2002). 이 기법은 대표적인 불균형 데이터 처리 방법으로서 다양한 연구에서 꾸준히 활용되고 있다(Liu et al., 2020; Chen et al., 2022; Kwon et al., 2024b; Song et al., 2024).

SMOTE를 활용한 데이터 증강은 다음과 같은 절차로 수행된다. 먼저, 임의의 기존 소수 등급 데이터( $x_{a}$ )를 기준으로 k개의 최근접 소수 등급 데이터를 탐색한다. 다음으로, 탐색된 k개의 데이터 중 임의로 하나의 데이터( $x_{b}$ )를 선택한다. 본 연구에서는 k 값으로 기본 설정 값인 5를 채택하였다. 마지막으로, 선택된 $x_{a}$ 와 $x_{b}$ 를 임의의 비율로 선형 내분하여 신규 소수 등급 데이터를 생성한다. SMOTE 기반 데이터 증강의 개략도를 Fig. 1에 도시하였다.

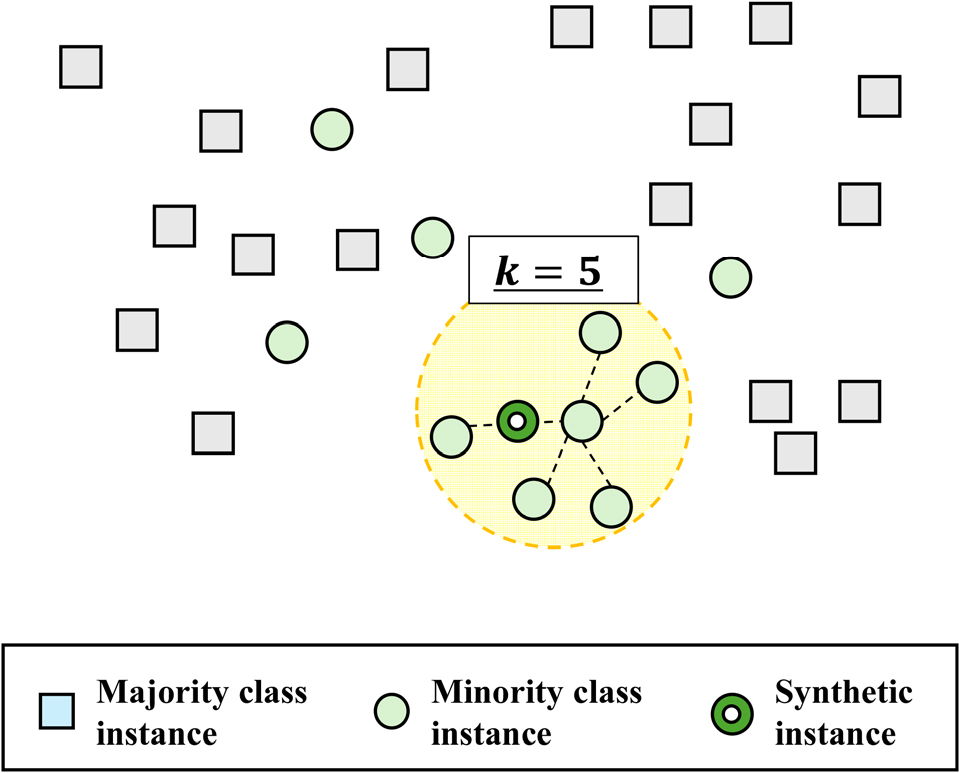
https://cdn.apub.kr/journalsite/sites/kta/2024-026-05/N0550260510/images/kta_2024_265_519_F1.jpg

Fig. 1.

Schematic of data augmentation using SMOTE

3. 머신러닝 예측 모델 개발

3.1 현장 개요

본 연구에서는 다수의 시설물을 복합적으로 수용할 수 있는 총 연장 2.2 km의 국내 멀티 유틸리티 터널 시공 현장 중 1.7 km에 해당하는 259번~1,400번 세그먼트 링을 연구대상 구역으로 선정하였다. 해당 구역에서는 굴착 직경 7.74 m의 토압식 쉴드 TBM이 적용되었으며, 세그먼트 라이닝의 제원은 외경 7.41 m, 내경 6.81 m, 길이 1.5 m이다. 현장에서 사용된 토압식 쉴드 TBM의 세부 사양은 Table 1에 요약하였다.

Table 1.

Specifications of TBM used in the studied site

Specification	Description
TBM type	EPB (earth pressure balance) shield TBM
TBM excavation diameter	7.74 m
TBM shield length	9.77 m
Max. thrust force	55.0 MN
Max. torque	10.4 MN ‧ m
Segment lining diameter	7.41 m (outer diameter), 6.81 m (inner diameter)
Segment width	1.5 m

연구대상 구역의 지층 분포는 지표로부터 매립층, 퇴적층, 풍화토, 풍화암, 연암, 경암으로 순차적으로 구성되어 있다. 통일분류법에 따라, 매립층은 SM, 퇴적층은 SM 혹은 SC, 풍화토는 SM 혹은 SW-SM으로 분류되었다. 지층별 N값 분포는 매립층 5/30~50/9, 퇴적층 4/30~30/30, 풍화토 1/30~50/12, 풍화암50/10~50/2이며, 연암과 경암의 RQD (rock quality designation)는 각각 0~75%와 34~100%로 도출되었다.

TBM 굴진 중 조우한 지반조건은 풍화토, 풍화암, 연암, 경암으로, 각 지반조건의 비배수 전단강도 대푯값은 풍화토 28.9 kPa, 풍화암 55.3 kPa, 연암 282.1 kPa, 경암 2,050.3 kPa이다. 선행연구에 의해 일축압축강도 및 비배수 전단강도 등의 지반강도와 굴진율이 반비례 관계에 있음이 확인되었으며(Frenzel et al., 2008; Gong and Zhao, 2009; Jamshidi, 2018), 본 연구에서는 굴진율 이상탐지에 비배수 전단강도를 활용하였다.

본 연구대상 구역의 터널 토피고는 5.8~23.5 m 범위에 존재하고, TBM은 0.5%의 상방향 구배로 굴진하였다. 지하수위는 터널 천장으로부터 상부 3.63~18.92 m에 위치하며, 토피고 및 지하수위 분포를 고려하여 산정된 수압은 TBM 굴진 방향에 따라 지속적으로 상승하는 경향을 보였다. 연구대상 구역의 종단면도를 Fig. 2에 도시하였다.

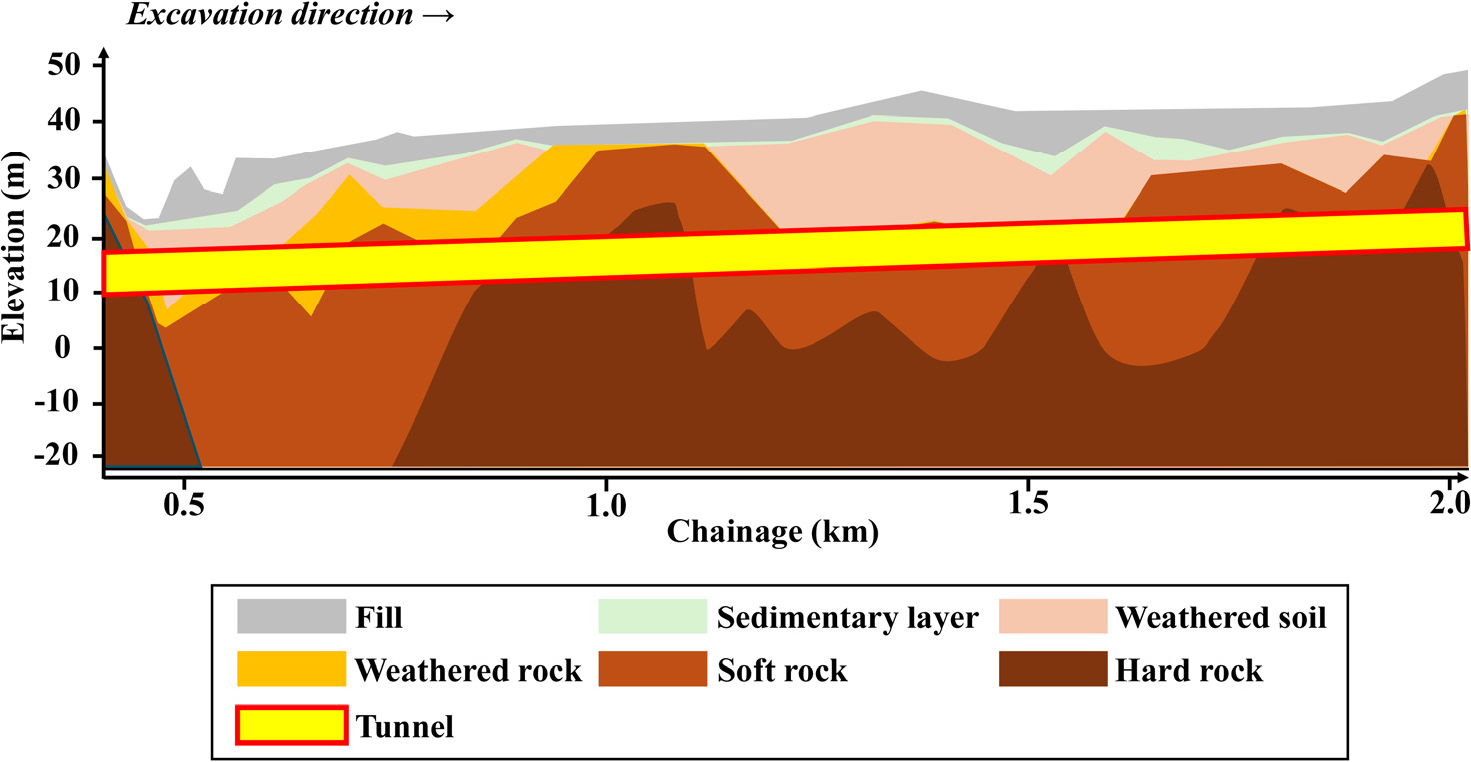
https://cdn.apub.kr/journalsite/sites/kta/2024-026-05/N0550260510/images/kta_2024_265_519_F2.jpg

Fig. 2.

Longitudinal profile of the TBM tunneling site

3.2 데이터세트 구성

TBM 굴진율에 영향을 미치는 인자는 지반조건과 TBM 운영인자로 구분된다(Grima et al., 2000). 본 연구에서는 3가지 지반조건과 4가지 운영인자 등 총 7가지 특성과 굴진율로 구성된 세그먼트 링 평균 데이터 중 결측치를 제외한 1,138개의 데이터가 수집되었다. 지반조건으로는 비배수 전단강도, 토피고, 터널 천장-지하수위 거리가 포함되었고, TBM 운영인자로는 추력, 토크, 챔버압, 테일보이드(tail void) 뒷채움량이 포함되었다. 전술한 7개의 특성 및 굴진율 데이터의 기술 통계량은 Table 2에 정리하였다.

Table 2.

Statistical descriptions of the dataset

Feature	Symbol	Min.	Q1*	Median	Q3*	Max.	Unit
Undrained shear strength	Su	28.9	55.3	282.1	282.1	2,050.3	kPa
Cover depth	C	5.8	18.6	19.2	19.7	23.5	m
Distance between tunnel crown and groundwater level	DTG	3.6	11.9	14.1	14.9	18.9	m
Thrust force	TF	6.4	10.5	12.7	16.3	34.8	MN
Torque	TQ	1.1	2.3	2.7	3.1	3.7	MN ‧ m
Chamber pressure	CP	0.01	0.08	0.15	0.25	1.68	kPa
Grouting volume for tail void	GV	4.1	6.0	6.2	6.5	21.1	m³
Penetration rate	PR	4.1	15.3	20.1	25.0	35.6	mm/min

*Q1: first quartile; Q3: third quartile

한편, 상관관계가 높은 입력특성들은 유사 정보를 제공하여 예측 모델의 복잡도를 증가시키고 과적합을 유발할 수 있다(Yu and Liu, 2004). 본 연구에서는 Fig. 3과 같이 유사 특성을 제거하기 위해 특성 간의 선형 관계를 측정하는 피어슨 상관계수(Pearson correlation coefficient)를 기준으로 상관관계 분석을 수행하였다(Liu et al., 2021; Xue et al., 2023). 그 결과, 토피고와 터널 천장-지하수위 거리 간 상관계수는 0.81로 도출되었고, 이는 두 특성 간의 강한 양의 상관관계가 있음을 의미한다(Moon et al., 2020). 이에 따라, 본 연구에서는 터널 천장-지하수위 거리를 제외한 6가지 특성을 TBM 굴진율 등급 예측 모델의 입력특성으로 선정하였다.

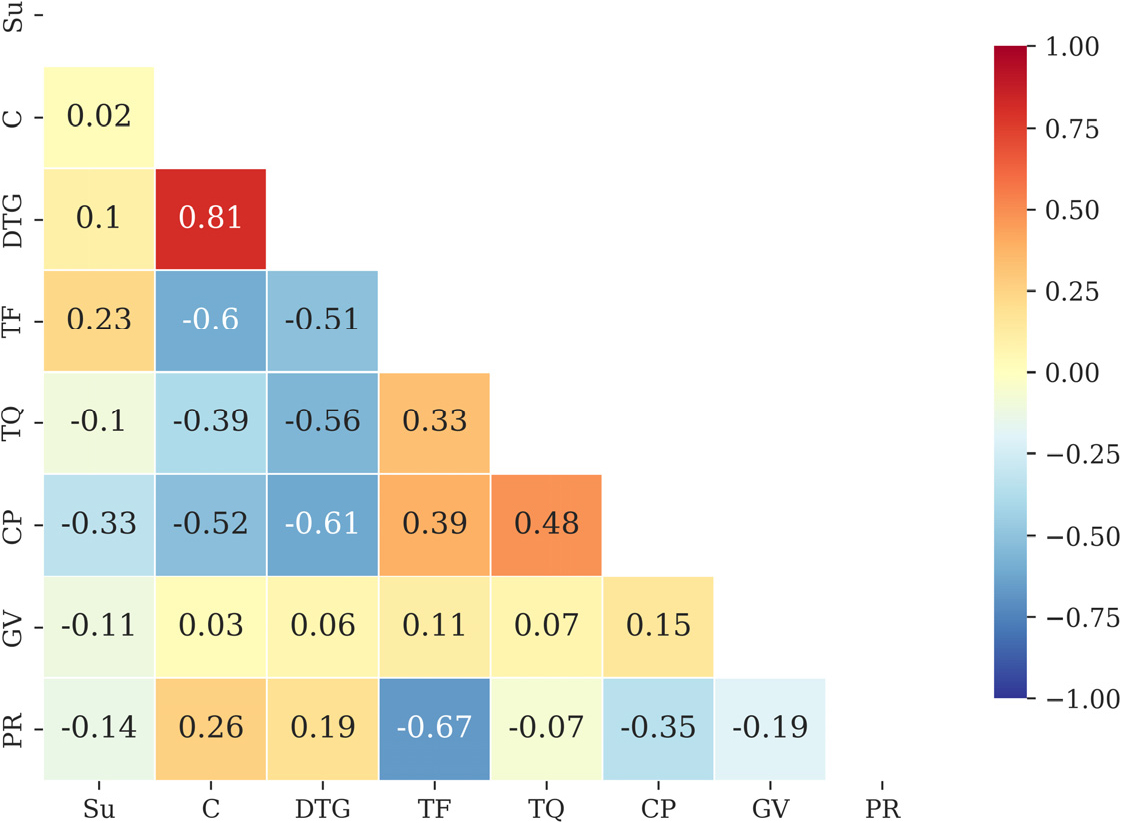
https://cdn.apub.kr/journalsite/sites/kta/2024-026-05/N0550260510/images/kta_2024_265_519_F3.jpg

Fig. 3.

Pearson correlation matrix of the dataset

본 연구에서는 수집된 굴진율 데이터에서 하위 10%와 상위 10%를 이상 범위로 설정하고 그 외의 범위를 정상 범위로 간주하여, Table 3과 같이 하위 10%를 low, 정상 범위를 medium, 상위 10%를 high로 굴진율 등급을 구분하였다. 하위 10%와 상위 10%의 기준 굴진율 값은 각각 11.4 mm/min와 28.0 mm/min이다.

Table 3.

Criteria for penetration rate classes

Class	Low	Medium	High
Range	PR < 11.4 mm/min	11.4 mm/min ≤ PR ≤ 28.0 mm/min	PR > 28.0 mm/min

3.3 예측 모델 구현

본 연구에서는 6가지 입력특성을 통해 3가지 굴진율 등급(low, medium, high)을 분류하는 두 가지 예측 모델을 구축하였다. 먼저, 1,138개의 수집 데이터를 굴진율 등급 분포를 유지한 상태로 80%는 학습 세트로, 나머지 20%는 시험 세트로 구분하였다. 전술한 바와 같이, 학습 세트 내 불균형 분포는 머신러닝 예측 모델을 다수 등급(medium)에 편향되게 하여 예측 모델의 소수 등급(low, high)에 대한 예측 성능을 저하시킬 수 있다. 따라서, 본 연구에서는 SMOTE 기반 기존 학습 세트 내 소수 등급 데이터 증강으로 불균형 데이터를 처리한 증강 학습 세트를 추가로 구성하였다. Fig. 4는 기존 학습 세트와 증강 학습 세트의 굴진율 등급 분포를 나타낸다.

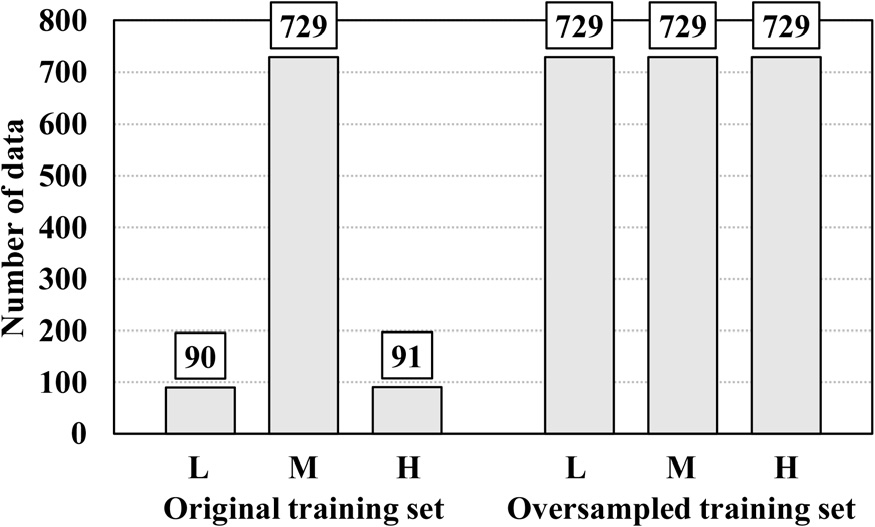
https://cdn.apub.kr/journalsite/sites/kta/2024-026-05/N0550260510/images/kta_2024_265_519_F4.jpg

Fig. 4.

Class distributions of original and oversampled training sets

본 연구의 목적인 불균형 데이터 처리를 통한 머신러닝 기반 TBM 굴진율 이상탐지 성능의 개선 여부를 확인하기 위해, 기존 및 증강 학습 세트를 각각 XGB와 결합하여 XGB 모델과 XGB-SMOTE 모델을 구축하였다. 이때, XGB의 초매개변수(hyperparameter) 탐색 공간은 Table 4에 제시하였다.

Table 4.

Search space of XGB hyperparameters

Search space	Hyperparameter
Search space	n_estimators	max_depth	min_child_weight	gamma	subsample	colsample_bytree	eta
Range	100~500	5~10	10~20	0.5~1	0.5~1	0.5~1	0.01~0.1

본 연구에서는 베이지안 최적화와 5겹 교차검증을 사용하여 예측 모델의 초매개변수를 최적화하였다. 베이지안 최적화는 베이지안 확률론에 기반하여 초매개변수 탐색 공간을 효율적으로 탐색하는 기법으로, 이전 탐색 결과를 바탕으로 확률적 모델을 이용하여 다음 탐색 지점을 순차적으로 선정한다. 5겹 교차검증은 학습 세트를 5개의 부분으로 나눈 후, 각 부분을 한 번씩 검증 세트로 사용하고 나머지 부분을 학습 세트로 사용하여 총 5번의 학습과 검증을 수행하는 기법으로, 모델의 일반화 성능을 평가하는 데 유용하다. 최종적으로, 동일한 시험 세트를 기준으로 XGB 모델과 XGB-SMOTE 모델의 굴진율 등급 분류 예측 성능을 비교하였다. 성능 지표로 정확도(accuracy), F1 score, 재현율(recall)을 사용하였으며, 이는 식 (1), (2), (3), (4)를 통해 산정할 수 있다.

(1)

A c c u r a c y = \frac{T P + T N}{T P + F P + T N + F N}

(2)

F 1 score = \frac{1}{n} \sum_{i = 1}^{n} 2 * \frac{{Precision}_{i} * {Recall}_{i}}{{Precision}_{i} + {Recall}_{i}}

(3)

{Precision}_{i} = \frac{T P_{i}}{T P_{i} + F P_{i}}

(4)

{Recall}_{i} = \frac{T P_{i}}{T P_{i} + F N_{i}}

여기서, $T P$ 는 특정 등급을 정확히 예측한 경우, $T N$ 은 특정 등급이 아닌 다른 등급을 정확히 예측한 경우, $F P$ 는 특정 등급이 아닌 다른 등급을 특정 등급으로 잘못 예측한 경우, $F N$ 은 특정 등급을 다른 등급으로 잘못 예측한 경우를 나타내며, $n$ 은 등급 수를 의미한다.

정확도는 전체 데이터 중 정확하게 예측된 데이터의 비율로 예측 성능을 포괄적으로 나타내는 지표이지만, 불균형 데이터의 경우 소수 등급에 대한 예측 성능을 충분히 반영하는 데 한계가 있다. 반면, F1 score는 모든 등급에 대해 비교적 균형 잡힌 예측 성능을 표현하고, 재현율은 각 등급에 대한 실제 데이터 중 정확히 분류된 데이터의 비율을 의미하여, F1 score와 재현율은 이상탐지 성능을 평가하고 비교하는 데 유용하다. 본 연구의 예측 모델 구현 절차는 Fig. 5에 도시하였다.

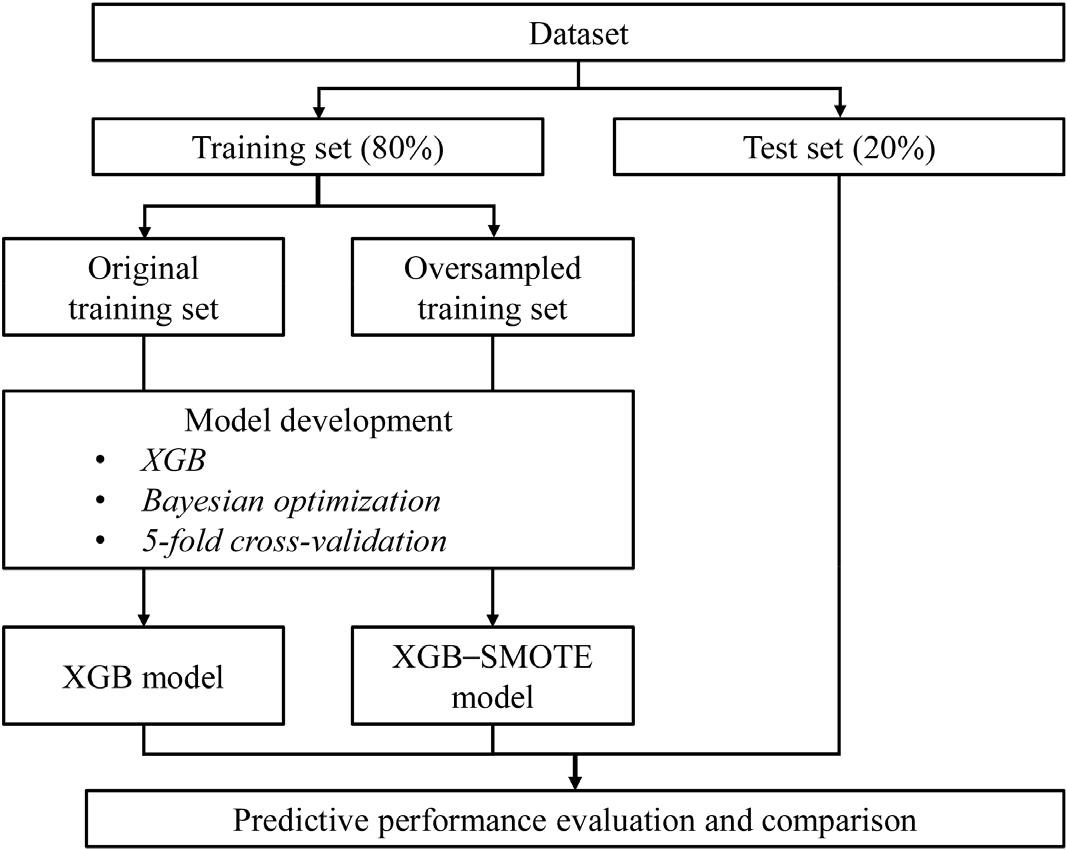
https://cdn.apub.kr/journalsite/sites/kta/2024-026-05/N0550260510/images/kta_2024_265_519_F5.jpg

Fig. 5.

Flowchart of development and comparison of prediction models

4. 결과 및 논의

XGB 모델과 XGB-SMOTE 모델에 동일한 시험 세트를 적용하여 도출된 오차 행렬(confusion matrix)과 성능지표는 각각 Fig. 6과 Fig. 7에 나타내었으며, 각 모델의 최적 초매개변수를 Table 5에 정리하였다.

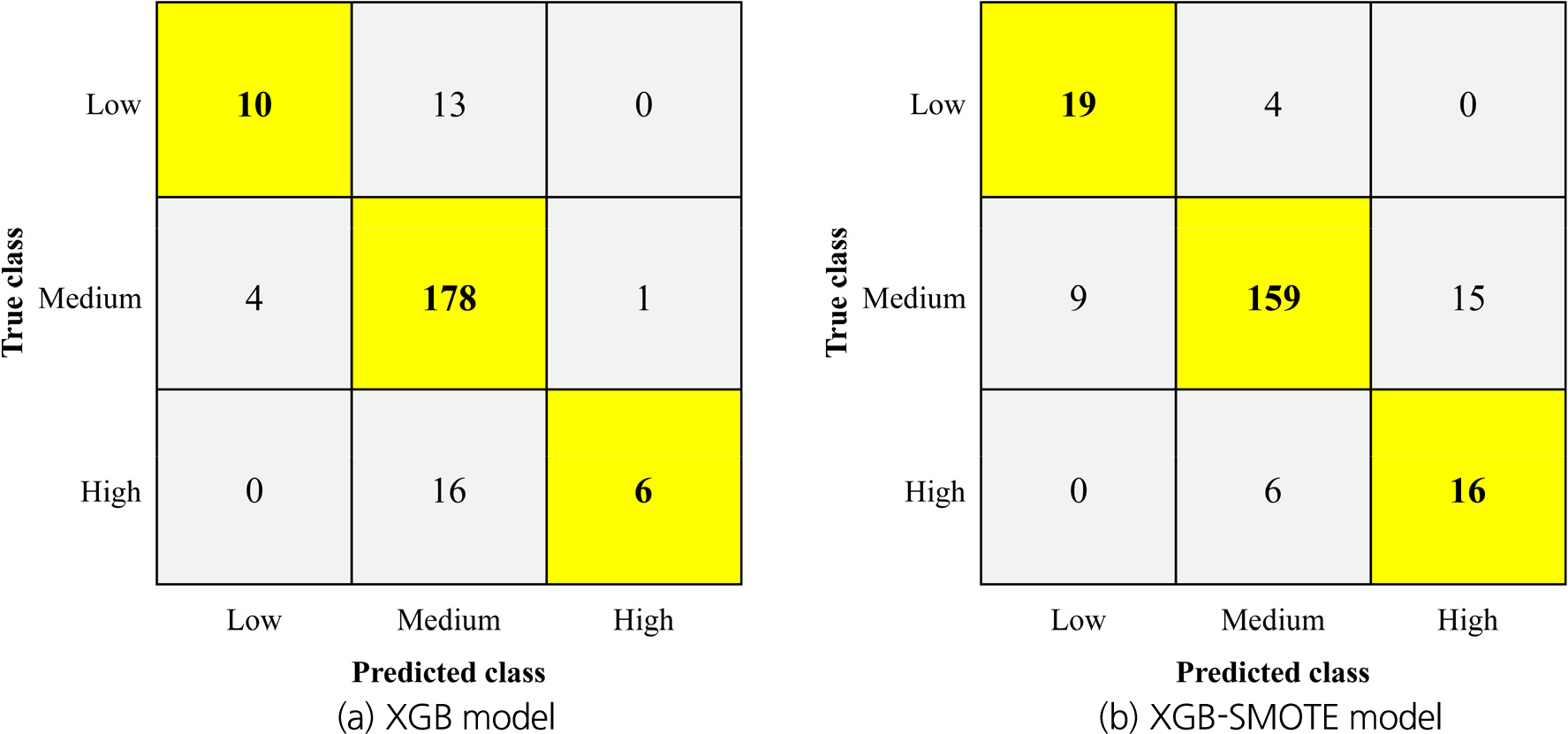
https://cdn.apub.kr/journalsite/sites/kta/2024-026-05/N0550260510/images/kta_2024_265_519_F6.jpg

Fig. 6.

Confusion matrix for developed models

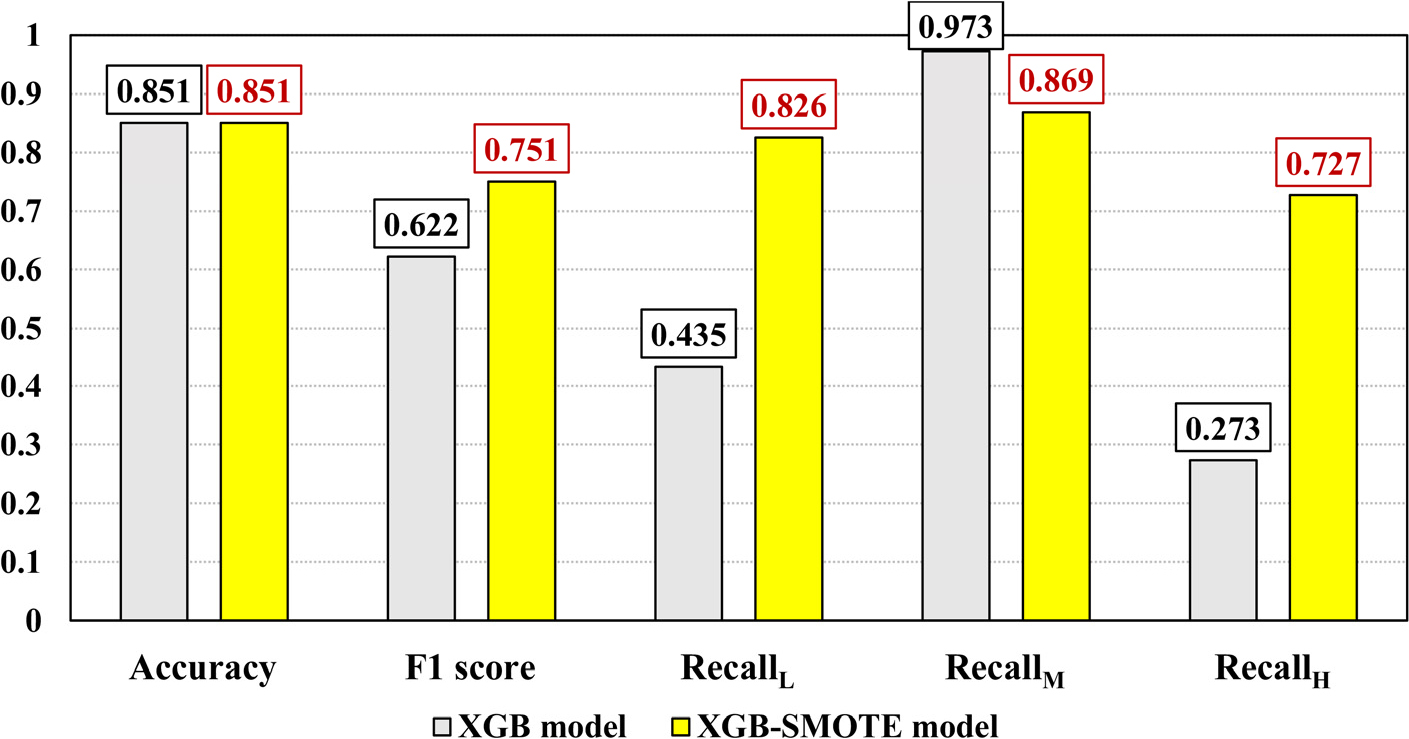
https://cdn.apub.kr/journalsite/sites/kta/2024-026-05/N0550260510/images/kta_2024_265_519_F7.jpg

Fig. 7.

Predictive performance of developed models

Table 5.

Optimal hyperparameters of each model

Model	Hyperparameter
Model	n_estimators	max_depth	min_child_ weight	gamma	subsample	colsample_ bytree	eta
XGB model	248	7	10	0.5	1.0	1.0	0.07
XGB-SMOTE model	500	8	10	0.5	0.8	1.0	0.1

두 모델의 예측 성능 비교 결과, 정확도는 0.851로 동일하였으나 F1 score는 XGB 모델이 0.622, XGB-SMOTE 모델이 0.751로 도출되었다. 이를 통해, XGB-SMOTE 모델이 모든 굴진율 등급에 대한 균형 잡힌 예측을 수행하여 이상탐지에 더욱 효과적임을 확인하였다.

리스크 관리 측면에서 정상 굴진율에 비해 이상 굴진율에 대한 정확한 탐지가 중요하므로, Fig. 7 내 각 모델의 굴진율 등급별 재현율( $R e c a l l_{L}$ , $R e c a l l_{M}$ , $R e c a l l_{H}$ )을 비교하였다. XGB 모델의 경우, 정상 범위인 medium에 대한 재현율은 0.973으로 높게 나타났으나, 이상 범위인 low와 high에 대한 재현율은 각각 0.435와 0.273으로 상당히 낮게 도출되었다. XGB-SMOTE 모델의 재현율은 low, medium, high에 대해 각각 0.826, 0.869, 0.727로 모든 굴진율 등급에서 일관되게 우수한 성능을 보였다. 이러한 결과는 XGB 모델이 정상 굴진율은 정확히 예측하지만 이상 굴진율을 탐지하는 데 한계가 있는 반면, XGB-SMOTE 모델은 모든 굴진율 범위에서 일관되게 우수한 예측을 제공함을 나타낸다. 이를 통해, 본 연구에서는 데이터 증강 기반 불균형 데이터 처리가 TBM 굴진율 이상탐지 성능을 개선하는 데 효과적임을 입증하였고, 이는 모델 학습 과정에서 이상 굴진율 데이터의 증강이 이상 굴진율과 관련된 지반조건 및 TBM 운영인자 간의 데이터 패턴 파악을 향상시켰기 때문으로 판단된다.

5. 결 론

본 연구에서는 불균형 데이터 처리를 통한 머신러닝 기반 TBM 굴진율 이상탐지 성능 개선 여부를 확인하였다. 상관관계 분석을 통해 유사 특성을 제외하고, 데이터 증강 기법인 SMOTE를 활용하여 불균형 데이터를 처리하였다. 데이터 증강 적용 유무에 따라 각각 다르게 구축된 예측 모델의 굴진율 등급 분류 성능을 비교하였다. 본 연구로부터 도출된 결론은 다음과 같다.

1. 상관계수 분석 결과, 토피고와 터널 천장-지하수위 거리 간 명확한 양의 상관관계를 확인하였다. 이에 따라, 예측 모델의 복잡도를 낮추고 과적합을 방지하기 위해 터널 천장-지하수위 거리를 입력특성에서 제외하였다.

2. XGB 모델과 XGB-SMOTE 모델의 정확도는 동일하였으나, F1 score는 XGB-SMOTE 모델이 더 우수하게 도출되었다. 또한, XGB 모델의 이상 굴진율 등급에 대한 재현율은 상대적으로 낮은 반면, XGB-SMOTE 모델은 모든 굴진율 등급에서 일관되게 높은 재현율을 보였다.

3. 예측 성능 분석 결과, 불균형 데이터 처리를 통한 TBM 굴진율 이상탐지 성능 개선 효과가 입증되었다. 이는 데이터 증강을 통해 예측 모델이 이상 굴진율을 나타내는 지반조건과 TBM 운영인자 간의 패턴을 보다 효과적으로 학습하였기 때문이다.

4. 본 연구에서 입증된 데이터 증강 기반 불균형 데이터 처리의 TBM 굴진율 이상탐지 성능 개선 효과는 TBM 시공 중 위험 상황에 대한 조기 경보 시스템 구축에 기여할 수 있다. 이와 함께, 후속 연구에서 SHAP (shapley additive explanations)를 활용하여 각 입력 특성이 머신러닝 모델의 이상 굴진율 탐지 결과에 미치는 영향도를 분석할 경우, TBM 시공의 안전성 및 경제성을 더욱 향상시킬 것으로 판단된다.

Acknowledgements

본 연구는 국토교통과학기술진흥원의 건설기술연구사업(No. RS-2022-00144188)의 지원으로 수행되었으며 이에 깊은 감사를 드립니다.

저자 기여도

권기범은 연구 개념 설계, 데이터 수집 및 해석, 원고작성을 하였고, 황병현은 데이터 해석, 원고검토를 하였고, 박현태는 데이터 분석 및 해석을 하였고, 오주영은 데이터 수집 및 분석을 하였고, 최항석은 연구 개념 설계, 데이터 해석, 원고검토를 하였다.

References

Agrawal, A.K., Murthy, V.M.S.R., Chattopadhyaya, S., Raina, A.K. (2022), "Prediction of TBM disc cutter wear and penetration rate in tunneling through hard and abrasive rock using multi-layer shallow neural network and response surface methods", Rock Mechanics and Rock Engineering, Vol. 55, No. 6, pp. 3489-3506.

10.1007/s00603-022-02834-7

Armaghani, D.J., Mohamad, E.T., Narayanasamy, M.S., Narita, N., Yagiz, S. (2017), "Development of hybrid intelligent models for predicting TBM penetration rate in hard rock condition", Tunnelling and Underground Space Technology, Vol. 63, pp. 29-43.

10.1016/j.tust.2016.12.009

Bae, S., Ham, S., Lee, I., Lee, G.P., Kim, D. (2022), "Deep learning based crack detection from tunnel cement concrete lining", Journal of Korean Tunnelling and Underground Space Association, Vol. 24, No. 6, pp. 583-598.

10.9711/KTAJ.2022.24.6.583

Benardos, A.G., Kaliampakos, D.C. (2004), "Modelling TBM performance with artificial neural networks", Tunnelling and Underground Space Technology, Vol. 19, No. 6, pp. 597-605.

10.1016/j.tust.2004.02.128

Broere, W. (2016), "Urban underground space: solving the problems of today's cities", Tunnelling and Underground Space Technology, Vol. 55, pp. 245-248.

10.1016/j.tust.2015.11.012

Chawla, N.V., Bowyer, K.W., Hall, L.O., Kegelmeyer, W.P. (2002), "SMOTE: Synthetic minority over-sampling technique", Journal of Artificial Intelligence Research, Vol. 16, pp. 321-357.

10.1613/jair.953

Chen, J., Huang, H., Cohn, A.G., Zhang, D., Zhou, M. (2022), "Machine learning-based classification of rock discontinuity trace: SMOTE oversampling integrated with GBT ensemble learning", International Journal of Mining Science and Technology, Vol. 32, No. 2, pp. 309-322.

10.1016/j.ijmst.2021.08.004

Chen, T., Guestrin, C. (2016), "Xgboost: A scalable tree boosting system", Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, USA, pp. 785-794.

10.1145/2939672.2939785

Farrokh, E. (2018), "Introducing hard rock TBMs' downtime analysis model with reference to past case histories' data", Journal of Mining and Environment, Vol. 9, No. 2, pp. 457-472.

10.22044/jme.2018.6815.1509

Frenzel, C., Käsling, H., Thuro, K. (2008), "Factors influencing disc cutter wear", Geomechanics and Tunnelling, Vol. 1, No. 1, pp. 55-60.

10.1002/geot.200800006

Gao, B., Wang, R., Lin, C., Guo, X., Liu, B., Zhang, W. (2021), "TBM penetration rate prediction based on the long short-term memory neural network", Underground Space, Vol. 6, No. 6, pp. 718-731.

10.1016/j.undsp.2020.01.003

Ghorbani, E., Yagiz, S. (2024), "Estimating the penetration rate of tunnel boring machines via gradient boosting algorithms", Engineering Applications of Artificial Intelligence, Vol. 136, 108985.

10.1016/j.engappai.2024.108985

Gong, Q.M., Zhao, J. (2009), "Development of a rock mass characteristics model for TBM penetration rate prediction", International Journal of Rock Mechanics and Mining Sciences, Vol. 46, No. 1, pp. 8-18.

10.1016/j.ijrmms.2008.03.003

Grima, M.A., Bruines, P.A., Verhoef, P.N.W. (2000), "Modeling tunnel boring machine performance by neuro-fuzzy methods", Tunnelling and Underground Space Technology, Vol. 15, No. 3, pp. 259-269.

10.1016/S0886-7798(00)00055-9

Hyun, K.C., Min, S., Choi, H., Park, J., Lee, I.M. (2015), "Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels", Tunnelling and Underground Space Technology, Vol. 49, pp. 121-129.

10.1016/j.tust.2015.04.007

Jamshidi, A. (2018), "Prediction of TBM penetration rate from brittleness indexes using multiple regression analysis", Modeling Earth Systems and Environment, Vol. 4, pp. 383-394.

10.1007/s40808-018-0432-2

Kim, D., Kwon, K., Pham, K., Oh, J.Y., Choi, H. (2022), "Surface settlement prediction for urban tunneling using machine learning algorithms with Bayesian optimization", Automation in Construction, Vol. 140, 104331.

10.1016/j.autcon.2022.104331

Kwon, K., Choi, H., Hwang, C., Park, S., Hwang, B. (2024a), "Risk assessment for development of consecutive shield TBM technology", Journal of Korean Tunnelling and Underground Space Association, Vol. 26, No. 4, pp. 303-314.

10.9711/KTAJ.2024.26.4.303

Kwon, K., Choi, H., Jung, J., Kim, D., Shin, Y.J. (2024b), "Prediction of abnormal TBM disc cutter wear in mixed ground condition using interpretable machine learning with data augmentation", Journal of Rock Mechanics and Geotechnical Engineering.

10.1016/j.jrmge.2024.05.027

Kwon, K., Choi, H., Oh, J.Y., Kim, D. (2022), "A study on EPB shield TBM face pressure prediction using machine learning algorithms", Journal of Korean Tunnelling and Underground Space Association, Vol. 24, No. 2, pp. 217-230.

10.9711/KTAJ.2022.24.2.217

Kwon, K., Choi, H., Pham, K., Kim, S., Bae, A. (2024c), "Influence analysis of pavement distress on international roughness index using machine learning", KSCE Journal of Civil Engineering, pp. 1-12.

10.1007/s12205-024-0093-9

Liu, Y., Yu, Z., Chen, C., Han, Y., Yu, B. (2020), "Prediction of protein crotonylation sites through LightGBM classifier based on SMOTE and elastic net", Analytical Biochemistry, Vol. 609, 113903.

10.1016/j.ab.2020.113903

Liu, Z., Li, L., Fang, X., Qi, W., Shen, J., Zhou, H., Zhang, Y. (2021), "Hard-rock tunnel lithology prediction with TBM construction big data using a global-attention-mechanism-based LSTM network", Automation in Construction, Vol. 125, 103647.

10.1016/j.autcon.2021.103647

Mahdevari, S., Shahriar, K., Yagiz, S., Shirazi, M.A. (2014), "A support vector regression model for predicting tunnel boring machine penetration rates", International Journal of Rock Mechanics and Mining Sciences, Vol. 72, pp. 214-229.

10.1016/j.ijrmms.2014.09.012

Moharrami, S., Bayat, A., AbouRizk, S. (2022), "Modeling microtunnel boring machine penetration rate using a mechanistic approach", Journal of Construction Engineering and Management, Vol. 148, No. 11, 04022128.

10.1061/(ASCE)CO.1943-7862.0002402

Moon, J.S., Kim, H.K., An, J.W., Lee, J.G. (2020), "A study on performance-based evaluation system for NATM tunnels in use: development of evaluation model and validation", Journal of Korean Tunnelling and Underground Space Association, Vol. 22, No. 1, pp. 107-120.

10.9711/KTAJ.2020.22.1.107

Pham, K., Kim, D., Le, C.V., Won, J. (2023), "Machine learning-based pedotransfer functions to predict soil water characteristics curves", Transportation Geotechnics, Vol. 42, 101052.

10.1016/j.trgeo.2023.101052

Rezapour, M. (2021), "Sentiment classification of skewed shoppers' reviews using machine learning techniques, examining the textual features", Engineering Reports, Vol. 3, No. 1, e12280.

10.1002/eng2.12280

Song, C., Peng, H., Xu, L., Zhao, T., Guo, Z., Chen, W. (2024), "Probabilistic evaluation of cultural soil heritage hazards in China from extremely imbalanced site investigation data using SMOTE-Gaussian process classification", Journal of Cultural Heritage, Vol. 67, pp. 121-133.

10.1016/j.culher.2024.02.014

Tóth, Á., Gong, Q., Zhao, J. (2013), "Case studies of TBM tunneling performance in rock-soil interface mixed ground", Tunnelling and Underground Space Technology, Vol. 38, pp. 140-150.

10.1016/j.tust.2013.06.001

Vergara, I.M., Saroglou, C. (2017), "Prediction of TBM performance in mixed-face ground conditions", Tunnelling and Underground Space Technology, Vol. 69, pp. 116-124.

10.1016/j.tust.2017.06.015

Xu, H., Zhou, J., Asteris, P.G., Armaghani, D.J., Tahir, M.M. (2019), "Supervised machine learning techniques to the prediction of tunnel boring machine penetration rate", Applied Sciences, Vol. 9, No. 18, 3715.

10.3390/app9183715

Xue, Y.D., Luo, W., Chen, L., Dong, H.X., Shu, L.S., Zhao, L. (2023), "An intelligent method for TBM surrounding rock classification based on time series segmentation of rock-machine interaction data", Tunnelling and Underground Space Technology, Vol. 140, 105317.

10.1016/j.tust.2023.105317

Yagiz, S., Gokceoglu, C., Sezer, E., Iplikci, S. (2009), "Application of two non-linear prediction tools to the estimation of tunnel boring machine performance", Engineering Applications of Artificial Intelligence, Vol. 22, No. 4-5, pp. 808-814.

10.1016/j.engappai.2009.03.007

Yang, J., Yagiz, S., Liu, Y.J., Laouafa, F. (2022), "Comprehensive evaluation of machine learning algorithms applied to TBM performance prediction", Underground Space, Vol. 7, No. 1, pp. 37-49.

10.1016/j.undsp.2021.04.003

Yu, L., Liu, H. (2004), "Efficient feature selection via analysis of relevance and redundancy", Journal of Machine Learning Research, Vol. 5, 1205-1224.

Zhou, J., Qiu, Y., Armaghani, D.J., Zhang, W., Li, C., Zhu, S., Tarinejad, R. (2021), "Predicting TBM penetration rate in hard rock condition: a comparative study among six XGB-based metaheuristic techniques", Geoscience Frontiers, Vol. 12, No. 3, 101091.

10.1016/j.gsf.2020.09.020

Journal of Korean Tunnelling and Underground Space Association ISSN:2233-8292(Print) 2287-4747(Online) 한국터널지하공간학회 논문집

Preview

Enhancing machine learning-based anomaly detection for TBM penetration rate with imbalanced data manipulation

ABSTRACT

MAIN

Fig. 1.

Schematic of data augmentation using SMOTE

Table 1.

Specifications of TBM used in the studied site

Fig. 2.

Longitudinal profile of the TBM tunneling site

Table 2.

Statistical descriptions of the dataset

Fig. 3.

Pearson correlation matrix of the dataset

Table 3.

Criteria for penetration rate classes

Fig. 4.

Class distributions of original and oversampled training sets

Table 4.

Search space of XGB hyperparameters

(1)

(2)

(3)

(4)

Fig. 5.

Flowchart of development and comparison of prediction models

Fig. 6.

Confusion matrix for developed models

Fig. 7.

Predictive performance of developed models

Table 5.

Optimal hyperparameters of each model

Acknowledgements

저자 기여도

References