1. 서 론
2. 현장계측
2.1 발파진동 허용기준
2.2 현장계측 개요
2.3 시험발파
3. 발파 이론
3.1 발파영역
3.2 발파하중 계산
4. 수치해석
4.1 해석 모델 및 입력 변수
4.2 경계조건
4.3 감쇠계수
4.4 데이터 계측 위치
4.5 수치해석 결과
5. 결 론
1. 서 론
도심지 상부구조물이 포화되면서 터널과 지하공간의 수요가 확대되고 있으며, 이 공간은 터널, 상하수도, 복합 문화 공간 등으로 다양하게 활용되고 있다. 우리나라의 지층구조는 얕은 심도에서 암반이 출현하는 특성을 가지고 있어, 지하공간 굴착 시 설계 단계에서부터 시공성과 경제성이 유리한 발파 굴착공법을 선정하는 것이 보편적이다(Choi, 2014). 그러나, 발파과정에서 발생하는 소음과 진동은 주변 환경에 영향을 미칠 수 있어 이에 대한 철저한 관리한 검토가 요구된다. 또한 발파로 인해 얕은 기초는 부등침하, 회전변위, 지지력파괴 등이 발생할 수 있기에 사회기반 시설물의 보호를 위해서도 발파에 대한 영향을 검토하는 것은 필수적이다(Castro et al., 2011).
특히, 사회기반 시설물 근처에서 발파를 수행할 때는 진동과 소음이 주변 구조물에 미치는 영향을 최소화하기 위해 더욱 신중한 접근이 필요하다. 사회기반 시설물이 영향을 받게 되면 구조물의 직접적인 피해뿐만 아니라, 서비스 중단, 복구비용 증가, 사용자 불편과 같은 사회경제적 파급효과가 발생할 수 있다. 이에 따라 발파진동의 영향을 평가하기 위한 다양한 이론적, 수치해석적 연구가 수행되어 왔다.
Kong et al. (2022)은 지반자료조사와 설계자료를 활용하여 동일 발파, 터널 조건에서 심도에 따른 발파 진동변화를 수치해석을 통해 예측하였다. 심도 40 m 깊이에서 터널굴착을 실시한 기존 현장 자료를 바탕으로, 심도에 따른 발파진동을 알아보기 위해 20 m, 30 m의 중심도와 50 m의 대심도 조건을 추가적으로 해석하였다. 터널굴착면 직상부 지표면에서 최대입자속도를 측정한 결과 심도 20 m 대비 30 m, 40 m, 50 m에서 각각 35.7%, 59.4%, 70.7%의 진동 감소율을 보였다. Kawk et al. (2023)은 상업운전 중인 발전소 부지 하부로 터널이 굴착될 때 발파진동의 특성과 영향을 3차원 유한요소해석법에 의한 동적수치해석을 수행하여 최대 입자진동속도를 산출하였다. 수치해석 결과 입자진동속도가 허용치의 95%를 상회하는 값을 나타내었고, 발전소 구조물의 중요도와 지반의 불확실성 등을 고려하여 일부 발파패턴을 추가적으로 구성하였다. 변경 발파패턴에 대한 시험발파를 수행하여 발파진동에 의한 최대 입자진동속도의 감소를 확인하고, 산업시설 근접발파 시 안정성을 확보할 수 있는 진동영향평가의 의사결정과정을 확립하였다.
Castro et al. (2011)은 자유장 발파 조건에서 최대입자속도(peak particle velocity, PPV)와 압력을 예측하기 위해 개발된 유한요소 모델의 성능을 평가한 연구 결과를 제시하였다. 또한 모델 성능에 미치는 영역 크기, 감쇠 계수의 영향을 경험식과 비교하여 보정하였고, 영역 크기는 500 m × 500 m, 감쇠계수는 α = 0.001,β = 0.01로 설정하였다. 보정이 완료된 수치해석의 결과를 사례 연구와 비교하여 수치해석 프로그램인 PLAXIS에서 발파를 합리적으로 모델링할 수 있음을 증명하였다. Yoon et al. (2008)은 터널굴착 시 전자뇌관과 비전기뇌관 발파를 비교하여 전자뇌관의 진동 ‧ 소음 저감효과와 시공성, 효율성을 검토하고자 하였다. 계측 데이터를 바탕으로 95% 신뢰도 발파진동 추정식을 산출한 결과 K값 및 n값 모두 값으로 전자뇌관이 발파진동 측면에서 유리한 결과를 보였다. 소음은 전자뇌관 사용 시 비전기뇌관 대비 8% 감소하였으며, 비산거리는 27.5% 감소, 파쇄입도는 약 50% 낮아 전자뇌관의 우수성이 확인되었다.
위 연구들에서 확인된 바와 같이, 도심지 개발 집중에 따른 발파진동의 영향을 최소화하고 발파의 효율성을 높이는 것이 터널 및 지하공간 설계에서 핵심적인 과제가 되고 있다. 최근에는 기준치 이하의 발파공해를 목표로 하는 새로운 발파공법이 요구되었고, 이에 다양한 대안공법 중 비전기식뇌관과 전자뇌관을 혼용하는 방안이 도입되었다(Lee et al., 2024). 비전기식뇌관과 전자뇌관의 혼용은 최근 터널 발파현장에서 주목받는 공법으로 실제 수도권 광역급행철도 등의 건설 현장에서 활용된 바 있는 대안공법이다(Hwang et al., 2021; 2022).
일반적인 발파작업은 전기 및 비전기뇌관을 이용하여 시행되고 있으나, 이들 뇌관은 Pyrotechnics (화학적 지연제)를 사용하므로, 초시의 오차가 ±10%로 매우 클 뿐만 아니라, 뇌관의 시차도 MS (millisecond, 20~25 ms) 또는 LS (long period, 100~1,000 ms)로 한정적이다(Hwang et al., 2016). 반면 전자뇌관은 전자 타이머에 의해 초 정밀시차로 특수한 용도에 사용하기 위해 개발되어 시차범위를 0~25,000 ms까지 부여할 수 있으며, IC 회로를 통해 기폭한다(Yoon et al., 2006). 또한 전자뇌관의 오차는 0.01% 이내의 초정밀도를 유지하기 때문에 일반뇌관(전기, 비전기)처럼 정밀도가 낮은 기폭시차로 인한 예기치 않는 진동 증폭현상을 제어할 수 있고, 발파 공간 및 열간 지연시차()의 선택을 통해 소멸간섭을 유도하여 진동을 저감할 수 있다는 장점이 있다(Oh et al., 2017).
본 연구에서는 ○○정수장 하부 터널굴착 발파로 인한 비전기뇌관과 전자뇌관을 적용하여 발생하는 진동영향을 분석하고, 두 뇌관의 성능을 정량적으로 비교한다. 이를 위해 현장계측 데이터를 활용하여 발파진동 추정식을 도출하고, 이격거리에 따른 허용장약량을 평가한다. 또한, 수치해석을 통해 발파진동의 최대입자속도(PPV)와 수직진동속도()를 비교하여 뇌관 종류에 따른 지반에 대한 진동간섭 및 감쇠특성을 확인한다.
2. 현장계측
2.1 발파진동 허용기준
○○정수장 하부를 통과하는 철도터널은 NATM 공법으로 설계되어, 터널굴착 과정에서 반복적인 발파 작업이 요구된다. 발파작업은 주변 구조물의 안정성과 기능에 중대한 영향을 미칠 수 있으므로, 이를 관리하기 위한 법적기준과 규정이 필수적이다. 발파진동 허용치는 일반적으로 관련기관의 고시 기준, 법원의 판례 기준, 중앙환경분쟁조정위원회의 조정사례를 기초로 설정된다. 대한민국에서는 환경부가 제정한 소음 ‧ 진동관리법 시행규칙 제 20조 제 3항 별표 8에 따라 발파작업의 특수성을 고려한 보정값을 반영하여 허용치를 결정한다. 그러나, 현행 환경부 소음진동관리법은 충격 진동으로서의 발파진동의 특성을 특별히 고려하지 않고 편의상 생활소음 ‧ 진동 규제기준에 +10 dB 하는것으로 규정이 되어있다(Choi and Ryu, 2012). 또한 데시벨(dB)은 인체감각을 기준으로 한 단위로, 진동레벨만을 기준으로 진동의 크기를 평가하는 데 한계가 존재한다(Lee and Chang, 2005). 따라서, 발파진동의 크기와 구조물에 미치는 영향을 보다 정밀하게 평가하기 위해 진동에 의하여 구조물에 피해가 발생되지 않도록 규제하는 범위의 진동치는 최대입자속도(PPV)를 허용진동치로 활용하는 것이 적합하다. PPV는 진동속도 파형 중에서 최대진폭을 뜻하며, 이는 진동현상에서 응력 증가와 연결되는 연결되는 가장 기본적이고 직접적인 매개변수이다. PPV를 기준으로 최대입자속도를 사용하는 사례를 정리하여 Table 1에 정리하였다.
Table 1.
Regulatory standards for environmental vibration
| Guideline |
Allowable vibration criteria (cm/s) | Remarks |
|
Design standard of tunnel (KTA, 2016) | 0.2~0.3 |
Cultural heritage & Vibration sensitive structure |
| 1.0 | Mansory walls | |
|
Tunnel standard specification (KTA, 2015) | 0.2~0.3 |
Cultural heritage & Vibration sensitive structure |
| 1.0 | Mansory walls | |
|
Highway construction standard specification (KEC, 2012) | 0.1 | Livestock |
| 0.2 | Cultural heritage | |
|
Highway environmental management manual (KEC, 2009) | 0.09 | Livestock |
| 0.2 |
Cultural heritage & Vibration sensitive structure | |
|
Seoul metro blast vibration allowance (MOLIT, 2002) | 0.2 | Cultural heritage |
| 0.5 | Mansonry walls |
본 연구에서는 기존 설계 및 시공사례, 공공기관 권고사항에 준용하여 발파진동 허용기준을 산정하였다. 국가주요 시설물인 ○○정수장에 미치는 영향을 최소화하기 위하여 구조물의 건축경과년수, 특성 등을 고려하여 발파진동 허용기준치는 0.2 cm/sec로 설정하였다.
2.2 현장계측 개요
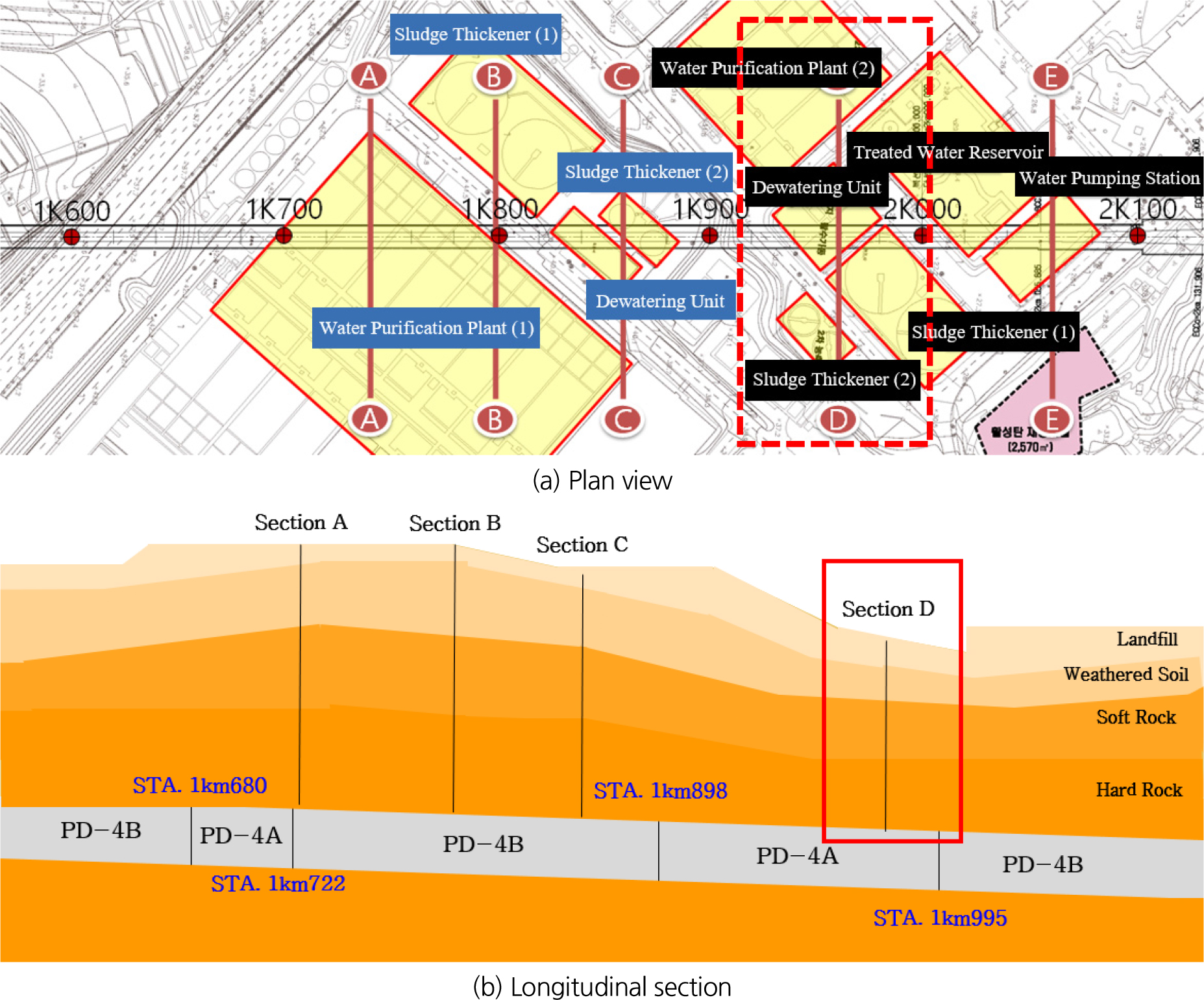
○○정수장 하부 NATM 터널굴착 시 발생하는 발파진동을 측정하기 위해 굴착공사가 진행 중인 STA.1km 630~STA.2km100에 계측기를 설치하였다. 본 구간의 대상 지반은 상부 매립층 및 토사층이 층후 1.5 m~12.5 m로 분포하고, 하부 풍화암 층후는 0.0~1.5 m로 분포, 터널 계획고 하부 1D 이상은 연 ‧ 경암층이 출현한다. 선형계획상 터널 직상부에 ○○정수장이 위치하고 있으며, 터널 심발부로부터 정수장까지 33.9~44.7 m 이격되어 있다. 본 연구에서는 전자뇌관이 적용된 D-D 단면을 선정하여 비교 연구를 수행하였다. Fig. 1은 이러한 지형 및 터널 위치를 포함한 현장의 평면도와 종단면도를 나타낸다.
발파설계의 경우 심발공법은 V-Cut 공법을 선정하였는데, 이는 시공성이 우수할 뿐만 아니라 국내 발파 기술자에게 가장 친숙하기 때문이다. 진동 제어발파 구간은 천공에 의한 2자유면 발파를 수행하여 심발부 진동저감이 가능한 대구경 발파공법을 적용하였다. 조절발파의 경우 국내 터널에서 일반적으로 사용하는 제어발파공법이며, 시공성이 우수한 공법을 선정하였다. 여굴최소화를 위해 smooth blasting 발파공법과 진동제어공간에 combination controlled blasting 발파공법을 적용하였다.
폭약은 폭속이 작아 발파 시 진동 ‧ 소음의 저감에 효과적이면서도 다이너마이트 폭력의 94% 정도로 폭력이 우수하며 적용성이 좋은 emulsion계 폭약을 적용하였다. 뇌관의 경우 일반적으로 비전기뇌관을 사용하되, 폭약에 대한 재원은 Table 2에 나타내었다. 뇌관의 경우 일반적으로 비전기뇌관을 사용하되, 발파진동 허용기준치(0.2 cm/sec)를 초과하는 것으로 추정되는 구간에는 전자뇌관을 사용하였다. 비전기뇌관은 전기발생지역, 낙뢰 및 정전기 발생과 무관하고 인장력이 우수하여 연결 작업 중 절단될 염려가 없기 때문에 안정적이고 시공성이 우수하다. 전자뇌관은 0.2 ms 이하의 오차범위로 무한단차를 사용할 수 있고, 진동저감 효과가 있어 진동 안정성 확보가 필요한 구간에 주로 사용한다.
Table 2.
Explosive material specification
| Category | Emulsion type | Precision explosive | |
|
Explosive performance | Detonation velocity (cm/s) | 5,700~5,900 | 3,900~4,400 |
| Apparent density (g/cm3) | 1.1 | 1.0 | |
| Heat of explosion (kcal/kg) | 880~1,398 | 640 | |
2.3 시험발파
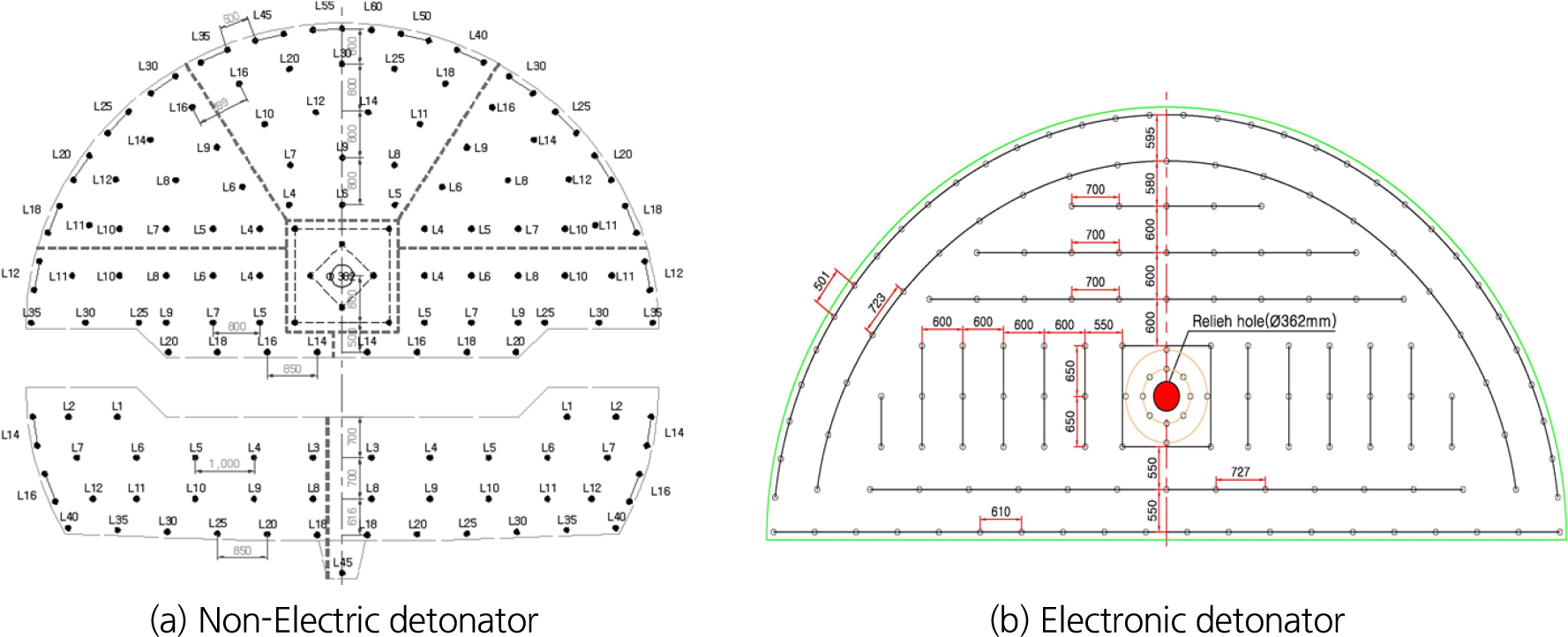
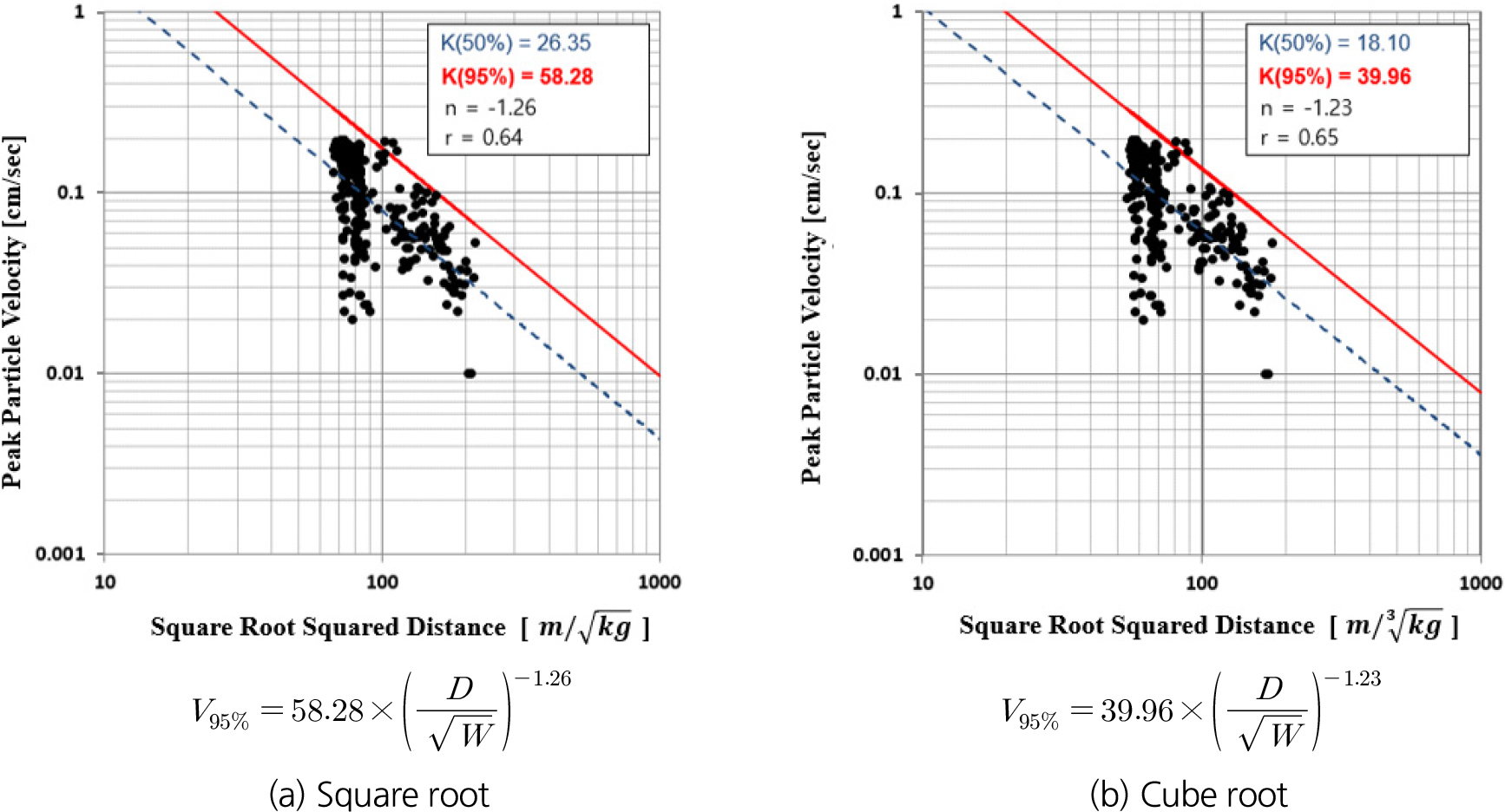
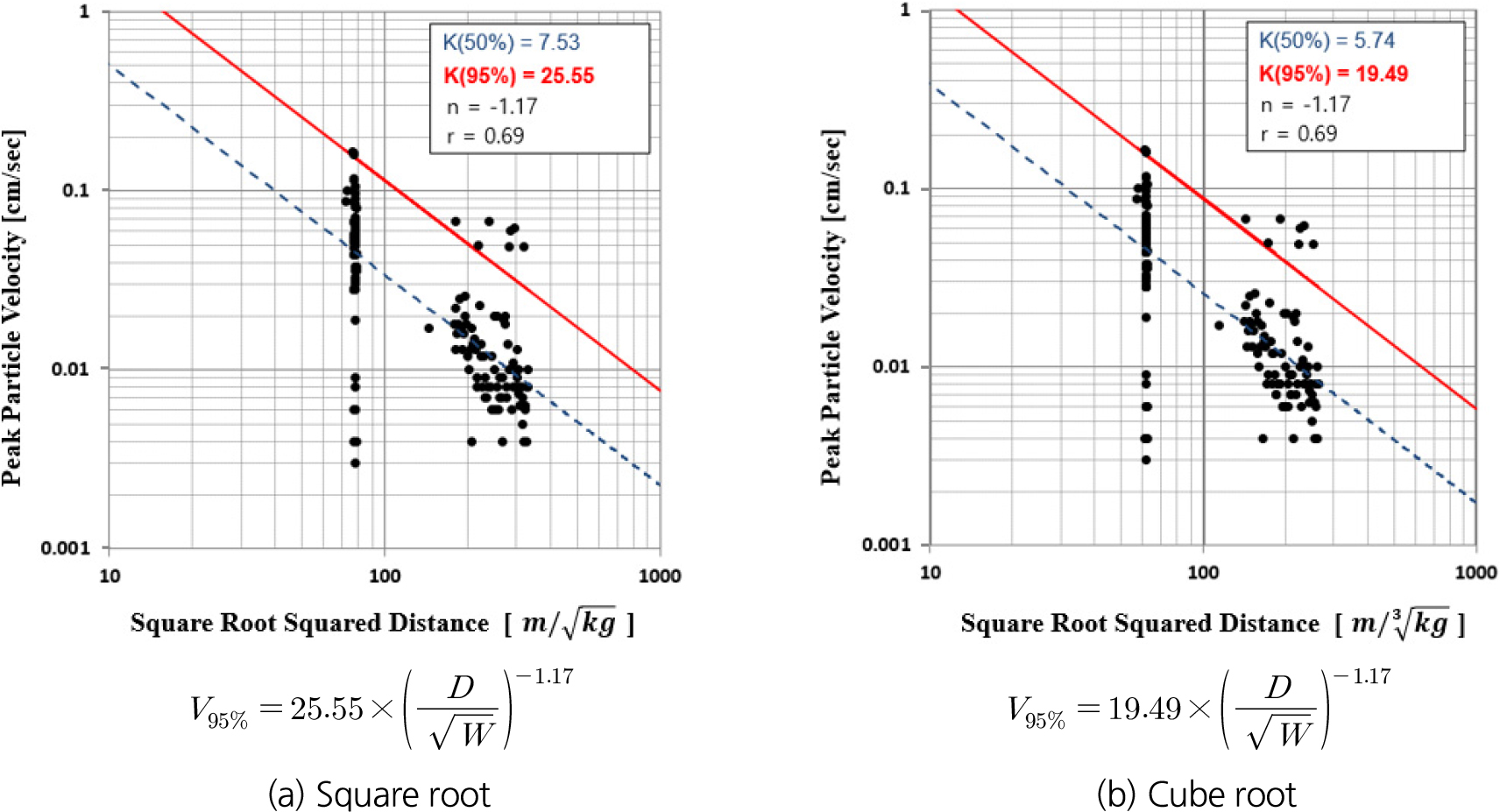
전자뇌관과 비전기뇌관을 비교하기 위하여 실험발파는 장약량과 천공 패턴에 따라 4차례 수행되었으며 현장에서 적용한 발파패턴도는 Fig. 2에 나타내었다. 획득한 발파진동 계측 데이터를 일반 비전기뇌관 사용 시와 전자뇌관 사용 시로 구분하여 각각 회귀분석을 진행하였으며, 일반 비전기뇌관 사용 시 데이터는 282개, 전자뇌관 사용 시 데이터는 158개를 사용하였다. 회귀분석은 자승근식과 삼승근식을 사용하였으며 회귀분석 그래프와 95% 신뢰도의 발파진동 추정식은 Figs. 3 and 4에 나타내었고, 발파진동 추정식은 식 (1)과 같은 식으로 나타낸다.
여기서, 는 최대입자속도(cm/sec), 는 폭원으로부터 측점까지의 거리(m), 는 지발당 장약량(kg)이다. 이때 를 환산거리라고 하며, n이 1/2일 경우 자승근, 1/3일 경우 삼승근이라고 표현한다. 일반적으로 근거리에서는 삼승근, 원거리에서는 자승근이 적절한 것으로 알려져 있다(Jeon et al., 2007).
계측된 데이터를 통한 95% 신뢰도의 발파진동 추정식 산출경과 K값과 n값 모두 전자뇌관이 낮으므로, 전자뇌관이 발파진동에 유리한 결과를 나타내었다. K값은 발파조건, 지반의 물리적 특성, 지반의 강성 등에 따라 달라지는 경험적 상수로, 값이 클수록 동일한 거리와 장약량에서 더 높은 PPV를 나타낸다. n값은 진동이 거리 D에 따라 감쇠하는 비율을 나타내며, 값이 작을수록 거리가 증가함에 따라 진동이 급격히 감소한다. 즉, K값과 n값이 작은 경우, 진동이 적어 발파에 의한 구조물의 피해 가능성이 낮아지고, 진동으로 의한 감쇠 효과가 커지게 된다.
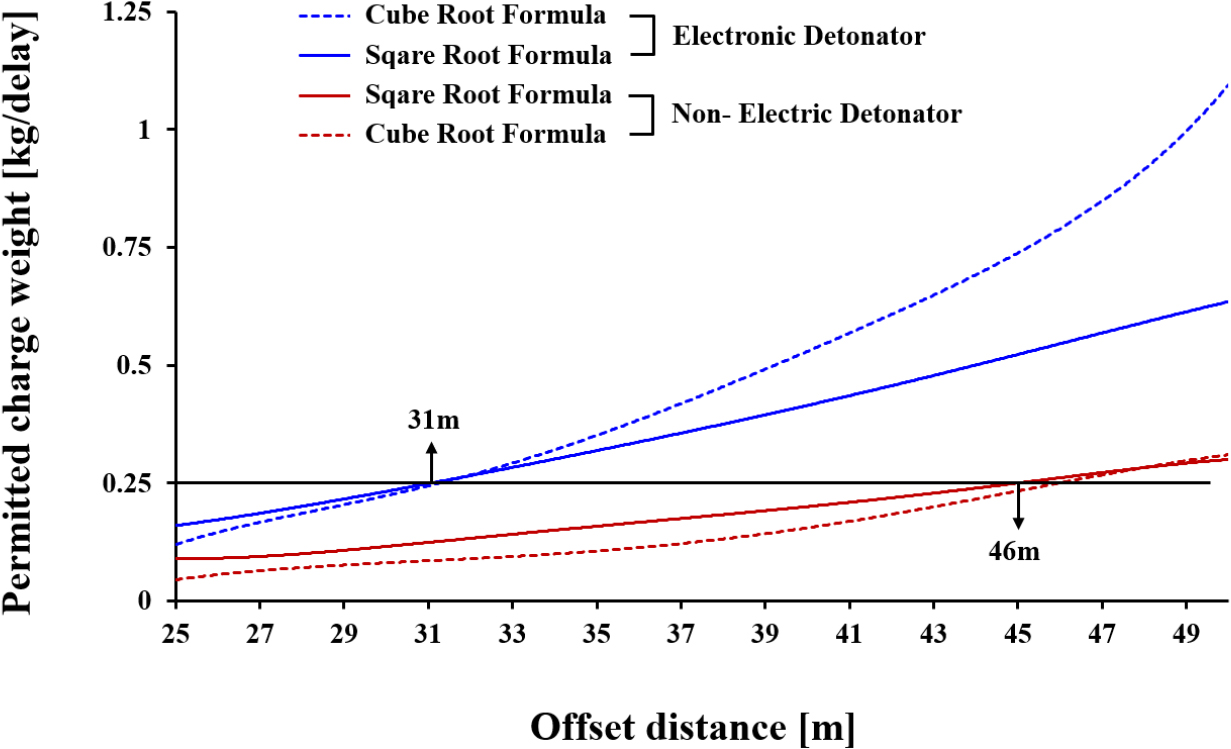
Fig. 5에서 보는 바와 같이 회귀분석을 통해 이격거리(사거리 = 수직+수평)에 따른 허용장약량을 분석한 결과, 지발당 장약량 0.25 kg으로 발파 시 일반 비전기뇌관은 이격거리 46 m 이상을 확보하는데 반해 전자뇌관은 이격거리 31 m 이상을 확보해야 하는 것으로 산정되었다. 현재 터널은 상부 구조물까지의 거리가 33.9~44.7 m 정도이므로, 일반 비전기뇌관으로는 허용진동치를 초과하고 전자뇌관 발파 시 허용진동치를 만족하는 것으로 분석되었다.
3. 발파 이론
3.1 발파영역
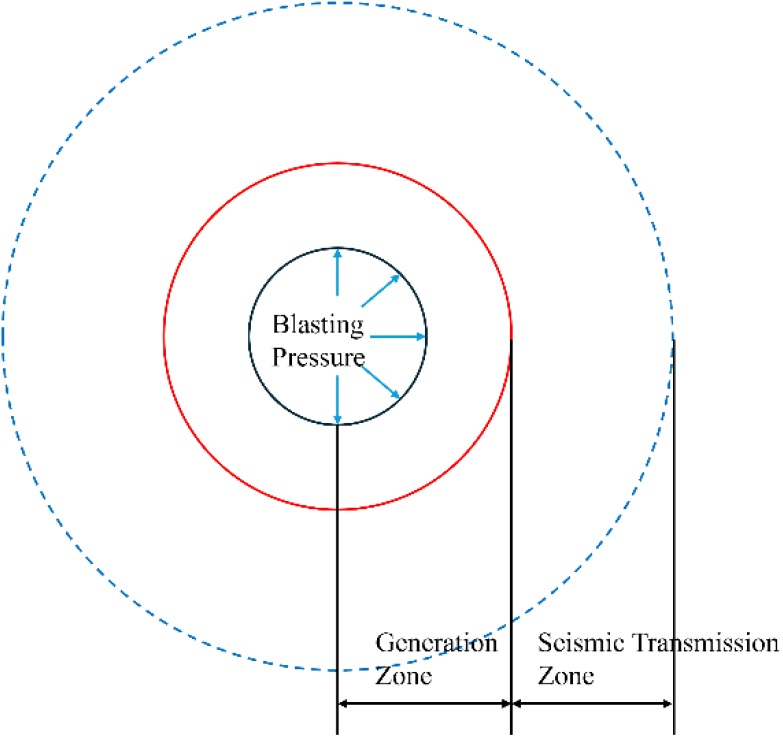
발파로 인해 일반적으로 두 가지의 영역이 발생하게 되는데, 생성영역(발원영역)과 전파(지진)영역으로 나뉘게 되고, 두 영역은 Fig. 6에 나타내었다(Enescu et al., 1973; Bollinger, 1980; Saharan et al., 2006). 생성영역(generation zone)은 폭발 화학반응에서 에너지가 집중되는 구역으로, 이 영역에서는 화학반응으로 인해 높은 압력과 고온이 발생함에 따라 매질의 비탄성적 현상과 큰 변형이 발생한다. 전파영역(seismic transmission zone)은 폭발지점으로부터 일정거리 떨어진 곳으로, 이 지점에서는 비탄성 현상이 종료되고 탄성거동이 매질을 지배하기 시작한다. 이 영역에서는 탄성적 교란이 지진파로서 전달되는데, 지진파는 다시 지중파와 표면파로 나뉘게 된다. 이 중 지중파는 토양 또는 암석과 같은 고체 매질 내부를 전파하는 파동이며, P파와 S파로 세분할 수 있다. 이에 대한 속도는 암반 강성에 따라 달라지기 때문에 암반 강성의 영향을 반영하기 위해, P파와 S파에 대한 속도를 수치해석 시 매질별로 다르게 적용하였다.
3.2 발파하중 계산
발파하중 산정 경험식은 다양하고 화약의 제원과 장약량에 따라 달라진다. 본 연구에서는 발파하중 산정 시 주로 사용하는 Hino (1959)에서 제안한 계산식을 사용하여 식 (2)에 나타내었다(Ahn et al., 2014; Kong et al., 2022).
여기서, 는 폭발하중(kg/cm2), 는 평균폭발속도(m/sec), 는 화약의 가비중(g/cm3)이다. 식 (2)는 장약량 1 kg에 따른 발파하중이다.
그러나, 식 (2)는 전색에 대한 발파하중을 고려하지 못한다. 전색은 폭약 충진 후 폭발 에너지가 손실되지 않도록 발파구멍의 입구를 밀봉하는 데 사용되는 재료이다. 전색의 효과는 폭발 에너지 유지 및 집중이 가능하고 발파 효율이 향상되고, 전색을 고려한 발파하중은 앞서 구한 Hino (1959)의 제안식에서 구한 발파하중에 전색제의 밀도와 충격파의 속도를 추가로 고려하며, 식은 식 (3)과 같다.
여기서, 는 전색을 고려한 폭발하중(kg/cm2), 는 모래의 밀도(g/cm2), 는 충격파 속도(m/sec)이다.
마지막으로, 전색을 고려한 발파하중을 등가 발파하중으로 변환하여 수치해석에 입력해야 한다. 실제 발파하중은 폭발에 의해 생성되는 비선형적이고 순간적인 동적하중으로, 시간 및 공간적으로 매우 복잡한 특성을 가지기에 이를 그대로 수치해석에 적용하게 되면, 계산 부담이 커지게 되고 모델링 과정에서 불확실성이 증가할 수 있다. 또한 폭발로 인한 충격파는 극히 짧은 시간에 매우 높은 압력을 생성하며, 이로 인해 수치해석에서 시간 분해능력이 지나치게 작아져 계산이 불안정해질 수 있다. 이를 보완하기 위해 등가 발파하중은 실제 폭발에 반응하는 전체 과정을 일정한 하중 형태로 단순화하여 구조물의 변형, 응력 분포, 파괴 등을 효과적으로 분석할 수 있고, Starfield and Pugliese (1968)가 제안한 식을 이용하여 등가 발파하중을 계산하는 식은 식 (4)와 같다.
여기서, 는 장약량(kg)이고, 보링의 직경은 45 mm, 천공장의 길이는 0.9 m로 설정하였다.
계산된 등가 발파하중을 기반으로 시간이력곡선(time history curve)을 도출해야 한다. 시간이력곡선은 시간축을 따라 발생하는 하중의 크기와 지속시간을 표현한 그래프로, 발파로 인한 동적 거동을 분석하는 데 필수적인 데이터이다.
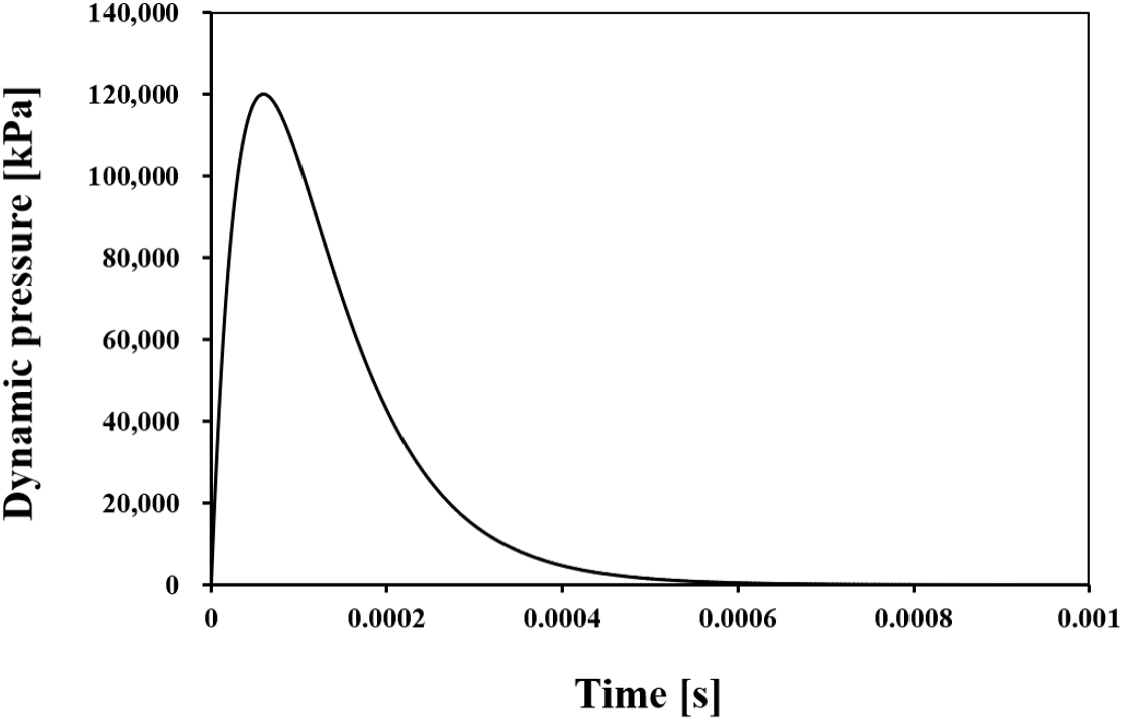
Fig. 7에서 보는 바와 같이 시간이력곡선의 x축은 시간을 나타내며, 발파 현상에서는 일반적으로 밀리초(ms) 단위를 사용한다. y축은 시간에 따라 변화하는 변수(예: 하중, 가속도, 변위)를 나타낸다. 곡선의 형태는 하중이 발생하고 소멸하는 과정을 시각적으로 보여주며, 발파하중의 급격한 상승 후 서서히 감소하는 형태를 보인다. 시간이력곡선을 사용한다면 시간에 따른 하중의 증감 패턴과 지속시간을 정량적으로 분석할 수 있다. 본 연구에서는 현장과 동일한 지발당 0.25 kg 기준의 총 장약량 40.75 kg을 발파하중으로 환산하여 수치해석에 적용하였다.
4. 수치해석
4.1 해석 모델 및 입력 변수
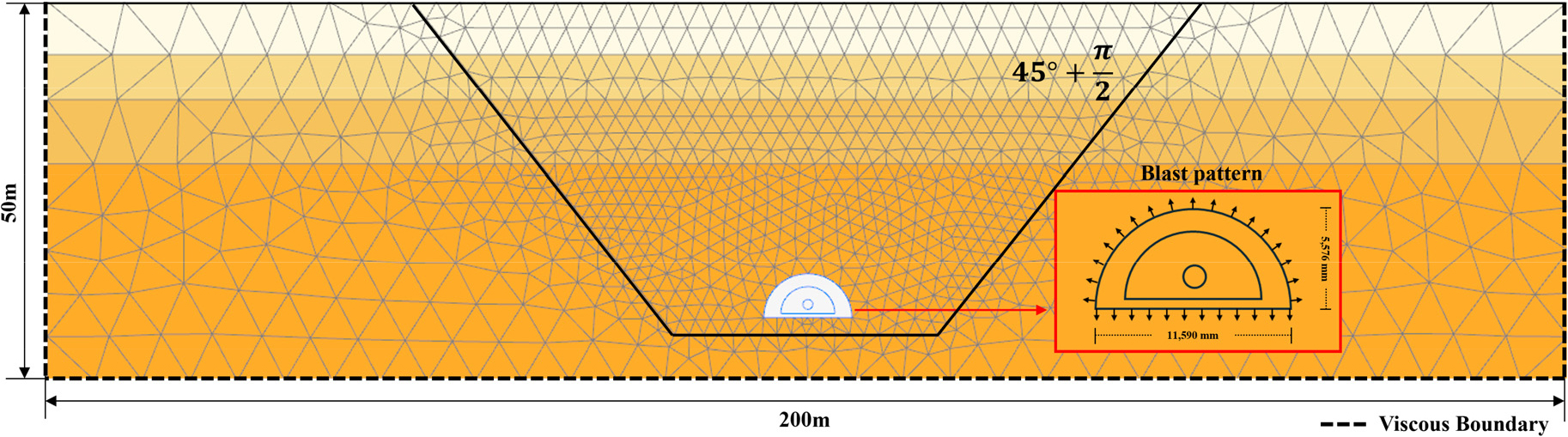
동일 단면에서의 이격거리별 PPV를 통한 전자뇌관과 비전기뇌관의 비교를 위해 현장의 D단면을 기반으로 모델링 하여 2차원 유한요소해석을 수행하였다. 발파단면의 크라운부로부터 지표면까지의 거리를 35 m로 설정하였으며, Fig. 1의 현장 지층자료를 기반으로 매립토, 풍화토, 연암, 경암으로 지반을 구성하였다. 지반종류에 따른 물성치는 Jeang (2004)을 참고하여 Table 3에 정리하였고, 발파가 수행되는 터널과 지층을 모델링한 수치해석 단면은 Fig. 8에 나타내었다. 터널의 직경과 토피고 및 지반의 크기는 실제 현장과 동일하게 설정하였으며, 터널 직상부로부터 수평 이격거리에 따른 지층에서의 PPV를 측정하기 위해 터널로부터 양측으로 100 m 거리만큼 확보된 수평 길이로 설정하였다. Castro et al. (2011)에 의하면, 유한요소해석을 통해 발파해석 시 요소의 크기가 해석의 정확도 측면에서 중요하게 작용하기 때문에 발파원 주변의 요소크기를 작게 조절해야 한다. 본 연구에서는 유한요소해석 프로그램 PLAXIS 2D, Ver. 2024의 자동 메쉬 생성 기능을 통해 전체 모델에서 45°+π/2 주동파괴 영역 내의 메쉬를 조밀(finesse)하게 생성하였다.
Table 3.
Material properties of the ground
4.2 경계조건
PLAXIS 2D매뉴얼(Bentley, 2014)에서는 동적해석을 위한 기본 경계조건을 제공하며, 이는 표준 고정경계(standard fixities)와 표준흡수경계(standard absorbent boundaries)로 구분된다. 동적하중으로 인해 발생하는 응력이 토체 내부로 반사되는 현상을 방지하기 위해서는 흡수경계를 사용해야 한다. 평면변형률(plain strain) 조건의 2차원 모델의 경우, 흡수경계는 모델의 하단과 양측경계에 적용되며, 상단경계는 지표면을 나타내기 때문에 흡수경계가 적용되지 않는다. 또한, 흡수경계를 위한 완화 계수(relaxation coefficients)인 C1, C2를 제공하며, 이는 파동흡수 성능을 향상시키기 위해 사용된다. 경계에 수직한 방향에서의 파동 감쇠는 C1, 경계에 접하는 방향에서는 C2로 보정한다. 흡수경계는 점성경계(viscous boundary)로 구성되며, 이는 댐퍼(damper) 역할을 하여 반사로 인해 발생하는 응력 증가를 소멸시킨다. 점성경계는 경계 근처의 재료 속도에 비례하는 저항력을 수직 및 접선응력으로 제공하도록 설정된다. Lysmer and Kuhlemeyer (1969)가 처음으로 점성경계 조건을 도입하였으며, PLAXIS는 댐퍼에서의 응력 성분을 다음 식 (5), (6)과 같이 정의한다.
여기서, 𝜎는 수직응력, 𝜏는 전단응력, 𝜌는 재료의 밀도, 는 압축파 속도, 는 전단파 속도, 수평 속도, 수직 속도를 의미한다.
모델의 기저에 점성경계를 적용할 경우, 입력데이터로 하중 시간이력(time history)을 제공해야 하며, 완화계수의 설정이 필요하다. 본 연구에서는 C = 1, C = 0.25를 사용하였고, 이는 동적하중을 받는 지반의 계산 결과가 이론 해와 가장 잘 일치하는 것으로 알려져 있다(Castro et al., 2011).
4.3 감쇠계수
진동의 감쇠는 토양 내 에너지 손실로 인해 발생하며, 이는 입자의 내부마찰, 점성특성, 비가역적변형 등의 요인에 의해 나타난다. 그러나 대부분의 지반모델은 탄성거동을 보이기 때문에 감쇠효과를 충분히 반영하지 못하는 한계가 있다. 이를 위해 수치해석에서는 Rayleigh 감쇠계수를 활용하여 현실적인 감쇠특성을 모사한다. Rayleigh 감쇠는 질량행렬()과 강성 행렬()의 조합을 통해 감쇠행렬()를 정의하며, 식 (7)에 나타냈다. 각 행렬의 계수는 고유진동수와 감쇠비율간의 관계를 통해 결정되며, 관계식은 식 (8)과 같다.
감쇠계수는 동적하중에 대한 시스템 응답을 결정하는 중요한 요소로, 이상적인 경우에는 실험적 방식을 통해 데이터를 산출할 수 있다. 그러나, 본 연구에서는 현장 여건상 관련 실험이 수행되지 않아, 시행착오적 보정방법(trial and error calibration)을 활용하여 계수를 결정하였다. 보정과정에서는 현장계측 데이터를 바탕으로, 발파원 직상부에서 측정된 최대입자속도(PPV) 값과 수치해석에서의 결과를 비교하였다. 이를 위해 감쇠계수 α와 β값을 0.1, 0.01, 0.001의 범위에서 조정하며 최적의 조합을 분석하였다.
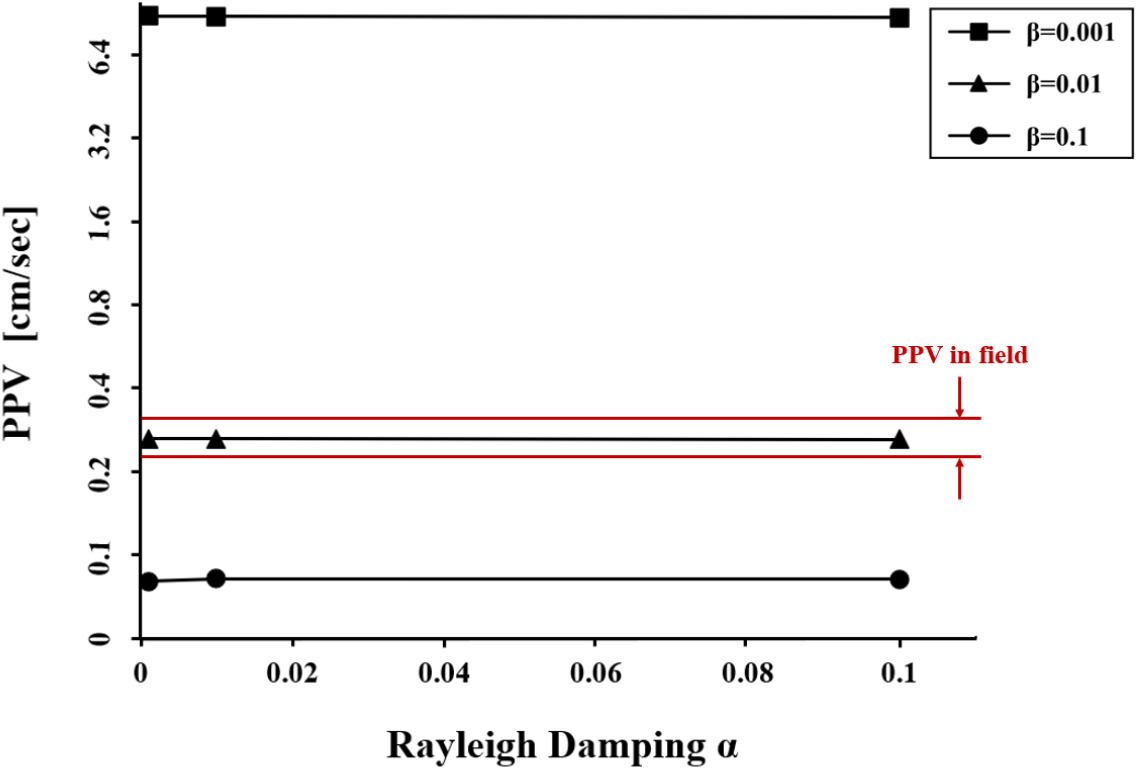
Fig. 9는 Rayleigh 감쇠계수(α, β)의 변화에 따른 최대입자속도(PPV) 결과를 나타낸 것이다. 다양한 조합을 적용한 수치해석 결과, α = 0.001, β = 0.01로 설정했을 때 도출된 PPV값이 현장계측값 범위와 일치하는 것으로 나타났다. 이는 본 연구에서 설정한 감쇠계수가 동적하중해석에서 토양의 실제 감쇠특성을 효과적으로 반영했음을 보여준다. α값의 변화에 따른 PPV 결과는 비교적 작은 편차를 보였으나, β값의 변화는 PPV값이 각각 0.08, 0.262, 8.8으로 큰 차이를 나타냈다. 이는 발파 시 발생하는 고주파 영역의 파동이 β값, 즉 강성 감쇠계수에 더 민감하게 반응하기 때문으로 판단된다. 따라서, 본 연구에서는 동적하중해석에서 지반의 실제 감쇠특성을 반영하기 위해 α = 0.001, β = 0.01의 Rayleigh 감쇠계수를 적용하였으며, 이는 현장 계측값과 수치해석 결과 간의 오차를 최소화하고, 해석의 신뢰성과 정확성을 높이는 데 적합한 값으로 판단된다.
4.4 데이터 계측 위치
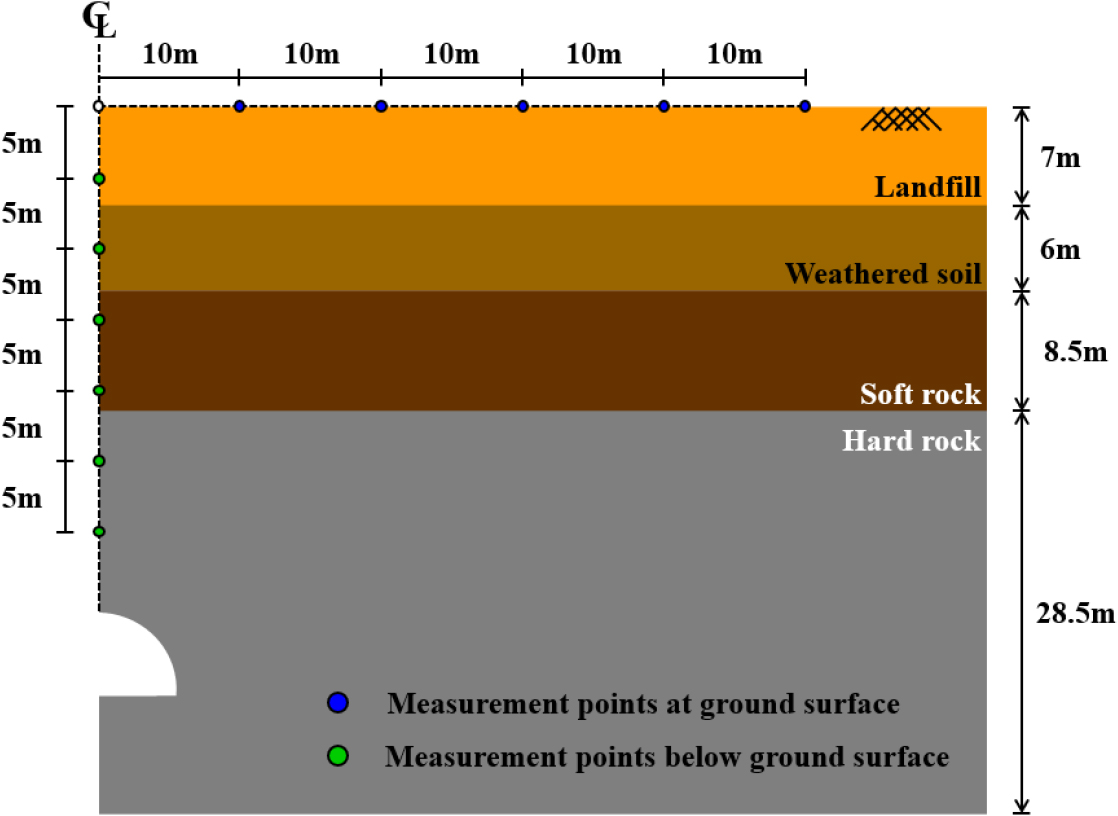
본 연구에서는 Fig. 10에서 보는 바와 같이 터널발파 시 수평 이격거리에 따른 진동영향을 분석하기 위해 터널 직상부 지표로부터 10 m 간격으로 측정점을 설정하였으며, 심도에 따른 영향을 분석하기 위해 터널 천정부로 부터 5 m 간격으로 지표층까지 측정점을 설정하였다. 총 12개의 측정 지점에서 최대입자속도(PPV)와 터널 직상부의 수직방향 진동속도() 데이터를 수집하였다.
4.5 수치해석 결과
4.5.1 지표면 수평이격거리에 따른 PPV
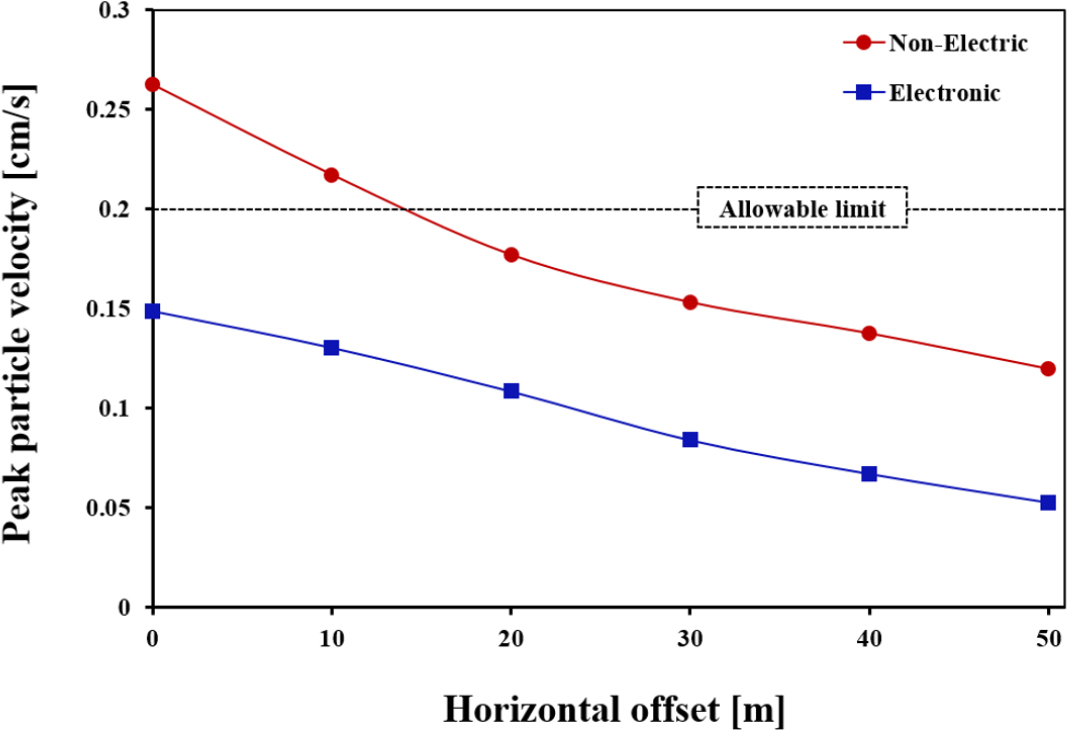
지표면 수평이격거리(10 m, 20 m, 30 m, 40 m, 50 m)에 따른 비전기뇌관과 전자뇌관의 발파 진동영향을 Fig. 11에 나타내었다. 비전기뇌관은 수평이격거리 0 m와 10 m에서 0.263 cm/s, 0.223 cm/s의 PPV값을 가져 환경부에서 제시한 진동허용치(0.2 m/sec)를 초과하였고, 15 m 이상부터 기준을 만족하였다. 반면, 전자뇌관은 모든 측정 지점에서 PPV가 최대 0.149 cm/s로 나타나 전 구간에서 허용기준을 만족하여 안정적인 성능을 보였다. 전자뇌관은 비전기뇌관 대비 0 m 지점에서 약 44%, 50 m 지점에서는 약 56% 낮은 PPV 값을 기록하였으며, 전체 측정지점에서 평균적으로 약 45%의 진동감소율을 나타냈다. 전자뇌관의 정밀한 시간제어 기능이 진동 간섭을 최소화하고 에너지를 효율적으로 분산시킨 결과로 판단된다.
4.5.2 터널 직상부로부터 수직이격거리에 따른 PPV
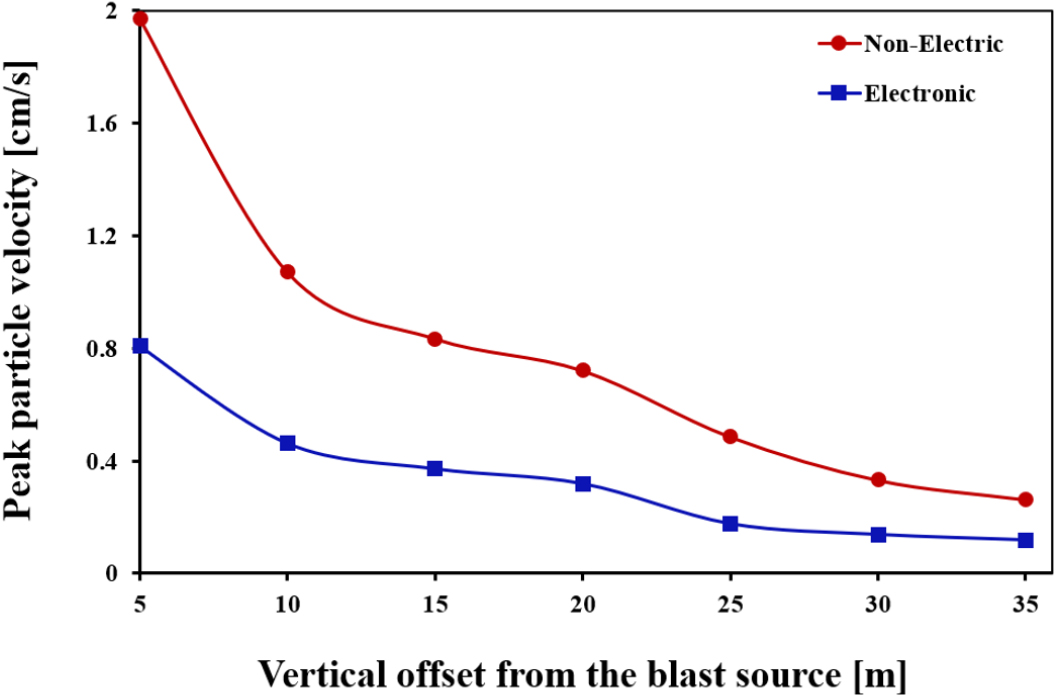
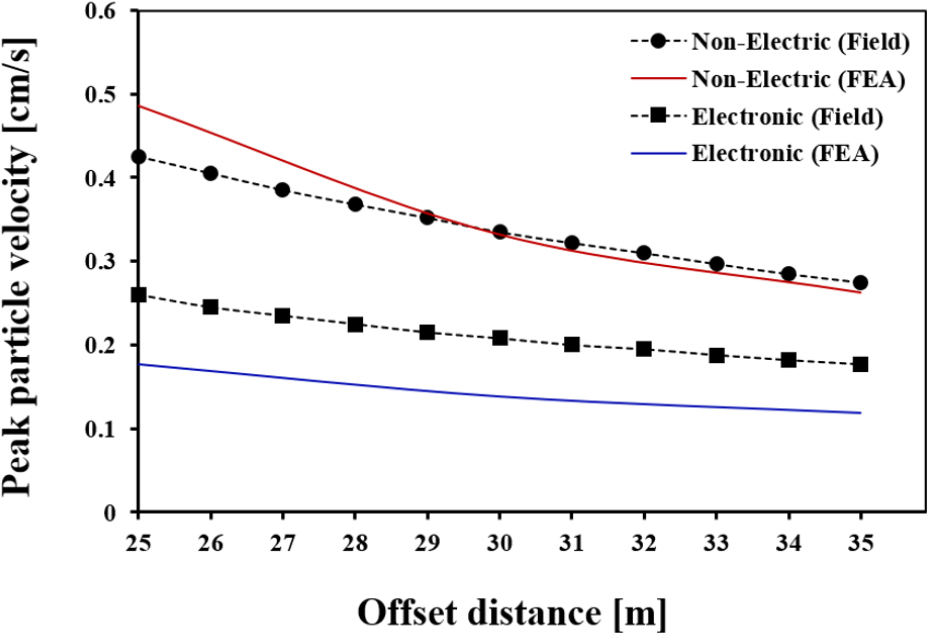
Fig. 12는 발파원으로부터 수직 이격거리에 따른 비전기뇌관과 전자뇌관의 발파 진동특성을 분석한 결과이다. 두 뇌관 모두 5~10 m 구간에서 진동이 급격히 감소하는 경향을 보였으며, 비전기뇌관은 발파원에서 가까운 5 m 지점에서 최대 1.97 cm/s의 PPV값을 기록하였고, 직상부 35 m 지점에서는 0.2625 cm/s로 감소하였다. 전자뇌관은 동일한 조건에서 5 m 지점에서 0.807 cm/s로 측정되어 비전기뇌관보다 약 59% 낮은 진동값을 보였고, 35 m 지점에서는 0.149 cm/s로 감소하였다. 이는 전자뇌관이 진동에너지를 효과적으로 제어함으로써 안정적인 진동특성을 나타냄을 보여준다. Fig. 13은 수치해석(FEA) 결과와 현장계측 데이터를 비교하여 허용진동치와의 상관성을 분석하였다. 비전기뇌관과 전자뇌관 모두 현장 계측 데이터와 수치해석 결과 간의 그래프 양상이 유사하게 나타났으며, 이는 수치해석이 실제 지반 조건을 효율적으로 반영했음을 보여준다. 특히, 비전기뇌관의 경우 수치해석과 현장계측 결과 모두 25 m-35 m 구간에서 허용 진동치를 초과하였으나, 전자뇌관의 경우 수치해석 결과가 허용진동치(0.2 cm/s)에 근접하면서도 모든 구간에서 허용치를 초과하지 않는 안정적인 경향을 보였다.
4.5.3 직상부에서의
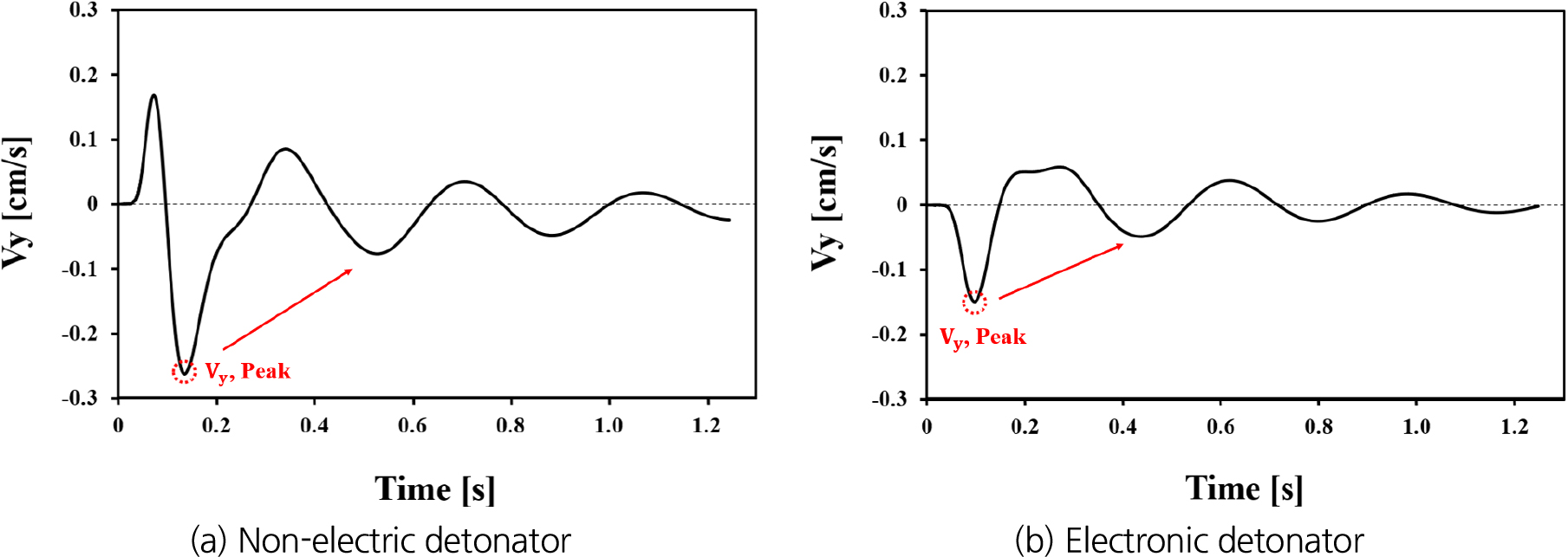
발파로 인한 진동의 감쇠메커니즘을 비교하기 위해 터널 직상부 지표에서 측정된 수직 진동속도()를 Fig. 14에 나타냈다. Fig. 14(a)와 (b)는 각각 비전기뇌관과 전자뇌관의 결과이다. 전자뇌관의 첨두 수직 진동속도는 -0.15 cm/s이며 지표층에 전달된 후 첫 번째 최대지점이 첨두 속도로 도출되었다. 비전기뇌관의 첨두 수직 진동속도는 -0.26 cm/s으로 전자뇌관에 비해 절대적으로 42%만큼 크게 발생하였다. 또한, 비전기뇌관은 진동이 지표층에 전달된 후 양의 값을 갖는 수직 진동속도로 첫 번째 최대지점을 거친 후, 음의 값을 갖는 두 번째 최대지점에서 첨두속도가 도출되었다. 따라서, 전자뇌관은 파동간의 간섭이 최소화되어 첫 번째 최대지점 이후 감소되는 양상이 나타나고, 비전기뇌관은 파동간의 간섭에 의해 파동합성이 발생한 것으로 판단된다. 진동감쇠 양상을 비교한 결과 전자뇌관이 비전기뇌관에 비해 약 15%만큼 짧은 주기를 가졌으며, 진폭의 경우 전자뇌관의 경우 68%, 48%, 53%로 평균 57%의 감쇠율이, 비전기뇌관의 경우 70%, 37%, 48%로 평균 52%의 감쇠율이 나타났다. 이는 전자뇌관이 지표층에서 상대적으로 고주파의 진동을 하며, 잔류진동의 감쇠가 더욱 빠르게 발생하여 지표층 구조물에 비교적 작은 진동영향을 미칠 가능성을 의미한다.
5. 결 론
본 연구는 ○○정수장 하부 터널발파 시 비전기뇌관과 전자뇌관의 성능을 비교하였다. 현장계측 데이터를 활용하여 이격거리에 따른 허용장약량을 평가하였으며, 수치해석을 통해 발파진동의 최대입자속도(PPV)와 수직 진동속도()를 비교하여 뇌관 종류에 따른 허용 진동 기준치 만족 여부와 진동저감 효과를 정량적으로 분석하였다. 결론을 요약하면 다음과 같다.
1. 현장계측을 통해 얻은 발파 진동계측 데이터를 비전기뇌관과 전자뇌관으로 구분하여 자승근식과 삼승근식을 적용한 회귀분석을 수행한 결과, 95% 신뢰도의 발파진동 추정식에서 K값, n값 모두 전자뇌관이 낮아 발파진동 저감에 유리한 것으로 평가되었다. 또한, 이격거리(사거리 = 수직+수평)에 따른 허용장약량 분석 결과, 지발당 0.25 kg의 장약량에서 비전기뇌관은 최소 46 m의 이격거리가 필요한 반면, 전자뇌관은 최소 31 m의 이격 거리만 확보하면 되는 것으로 나타났다
2. 수치해석의 지표면 수평이격거리(10 m, 20 m, 30 m, 40 m, 50 m)에 따른 발파 진동을 분석한 결과, 비전기뇌관은 0 m와 10 m에서 각각 0.263 cm/s와 0.223 cm/s의 PPV값을 기록하여 환경부의 진동 허용 기준(0.2 cm/s)을 초과하였으며, 최소 15 m 이상의 이격거리가 필요하였다. 전자뇌관은 모든 측정 지점에서 최대 0.149 cm/s의 PPV값을 나타내어 기준을 충족하였으며, 평균적으로 비전기뇌관보다 약 45% 낮은 진동 감소율을 보였다. 이는 전자뇌관의 정밀한 시간 제어 기능으로 진동 간섭을 최소화하고 에너지를 효율적으로 분산시킨 결과로 판단된다.
3. 발파원으로부터 수직 이격거리에 따른 진동 분석 결과, 비전기뇌관은 발파원 근처 5 m 지점에서 최대 1.97 cm/s, 직상부 35 m 지점에서 0.2625 cm/s로 진동이 감소하였다. 전자뇌관은 동일한 조건에서 각각 0.807 cm/s와 0.149 cm/s로 측정되어 비전기뇌관보다 약 59% 낮은 진동값을 보였으며, 전자뇌관은 31 m, 비전기뇌관은 45 m 이상의 수직 이격거리가 필요함을 확인하였다. 수치해석과 현장계측 데이터를 비교한 결과, 전자뇌관은 모든 구간에서 허용진동치를 초과하지 않는 안정적인 특성을 확인할 수 있었다.
4. 발파로 인한 수직 진동속도()를 비교한 결과, 전자뇌관의 첨두 수직 진동속도는 -0.15 cm/s로 비전기뇌관(-0.26 cm/s)보다 약 42% 낮았다. 또한, 전자뇌관은 첫 번째 최대 진동 이후 감소되는 양상을 보였으며, 비전기뇌관은 파동 간섭으로 인해 파동합성이 발생하였다. 진동 감쇠율은 전자뇌관이 평균 57%, 비전기뇌관이 52%로 나타났으며, 잔류 진동의 감쇠가 더욱 빠르게 발생하여 지표층 구조물에 비교적 작은 진동영향을 줄 것으로 예상된다.
5. 향후 연구에서는 역해석 외에도 지하수위의 존재 유무 및 위치, 암반의 등급, 터널의 깊이와 같은 변수를 고려하여, 이러한 요소가 발파진동에 미치는 영향을 추가적으로 분석할 필요가 있다고 판단된다.