Comparison of performance of automatic detection model of GPR signal considering the heterogeneous ground

Sang Yun Lee; Ki-Il Song; Kyung Nam Kang; Hee Hwan Ryu

doi:10.9711/KTAJ.2022.24.4.341

Preview

Research Paper

Journal of Korean Tunnelling and Underground Space Association. 31 July 2022. 341-353
https://doi.org/10.9711/KTAJ.2022.24.4.341

Comparison of performance of automatic detection model of GPR signal considering the heterogeneous ground

지반의 불균질성을 고려한 GPR 신호의 자동탐지모델 성능 비교

Sang Yun Lee¹

Ki-Il Song²^*

Kyung Nam Kang³

Hee Hwan Ryu⁴

이 상연¹

송 기일²^*

강 경남³

류 희환⁴

¹Ph.D. Student, Dept. of Civil Engineering, Inha University

²Professor, Dept. of Civil Engineering, Inha University

³Senior Researcher, Research Institute of Construction & Environmental System, Inha University

⁴Principal Researcher, Structural & Seismic Technology Group, Korea Electric Power Corporation Research Institute

¹학생회원, 인하대학교 토목공학과 박사과정

²정회원, 인하대학교 토목공학과 정교수

³정회원, 인하대학교 건설환경시스템연구소 책임연구원

⁴정회원, 한국전력공사 전력연구원 구조내진연구실 책임연구원

^{*Corresponding Author}

ABSTRACT

Pipelines are buried in urban area, and the position (depth and orientation) of buried pipeline should be clearly identified before ground excavation. Although various geophysical methods can be used to detect the buried pipeline, it is not easy to identify the exact information of pipeline due to heterogeneous ground condition. Among various non-destructive geo-exploration methods, ground penetration radar (GPR) can explore the ground subsurface rapidly with relatively low cost compared to other exploration methods. However, the exploration data obtained from GPR requires considerable experiences because interpretation is not intuitive. Recently, researches on automated detection technology for GPR data using deep learning have been conducted. However, the lack of GPR data which is essential for training makes it difficult to build up the reliable detection model. To overcome this problem, we conducted a preliminary study to improve the performance of the detection model using finite difference time domain (FDTD)-based numerical analysis. Firstly, numerical analysis was performed with homogeneous soil media having single permittivity. In case of heterogeneous ground, numerical analysis was performed considering the ground heterogeneity using fractal technique. Secondly, deep learning was carried out using convolutional neural network. Detection Model-A is trained with data set obtained from homogeneous ground. And, detection Model-B is trained with data set obtained from homogeneous ground and heterogeneous ground. As a result, it is found that the detection Model-B which is trained including heterogeneous ground shows better performance than detection Model-A. It indicates the ground heterogeneity should be considered to increase the performance of automated detection model for GPR exploration.

Keywords

Ground penetrating radar

Finite difference time domain (FDTD)

Fractal model

Convolutional neural network

도심지에는 많은 지중 매설관이 설치되어 있으며, 이러한 지중 관로의 위치(깊이, 방향 등)은 굴착을 수행하기 전에 특정되어야 한다. 지중 매설관을 탐지하기 위해 다양한 지구물리학적인 방법을 사용할 수 있으나, 지반의 불균질성으로 인해 정확한 위치정보를 파악하는 것은 어렵다. 다양한 비파괴 탐사 방법 중 GPR (ground penetrating radar)는 고속으로 실험이 가능하며, 다른 탐사 방법에 비해 상대적으로 저렴한 탐사비용 등의 장점을 갖는다. 그러나 GPR의 탐사 데이터는 해석이 직관적이지 않아 상당한 전문적 지식이 요구된다. 최근 딥러닝을 이용한 탐사 데이터의 자동판독 기술에 대한 연구가 증가하고 있으나, 매설물의 위치를 정확히 알고 있는 탐사 데이터가 부족하여 학습모델 구축에 어려움이 있다. 이를 해결하기 위해 본 연구에서는 이러한 문제를 FDTD (finite difference time domain)수치해석을 통해 해결하고 자동탐지 학습 모델의 성능을 향상시키기 위한 기초연구를 수행하였다. 첫째, 단일유전율로 구성된 균질지반을 구성하고 해석을 수행하였다. 불균질 지반의 경우 프랙탈 기법을 이용하여 모델을 구성하고 해석을 수행하였다. 둘째, 합성곱 신경망을 이용하여 딥러닝 학습을 수행하였다. Model-A는 균질 지반 해석 데이터만 이용하여 학습을 수행하였으며, Model-B는 균질 및 불균질 지반 해석 데이터를 이용하여 학습을 수행하였다. 그 결과 Model-B가 Model-A보다 탐지성능이 우수한 것을 확인하였다. 이는 자동탐지 모델의 학습 시, 지반의 불균질성을 포함하여 학습을 수행하면 탐지 모델의 성능이 개선됨을 의미한다.

키워드

지표 투과 레이더

시간영역 유한차분 수치해석

프랙탈 기법

합성곱 신경망

MAIN

1. 서 론
2. FDTD수치해석을 통한 학습데이터 셋 구축
3. YOLO v5를 이용한 객체 탐지
3.1 균질지반의 지중관로 탐지
3.2 불균질지반을 고려한 지중관로 탐지
4. 결 론

1. 서 론

도심지에는 상하수관, 전력관, 통신관 등 많은 지중 매설관이 설치되어 있으며, 매설관의 노후화로 인해 균열, 파손 등 손상이 발생한다(Lee, 2018). 이러한 매설관의 유지관리를 위해서는 지중 매설관의 위치정보가 중요하지만, 도심지에서 매설관의 위치정보를 획득하기는 쉽지 않다. Ground penetrating radar (GPR)은 기존의 지반조사 방법들에 비해 비파괴성 및 고속데이터 수집, 상대적으로 저렴한 탐사 비용 등의 장점을 갖는다(Benedetto and Pajewski, 2015). 그러나 탐사를 효과적으로 설계하고 수행하려면 상당한 전문 지식이 필요하다는 단점이 있으며, 탐사 데이터의 해석은 직관적이지 않아 측정값을 판독하려면 전문적인 지식이 필요하다(Benedetto and Pajewski, 2015; Chae et al., 2019).

최근 GPR탐사 결과에서 지중 시설물 등을 판독하기 위해 딥러닝 기법을 이용한 연구가 수행되고 있다(Al-Nuaimy et al., 2000; Pham and Lefèvre, 2018; Yuan et al., 2018; Chae et al., 2019; Kim and Bae, 2021). 이러한 연구에서는 대부분 합성곱 신경망(Convolution neural network, CNN)을 이용하여 B-Scan 데이터를 자동으로 판독하는 알고리즘을 연구하였다. 학습데이터로는 GPR 실험 데이터를 이용하여 학습을 진행하였으며, 일부 연구에서는 학습데이터 양의 부족으로 FDTD (Finite difference time domain) 수치해석 결과를 포함하여 학습데이터를 구성하였다. 그러나 FDTD 수치해석의 경우, 대부분 지반의 모델을 균질하게 모델링하고, 이에 대한 수치해석 결과를 사용하여 딥러닝 모델을 학습하고 있는 실정이다. 그러나 실제 지반의 경우, 지반의 함수비 및 구성비에 따라 균질하지 않기 때문에 균질지반에 비해 많은 반사파가 생기며, 이는 측정되는 반사파 신호에 영향을 미친다. 따라서 불균질 지반에서의 반사 신호는 균질 지반에서의 반사신호보다 많은 노이즈를 포함하고 있기 때문에, 자동탐지 학습을 위해 이러한 영향을 고려할 필요가 있다.

Peplinski et al. (1995)의 연구에 따르면, 0.3~1.3 GHz의 주파수에서 지반을 구성하는 사질토와 점성토의 비율, 함수비, 사질토의 단위중량 등을 이용하여 지반의 유전율을 추정하는 연구를 수행하였다. Giannakis (2016)는 Peplinski et al. (1995)의 연구결과와 프랙탈 기법(Fractal method)을 이용하여 불균질성을 고려한 지반모델을 생성하고, 과거 전쟁 중 매설된 지뢰를 탐사하기 위한 FDTD 수치해석을 수행한 바 있다. 또한 ANN (Artificial neural network)을 사용하여 지뢰를 탐지하기 위한 학습과 탐지를 진행한 바 있다.

본 연구에서는 GPR 탐사결과의 자동 판독을 위한 기초연구로 프랙탈 기법을 이용하여 지반의 불균질성을 고려한 해석을 수행하고, 이를 학습데이터로 사용하여 균질 지반 데이터로만 학습한 모델과 불균질 지반데이터를 포함하여 학습한 모델을 비교 및 분석하는 연구를 수행하였다. 학습에 사용된 알고리즘으로는 CNN을 이용한 객체 탐지 알고리즘을 사용하였으며, 탐지속도가 상대적으로 빠른 YOLO v5를 이용하여 연구를 진행하였다.

2. FDTD수치해석을 통한 학습데이터 셋 구축

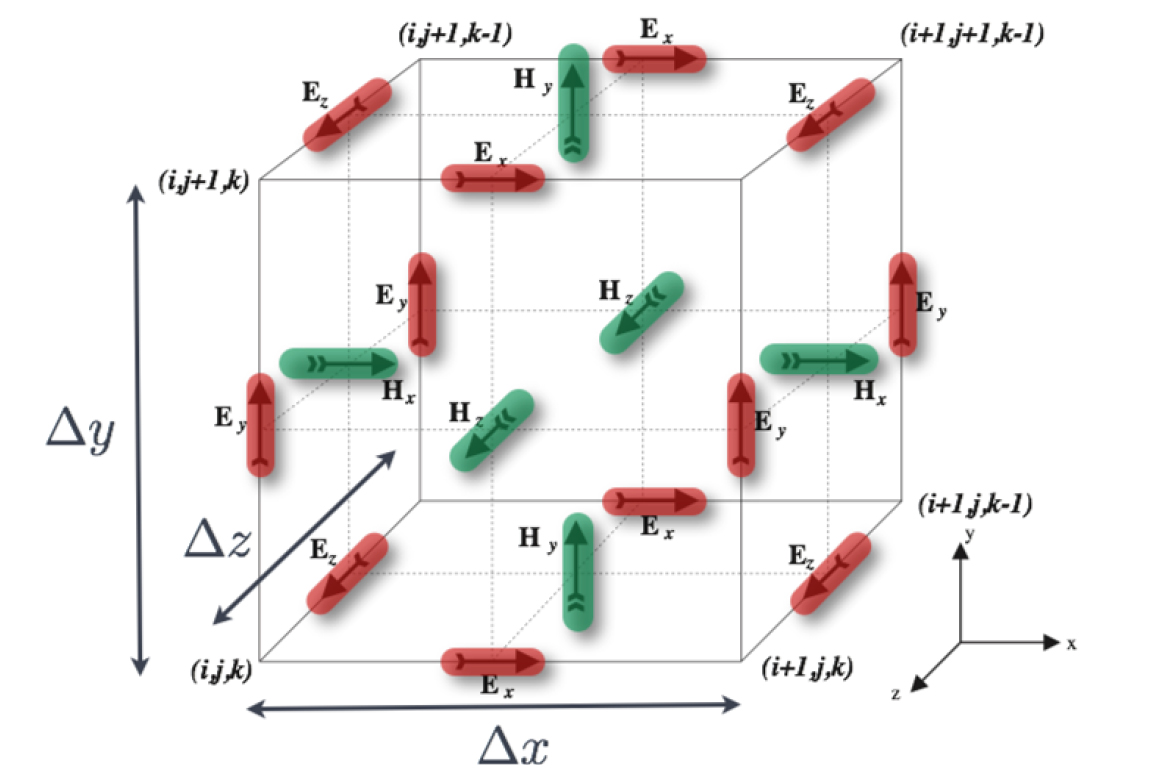
균질 지반과 불균질 지반의 학습모델을 비교하기 위해 본 연구에서는 FDTD 수치해석을 이용하여 균질지반의 GPR 데이터와 불균질 지반의 GPR 데이터를 축적하였다. FDTD 수치해석은 시간영역 유한차분법이라고 하며, 해석 대상을 Yee 셀로 정의된 영역으로 이산화하고 각각의 셀에서 맥스웰 방정식을 풀어내는 것으로 해석을 수행한다(Taflove et al., 2005). FDTD 수치해석은 간단하며, 명시적인 장점이 있는 반면 해석영역이 넓을 경우 해석에 많은 리소스를 사용해야 된다는 단점이 있다(Warren et al., 2016). Fig. 1은 Yee 셀을 나타내며, E는 전기장, H는 자기장을 의미하며 하나의 셀은 x, y, z 축으로 단위 길이를 갖게 된다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F1.jpg

Fig. 1

Single FDTD Yee cell (Warren and Giannopoulos, 2022)

FDTD 수치해석은 미소 시간을 설정하고, 미소시간영역에 대한 해석을 반복적으로 수행하여 전체 시간영역에 대한 해석을 수행한다. 이 때 미소시간영역에 대한 안정조건은 CFL조건으로 알려져 있으며 식 (1)과 같이 나타낼 수 있다. 여기서, $c$ 는 빛의 속도(m/sec)를 의미하며, $Δ x$ , $Δ y$ , $Δ z$ 는 각각 Yee 셀의 x, y, z축의 단위 길이를 의미한다. 식 (1)은 3차원 해석에 대한 안정조건이며 2차원 해석에 대한 안정조건은 상기 식에서 $Δ z \to \infty$ 로 설정하여 미소시간영역을 결정한다.

(1)

Δ t \leq \frac{1}{c \sqrt{\frac{1}{(Δ x)^{2}} + \frac{1}{(Δ y)^{2}} + \frac{1}{(Δ z)^{2}}}}

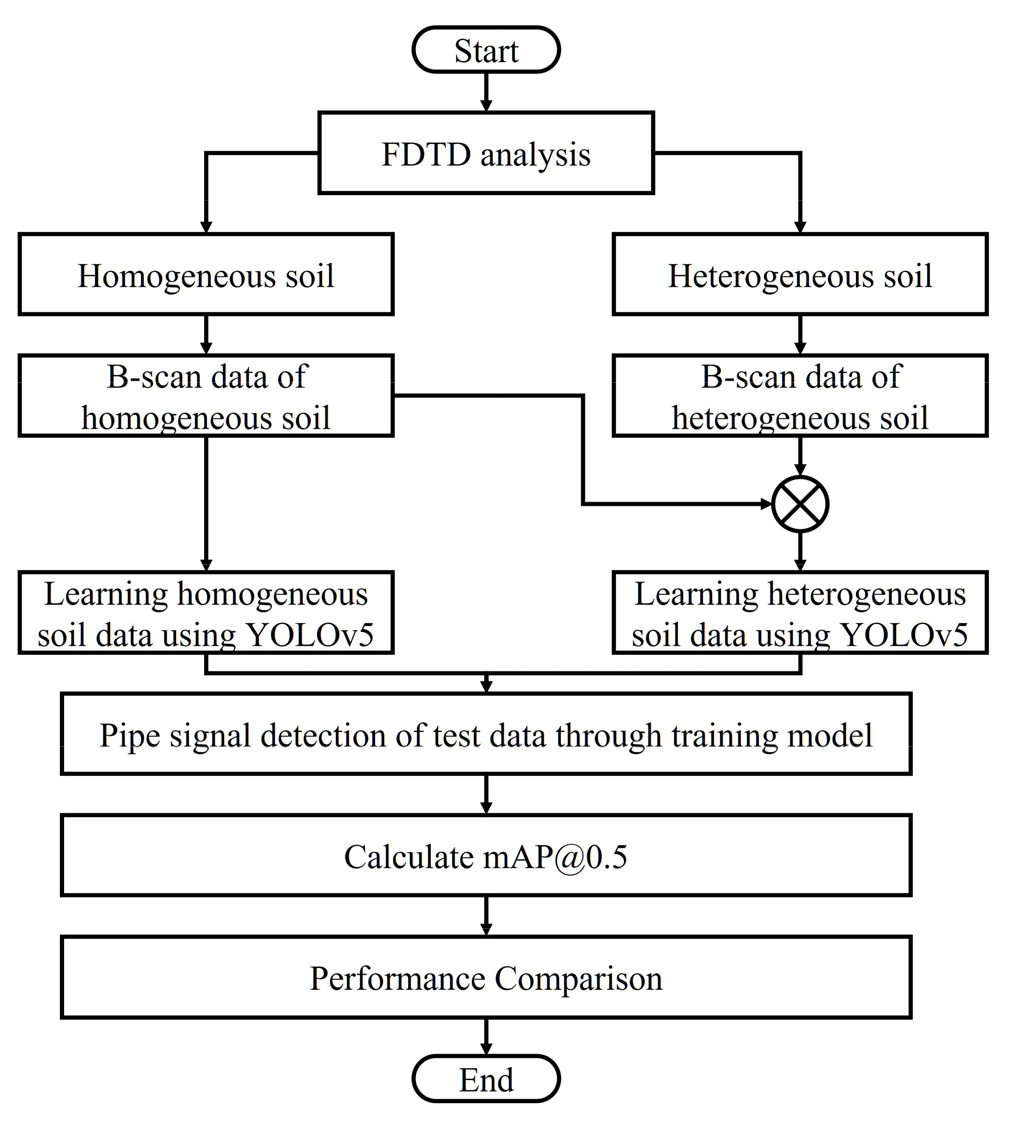
오픈소스 프로그램인 gprMax를 이용하여 수치해석을 진행하였으며, 사용된 입력 파라미터는 Table 1, Table 2에 나타내었다. Table 1, Table 2는 각각 균질한 지반과 불균질한 지반의 입력파라미터이다. 본 연구에서 균질한 지반은 단일 유전율을 통해 형성된 수치해석 모델을 의미하며, 불균질한 지반은 지반의 함수비에 따라 생성된 재료가 프랙탈 기법을 통해 분포된 모델을 불균질한 지반 모델로 설정하였다. 본 연구의 흐름도는 Fig. 2에 도시하였다.

Table 1.

Input parameters about homogeneous soil

$Δ l$ (m)		0.0142
$t_{w}$ (ns)		72
Soil	$ε_{r}$	5.5
	$σ$ (S/m)	0
	$μ_{r}$ (g/cm³)	1.0
	$σ_{*}$ (g/cm³)	0
Waveform	Type	Ricker
Waveform	$f$ (MHz)	300

Table 2.

Input parameters about heterogeneous soil

$Δ l$ (m)		0.003
$t_{w}$ (ns)		110
Soil	$S$	0.5
	$C$	0.5
	$ρ_{s}$ (g/cm³)	2
	$ρ_{b}$ (g/cm³)	2.66
	$m_{u}$	0.15~0.2
Waveform	Type	Ricker
Waveform	$f$ (MHz)	300

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F2.jpg

Fig. 2

Flowchart for this research

Table 1은 균질지반에서 사용되는 입력물성을 나타내었다. $Δ l$ 는 단위 셀의 길이를 의미하며, $t_{w}$ 는 해석을 수행하는 시간, $ϵ_{r}$ 는 상대 유전율, $σ$ 는 전도도, $μ_{r}$ 는 상대투자율, $σ_{*}$ 는 자기 손실을 의미한다. Table 2는 불균질 지반의 입력물성을 나타낸 것이며 균질지반과 다르게 사질토( $S$ )와 점성토( $C$ )의 비, 사질토의 단위중량( $ρ_{s}$ ), 지반의 체적 단위 중량( $ρ_{b}$ ), 함수비( $m_{u}$ ) 등을 입력물성으로 사용한다. 불균질 지반의 재료모델은 함수비의 값에 따라 총 50가지 물성을 생성하고 이를 프랙탈 기법을 통해 배열하여 도시하였다. Peplinski et al. (1995)이 제안한 식을 통해 지반의 함수비에 따른 유전율과 전도도가 계산되어 입력되었으며, 상대 유전율 8.57~9.87과 전도도 0.0628~0.0718 S/m로 설정되었다.

현실에서 전자기파의 진행은 방향과 주파수에 관계없이 동일한 속도로 전파되나, FDTD 수치해석의 경우해석 모델을 이산화하여 현실과 같이 전달되지 않는다. 이러한 오차를 최소화하기 위해 단위 셀의 길이는 해석영역에서 가장 작은 파장의 길이보다 10배 이상 작도록 모델을 구성해야 된다고 알려져 있다(Giannopoulos, 1998; 2005). 따라서 지반의 상대 유전율에 따라 매질 내에서 전자기 파의 파장이 변화되며 이로 인해 단위 셀의 길이가 변하게 된다. 따라서 지반의 유전율의 값이 차이가 나는 Table 1과 Table 2의 단위 셀의 길이는 다르게 설정되었다.

해석 대상 모델은 실린더의 위치와 크기를 임의로 생성하며 해석하기 위해 가로 10 m 깊이 5 m의 지반을 모사하였으며, 2D 단면의 해석을 진행하였다. 또한 원형 실린더 모델을 해석 대상 모델 내에 임의의 위치에 생성하여 해석을 수행하였다. 원형 실린더의 직경은 50~100 cm의 범위에서 임의로 선택되었으며, 완전한 전기 도체로 모델링하여 $ϵ_{r} = 1$ , $σ = 0$ 으로 설정하였다. 해석에 사용된 송신신호는 균질 모델 및 불균질 모델에서 리커(Ricker) 파형을 사용하였으며, 송신 주파수는 300 MHz로 설정하였다.

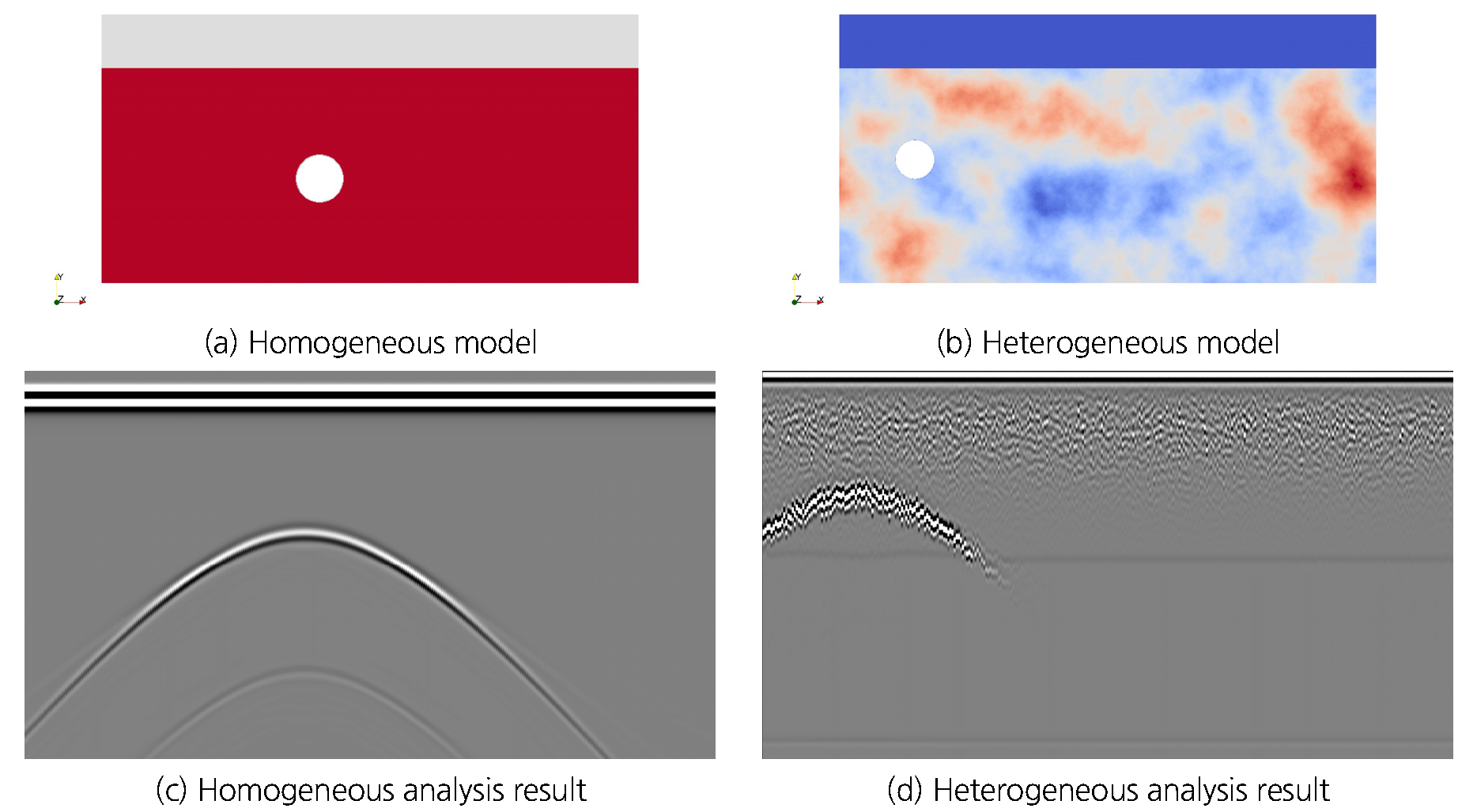
해석은 관로의 위치와 크기를 변경하며 균질 및 불균질 지반 모델에서 각각 100회 수행하여 학습데이터를 축적하였으며, Fig. 3은 균질 및 비균질 해석 모델과 B-Scan 데이터의 예시이다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F3.jpg

Fig. 3

FDTD analysis model and result

모델링 된 원형 실린더 반경의 범위는 25~50 cm이며, 위치는 지반 내 무작위 위치에 생성하고 해석을 진행하도록 설정하였다.

3. YOLO v5를 이용한 객체 탐지

균질 지반의 반사파 특성으로 학습한 모델과 불균질 모델의 특성을 포함한 학습 모델을 비교하기 위해 앞서 구축된 해석 데이터 셋을 이용하여 객체탐지 학습을 진행하였다. Redmon et al. (2016)에 따르면, 대표적인 객체탐지 모델은 DPM (Deformable parts models)과 R-CNN (Regions with convolution neural network)가 있다. DPM은 이미지 전체에서 슬라이딩 윈도우(Sliding window) 방식으로 객체를 검출하는 모델이며, R-CNN은 이미지 안에 무작위로 생성된 bounding box에서 객체가 검출되면 bounding box의 크기 및 위치를 조정하며 오차를 줄여가는 방식으로 객체를 검출하는 모델이다. 그러나 두 모델 모두 복잡한 과정으로 인해 학습 및 분류가 느리다는 단점이 있다.

YOLO는 You only look once의 약자로 Redmon et al. (2016)에 의해 처음 발표되었으며, 다른 객체 탐지 알고리즘에 비해 탐지속도가 빠르고 작은 표적탐지에도 잘 작동한다(Tian et al., 2019). 따라서 본 연구에서는 실시간 분류가 가능하도록 탐지속도가 상대적으로 빠른 YOLO v5를 이용하여 학습 결과를 비교하였다.

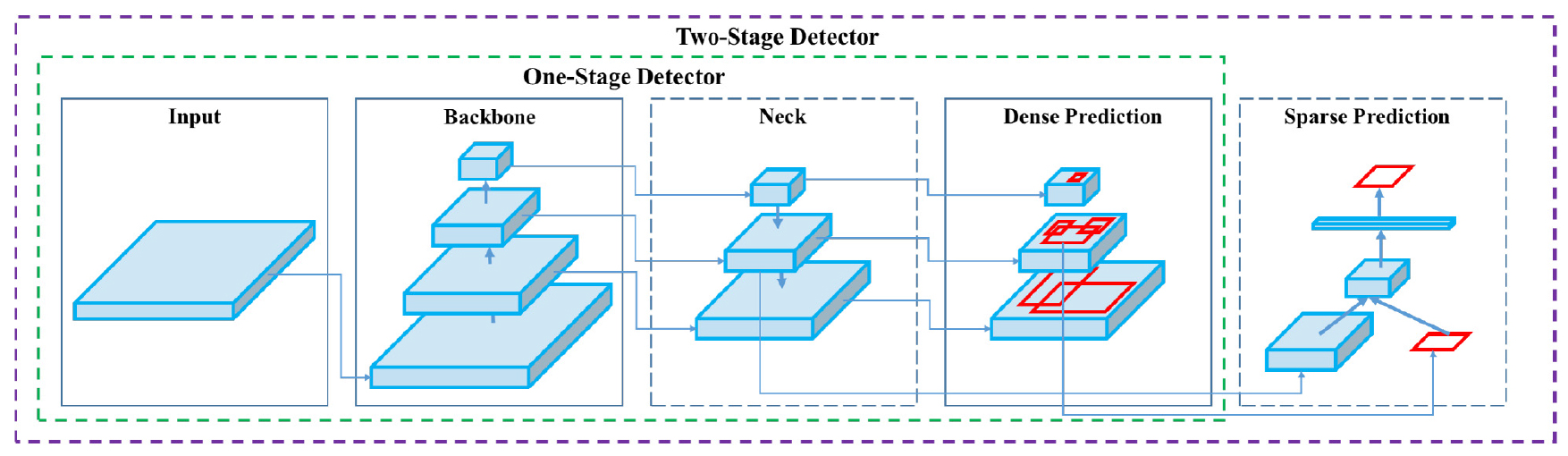
YOLO v5 알고리즘의 구조는 YOLO v4와 유사하며 크게 3가지(backbone, neck, head)로 구분할 수 있다(Fig. 4). Backbone에서는 입력 이미지에서 중요한 특징들을 추출하며, neck에서는 이미지의 크기와 축적에 무관하게 동일한 객체를 식별하기 위한 일반화 작업에 도움 주고, 마지막인 head에서 앵커박스 및 객체 분류 확률 등의 최종 벡터를 출력한다(Fang et al., 2021). 반면 YOLO v5는 YOLO v3에서 사용되었던 K-mean clustering과 genetic learning algorithm의 성능을 향상시켜 이전버젼에 비해 속도가 좋아졌다고 알려져 있다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F4.jpg

Fig. 4

YOLO v4 structure (Bochkovskiy et al., 2020)

3.1 균질지반의 지중관로 탐지

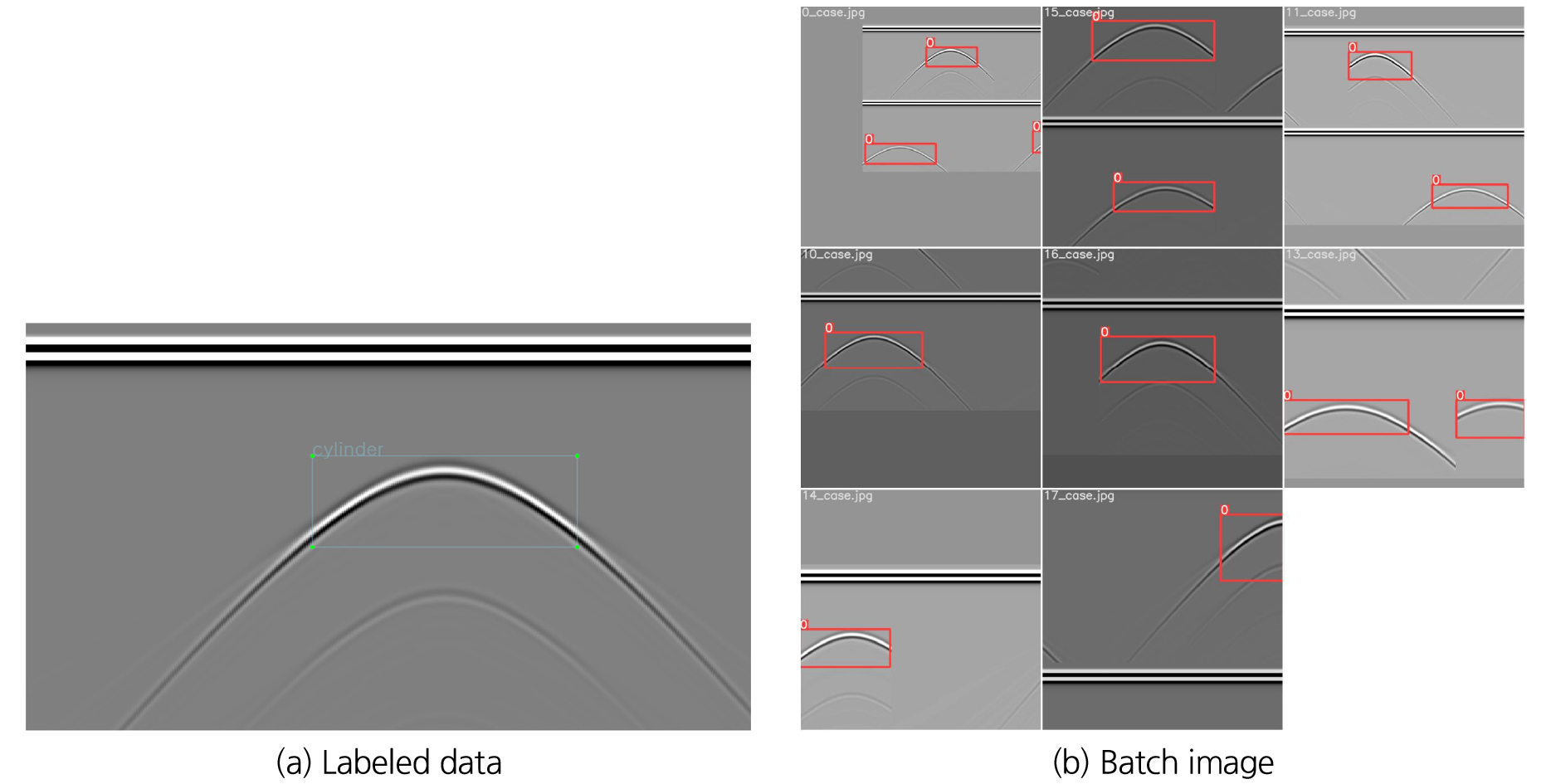
본 절에서는 균질지반의 해석결과만 이용하여 학습을 수행하고 균질지반에서의 탐지 결과와 불균질 지반의 탐지 결과를 비교하여 나타내었다. 학습에 사용된 데이터는 100개의 균질 지반 해석 데이터를 사용하였으며, 90개의 학습데이터와 10개의 검증데이터로 구분하여 학습을 진행하였다. Fig. 5는 학습에 사용된 라벨 데이터의 예시와 배치 이미지의 예시이다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F5.jpg

Fig. 5

Labeled data and batch image of homogeneous model

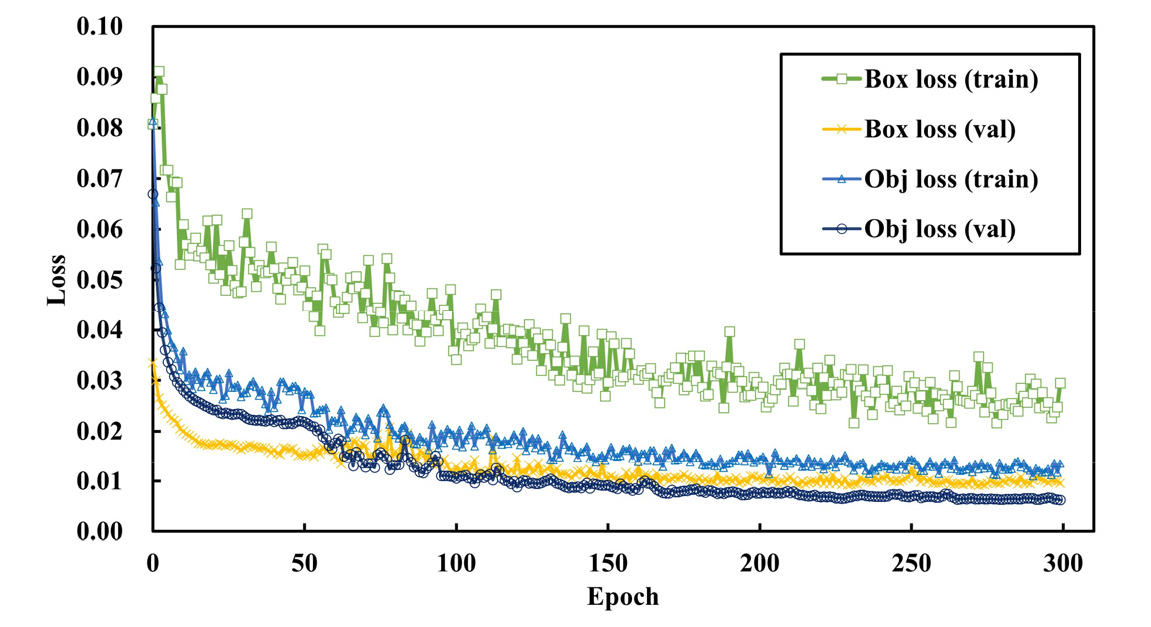
학습은 8의 배치사이즈로 총 300 epoch를 학습하였으며, 각 epoch에 따른 학습 결과는 Fig. 6에 도시하였다. Fig. 6에서 Box loss는 bounding box에 대한 오차를 의미하며, obj loss는 해당 객체의 class에 대한 오차를 의미한다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F6.jpg

Fig. 6

Box and object loss about train and validation result (homogeneous)

균질지반의 데이터로 학습된 모델(Model-A)을 통해 균질지반 및 불균질 지반의 수치해석 결과를 탐지하여 Fig. 7에 도시하였다. 검증에 사용된 이미지는 46개이며 Model-A를 이용하여 균질지반 및 불균질 지반 해석결과를 탐지한 결과, 관로특성이 육안으로 확인 가능한 46개의 균질, 불균질 해석결과 중 40개의 관로 특성을 탐지하였으며, 6개의 이미지에서 탐지를 실패하였다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F7.jpg

Fig. 7

Signal detection result using homogeneous soil training model

탐지된 이미지들을 분석한 결과, 균질지반의 해석결과에서 반사신호를 대부분 탐지하는 것으로 확인하였다. 그러나 불균질 지반의 경우 반사신호로 생기는 쌍곡선형태가 육안으로 확인이 가능하나 학습모델은 이를 탐지하지 못하는 경우가 다수 발생한 것을 확인할 수 있었다. 이는 균질지반에서의 반사신호는 노이즈가 거의 측정되지 않아 이를 이용하여 학습한 모델은 불균질 지반에서 발생하는 노이즈로 인해 탐지 성능이 떨어지는 것으로 사료된다.

3.2 불균질지반을 고려한 지중관로 탐지

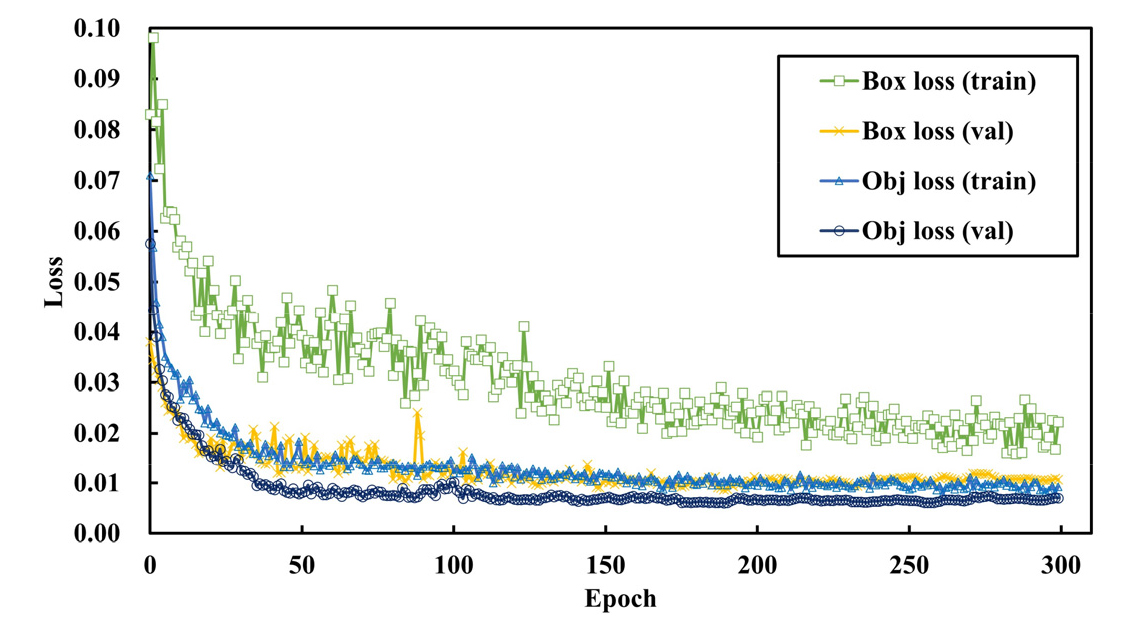
앞서 균질지반에서 학습에 사용한 데이터 일부와 불균질 지반에서의 데이터 일부를 이용하여 학습을 진행하고 그 결과를 확인하였다. 이때 학습데이터의 양이 늘어나면 정확한 비교가 불가능할 것으로 판단하여 앞선 Model-A의 학습과 동일하게 90개의 학습데이터와 10개의 검증데이터를 구성하였으며 균질지반의 데이터 수와 불균질 지반의 데이터 수는 같게 설정하였다. 8배치, 300 epoch로 설정하여 학습을 진행하였으며, 각각의 epoch에 따른 학습결과는 Fig. 8과 같다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F8.jpg

Fig. 8

Box and object loss about train and validation result (homogeneous and heterogeneous)

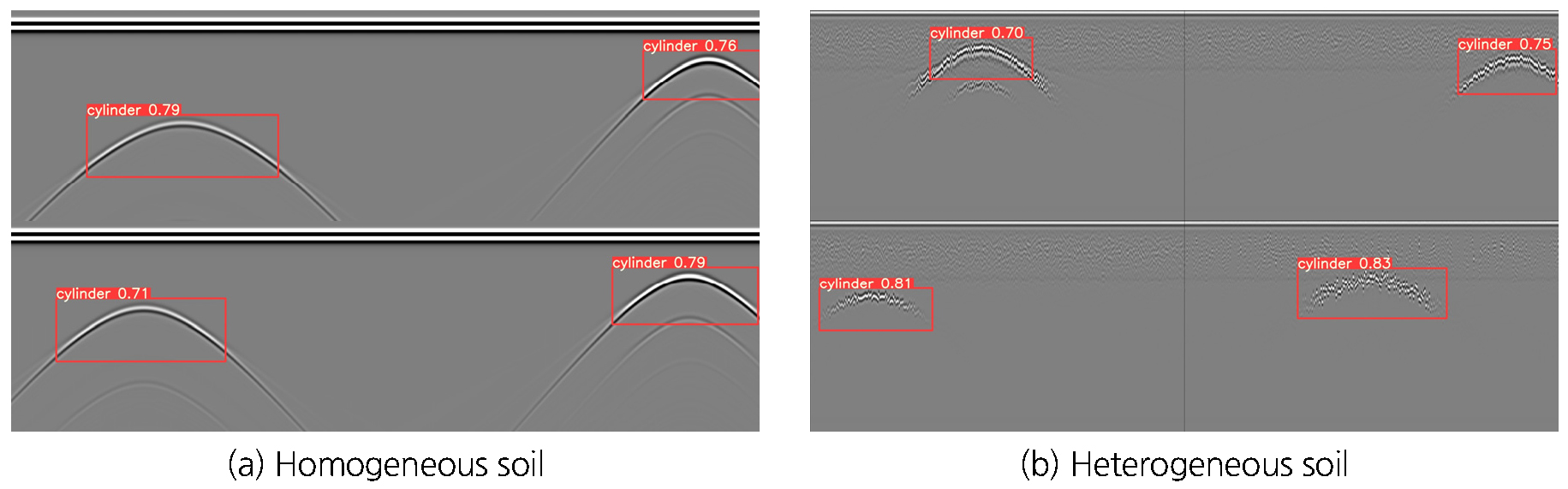
균질지반의 학습모델과의 비교를 위해 탐지를 수행했던 46개의 이미지에 대한 객체탐지를 수행하여 Fig. 9에 도시하였다. 불균질 이미지를 포함하여 학습을 수행한 모델(Model-B)의 경우 46개의 이미지에서 모두 관로 특성을 찾아낸 것으로 확인하였다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F9.jpg

Fig. 9

Signal detection result using training model including heterogeneous soil

불균질 지반의 경우, 지반의 함수비에 따라 유전율이 큰 폭으로 변하게 되며 지반의 유전율 차이가 커지면 매질 내에서의 송신신호의 속도의 차이가 벌어져 수신 데이터의 노이즈는 커지게 된다. 따라서 학습모델의 성능을 확인하기 위해 지반의 함수비의 범위를 0.05~0.25까지 넓혀 해석을 수행하고 그 결과를 학습모델을 통해 검증해 보았다.

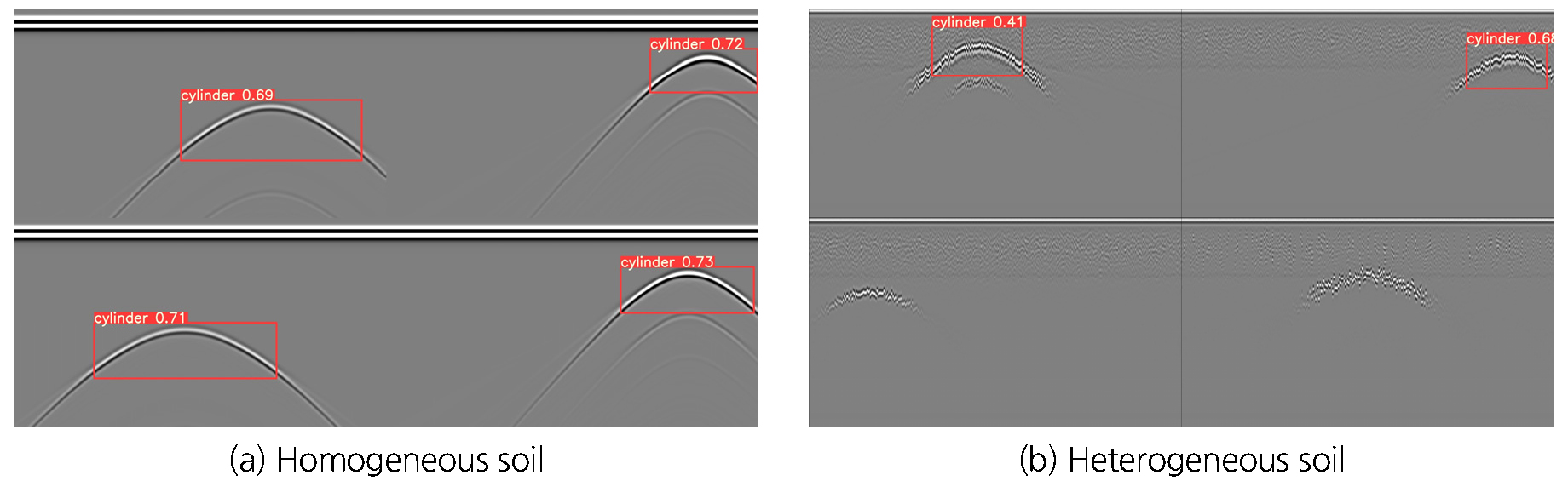
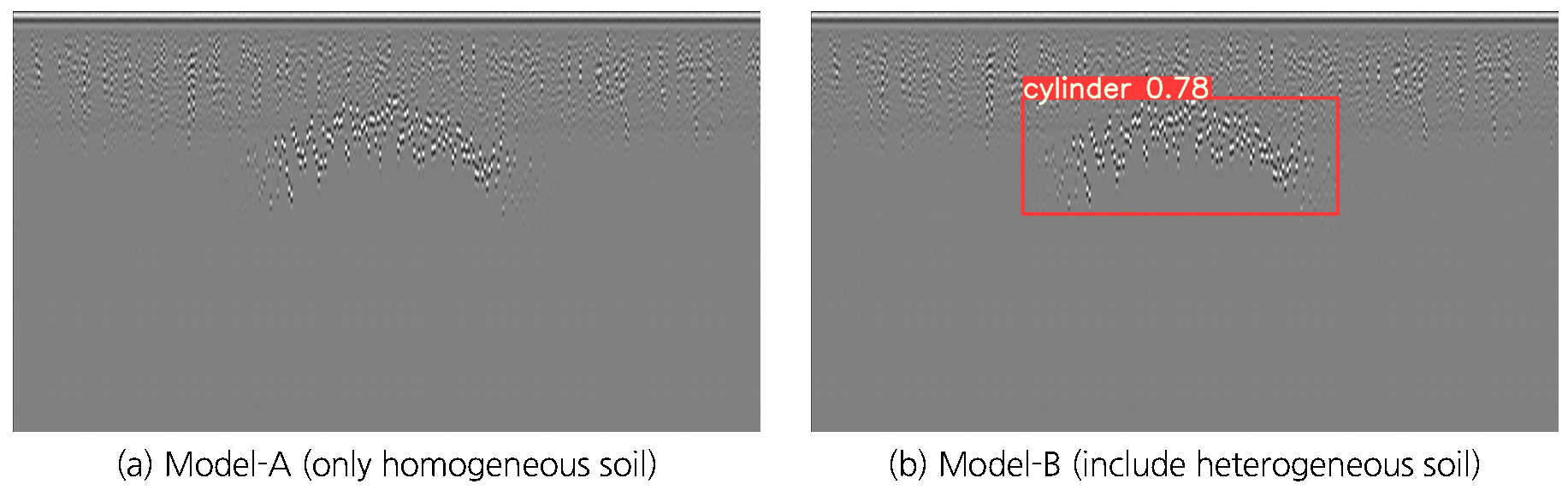
검증을 수행한 결과, Model-A는 관로의 위치를 탐지하지 못한 반면, Model-B는 노이즈가 많은 반사 신호에서도 관로의 반사 특성을 탐지하는 것을 확인할 수 있었다. Fig. 10의 (a)는 Model-A를 통한 탐지 결과이며, (b)는 Model-B를 통한 탐지 결과이다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F10.jpg

Fig. 10

Signal detection results according to the training model in large water content range

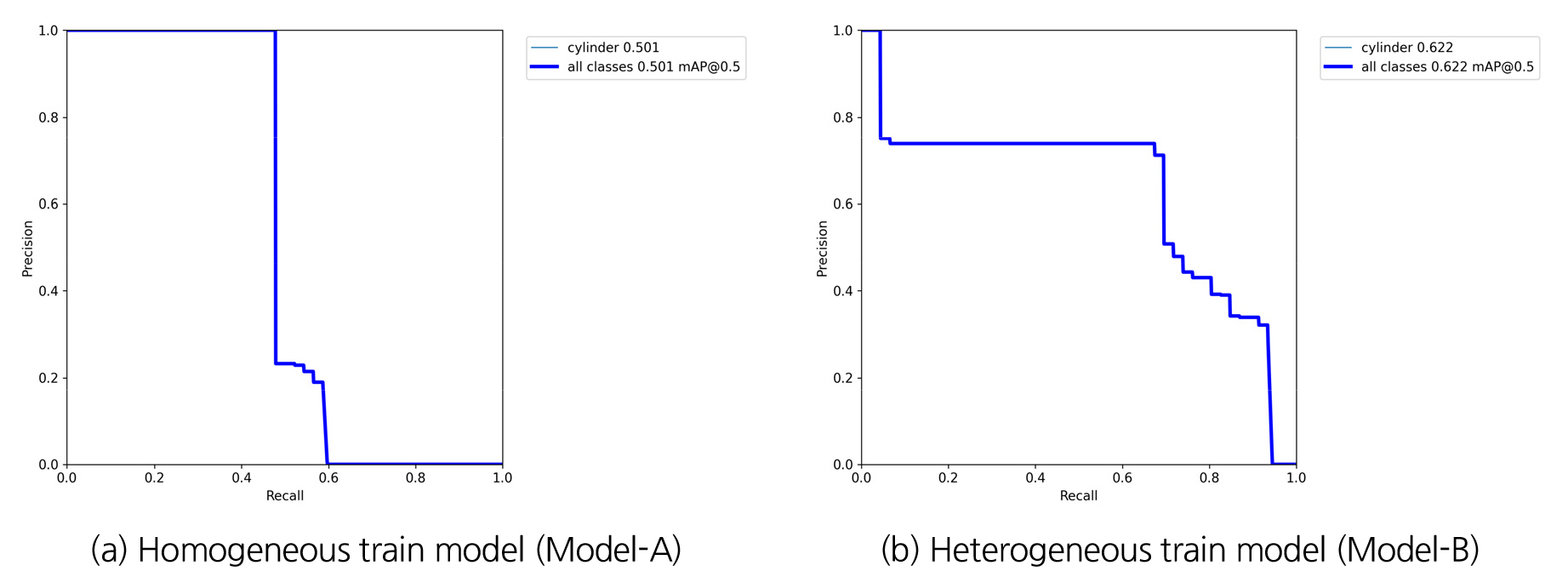
본 연구를 통해 학습된 모델에 대한 mAP를 계산하여 Fig. 11에 도시하였다. mAP는 mean average precision의 약자로 객체 탐지 모델의 정확도를 측정하는 일반적인 기준이며 1에 가까울수록 모델의 정확도가 높다는 것을 의미한다. Model-A에 비해 Model-B의 mAP가 0.622로 더 높은 것으로 조사되었다. 이는 균질 및 불균질 지반의 해석 데이터를 학습한 모델이 균질지반만 학습한 모델보다 더 좋은 정확도를 보이는 것을 의미한다.

https://static.apub.kr/journalsite/sites/kta/2022-024-04/N0550240404/images/kta_24_04_04_F11.jpg

Fig. 11

PR curve and mAP@0.5

4. 결 론

본 연구에서는 GPR 탐사 후 지중 관로의 자동인식기술을 위한 기초연구로써 FDTD 수치해석을 통한 학습데이터의 축적과 그 성능을 검증하는 연구를 수행하였다. 학습에 사용된 데이터 셋은 크게 두 분류로 구분하였으며, 1) 단일 유전율 지반(균질 지반)으로 생성된 모델의 해석결과, 2) 단일 유전율 데이터와 프랙탈 기법을 이용한 불균질 지반 해석결과(균질 지반 + 불균질 지반)를 학습데이터 셋을 구성하였다. 이를 이용하여 균질 지반의 데이터만 이용하여 학습된 모델과 균질 및 불균질 지반으로 학습된 모델의 탐지 성능을 비교하였다. 학습에 사용한 알고리즘은 객체 탐지 알고리즘 중 하나인 YOLO v5를 이용하여 학습을 수행하였다. 본 연구의 결론은 다음과 같다.

균질한 지반의 해석데이터만 이용하여 학습된 모델(Model-A)의 경우, 균질한 지반에서 측정된 단일 관로의 위치는 정확하게 찾아내는 것을 확인할 수 있었다. 반면 불균질한 지반의 해석데이터에 대한 탐지 결과, 단일 관로의 특성에 대한 탐지 성능이 떨어지는 단점을 보였다. 불균질 지반의 경우, 지중 유전율 및 전도도의 차이로 인해 관로의 반사신호에 노이즈가 발생하게 되는데 균질 지반의 데이터만 학습한 모델은 노이즈가 없는 반사신호에 과적합되어 노이즈가 있는 데이터에 대한 탐지 성능이 감소하는 것으로 사료된다.

균질한 지반 및 불균질한 지반의 해석 데이터를 이용하여 학습모델(Model-B)을 학습시키고 테스트 데이터를 통해 학습결과를 확인하였다. 이때, 학습데이터의 양에 따른 편차를 줄이고자 균질 및 불균질 지반의 학습데이터 및 검증 데이터의 수를 동일하게 유지하였다. Model-B의 경우, 균질한 지반의 학습모델은 탐지하지 못했던 데이터에서 정확하게 탐지를 한 것을 확인할 수 있어 기존의 학습모델에 비해 비교적 잘 탐지하는 것을 확인할 수 있었다.

앞선 결론을 통해 균질지반의 해석데이터 만을 이용하여 학습을 수행하는 경우, 노이즈가 있는 불균질한 지반에 대한 탐지 성능이 감소할 수 있을 것으로 사료된다. 그러나 본 연구는 기초 단계 연구로 추후 실제 GPR 탐사 데이터를 확보하여 실제 GPR 데이터에서의 탐지성능을 확인할 필요가 있다. 또한 다중 지중시설물에 의해 반사 신호의 중첩이 일어나는 경우에 대한 학습데이터를 추가로 학습하여 다중 관로의 탐지 성능 또한 검증할 필요가 있을 것으로 판단된다.

Acknowledgements

본 연구는 한국전력공사 자체연구개발과제(R21SA02)와 기초연구과제(R21XO01-47)의 지원을 받았습니다. 이에 감사드립니다.

저자 기여도

이상연은 데이터 분석, 원고작성을 하였고, 송기일은 연구 개념 및 설계, 원고 검토를 하였고, 강경남은 데이터 해석을 하였고, 류희환은 데이터 수집을 하였다.

References

Al-Nuaimy, W., Huang, Y., Nakhkash, M., Fang, M.T.C., Nguyen, V.T., Eriksen, A. (2000), "Automatic detection of buried utilities and solid objects with GPR using neural networks and pattern recognition", Journal of applied Geophysics, Vol. 43, No. 2-4, pp. 157-165. 10.1016/S0926-9851(99)00055-5

Benedetto, A., Pajewski, L. (2015), Civil Engineering Applications of Ground Penetrating Radar, Springer, London, pp. i-xi. 10.1007/978-3-319-04813-0

Bochkovskiy, A., Wang, C.Y., Liao, H.Y.M. (2020), "Yolov4: Optimal speed and accuracy of object detection", arXiv preprint arXiv:2004.10934, pp. 1-17.

Chae, J.H., Ko, H.Y., Lee, B.G., Kim, N.G. (2019), "A study on the pipe position estimation in GPR images using deep learning based convolutional neural network", Journal of Internet Computing and Services, Vol. 20, No. 4, pp. 39-46. 10.7472/jksii.2019.20.4.39

Fang, Y., Guo, X., Chen, K., Zhou, Z., Ye, Q. (2021), "Accurate and automated detection of surface knots on sawn timbers using YOLO-V5 model", BioResources, Vol. 16, No. 3, pp. 5390-5406. 10.15376/biores.16.3.5390-5406

Giannakis, I. (2016), Realistic numerical modelling of ground penetrating radar for landmine detection, Ph.D. Thesis, University of Edinburgh, pp. 1-268.

Giannopoulos, A. (1998), The investigation of transmission-line matrix and finite-difference time-domain methods for the forward problem of ground probing radar, Ph.D. Thesis, University of York, pp. 1-258.

Giannopoulos, A. (2005), "Modelling ground penetrating radar by GprMax", Construction and Building Materials, Vol. 19, No. 10, pp. 755-762. 10.1016/j.conbuildmat.2005.06.007

Kim, H.M., Bae, H.R. (2021), "A study on GPR image classification by semi-supervised learning with CNN", The Journal of Bigdata, Vol. 6, No. 1, pp. 197-206. 10.36498/kbigdt.2021.6.1.197

Lee, D.Y. (2018), "Analysis of sewer pipe defect and ground subsidence risk by using CCTV and GPR monitering results", Journal of the Korean Geosynthetics Society, Vol. 17, No. 3, pp. 47-55. 10.12814/jkgss.2018.17.3.047

Peplinski, N.R., Ulaby, F.T., Dobson, M.C. (1995), "Dielectric properties of soils in the 0.3-1.3-GHz range", IEEE Transactions on Geoscience and Remote Sensing, Vol. 33, No. 3, pp. 803-807. 10.1109/36.387598

Pham, M.T., Lefèvre, S. (2018), "Buried object detection from B-scan ground penetrating radar data using Faster-RCNN", Proceedings of the IGARSS 2018 - 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, pp. 6804-6807. 10.1109/IGARSS.2018.8517683

Redmon, J., Divvala, S., Girshick, R., Farhadi, A. (2016), "You only look once: Unified, real-time object detection", Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 779-788. 10.1109/CVPR.2016.91

Taflove, A., Hagness, S.C., Piket-May, M. (2005), Computational Electrodynamics: The Finite-Difference Time-Domain Method, The Electrical Engineering Handbook, 3, Elsevier, Burlington, pp. 629-670. 10.1016/B978-012170960-0/50046-3

Tian, Y., Yang, G., Wang, Z., Wang, H., Li, E., Liang, Z. (2019), "Apple detection during different growth stages in orchards using the improved YOLO-V3 model", Computers and Electronics in Agriculture, Vol. 157, pp. 417-426. 10.1016/j.compag.2019.01.012

Warren, C., Giannopoulos, A. gprMax user guide, https://docs.gprmax.com/en/latest/ (Apr 14, 2022)

Warren, C., Giannopoulos, A., Giannakis, I. (2016), "gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar", Computer Physics Communications, Vol. 209, pp. 163-170. 10.1016/j.cpc.2016.08.020

Yuan, C., Li, S., Cai, H., Kamat, V.R. (2018), "GPR signature detection and decomposition for mapping buried utilities with complex spatial configuration", Journal of Computing in Civil Engineering, Vol. 32, No. 4, pp. 1-15. 10.1061/(ASCE)CP.1943-5487.0000764

Journal of Korean Tunnelling and Underground Space Association ISSN:2233-8292(Print) 2287-4747(Online) 한국터널지하공간학회 논문집

Preview

Comparison of performance of automatic detection model of GPR signal considering the heterogeneous ground

ABSTRACT

MAIN

Fig. 1

Single FDTD Yee cell (Warren and Giannopoulos, 2022)

(1)

Table 1.

Input parameters about homogeneous soil

Table 2.

Input parameters about heterogeneous soil

Fig. 2

Flowchart for this research

Fig. 3

FDTD analysis model and result

Fig. 4

YOLO v4 structure (Bochkovskiy et al., 2020)

Fig. 5

Labeled data and batch image of homogeneous model

Fig. 6

Box and object loss about train and validation result (homogeneous)

Fig. 7

Signal detection result using homogeneous soil training model

Fig. 8

Box and object loss about train and validation result (homogeneous and heterogeneous)

Fig. 9

Signal detection result using training model including heterogeneous soil

Fig. 10

Signal detection results according to the training model in large water content range

Fig. 11

PR curve and mAP@0.5

Acknowledgements

저자 기여도

References