1. 서 론
2. 콘크리트의 탄소배출량 추정
2.1 내재탄소와 운영탄소
2.2 내재탄소의 계산
2.3 탄소배출량 계산
3. 유한요소 수치해석 모델
3.1 수치해석 개요
3.2 물성치 산정
3.3 지보패턴
3.4 안정성 검토 기준
4. 유한요소 수치해석 결과 분석
4.1 라이닝 해석 개요
4.2 축력 결과
4.3 전단력 결과
4.4 모멘트 결과
5. 결 론
1. 서 론
세계적으로 기후변화가 심각해지면서 한국 정부는 2020년에 2050 탄소중립을 선언하였다. 특히 건설산업은 전 세계 온실가스 배출의 25%, 이산화탄소의 37%를 차지하고 있어(Mckinsey & Company, 2025), 건설산업의 지속가능한 전환을 위해 탄소배출 감소가 필수적이다. 이와 관련하여 콘크리트는 현대 건설에서 가장 널리 사용되는 재료 중 하나로 생산 과정에서 상당한 양의 이산화탄소(CO2)를 배출하고 있어 지구온난화에 많은 영향을 끼치고 있다. 이산화탄소는 주로 시멘트 제조 과정에서 발생하며 1,000 kg의 시멘트 생성 시 약 900 kg의 탄소가 배출된다(Nukah et al., 2024). 전 세계적으로 콘크리트 수요는 인구 증가와 도시 확장, 그리고 인프라 개발로 인해 급증하고 있으며 1990년부터 2020년까지 콘크리트와 모르타르의 생산은 네 배로 증가하였다(Watari et al., 2023). 이에 따라 저탄소 콘크리트의 개발이 활발히 진행되고 있으며 이러한 연구들은 산업 폐기물로부터 제조된 대체 결합재(supplementary cementitious materials, SCMs)를 활용해 구조적 성능을 유지하면서도 탄소 배출을 줄이기 위한 노력을 포함하고 있다.
일반적인 혼화재는 고로슬래그 미분말(ground granulated blast furnace slag, GGBS), 플라이애시(fly ash, FA), 등이 있다. 고로슬래그는 철을 제조하는 과정에서 발생하는 부산물로, 내구성에서의 우수성 덕분에 건물의 수명을 50년에서 100년으로 연장할 수 있다(Suresh and Nagaraju, 2015). 플라이애시는 석탄을 연소하여 에너지를 생산할 때 발생하는 산업 부산물로 처치가 곤란하였으나 현재는 건설산업에서 재사용을 통해 효과적으로 사용되고 있다. 위와 같은 산업 부산물은 포졸란 특성을 통해 콘크리트의 강도, 내구성, 작업성을 향상시킬 뿐 아니라 보통 포틀랜드 시멘트(ordinary Portland cement, OPC) 대비 낮은 탄소 배출량을 보이기 때문에 CO2 배출을 효과적으로 줄이는 것이 가능하다. Huntzinger and Eatmon (2009)에 따르면 표준 콘크리트 혼합물에 고로슬래그와 플라이애시를 혼합하면 CO2 배출량을 크게 줄일 수 있으며 고로슬래그의 경우 22%, 플라이애시의 경우 14%의 배출저감 효과를 보였다.
그러나 혼화재를 사용한 저탄소 콘크리트(low-carbon concrete, LCC)의 경우 초기강도 저하 문제가 발생한다. 사우디 애시를 사용한 연구에서 플라이애시의 비율이 10%에서 50%로 증가할수록 1년동안 콘크리트의 압축강도가 감소했다고 보고하였다(Amran et al., 2020). 이 연구에서는 보통 포틀랜드 시멘트를 플라이애시로 50% 치환 시 초기 압축강도가 크게 감소하는 것으로 나타났다. 반면 고로슬래그 미분말을 50% 치환한 경우 초기 강도는 감소하지만 재령 119일 이후에는 기존 콘크리트와 유사하거나 더 높은 강도를 보였고, 이는 포졸란 반응이 느리게 진행되게 때문이다(Oner and Akyuz, 2007). 즉, 고로슬래그와 플라이애시 모두 포졸란 반응으로 인해 장기강도가 우수한 특성이 있으나, 초기강도의 경우 모두 기존 콘크리트에 비해 감소하는 경향이 있기 때문에 시공 시 주의를 요해야 한다.
터널 및 지하공간의 개발 또한 대량의 콘크리트를 사용하는 자재 집약적 산업이며, 새로운 터널 건설 과정에서 발생하는 CO2의 67%는 시멘트와 그 안의 클링커(clinker)로부터 직접적으로 발생하기에 이에 대한 사용량을 줄이는 것이 중요하다(Sauer, 2016). 강도와 내구성 요구 사항 및 노출 등급은 지침과 입찰 사양에 명확히 규정되어 있지만 현재 프로젝트 설계, 수주 및 구현에서 콘크리트 1 m3당 CO2 배출량이 관련 기준으로 고려되지 않기에(Aldrian et al., 2022), 터널 산업 또한 탄소 중립 목표를 위한 패러다임 전환이 필요하다.
본 연구에서는 저탄소 콘크리트를 콘크리트라이닝에 적용 시, 기존 콘크리트 대비 CO2 배출 저감효과를 이론적으로 계산하고, 동시에 구조적 안정성을 확보하는지 분석하였다. CO2 배출량은 건설상품의 전 생애주기 단계별 탄소배출 현황을 파악 및 비중 분석을 위해 전과정평가(life cycle assessment, LCA) 방법론을 활용하였다. 생애주기 관점의 탄소배출량은 환경성적표지제도를 활용한다. 한국환경산업기술연구원의 국가 전과정목록 데이터베이스(life cycle inventory database, LCI DB)를 활용하여 제품 투입대비 CO2 배출량을 계산해 기존 콘크리트와 저탄소 콘크리트의 CO2 배출량을 비교하였다. 구조적 안정성 계산은 유한요소 수치해석 프로그램인 PLAXIS 3D (Ver. 2024)를 통해 계산하며, 체적손실 및 토압계수 변화 조건에서 재료특성이 구조적 응답에 미치는 영향을 분석하였다. 콘크리트라이닝의 안정성 판단은 허용응력설계법을 통해 계산하고 발생응력과 허용응력의 비교를 통해 안전율을 산정한다. 허용응력은 콘크리트 설계기준을 통해 계산하였으며, 발생응력은 콘크리트라이닝의 부재력인 축력, 전단력, 모멘트를 각각 압축응력, 전단응력, 인장응력으로 변환하여 계산하였다. 이를 통해 저탄소 콘크리트의 적용이 구조적 안정성을 유지하면서 탄소배출 저감 효과를 제공할 수 있음을 이론적으로 제시하였다.
2. 콘크리트의 탄소배출량 추정
2.1 내재탄소와 운영탄소
생애주기평가는 건설제품의 지구 온난화 잠재력(global warming potential, GWP) 및 기타 환경적 영향을 정량화하기 위한 국제적으로 인정된 방법이다(Hammond et al., 2011). 이를 통해 건설 제품의 환경적 영향을 평가할 때, 생애주기 단계별로 배출되는 탄소를 보다 구체적으로 구분할 수 있고 배출된 탄소는 운영탄소(operational carbon)와 내재탄소(embodied carbon)로 나누어 분석이 가능하다. 운영탄소는 주로 건축물의 운영과정에서 배출되는데 난방, 온수, 환기, 조명, 시스템, 장비 및 엘리베이터를 포함한다. 인프라 부문의 운영탄소는 건축물의 운영탄소에 비해 현저히 적지만, 도로, 철도, 댐 등 인프라 시설의 운영과정에서도 부대시설과 설비 운영에 에너지가 소비되고 이로 인해 운영탄소가 배출된다. 한편 내재탄소는 건설상품의 운영과정에서 배출되는 탄소를 제외한 건설자재 생산과정을 포함한 건설단계, 개보수과정, 해체과정에서 배출된 모든 탄소를 포함한다. 특히 건설제품이 준공되기 직전까지 건설자재 생산과정과 시공과정에서 배출된 탄소를 내재탄소라고 일컫는다.
국제에너지기구(IEA)의 2018년 CO2 배출 통계를 기초로 분석한 Mckinsey & Company (2025)의 보고서에 따르면, 인프라 시설의 내재탄소가 전체 탄소배출량의 99%를 차지하는 것으로 분석되었고, Table 1에 통계 보고서의 결과를 나타내었다. 인프라 부문의 운영탄소 비중이 1%만 차지하는 이유는 건축물과 다르게 운영 중 발생하는 냉난방설비, 가전제품 사용 등의 에너지 소비가 훨씬 작기 때문이다. 특히, 인프라 부문의 생애주기 단계별 탄소배출 비중에서 자재생산 단계는 전체 탄소배출의 89.71%를 차지하고 있으며 이는 자재 생산 과정에서의 배출이 훨씬 지배적임을 나타낸다. 따라서, 본 연구에서는 탄소배출량을 효과적으로 줄이기 위해 내재탄소를 줄이는 데 중점을 두어 콘크리트라이닝 건설 과정에서 기존 콘크리트와 저탄소 콘크리트의 내재탄소 감소율을 추정하였다.
Table 1.
Analysis of carbon emissions by lifecycle stages in infrastructure (Mckinsey & Company, 2025)
2.2 내재탄소의 계산
내재탄소 계산은 제품 기능단위당 생산에 필요한 원료의 채취, 생산, 수송 ‧ 유통, 폐기까지의 제품 시스템으로 투입되는 양 대비 산출되는 양을 탄소배출계수로 나타내어 목록화한 데이터인 LCI DB를 이용하여 배출량을 산출할 수 있고, 탄소배출계수는 Table 2에 나타내었다. LCI DB는 제품에 대한 전과정평가를 수행하는 기초데이터로 활용되고 있으며, 콘크리트 배합비에 LCI DB를 적용한다면 콘크리트의 내재탄소를 구할 수 있다. 콘크리트 배합비에 사용된 각 재료의 단위중량(𝛾)과 재료의 LCI DB에서의 탄소배출계수를 곱하여 다 더하면, 이는 콘크리트 1 kg 생산 시 발생하는 CO2의 질량으로 환산되며 식 (1)로 나타낼 수 있다. 탄소배출계수의 경우 GWP 단위를 사용하며, 보통 100년의 기간 동안 CO2 한 분자의 영향을 기준으로 측정한다(Hammond et al., 2011). 예를 들어 1 kg의 CO2는 1 kgCO2eq의 GWP를 가지며, 메탄 1 kg은 약 28 kgCO2eq의 GWP를 가진다.
Table 2.
Carbon emission factor of LCI DB (KEITI, 2025)
| Material | OPC | GGBS | FA | Sand | Aggregate |
|
Carbon emissions (kgCO2eq) | 0.926 | 0.01 | 1.22 | 0.08 | 0.01 |
콘크리트 배합비는 저탄소 콘크리트 국가기준 개정 연구를 참고하여 사용하였고, Table 3에 나타내었다. 콘크리트 배합의 경우 양생은 20°C에서 진행하였으며 콘크리트의 단위중량은 2,205 kg/m3, 결합재량(binder, B) 374 kg/m3, 단위수량(water content, W) 165 kg/m3를 적용하였다. 결합재의 혼합비율은 고로슬래그 미분말과 플라이애시를 합산한 치환율을 50~90%까지 치환하였고, 그 외 결합재는 보통 포틀랜드 시멘트를 사용하였다. 저탄소 콘크리트의 경우 플라이애시의 치환율을 20%로 고정하였으며 고로슬래그 미분말의 치환율을 30%, 50%, 70%로 각각 다르게 적용하여 이를 순서대로 R50, R70, R90으로 명명하였다. 기존 콘크리트의 경우 보통 포틀랜드 시멘트를 100% 결합재로 사용하였으며, PC (plain concrete)로 명명하였다. 기존 콘크리트는 대조군, 저탄소 콘크리트는 실험군으로 설정하였다. 잔골재와 굵은골재는 각각 841 kg/m3, 825 kg/m3를 적용하였다. 추가로 콘크리트 내에 미세한 공기를 균일하게 분포시키기 위한 AE제(air entraining agent)를 0.1%, 콘크리트의 유동성을 향상시키고, W/B를 줄이면서도 동일한 작업성을 유지하기 위한 고성능 감수제(superplasticizer, SP)를 0.6% 사용하였다.
Table 3.
Concrete mix ratio (KICT, 2015)
| Raw material | W/B | OPC | FA | GGBS | S | A | AE | SP |
| (%) | Unit weight (kg/m3) | (%) | ||||||
| PC | 44.1 | 374 | 0 | 0 | 841 | 825 | 0.001 | 0.6 |
| R50 | 187 | 75 | 112 | |||||
| R70 | 112 | 75 | 187 | |||||
| R90 | 37 | 75 | 262 | |||||
2.3 탄소배출량 계산
탄소배출량 계산은 Yang et al. (2017)과 동일한 계산 방식으로 수행하였다. 탄소배출량계산 결과, 기존 콘크리트의 경우 1 m3의 자재에서 약 460.8 kg만큼의 CO2가 발생하고, 보통 포틀랜드 시멘트를 50% 치환한 R50 콘크리트 사용 시 297.5 kg의 CO2가 발생하여 기존 콘크리트 대비 약 35%의 이산화탄소 배출 감소 효과가 있을 것으로 추정하였다. 이는 플라이애시와 고로슬래그 미분말이 상대적으로 낮은 탄소배출계수를 갖기 때문에 시멘트 치환 시 배합 내 탄소 집약도가 낮아지기 때문이다. 보통 포틀랜드 시멘트를 70% 치환한 R70 콘크리트는 231.5 kg의 CO2가 발생하여 기존 콘크리트 대비 49.76%의 이산화탄소 배출 감소 효과가 있을 것으로 추정하였다. 보통 포틀랜드 시멘트를 90% 치환한 R90 콘크리트의 경우 167.3 kg의 CO2가 발생하여 기존 콘크리트 대비 65%의 이산화탄소 배출 감소 효과가 있을 것으로 추정하였고, 각 콘크리트에 대한 탄소배출량을 Table 4에 정리하였다.
3. 유한요소 수치해석 모델
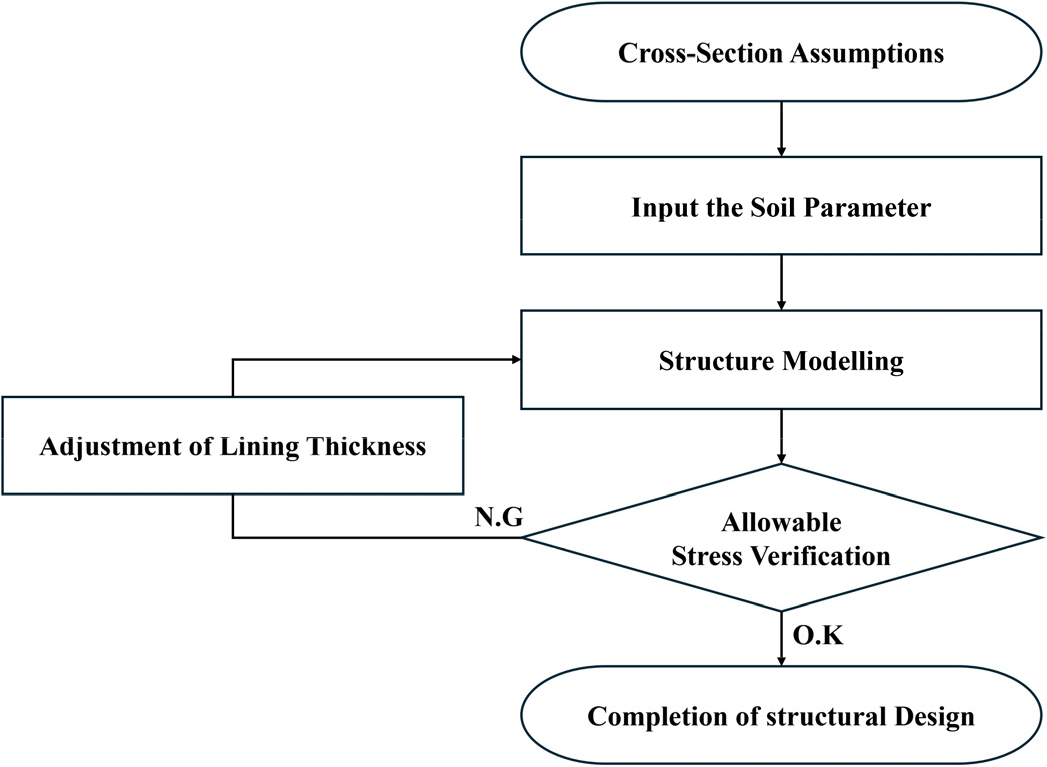
본 절에서는 콘크리트라이닝에 기존 콘크리트와 저탄소 콘크리트를 각각 적용하여 구조적 안정성을 비교하고자 했다. 수치해석은 3차원 유한요소법 기반의 수치해석 프로그램인 PLAXIS 3D (Ver. 2024)를 이용하였다. PLAXIS 3D는 복잡한 지반-구조물 상호작용 해석을 수행하는 데 특화된 유한요소해석(finite element analysis, FEA) 소프트웨어로서, 토목 및 지반 공학 분야에서 광범위하게 사용되고 있다. 본 프로그램은 3차원 해석을 통해 지반의 거동 및 터널, 흙막이 벽체, 기초 구조물의 안정성을 정밀하게 평가할 수 있는 기능을 제공한다. 해당 프로그램을 통해 암반과 같은 복합 지반의 비등방성 및 소성 거동을 정밀하게 모사하고, 지층의 단계적 굴착과 같은 단계적 해석 기능을 사용하여 지반의 시간 의존적 변형 및 응력 변화 과정을 현실적으로 해석하고자 하였다. 수치해석에 대한 흐름도는 Fig. 1과 같다.
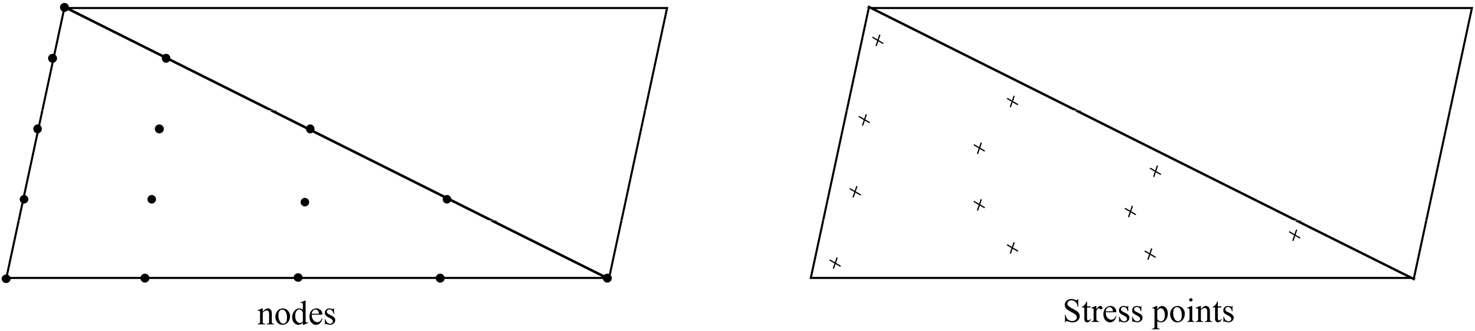
정확한 수준의 응력 결과를 확인하기 위해 요소는 15-절점 삼각형 요소를 사용하여 지층과 다른 체적 영역을 모델링하였다. 15-절점 삼각형 요소는 총 15개의 절점으로 구성되며, 각 요소는 인접한 요소와 절점을 통해 연결된다. 15-절점 요소는 고차 요소로서 6-절점 요소보다 더 정밀한 변위 및 응력이 가능하다. 또한, 각 요소 내 변위는 절점에서 계산되며, 응력 및 변형률은 개별 가우스 적분점에서 산정된다. 15-절점 삼각형 요소는 12개의 응력점을 가지며, 이는 6-절점 요소의 3개 응력점보다 더 세밀한 응력 해석을 가능하게 한다. 15-절점 삼각형 요소는 Fig. 2에 나타내었다.
3.1 수치해석 개요
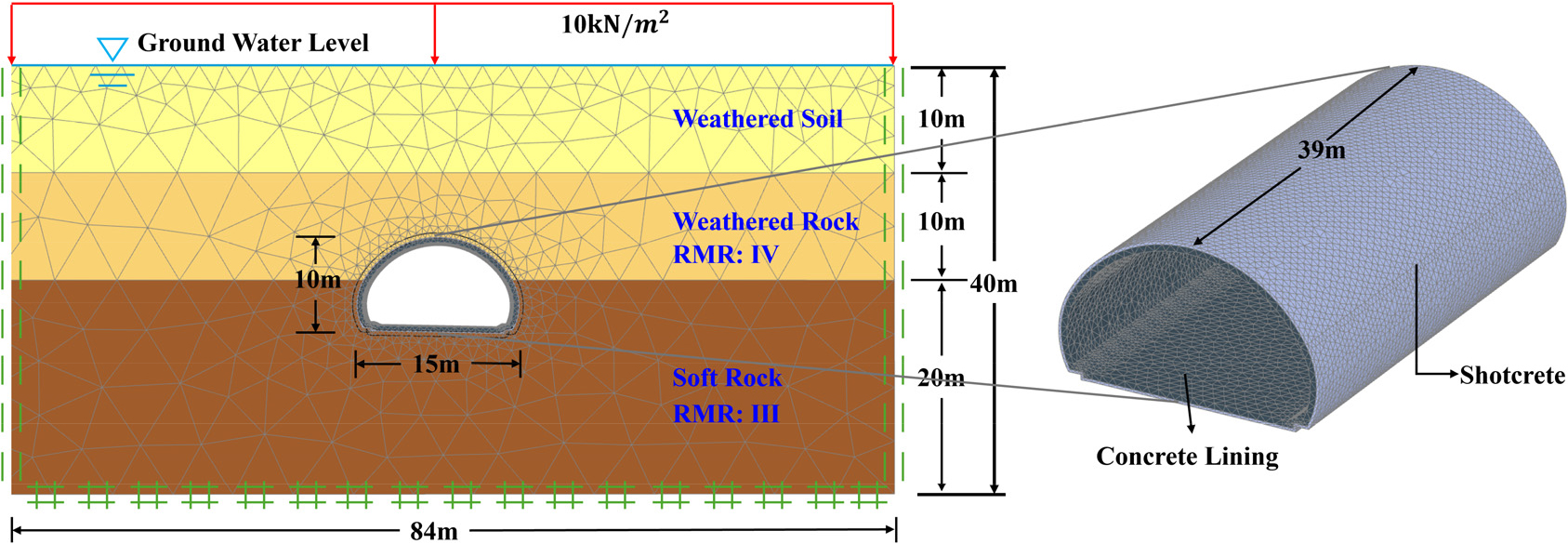
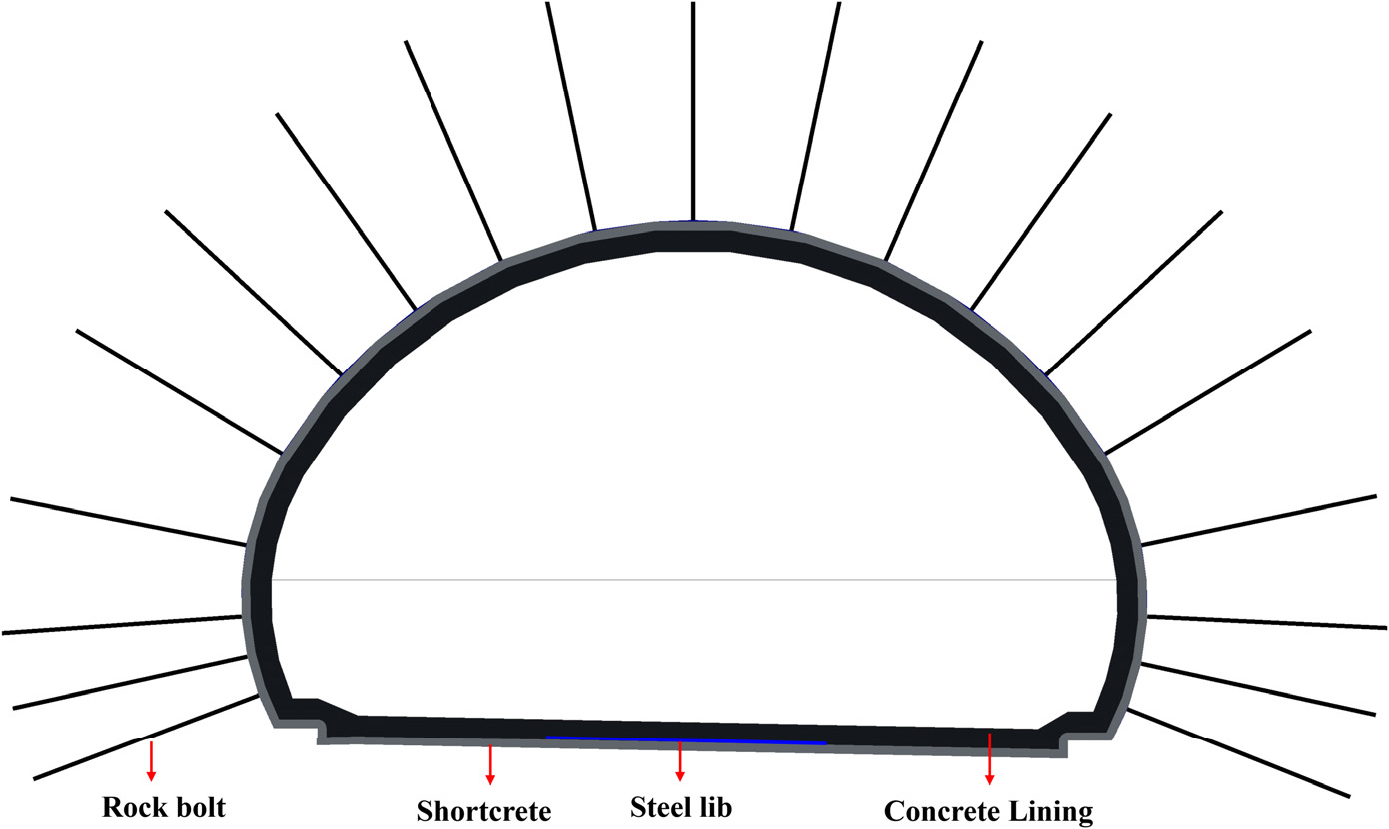
본 연구에서는 굴착 과정 및 숏크리트, 록볼트, 강지보재과 같은 주 지보재 이후, 보조 지보재로서 콘크리트라이닝을 시공하였다. 수치해석을 위한 mesh, 지층 구조, 경계조건은 Fig. 3에 제시하였다. 지표면의 등분포하중은 국도건설공사 설계실무 요령(MOLIT, 2021)에 따라 활하중 10 kN/m2으로 설정하였다. 콘크리트라이닝이 지보재 역할을 담당하는 경우는 대체로 지반조건이 불량한 경우이다. 이에 따라 지반은 풍화토, 풍화암, 연암의 3개 층으로 구성되었으며 터널 단면은 풍화암층과 연암층을 동시에 통과하도록 설계하였다. 해석모델 경계조건은 터널굴착 영향권을 반영하기 위해 터널측방 1.5 D 이상, 터널 하부 1.0 D 이상을 경계로 모델링하였고 Fig. 3에 나타내었다. 경계 터널의 폭과 높이는 외부 경계면을 기준으로 숏크리트 두께와 콘크리트라이닝 두께를 포함하여 각각 15 m와 10 m로 설정하였다.
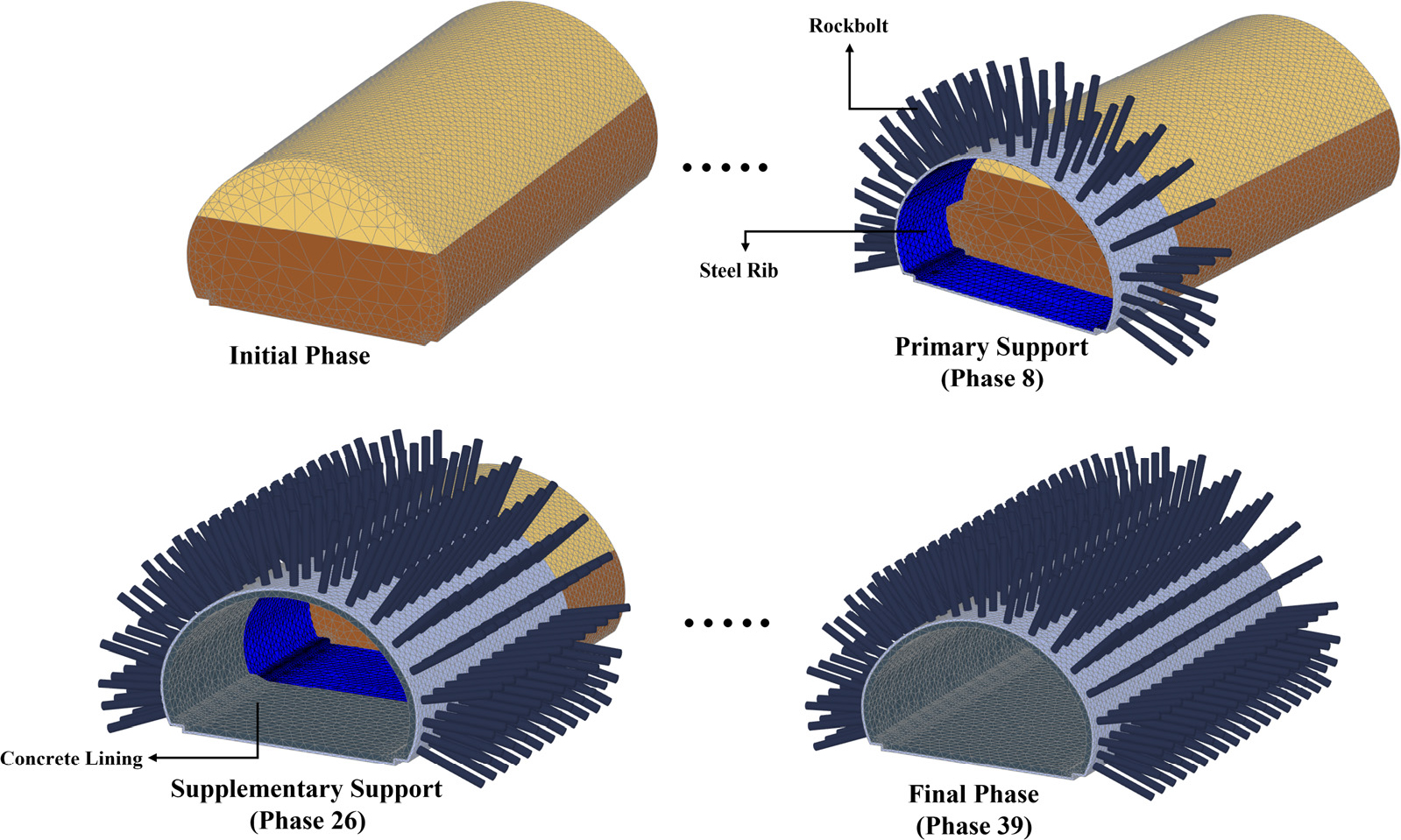
수치해석은 초기단계, 굴착 및 주 지보단계, 보조 지보단계(라이닝)으로 나누어 수행하였고, Fig. 4에 나타내었다. 굴착단계에서는 굴착과 동시에 숏크리트, 록볼트, 강지보재 순으로 지보단계를 수행하였다. 강지보재는 지반이 풍화암이고 상재하중에 의한 변형 억제를 위해 적용되었다. 콘크리트라이닝 시공은 공기 단축 상황을 가정하여 굴착 과정과 동시에 진행되었으며, 발파진동으로 인한 안정성을 고려하여 굴착과 라이닝 시공 간 이격거리를 Jeon and Jang (2009)의 연구에 따라 10 m로 설정하였다. 콘크리트 라이닝 구조검토를 위한 지반이완하중은 보수적 설계를 위해 전토피하중으로 선정 및 적용하였다. 시공순서 및 과정에 대한 그림은 Fig. 3에 나타내었다. 특히, 라이닝 단계에서는 저탄소 콘크리트의 초기 압축강도 저하를 모사하기 위해 해석에서 특정 시간 간격으로 데이터를 계산하고 저장하는 기준을 제공하는 time interval 기반의 동해석을 수행하였다. 초기 강도발현이 중요한 3일은 0~12시간, 12~24시간, 1일~3일 간격으로 짧게 설정하였으며 이후 강도 발현 속도가 비교적 완만해지는 시간은 3~7일, 7~28일로 나누어 간격을 길게 설정하였다.
토압계수(K)는 도심지 지하철 공사 기준을 바탕으로 0.5, 1, 1.5로 구분하였으며, 체적손실(volume loss, VL)은 보수적 설계를 위해 2%, 2.5%, 3%로 구분하여 Atkinson and Mair (1981)의 제안인 1~2%보다 크게 설정하였다. 체적손실은 PLAXIS 내에 surface contraction 기능을 통해 모사하였으며, 이는 터널 굴착 후 발생하는 지반 이완에 따른 터널 단면의 수축률을 나타낸다. 굴착 이후 지반의 이완이 발생터널 단면을 기준으로 각 Case는 토압계수별로 A, B, C로 분류하고, 체적손실 값에 따라 Ⅰ~Ⅲ 로 나누어 Table 5에 나타내었다.
Table 5.
Case for numerical analysis
| Case | Coefficient of earth pressure (K) | Volume loss (VL, %) | |
| A | Ⅰ | 0.5 | 2 |
| Ⅱ | 2.5 | ||
| Ⅲ | 3 | ||
| B | Ⅰ | 1 | 2 |
| Ⅱ | 2.5 | ||
| Ⅲ | 3 | ||
| C | Ⅰ | 1.5 | 2 |
| Ⅱ | 2.5 | ||
| Ⅲ | 3 | ||
3.2 물성치 산정
지반의 물성치는 국내의 터널 현장 및 실내시험 자료를 기반으로 암반 특성을 분석한 논문(Seo et al., 2016)을 참고하여 설정하였다. 암종은 국내에 널리 분포된 화강암으로 설정하고, 물성치는 각 암종별 평균값을 적용하였다. 경계면 조건을 나타내는 인터페이스 요소는 구조물의 강성과 지반의 강성차에서 발생하는 상대변위(slip, relative displacement)를 나타내기 위한 요소로, 강도감소계수(Rinter)를 사용하였다. 암반의 경우 구조물과의 강성 차가 크지 않아 강도감소계수를 1로 설정하였다.
지반의 구성모델은 일반적으로 널리 사용되는 Mohr-Coulomb 모델을 적용하였다. 이 모델은 선형 탄성-완전소성 모델로, 토층의 평균 강성을 가정하여 지반 거동을 모사하며, 해석 과정의 효율성을 높이는 장점이 있다. 단, 깊이에 따른 강성 증가와 같은 비선형 특성은 고려하지 않았다. 지층별 상세 물성치는 Table 6에 요약되어 있다.
Table 6.
Material properties of ground
콘크리트라이닝에 사용될 콘크리트의 경우, 재료의 강성을 나타내는 탄성계수를 입력해야 한다. 본 연구에서는 이를 추론하기 위해 콘크리트 구조기준(KCI, 2012), 미국 콘크리트 학회 기준(ACI Committee 318, 1995), Eurocode 2 (CEN, 2010)에서 제안된 경험식을 검토하였다. 세 경험식은 모두 단위중량과 압축강도를 통해 탄성계수를 추정하며, 본 연구에서는 저탄소 콘크리트 국가기준 개정 연구에서 도출된 압축강도를 사용하여 계산하였다. 보수적 설계를 위해 탄성계수를 가장 작게 예측하는 ACI 318을 최종적으로 선정하여 설계 및 해석에 반영하였다.
사용된 경험식은 식 (2)에 나타내었으며, 각 재료의 압축강도와 탄성계수는 Table 7에 정리되어 있다. R50은 플라이애시와 고로슬래그 미분말의 포졸란 반응에 의해 장기 강도가 더 크게 발현되어, 28일 압축강도가 기존 콘크리트보다 크게 측정되었다. 고치환율 콘크리트(R70, R90)의 28일 압축강도는 모두 21 MPa를 초과하며, 이는 KR C-12040 콘크리트라이닝 기준(21~24 MPa)을 만족한다. 이러한 결과는 저탄소 콘크리트가 구조적 성능을 유지하면서도 설계 기준을 충족할 수 있음을 보여준다.
여기서, 는 콘크리트 탄성계수, 는 콘크리트 단위중량, 는 콘크리트 압축강도이다.
Table 7.
Compressive strength and young’s modulus of concrete (KICT, 2015)
3.3 지보패턴
본 연구에서는 국토교통부 제정 터널공사 표준시방서(KTA, 2018) 및 적용 지반조건에 근거하여 작성된 지보 패턴 및 굴착패턴(PD-3B)을 적용하였고 정면도를 Fig. 5에 나타내었다. 숏크리트의 경우 단면 크기와 지반 조건, 터널 단면을 고려하여 두께를 150 mm로 설정하였으며 설계강도는 21 MPa를 적용하였다. 숏크리트는 선형 탄성을 가정한 linear elastic 모델을 적용하여 해석하였다. 록볼트의 경우 D25, SD400 이형강봉을 적용하였으며 시스템 록볼트를 하였다. 록볼트의 길이는 4 m, 간격은 1.5 m로 설정하였다. 록볼트 모델링에는 embedded beam 요소를 사용하였으며 경계 변위를 모사하기 위해 인터페이스 요소 대신 주면 마찰력을 입력하였다. 강지보재는 일반적으로 사용하는 H형강을 사용하였으며 본 논문에서는 H-125×125×6.5×9 (mm) 규격의 강지보재 SS275를 적용하였다. 강지보재는 plate 요소를 통해 셀(shell)의 영향을 모사하였다. 1차 지보에 대한 물성치는 Table 8에 나타내었다.
Table 8.
Properties of primary support members (KTA, 2018)
2차 지보재로 사용된 콘크리트라이닝은 현장 타설 무근 콘크리트를 기준으로 설정하였으며, 설계기준(24~27 MPa) 이상의 강도를 적용하였다. 라이닝 두께는 한국도로공사 도로설계요령 제4권(KEC, 2021)에서의 제안값인 30~40 cm의 중간값인 35 cm로 설정하였다, 라이닝 모델은 linear elastic 모델을 적용하였다.
3.4 안정성 검토 기준
터널 콘크리트라이닝 설계에서는 지반 조건, 작용 하중, 구조적 안정성, 장기 내구성을 종합적으로 고려하여 설계 기준을 설정하는 것이 필수적이다. 앞서 콘크리트라이닝에 linear elastic 구성 모델을 적용했기 때문에 콘크리트를 탄성체로 보는 허용응력설계법을 채택하였다. 국가철도공단에서 채택한 허용응력설계법(KR, 2012)은 구조물에 작용하는 최대 응력이 허용 가능한 한계를 초과하지 않도록 하는 방식으로, 터널 콘크리트라이닝 설계에서 있어 신뢰할 수 있는 설계 방법으로 널리 사용된다. 라이닝의 안정성을 평가할 때 검토되는 단면력은 축력, 전단력, 휨 모멘트이며 이를 허용응력과 비교하여 안전율(factor of safety, F.S)을 계산하고 안정성을 평가한다. 축력과 전단력은 단면적으로 나누어 각각 압축응력과 전단응력으로 변환 후 허용응력과 비교하였다. 휨 모멘트는 단면 2차 모멘트와 중립축 거리를 이용해 인장응력으로 변환한 뒤 허용응력과 비교하였다. 이러한 부재력별 허용응력 산정식은 Table 9에 정리하였다.
Table 9.
Allowable stress design criteria (KR, 2012)
| Category | Allowable compressive stress | Allowable shear stress | Allowable tensile stress |
| Stress formula |
4. 유한요소 수치해석 결과 분석
4.1 라이닝 해석 개요
본 연구에서는 NATM 터널의 콘크리트라이닝 시공 시 발생하는 구조적 안정성을 판단하기 위해 기존 콘크리트를 대조군, 저탄소 콘크리트를 실험군으로 설정하여 단면의 부재력과 응력을 비교하였다. 수치해석은 Table 5에 제시된 Case를 기준으로 진행하였으며 콘크리트라이닝에 적용된 재료 특성, 토압계수, 체적손실 변화에 따른 부재력과 안전율을 분석하였다.
Fig. 6(a)는 콘크리트라이닝 축력 분포를 나타내며, 아치형 구조로 인해 천단부에서 발생한 압축력이 측면부로 전달되었고, 저면부에서는 하중 전달 감소로 인해 인장력이 나타났다. 이때, 축력의 양의 값은 콘크리트라이닝이 압축을 받는 상태를 의미하며, 음의 값은 라이닝이 인장력을 받는 상태를 나타낸다. Fig. 6(b)는 전단력 분포를 보여주며 천단부에서는 응력이 분산되어 축력이 우세하고, 저면부는 반발력으로 인해 전단력이 집중되는 양상을 보였다. Fig. 6(c)의 휨 모멘트 분포도에서 천단부는 상부 하중 집중과 곡률의 영향으로 양의 값을, 측면부는 지반 횡압력의 영향으로 음의 값을 나타냈다. 저면부 중앙은 반발력 증가로 인해 양의 값을, 양측 끝은 반발력 감소로 인해 음의 분포를 보인다. 이러한 결과는 터널 콘크리트라이닝 구조의 각 부재력이 지반과 하중의 상호작용에 따라 복합적으로 발생함을 보여주며 안정적인 설계를 위해 각 부재력의 분포를 면밀히 고려해야 한다.
4.2 축력 결과
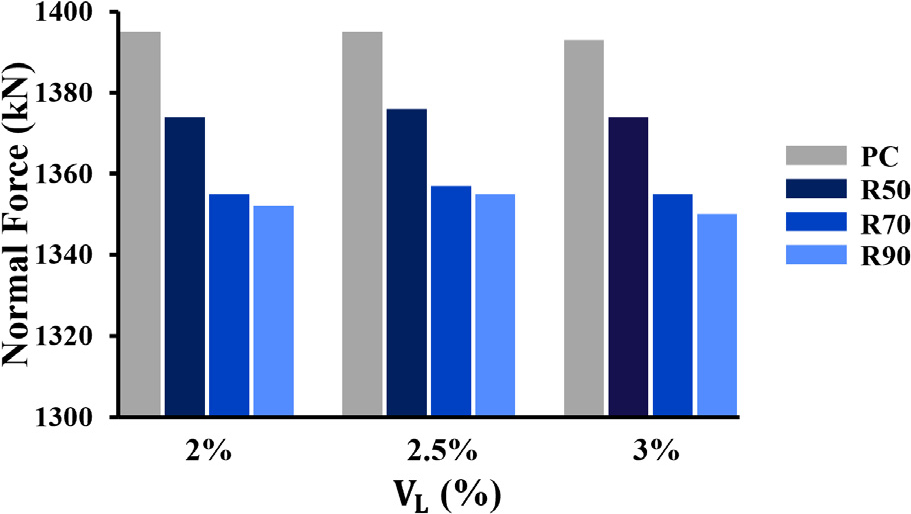
축력은 1,329~1,398 kN의 값을 보였으며, Table 10에 결과값을 나타내었다. PC (기존 콘크리트)에서 가장 높게 나타나고, R90에서 가장 낮았다. R50의 경우 28일 기준 압축강도가 기존 콘크리트보다 크지만 축력이 적게 나타난 이유는 초기강도의 저하로 초기 시공과정에서 하중분담 능력이 감소했기 때문이다. 재료에 따른 축력의 최대 변동폭은 Case B-Ⅰ에서의 PC와 R90의 차이인 67 kN (변동률 4.5%)이며 축력 변동에 가장 큰 영향을 끼쳤다.
Table 10.
Result of axial force (kN)
체적손실이 증가할수록 축력은 거의 일정하거나 소폭 증가하였다. 일반적으로 체적손실이 증가하면 라이닝 축력이 증가하지만, 소성 변형의 발생으로 인해 일부 응력이 지반 내부에 흡수되어 라이닝으로 전달되는 하중이 상대적으로 작아졌다. 체적손실에 따른 축력의 최대 변동폭은 25 kN (변동률 1.8%)으로 나타났다. 토압계수는 증가할수록 축력이 감소하는 경향을 보였는데, 지반의 수평응력이 증가함에 따라 축력 분포가 완화되었기 때문이다. 토압계수에 따른 축력의 최대 변동폭은 13 kN (변동률 0.9%)으로 나타났다. 토압계수에 따른 변동폭이 1% 미만으로 Case 간 차이가 적어, Case A만을 Fig. 7에 나타내었다.
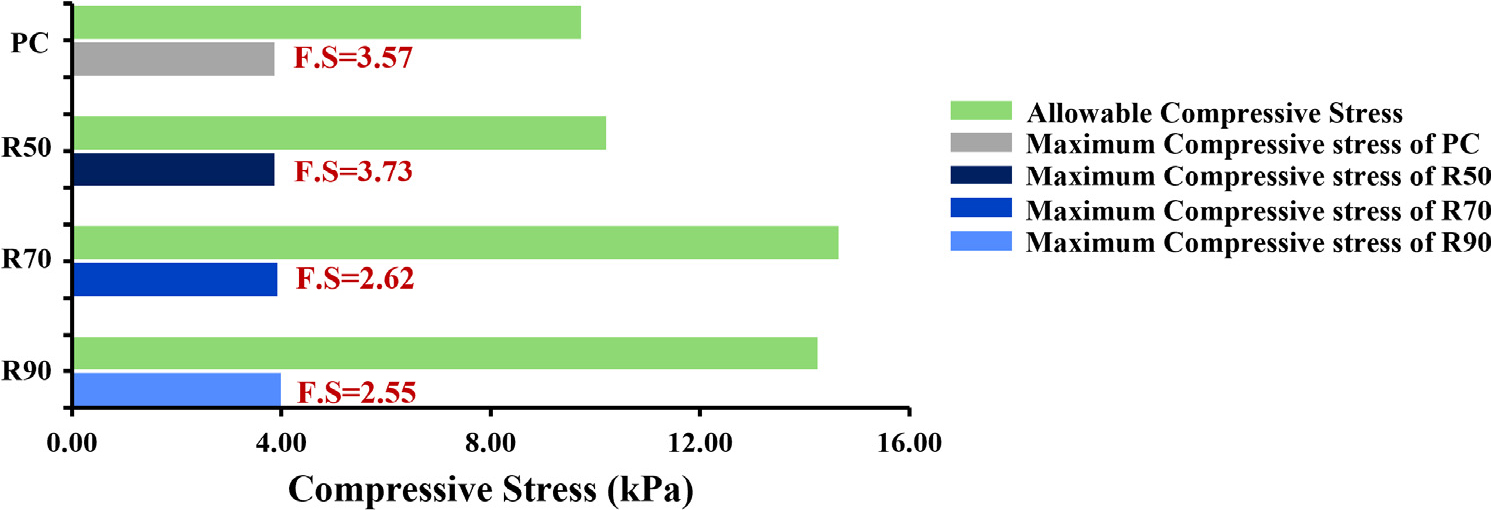
축력을 단면적으로 나누어 계산한 최대압축응력은 3.84~3.98 MPa로 나타났다. 허용압축응력은 체적손실 및 토압계수와는 무관하게 재료의 압축강도에 비례하였으며 재료에 따라 9.72~14.64 MPa로 나타났다. 안전율은 허용압축응력을 최대압축응력으로 나누어 계산하였으며 기존 콘크리트는 3.58, 저탄소 콘크리트(R50, R70, R90)는 각각 3.73, 2.64, 2.53으로 모두 안전율 1을 넘어 안정성을 확보하였다. 체적손실, 토압계수 변동은 안전율에 영향을 끼치지 않아 재료에 따른 최대압축응력, 허용압축응력, 안전율만을 Fig. 8에 나타내었다.
저탄소 콘크리트의 치환율이 증가할수록 안전율이 감소하는 경향이 확인되었다. 안전율이 가장 높은 R50은 치환율이 적정 수준으로 설정되어 초기 하중분담 능력이 유지된 결과로 해석된다. 반면, R70과 R90은 초기 및 장기 강도 저하로 인해 안전율이 상대적으로 낮게 나타났다. 그러나, 포졸란 반응이 우수한 R70과 R90은 시간이 지남에 따라 강도 회복과 내구성 향상이 기대되어 장기적 안정성이 우수할 가능성이 있다.
4.3 전단력 결과
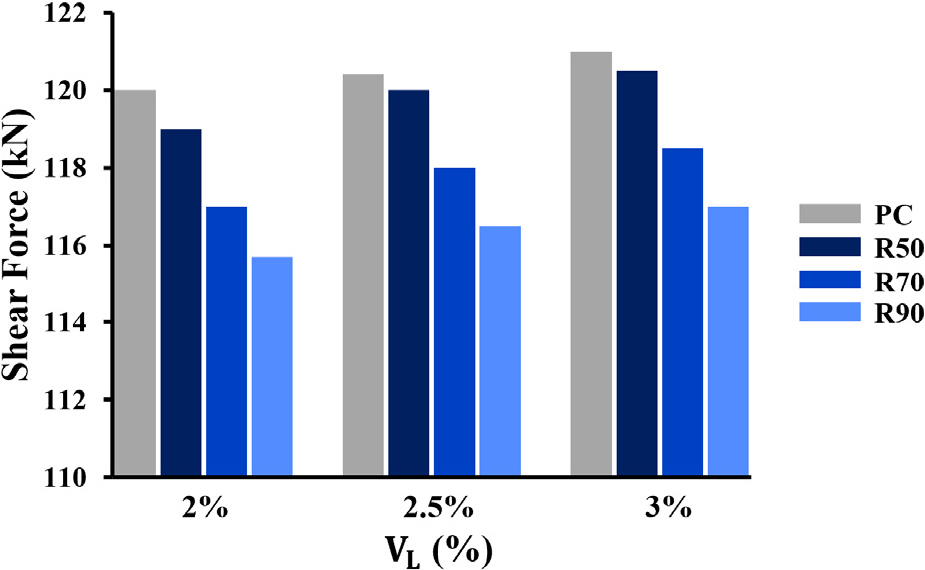
전단력은 115~120.4 kN의 값을 보였으며 전단력 결과값을 Table 11에 나타내었다. PC는 가장 높은 전단력을 보였고 R90은 가장 낮은 전단력을 보였다. R50은 28일 기준 압축강도가 기존 콘크리트보다 크지만, 초기강도 저하로 시공 초기 하중 분담 능력이 감소하여 전단력이 적게 나타났다. 재료에 따른 전단력의 최대 변동폭은 Case A-Ⅲ에서의 PC와 R90의 차이인 4.6 kN (변동률 4.1%)으로 가장 큰 변동폭을 보였다.
Table 11.
Result of shear force (kN)
체적손실이 증가할수록 전단력이 소폭 증가하는 경향을 보였다. 이는 굴착 과정에서 지반응력이 재분배되며 라이닝에 추가적인 하중이 작용한 결과로 판단된다. 체적손실에 따른 전단력의 최대 변동폭은 1 kN (변동률 0.85%)으로 나타났다. 토압계수의 경우 가장 작은 변동폭을 보였으며, K = 1에서 전단력이 가장 낮았고 이는 수평응력과 수직응력 간의 균형으로 인해 전단력이 최소화된 결과로 이어졌다. 토압계수에 따른 최대 변동폭은 0.7 kN (변동률 0.6%)로 나타났다. 토압계수에 따른 변동폭이 1% 미만으로 Case 간 차이가 적어, Case A만을 Fig. 9에 나타내었다.
전단력을 단면적으로 나누어 계산한 최대전단응력은 0.33~0.34 MPa로 나타났다. 허용전단응력은 체적손실 및 토압계수와는 무관하게 재료의 압축강도에 비례하였으며, 재료에 따라 0.39~0.48 MPa로 나타났다. 전단응력과 안전율 분석결과, 재료 특성이 전단력 분포와 안전율에 가장 큰 영향을 미치는 요인으로 나타났다. 기존 콘크리트와 R50은 각각 안전율 1.39, 1.42를 기록하였다. 고치환율 저탄소 콘크리트(R70, R90)는 안전율이 1.2~1.21로 하한값에 근접하였으나, 허용기준을 만족하여 안전율을 확보하였다. 체적손실와 토압계수 변동은 안전율에 영향을 끼치지 않아 재료에 따른 최대전단응력, 허용전단응력, 안전율만을 Fig. 10에 나타내었다.
전단력은 구조적 안정성에 미치는 영향이 제한적이지만, 초기강도 발현 저하로 인한 설계적 개선이 필요한 경우 전단철근 보강을 통해 안정성을 향상시킬 수 있다. 이러한 결과는 저탄소 콘크리트가 구조적 안정성을 유지하면서도 환경적 이점을 제공할 수 있음을 시사한다.
4.4 모멘트 결과
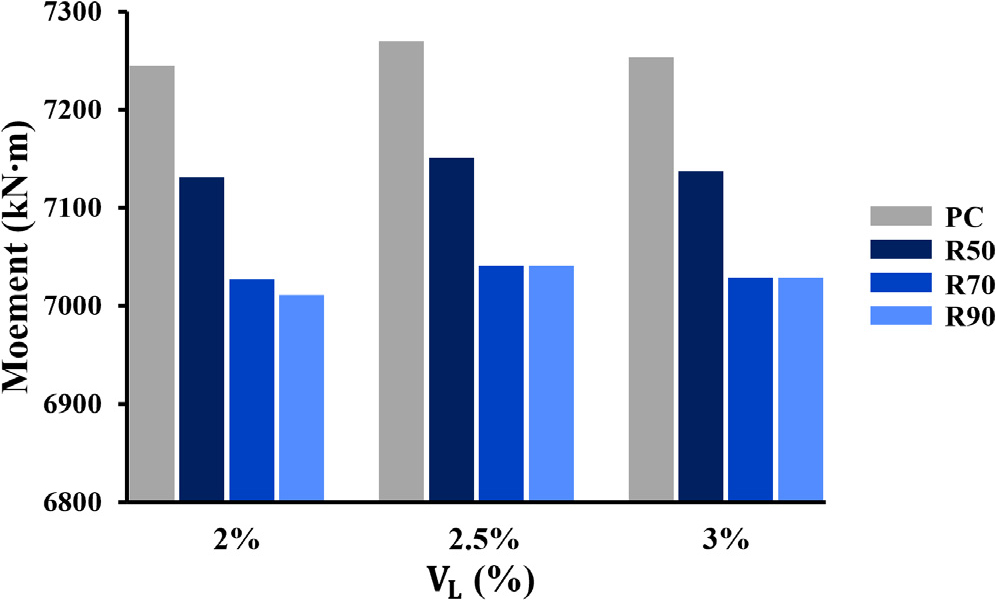
모멘트는 6,928~7,270 kN ‧ m의 값을 보였으며 Table 12에 나타내었다. PC는 높은 초기강도로 인해 모든 경우에서 가장 높은 모멘트를 보였다. 저탄소 콘크리트의 경우 초기강도 저하에 따른 하중분담 능력감소로 인해 재료 치환율이 높아질수록 모멘트가 점진적으로 감소하였다. 재료에 따른 최대 변동폭은 Case B-Ⅰ에서의 PC와 R90의 차이인 293 kN ‧ m (변동률 4%)으로 나타났다.
Table 12.
Result of bending moment (kN ‧ m)
체적손실이 증가함에 따라 모멘트는 소폭 증가하거나 일정한 값을 유지하였다. 이는 체적손실 증가로 인해 주변 지반의 소성변형이 발생해 라이닝에 전달되는 응력이 감소했기 때문이다. 고치환율 저탄소 콘크리트는 초기강도가 낮아 하중 흡수 능력이 상대적으로 부족하여 일부 하중이 지반으로 분산되었으며, 이로 인해 모멘트 증가율이 감소하고 일정한 값을 유지하는 경향을 보였다. 체적손실에 따른 모멘트 최대 변동폭은 93 kN ‧ m (변동률 1.3%)로 나타났다. 토압계수는 작을수록 모멘트 값이 증가하였으며 이는 수평응력이 약화되면서 수직응력이 구조물 상하단에 집중되고, 라이닝에 추가적인 하중이 작용했기 때문이다. 이러한 영향은 라이닝의 압축 영역에서 더 큰 모멘트를 발생시키는 주요 원인으로 작용하였다. 토압계수에 따른 변동폭은 57 kN ‧ m (변동률 0.8%)로 1% 미만으로 Case 간 차이가 적어, Case A만을 Fig. 11에 나타내었다.
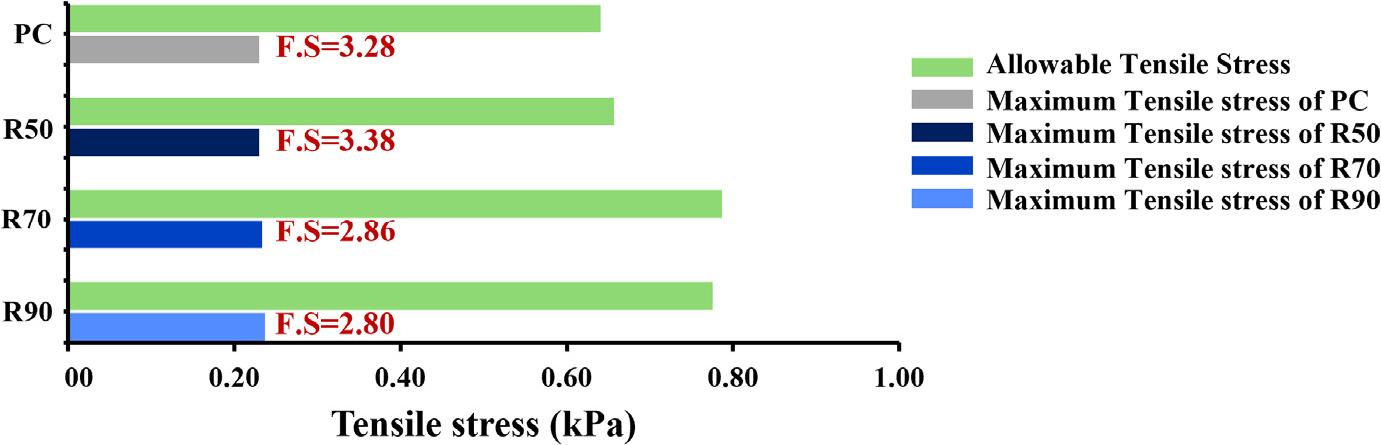
최대 인장응력은 기존 콘크리트와 R50은 0.24 MPa, R70, R90은 각각 0.23 MPa로 나타났으며, 체적손실 및 토압계수 변화는 인장응력에 유의미한 영향을 미치지 않았다. 허용인장응력은 압축강도의 자승근에 비례하여 0.64~0.79 MPa로 나타났으며 안전율은 기존 콘크리트에서 3.28, 저탄소 콘크리트(R50, R70, R90)에서 3.38, 2.86, 2.80으로 모두 허용응력설계법 기준을 충족하였다. 체적손실과 토압계수 변동은 안전율에 영향을 끼치지 않아 재료에 따른 최대인장응력, 허용인장응력, 안전율만을 Fig. 12에 나타내었다.
분석 결과, 재료 특성에 가장 큰 영향을 받았으며 고치환율 저탄소 콘크리트는 축력, 전단력보다 높은 안전율을 보였다. 이는 모멘트가 단면의 회전 강성과 구조물의 하중분산 특성에 따라 영향을 받기 때문으로, 저탄소 콘크리트의 초기강도 저하에도 불구하고 구조적 안정성을 유지할 수 있음을 시사한다.
5. 결 론
본 연구에서는 내재탄소 개념과 LCI DB를 활용하여 저탄소 콘크리트 사용 시 CO2 배출저감 효과를 추정하고, 기존 콘크리트와 저탄소 콘크리트를 각각 NATM 터널의 콘크리트라이닝 과정에 적용하여 단면의 부재력 검토를 통한 안정성 검토를 진행하였다. 저탄소 콘크리트의 CO2 배출저감 효과 및 단면의 안정성 검토의 결과를 정리하면 다음과 같다.
1. 기존 콘크리트는 1 kg/m3당 460.8 kg의 CO2를 배출하고, 보통 포틀랜드 시멘트를 치환한 저탄소 콘크리트는 167.3~297.5 kg의 CO2를 배출하는 것으로 추정되었다. 저탄소 콘크리트 사용 시 약 35~65%의 CO2 저감효과가 나타날 것이라는 기대효과를 확인했으며 이는 플라이애시와 고로슬래그가 낮은 탄소배출계수를 가져 배합 내 탄소 집약도를 감소시키기 때문이다.
2. 수치해석 결과, 축력, 전단력, 모멘트 결과 모두 재료특성에 가장 큰 영향을 받았다. 축력은 안전율이 2.52~3.73, 전단력은 안전율 1.2~1.42, 모멘트는 안전율 2.8~3.38로 모두 안전율 1을 넘어 허용응력설계기준을 만족하였다. 체적손실과 토압계수는 안전율 계산에 영향을 미치지 못했고, 부재력에 제한적인 영향을 미친다는 점을 확인하였다.
3. 터널의 설계과정 중 기존 콘크리트 대신 저탄소 콘크리트를 적용한다면, CO2 배출량이 35% 이상 감소하면서도 허용응력설계기준을 만족하는 것으로 나타났다. 저탄소 콘크리트를 콘크리트라이닝에 적용하는 것은 환경적 이점 뿐 아니라 구조적 안정성을 만족할 수 있음을 시사한다.